2. 柏林工业大学大地测量与地球信息科学系, STRAßE des 17, Juni 135, Berlin 10623
众多学者研究了地影期间GNSS卫星偏航姿态对PPP的影响。Lou等[1]分析地影期间不同类型GPS卫星偏航姿态对动态PPP的影响,结果表明,采用模型姿态可以显著提高动态PPP的定位精度;Cao等[2]指出偏航姿态对PPP的影响和卫星端天线相位中心偏差(PCO)量级、姿态差异、轨道机动时间、太阳与卫星轨道面夹角以及卫星几何构型有关;叶世榕等[3]详细调查深地影期间BDS-2卫星偏航姿态对PPP的影响,得出相比于动偏模式,在零偏期间采用零偏姿态可显著提高定位和ZTD的估计精度。但这些研究主要针对GPS/GLONASS/Galileo/BDS-2卫星,缺乏BDS-3卫星偏航姿态对PPP的影响分析。因此,本文拟分析BDS-3 MEO卫星在地影期间采用名义姿态和模型姿态对PPP的影响。
1 BDS-3卫星偏航姿态模型卫星星固系Z轴指向已知,只需星固系X轴指向或姿态角Ψ(X轴与卫星速度矢量的夹角)就能精确确定卫星空间指向或姿态。因此,精确重现偏航姿态的核心在于确定卫星在轨姿态角。BDS-3 GEO卫星与BDS-2 GEO卫星一样,全时段采用零偏模式,即Ψ=0°,无需特别考虑其在地影期间的偏航姿态。BDS-3非GEO卫星大部分时间保持名义姿态,其名义偏航角可以通过太阳高度角β和卫星轨道角μ计算[4]:
| $ \mathit{\Psi}=\operatorname{atan} 2(-\tan \beta, \sin \mu) $ | (1) |
在深地影期间,BDS-3 IGSO/MEO卫星均采用连续动偏模式。但BDS-3 SECM和CAST MEO卫星在地影期间的姿态控制模式存在一定差异。其中,SECM MEO卫星在|β|<3°后立刻进行偏航角机动,其偏航姿态模型可表示为[5]:
| $ \mathit{\Psi}=\left\{\begin{array}{l} \operatorname{atan} 2\left(-\tan \beta_0, \sin \mu\right), 0 \leqslant \beta<\beta_0 \\ \operatorname{atan} 2\left(\tan \beta_0, \sin \mu\right), -\beta_0<\beta<0 \end{array}\right. $ | (2) |
式中,β0=3°为设定阈值,|β|<3°时,采用式(2)的理论偏航角;|β|>3°时,采用名义偏航角。
欧空局和武汉大学都对BDS-3 CAST MEO卫星的偏航姿态进行研究,并发布各自的模型,分别为ESOC和WHU,两者一致性很好[6]。本文采用WHU模型,其可以表示为[7]:
| $ \begin{gathered} \mathit{\Psi}(\mu)=90^{\circ} \operatorname{sign}\left(1, \mathit{\Psi}\left(\mu_s\right)\right)+\left[\mathit{\Psi}\left(\mu_s\right)-90^{\circ} \cdot\right. \\ \left.\operatorname{sign}\left(1, \mathit{\Psi}\left(\mu_s\right)\right)\right] \cos \left(\frac{2 {\rm{ \mathsf{ π} }}}{t_{\max }} \cdot \frac{\mu-\mu_s}{\mu}\right) \end{gathered} $ | (3) |
式中,sign(a, b)为符号函数,其返回值取a的值且与b同符号;μs为开始进行轨道机动时的卫星轨道角,子夜和正午机动的模型值μs分别为-6°和174°;Ψ(μs)为其对应的名义姿态偏航角;tmax为轨道机动的持续时间,IGSO和MEO卫星的tmax分别为5 740 s和3 090 s;
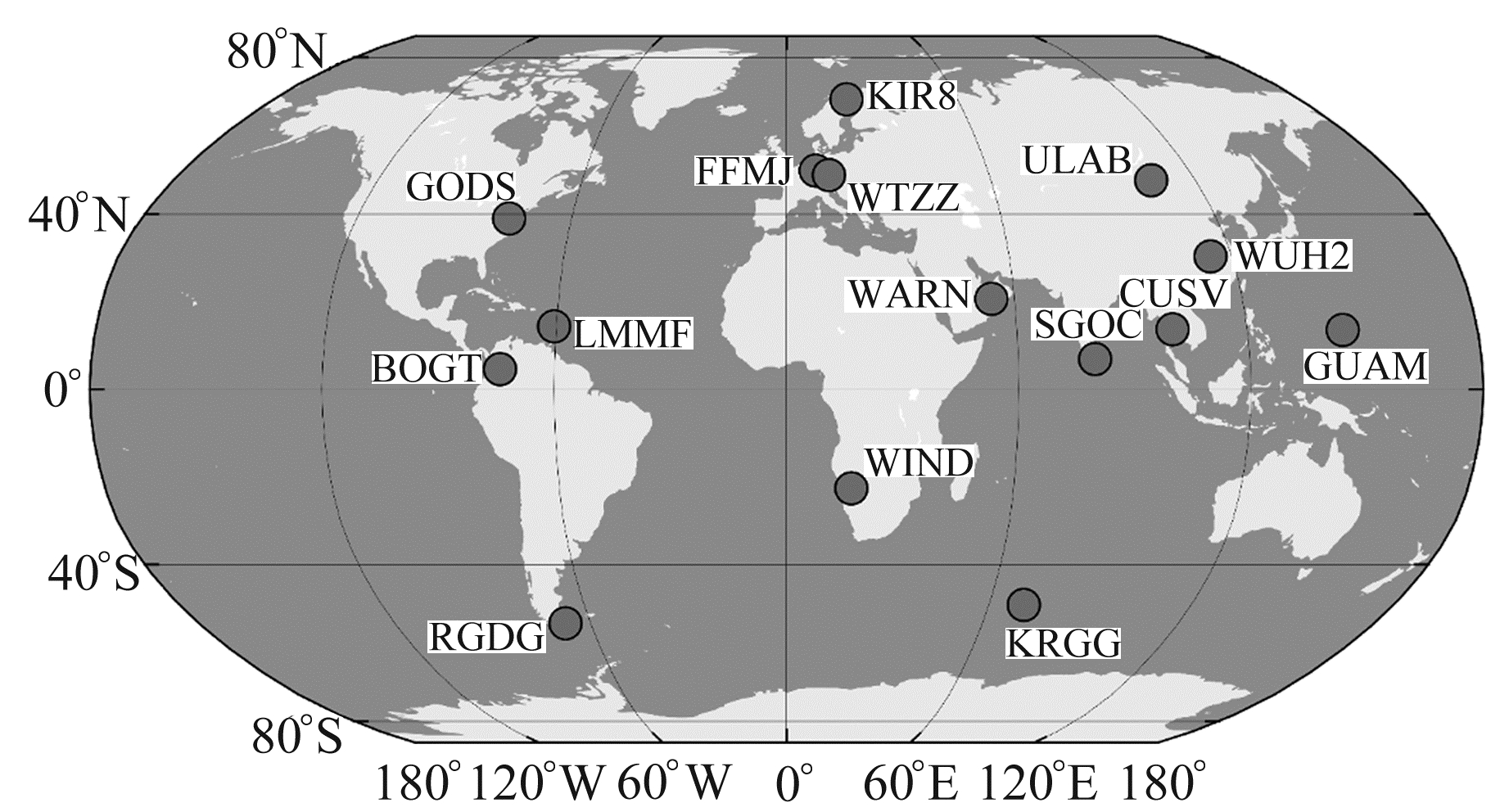
基于GBM、WUM和ESA的精密轨道和钟差产品,选择全球均匀分布的15个可观测到BDS-2/3信号的MGEX测站的数据进行BDS-2/3静态和动态PPP解算,测站分布见图 1,PPP处理策略见表 1。PPP解算采用改进的GAMP软件[8],其支持处理BDS-3数据并考虑了不同卫星的偏航姿态。GBM产品支持北斗全星座卫星,WUM和ESA产品不支持北斗C37后的卫星,且ESA产品不支持GEO卫星,实验过程中将GEO卫星进行剔除。通过联系GFZ MGEX产品负责人,以及查看WUM和ESA产品处理策略文件可知,WHU、ESA及GFZ在进行BDS数据处理时均采用模型姿态。数据时段为2020年doy143~149,该时段内共有8颗BDS-3 MEO卫星的|β|<3°,包括2颗SECM MEO卫星(C25、C26)和6颗CAST MEO卫星(C23、C24、C36、C37、C45、C46)。对比分析8颗BDS-3 MEO卫星地影期分别采用名义姿态和相应模型姿态时BDS-2/3静态和动态PPP的解算结果。
|
图 1 测站分布 Fig. 1 Distribution of the stations |
|
|
表 1 PPP处理策略 Tab. 1 PPP processing strategy |
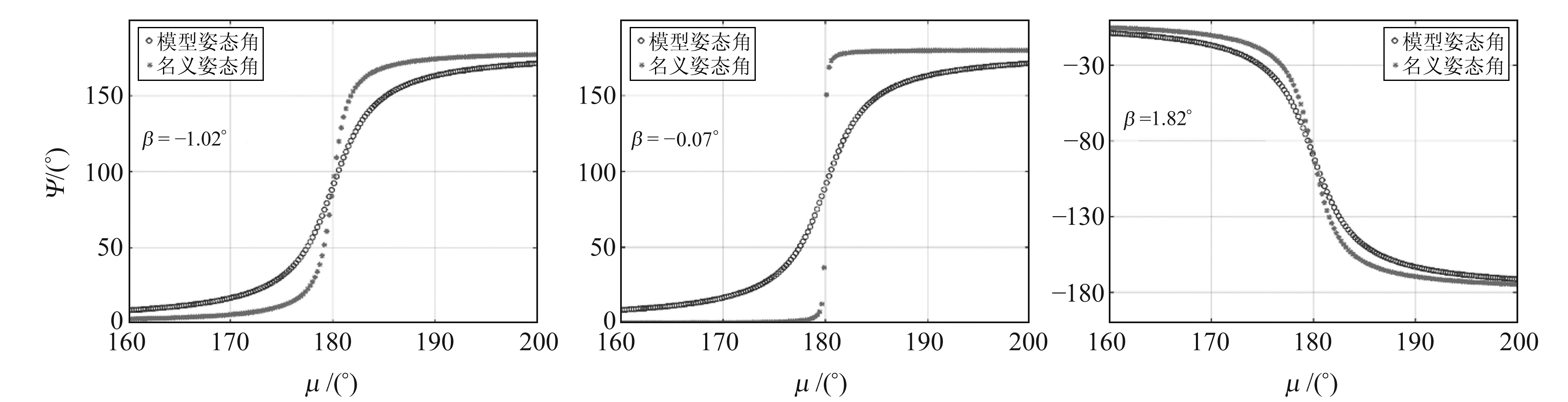
地影期时,SECM和CAST MEO卫星的模型姿态角分别用式(2)和式(3)计算,名义姿态角用式(1)计算。图 2和图 3分别给出不同β值下SECM C25卫星和CAST C37卫星在正午点附近名义姿态角与模型姿态角的变化。可以看出,名义姿态角和模型姿态角的差异与β值的大小及卫星离正午点的距离相关,β值越接近于0,两者间的差异越大,且卫星越靠近正午点差异越大。由于SECM卫星在|β|<3°时便进行轨道机动,其名义姿态角和模型姿态角的差异在地影期会一直存在,在β=-0.07°时最大差异可达70°左右。CAST卫星在|β|<3°且位于正午点6°范围内时才进行轨道机动,其他时间名义姿态角与模型姿态角的差异为0,在β=0.02°时最大差异可达80°左右。在午夜点结论相同。
|
图 2 地影期间BDS-3 SECM C25卫星在正午点附近的偏航姿态角 Fig. 2 The yaw attitude angles of BDS-3 SECM C25 satellite around perihelion during eclipse seasons |

|
图 3 地影期间BDS-3 CAST C37卫星在正午点附近的偏航姿态角 Fig. 3 The yaw attitude angles of BDS-3 CAST C37 satellite around perihelion during eclipse seasons |
因使用模型姿态对BDS-3 SECM和CAST MEO卫星的影响存在差异,故分析偏航姿态对PPP的影响时将SECM和CAST卫星分开讨论。
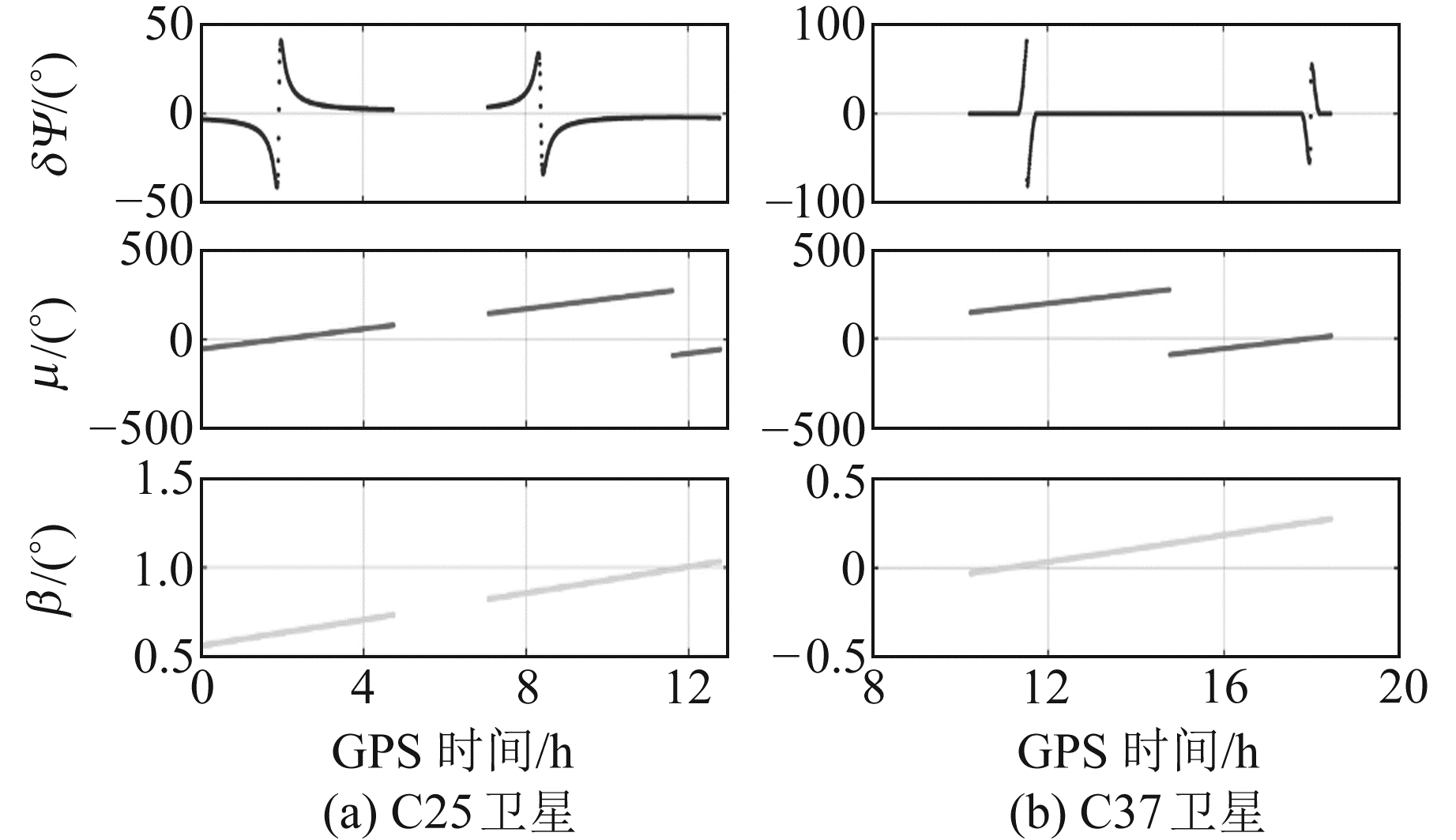
3.2 偏航姿态对PPP的影响选取2020年doy145 WIND测站观测数据,分别采用名义姿态和模型姿态对上述8颗卫星地影期进行静态和动态的BDS-2/3 PPP解算,解算过程中剔除GEO卫星。仍以C25和C37卫星为例,从偏航姿态角的差异、天线相位缠绕和PCO改正、相位观测值残差及定位误差等方面分析SECM和CAST卫星的偏航姿态对PPP的影响。图 4给出2020年doy145 C25和C37卫星在WIND测站可观测期间的太阳高度角β、轨道角μ以及名义姿态和模型姿态差异δΨ的变化曲线。可以看出,C25卫星的可观测时间段约为0~5 h和7~13 h,C37卫星的可观测时间段约为10~18 h。C25卫星的姿态角差异在可观测时间段内一直存在,C37卫星的姿态角差异在轨道角μ为(-6°, 6°)或者(174°, 186°)时存在,持续时间约为52 min。C25和C37卫星的名义姿态与模型姿态之间的最大差异分别为40°和80°,分别发生在正午点和午夜点。而当卫星逐渐远离正午点和午夜点时,其姿态差异可忽略不计。
|
图 4 C25和C37卫星的太阳高度角β、轨道角μ及名义姿态和模型姿态差异δΨ的变化 Fig. 4 Variations of the sun angles β, orbit angles μ and differences between nominal and modeled attitudes δΨ for C25 and C37 satellites |
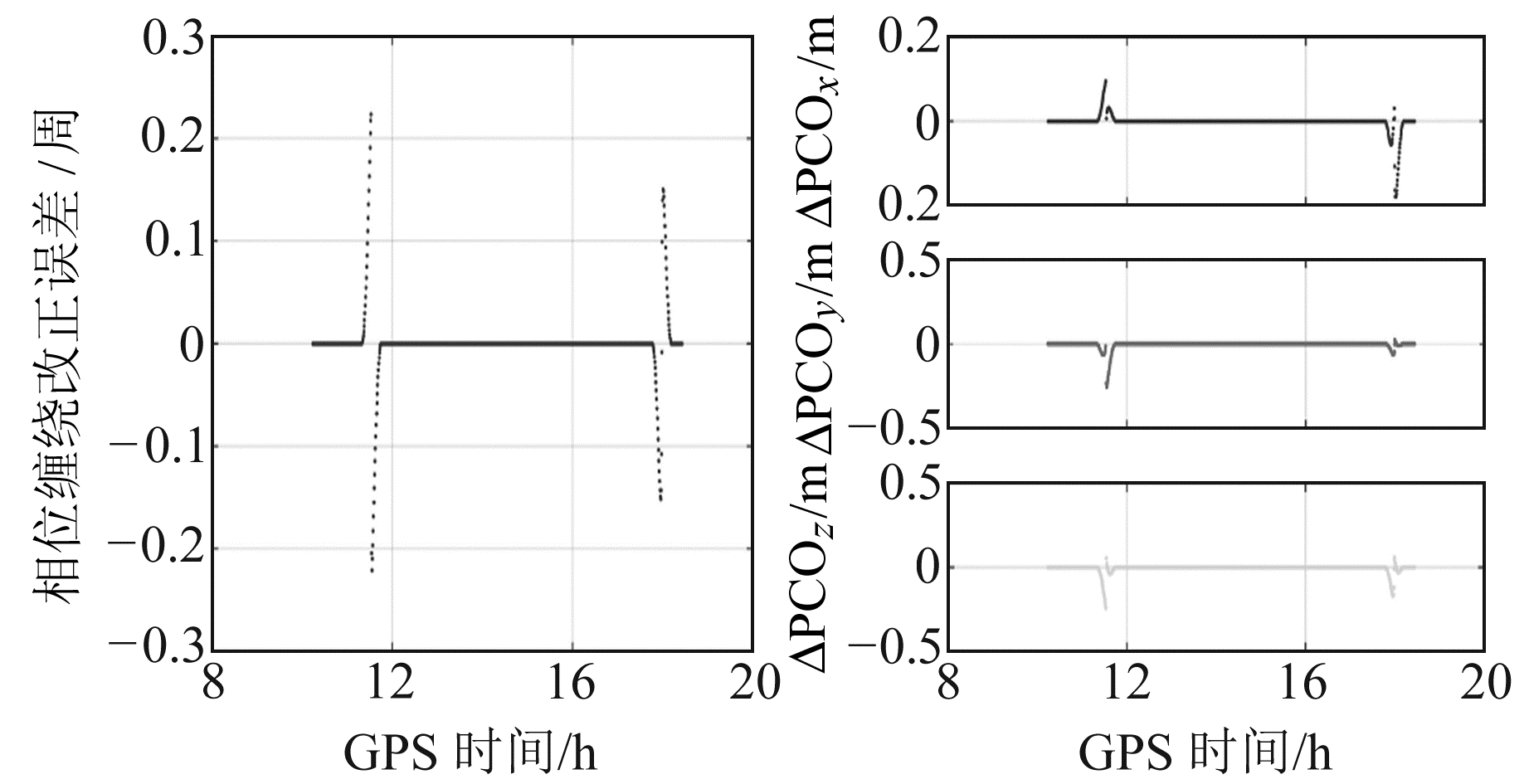
偏航姿态在PPP中会直接影响天线相位缠绕和PCO改正的计算,进而影响PPP的解算结果,图 5、6分别给出对应图 4中C25和C37卫星采用名义姿态和模型姿态对天线相位缠绕和PCO改正的影响。可以看出,当姿态差异接近0°时,对相位缠绕和PCO改正的影响较小;当姿态差异变大时,相位缠绕和PCO改正的误差逐渐变大,其中C25和C37卫星最大相位缠绕改正误差分别为0.1周和0.2周左右,基本相同。而两者PCO改正误差存在显著差异,最大分别为0.02 m和0.2 m左右,这主要是由于C37卫星的水平PCO(x=-200.0 mm, y= 0.0 mm)的量级显著大于C25卫星(x=40.0 mm, y= -10.0 mm)。

|
图 5 C25卫星名义姿态和模型姿态差异引起的天线相位缠绕和PCO改正误差 Fig. 5 The errors of the corrections of antenna wind-up and PCO caused by the differences of nominal and modeled attitudes for C25 satellite |
|
图 6 C37卫星名义姿态和模型姿态差异造成的天线相位缠绕和PCO改正误差 Fig. 6 The errors of the corrections of antenna wind-up and PCO caused by the differences of nominal and modeled attitudes for C37 satellite |
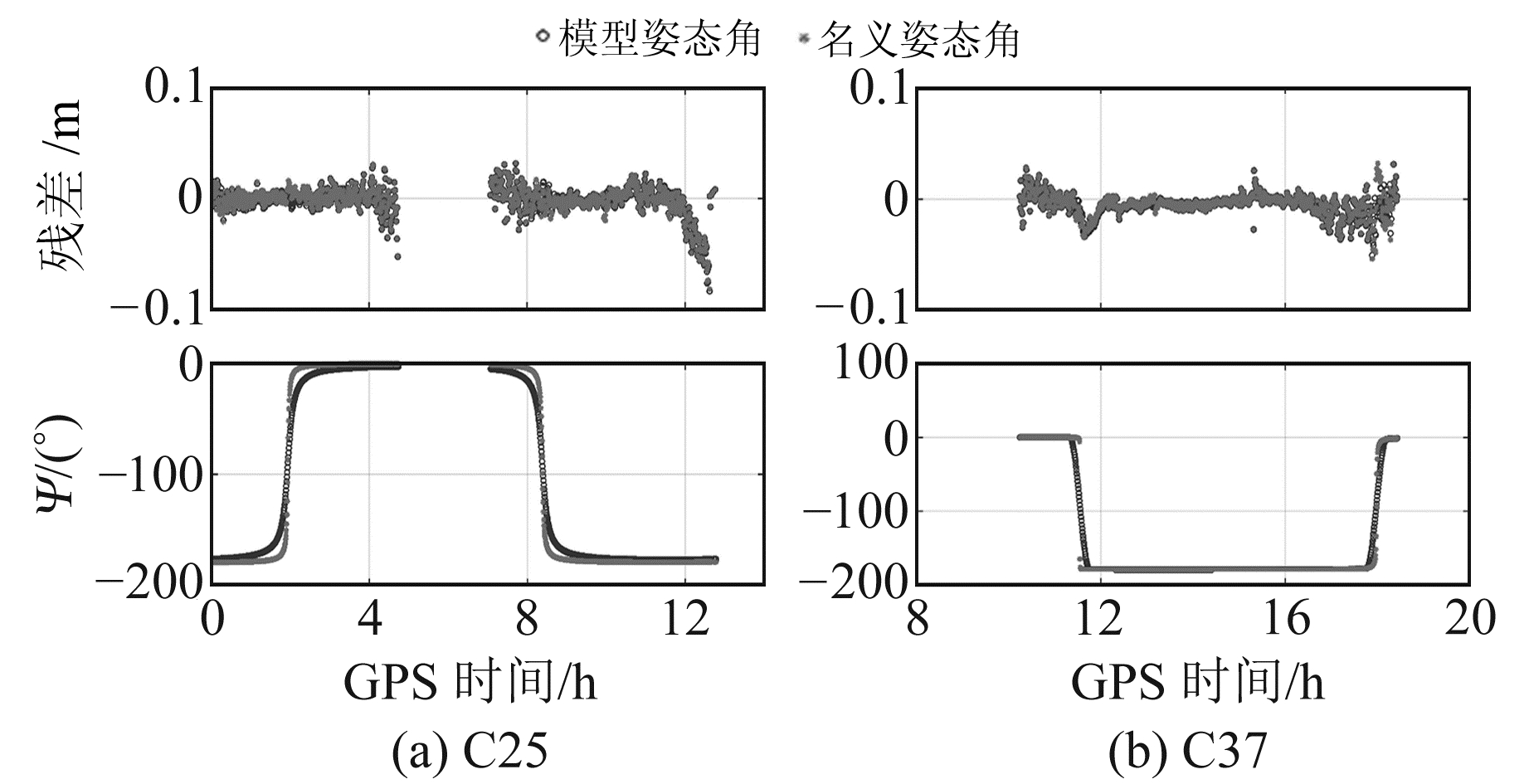
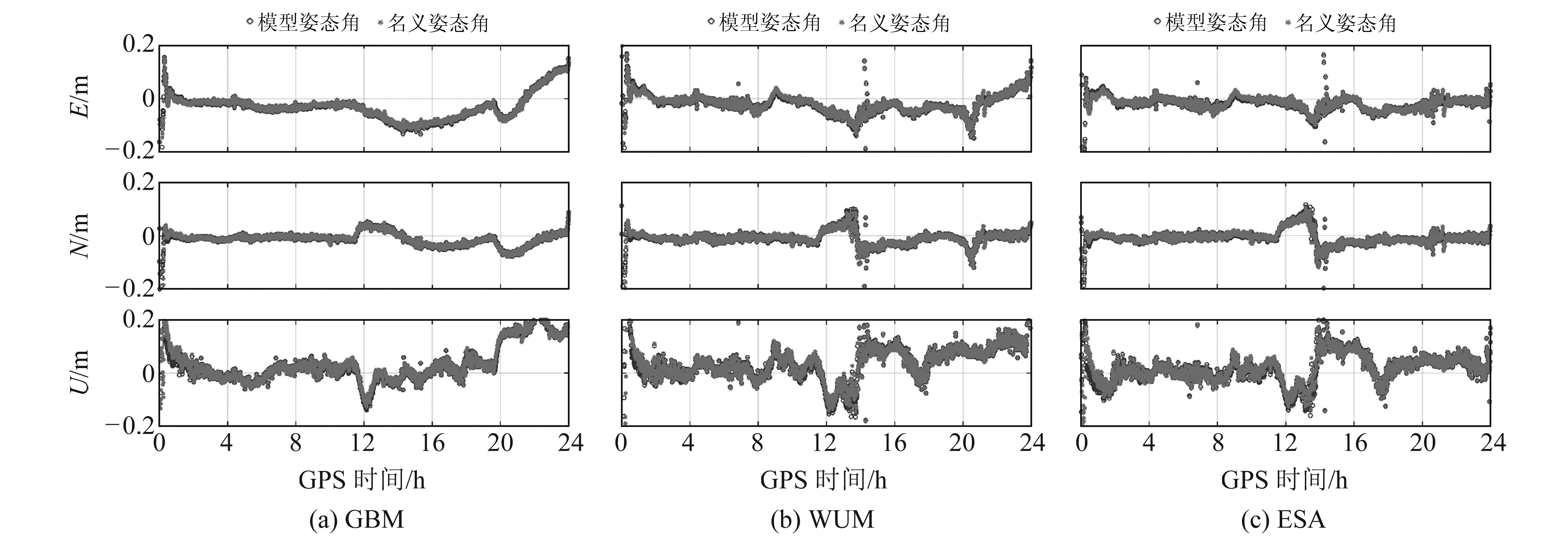
图 7给出用GBM精密轨道和钟差产品解算的WIND测站BDS-2/3动态PPP中滤波后的C25和C37卫星的无电离层组合载波相位观测值残差。可以看出,当名义姿态和模型姿态差异较大时,载波相位观测值残差存在一定差异,但整体上可以忽略不计。图 8为分别使用GBM、WUM和ESA产品解算的WIND测站BDS-2/3动态PPP的位置误差序列,其中,使用WUM和ESA产品时由于部分历元的可用卫星数较少,定位结果存在一定的跳变;使用GBM产品时可用卫星数较多,但由于可跟踪C38~C46卫星的测站较少,导致这部分卫星轨道精度较差[12],使得12 h后的结果有发散现象。但整体上,使用名义姿态和模型姿态的PPP定位结果并无明显差异。
|
图 7 WIND测站C25和C37卫星姿态及相位观测值残差变化 Fig. 7 Variations of C25 and C37 satellite attitudes and phase residuals at WIND station |
|
图 8 WIND测站BDS-2/3动态PPP定位结果 Fig. 8 The positioning performance of BDS-2/3 kinematic PPP at WIND station |
综上可知,当β值较小且卫星处于正午点或者午夜点附近时,BDS-3 SECM和CAST卫星的名义姿态角和模型姿态角的差异较大,这会对相位缠绕和PCO改正造成较大影响。但由于BDS-3 SECM和CAST卫星的较大姿态角差异维持的时间均较短,加上BDS-2/3联合处理时卫星几何构型较优,姿态角差异对滤波后的载波相位观测值残差以及PPP定位误差影响不大。
为进一步统计BDS-3 MEO卫星地影期使用名义姿态和模型姿态对静态和动态PPP定位结果的影响,分别使用GBM、WUM和ESA的北斗精密轨道和钟差产品对2020年doy143~149期间15个MGEX测站的观测数据进行静态和动态的BDS-2/3 PPP解算。统计定位误差的RMS值和PPP收敛时间,将IGS周解文件中的坐标作为测站参考坐标,计算定位误差时统一收敛时间为滤波开始后2 h,收敛时间判定条件为连续20个历元的三维误差小于10 cm。表 2、3分别统计了PPP定位误差RMS的均值和PPP的收敛时间均值。可以看出,无论是静态还是动态PPP,使用模型姿态的定位精度和收敛速度均优于使用名义姿态,但两者差异较小,定位误差差异几乎都在0.1 mm之内,收敛时间差异在1 min之内,这与前文分析结果相符。
|
|
表 2 BDS-2/3静态和动态PPP定位误差RMS均值 Tab. 2 Average RMS of positioning errors of BDS-2/3 static and kinematic PPP |
|
|
表 3 BDS-2/3静态和动态PPP收敛时间均值 Tab. 3 Average convergence time of BDS-2/3 static and kinematic PPP |
1) BDS-3 MEO卫星在地影期间的名义姿态和模型姿态的差异与太阳高度角和离正午或子夜点的时间相关。由于偏航姿态模型的差异,地影期间SECM卫星的名义姿态与模型姿态的差异持续时间要远长于CAST卫星。
2) BDS-3 MEO卫星在较小的太阳高度角以及正午点或午夜点附近时,较大的名义姿态角与模型姿态角差异使得天线相位缠绕和PCO改正计算差异明显, 其中天线相位缠绕改正误差可达0.1~0.2周。而由于CAST卫星的PCO具有较大的量级,其姿态角差异引起的PCO改正误差明显大于SECM卫星,两者的最大值分别约为0.2 m和0.02 m。但较大的姿态角差异维持的时间较短,加上BDS-2/3联合处理时卫星几何构型较优,姿态角差异对载波相位观测值残差以及定位误差影响不大。
3) 根据多个MGEX测站的观测数据以及GBM、WUM和ESA的精密轨道和钟差产品解算的BDS-2/3静态和动态PPP结果可以发现,针对地影期间的BDS-3 MEO卫星,采用模型姿态相较于采用名义姿态在PPP定位精度和收敛速度上均有一定的提高,但整体差异不大,定位误差的差异基本在0.1 mm之内,收敛时间的差异在1 min之内。
| [1] |
Lou Y D, Zheng F, Gu S F, et al. The Impact of Non-Nominal Yaw Attitudes of GPS Satellites on Kinematic PPP Solutions and Their Mitigation Strategies[J]. Journal of Navigation, 2015, 68(4): 718-734 DOI:10.1017/S0373463315000041
(  0) 0) |
| [2] |
Cao X Y, Zhang S J, Kuang K F, et al. The Impact of Eclipsing GNSS Satellites on the Precise Point Positioning[J]. Remote Sensing, 2018, 10(2)
(  0) 0) |
| [3] |
叶世榕, 夏凤雨, 赵乐文, 等. 偏航姿态对北斗精密单点定位的影响分析[J]. 测绘学报, 2017, 46(8): 971-977 (Ye Shirong, Xia Fengyu, Zhao Lewen, et al. Impact Analysis of Yaw Attitude on BDS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(8): 971-977)
(  0) 0) |
| [4] |
Dilssner F, Springer T, Gienger G, et al. The GLONASS-M Satellite Yaw-Attitude Model[J]. Advances in Space Research, 2011, 47(1): 160-171 DOI:10.1016/j.asr.2010.09.007
(  0) 0) |
| [5] |
Xia L, Lin B J, Liu Y C, et al. Satellite Geometry and Attitude Mode of BDS-3 MEO Satellites Developed by SECM[C]. 31st International Technical Meeting of the Satellite Division of the Institute of Navigation, Miami, 2018
(  0) 0) |
| [6] |
Xia F Y, Ye S R, Chen D Z, et al. Observation of BDS-2 IGSO/MEOs Yaw-Attitude Behavior during Eclipse Seasons[J]. GPS Solutions, 2019, 23(3): 1-16
(  0) 0) |
| [7] |
Wang C, Guo J, Zhao Q L, et al. Yaw Attitude Modeling for Beidou I06 and Beidou-3 Satellites[J]. GPS Solutions, 2018, 22(4): 1-10
(  0) 0) |
| [8] |
Zhou F, Dong D N, Li W W, et al. GAMP: An Open-Source Software of Multi-GNSS Precise Point Positioning Using Undifferenced and Uncombined Observations[J]. GPS Solutions, 2018, 22(2): 1-10
(  0) 0) |
| [9] |
Boehm J, Niell A, Tregoning P, et al. Global Mapping Function(GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters, 2006, 33(7)
(  0) 0) |
| [10] |
Wang N B, Yuan Y B, Li Z S, et al. Determination of Differential Code Biases with Multi-GNSS Observations[J]. Journal of Geodesy, 2016, 90(3): 209-228
(  0) 0) |
| [11] |
Zhou S S, Hu X G, Zhou J H, et al. Accuracy Analyses of Precise Orbit Determination and Timing for COMPASS/Beidou-2 4GEO/5IGSO/4MEO Constellation[C]. China Satellite Navigation Conference, Wuhan, 2013
(  0) 0) |
| [12] |
Shen P L, Cheng F, Lu X C, et al. An Investigation of Precise Orbit and Clock Products for BDS-3 from Different Analysis Centers[J]. Sensors, 2021, 21(5)
(  0) 0) |
2. Department of Geodesy and Geoinformation Science, Technical University of Berlin, STRAßE des 17, Juni 135, Berlin 10623, Germany
 2022, Vol. 42
2022, Vol. 42

