2. 上海海事大学商船学院, 上海市海港大道1550 号, 201306
星载全球导航卫星系统反射技术(global navigation satellite system reflectometry, GNSS-R)可以利用目标周围海面与目标之间反射系数的差异进行海面目标检测研究[1-3]。Schiavulli等[4]使用奇异值分解(singular value decomposition,SVD)抑制噪声,舍弃了噪声中最大的奇异值,在二维SVD中只保留前k个奇异值,但此方法处理DDM计算量较大。为了减少计算量,Simone等[5]提出一种特殊的海杂波抑制算法,利用拟合的DDM抑制原始DDM中的海杂波,但此方法需要对得到的每组DDM进行拟合,处理过程繁琐。
本文提出使用PCA方法对原始DDM进行海杂波抑制,可以降低拟合DDM的复杂性,并提高反演海面目标的精度。首先对TDS-1数据进行筛选,选取包含采气平台的DDM;然后使用PCA对DDM的海杂波进行抑制,再使用固定阈值筛选可疑目标位置;最后基于雅可比算法对可疑目标进行物理位置反演。
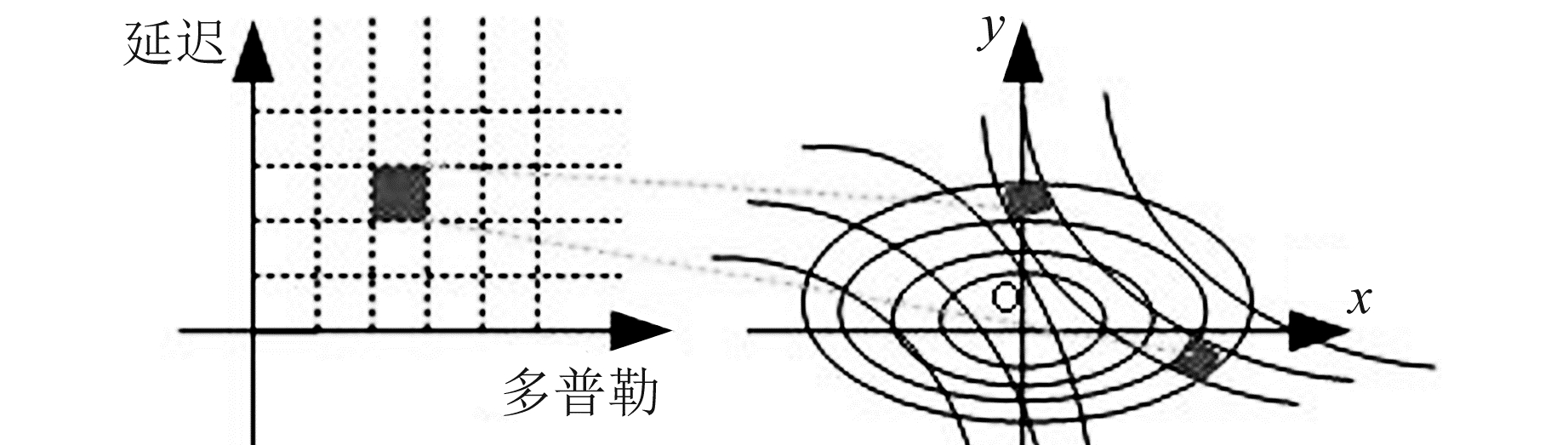
1 原理介绍 1.1 GNSS-R DDM信号反射表面越粗糙,收集GNSS-R信号的区域(称为闪光区)就越大。如果这个表面是一个平面,恒定延迟(等距离)区域和恒定多普勒频移(等多普勒)轨迹是一组双曲线。因此,每个表面点都有一个特定的延迟和多普勒(实际上有2个点具有相同的延迟和多普勒),见图 1。
|
图 1 DDM与物理域示意图 Fig. 1 Diagram of DDM and physical domain |
GNSS-R的DDM由反射信号在延迟偏移和多普勒偏移的二维空间上的功率分布组成。该功率分布可表示为[6]:
| $ \begin{gathered} \left\langle\left|Y\left(\tau, f_d\right)\right|^2\right\rangle= \\ \left(\mathit{\Lambda}^2(\tau) \cdot\left|S\left(f_d\right)\right|^2\right) * * \mathit{Σ}\left(\tau, f_d\right) \end{gathered} $ | (1) |
式中,τ、fd分别为任意一点相对于镜面反射点的延迟偏移和多普勒偏移,Λ=1-|τ|/τc(τc=1 ms/1 023),|S(f)|=|sin (πf)/(πf)|, ** 为二重卷积:
| $ \begin{gathered} \mathit{Σ}\left(\tau, f_d\right)= \\ T_i^2 \frac{D^2\left(\vec{\rho}\left(\tau, f_d\right)\right) \sigma^0\left(\vec{\rho}\left(\tau, f_d\right)\right)}{4 {\rm{ \mathsf{ π} }} R_0^2\left(\vec{\rho}\left(\tau, f_d\right)\right) R^2\left(\vec{\rho}\left(\tau, f_d\right)\right)}\left|\boldsymbol{J}\left(\tau, f_d\right)\right| \end{gathered} $ | (2) |
式中,Ti为相干积分时间,
PCA是一种广泛使用的数据降维去噪算法,其将n维特征映射到k维上,这k维全新的正交特征被称为主成分。如果源于噪声的奇异值较低,则PCA估计的较高奇异值(singular value,SV)对应于期望信号的SV。为了获得多个观测功率,由DDM创建功率矩阵X (n):
| $ \boldsymbol{X}(n)=\left[\boldsymbol{x}_1(n), \boldsymbol{x}_2(n), \cdots, \boldsymbol{x}_i(n)\right]^{\mathrm{T}} $ | (3) |
式中,xi(n) 表示第i个数据样本。需要对xi数据进行归一化,即
| $ \overline{\boldsymbol{x}}=\frac{1}{m} \sum\limits_{i=1}^m \boldsymbol{x}_i $ | (4) |
对所有的数据样本求对应元素的均值,得到均值列向量x, 然后求取归一化后的结果,即
| $ \boldsymbol{x}_i=\boldsymbol{x}_i-\overline{\boldsymbol{x}} $ | (5) |
计算去平均值后的功率矩阵的协方差,得到协方差矩阵,即
| $ \boldsymbol{Z}=\frac{1}{n} \boldsymbol{X} \boldsymbol{X}^{\mathrm{T}} $ | (6) |
对协方差矩阵Z进行SVD,SV相对较低的杂波分量被消除。抑制海杂波后的信号矩阵Y表示为:
| $ \boldsymbol{Y}=\left[\boldsymbol{y}_1, \boldsymbol{y}_2, \boldsymbol{\cdots}, \boldsymbol{y}_p\right]^{\mathrm{T}}=\boldsymbol{U}^{\mathrm{T}} \boldsymbol{Z}=\boldsymbol{D} \boldsymbol{V}^{\mathrm{T}} $ | (7) |
式中,U、V是由Z的奇异向量创建的正交基矩阵,D是奇异值为Z的对角矩阵,是由Z的奇异向量创建的正交基矩阵。
1.3 基于雅可比矩阵的反演算法利用阈值对抑制海杂波后的DDM进行筛选,得到可疑目标的延迟和多普勒值;再基于雅可比矩阵算法反演其相对于镜面反射点的物理域位置。
式(2)中雅可比矩阵| J |表示物理空间与延迟-多普勒单元的对应关系(图 1),可表示为[7]:
| $ \left|\boldsymbol{J}_i\left(\tau_{x y}, f_{\mathrm{d} x y}\right)\right|=\operatorname{det}\left|\begin{array}{ll} \frac{\partial x_i}{\partial \tau_{x y}} & \frac{\partial x_i}{\partial f_{\mathrm{d} x y}} \\ \frac{\partial y_i}{\partial \tau_{x y}} & \frac{\partial y_i}{\partial f_{\mathrm{d} x y}} \end{array}\right| $ | (8) |
如图 1所示,延迟多普勒域中的1个点对应xy坐标中的2个点, 所以i=1, 2表示物理空间坐标的第1个或第2个解。其中,
| $ \tau_{x y} \approx \sqrt{x^2+\left(y+\frac{h}{\tan \gamma}\right)^2+h^2}-\frac{h}{\sin \gamma}-y \cos \gamma $ | (9) |
| $ \begin{aligned} &f_{\mathrm{d} x y} \approx-V_{T_y} \cos \gamma-V_{T_z} \sin \gamma+ \\ &\frac{V_{R_x} x+V_{R_y}\left(y+\frac{h}{\tan \gamma}\right)-V_{R_z} h}{\sqrt{x^2+\left(y+\frac{h}{\tan \gamma}\right)^2+h^2}} \end{aligned} $ | (10) |
式中,(x, y)为闪光区任一反射点相对于镜面反射点的坐标,γ为全接收机卫星仰角,h为接收机到闪光区的高度,VT=(VTx,VTy,VTz)、VR=(VRx, VRy, VRz)分别为GPS卫星和接收卫星的速度。
2 实验数据为验证使用PCA可以抑制DDM中的海杂波,选用挪威Snøhvit采气平台(71°36′N,21°00′E)DDM数据进行实验。
首先对得到的TDS-1数据按照平台和DDM的镜面反射点的经纬度之差小于1°的原则进行筛选;然后对筛选后的数据进行目标反演,反演位置与实际位置误差小于30 km为有效结果,共得到9组有效反演DDM(表 1)。
|
|
表 1 实验数据 Tab. 1 Experimental data |
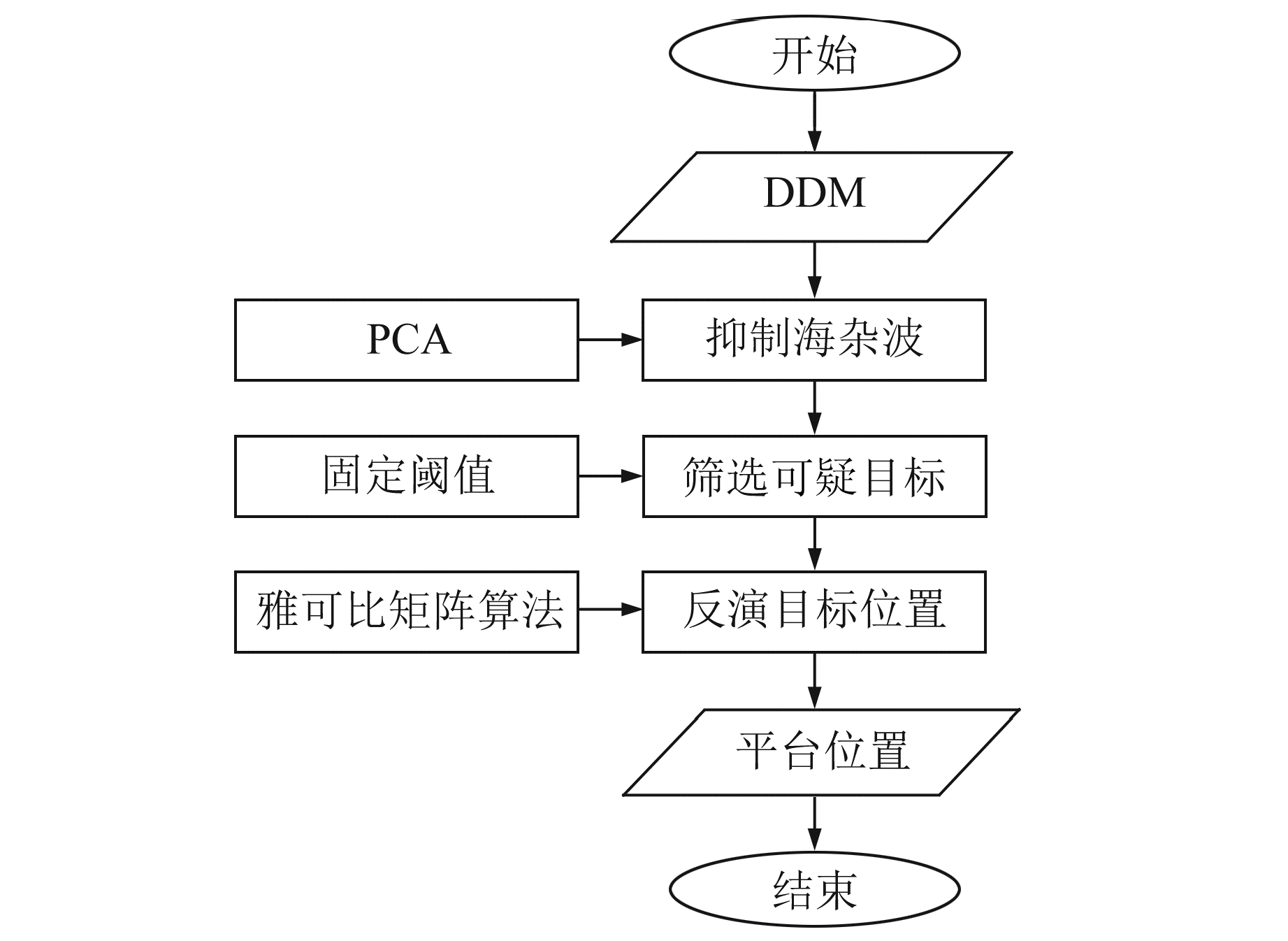
为了提高实验效率,使用筛选后的TDS-1数据作为原始DDM,数据参数如表 1所述。检测海面目标的实验流程见图 2,具体步骤为:1)输入原始DDM;2)使用PCA对原始DDM进行海杂波抑制;3)使用固定阈值从抑制海杂波后的DDM中得到可疑目标,可疑目标的出现会使DDM中对应的功率值远大于闪光区其他点的功率值,因此需要根据DDM的不同进行调整,使用每个DDM中对应的最大功率值作为筛选可疑目标的固定阈值;4)利用实际物理域和延迟多普勒域的对应关系,使用雅可比矩阵进行可疑目标的物理位置反演;5)反演出平台位置。
|
图 2 目标检测流程 Fig. 2 Target detection process |
图 3为索引号244的实验结果。使用实际位置与反演位置的误差分析PCA抑制DDM中海杂波的有效性,即
| $ \mathit{\Delta}=\left|\boldsymbol{P}_{\text {突示位置 }}-\boldsymbol{P}_{\text {反演位置 }}\right| $ | (11) |

|
图 3 索引号244的实验结果 Fig. 3 Experimental results of index 244 |
式中,P实际位置为平台相对于镜面反射点的实际位置,P反演位置为反演得到的平台相对于镜面反射点的位置,Δ为位置误差。
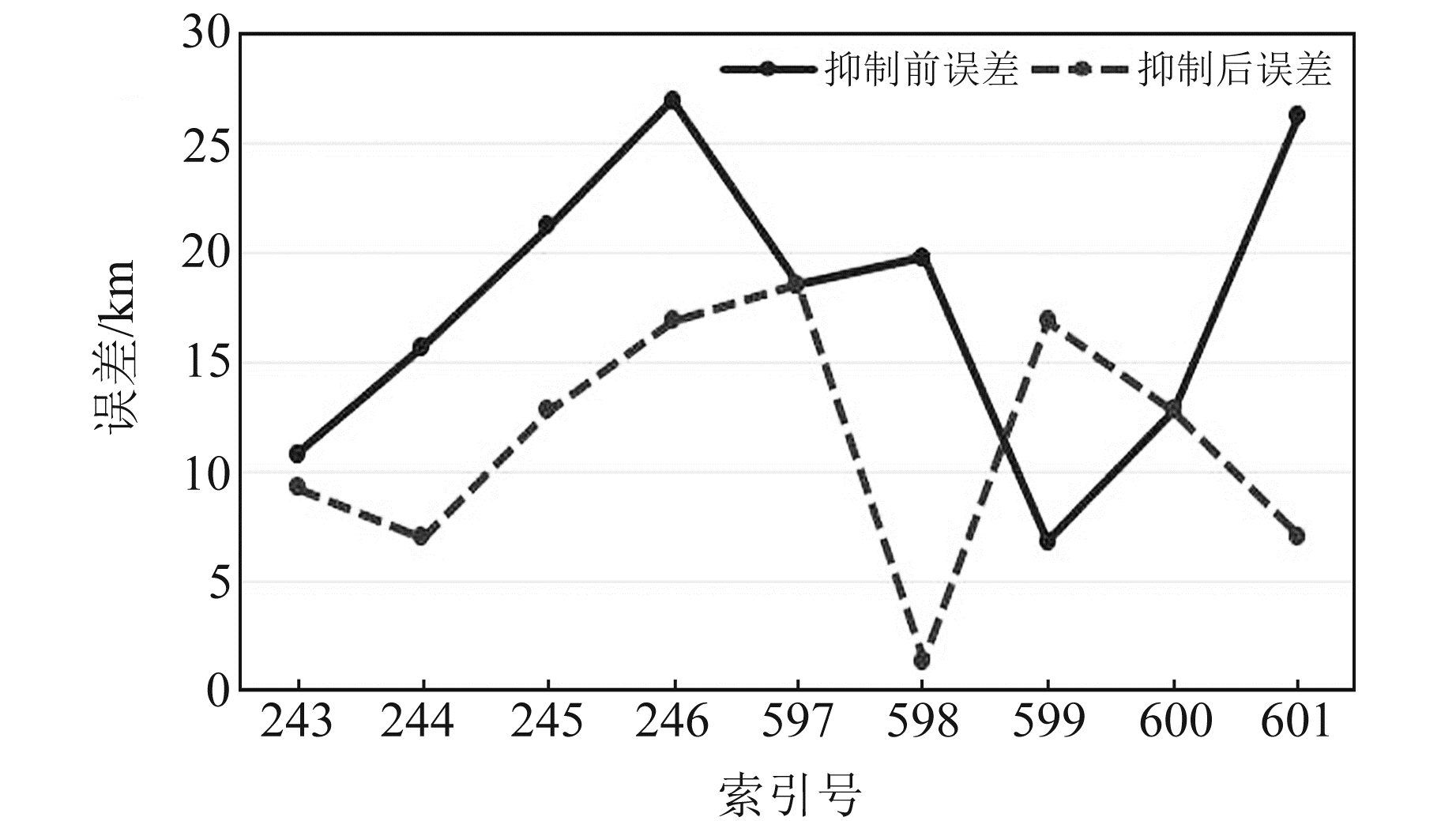
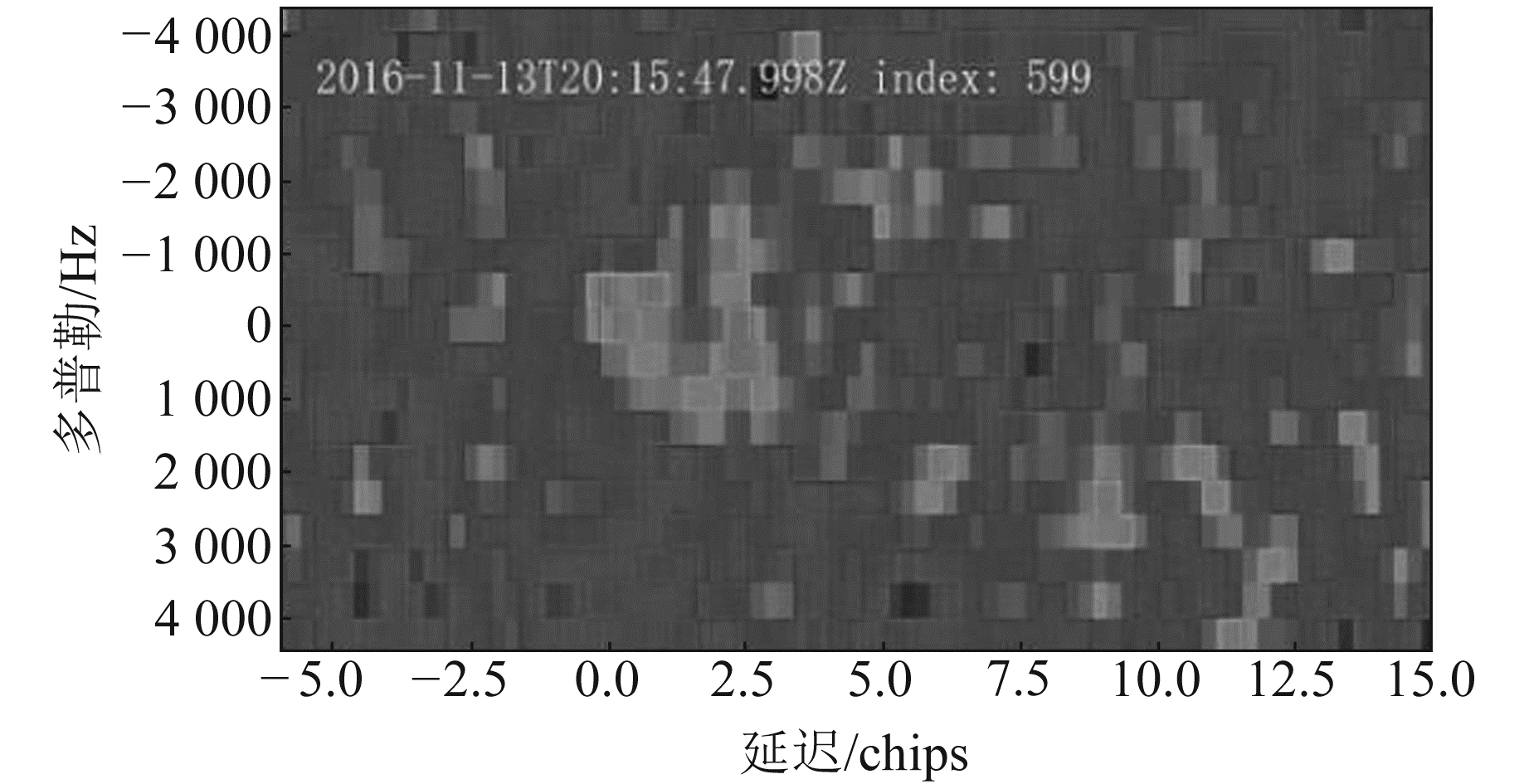
通过对选取的DDM进行海杂波抑制、阈值过滤及雅可比矩阵算法反演,得到Snøhvit采气平台位置,具体实验结果见表 2。为了验证使用PCA抑制海杂波的有效性,在原始DDM中使用阈值过滤得到的反演位置作为对照组,即抑制前Δ的值。分析表 2中抑制前后位置误差的平均值可知,使用海杂波抑制前均值为17.65 km,而抑制海杂波后均值为11.42 km,精度提升35.30%,详细误差对比见图 4。分析发现,索引号599的DDM使用PCA抑制海杂波后位置误差变大,其原始DDM见图 5,抑制海杂波后的DDM见图 6。可以看出,索引号599的原始DDM功率分布杂乱,呈非马蹄形。对比原始DDM与使用PCA抑制海杂波后的DDM发现,由于原始DDM海杂波分布杂乱,使得最大功率值附近存在众多干扰;当使用PCA抑制非马蹄形DDM中的海杂波时,由于海面粗糙,反射信号的功率在DDM中分布杂乱,使得PCA抑制海杂波后奇异值差异小,出现误差值变大的情况。
|
|
表 2 实验结果 Tab. 2 Experimental results |
|
图 4 抑制海杂波前后误差分析 Fig. 4 Error analysis before and after sea clutter suppression |
|
图 5 索引号599原始DDM Fig. 5 Original DDM of index 599 |
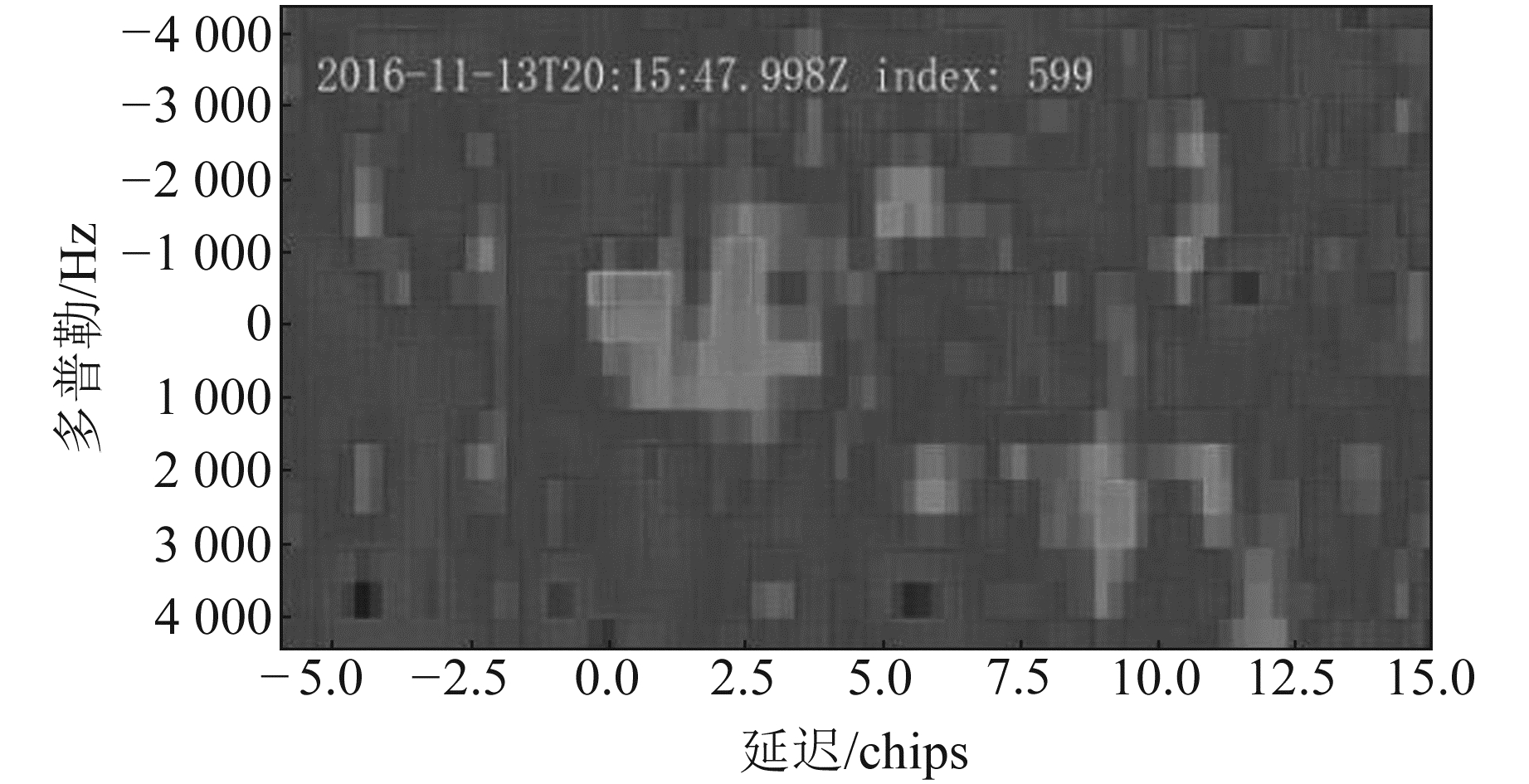
|
图 6 索引号599抑制海杂波后的DDM Fig. 6 DDM of index 599 after sea clutter suppression |
本文以挪威Snøhvit采气平台作为海面目标,提出使用PCA抑制海杂波,提高海面目标反演精度。为验证PCA抑制海杂波的有效性,使用镜面反射点的经纬度来筛选DDM,以减少实验的干扰性。实验结果显示,在使用PCA抑制海杂波前,反演位置平均误差为17.65 km,而抑制海杂波后的反演位置平均误差为11.42 km,位置精度提升35.30%。
致谢: 感谢萨里卫星技术有限公司提供TDS-1数据。
| [1] |
Valencia E, Camps A, Rodriguez-Alvarez N, et al. Using GNSS-R Imaging of the Ocean Surface for Oil Slick Detection[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(1): 217-223 DOI:10.1109/JSTARS.2012.2210392
(  0) 0) |
| [2] |
Carrie G, Deloues T, Mametsa J, et al. Ship Detection Based on GNSS Reflected Signals: An Experimental Plan[C]. Space Reflecto, Calais, 2011
(  0) 0) |
| [3] |
Ji W X, Xiu C D, Li W Q, et al. Ocean Surface Target Detection and Positioning Using the Spaceborne GNSS-R Delay-Doppler Maps[C]. 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec, 2014
(  0) 0) |
| [4] |
Schiavulli D, Frappart F, Ramillien G, et al. Observing Sea/Ice Transition Using Radar Images Generated from TechDemoSat-1 Delay Doppler Maps[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(5): 734-738
(  0) 0) |
| [5] |
Simone A D, Park H, Riccio D, et al. Sea Target Detection Using Spaceborne GNSS-R Delay-Doppler Maps: Theory and Experimental Proof of Concept Using TDS-1 Data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(9): 4 237-4 255 DOI:10.1109/JSTARS.2017.2705350
(  0) 0) |
| [6] |
Zavorotny V U, Voronovich A G. Scattering of GPS Signals from the Ocean with Wind Remote Sensing Application[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(2): 951-964 DOI:10.1109/36.841977
(  0) 0) |
| [7] |
Valencia E, Camps A, Marchan-Hernandez J F, et al. Ocean Surface's Scattering Coefficient Retrieval by Delay-Doppler Map Inversion[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 750-754 DOI:10.1109/LGRS.2011.2107500
(  0) 0) |
2. Merchant Marine College, Shanghai Maritime University, 1550 Haigang Road, Shanghai 201306, China
 2022, Vol. 42
2022, Vol. 42


