2. 武汉引力与固体潮国家野外科学观测研究站,武汉市洪山侧路40号,430071;
3. 航天工程大学电子与光学工程系,北京市八一路1号,101416
人工爆破事件与天然地震事件在发震原理、地震波传播方式以及能量释放大小等方面均有较大区别,但二者波形特征具有一定的相似性。如何精确区分天然地震和人工地震信号是当前地震学研究的重要方向之一。
信号特征提取是地震识别的重要前提工作,但天然地震信号往往掺杂大量环境噪声,直接进行波形特征提取或地震识别会导致结果不够精确,甚至造成较大的识别误差[1]。集合经验模态分解[2](EEMD)是一种从经验模态分解[3](EMD)发展而来的新型信号降噪方法,其利用多个白噪声数据来消除初始信号中的干扰成分,并利用均值化得到最终的本征模态函数(IMF)分量。
人工神经网络(artificial neural networks,ANN) 在天然地震事件与人工爆破事件的震相识别或波形分类等[4-8]方面具有较好效果。但许多神经网络模型,如BPNN[5]、GRNN[6]、CNN[7]以及SOM[8]等存在识别率不高、部分超参数需凭借人工预设合适经验值、预测结果不稳定等问题,从而给地震事件类型的精准性及可靠性识别带来极大挑战。
本文从天然地震事件和人工爆破事件的振动波形信号中选取固定长度数据,归一化处理后利用EEMD对信号进行降噪与分解,对前10阶IMF进行分布熵计算,得到10维多尺度分布熵输入矩阵,并按照固定比例随机抽取并拆分成训练集和测试集,使用鲸鱼优化算法(WOA)对自组织特征映射(SOM)神经网络进行参数寻优,得到新的地震波形分类器。
1 WOA-SOM辨识模型 1.1 鲸鱼算法鲸鱼优化算法[9](whale optimization algorithm,WOA)是一种源自座头鲸狩猎习性的仿生优化方法,其原理是鲸鱼群利用自身巨大的浮力和行动缓慢的特点,发现猎物后采取空间螺旋式游行并吐泡标记与更新猎物最新位置,最后实施目标猎捕行动。
设定猎物位置为寻优对象,鲸鱼群在发动空间螺旋气泡式攻击前首先会进行针对猎物的包围动作,鲸鱼个体会把当前最优位置方位作为移动目标。鲸鱼位置更新方式为:
| $ \boldsymbol{D}=\left|C \cdot \boldsymbol{L}^*(t)-\boldsymbol{L}(t)\right| $ | (1) |
| $ \boldsymbol{L}(t+1)=\boldsymbol{L}^*(t)-A \cdot \boldsymbol{D} $ | (2) |
式中,t为当前迭代次数;A和C为鲸鱼位置调节系数,其中A为受迭代次数t影响的随机数,C为值域在[0, 2]的完全随机数;L*(t)为当前时刻鲸鱼群的最佳位置向量;L(t)为当前时刻鲸鱼位置;D为当前鲸鱼位置与鲸群最佳鲸鱼位置之间的距离向量。
在发现目标猎物后,WOA算法根据p值大小制定合适的鲸鱼群猎捕行动策略并更新鲸鱼位置:当p < 0.5时,WOA算法选择收缩包围的方法对猎物进行攻击;当p≥0.5时,WOA算法选择螺旋气泡式行动捕食猎物。相关公式为:
| $ \boldsymbol{L}(t+1)=\left\{\begin{array}{l} \boldsymbol{L}^*(t)-A \cdot \boldsymbol{D}, p<0.5 \\ D^{\prime} \mathrm{e}^{b p} \cos (2 \pi q)+\boldsymbol{L}^*(t), p \geqslant 0.5 \end{array}\right. $ | (3) |
式中,随机数p∈[0, 1],q∈[-1, 1];D′为当前鲸鱼位置与鲸群最佳鲸鱼位置之间的绝对距离,即D′=| L*(t)- L(t)|;定常数b为螺旋形状控制参数;常数0.5为预设的捕食方法选择概率阈值的经验值。最后得到满足迭代停止条件的L*(t),即WOA算法的最终寻优结果。
1.2 WOA-SOM模型识别原理SOM神经网络[8]是一种由输入层与各竞争层神经元之间全互联而成的无监督型学习模型,可在无属性标签的情况下对输入样本进行自动聚类。SOM网络识别结果会受到网络参数的影响,为了获得较准确的地震辨识结果,引入WOA对SOM部分超参数进行寻优,以得到一个新型的地震辨识模型。
WOA-SOM模型识别流程如图 1所示,WOA将SOM中竞争层维数、网络训练次数等超参数作为优化自变量,将SOM识别结果向量R与真实类别标签向量T的均方根误差(RMSE)作为适应度函数,即
| $ \text { fitness }=\operatorname{RMSE}(\boldsymbol{R}, \boldsymbol{T}) $ | (4) |

|
图 1 WOA-SOM模型识别流程 Fig. 1 Flow chart of WOA-SOM recognition |
基于训练集得到满足迭代停止条件的最优超参数值,最后使用WOA-SOM辨识模型对测试集进行识别。
2 EEMD多尺度分布熵特征提取 2.1 EEMDEEMD区别于EMD的关键是在原始信号x(t)中分别添加m个高斯白噪声,构成m个合成信号,依次进行EMD分解得到K个本征模态函数分量(IMF)Iij(t)及一个剩余信号分量ri(t);按照对应阶数j,循环对m个Iij(t)求和后取均值,得到最终的本征模态函数分量Ij(t)与剩余分量r(t),可显著消除白噪声影响,即
| $ I_j(t)=\frac{1}{m} \sum\limits_{i=1}^m I_{i j}(t) $ | (5) |
| $ \bar{r}(t)=\sum\limits_{i=1}^m r_i(t) $ | (6) |
图 2为天然地震信号及人工爆破信号的EEMD分解结果,其中第1行为初始波形信号通过固定长度(l=4 000)截取的归一化处理结果,第2~11行分别为EEMD分解得到的IMF1~IMF10分量,并按照频率或幅值大小降序排列,第12行为剩余分量(趋势项)。EEMD算法的参数设置为:STD(白噪声)=0.1*STD(x(t)), K为10, m为20,其中STD为信号标准差。
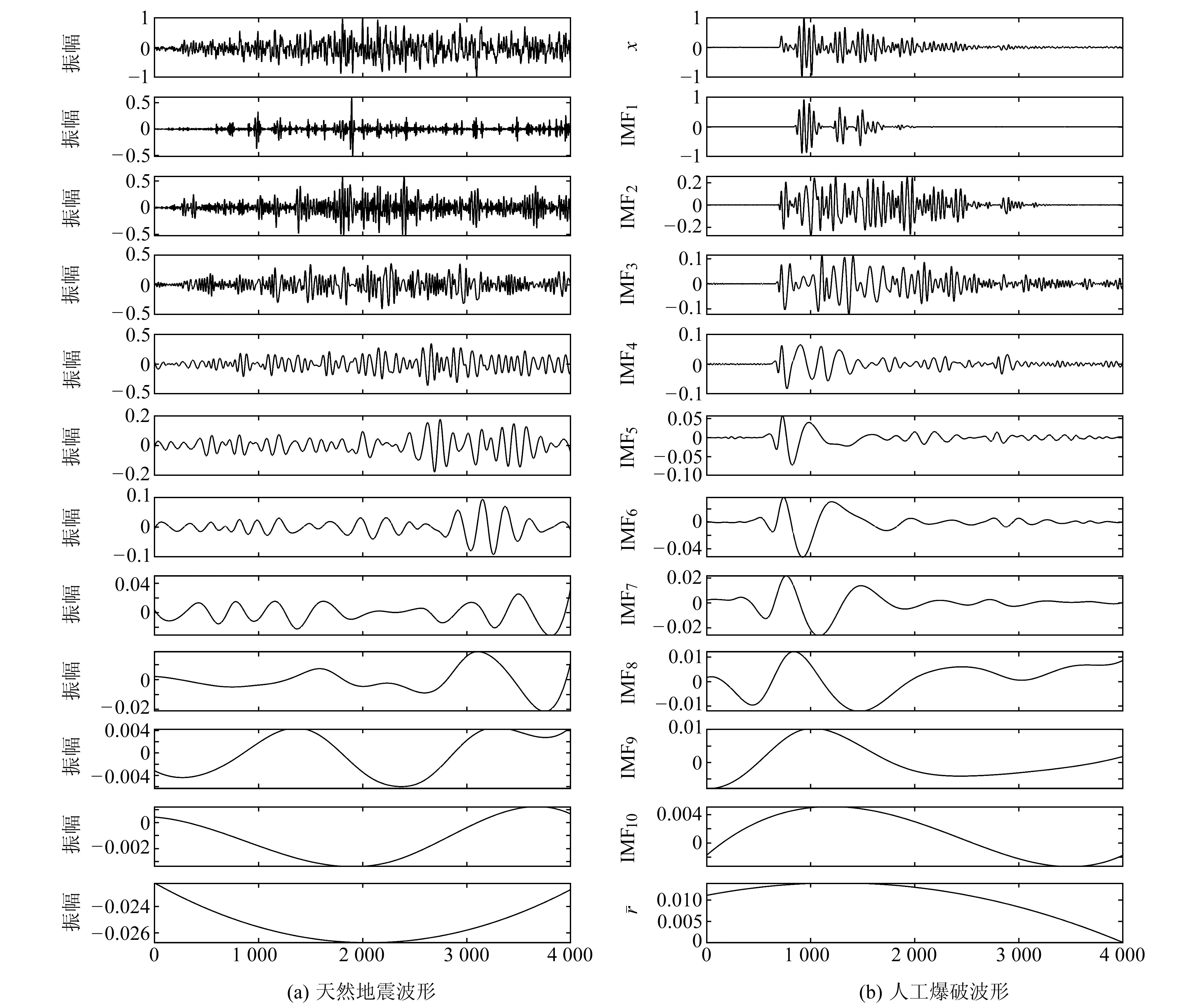
|
图 2 单个波形的EEMD分解结果 Fig. 2 Results of EEMD for a single waveform |
分布熵[10]可以描述时间序列或一维离散信号的不规律性和混乱程度,其计算方法为:
1) 信号重构。设时序信号为x={x(1), x(2), …, x(l)},其长度为l,自定义参数嵌入维数为p,重新构造(l-p)个一维向量
2) 切比雪夫距离计算。计算向量
3) 直方图估算EPDF:预先设定直方图柱数为q,则直方图频数分布为N=[n1, n2, …, nk, …, nq],距离矩阵Q的经验概率密度函数(EPDF)为
4) 计算分布熵。
| $ \text { Dist }_{\mathrm{en}}=-\sum\limits_{k=1}^q f_k \log _2 f_k $ | (7) |
利用EEMD从地震信号中提取若干个频率逐渐递减且振幅差异较大的IMF分量,再计算得到这些分量的分布熵,组成多尺度分布熵。基于EEMD的多尺度分布熵(图 3)能有效降低噪声对信号的污染,得到更加纯净的信号特征,以有效区分不同混乱状态的信号。
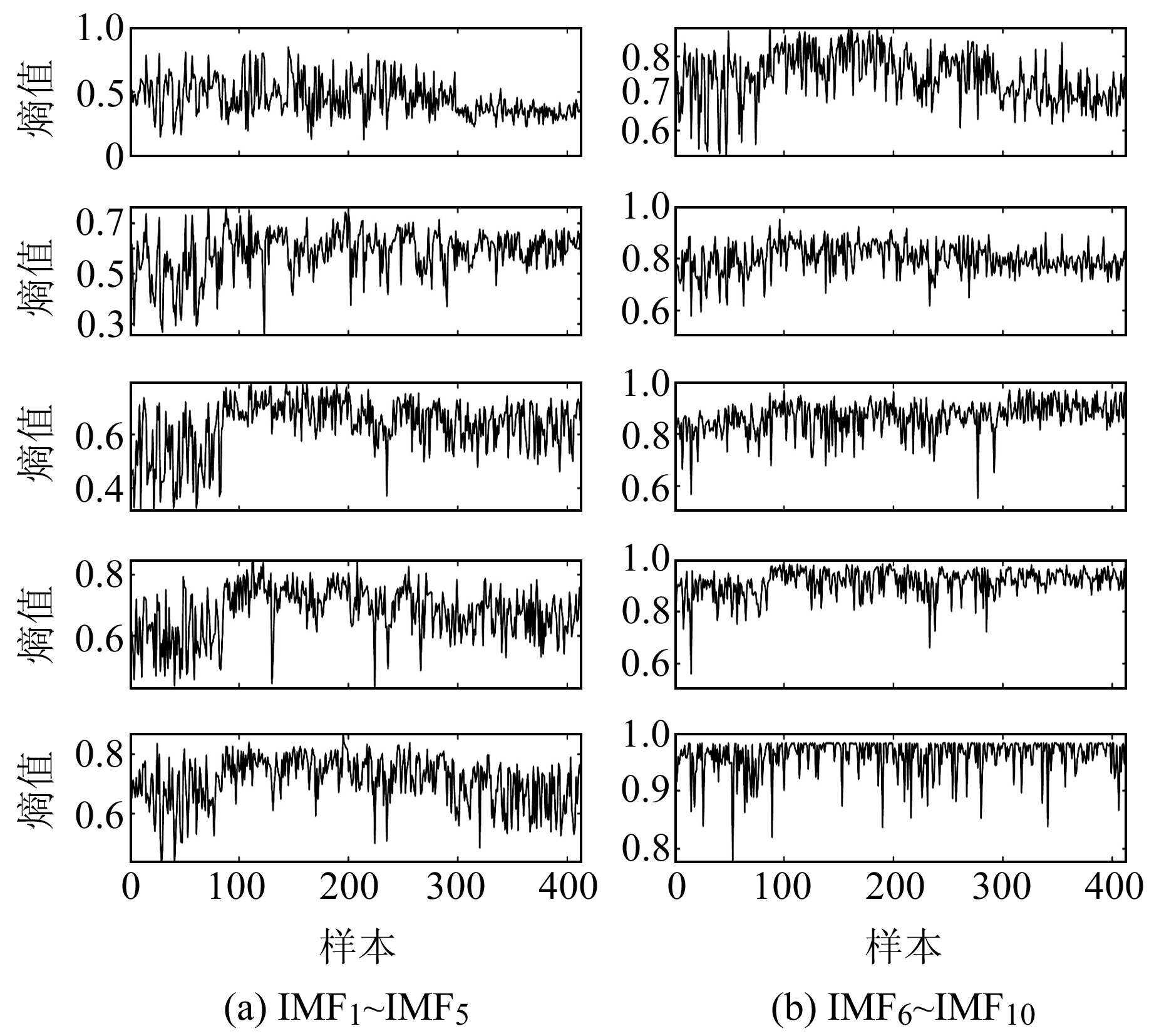
|
图 3 EEMD多尺度分布熵计算结果 Fig. 3 Results of EEMD multiscale distribution entropy |
本实验选取国家地震科学数据中心与中国地震局工程力学研究所提供的2021年江苏天宁MS4.2地震的96条强震动加速度波形记录、2021年江苏大丰海域MS5.0地震的117条强震动加速度波形记录、2021年云南漾濞MS6.4地震的84条余震记录(2.9≤MS≤3.9)和中国水利水电科学研究院岩土工程研究所(www.geoeng.iwhr.com)人工爆破实验得到的117条爆破加速度波形记录,数据仿真平台采用MATLAB 2019A。
由于神经网络的权值和阈值等参数具有一定随机性,该类模型的网络预测结果并不完全一致,甚至会出现较大误差。为了探究WOA-SOM模型的有效性和稳健性,设计100次循环条件的地震辨识子实验,测试该模型在部分超参数发生变化后的辨识效果与模型稳健性,训练集与测试集比例为8:2,即331:83,具体实验结果如图 4、5和表 1所示。

|
图 4 100次辨识子实验结果 Fig. 4 Results of 100 identification sub-tests |
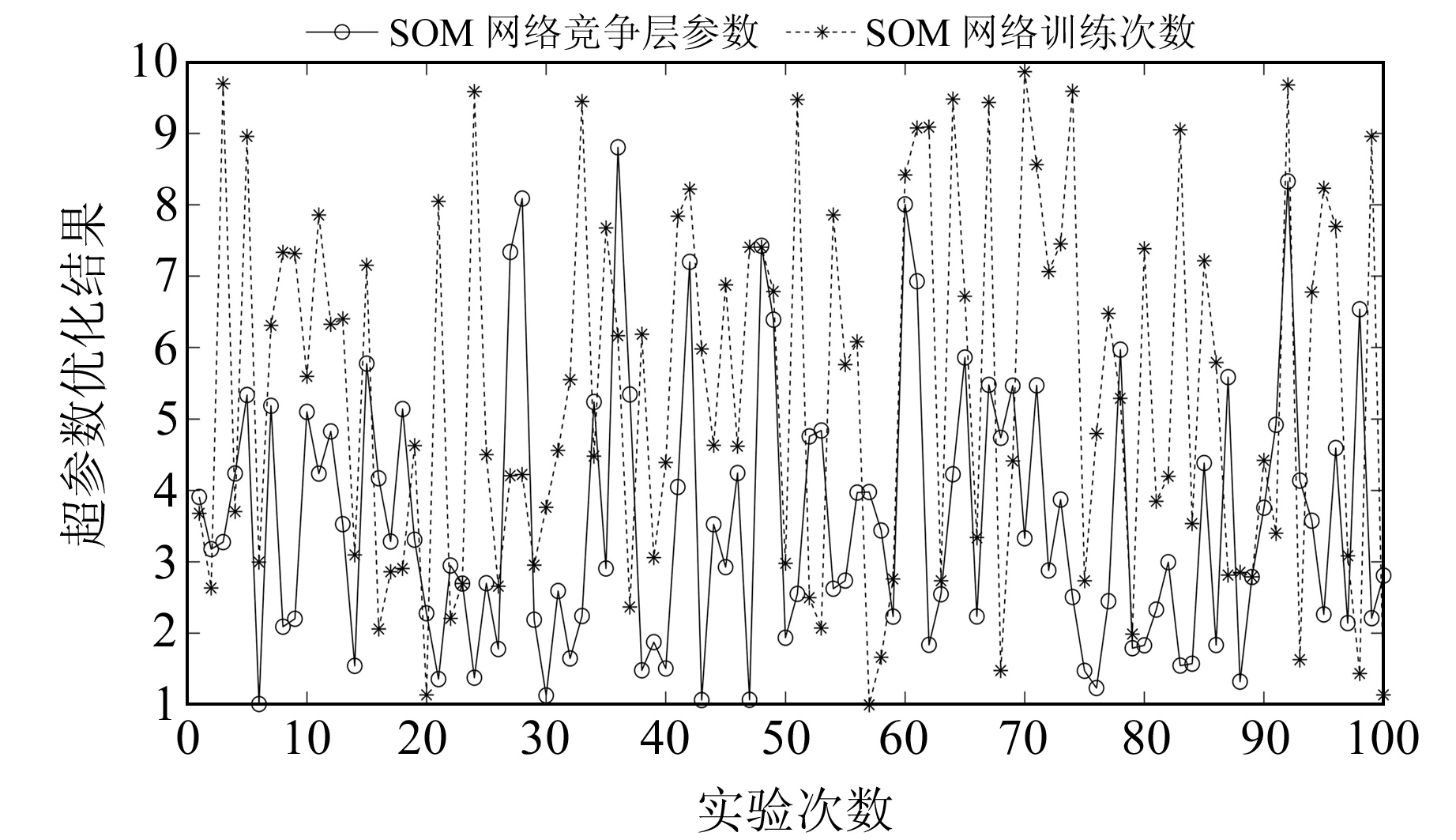
|
图 5 100次辨识子实验情况下SOM超参数优化结果 Fig. 5 Optimization results of SOM hyperparameter under 100 identification sub-tests |
|
|
表 1 100次辨识子实验条件下的统计学结果 Tab. 1 Statistical results under 100 identification sub-tests |
计算100次辨识子实验识别率的均值期望(mean)、标准差(STD)、极差、变异系数(CV)以及四分位距(interquartile range, IQR)等统计指标,综合评价WOA-SOM模型的地震识别性能与算法稳健性。结合表 1和图 4、5可知,100次重复实验条件下WOA-SOM模型相较于标准SOM模型,辨识结果更加可靠,准确率更高,表征结果波动程度的标准差、极差、CV、IQR等指标值均明显减小,尤其是IQR值从2.409 6变为0,表明利用WOA优化SOM模型具有良好效果。
由图 4可知,WOA优化后的SOM模型识别曲线虽然仍存在局部波动现象,但其相较于标准SOM模型辨识效果具有明显改善,辨识准确率曲线整体较平稳,峰值突降现象得到有效抑制。由图 5可知,四舍五入后的SOM网络竞争层维数优化值多集中在6以下,网络训练次数优化结果虽然差异较大,但其对辨识结果并无显著影响。
为了测算WOA-SOM模型与其他方法在同等实验条件下的性能差异,采用K近邻(KNN)、线性判别分析(LDA)、朴素贝叶斯、决策树、支持向量机(SVM)等学习模型作为参照,辨识实验仍然采取100次循环子实验方式,训练集与测试集比例统一设定为8∶2,准确率、召回率、F1等指标的均值对比结果如表 2所示。
|
|
表 2 机器学习模型辨识效果对比 Tab. 2 Comparison of identification effects of machine learning methods |
由表 2可知,WOA-SOM模型性能优异,与KNN、LDA及朴素贝叶斯等多种经典机器学习方法相比,在准确率、召回率及F1等性能指标上均有明显提升,说明该模型在地震波形辨识上具有一定价值。
4 结语本文主要对天然地震波形信号与人工爆破波形信号进行EEMD多尺度分布熵提取和WOA-SOM神经网络识别,并取得良好的地震信号识别效果。
1) EEMD作为一种新型非平稳信号处理方法,可用于地震信号的分析和识别;EEMD方法结合分布熵概念可形成一种新的地震信号辨识判据,即EEMD多尺度分布熵。
2) 标准SOM神经网络模型的超参数具有一定随机性,这对辨识结果的可靠性具有一定影响;通过引入鲸鱼算法对竞争层维数、网络训练次数等参数进行全局寻优,得到新型的地震信号辨识模型,即WOA-SOM神经网络模型。
3) 实测数据计算结果表明,利用EEMD提取多尺度分布熵特征,再利用WOA寻优SOM模型部分参数能较好地识别地震波形类型。
本文WOA-SOM模型仍具有一定改进空间,EEMD多尺度分布熵提取平均耗时为0.527 1 s,而WOA-SOM模型平均耗时接近74.664 4 s,WOA寻优时间较长,同时实验数据的选择存在一定局限性。
致谢: 感谢中国地震局工程力学研究所及中国水利水电科学研究院岩土工程研究所为本研究提供数据。
| [1] |
何光林, 陶斯倩, 范红波. 基于噪声特征的地震动信号目标预警和识别算法研究[J]. 北京理工大学学报, 2014, 34(1): 64-67 (He Guanglin, Tao Siqian, Fan Hongbo. Research on Early-Warming and Target Identification Algorithm of Seismic Signal Based on Characteristics of Noise[J]. Transactions of Beijing Institute of Technology, 2014, 34(1): 64-67)
(  0) 0) |
| [2] |
李大虎, 赖敏, 何强, 等. 基于聚类经验模态分解(EEMD)的汶川MS8.0强震动记录时频特性分析[J]. 地震学报, 2012, 34(3): 350-362 (Li Dahu, Lai Min, He Qiang, et al. Time-Frequency Characteristics Analysis of Wenchuan MS8.0 Strong Motion Records Based on EEMD Decomposition[J]. Acta Seismologica Sinica, 2012, 34(3): 350-362 DOI:10.3969/j.issn.0253-3782.2012.03.007)
(  0) 0) |
| [3] |
杨凯, 刘伟. 基于改进EMD的地震信号去噪[J]. 西南石油大学学报: 自然科学版, 2012, 34(4): 75-82 (Yang Kai, Liu Wei. Random Noise Attenuation of Seismic Signal Based on Improved EMD[J]. Journal of Southwest Petroleum University: Science and Technology Edition, 2012, 34(4): 75-82 DOI:10.3863/j.issn.1674-5086.2012.04.010)
(  0) 0) |
| [4] |
曲均浩, 刘希强, 吴丹彤, 等. 基于神经网络的近震与远震识别[J]. 地震研究, 2012, 35(3): 360-366 (Qu Junhao, Liu Xiqiang, Wu Dantong, et al. Identification between Near and Distant Earthquakes Based on Neutral Network[J]. Journal of Seismological Research, 2012, 35(3): 360-366 DOI:10.3969/j.issn.1000-0666.2012.03.011)
(  0) 0) |
| [5] |
刘方斌, 曲均浩, 张志慧. 基于BP神经网络的天然与非天然地震识别[J]. 计算机应用与软件, 2020, 37(1): 106-109 (Liu Fangbin, Qu Junhao, Zhang Zhihui. Identification of Natural and Non-Natural Earthquakes Based on BP Neural Network[J]. Computer Applications and Software, 2020, 37(1): 106-109)
(  0) 0) |
| [6] |
韩晓飞, 潘存英, 罗词建. 基于遗传算法的广义回归神经网络在地震预测中的应用[J]. 华北地震科学, 2012, 30(1): 48-53 (Han Xiaofei, Pan Cunying, Luo Cijian. Application of Generalized Regression Neural Network Based on Genetic Algorithm in Earthquake Predication[J]. North China Earthquake Sciences, 2012, 30(1): 48-53 DOI:10.3969/j.issn.1003-1375.2012.01.010)
(  0) 0) |
| [7] |
赵明, 陈石, Dave Yuen. 基于深度学习卷积神经网络的地震波形自动分类与识别[J]. 地球物理学报, 2019, 62(1): 374-382 (Zhao Ming, Chen Shi, Dave Yuen. Waveform Classification and Seismic Recognition by Convolution Neural Network[J]. Chinese Journal of Geophysics, 2019, 62(1): 374-382)
(  0) 0) |
| [8] |
蔡润, 武震, 云欢, 等. 基于BP和SOM神经网络相结合的地震预测研究[J]. 四川大学学报: 自然科学版, 2018, 55(2): 307-315 (Cai Run, Wu Zhen, Yun Huan, et al. Research on Earthquake Prediction Based on BP and SOM Neural Network[J]. Journal of Sichuan University: Natural Science Edition, 2018, 55(2): 307-315 DOI:10.3969/j.issn.0490-6756.2018.02.016)
(  0) 0) |
| [9] |
Mirjalili S, Lewis A. The Whale Optimization Algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67 DOI:10.1016/j.advengsoft.2016.01.008
(  0) 0) |
| [10] |
Li P, Liu C Y, Li K, et al. Assessing the Complexity of Short-Term Heartbeat Interval Series by Distribution Entropy[J]. Medical and Biological Engineering and Computing, 2015, 53(1): 77-87 DOI:10.1007/s11517-014-1216-0
(  0) 0) |
2. Wuhan Gravitation and Solid Earth Tides, National Observation and Research Station, 40 Hongshance Road, Wuhan 430071, China;
3. Department of Electronic and Optical Engineering, Space Engineering University, 1 Bayi Road, Beijing 101416, China
 2022, Vol. 42
2022, Vol. 42


