2. 华南师范大学地理科学学院,广州市中山大道西55号,510631;
3. 广东省智慧国土工程技术研究中心,广州市中山大道西55号,510631
在高程测量中,GPS获取的高程数据为大地高,而我国所采用的高程系统为正常高[1],两者存在差值,即高程异常。因此,如何获取高精度的高程异常是区域似大地水准面拟合的关键。
LSSVM是一种常用的区域似大地水准面拟合方法,其以支持向量机为基础改进而来,在高程转换过程中能够取得较好的效果[2]。但单一的LSSVM会存在模型误差,精度有限,且会造成拟合残差序列信息浪费。基于此,本文以LSSVM为基础,提出LSSVM-Shepard组合区域似大地水准面拟合方法,充分利用拟合的残差序列信息,减少模型误差影响,提高高程转换精度。
1 原理与方法 1.1 LSSVM原理LSSVM对支持向量机优化方程中的损失函数进行改进,采用误差的二次项之和代替
假设(xi, yi)为一组高程异常数据集,其中,i=1, 2,…,n,xi∈Rl,yi∈R。xi为数据集的平面坐标,yi为数据集的高程异常。则LSSVM优化问题为:
| $ \begin{aligned} &\min _{\boldsymbol{\omega}, b, e} J(\boldsymbol{\omega}, e)=\frac{1}{2} \boldsymbol{\omega}^{\mathrm{T}} \boldsymbol{\omega}+\frac{1}{2} \gamma \sum\limits_{i=1}^n e_i^2 \\ &\text { s. t } \quad y_i=\boldsymbol{\omega}^{\mathrm{T}} \boldsymbol{\varphi}\left(x_i\right)+b+e_i, \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ i=1, 2, 3, \cdots, n \end{aligned} $ | (1) |
式中,ω为系数序列,e为误差项,γ为正则化参数,φ(·)为映射函数,b为偏差量。根据拉格朗日定理可得:
| $ \begin{gathered} L(\boldsymbol{\omega}, b, e, \alpha)=J(\boldsymbol{\omega}, e)- \\ \sum\limits_{i=1}^n \alpha_i\left\{\boldsymbol{\omega}^{\mathrm{T}} \boldsymbol{\varphi}\left(x_i\right)+b+e_i-y_i\right\} \end{gathered} $ | (2) |
分别对ω、b、ei、αi求偏导数,并使偏导数等于0。整理得:
| $ \left\{\begin{array}{l} \boldsymbol{\omega}=\sum\limits_{i=1}^n \alpha_i \boldsymbol{\varphi}\left(x_i\right), \sum\limits_{i=1}^n \alpha_i=0 \\ \alpha_i=\gamma_{e_i}, \boldsymbol{\omega}^{\mathrm{T}} \boldsymbol{\varphi}\left(x_i\right)+b+e_i-y_i=0 \end{array}\right. $ | (3) |
根据Mercer条件可知[6-7],存在映射函数φ和核函数K,使得K(xk, xl)= φ(xk)Tφ(xl)。线性方程组(3)整理可得:
| $ \left[\begin{array}{ccccc} 0 & 1 & 1 & \cdots & 1 \\ 1 & K\left(x_1, x_1\right)+1 / \gamma & K\left(x_1, x_2\right) & \cdots & K\left(x_1, x_n\right) \\ 1 & K\left(x_2, x_1\right) & K\left(x_2, x_2\right)+1 / \gamma & \cdots & K\left(x_2, x_n\right) \\ \vdots & \vdots & \vdots & \vdots & \\ 1 & K\left(x_n, x_1\right) & K\left(x_n, x_2\right) & \cdots & K\left(x_n, x_n\right)+1 / \gamma \end{array}\right]\left[\begin{array}{c} b \\ \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_n \end{array}\right]=\left[\begin{array}{c} 0 \\ y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right] $ | (4) |
通过解方程(4)可得αi和b,则LSSVM模型函数可表示为:
| $ y(x)=\sum\limits_{i=1}^n \alpha_i K\left(x_i, x\right)+b $ | (5) |
Shepard插值模型是针对大量离散点提出的局部逼近模型,是一种改进的加权平均法[8]。该模型应用于高程转换的主要原理为:对于给定的数据集(xi, yi, ξi),i=1, 2,…,n,(xi, yi)为平面位置坐标,ξi为对应的高程异常,则未知点高程异常可通过下式进行求解:
| $ \xi(x, y)=\left\{\begin{array}{l} \frac{\sum\limits_{i=1}^n \xi_i\left(\rho\left(r_i\right)\right)^u}{\sum\limits_{i=1}^n\left(\rho\left(r_i\right)\right)^u}, r_i \neq 0 \\ \xi_i, r_i=0 \end{array}\right. $ | (6) |
式中,u为拟合度,u>1;ri为未知点到各已知点的距离;ρ(ri)为已知点关于未知点的距离权函数:
| $ \rho(r)=\left\{\begin{array}{l} \frac{1}{r}, 0<r \leqslant \frac{R}{3} \\ \frac{27}{4 R}\left(\frac{r}{R}-1\right)^2, \frac{R}{3}<r \leqslant R \\ 0, r>R \end{array}\right. $ | (7) |
从式(7)可以看出,影响范围内会形成两个环带。
1.3 LSSVM-Shepard组合模型根据物理大地测量学理论,高程异常可分为3个分量[9],其公式为:
| $ \xi=\xi_{\text {长 }}+\xi_{\text {中 }}+\xi_{\text {短 }} $ | (8) |
式中,ξ长、ξ中、ξ短分别为长波、中波、短波分量。高程异常在中长波项部分趋势变化平缓,而在短波项部分变化较大,容易受到地形等因素影响。
LSSVM将最小二乘思想引入到支持向量机,趋势面变化相对平缓,同时保持支持向量机良好的非线性问题处理能力,可提高计算效率。与二次曲面拟合“移去-恢复”模型的中长波项相比,LSSVM能够更好地处理中长波项中存在的非线性问题。Shepard插值模型可以充分利用周围已知点信息,能够有效处理局部变化信息。本文将两个单一模型进行结合,采用LSSVM拟合高程异常的中长波项,利用Shepard插值模型拟合包含模型误差的短波项,综合两个单一模型的优点,同时充分利用单一模型的拟合残差信息。其主要步骤如下:
1) 利用LSSVM对高程异常的中长波项进行拟合,确定模型系数,并计算包含LSSVM模型误差和短波项的残差序列。
2) 利用Shepard插值模型对残差序列进行训练,使用交叉验证方法确定模型系数。
3) 利用组合模型计算区域内任意一点的高程异常值。
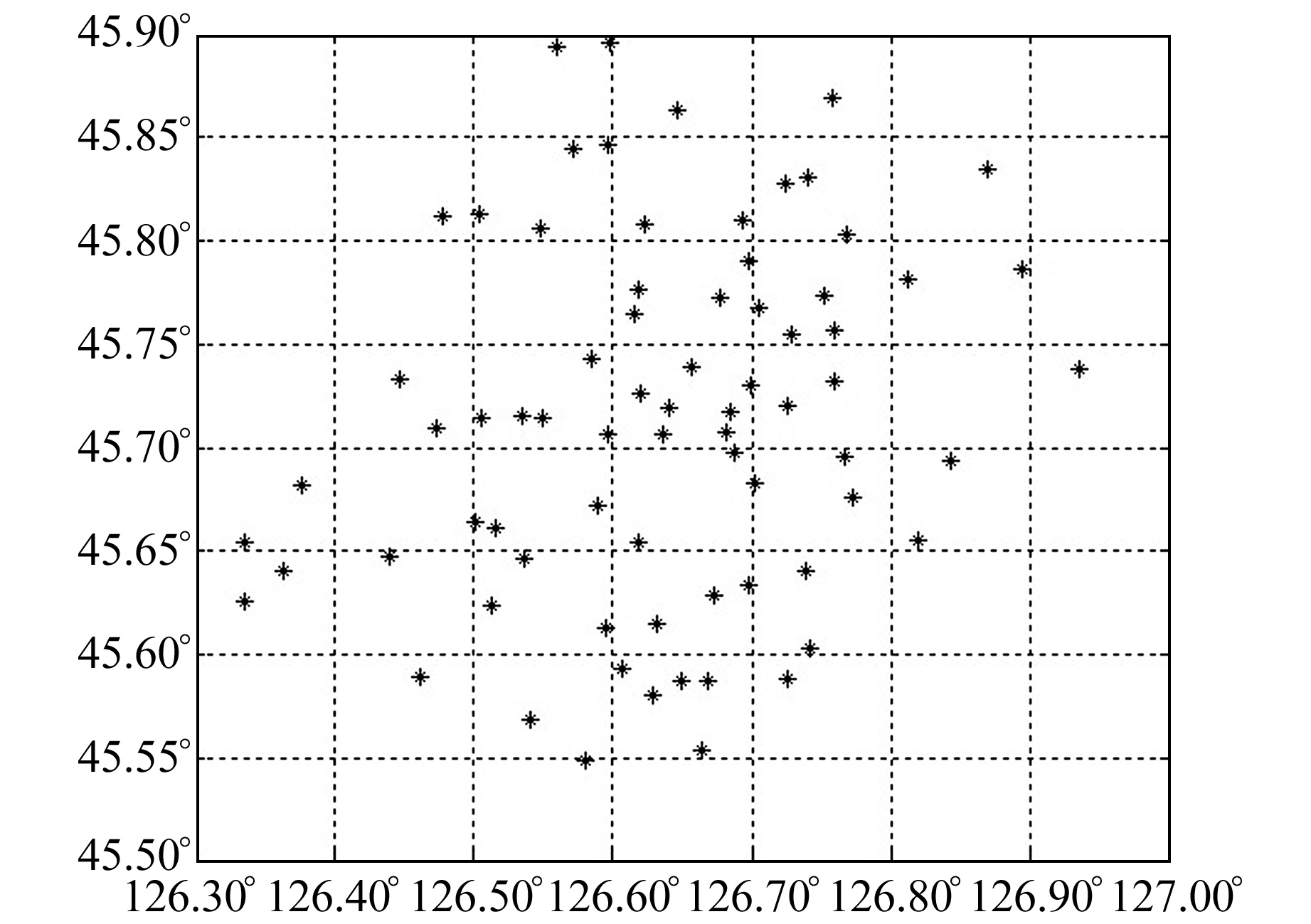
2 算例分析 2.1 项目概况实例1 项目区位于黑龙江省某市,地势较为平坦,属于平原地区。项目区共有74个GPS C级网点,且均已进行二等水准联测[10],测区面积为1 100 km2。点位分布见图 1。
|
图 1 平原地区GPS点位分布 Fig. 1 Distribution of GPS points in plain area |
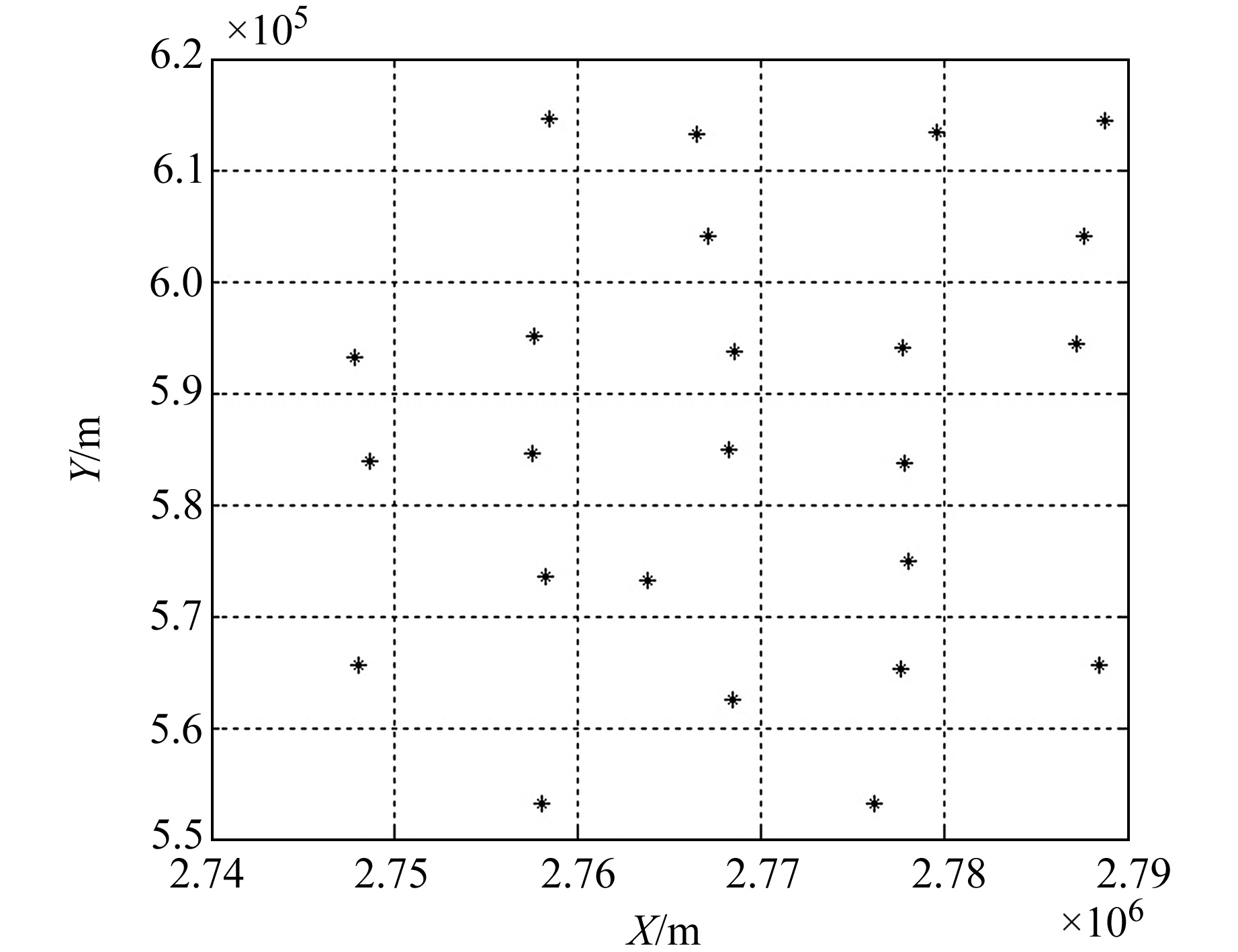
实例2 似大地水准面拟合项目区位于云南某地区,区域内地形起伏大,属于高原山区地形。区域内共布设24个C级GPS控制点,并已进行三等水准联测[11],测区面积约为2 159 km2。点位分布见图 2。
|
图 2 高原山区GPS点位分布 Fig. 2 Distribution of GPS points in plateau mountainous area |
LSSVM模型采用径向基函数作为核函数,其公式为:K(x, xi)=exp(-‖x-xi‖2/2σ2)。该模型含有2个参数,分别为惩罚系数γ和核函数参数σ,模型参数以双层方格网法进行寻优。同时为减少取样随机性所产生的训练偏差,采用交叉验证法进行参数精度评定,将原始数据分为n等份,通过n次循环,每次以其中一份作为测试数据,其余n-1份作为训练数据,得到模型并对测试数据进行预测。统计测试结果,最终获得n次统计结果的平均值,并以此作为参数的评价因子。Shepard插值模型参数为拟合度u和影响半径R,为防止模型陷入局部最优,文中将u和R范围分别设置为[1, 50]和[0.1, 20],搜索步长分别设置为1和0.02,同时通过循环操作使寻优过程遍历每一个节点。
2.3 实验对比分析为增加实验的可靠性,选取10、20、30、40、50个均匀分布的联测点分别作为平原地区实验拟合点,选取7、9、11、13、15个均匀分布的联测点分别作为高原山区实验拟合点,剩余点作为检测点进行计算。为使高程异常数据集处于同一量级,在实验前对两组数据分别进行标准化处理。
实验分别采用二次曲面法、LSSVM、Shepard插值模型、二次曲面-Shepard、LSSVM-Shepard模型等5种方法进行似大地水准面拟合,采用检测点的外符合精度作为评定指标。实验计算结果如表 1(单位m)和表 2(单位m)所示。
|
|
表 1 平原地区似大地水准面拟合结果统计 Tab. 1 Statistics of fitting results of quasi-geoid in plain area |
|
|
表 2 高原山区似大地水准面拟合结果统计 Tab. 2 Statistics of fitting results of quasi-geoid in plateau mountainous area |
表 1为平原地区各模型计算结果对比。当拟合点个数从10增加至50时,LSSVM-Shepard模型的外符合精度从0.035 m降至0.015 m,且数值均小于二次曲面、LSSVM、Shepard插值等3种单一模型,说明该组合模型的拟合效果优于这3种单一模型。二次曲面-Shepard模型随着拟合点数增加,外符合精度从0.034 m降为0.013 m,且数值均小于二次曲面和Shepard插值模型,说明拟合效果优于这两种单一模型。当拟合点个数一定时,二次曲面-Shepard和LSSVM-Shepard模型的外符合精度最大差值的绝对值为0.002 m,表明两个组合模型的拟合效果基本一致。
表 2为高原山区各模型计算结果对比。当拟合点个数一定时,LSSVM-Shepard模型的外符合精度小于其他4种模型,说明该组合模型高程转换效果最优。当拟合点个数由7增加至11时,二次曲面-Shepard模型的外符合精度分别为0.097 m、0.103 m、0.110 m,而Shepard插值模型的外符合精度分别为0.095 m、0.094 m、0.089 m,Shepard插值模型的拟合效果略优,说明二次曲面-Shepard模型在复杂的高原山区进行高程转换时适用性受限。
综上所述,无论是在平原还是高原山区实验区,LSSVM-Shepard模型的拟合效果均优于二次曲面、LSSVM、Shepard插值等3种单一模型。在平原实验区,LSSVM-Shepard模型和二次曲面-Shepard模型均能取得较好的拟合效果,但在高原山区实验区,二次曲面-Shepard模型适用性受限,而LSSVM-Shepard模型仍能取得较好的拟合效果。
3 结语本文提出LSSVM-Shepard组合区域似大地水准面拟合方法,并结合平原地区和高原山区两个工程实例进行实验,得到以下结论:
1) 无论是在平原地区还是高原山区,LSSVM-Shepard模型的拟合效果均优于二次曲面法、LSSVM、Shepard插值等3种单一模型,是一种可行的似大地水准面拟合方法。
2) 二次曲面-Shepard模型在平原实验区进行高程转换时,能够取得较好的拟合效果,但在高原山区实验中,转换度低于Shepard插值模型,适用性受限。LSSVM-Shepard模型以LSSVM代替二次曲面模型,能够有效处理转换过程中的非线性问题,在两个实验中均能取得较好的高程转换效果,具有较强的适用性。
| [1] |
甘勇, 刘新新, 郑远攀. CPSO优化FLS-SVM应用于山区地形的GPS高程拟合研究[J]. 测绘通报, 2014(4): 5-9 (Gan Yong, Liu Xinxin, Zheng Yuanpan. A Study of GPS Height Fitting in Mountainous Terrain by CPSO Optimizing FLS-SVM[J]. Bulletin of Surveying and Mapping, 2014(4): 5-9)
(  0) 0) |
| [2] |
周理含. 最小二乘支持向量机在GPS高程转换中的应用[J]. 工程地球物理学报, 2010, 7(2): 243-247 (Zhou Lihan. Least Square Support Vector Machine in GPS Height Conversion[J]. Chinese Journal of Engineering Geophysics, 2010, 7(2): 243-247 DOI:10.3969/j.issn.1672-7940.2010.02.021)
(  0) 0) |
| [3] |
李明飞, 吴军超. 基于混合核函数的LSSVM在GNSS高程拟合中的应用[J]. 工程勘察, 2019, 47(12): 64-68 (Li Mingfei, Wu Junchao. Application of LSSVM Based on Hybrid Kernel Functions in GNSS Height Fitting[J]. Geotechnical Investigation and Surveying, 2019, 47(12): 64-68)
(  0) 0) |
| [4] |
Suykens J A K, Vandewalle J. Least Squares Support Vector Machine Classifiers[J]. Neural Processing Letters, 1999, 9(3): 293-300 DOI:10.1023/A:1018628609742
(  0) 0) |
| [5] |
马文涛. 基于灰色最小二乘支持向量机的边坡位移预测[J]. 岩土力学, 2010, 31(5): 1670-1674 (Ma Wentao. Forecasting Slope Displacements Based on Grey Least Square Support Vector Machines[J]. Rock and Soil Mechanics, 2010, 31(5): 1670-1674 DOI:10.3969/j.issn.1000-7598.2010.05.055)
(  0) 0) |
| [6] |
孙凯, 王颖龙. 支持向量机中Mercer核函数的构造研究[J]. 兵工自动化, 2008, 27(11): 40-42 (Sun Kai, Wang Yinglong. Research on Construction of Mercer Kernel-Function in Support Vector Machine[J]. Ordnance Industry Automation, 2008, 27(11): 40-42 DOI:10.3969/j.issn.1006-1576.2008.11.015)
(  0) 0) |
| [7] |
唐杰明, 刘俊勇, 杨可, 等. 基于灰色模型和最小二乘支持向量机的电力短期负荷组合预测[J]. 电网技术, 2009, 33(3): 63-68 (Tang Jieming, Liu Junyong, Yang Ke, et al. Short-Term Load Combination Forecasting by Grey Model and Least Square Support Vector Machine[J]. Power System Technology, 2009, 33(3): 63-68)
(  0) 0) |
| [8] |
钟波, 罗志才. GPS水准综合模型的应用研究[J]. 测绘通报, 2007(6): 5-7 (Zhong Bo, Luo Zhicai. Research on Application of Combined Model for GPS Leveling[J]. Bulletin of Surveying and Mapping, 2007(6): 5-7 DOI:10.3969/j.issn.0494-0911.2007.06.002)
(  0) 0) |
| [9] |
康靖玉. 综合EGM2008、剩余地势模型及地面重力数据的大地水准面精化[D]. 长春: 吉林大学, 2017 (Kang Jingyu. Geoid Refinement Based on EGM2008, Residual Terrain Model and Ground Gravity Data[D]. Changchun: Jilin University, 2017)
(  0) 0) |
| [10] |
朱君俊. 基于重力场模型EGM2008的高程拟合方法研究[D]. 呼和浩特: 内蒙古农业大学, 2012 (Zhu Junjun. Study on Elevation Fitting Method Based on EGM2008 Model[D]. Hohhot: Inner Mongolia Agricultural University, 2012)
(  0) 0) |
| [11] |
黎剑. 区域GPS高程异常拟合及建模方法研究[D]. 昆明: 昆明理工大学, 2013 (Li Jian. Research on Regional GPS Height Abnormal Fitting and Modeling Method[D]. Kunming: Kunming University of Science and Technology, 2013)
(  0) 0) |
2. School of Geography, South China Normal University, 55 West-Zhongshan Road, Guangzhou 510631, China;
3. Guangdong Provincial Center for Smart Land Research, 55 West-Zhongshan Road, Guangzhou 510631, China
 2022, Vol. 42
2022, Vol. 42

