2. 中国地震局地质研究所地震动力学国家重点实验室,北京市华严里甲1号,100029
对流层延迟指电磁波信号在通过高度40 km以下未被电离的中性大气层时所产生的一种信号延迟,是GNSS领域主要误差源之一。对流层延迟可用天顶对流层延迟(zenith tropospheric delay, ZTD) 和与高度角相关的映射函数的乘积表示。GNSS中消除(削弱)对流层延迟的方法大致可以归纳为随机模型、待定参数估计、差分法、模型改正等。对流层延迟改正模型既可以为高精度GNSS测量提供较精确的对流层延迟先验值,又可以显著降低相对定位差分后的残余对流层延迟误差,因此模型改正成为常用的对流层延迟处理策略。
早期的对流层延迟模型主要有Hopfield、Saastamoinen和Black模型,需代入实测气象参数进行计算,使得模型使用受到限制。鉴于此,部分学者直接针对气象参数建立时空模型,以Saastamoinen为基础衍生出UNB、EGNOS、GPT等一系列无气象参数的对流层延迟模型。随着全球四维天顶对流层延迟信息的不断累积,由回归参数直接模拟对流层延迟时空变化成为目前主流的对流层延迟建模方法[1]。TropGrid2模型、SHAO系列模型(SHAO-C、SHAO-G、SHAO-H)、IGGtrop模型、GZTD系列模型均是基于高精度ZTD时间序列建立的全球数值模型,相比UNB、EGNOS精度得到进一步提高,可达4 cm。由于全球范围内不同区域的气候差异较大,这类全球ZTD模型在局部地区会存在明显偏差[2]。因此,部分学者依托CORS网基站建立了区域精密对流层延迟模型[3-4],虽然可缩小系统偏差,但精度仍约为4 cm。主要原因在于模型时间域内仅由傅里叶级数拟合,只能反映ZTD变化主趋势,且较难精细描述ZTD序列的快速变化特征。另一方面,空间域采用函数(球谐函数+指数函数、多面函数)拟合或三维网格表征精度有限,且存在参数过多、模型复杂、使用不便等问题。此外,通过相关实验来验证模型实用效果的研究较少。
针对上述问题,本文提出一种结合小波变换、傅里叶级数拟合、AR和SVR的ZTD建模方法。该模型将ZTD时间序列分解为高、低频序列分别进行建模,可最大程度还原ZTD时间变化特性;空间部分则采用以统计学习理论为基础的SVR机器学习算法建立关于空间位置的非线性模型,且只需确定核函数类型和3个参数即可完成建模。本文基于一定数量的GNSS基站ZTD数据完成建模,并进行模型内、外符合精度检验。最后通过伪距单点定位实验测试该模型的实用效果。
1 建模方法及原理利用区域内GNSS基站观测数据解算的对流层延迟序列,可研究该区域内对流层延迟时空变化,是建立区域精密对流层延迟模型的可靠数据源。本文所用数据为NOAA(national oceanic and atmospheric administration)CORS网在加州境内的部分GNSS基站2016~2018年的RINEX观测值文件(https://geodesy.noaa.gov/corsdata/rinex/)经GAMIT解算得到的ZTD和ZHD(天顶干延迟)序列,其中94个站点用于建模,24个站点(靠近海岸线,对流层延迟变化相对剧烈)用于模型预报测试。
GAMIT采用双差观测值,需引入长距离测站来获取绝对延迟。本文采用GAMIT进行数据处理时引入周边4个长距离IGS站(MKEA、BAKE、SASK、WHIT)参与解算。详细解算流程参考文献[5]。
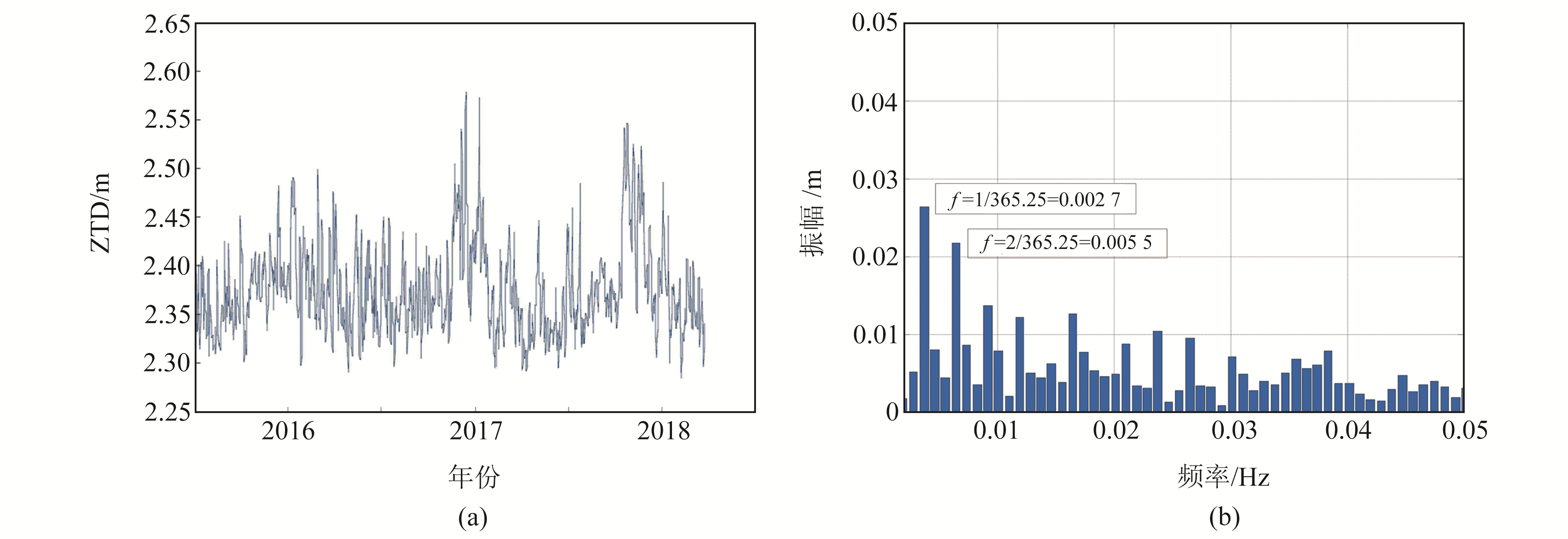
为研究ZTD的时间变化特征,随机选取1个站点(AZU1)2016~2018年的ZTD时间序列进行快速傅里叶变换,图 1为时间序列和对应的频谱图。
|
图 1 AZU1站ZTD时间序列及其频谱图 Fig. 1 ZTD time series and its sequence spectrum of AZU1 station |
从图 1(b)可以看出,AZU1测站ZTD序列含有2个显著频率(0.002 7 Hz和0.005 8 Hz),其对应周期分别为365.25 d和365.25/2 d,表现出明显的年周期和半年周期特性,符合ZTD普遍时间变化规律。因此大部分学者在时间域均采用式(1),即傅里叶级数进行最小二乘拟合:
| $ \begin{aligned} \mathrm{ZTD}(\operatorname{doy}) &=A_0+A_1 \cos \left(2 {\rm{ \mathsf{ π} }} \frac{\mathrm{doy}-\varphi_1}{T_1}\right)+\\ & A_2 \cos \left(2 {\rm{ \mathsf{ π} }} \frac{\mathrm{doy}-\varphi_2}{T_2}\right) \end{aligned} $ | (1) |
式中,T1=365.25,T2=365.25/2,doy为年积日,A0(年均值)、A1(年振幅)、A2(半年振幅)、φ1(年相位)、φ2(半年相位)为待拟合参数。
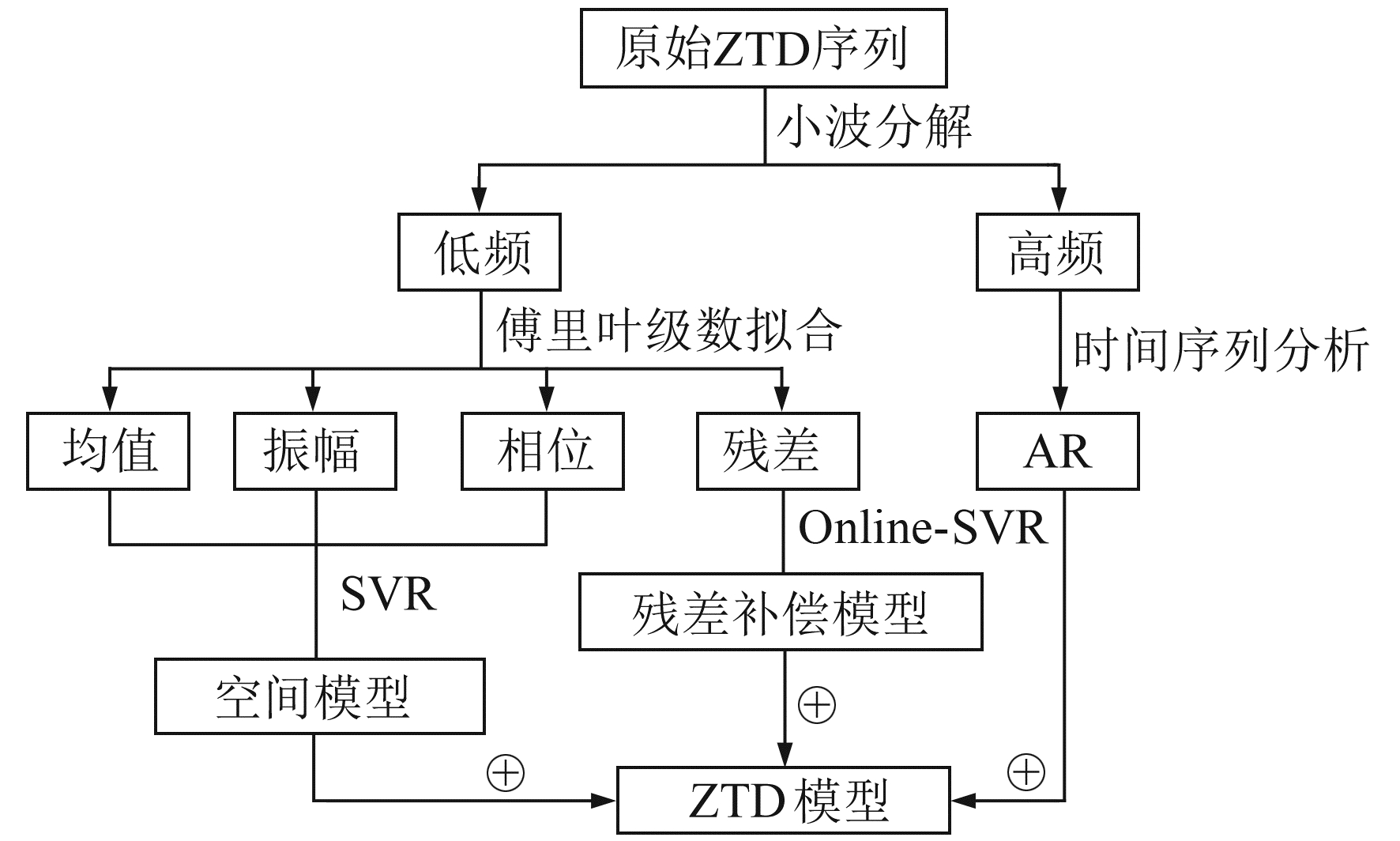
天顶对流层延迟包含ZHD和ZWD(天顶湿延迟),其中ZWD受水汽含量影响变化较为剧烈,导致ZTD整体出现图 1(a)所示的高频振荡特性。若采用式(1)直接拟合ZTD序列,拟合残差较大。文献[6]利用小波分解技术提取ZTD序列的低频部分来研究其变化规律,结果表明ZTD低频序列可反映ZTD序列主变化趋势,但文献未对高频序列进行分析,而该部分包含ZTD细节信息。因此,本文采用AR模型剔除噪声,进一步提取这部分细节信息。对低频序列则直接采用式(1)进行拟合,并对拟合残差采用在线支持向量回归(Online-SVR)建立实时残差补偿模型。另外,ZTD空间变化特性体现在均值A0、振幅(A1、A2)、相位(φ1、φ2)与其空间位置相关,因此建立空间位置向上述5个参数映射的SVR空间模型。本文仅以ZTD建模为例进行说明(ZHD建模方法同ZTD)。组合模型结构如图 2所示,各部分在下文中详细说明。
|
图 2 ZTD组合预报模型框架 Fig. 2 Framework of ZTD combined prediction model |
离散小波变换是用一对共轭的低通和高通滤波器将信号分解成近似值(低频)和细节值(高频)两部分。小波重构为分解的逆过程,可用下式表示:
| $ a_0=a_m+\sum\limits_{i=1}^m d_m $ | (2) |
式中,a0为原始信号,ai、di分别为低频和高频信号。
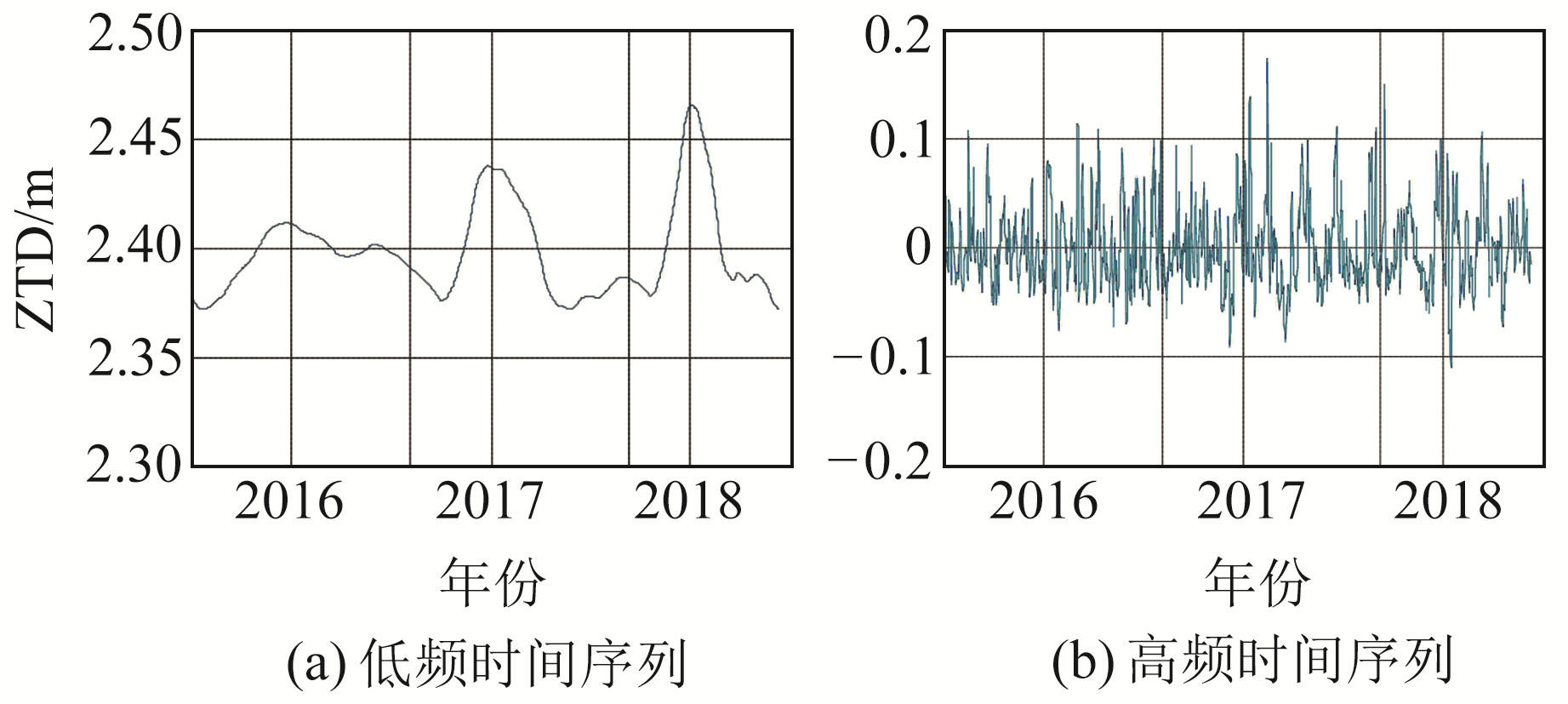
通过实验发现,ZTD序列经db4滤波器6层分解后的低频序列可反映ZTD序列的主要趋势。图 3为小波分解后的AZU1站低频序列和高频序列,从图中可观察到低频序列曲线已变得光滑。
|
图 3 AZU1站ZTD采用db4小波基6层分解后的低频序列和高频序列 Fig. 3 Low-frequency and high-frequency ZTD sequences of AZU1 station generated by 6-layer decomposition with db4 wavelet basis function |
高频序列包含ZTD细节信息,建立AR模型的目的在于过滤白噪声,最大程度提取出ZTD细节信息,AR模型表达式如下:
| $ \begin{gathered} x_t=\varphi_1 x_{t-1}+\varphi_2 x_{t-2}+\cdots+\varphi_n x_{t-n}+ \\ a_t, a_t \sim N\left(0, \sigma_a^2\right) \end{gathered} $ | (3) |
式中,φi(i=1, 2, …, n)为自回归参数,at为白噪声序列。
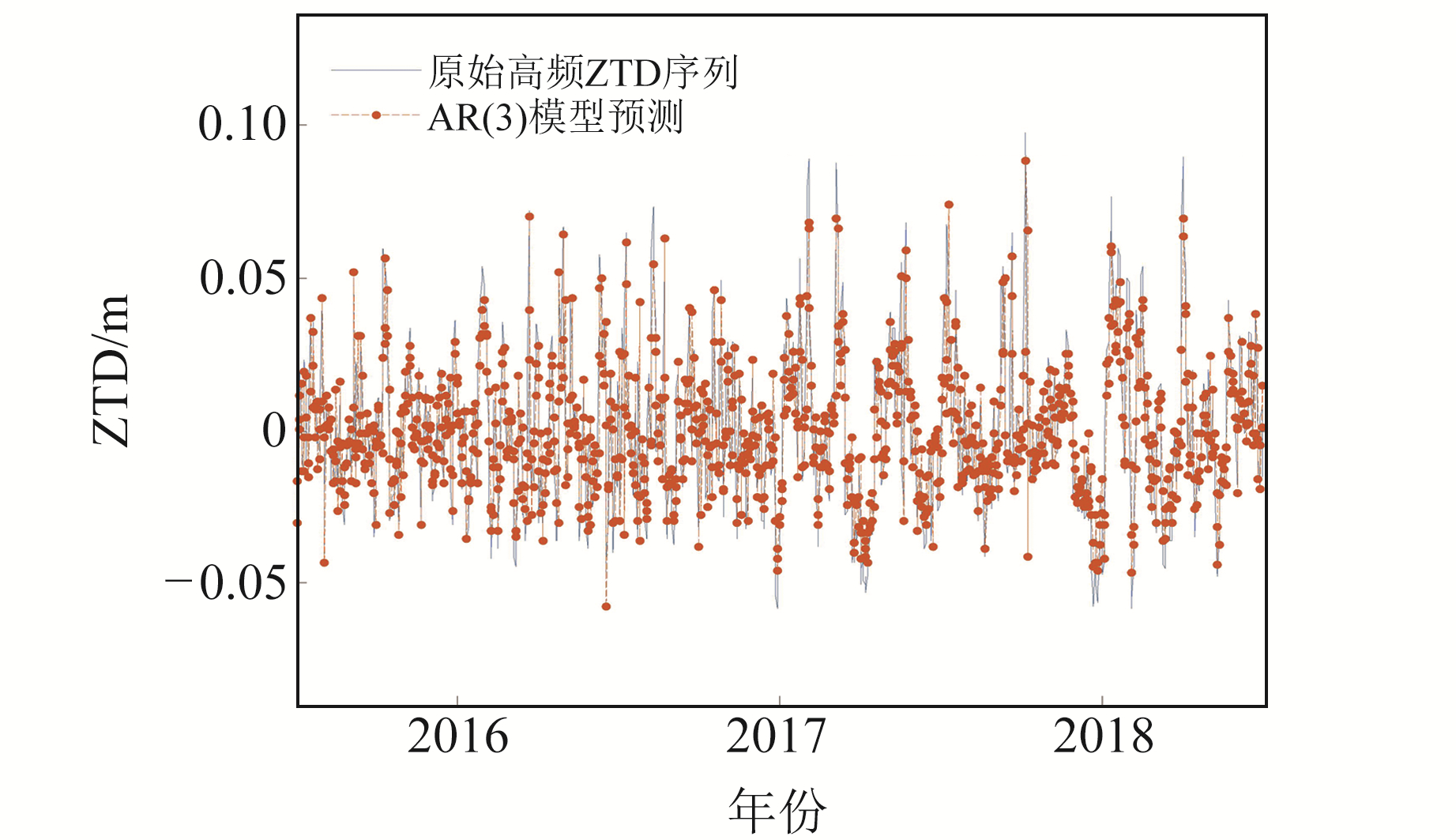
本文选用相关系数函数(ACF)和偏自相关系数函数(PACF)中截尾和拖尾进行模型识别和定阶,具体过程可参考文献[7],经计算可对AUZ1站高频ZTD序列建立3阶AR模型(ACF拖尾,PACF截尾,模型参数为:φ1 =1.145 7,φ2 =-0.560 8,φ3 =0.194 1)。按式(3)进行预测,实测值与预测值对比结果见图 4。选用平均偏差(bias)和均方根误差(RMSE)来检验AR模型预测高频ZTD序列的效果,计算公式如下:
| $ \left\{\begin{array}{l} \text { bias }=\frac{1}{N} \sum\limits_{i=1}^N\left(X_i-X_i^0\right) \\ \mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(X_i-X_i^0\right)^2} \end{array}\right. $ | (4) |
|
图 4 AZU1站高频ZTD AR模型预测值与原始值对比 Fig. 4 Comparison between predicted value obtained by AR model and original value of high frequency ZTD in AZU1 station |
式中,Xi为预报值,Xi0为实测值。
经计算可得bias=0.015 mm,RMSE=0.197 mm,表明预测值与实测值符合较好。结合图 4可以发现,预测值序列仍保留高频振荡特性,说明AR模型可有效提取高频ZTD序列的细节信息。
1.3 空间SVR模型非线性规划的支持向量回归(SVR)问题可以表述为:给定一个训练样本集T={(x1, y1), (x2, y2), …, (xl, yl)}∈(Rn×R)l,其中x∈ Rn为输入指标向量,其分量称为特征,y∈R为输出指标,在特征空间中构造回归函数:
| $ f(x)=\boldsymbol{W}^{\mathrm{T}} {\mathit{\Phi}}(\boldsymbol{x})+b $ | (5) |
式中,W为权向量,Φ(x)为核函数,可将输入向量从Rn映射到Hilbert特征空间,b为偏置,求解带约束的凸二次优化问题可得W、b。
由于ZTD的空间变化特性在于均值、振幅、相位参数与其空间位置相关,统一以纬度B、经度L、大地高H为SVR的输入向量,分别对A0、A1、A2、φ1、φ2参数进行空间回归模型训练。
由SVR算法可知,核函数类型选取以及核参数γ、不敏感损失函数系数ε、惩罚参数C的取值会直接影响SVR的拟合、泛化能力。在进行样本训练时,需要进行参数优化。本文选取高斯径向基核函数,参数寻优方法为PSO(粒子群算法),以k-fold交叉验证误差作为SVR参数选择的目标值,详细算法流程见文献[8]。
1.4 残差补偿模型Online-SVR的基本思想是通过更新回归函数,使加入样本后的新训练集继续满足KKT条件。Online-SVR比SVR样本更新后的训练速度更快,详细算法参照文献[9-10]。
对应一组残差序列{v1, v2, …, vn},Online-SVR残差补偿模型采用的训练样本组成为:
| $ \boldsymbol{T}=\left[\begin{array}{cccc} v_1 & v_2 & \cdots & v_m \\ v_2 & v_3 & \cdots & v_{m+1} \\ \vdots & \vdots & \cdots & \vdots \\ v_{n-m} & v_{n-m+1} & \cdots & v_{n-1} \end{array}\right]\left[\begin{array}{c} v_{m+1} \\ v_{m+2} \\ \vdots \\ v_n \end{array}\right] $ | (6) |
式中,左边矩阵为输入向量,右边矩阵为输出向量。即建立滑动时间窗口{vt-1, vt-2, …, vt-m}与vt之间的映射关系f: Rm→R。将一维时间序列转化成矩阵形式获得数据间的关联关系,以挖掘到尽可能多的信息量,也称为相空间重构。式中m为嵌入维数,可反映转换后矩阵蕴涵的知识量[11]。
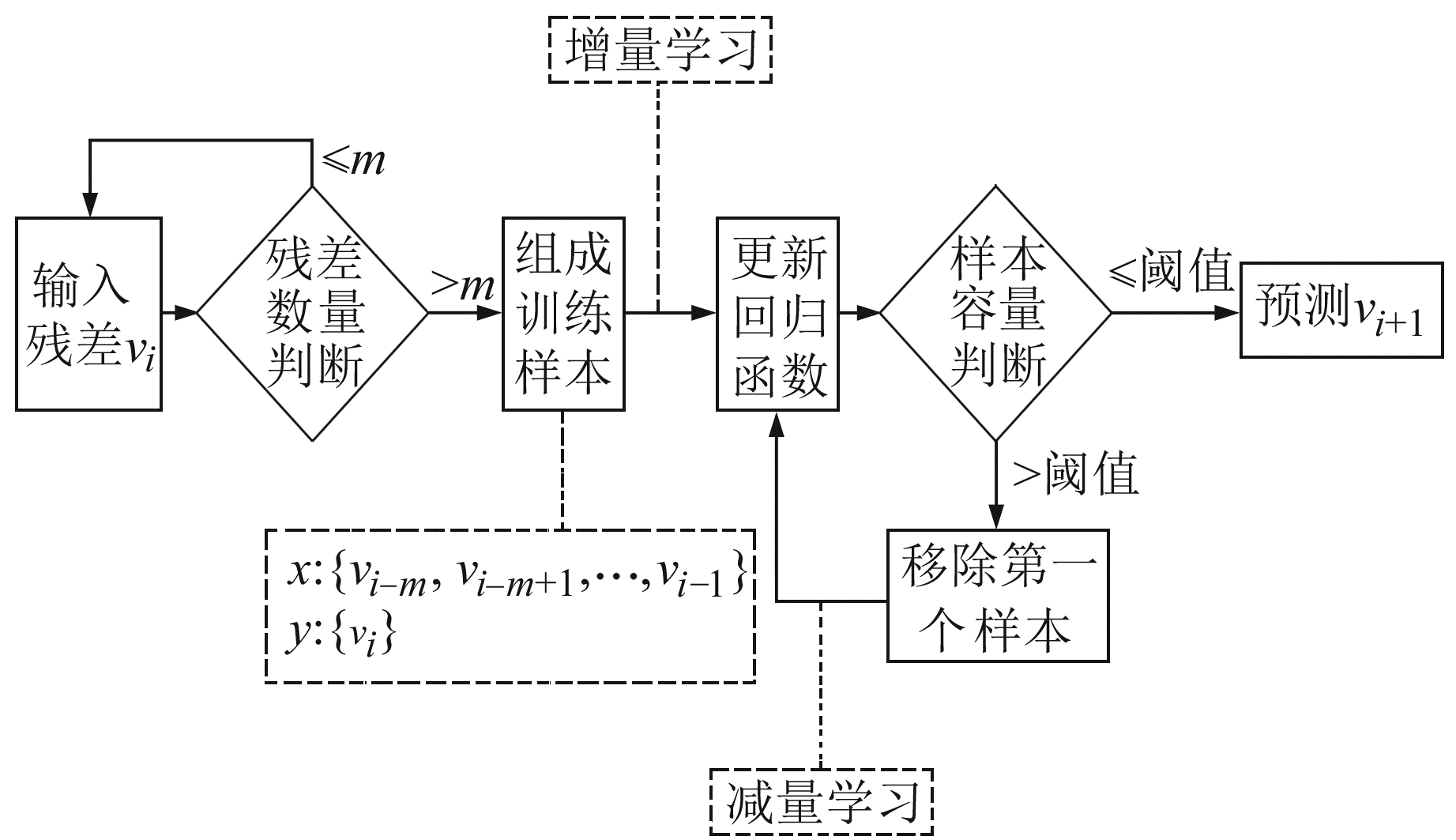
本文采用贝叶斯信息准则(BIC)来确定维数m。由于样本不断更新,为提高计算效率,采用文献[12]中的方法快速确定C、γ、ε(相关公式及参数详见参考文献)。为提高Online-SVR残差补偿模型的训练速度,保证训练样本之间的相关性,样本容量不宜过大。本文初步确定样本容量阈值为10,当达到阈值后,每加入1个新样本,就需要移除最早时刻的1个样本。Online-SVR残差补偿模型预报流程如图 5所示。
|
图 5 Online-SVR残差补偿模型预报流程 Fig. 5 Prediction process of online-SVR residual compensation model |
采用2016~2017年ZTD和ZHD序列数据进行建模,以2018年ZTD和ZHD序列为真值进行预报精度检验,模型精度评价指标选用bias和RMSE。由于建模采用多个GNSS基站数据,ZTD/ZHD预报模型的AR阶数和残差补偿模型的嵌入维数采用建模站点的平均值序列进行计算。表 1为最后确定的ZTD/ZHD模型参数。
|
|
表 1 模型参数设置 Tab. 1 Model parameters setting |
根据建立的区域对流层延迟预报模型可计算区域内任意位置对应某个年积日的ZTD/ZHD,计算流程如下:
1) 输入B、L、H,由空间SVR模型计算A0、A1、A2、φ1、φ2;
2) 输入doy,按式(1)计算ZTD/ZHD初始值;
3) 残差补偿模型补偿ZTD/ZHD初始值;
4) 按式(2)叠加AR模型预报的高频ZTD/ZHD值;
5) 输出ZTD/ZHD最终预报值。
任意位置步骤3)、4)数值可由周边一定数量建模站点的预报值反距离加权内插得到。
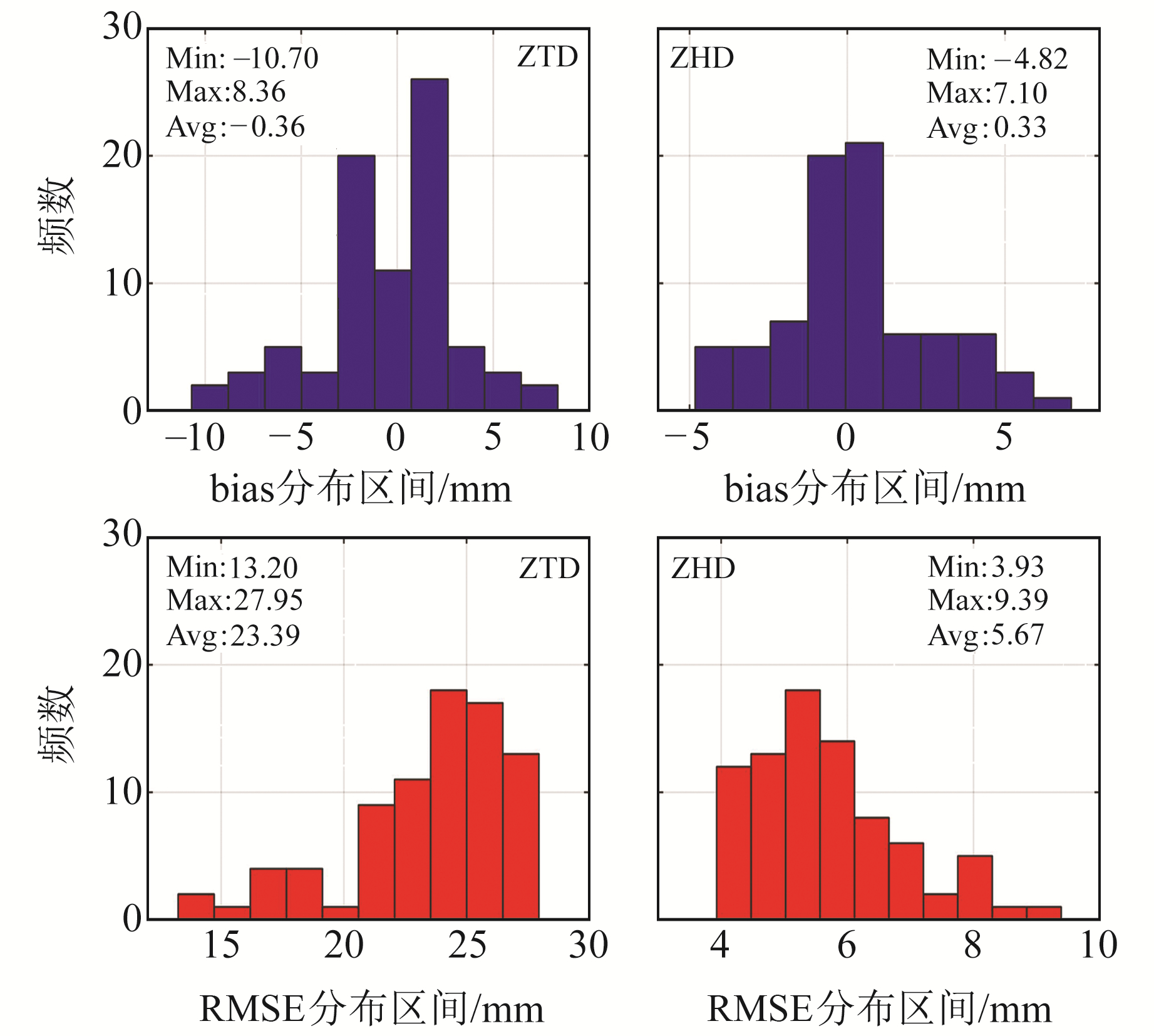
2.1 内符合精度检验从建模站点中挑选观测数据较完整的80个基站2018年的ZTD/ZHD值与模型预报值进行对比,检验模型的可靠程度。内符合精度统计如图 6所示。
|
图 6 建模站点ZTD/ZHD内符合检验精度统计 Fig. 6 Statistics of internal coincidence accuracy of ZTD/ZHD of modeling stations |
统计数据表明,ZHD和ZTD的平均bias均为0.3 mm左右,RMSE分别为5.67 mm和2.34 cm。模型预报ZTD精度较ZHD低,原因在于ZTD包含变化相对更剧烈的ZWD。但总体上模型内符合程度较好。
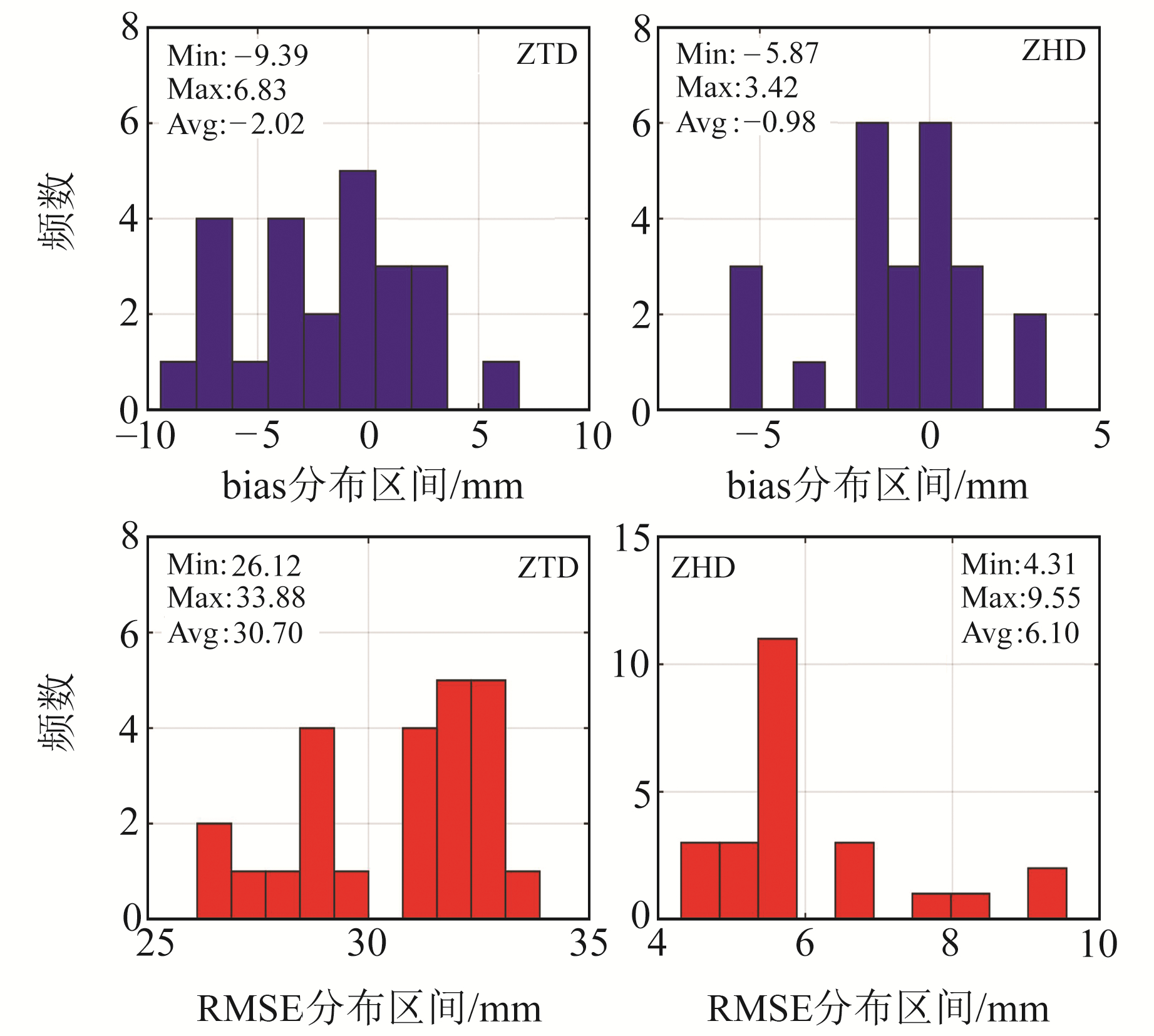
2.2 外符合精度检验将24个测站2018年的ZTD/ZHD值与模型预测值进行对比,测试模型的适用性(泛化能力)。图 7为模型外符合精度,从图中可以看出,外符合精度稍低于内符合精度(mm级差别),说明模型泛化能力好。此外,ZTD和ZHD的RMSE最大、最小值相差较小,表明模型在区域内的预报精度较均匀。
|
图 7 测站ZTD/ZHD外符合检验精度统计 Fig. 7 Statistics of external coincidence accuracy of ZTD/ZHD |
本文将该模型应用到伪距单点定位中,通过分析模型对定位结果产生的影响来检验模型预测ZTD/ZHD的可靠性。实验数据为测站(BRIB、FARB、MASW、MLFP、OHLN)2018-01-22全天的原始观测值。对流层延迟分别采用模型预报值改正和不加改正两种模式。
3.1 伪距单点定位解算策略观测值为无电离层组合伪距(削弱电离层延迟),截止高度角取15°,采用精密星历,对流层延迟映射函数为VMF1。为尽可能削弱其他误差对定位结果的影响,本文实验还进行地球自转改正、卫星天线相位中心改正、相位缠绕改正和DCB补偿。
3.2 伪距单点定位结果分析两种模式下伪距单点定位在N、E、U方向的偏差如表 2所示。经模型ZTD预测值改正后U方向的定位偏差从6~8 m缩小至dm级,同文献[13]中对流层延迟对单点定位U方向影响最大(可达7~15 m)的结论一致。另外,本实验取截止高度角15°使得低高度角卫星不参与解算,对流层延迟对平面定位结果的影响会进一步降低。因此改正后N、E方向的偏差与不改正模式差别较小。
|
|
表 2 两种模式下伪距单点定位N、E、U方向偏差对比 Tab. 2 Comparison of deviation in N, E and U directions of pseudorange single point positioning of two models |
表 3为两种模式下伪距单点定位在N、E、U三个方向的中误差。从表中可以看出,二者基本保持一致,说明本文所建的组合模型在对伪距观测值的对流层延迟进行有效改正时,未引入多余噪声而降低单点定位精度。
|
|
表 3 两种模式下伪距单点定位N、E、U方向中误差对比 Tab. 3 Comparison of mean square error of pseudorange single point positioning in N, E and U directions of two models |
本文提出一种结合小波变换、傅里叶级数拟合、AR和SVR的对流层延迟建模新方法,选用NOAA CORS网在加州境内的94个GNSS基站2016~2017年数据建立区域ZTD/ZHD数值预报模型,并对模型内、外符合精度进行检验。总体来说,预报模型内、外符合精度相差较小,表现出较好的泛化性能。
分析组合模型结构可以看出,该模型包含函数和预测两部分,使得模型预测值既符合ZTD/ZHD变化趋势又可保留部分细节变化属性,能更好地描述ZTD/ZHD的时空变化特征。24个测站1 a的ZTD/ZHD预测结果表明,平均bias为-2.02 mm/-0.98 mm,RMSE为3.07 cm/6.10 mm,精度优于现有的大部分区域对流层延迟模型。将该模型应用到伪距单点定位中可取得较好的对流层延迟改正效果,可显著提高单点定位U方向精度。
综上所述,该组合模型具有较高的预报精度和可靠性,在GNSS领域具有一定的应用价值。
致谢: 感谢NOAA CORS提供的部分GNSS基站观测数据。
| [1] |
赵静旸, 时爽爽. 对流层天顶延迟模型研究进展及其在中国区域的精度分析[J]. 地球物理学进展, 2018, 33(1): 148-155 (Zhao Jingyang, Shi Shuangshuang. Research Progress of Zenith Tropospheric Delay Model and Its Accuracy Analysis over China[J]. Progress in Geophysics, 2018, 33(1): 148-155)
(  0) 0) |
| [2] |
夏晓明. 无气象参数的对流层延迟改正模型研究[D]. 南京: 东南大学, 2017 (Xia Xiaoming. Research on Tropospheric Delay Correction Model without Meteorological Parameters[D]. Nanjing: Southeast University, 2017)
(  0) 0) |
| [3] |
黄良珂, 刘立龙, 姚朝龙, 等. 基于区域CORS网精密天顶对流层延迟建模方法研究[J]. 大地测量与地球动力学, 2013, 33(6): 141-144 (Huang Liangke, Liu Lilong, Yao Chaolong, et al. Modeling for Precise Zenith Tropospheric Delay Based on Regional CORS Network[J]. Journal of Geodesy and Geodynamics, 2013, 33(6): 141-144)
(  0) 0) |
| [4] |
戴吾蛟, 赵岩. 区域对流层干湿延迟建模[J]. 大地测量与地球动力学, 2013, 33(2): 72-76 (Dai Wujiao, Zhao Yan. Modeling the Dry and Wet Component of Regional Ropospheric Delay[J]. Journal of Geodesy and Geodynamics, 2013, 33(2): 72-76)
(  0) 0) |
| [5] |
李国平. 地基GPS气象学[M]. 北京: 科学出版社, 2010 (Li Guoping. Ground-Based GPS Meteorology[M]. Beijing: Science Press, 2010)
(  0) 0) |
| [6] |
杨晶, 顾慧, 刘严萍, 等. 基于小波分析的GPS对流层延迟变化研究[J]. 测绘通报, 2015(5): 60-62 (Yang Jing, Gu Hui, Liu Yanping, et al. Study on GPS Tropospheric Delay Variation Based on Wavelet Analysis[J]. Bulletin of Surveying and Mapping, 2015(5): 60-62)
(  0) 0) |
| [7] |
黄声享, 尹晖, 蒋征. 变形监测数据处理[M]. 武汉: 武汉大学出版社, 2003 (Huang Shengxiang, Yin Hui, Jiang Zheng. Deformation Monitoring Data Processing[M]. Wuhan: Wuhan University Press, 2003)
(  0) 0) |
| [8] |
邵信光, 杨慧中, 陈刚. 基于粒子群优化算法的支持向量机参数选择及其应用[J]. 控制理论与应用, 2006, 23(5): 740-743 (Shao Xinguang, Yang Huizhong, Chen Gang. Parameters Selection and Application of Support Vector Machines Based on Particle Swarm Optimization Algorithm[J]. Control Theory and Applications, 2006, 23(5): 740-743 DOI:10.3969/j.issn.1000-8152.2006.05.014)
(  0) 0) |
| [9] |
Ma J S, Theiler J, Perkins S. Accurate On-Line Support Vector Regression[J]. Neural Computation, 2003, 15(11): 2 683-2 703 DOI:10.1162/089976603322385117
(  0) 0) |
| [10] |
Parrella F. Online Support Vector Regression[D]. Genoa: University of Genoa, 2007
(  0) 0) |
| [11] |
尉询楷, 李应红, 张朴, 等. 基于支持向量机的时间序列预测模型分析与应用[J]. 系统工程与电子技术, 2005, 27(3): 529-532 (Wei Xunkai, Li Yinghong, Zhang Pu, et al. Analysis and Applications of Time Series Forecasting Model via Support Vector Machines[J]. Systems Engineering and Electronics, 2005, 27(3): 529-532)
(  0) 0) |
| [12] |
Cherkassky V, Ma Y Q. Practical Selection of SVM Parameters and Noise Estimation for SVM Regression[J]. Neural Networks, 2004, 17(1): 113-126
(  0) 0) |
| [13] |
王瑾芳, 杨玲. 对流层延迟对GNSS单点定位影响的全球评估[J]. 大地测量与地球动力学, 2020, 40(11): 1 194-1 199 (Wang Jinfang, Yang Ling. Global Assessment on GNSS Single Point Positioning Accuracy Impacted by Tropospheric Delay[J]. Journal of Geodesy and Geodynamics, 2020, 40(11): 1 194-1 199)
(  0) 0) |
2. State Key Laboratory of Earthquake Dynamics, Institute of Geology, CEA, A1 Huayanli, Beijing 100029, China
 2022, Vol. 42
2022, Vol. 42


