行星历表广泛应用于航天器导航、对行星及其卫星等的空间观测、天文年历编制、地球物理及引力理论验证等领域[1]。目前行星和月球历表编制主要有分析与半分析法及数值积分法两大类[2],分析与半分析历表主要有法国巴黎天文台VSOP系列历表,数值历表主要有美国喷气推进实验室(JPL)发布的DE系列历表[1, 3]、欧空局(ESA)支持编制的INPOP历表[4]以及俄罗斯应用天文研究所发布的EPM系列历表[5]。我国紫金山天文台也自行编制了PMOE系列历表,但目前其精度不及上述高精度历表[6-8]。
DE系列历表发展于20世纪60年代,是以运动方程的数值积分为基础推出的历表[9],在国际上广泛应用。DE系列历表中比较著名的有1984年以来广泛使用的DE200、国际地球自转与参考系服务(IERS)在2003、2010规范中推荐的DE405以及DE421历表。DE405可被用于天体视位置计算,DE421历表中月球天平动角可被用于GRAIL任务中月心惯性系和月固系间的坐标转换。目前使用比较广泛的为DE430,于2013-04发布,时间跨度为1550~2650年,采用IAU1980章动模型,包含月球天平动[10],曾被用于天体物理学研究。目前最新版本为DE440和DE441,后者假定月球液体核和固体幔间无阻尼,时间跨度更长[11]。
由于观测数据和动力学模型不同,DE系列模型的精度存在差异。本文以DE405、DE421、DE430、DE440为例给出不同行星历表拟合深空数据适用范围的差异,同时比较不同历表中大行星在地心惯性系及太阳系质心惯性系中的位置差异,最后分析各历表用于月球月固系和惯性坐标系间坐标和速度转换的精度。
1 基本行星历表近年来,随着科学技术的不断提升以及深空探测任务的不断增多,行星历表的更新也越来越频繁,从而出现很多为特定飞行任务服务的临时星历。观测数据的增多也使得历表精度不断提高。
DE405[12]星历对内部坐标系指向进行改进,主要通过对绕金星的麦哲伦号探测器进行甚长基线干涉(very long baseline interferometry,VLBI)观测,使其指向国际天球参考框架(ICRF),整体精度为1 mas,距离相当于1 km。DE421[13]星历中动力学参考框架同ICRF的对准由包括火星侦察轨道器MRO、火星奥德赛(ODY)、火星全球探测者MGS在内的火星探测器VLBI测量完成,精度为0.25 mas[1]。DE430星历通过对火星轨道航天器进行VLBI观测来实现内部行星轨道与ICRF2的对准,精度为0.2 mas[10]。DE440星历通过VLBI测量火星轨道航天器相对于ICRF中位置已知的类星体来实现同ICRF3的对准,整体精度为0.2 mas[11]。DE440星历和DE430星历相比,主要有以下改进:Lense-Thirring效应、柯伊伯带(Kuiper belt)新模型、Vondrak岁差模型、考虑地心进动对月球轨道的影响、考虑太阳辐射压对地月系统轨道的影响、内部行星动力学框架同ICRF的连接由ICRF2[14]变为ICRF3[15]、2013~2020年新的航天器和LLR数据。
2 拟合行星历表的高精度观测数据拟合行星历表采用的观测资料主要包括行星的光学观测、地面雷达测距、行星探测器测量以及激光测月4类数据。自DE102星历以来,DE系列历表已拟合越来越多的深空探测器测量数据,数据类型覆盖更全面,同时动力学模型也不断精化,这都有利于历表精度的提高。考虑到历表使用的广泛性及国际标准性,本文选取4个星历,对比其月球、火星、木星轨道拟合使用的观测数据。具体来讲,相比于DE405,DE421放弃使用部分天文观测数据,数据时间跨度增长、航天器观测数据增多。DE430剔除了DE421中部分精度较低的观测数据,同时使用更高精度的数据,通过信使号的距离测量以及2008~2009年3次飞掠的无线电跟踪测量来改进水星轨道;对卡西尼(Cassini)探测器进行VLBI测量以及测距使得土星轨道精度有所提升。DE430中探测器观测数据时间跨度的增加也可提升金星、地球和火星轨道精度。相比于DE430,DE440拟合朱诺号(Juno)探测器无线电测距和超长基线阵列(VLBA)测量,使得木星轨道显著提升。得益于卡西尼探测器的VLBA测量,土星轨道也有所改进。7 a跨度的新数据使得月球、金星、水星、火星轨道精度均有所提升。利用高精度观测数据得到行星位置和速度的过程,实际上是动力学法确定行星状态矢量及其他参数的过程。在建立DE历表时,考虑的因素主要有星体的点质量、非球形引力场的影响、地球潮汐对月球加速度的影响、月球天平动、相对论加速度以及太阳辐射压等。对于动力学模型,4种历表均基于参数化后牛顿N体引力模型进行数值积分(PPN-EIH)。DE421、DE430、DE440模型中所有参数个数均为228个,DE405为156个。对于太阳系中的小行星,DE440除包含DE421和DE430中考虑的谷神星的牛顿力以及342颗主带小行星外,还包含30颗柯伊伯带星体,其余的柯伊伯带星体被当作一个环。
3 行星历表比较 3.1 不同历表大行星位置比较在进行深空探测过程中,对探测器进行观测的射电或光学望远镜多位于地球,观测数据具有显著的地基属性,数据处理也需要使用地心天球坐标系。作为基本空间参考系之一,太阳系质心天球坐标系也常用于深空探测。因此,比较不同星历间大行星相对于太阳系质心及地心的位置分量差异对于深空探测及导航等具有重要意义。本文计算4个不同历表间大行星(包括太阳、冥王星、月球)在太阳系质心以及地心惯性系中位置差异的最大值(max)及均方根(RMS),数据时间跨度为1960~2020年,时间间隔为1 d,结果见表 1和表 2(单位km)。本文精度分析均以DE440星历作为参考,将DE405、DE421、DE430与之作差。Park等[11]给出DE440星历中各天体的部分观测数据残差以表征星历精度,如月球轨道的LLR数据残差为20 cm(早期)和1.3 cm(近期),水星轨道的Messenger测距残差为0.7 m,金星、火星、木星、土星的观测数据残差分别为8 m、0.7 m、13 m、3 m。Folkner等[10]也基于各种观测数据的残差对DE430星历精度进行分析。但需要注意的是,上述精度结果应乘以2倍尺度因子来合理评估轨道变化[16]。尽管本文的差值并不能代表历表用于测量行星位置的绝对误差,但在一定程度上可以反映历表的相对精度。
|
|
表 1 1960~2020年大行星相对地心位置差异的最大值max和均方根RMS Tab. 1 Max and RMS of the position difference of the major planets relative to geocenter from 1960 to 2020 |
|
|
表 2 1960~2020年大行星相对太阳系质心位置差异的最大值max和均方根RMS Tab. 2 Max and RMS of the position difference of the major planets relative to the mass center of the solar system from 1960 to 2020 |
由表 1可知,月球在所有天体中位置精度最高,DE421和DE430星历精度为1~2 m,DE405历表精度略差,为7 m。月球历表的高精度得益于月球LLR测量数据的大体量和高精度。对于太阳、水星、金星、火星,DE405历表精度均在103 m量级,DE421和DE430历表精度在102 m量级(DE421星历中水星位置精度为2 km除外),可提高一个数量级。其中,除金星外,DE430相对于DE421在精度上至少可提高50%,这是因为水星、火星的航天器测量数据时间跨度变长以及观测精度提高。对于木星和土星,DE405历表精度在105 m量级,比DE421和DE430历表精度高1~2个量级。其中,DE430历表精度相对于DE421依然有50%的提高。由于卡西尼号测量,土星轨道精度比木星轨道精度高。天王星、海王星历表精度从DE405的106 m量级提高到DE421和DE430的105 m量级。对于冥王星,DE405和DE421历表精度均在106 m量级,DE430历表精度有一个量级的提高。天王星、海王星和冥王星的轨道主要由天文测量观测确定,受制于地球大气测量以及恒星目录的不确定性,DE430之前位置精度均限制在105~106 m量级。
由表 2可知,相对于太阳系质心的位置偏差,地球、水星、金星和火星的DE405、DE421和DE430同DE440历表的差异均为数10 km到100 km,而DE405、DE421和DE430之间的差异在数km。以金星为例,时间跨度为1960~2020年,步长为1 d,结果如图 1所示。这是由于DE440历表在计算太阳系质心时加入了30个柯伊伯带星体(KBOs)的扰动,同时将其他柯伊伯带星体当作一个圆环,其结果与DE430历表相比,太阳系质心移动100 km左右。天王星、冥王星和海王星相对于太阳系质心的位置差异随着新星历的发布也越来越小。

|
图 1 不同历表间金星相对于太阳系质心的位置差异 Fig. 1 The position difference of Venus relative to the mass center of solar system based on different ephemerides |
DE405与其他星历的差距明显,可能由于DE405、DE421、DE430、DE440均采用参数化后牛顿N体运动方程描述太阳系天体运动,其中DE405仅包含156个参数,而DE421、DE430、DE440均包含228个参数。
3.2 不同历表中月球相对于地心的位置差异月球是地球唯一的天然卫星,同时也是离地球最近的天体,月球超高真空、无磁场的环境可为科学研究提供良好条件,因此月球探测一直是深空探测的重要部分。随着激光测月数据量的增多,月球轨道的测量精度越来越高。同时,随着探月任务的发展,对月球探测器位置的精度要求也越来越高。设一个绕月探测器的地心位置矢量为rES,月心位置矢量为rLS,月球的地心位置矢量为rEL,则存在以下关系式:
| $ \boldsymbol{r}_{\mathrm{ES}}=\boldsymbol{r}_{\mathrm{EL}}+\boldsymbol{r}_{\mathrm{LS}} $ | (1) |
由式(1)可知,历表造成的月球地心惯性系下的位置和速度差异会影响绕月探测器在地心惯性系下的位置和速度。本文基于不同星历计算和比较月球在地心天球坐标系下的位置及速度差异,分析其对绕月探测器的位置影响。
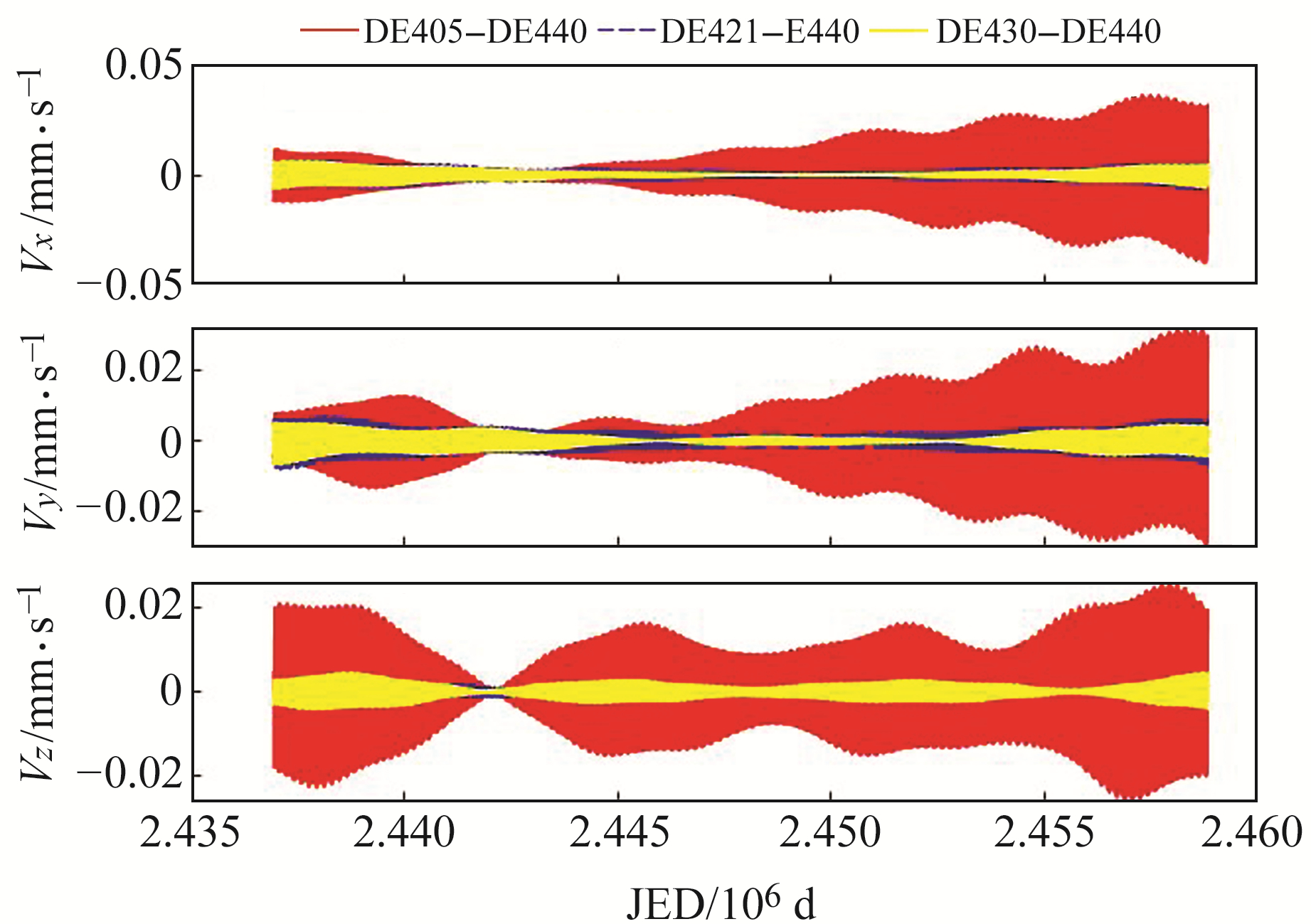
基于不同历表计算1960~2020年月球在J2000.0地心天球坐标系下的位置和速度,以DE440结果为参考值,研究其他不同历表(DE405、DE421、DE430)引起的月球在地心天球坐标系下的位置和速度误差,结果如图 2、3所示。由图可知,DE405位置矢量误差为7 m,DE421和DE430误差分别为1.5 m、1.3 m。DE405速度误差在0.02 mm/s左右,DE421和DE430速度误差在0.005 mm/s以内。DE430在X和Y方向的位置误差均值比DE421小0.25 m左右。可以发现,相比于DE405历表,DE421和DE430的误差明显减小,这是因为DE421比DE405所用数据跨度更长、精度更高。相比于DE421历表,DE430历表使用了更高精度的重力场数据以及更长跨度的LLR数据。在DE430基础上,DE440历表又使用7 a的LLR数据,同时LLR测距数据的残差为1.3 cm,较DE430有所提升。因此,在绕月探测任务中,若要求探测器位置精度在亚米级,则需要采用DE421和DE430,甚至DE440星历。

|
图 2 不同历表间月球的地球质心位置差异 Fig. 2 The position difference of Moon relative to the mass center of Earth based on different ephemerides |
|
图 3 不同历表间月球的地球质心速度差异 Fig. 3 The velocity difference of Moon relative to the mass center of Earth based on different ephemerides |
在月球参考系中建立运动方程时,通常选择月心惯性系,而月球非球形引力作为最主要的摄动力,在月固系下通常采用球谐函数展开形式来表示,因此需要进行月固系与月心惯性系间的转换,以建立环月探测器的运动方程。JPL中定义的月固坐标系原点在月球质心,3个轴由月球的3个惯性主轴确定。本文提及的4个历表中均已给出月球天平动,月球天平动的3个欧拉角可以用来实现从月心惯性坐标系到月固坐标系的转换,具体转换过程可参考文献[17]。
本文利用美国国家航空航天局(NASA)提供的重力恢复数据和内部结构实验室GRAIL的Level 1B数据研究星历对月固系坐标的影响。其中,GNI1B数据为GRAIL A/B探测器的月心惯性系坐标。选取2012-03-20的GRAIL B探测器GNI1B数据,将其转换为月固坐标系坐标,时间间隔为1 min。将基于不同行星历表得到的月固系位置与速度矢量分别同DE440历表转换得到的结果作差,并将差值视为利用不同历表进行坐标转换时的位置和速度矢量误差,结果见表 3。由表可知,对于位置矢量,DE405历表误差高达30 m,均值偏离也达m级,DE421和DE430历表误差分别为1.3 m、1 m,两者均值也较小,为cm级;对于速度矢量,DE405历表误差为3 cm/s,DE421历表误差为1.2 mm/s,DE430历表误差为0.9 mm/s。DE405在Y方向精度最差,而DE421在Y方向精度最好,甚至比DE430精度略高,但DE430历表在Z方向精度有较大提高。综上可知,在进行月球探测器定轨及其他涉及月球坐标系转换任务时,当精度要求在m级时,不建议使用DE405历表。若要求导航精度在亚米级别时,需要选用较新的DE430或DE440历表。
|
|
表 3 利用不同历表进行坐标及速度转换时误差最大值、均值及RMS Tab. 3 The maximum values, average values and RMS of the position and velocity conversion error based on different ephemerides |
本文选取DE405、DE421、DE430、DE440星历计算大行星相对于地球及太阳系质心位置,分析各大行星的星历位置精度。对于地心位置,由于受观测数据等因素影响,各大行星的位置精度不同,从最高的月球m级精度,到太阳、水星、金星和火星的103 m级精度,到木星、土星的105 m量级,到天王星、海王星和冥王星的106 m量级。总体而言,DE421和DE430星历相对DE405在行星位置精度方面有1~2个量级的提高,DE430星历精度相对DE421提高50%。对于太阳系质心位置,DE440历表由于加入30个柯伊伯带星体的扰动,和其他3个历表存在几百到几千km量级的差异。同时,针对我国正在进行的“嫦娥”系列探月工程以及其他月球科学任务,比较不同历表对于月球地心位置以及月固和月惯坐标系间转换的影响。对于月球地心位置和速度,DE405历表精度为7 m和0.02 mm/s,DE421历表精度约为1.5 m和0.004 mm/s,DE430历表精度为1.3 m和0.003 5 mm/s。利用DE405历表进行坐标转换时位置和速度误差高达30 m和3 cm/s,DE421和DE430历表位置和速度误差分别为1.3 m、1.2 mm/s和1 m、0.9 mm/s。因此对于高精度的探月导航及科学研究,推荐使用高精度的DE430或DE440历表。
随着我国“嫦娥”计划的持续推进,以及地月激光测距技术的提升,将提供类型更多、精度更高的测月数据,有利于我国建立自主的月球历表,也可为我国开展月基观测及导航奠定基础。
| [1] |
邓雪梅, 樊敏, 谢懿. JPL行星历表的比较及评估[J]. 天文学报, 2013, 54(6): 550-561 (Deng Xuemei, Fan Min, Xie Yi. Comparisons and Evaluations of JPL Ephemerides[J]. Acta Astronomica Sinica, 2013, 54(6): 550-561 DOI:10.3969/j.issn.0001-5245.2013.06.005)
(  0) 0) |
| [2] |
金文敬. 太阳系行星和月球历表的发展[J]. 天文学进展, 2015, 33(1): 103-121 (Jin Wenjing. Development of Planetary and Lunar Ephemeris in the Solar System[J]. Progress in Astronomy, 2015, 33(1): 103-121 DOI:10.3969/j.issn.1000-8349.2015.01.06)
(  0) 0) |
| [3] |
杨永章, 李金岭, 平劲松, 等. NASA历表在深空导航中的发展和比较[J]. 深空探测学报, 2017, 4(1): 89-98 (Yang Yongzhang, Li Jinling, Ping Jinsong, et al. Development and Comparison of the JPL Ephemerides in Deep Space Exploration[J]. Journal of Deep Space Exploration, 2017, 4(1): 89-98)
(  0) 0) |
| [4] |
Fienga A, Laskar J, Kuchynka P, et al. The INPOP10a Planetary Ephemeris and Its Applications in Fundamental Physics[J]. Celestial Mechanics and Dynamical Astronomy, 2011, 111(3): 363-385 DOI:10.1007/s10569-011-9377-8
(  0) 0) |
| [5] |
Vasilyev M V, Yagudina E I. 俄罗斯应用天文研究所月球历表研究现状[J]. 深空探测学报, 2014, 1(3): 187-191 (Vasilyev M V, Yagudina E I. Current State and Prospects of Lunar Ephemeris in IAA RAS[J]. Journal of Deep Space Exploration, 2014, 1(3): 187-191)
(  0) 0) |
| [6] |
李广宇, 倪维斗, 田兰兰. PMOE2003精密行星历表框架(Ⅰ)数学模型[J]. 紫金山天文台台刊, 2003, 22(3/4): 12-30 (Li Guangyu, Ni Weidou, Tian Lanlan. PMOE2003 Planetary Ephemeris Framework(Ⅰ) Mathematical Model[J]. Publications of Purple Mountain Observatory, 2003, 22(3/4): 12-30)
(  0) 0) |
| [7] |
李广宇, 田兰兰. PMOE2003精密行星历表框架(Ⅱ)积分器和程序设计[J]. 紫金山天文台台刊, 2003, 22(3/4): 32-56 (Li Guangyu, Tian Lanlan. PMOE2003 Planetary Ephemeris Framework(Ⅱ) Integrators and Programs[J]. Publications of Purple Mountain Observatory, 2003, 22(3/4): 32-56)
(  0) 0) |
| [8] |
李广宇, 田兰兰. PMOE2003行星历表框架(Ⅴ)历表文件的生成和使用[J]. 紫金山天文台台刊, 2004, 23(1-4): 160-170 (Li Guangyu, Tian Lanlan. PMOE2003 Planetary Ephemeris Framework(Ⅴ) Creating and Using of Ephemeris Files[J]. Publications of Purple Mountain Observatory, 2004, 23(1-4): 160-170)
(  0) 0) |
| [9] |
Newhall X X, Standish E M, Williams J G. DE 102: A Numerically Integrated Ephemeris of the Moon and Planets Spanning Forty-Four Centuries[J]. Astronomy and Astrophysics, 1983, 125(1): 150-167
(  0) 0) |
| [10] |
Folkner W M, Williams J G, Boggs D H, et al. The Planetary and Lunar Ephemerides DE430 and DE431[J]. Interplanetary Network Progress Report, 2014, 196
(  0) 0) |
| [11] |
Park R S, Folkner W M, Williams J G, et al. The JPL Planetary and Lunar Ephemerides DE440 and DE441[J]. The Astronomical Journal, 2021, 161(3)
(  0) 0) |
| [12] |
Standish E M. JPL Planetary and Lunar Ephemerides DE405/LE405[R]. Pasadena: JPL, 1998
(  0) 0) |
| [13] |
Folkner W M, Williams J G, Boggs D H. The Planetary and Lunar Ephemeris DE421[J]. Interplanetary Network Progress Report, 2009, 178
(  0) 0) |
| [14] |
Fey A L, Gordon D, Jacobs C S, et al. The Second Realization of the International Celestial Reference Frame by Very Long Baseline Interferometry[J]. The Astronomical Journal, 2015, 150(2)
(  0) 0) |
| [15] |
Charlot P, Jacobs C S, Gordon D, et al. The Third Realization of the International Celestial Reference Frame by Very Long Baseline Interferometry[J]. Astronomy and Astrophysics, 2020, 644
(  0) 0) |
| [16] |
Folkner W M. Uncertainties in the JPL Planetary Ephemeris[C]. Proceedings of the Journées, Paris, 2010
(  0) 0) |
| [17] |
马高峰. 地-月参考系及其转换研究[D]. 郑州: 信息工程大学, 2005 (Ma Gaofeng. Research on Earth-Moon Reference System and Its Transformation[D]. Zhengzhou: Information Engineering University, 2005)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


