2. 九江学院电子工程学院,江西省九江市前进东路551号,332005
在全球导航卫星系统GNSS中,星载原子钟的钟差预报在维持卫星导航系统时间同步、优化导航电文钟差参数、满足实时动态精密单点定位需求、提供卫星自主导航所需的先验信息等方面具有重要意义[1]。灰色模型以其表达式简单、所需建模数据较少等优势在钟差预报中发挥着重要作用[2-3]。单变量一阶微分模型GM(1, 1)是灰色模型的重要组成部分,被广泛应用于GNSS导航卫星钟差预报。部分学者[4-5]采用GM(1, 1)模型对GPS、GLONASS等导航卫星钟差进行预报处理,验证其可行性和有效性,并获得较高的预报精度。但经过深入剖析GM(1, 1)模型的建模机理发现,灰微分方程与所拟合的微分方程很难做到严格近似,而且参与建模的初始序列的光滑程度也会影响GM(1, 1)模型的预报精度。针对GM(1, 1)预报模型存在的问题,众多学者从初始序列预处理、背景值重构、时间响应函数优化以及初始条件优化等方面展开研究。
在初始条件优化方面,现有的生成方法主要有3类:采用一阶累加生成(first-order accumulated generating operation,1-AGO)序列的单个分量作为初始条件、采用1-AGO序列的多个分量进行线性组合作为初始条件、将系数乘以或添加到特定分量中获得初始条件。上述方法都是基于白化方程的时间响应函数,以1-AGO序列的某个或多个分量进行线性组合作为已知参量求解初始条件。这类方法着重强调参与初始条件计算信息的挖掘和利用以及信息的权重分配,忽视了建模参数和表达形式对模型自身的影响,从而导致模型不稳定,预报效果不佳。本文提出一种利用原始序列生成初始条件的新方法,更注重预报模型的构建和参数对模型的影响。首先利用1-AGO和最小二乘法估计发展系数和灰作用量,然后运用一阶累减运算(first-order inverse accumulated generating operation,1-IAGO)将白化方程的时间响应函数还原得到原始序列的拟合模型,最后将原始序列的最新分量代入拟合模型,求解初始条件得到GM(1, 1)预报模型。利用新方法构建的GM(1, 1)模型对IGS提供的精密卫星钟差进行预报实验,通过与其他方法构建的GM(1, 1)模型进行对比分析来验证新方法的有效性和优越性。
1 GM(1, 1)模型及初始条件优化 1.1 GM(1, 1)基本模型设非负原始数据序列为X(0)={x(0)(1), x(0)(2), …, x(0)(N)},N为原始数据个数,与之对应的时间为ti(i=1, 2, …, N)。X(0)的1-AGO序列为X(1)={x(1)(1), x(1)(2), …, x(1)(N)},其中
定义GM(1, 1)模型的灰微分方程为:
| $x^{(0)}(k)+a z^{(1)}(k)=b, k=2, 3, \cdots, N$ | (1) |
式中,a为发展系数,b为灰作用量,z(1)(k)称为GM(1, 1)模型的背景值,用序列Z(1)={z(1)(1), z(1)(2), …, z(1)(N)}表示。z(1)(k)可由x(1)(k)的紧邻均值生成,即
| $ \begin{gathered} z^{(1)}(k)=\frac{1}{2}\left[x^{(1)}(k-1)+x^{(1)}(k)\right], \\ k=2, 3, \cdots, N \end{gathered} $ | (2) |
令
GM(1, 1)模型的白化方程为:
| $\frac{\mathrm{d} x^{(1)}}{\mathrm{d} t}+a x^{(1)}=b$ | (3) |
式(3)为线性微分方程,其通解可近似为:
| $\hat{x}^{(1)}(t)=\frac{\hat{b}}{\hat{a}}+c \mathrm{e}^{-\hat{a} t}$ | (4) |
该通解也称为白化方程的时间响应函数,待定系数c为GM(1, 1)模型的初始条件。离散化
| $ \begin{gathered} \hat{x}^{(1)}(n)=\frac{\hat{b}}{\hat{a}}+c \mathrm{e}^{-\hat{a} n}, \\ n=1, 2, \cdots, N, N+1, \cdots \end{gathered} $ | (5) |
将式(5)进行1-IAGO运算,得到
| $ \begin{aligned} &\hat{x}^{(0)}(n)=\left(1-\mathrm{e}^{\hat{a}}\right) c \mathrm{e}^{-\hat{a} n}, \\ &n=1, 2, \cdots, N, N+1, \cdots \end{aligned} $ | (6) |
式(6)为GM(1, 1)预报模型,其时间序号已外推至大于N的范围。在初始条件c已知的情况下,利用式(6)能够求得n≥N+1时的
|
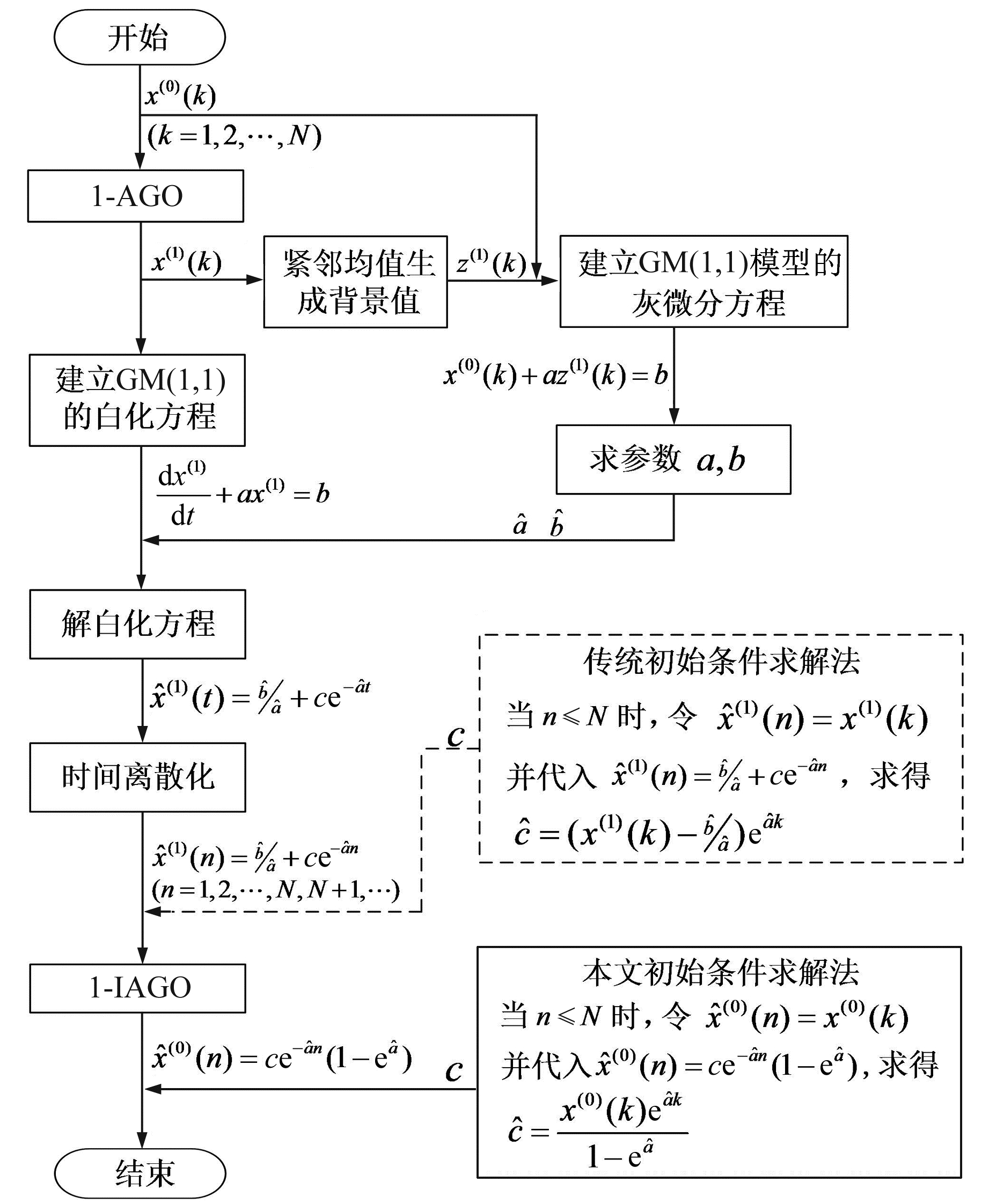
图 1 GM(1, 1)模型预报流程 Fig. 1 Prediction flow of GM(1, 1) model |
初始条件的计算对GM(1, 1)模型的确定至关重要,其估计水平高低直接影响模型预报精度。传统GM(1, 1)模型及部分改进模型的初始条件求解法是将1-AGO序列的某一分量或加权分量代入GM(1, 1)模型的时间响应函数中计算得到c,该求解法在GM(1, 1)模型预报流程中所处的位置和简单过程如图 1中虚线箭头和虚线框所示。获得时间响应函数
| $\hat{c}=\left(x^{(1)}(k)-\frac{\hat{b}}{\hat{a}}\right) \mathrm{e}^{\hat{a} k}$ | (7) |
以下为4种利用1-AGO序列求初始条件的方法:
1) 方法1:取1-AGO最旧分量,将k=1代入式(7),求得
2) 方法2:取1-AGO最新分量,将k=N代入式(7),求得
3) 方法3:取1-AGO最新最旧分量的加权分量,利用式(7)计算加权表达式wx(1)(1)+(1-w)x(1)(N),求得
4) 方法4:取1-AGO所有分量加权值之和,即P1x(1)(1)+P2x(1)(2)+…+PNx(1)(N),P1, P2, …, PN为对应分量的权值系数,利用式(7)求得
令
|
|
表 1 4种方法对应的GM(1, 1)预报模型 Tab. 1 GM(1, 1) prediction model corresponding to the four methods |
本文提出的初始条件求解思路是将原始序列的最新分量代入GM(1, 1)预报模型中计算获得c,这种初始条件求解法在GM(1, 1)预报流程中所处的位置和简单过程如图 1中实线箭头和实线框所示。GM(1, 1)模型的时间响应函数经过1-IAGO运算后得到
| $\hat{c}=\frac{x^{(0)}(k) \mathrm{e}^{\hat{a} k}}{1-\mathrm{e}^{\hat{a}}}$ | (8) |
式中,x0(k)可以取原始序列的某个分量或多个分量的加权和,本文依据新信息优先原则取其最新分量,将k=N代入式(8)得到初始条件的估计值为:
| $\hat{c}=\frac{x^{(0)}(N) \mathrm{e}^{\hat{a} N}}{1-\mathrm{e}^{\hat{a}}}$ | (9) |
令
| $ \begin{aligned} &\hat{x}^{(0)}(n)=x^0(N) \mathrm{e}^{-\hat{a}(n-N)}, \\ &N=1, 2, \cdots, N, N+1, \cdots \end{aligned} $ | (10) |
当n>N时,利用式(10)就可以求得优化初始条件后的GM(1, 1)模型的预报值。
由图 1可知,相比于传统方法,本文提出的初始条件求解法是在1-IAGO流程后代入原始序列的最新分量来获得c。由式(10)和表 1中各方法对应的
为验证优化初始条件后GM(1, 1)模型的有效性,采用IGS提供的采样间隔为5 min的最终精密星历钟差作为原始数据进行钟差预报,并与传统初始条件的GM(1, 1)模型进行对比分析。IGS最终精密星历钟差的精度优于75 ps,可作为真值用于检验模型的预报精度。假设采用§1.2中方法1~4获得的GM(1, 1)模型分别为模型1、模型2、模型3和模型4,本文提出的初始条件生成法构建的GM(1, 1)模型为模型5。采用预报值与真值的均方根误差(RMSE)定量分析模型的预报精度,RMSE越小,说明钟差预报精度越高;采用预报值与真值的残差图定性分析模型的预报误差,残差图偏离0越远则误差越大。RMSE计算公式为:
| $\mathrm{RMSE}=\sqrt{\frac{\sum\limits_{i=1}^L\left[\hat{x}\left(t_i\right)-x\left(t_i\right)\right]^2}{L}}$ | (11) |
式中,
采用2021-10-17~23采样间隔为5 min的GPS最终精密星历钟差作为实验数据。由于GPS卫星钟绝大部分为铷原子钟,选取该时间段内钟差数据完整性较好的4种类型铷原子钟各1颗,4颗卫星的类型和编号分别为ⅡF Rb G01、ⅢRb G04、ⅡR-M Rb G15和ⅡR Rb G19。其中G01钟差信号呈递减趋势,其余3颗卫星的钟差信号均递增。除G01钟差数据线性特性极好外,其他卫星的钟差数据均出现不同程度的波动,G15卫星波动幅度和频率最大。
2.2 钟差预报及结果分析在实际预报中,首先选取2021-10-17前12 h(00:00~12:00)的钟差数据进行建模,然后分别预报未来6 h和24 h的卫星钟差,并将模型5的预报结果与模型1~4进行对比分析。表 2和表 3分别为预报6 h和24 h的RMSE(单位ns)。
|
|
表 2 钟差数据预报6 h的RMSE Tab. 2 RMSE for 6 h of clock offset data forecasting |
|
|
表 3 钟差数据预报24 h的RMSE Tab. 3 RMSE for 24 h of clock offset data forecasting |
1) 模型2和模型3对4种类型卫星的6 h和24 h预测结果与传统GM(1, 1)模型(模型1)几乎相同,说明采用1-AGO序列的最旧分量、最新分量、最新最旧分量加权和生成初始条件构建的GM(1, 1)模型进行卫星钟差预报的精度相当。经多次实验发现,卫星类型、建模数量和预报时间的选择与3种模型钟差预报精度几乎一致的结论无关,这是由卫星钟差序列之间的差值太小所致。对于数据差别较大的序列,模型预报精度完全不同,如文献[6]中采用模型3对序列值之差为个位数的实验数据进行预报处理,结果表明模型3的预报精度优于模型1。
2) 模型4与模型1的RMSE虽然不相等,但是除了对G19卫星进行24 h预报时模型4的RMSE低于模型1外,其他情况下模型4的RMSE均远远高于模型1,尤其是Ⅱ F和Ⅱ R-M两种类型铷钟。说明在钟差预报中用于生成GM(1, 1) 模型初始条件的分量并不是越多越好,分量过多反而会弱化最新序列与预报序列之间的关系,导致预报效果不佳。
3) 相比于模型1和模型4,模型5进行钟差预报的RMSE最小,精度最高。6 h预报时模型5的RMSE约为0.3 ns;24 h预报时,除G15外其余卫星钟差预报的RMSE均在0.8 ns以内。由此可见,采用原始序列生成初始条件的方法具有可行性,在钟差预报中能够获得较好的预报效果。
4) 除G01外大多数卫星的RMSE均随着预报时长的增加而增大,其中G15卫星的RMSE变化较为明显。这是因为G01卫星的钟差信号线性特性极好,而G15卫星钟差波动较为严重。说明5种GM(1, 1)模型对卫星钟差的波动都很敏感,波动幅度越大、频率越高,预报效果越差。
由于模型1~3的预报精度相当,后续图表只给出模型1、模型4和模型5的处理结果。图 2和图 3分别为采用2021-10-17数据预报未来6 h和24 h的残差结果。

|
图 2 4种模型6 h预报误差 Fig. 2 The 6 h prediction errors of four models |

|
图 3 4种模型24 h预报误差 Fig. 3 The 24 h prediction errors of four models |
由图 2和图 3可见,模型5的误差基本在0值附近波动,尤其是6 h预报时长;而模型1和模型4的误差值偏离0值相对较远,且预报时间越长该现象越明显。模型5预报误差的变化趋势与模型1和模型4基本保持一致,随着预报时长的增加,绝大部分卫星的误差绝对值均缓慢增大。由此说明,模型4的预报精度得到很大提升,但稳定度还有待改善。
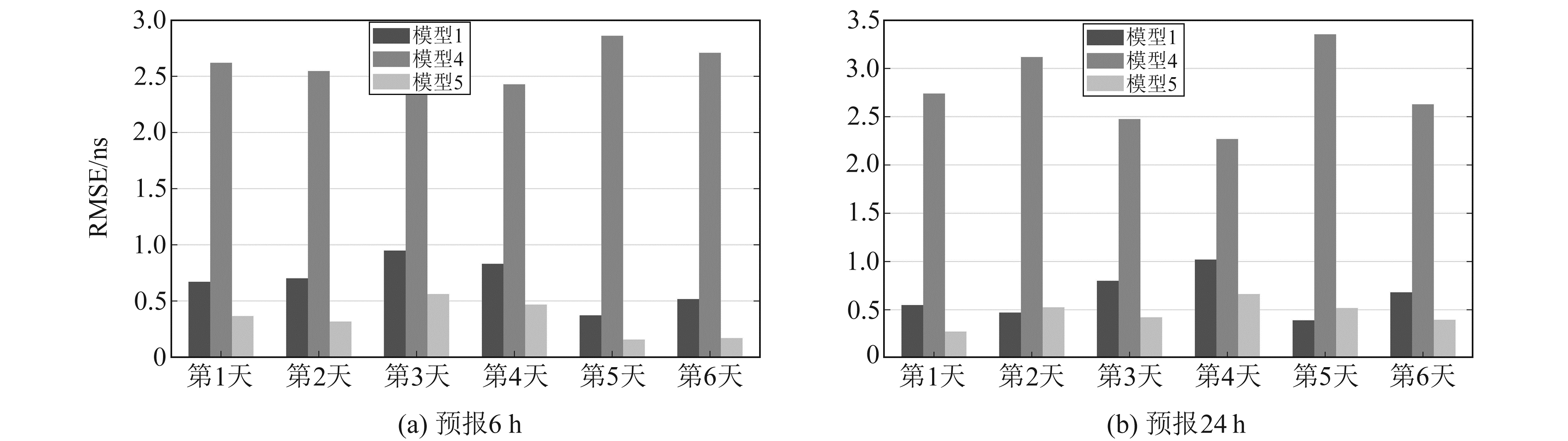
为进一步验证模型5预报性能的优越性,将2021-10-17~22连续6 d的钟差数据进行预报处理。由于篇幅有限,图 4只给出G01卫星2021-10-17~22的预报精度,表 4(单位ns)为4颗卫星6 d预报结果的平均值,表 5(单位%)为模型5相对于模型1和模型4的平均精度提高率。
|
图 4 G01卫星6 d的预报精度 Fig. 4 The 6 d prediction accuracy of G01 satellite |
|
|
表 4 6 d钟差预报的RMSE平均值 Tab. 4 The average RMSE of 6 d clock offset forecasting |
|
|
表 5 模型5相对于模型1和模型4的平均精度提高率 Tab. 5 The accuracy improvement rate of model 5 compared with model 1 and model 4 |
由图 4可知,除个别时间段模型5的预报精度略低于模型1外,其他预报时长和时间段内模型5的预报精度均远远高于模型1和模型4。由表 4和表 5可知,所有卫星6 d的平均预报精度均有不同程度提升,钟差信号变化越平稳,模型5的预报精度提升越明显。由此可见,对2021-10-17~22连续6 d的钟差数据作与2021-10-17钟差数据同样的预报处理,能够得到与2021-10-17相似的结论。
3 结语本文提出利用原始序列的最新分量生成初始条件的新方法,该方法既充分利用已知信息,又遵循新信息优先原则。理论分析和实验结果表明,采用新的初始条件构建的GM(1, 1)模型可以有效预报卫星钟差,且预报精度明显优于利用1-AGO序列的某个或多个分量加权和生成初始条件构建的GM(1, 1)模型。但本文构建的GM(1, 1)模型钟差预报的稳定度相比于传统GM(1, 1) 模型并未明显改善,在以后的研究工作中可以从卫星钟差序列的实际特征出发,结合信号预处理、背景值优化及其他辅助手段优化GM(1, 1)模型,进一步提高钟差预报的精度和稳定性。
| [1] |
王润, 王井利, 吕栋. 导航卫星钟差预报的Elman神经网络算法研究[J]. 大地测量与地球动力学, 2021, 41(3): 285-289 (Wang Run, Wang Jingli, Lü Dong. Research on the Elman Neural Network Algorithm to Predict Navigation Satellite Clock Bias[J]. Journal of Geodesy and Geodynamics, 2021, 41(3): 285-289)
(  0) 0) |
| [2] |
于烨, 黄默, 王小青, 等. 利用最小一乘法改进的灰色模型的导航卫星钟差预报[J]. 测绘通报, 2019(4): 1-6 (Yu Ye, Huang Mo, Wang Xiaoqing, et al. Navigation Satellite Clock Bias Prediction Based on Grey Model Improved by Least Absolute Deviations[J]. Bulletin of Surveying and Mapping, 2019(4): 1-6)
(  0) 0) |
| [3] |
梅长松, 黄海军, 蒋可, 等. 级比离散灰色模型在卫星钟差预报中的应用[J]. 武汉大学学报: 信息科学版, 2021, 46(8): 1 154-1 160 (Mei Changsong, Huang Haijun, Jiang Ke, et al. Application of Discrete Grey Model Based on Stepwise Ratio Sequence in the Satellite Clock Offset Prediction[J]. Geomatics and Information Science of Wuhan University, 2021, 46(8): 1 154-1 160)
(  0) 0) |
| [4] |
崔先强, 焦文海. 灰色系统模型在卫星钟差预报中的应用[J]. 武汉大学学报: 信息科学版, 2005, 30(5): 447-450 (Cui Xianqiang, Jiao Wenhai. Grey System Model for the Satellite Clock Error Predicting[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 447-450)
(  0) 0) |
| [5] |
李超, 党亚民, 谷守周. 灰色模型的GLONASS卫星钟差预报[J]. 导航定位学报, 2016, 4(4): 24-29 (Li Chao, Dang Yamin, Gu Shouzhou. Prediction of GLONASS Satellite Clock Error Based on Grey Model[J]. Journal of Navigation and Positioning, 2016, 4(4): 24-29)
(  0) 0) |
| [6] |
Wang Y H, Dang Y G, Li Y Q, et al. An Approach to Increase Prediction Precision of GM(1, 1) Model Based on Optimization of the Initial Condition[J]. Expert Systems With Applications, 2010, 37(8): 5 640-5 644 DOI:10.1016/j.eswa.2010.02.048
(  0) 0) |
| [7] |
Xiong P P, Dang Y G, Yao T X, et al. Optimal Modeling and Forecasting of the Energy Consumption and Production in China[J]. Energy, 2014, 77: 623-634 DOI:10.1016/j.energy.2014.09.056
(  0) 0) |
2. School of Electronic Engineering, Jiujiang University, 551 East-Qianjin Road, Jiujiang 332005, China
 2022, Vol. 42
2022, Vol. 42


