虽然目前IGS提供的事后GPS轨道和各分析中心轨道的一维精度互差在1 cm左右,但是光压摄动力等非保守力的处理模型还未统一,太阳光压摄动依然是影响GPS卫星轨道精度的主要因素。在精密定轨中,ECOM1[1]和ECOM2[2]常作为参数化光压模型,Box-Wing(以下简称BW)常作为先验模型。在IGS第3次重处理中,欧洲定轨中心(center for orbit determination in Europe, CODE)提供的ECOM1模型被推荐应用于Block Ⅱ R和Ⅱ F卫星,ECOM2和美国喷气推进实验室(JPL)提供的GSPM模型被推荐用于其他类型的卫星。鉴于GPS有多种可用的光压模型,而关于不同光压模型对PPP性能影响的研究很少,本文分别使用ECOM1、ECOM1+BW和ECOM1+ABW等3种不同的光压模型进行GPS卫星精密定轨,然后利用得到的GPS精密轨道分别进行静态和动态PPP实验,并对定位效果进行统计分析。
1 PPP模型与数据处理策略采用双频伪距和载波的无电离层组合消除电离层一阶误差项的影响,具体GPS PPP观测方程见文献[3],本文不再复述。
利用武汉大学自主研发的PANDA软件进行GPS精密定轨,采用MW组合及电离层残差组合探测周跳[4],采用最小二乘配置法进行参数估计。具体定轨处理策略如表 1所示。PPP待估参数包括测站坐标、天顶对流层延迟、接收机钟差以及模糊度参数,其中接收机位置参数(x, y, z)分别进行静态和动态处理[5];对流层延迟采用Saastamoinen模型进行改正,湿分量剩余通过参数进行估计[6-8];相对论效应、固体潮汐、相位缠绕使用模型进行改正[9];卫星端和接收机端天线相位中心偏移(phase center offset, PCO)和天线相位中心变化(phase center variation, PCV)使用IGS提供的ANTEX文件进行改正[10]。具体参数估计策略见表 2。
|
|
表 1 GPS定轨处理策略 Tab. 1 GPS orbit determination processing strategy |
|
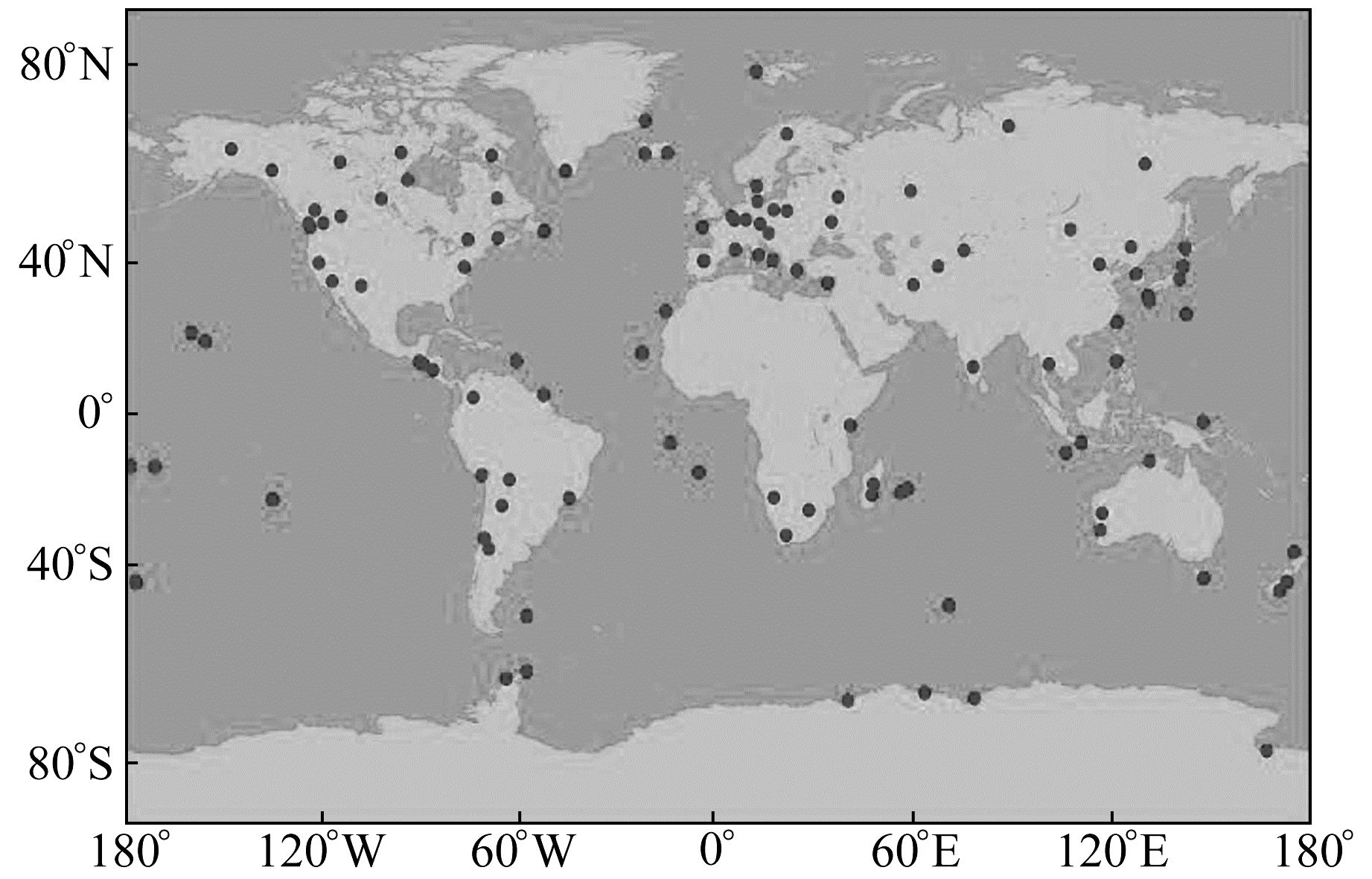
图 1 测站分布 Fig. 1 Distribution of the stations |
|
|
表 2 PPP参数估计策略 Tab. 2 The parameter estimation strategy of PPP |
首先利用全球120个跟踪站(图 1)2019年doy110~139观测数据进行GPS精密定轨。结合IGS重处理建议,设计3种实验方案: 1)仅使用5参数ECOM1模型;2)使用ECOM1及BW模型,其系数来自厂商[1, 3],简称ECOM1+BW;3)使用ECOM1及BW模型,其系数来自文献[17],简称ECOM1+ABW。除光压模型外,其余待估参数设置均与IGS第3次重处理相同。
基于3种方案计算得到的轨道结果,选取未参与定轨的7个测站2019年doy110~139观测数据进行PPP实验。测站经度、纬度、天线类型见表 3。
|
|
表 3 测站信息 Tab. 3 Information of the stations |
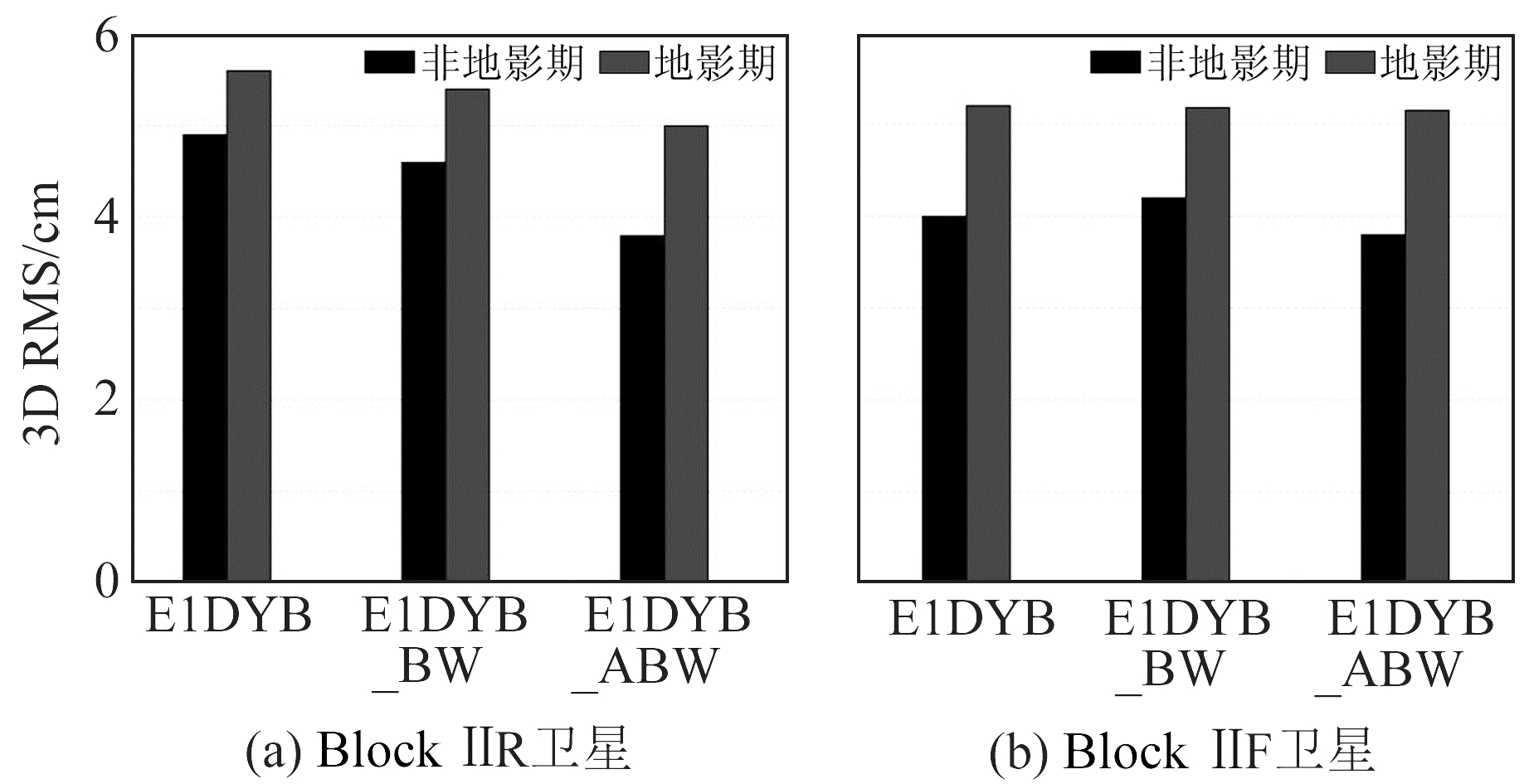
不同光压模型处理的轨道精度如图 2所示。从图中可以看出,对于Block Ⅱ R卫星,在非地影期,采用ECOM1、ECOM1+BW光压模型的轨道三维RMS精度优于5 cm,而采用ECOM1+ABW的精度优于4 cm;在地影期,采用ECOM1、ECOM1+BW光压模型的轨道三维RMS精度优于6 cm,而采用ECOM1+ABW光压模型的轨道精度优于5 cm。
|
图 2 不同光压模型对轨道精度的影响 Fig. 2 Influence of different solar radiation pressure models on orbit accuracy |
对于Block Ⅱ F卫星,在地影期,采用ECOM1+ABW光压模型的轨道精度略优于ECOM1和ECOM1+BW光压模型。因此,对于Block Ⅱ R和Ⅱ F卫星,在地影期及非地影期,采用ECOM1+ABW光压模型的轨道精度均优于ECOM1和ECOM1+BW光压模型。
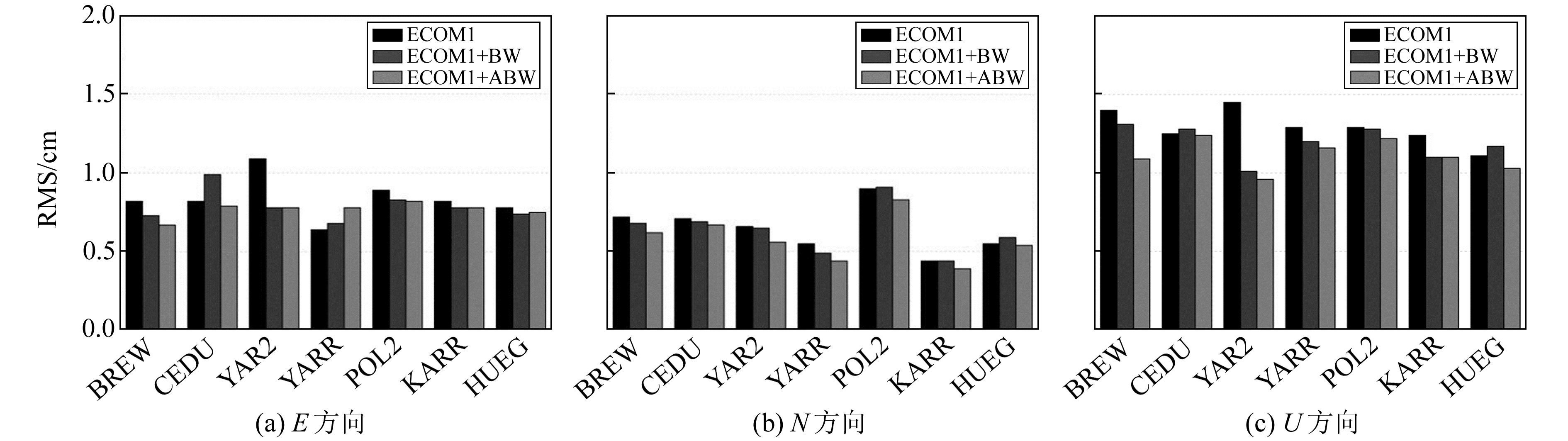
2.2 不同光压模型对静态PPP的影响本文分别使用ECOM1、ECOM1+BW和ECOM1+ABW等3种不同光压模型进行静态PPP解算并对解算结果进行统计(测站参考坐标为IGS SINEX单天解)。图 3为各测站静态PPP定位误差RMS。以BREW站为例,ECOM1方案E、N、U分量定位误差RMS值约为0.82 cm、0.72 cm、1.40 cm,ECOM1+BW方案约为0.73 cm、0.68 cm、1.31 cm,ECOM1+ABW方案约为0.67 cm、0.62 cm、1.09 cm。7个测站的平均静态PPP定位误差RMS值见表 4。从表中可以看出,ECOM1+ABW光压模型的定位精度最优,相比于ECOM1和ECOM1+BW光压模型,其E、N、U分量定位精度分别提高8.4%、10.9%、13.9%和3.7%、9.5%、6.7%。
|
图 3 各测站静态PPP定位误差RMS Fig. 3 RMS of static PPP error of each station |
|
|
表 4 各测站RMS均值 Tab. 4 Average RMS of each station |
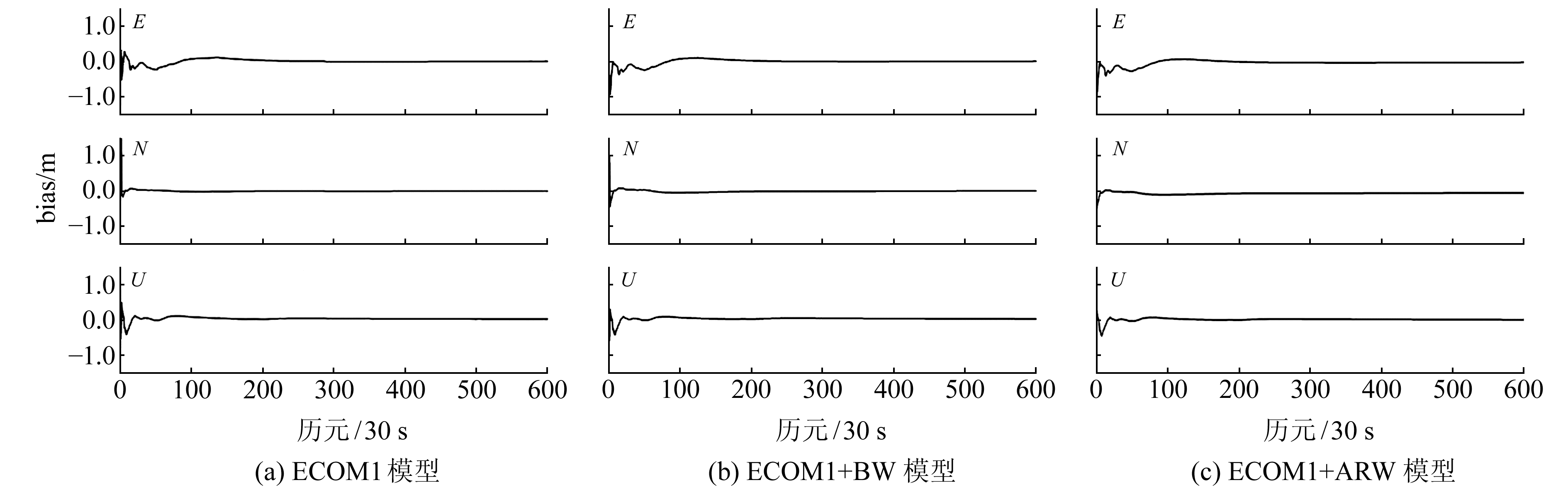
将单天解的PPP动态解算结果与IGS SINEX单天解参考值作差,获得E、N、U方向的坐标偏差以分析动态PPP的收敛时间和定位精度。当E、N、U方向连续20个历元的定位偏差均优于0.1 m时认为收敛。以2019-05-06 BREW站为例(图 4),分析3种不同光压模型PPP的偏差。从图中可以看出,ECOM1、ECOM1+BW和ECOM1+ABW模型的收敛时间分别为45 min、35 min和30 min。
|
图 4 BREW站PPP偏差 Fig. 4 PPP bias of BREW station |
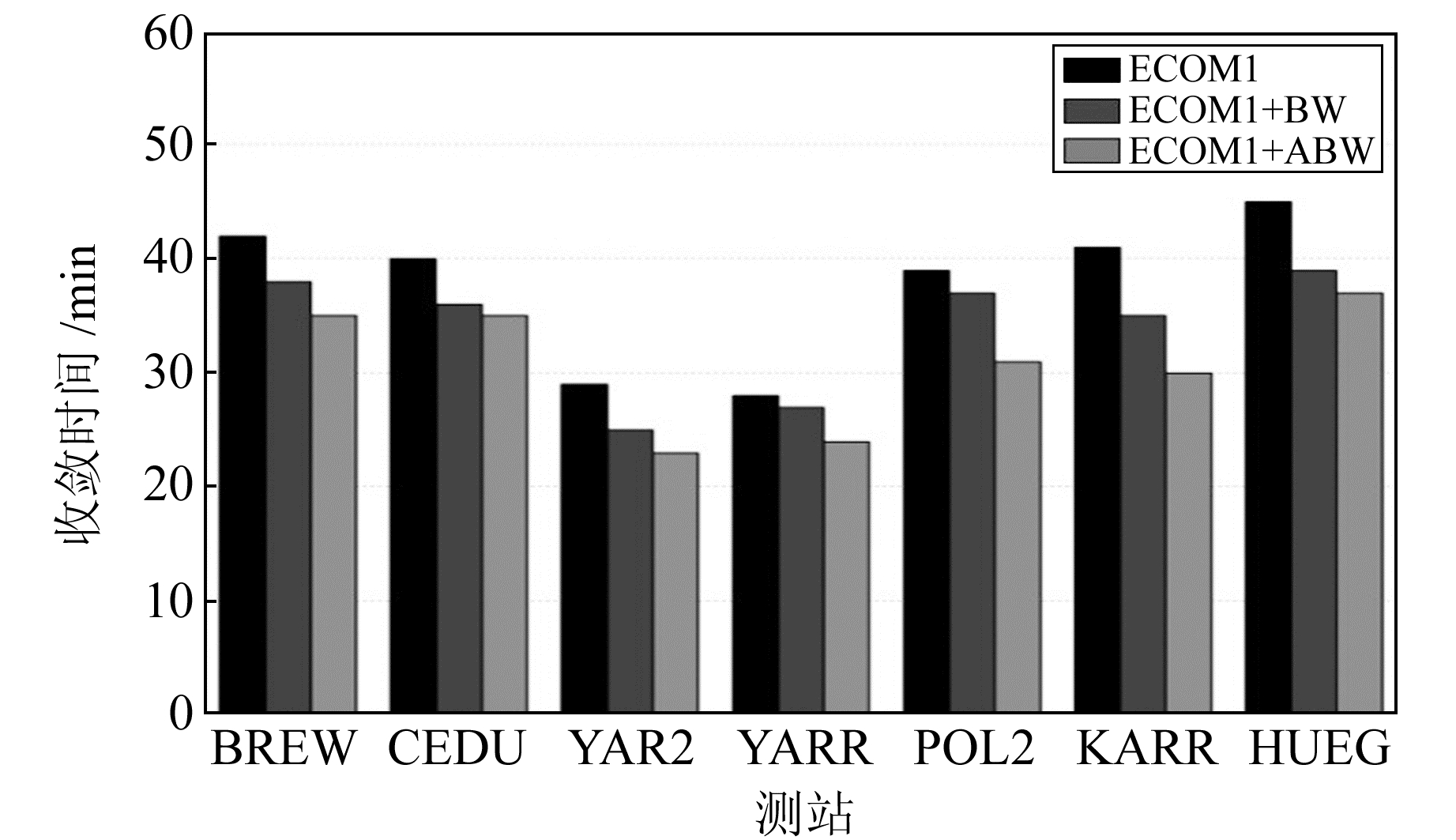
各测站平均收敛时间如图 5所示。从图中可以看出,ECOM1、ECOM1+BW和ECOM1+ABW模型的平均收敛时间分别约为37 min、33 min和30 min。
|
图 5 不同光压模型平均收敛时间 Fig. 5 Average convergence time of different solar radiation pressure models |
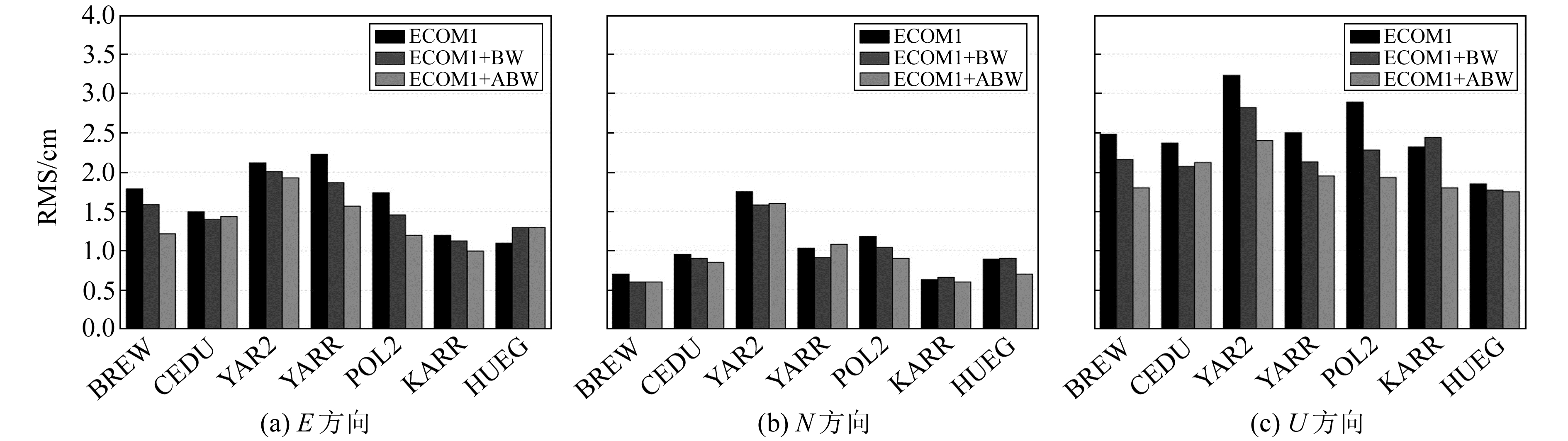
图 6为3种光压模型的GPS动态定位结果精度。从图中可以看出,ECOM1、ECOM1+BW、ECOM1+ABW模型的水平和垂直方向平均精度分别优于1.7 cm和2.6 cm、1.6 cm和2.3 cm、1.4 cm和2.0 cm。7个测站的平均动态定位精度见表 5。由表可知,对于动态定位结果,相比于ECOM1和ECOM1+BW模型,ECOM1+ABW模型在E、N、U方向的定位精度分别提高16.8%、10.8%、22.2%和9.8%、4.2%、12.1%。
|
图 6 各测站动态PPP定位误差RMS Fig. 6 RMS of kinematic PPP error of each station |
|
|
表 5 各测站RMS均值 Tab. 5 Average RMS of each station |
本文首先利用ECOM1、ECOM1+BW、ECOM1+ABW光压模型进行精密定轨,然后利用得到的轨道进行GPS静态、动态PPP实验,经分析得出以下结论:
1) 在轨道精度方面,当卫星处于地影期和非地影期时,采用ECOM1+ABW模型的轨道精度均最优。
2) 在静态定位精度方面,ECOM1+ABW模型与ECOM1模型差异最明显,前者精度比后者在E、N、U方向分别提高8.4%、10.9%、13.9%。
3) 在动态定位方面,ECOM1、ECOM1+BW和ECOM1+ABW模型的收敛时间分别为37 min、33 min和30 min;相比于ECOM1和ECOM1+BW模型,ECOM1+ABW模型在E、N、U方向的定位精度分别提高16.8%、10.8%、22.2%和9.8%、4.2%、12.1%。
综上所述,从不同模型定位的收敛时间和精度来看,ECOM1+ABW模型对PPP性能提升均最大。
| [1] |
Springer T A, Beutler G, Rothacher M. A New Solar Radiation Pressure Model for GPS[J]. Advances in Space Research, 1999, 23(4): 673-676 DOI:10.1016/S0273-1177(99)00158-1
(  0) 0) |
| [2] |
Arnold D, Meindl M, Beutler G, et al. CODE's New Solar Radiation Pressure Model for GNSS Orbit Determination[J]. Journal of Geodesy, 2015, 89(8): 775-791 DOI:10.1007/s00190-015-0814-4
(  0) 0) |
| [3] |
周锋. 多系统GNSS非差非组合精密单点定位相关理论和方法研究[D]. 上海: 华东师范大学, 2018 (Zhou Feng. Theory and Methodology of Multi-GNSS Undifferenced and Uncombined Precise Point Positioning[D]. Shanghai: East China Normal University, 2018)
(  0) 0) |
| [4] |
刘经南, 叶世榕. GPS非差相位精密单点定位技术探讨[J]. 武汉大学学报: 信息科学版, 2002, 27(3): 234-240 (Liu Jingnan, Ye Shirong. GPS Precise Point Positioning Using Undifferenced Phase Observation[J]. Geomatics and Information Science of Wuhan University, 2002, 27(3): 234-240)
(  0) 0) |
| [5] |
任晓东, 张柯柯, 李星星, 等. Beidou、Galileo、GLONASS、GPS多系统融合精密单点[J]. 测绘学报, 2015, 44(12): 1 307-1 313 (Ren Xiaodong, Zhang Keke, Li Xingxing, et al. Precise Point Positioning with Multi-Constellation Satellite Systems: Beidou、Galileo、GLONASS、GPS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1 307-1 313)
(  0) 0) |
| [6] |
王趁香, 徐爱功, 葛茂荣, 等. GPS/BDS组合的精密单点定位算法实现[J]. 导航定位学报, 2018, 6(1): 67-75 (Wang Chenxiang, Xu Aigong, Ge Maorong, et al. Algorithm Implementation of Precision Point Positioning for GPS/BDS Combination[J]. Journal of Navigation and Positioning, 2018, 6(1): 67-75)
(  0) 0) |
| [7] |
Guevara J, Auat Cheein F A, Gené-Mola J, et al. Analyzing and Overcoming the Effects of GNSS Error on LiDAR Based Orchard Parameters Estimation[J]. Computers and Electronics in Agriculture, 2020, 170
(  0) 0) |
| [8] |
赵齐乐, 刘经南, 葛茂荣, 等. 用PANDA对GPS和CHAMP卫星精密定轨[J]. 大地测量与地球动力学, 2005, 25(2): 113-116 (Zhao Qile, Liu Jingnan, Ge Maorong, et al. Precise Orbit Determination of GPS and CHAMP Satellites with PANDA Software[J]. Journal of Geodesy and Geodynamics, 2005, 25(2): 113-116)
(  0) 0) |
| [9] |
张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250-256 (Zhang Xiaohong, Zuo Xiang, Li Pan, et al. Convergence Time and Positioning Accuracy Comparison between BDS and GPS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 250-256)
(  0) 0) |
| [10] |
祝会忠, 杨添宇, 赵洪涛, 等. GNSS多系统精密单点定位方法与性能分析[J]. 测绘科学, 2020, 45(12): 1-7 (Zhu Huizhong, Yang Tianyu, Zhao Hongtao, et al. GNSS Multi-System Precise Point Positioning Method and Performance Analysis[J]. Science of Surveying and Mapping, 2020, 45(12): 1-7)
(  0) 0) |
| [11] |
Kouba J. A Simplified Yaw-Attitude Model for Eclipsing GPS Satellites[J]. GPS Solutions, 2009, 13(1): 1-12 DOI:10.1007/s10291-008-0092-1
(  0) 0) |
| [12] |
Bar-Sever Y E. A New Model for GPS Yaw Attitude[J]. Journal of Geodesy, 1996, 70(11): 714-723 DOI:10.1007/BF00867149
(  0) 0) |
| [13] |
Dilssner F, Springer T, Enderle W. GPS Ⅱ F Yaw Attitude Control during Eclipse Season[C]. AGU Fall Meeting, San Francisco, 2011
(  0) 0) |
| [14] |
Rodríguez-Solano C J. Impact of Non-Conservative Force Modeling on GNSS Satellite Orbits and Global Solutions[D]. München: Technische Universität München, 2014
(  0) 0) |
| [15] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere(GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [16] |
Boehm J, Niell A, Tregoning P, et al. Global Mapping Function(GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters, 2006, 33(7)
(  0) 0) |
| [17] |
Duan B B, Hugentobler U. Enhanced Solar Radiation Pressure Model for GPS Satellites Considering Various Physical Effects[J]. GPS Solutions, 2021, 25(2)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

