2. 中国地质大学(武汉)地理与信息工程学院,武汉市鲁磨路388号,430074;
3. 湖北经济学院信息管理与统计学院,武汉市杨桥湖大道8号,430205
GPS坐标时间序列主要包括长期趋势项、周期项以及噪声项,对GPS坐标时间序列进行精确重构,不仅可以提取该站点的周期性信号,还可以准确估计噪声振幅、速度不确定度等参数。近年来,国内外学者提出多种方法估计时变振幅的周期信号,如奇异谱分析法(singular spectrum analysis, SSA)[1]、小波分解法(wavelet decomposition, WD)[2]、滑动最小二乘法(moving ordinary least squares, MOLS)[3]以及经验模态分解法(empirical mode decomposition, EMD)[4]等。其中,EMD法本身存在模态混叠,且在提取闪烁噪声环境下的周期信号时存在吸收噪声的现象,会导致重构精度降低。
针对EMD算法本身的局限性,有学者提出自适应噪声完备集成经验模态分解(CEEMD with adaptive noise, CEEMDAN)[5]和改进的自适应噪声完备集成经验模态分解(improved CEEMDAN, ICEEMDAN)[6]等算法。ICEEMDAN方法由CEEMDAN方法改进而来,采用局部均值的估计值替换模态估计值以减少冗余模态的影响。k阶模态由信号的局部均值来提取而不直接使用白噪声,可降低分解后模态的噪声残余,基本可解决模态混叠问题,可以稳定提取低频信息。然而实际的GPS坐标时间序列中往往存在振幅较小的弱周期信号[7],这些弱周期信号对应的奇异值与噪声的奇异值往往较为接近,在提取时容易被噪声掩盖而难以顺利提取。基于上述分析,本文首先利用ICEEMDAN方法提取GPS坐标时间序列中不同时间尺度下的趋势以及周期信号,然后将ICEEMDAN方法分解得到的各个本征模态分量排成Hankel矩阵并利用SSA对分解得到的每个本征模态分量进行重构,最后获得整个GPS坐标时间序列的重构结果。模拟结果表明,本文提出的ICEEMDAN-SSA联合算法在重构精度上优于多个现有方法,对于闪烁噪声具有更好的压制效果,可以更好地分离出趋势和周期信号。
1 具有时变振幅的GPS坐标时间序列模型GPS坐标时间序列一般由长期趋势、周期项以及噪声项组成,一般建模如下:
| $ y(t)=h_0+v t+s(t)+\varepsilon(t), t=1, 2, \cdots, N $ | (1) |
式中,h0为初始位置,v为速度,s(t) 为周期项,ε(t) 为噪声项。其中,周期项s(t) 通常认为由年周期信号和半年周期信号构成。研究表明[7-8],对流层和地磁活动中存在准两年振荡,可能会对日长和极移产生潜在影响,从而影响GPS观测结果。准两年信号会使速度估计产生偏差,因此有必要在周期信号模型中考虑准两年周期信号。由于准两年周期与两年周期的频率信息较为接近,本文模型由半年、年以及较小振幅的两年周期信号构成,即
| $ \begin{aligned} s(t)=& \sum\limits_{i=1}^3 a_i(t) \cos \left(2 \pi f_i t\right)+\\ & b_i(t) \sin \left(2 \pi f_i t\right) \end{aligned} $ | (2) |
式中,ai(t)、bi(t) 为时变振幅项,数学形式上表现为振幅项随着时间的变化而波动,时变振幅选取以下形式[1]:
| $ a_i(t)=a_i+{\mathrm{e}}^{p \sin (t)}, b_i(t)=b_i+{\mathrm{e}}^{q \sin (t)} $ | (3) |
式中,ai、bi(i=1, 2, 3) 为周期项振幅的常数项,p、q为周期波动参数。
2 基于ICEEMDAN-SSA的GPS坐标时间序列分解和重构基于ICEEMDAN-SSA算法的信号分解和重构具体步骤如下:
1) 输入GPS坐标时间序列x,通过EMD法进行第i次迭代(i=1, 2, …, I),迭代公式如下:
| $ x^{(i)}=x+\beta_0 E_1\left(w^{(i)}\right) $ | (4) |
式中,E1为对输入信号进行EMD分解并获得的第一个模态分量;i为迭代次数;w(i)为标准正态分布的白噪声;β0为噪声系数,即加入白噪声的标准差和输入信号的标准差的比值。通过计算其局部均值获得第一个残差序列r1:
| $ r_1=\frac{1}{I} \sum\limits_{i=1}^I M\left(x^{(i)}\right) $ | (5) |
式中,M为产生信号局部均值的算子。第一个模态计算公式如下:
| $ {\mathrm{IMF}}_1=x-r_1 $ | (6) |
2) 第二个残差序列r2以及第二个模态IMF2计算公式如下:
| $ r_2=\frac{1}{I} \sum\limits_{i=1}^I M\left(r_1+\beta_1 E_2\left(w^{(i)}\right)\right) $ | (7) |
| $ {\mathrm{IMF}}_2=r_1-r_2 $ | (8) |
3) 循环计算IMFk和rk,公式如下:
| $ r_k=\frac{1}{I} \sum\limits_{i=1}^T M\left(r_{k-1}+\beta_{k-1} E_k\left(w^{(i)}\right)\right) $ | (9) |
| $ {\mathrm{IMF}}_k=r_{k-1}-r_k $ | (10) |
式中,k=3, 4, 5, …, Q, Q为满足分解结束条件时共产生的模态分量个数。循环计算式(9)、式(10)直至残差序列极值点小于2,分解步骤结束。
4) 得到Q个不同时间尺度下的模态{IMF1, IMF2, …, IMFQ},通过计算各模态分量与原GPS信号的相关系数和方差贡献率筛选出噪声模态和信号模态,此时有:
| $ x=\sum\limits_{i=1}^q {\rm{IMF}}_i({\rm { noise }})+\sum\limits_{j=q+1}^Q {\mathrm{IMF}}_j(\rm{signal}) $ | (11) |
式中,q为噪声模态的数量。
5) 将各信号模态分别排成Hankel矩阵Ds(L, K) 形式,其中s为第s个信号模态分量(s=q+1, q+2, …, Q),L=N-K+1≤N/2:
| $ {\boldsymbol{D}}^s=\left[\begin{array}{ccccc} x_1^s & x_2^s & x_3^s & \cdots & x_K^s \\ x_2^s & x_3^s & x_4^s & \cdots & x_{K+1}^s \\ x_3^s & x_4^s & \ddots & \cdots & x_{K+2}^s \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_L^s & x_{L+1}^s & x_{L+2}^s & \cdots & x_N^s \end{array}\right] $ | (12) |
计算其协方差矩阵Cj:
| $ {\boldsymbol{C}}_j=\frac{1}{N} {\boldsymbol{D}}_j^{\mathrm{T}} {\boldsymbol{D}}_j $ | (13) |
对Cj进行特征值分解得到各特征值λij和特征向量Eij,将特征值降序排列后计算得到各主成分aij,表达式如下:
| $ a_i^j=\sum\limits_{m=1}^M x_{i+m} E_m^j, 0 \leqslant i \leqslant N-L $ | (14) |
6) 计算重建成分:
| $ \begin{array}{l} x_i^p=\\ \left\{\begin{array}{l} \frac{1}{i} \sum\limits_{j=1}^i a_{i-j}^p E_j^p, 1 \leqslant i \leqslant L-1 \\ \frac{1}{L} \sum\limits_{j=1}^L a_{i-j}^p E_j^p, L \leqslant i \leqslant N-L+1 \\ \frac{1}{N-i+1} \sum\limits_{j=i-N+L}^L a_{i-j}^p E_j^p, N-L+2 \leqslant i \leqslant N \end{array}\right. \end{array} $ | (15) |
7) 根据特征值贡献率选取前p个重建成分累加得到重建后的模态{IMFq+1R, …, IMFQR},并计算得到重构信号xD:
| $ x^D={\mathrm{IMF}}_{q+1}^R+\cdots+{\mathrm{IMF}}_Q^R $ | (16) |
基于文献[3]与文献[7]中对垂直方向GPS坐标时间序列中半年周期、年周期、准两年周期振幅大小的研究结果,本文模拟实验将半年周期、年周期、两年周期振幅参数ai和bi(i=1, 2, 3)设置为2 mm、3 mm、1.2 mm,时变振幅参数p、q均设置为0.3。趋势项中取初始位置h0=10 mm,速度v=5 mm/a。为避免白噪声对算法性能的影响,本文模拟实验添加接近于真实噪声振幅10 mm/
在模拟实验与实际站点实验中,ICEEMDAN-SSA方法的噪声系数βj=5,迭代次数i=1 000,滑动窗口长度L=5。对于SSA方法,窗口长度选为3 a[1]。WD方法采用Meyer小波滤波器,将信号分解后得到的第7道和第8道信号作为提取的周期信号[2]。对于MOLS方法,在模拟实验中对长度为6 000 d的GPS坐标时间序列进行分段处理,每3 a为一小段,相邻两段重叠时间段为1 a,取均值作为重叠部分进行周期信号重构。
本文选取4个评价指标来衡量各个算法对GPS坐标时间序列周期信号的重构精度,并对比各算法来检验ICEEMDAN-SSA方法的有效性。评价指标包括:1)Misfit:估计信号与不带噪的真实周期信号的标准差;2)谱指数κ:噪声在功率谱密度对数形式下的斜率[9];3)残差振幅Apl:残差估计振幅;4)速度不确定度:由谱指数κ和残差振幅Apl计算得出,具体公式见文献[10]。
3.2 实验结果分析对加入振幅为10 mm/

|
图 1 ICEEMDAN方法提取的周期信号 Fig. 1 Periodic signals extracted by the ICEEMDAN method |
由图 1可知,在ICEEMDAN方法的处理阶段,已初步分解出含有半年、一年、两年周期信号的模态分量。但由于GPS信号的有色噪声规模较大,初步分解后得到的模态分量仍有部分噪声残余。
由图 2可知,在SSA方法的处理阶段,通过对每一个周期信号选取贡献率更高的特征值来重构模态分量,可以对各模态分量进一步去噪,提取出精度更高的各周期分量以及趋势信号。将各个重构的趋势、周期模态分量累加即可得到重构后的时间序列。将ICEEMDAN-SSA与SSA、WD、MOLS、ICEEMDAN方法进行比较,对比结果如图 3、图 4、表 1所示。

|
图 2 基于ICEEMDAN和ICEEMDAN-SSA提取周期信息与趋势信息 Fig. 2 Periodic information and trend information extracted by ICEEMDAN and ICEEMDAN-SSA |
|
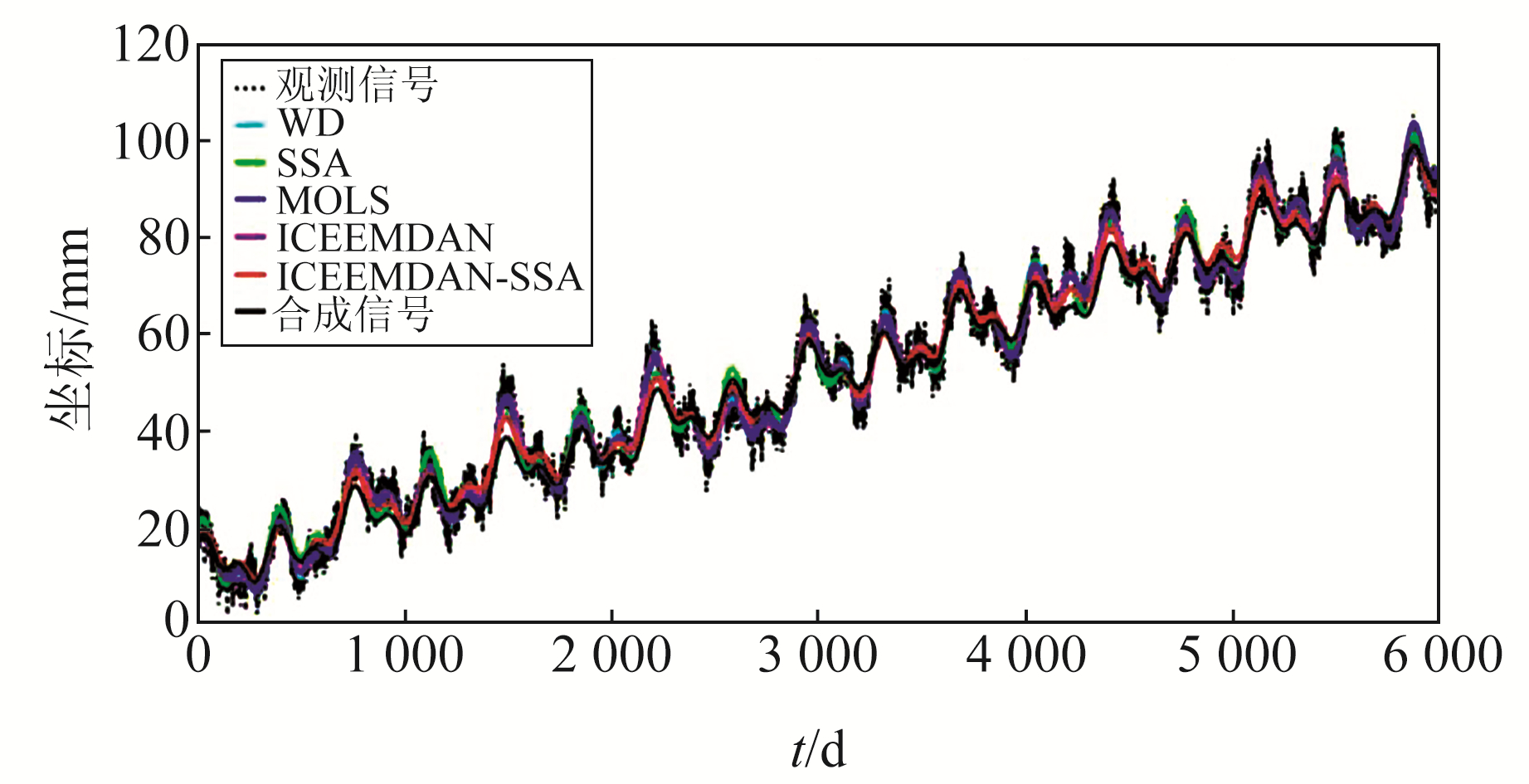
图 3 闪烁噪声振幅为10 mm/ |

|
图 4 闪烁噪声振幅为10 mm/ |
|
|
表 1 闪烁噪声振幅为10 mm/ |
由图 3可知,SSA、MOLS、ICEEMDAN-SSA方法对周期信号均有较好的拟合精度,其中ICEEMDAN-SSA方法的Misfit指标最小,说明该方法的拟合效果最好。结合图 4各方法残差序列的PSD可知,在噪声振幅较大时,WD吸收噪声情况严重。ICEEMDAN方法在2 cpy处与噪声PSD较为相近,在0.5 cpy与1 cpy处均吸收大量噪声,说明ICEEMDAN方法对闪烁噪声去噪效果有限。SSA与MOLS方法效果相近,这两种方法均在0.5 cpy处与噪声PSD较为吻合,在1 cpy以及2 cpy处对噪声PSD曲线拟合较差,说明两者在估计年周期和半年周期信号时存在吸收噪声的情况。ICEEMDAN-SSA方法在2 cpy处与噪声曲线几乎完全吻合,但在0.5 cpy以及1 cpy处与噪声曲线存在少量偏差,说明该方法对半年周期信号的估计精度较高,在估计年、两年周期信号时会吸收少量噪声。
由表 1可知,在闪烁噪声振幅为10 mm/
选取昆明(KUNM)GPS观测站的带趋势数据进行分析,同时也将ICEEMDAN-SSA联合算法与其他几种经典方法进行对比来检验其提取时变振幅周期信号的有效性。以下真实站点数据可通过IGS全球数据中心SOPAC网站下载。本文选取的KUNM站点信息如表 2所示。
|
|
表 2 GPS站点信息 Tab. 2 GPS station information |
为尽可能地减少系统误差,只选取各站点最近3 000 d的数据进行实验。由于GPS坐标时间序列存在数据缺失以及野值干扰的问题,实验开始前需要对数据进行偏移量检测和缺失数据插值等预处理,本文根据3σ准则去除野值[11],然后通过KKF插值方法进行插值[12]。
对于插值后的时间序列,使用ICEEMDAN-SSA方法和其他传统方法分别对KUNM站点N、E、U方向的时间序列进行重构,结果如图 5所示。

|
图 5 KUNM站各方向时间序列重构结果 Fig. 5 Reconstruction results of time series in each direction of KUNM station |
与模拟实验不同的是,在处理实际数据时无法得到真实无噪的干净信号,因此Misfit指标不予计算,在评价各方法时仅考虑速度不确定度、谱指数κ以及残差振幅Apl(表 3)。由表可知,相比于MOLS方法,ICEEMDAN-SSA方法的重构曲线更加平滑,与其他传统方法在拟合效果上更为接近;ICEEMDAN-SSA方法的残差振幅与SSA方法较为接近;与ICEEMDAN方法相比,ICEEMDAN-SSA方法在重构稳定性方面有所提高,不会出现噪声分离失败的现象。
|
|
表 3 通过不同方法得到KUNM站点各指标值 Tab. 3 Index values of KUNM station with different methods |
本文通过计算各种方法得到的重构信号之间的相关系数来了解各个估计方法的有效性(表 4)。由表可知,SSA方法和ICEEMDAN方法与ICEEMDAN-SSA联合重构算法的重构结果更为接近。除此之外,本文涉及的各算法重构结果之间的相关系数在N方向和E方向上均为0.99左右,U方向均不小于0.91,说明本文涉及的所有方法均对实际GPS观测信号具备有效性。
|
|
表 4 ICEEMDAN-SSA在KUNM站N、E、U方向的重建结果与SSA、WD、MOLS、ICEEMDAN重建结果之间的相关系数 Tab. 4 Correlation coefficients between the reconstruction result of ICEEMDAN-SSA and SSA, WD and MOLS in the N, E and U direction of KUNM station |
本文利用ICEEMDAN算法多尺度分解的优势,结合SSA提出基于ICEEMDAN-SSA的GPS坐标时间序列联合估计方法。该方法利用ICEEMDAN在提取周期、趋势时可以将信号和噪声分离的优势,同时可保留不同振幅大小的周期信号;对于单个分离信号,利用SSA精确提取时间序列中的主要特征,可以更好地提升GPS坐标时间序列的重构精度。通过对比模拟数据和实际观测数据,将ICEEMDAN-SSA方法与SSA、WD、MOLS三种传统方法进行对比。
模拟实验表明,本文提出的ICEEMDAN-SSA方法相比上述方法对GPS坐标时间序列的重构效果相对更优。实验结果表明,ICEEMDAN-SSA方法的重构信号与各方法的重构信号均具备较高的相关度,这也表明本文方法具备有效性。综上所述,ICEEMDAN-SSA方法对于GPS坐标时间序列的周期、趋势信号具有更好的估计精度与重构效果。
| [1] |
Chen Q, Dam T, Sneeuw N, et al. Singular Spectrum Analysis for Modeling Seasonal Signals from GPS Time Series[J]. Journal of Geodynamics, 2013, 72: 25-35 DOI:10.1016/j.jog.2013.05.005
(  0) 0) |
| [2] |
Bogusz J. Geodetic Aspects of GPS Permanent Station Non-Linearity Studies[J]. Acta Geodynamica et Geomaterialia, 2015, 12(4): 323-333
(  0) 0) |
| [3] |
Klos A, Bos M S, Bogusz J. Detecting Time-Varying Seasonal Signal in GPS Position Time Series with Different Noise Levels[J]. GPS Solutions, 2018, 22(1)
(  0) 0) |
| [4] |
张双成, 李振宇, 何月帆, 等. GNSS高程时间序列周期项的经验模态分解提取[J]. 测绘科学, 2018, 43(8): 80-84 (Zhang Shuangcheng, Li Zhenyu, He Yuefan, et al. Extracting of Periodic Component of GNSS Vertical Time Series Using EMD[J]. Science of Surveying and Mapping, 2018, 43(8): 80-84)
(  0) 0) |
| [5] |
Torres M E, Colominas M A, Schlotthauer G, et al. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise[C]. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing, Prague, 2011
(  0) 0) |
| [6] |
Colominas M A, Schlotthauer G, Torres M E. Improved Complete Ensemble EMD: A Suitable Tool for Biomedical Signal Processing[J]. Biomedical Signal Processing and Control, 2014, 14(1): 19-29
(  0) 0) |
| [7] |
Pan Y J, Shen W B, Ding H, et al. The Quasi-Biennial Vertical Oscillations at Global GPS Stations: Identification by Ensemble Empirical Mode Decomposition[J]. Sensors, 2015, 15(10): 26 096-26 114 DOI:10.3390/s151026096
(  0) 0) |
| [8] |
Scaife A A, Athanassiadou M, Andrews M, et al. Predictability of the Quasi-Biennial Oscillation and Its Northern Winter Teleconnection on Seasonal to Decadal Timescales[J]. Geophysical Research Letters, 2014, 41(5): 1 752-1 758
(  0) 0) |
| [9] |
Bos M S, Fernandes R M S, Williams S D P, et al. Fast Error Analysis of Continuous GPS Observations[J]. Journal of Geodesy, 2008, 82(3): 157-166 DOI:10.1007/s00190-007-0165-x
(  0) 0) |
| [10] |
Gazeaux J, Williams S, King M, et al. Detecting Offsets in GPS Time Series: First Results from the Detection of Offsets in GPS Experiment[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(5): 2 397-2 407
(  0) 0) |
| [11] |
吴浩, 卢楠, 邹进贵, 等. GNSS变形监测时间序列的改进型3σ粗差探测方法[J]. 武汉大学学报: 信息科学版, 2019, 44(9): 1 282-1 288 (Wu Hao, Lu Nan, Zou Jingui, et al. An Improved 3σ Gross Error Detection Method for GNSS Deformation Monitoring Time Series[J]. Geomatics and Information Science of Wuhan University, 2019, 44(9): 1 282-1 288)
(  0) 0) |
| [12] |
Liu N, Dai W J, Santerre R, et al. A MATLAB-Based Kriged Kalman Filter Software for Interpolating Missing Data in GNSS Coordinate Time Series[J]. GPS Solutions, 2017, 22(1)
(  0) 0) |
2. School of Geography and Information Engineering, China University of Geosciences, 388 Lumo Road, Wuhan 430074, China;
3. School of Information Management and Statistics, Hubei University of Economics, 8 Yangqiaohu Avenue, Wuhan 430205, China
 2022, Vol. 42
2022, Vol. 42


