近20 a来,全球IGS基准站不断积累的时间序列数据为大地测量和地球动力学研究提供了宝贵的数据基础[1-3]。这些数据可有效反映由地球物理效应引起的长期变化趋势和非线性变化[4],因此对GNSS坐标时间序列进行分析有助于地壳板块运动监测[5]、大坝或桥梁变形监测[6-7]、全球或区域坐标系维护[8-9]等领域的发展。通过分析GNSS坐标时间序列,可以预测连续时间点坐标,为判断运动趋势提供重要依据。研究发现,GNSS坐标时间序列中高程方向的噪声分量通常大于水平方向,且噪声组合模型丰富,因此构建高精度的GNSS高程时间序列预测模型具有较大困难[10-12]。
目前,已有许多学者在GNSS高程坐标时间序列预测研究中基于机器学习、深度学习等算法构建相应的预测模型,并针对GNSS高程坐标时间序列的信号特征进行高精度的预测研究工作[11]。但是相关研究仍存在一定不足:1)模型预测精度容易受到异常值以及缺失值影响,抗干扰能力较弱,导致使用模型时对数据质量具有较高的要求。2)模型单次预测精度无法保证随着预测时间跨度的增长持续保持在较高水平上,在进行长期预测时需要进行滚动预测以保持模型精度,从而会增大模型的运行载荷。3)在相同参数设置和数据集下,部分模型的预测结果存在差异,并且无法进行动态调整。
针对这些问题,本文提出一种Prophet-XGBoost组合预测模型用于GNSS高程时间序列预测,并通过SOPAC公布的实测高程数据对本文方法的适用性和有效性进行检验。首先检验XGBoost模型和Prophet模型在GNSS时间序列中的适应度;再基于单模型在长期预测中表现出的特点,针对XGBoost模型对于趋势项部分预测能力较弱和Prophet模型对于非线性部分预测能力较弱的问题,构建Prophet-XGBoost组合预测模型;最后通过ALGO、ALRT和BRST基准站U分量坐标时间序列数据对模型预测精度进行检验。
1 模型原理与评价指标 1.1 XGBoost模型XGBoost作为一种集成学习算法,可通过构建多个CART树对数据集进行预测,然后集成多个树模型的预测结果,从而输出最终预测数据。与同属于树模型算法的GBDT算法相比,XGBoost算法更为高效,并且在算法方面也进行过改进。XGBoost使用二阶泰勒展开式逼近目标函数的泛化误差部分,可有效简化目标函数的计算;XGBoost还可通过在目标函数中加入正则项来降低模型预测的波动性以及改善模型过拟合现象[13]。
假设存在数据集A={(xi, yi): i=1,…,n, xi∈
| $ \hat{y}_i=\varphi\left(x_i\right)=\sum\limits_{k=1}^K f_k\left(x_i\right) $ | (1) |
式中,fk表示决策树,fk(xi) 表示第k棵树赋予第i个观测值的分数。同时,使用函数fk时,下述正则化目标函数应被最小化:
| $ L(\varphi)=\sum\limits_i l\left(y_i, \hat{y}_i\right)+\sum\limits_k \varOmega\left(f_k\right) $ | (2) |
式中,l为损失函数。为防止模型过于复杂,在模型中设置惩罚项Ω:
| $ \varOmega\left(f_k\right)=\gamma T+\frac{1}{2} \lambda\|w\|^2 $ | (3) |
式中,γ可控制惩罚项中枝叶数量T,λ可控制惩罚项中枝叶重量w。设置Ω(fk) 项不仅可以简化算法生成模型,同时可以防止模型过拟合。
XGBoost算法采用迭代法最小化目标函数。模型通过增加fj项在第j次迭代后得到减小的目标函数:
| $ L^j=\sum\limits_{i=1}^n l\left(y_i, \hat{y}_i^{(j-1)}+f_j\left(x_i\right)\right)+\varOmega\left(f_j\right) $ | (4) |
式(4)可以通过泰勒展开进行简化,并且可以推导出决策树从给定节点分裂后的损失减少公式:
| $ \begin{gathered} L_{\text {split }}= \\ \frac{1}{2}\left[\frac{\left(\sum\limits_{i \in I_L} g_i\right)^2}{\sum\limits_{i \in I_L} h_i+\lambda}+\frac{\left(\sum\limits_{i \in I_R} g_i\right)^2}{\sum\limits_{i \in I_R} h_i+\lambda}-\frac{\left(\sum\limits_{i \in I} g_i\right)^2}{\sum\limits_{i \in I} h_i+\lambda}\right]-\gamma \end{gathered} $ | (5) |
式中,I为当前节点中可用观测数据的一个子集,IL和IR分别为分裂后左右节点中可用观测数据的一个子集。函数gi和hi可表示为:
| $ g_i=\partial_{\hat{y}_i^{(j-1)}} l\left(y_i, \hat{y}_i^{(j-1)}\right) $ | (6) |
| $ h_i=\partial_{\hat{y}_i^{(j-1)}}^2 l\left(y_i, \hat{y}_i^{(j-1)}\right) $ | (7) |
从推导Lsplit公式中可找到任意给定节点的最佳分裂,该函数只依赖于损失函数和正则化参数γ。同时,基于式(5),XGBoost算法可以优化任何损失函数,并且提供一阶和二阶梯度。
1.2 Prophet模型Prophet模型是一种基于加性模型的时间序列预测模型,由趋势项、周期项和假日项组成[14-15],表达式为:
| $ y(t)=g(t)+s(t)+h(t)+\varepsilon_t $ | (8) |
式中,g(t) 为趋势项;s(t) 为周期项;h(t) 为假日项,该项在GNSS时间序列中通常不存在,因此建模过程中不予考虑;εt为残差项,即模型未能预测到的随机趋势。
在Prophet模型中,趋势项包含逻辑回归函数和分段线性函数两个重要函数。根据GNSS高程时间序列的趋势变化特点,选用逻辑回归函数来计算趋势项。同时,Prophet模型使用傅里叶级数表示时间序列的周期性:
| $ s(t)=\sum\limits_{n=1}^N\left(a_n \cos \left(\frac{2 \pi n t}{P}\right)+b_n \sin \left(\frac{2 \pi n t}{P}\right)\right) $ | (9) |
式中,P为时间序列周期,P=365.25时为年周期项,P=7时为周周期项。因此,Prophet模型在进行GNSS日坐标时间序列分解时会分别输出年周期项和周周期项。
1.3 精度评价指标使用平均绝对误差(MAE)和均方根误差(RMSE)作为模型预测精度的评价指标:
| $ {\mathrm{MAE}}=\frac{1}{n} \sum\limits_{i=1}^n\left|y_i-\hat{y}_i\right| $ | (10) |
| $ {\mathrm{RMSE}}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(y_i-\hat{y}_i\right)^2} $ | (11) |
式中,yi为原始值,
通过引入Pearson相关系数判断预测时间序列和原始时间序列之间的相关性。Pearson相关系数将时间序列视为变量,从而计算两个时间序列之间的相关性,其计算公式为:
| $ \rho_{Y \hat{Y}}=\frac{E(Y \hat{Y})-E(Y) E(\hat{Y})}{\sigma_Y \sigma_{\hat{Y}}} $ | (12) |
式中,Y和
为验证Prophet-XGBoost模型的有效性,选取IGS基准站实测数据作为数据集。选用ALGO、ALRT和BRST站2010~2015年U分量日坐标时间序列作为实验数据,该数据来源于SOPAC(scripps orbit and permanent array center)。数据基本情况如表 1(单位mm)所示。
|
|
表 1 数据基本情况 Tab. 1 Basic information of data |
为检验XGBoost模型和Prophet模型对于GNSS坐标时间序列预测的适用性,引入经典时间序列预测模型ARIMA模型作为对比。选用ALGO站数据作为实验数据,分别用ARIMA模型、XGBoost模型和Prophet模型对数据集进行预测,将预测值与原始数据值进行对比,得到相应的MAE值和RMSE值。
该实验数据集中2010~2014年数据为训练集,2015年数据为验证集,共包含2 149个日坐标数据,缺失数据天数为42,数据完整率为98.08%,训练中最大连续缺失数据时间跨度为7 d。
由表 1和四分位距值(interquartile range,IQR)计算可知,该实验数据集中含有少量异常值。因此,该数据训练集中包含异常值、缺失值、连续缺失值等条件,可以更好地检验模型对于GNSS实测数据预测的适用性。各模型精度见表 2(单位mm)。
|
|
表 2 不同模型精度对比 Tab. 2 Comparison of accuracy of different models |
由表 2可知,相较于ARIMA模型,XGBoost模型和Prophet模型在MAE和RMSE两个精度评价指标上均有优势。基于3个模型的预测原理可知,在长时间跨度的GNSS坐标时间序列预测研究中,ARIMA模型精度更容易受到预测时间长度的影响,而XGBoost模型和Prophet模型的预测精度随预测跨度变化而变化的幅度较小,且XGBoost模型的算法实现更为简便,具有更高的预测效率。因此,XGBoost模型和Prophet模型均可应用于GNSS坐标时间序列预测,并在实测数据实验中具有适用性。图 1为ALGO站Prophet模型预测结果,其中离散点为原始时间序列值,曲线为拟合预测值。
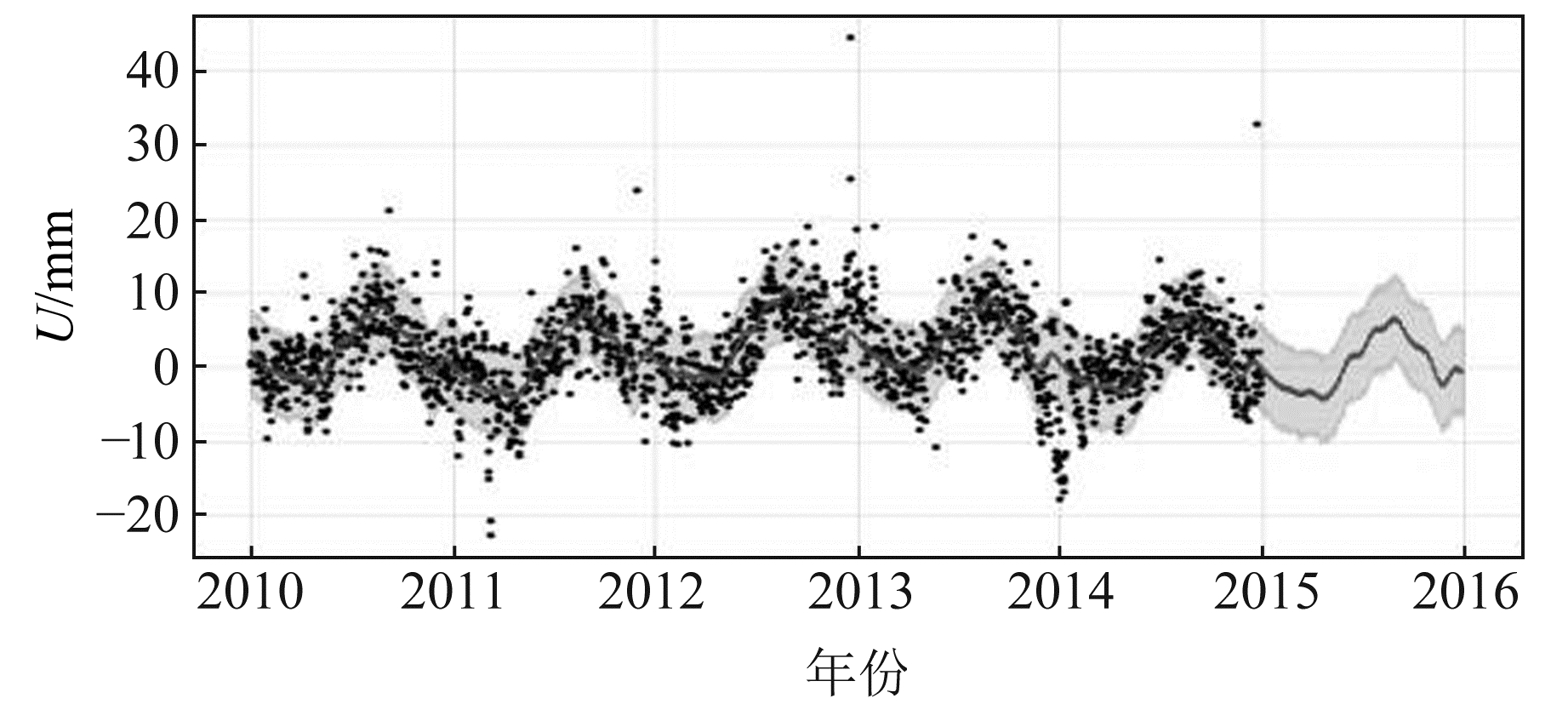
|
图 1 ALGO站Prophet模型预测结果 Fig. 1 Prediction results of Prophet model of ALGO station |
基于XGBoost模型和Prophet模型在GNSS坐标时间序列预测中表现出的模型特性,构建Prophet-XGBoost组合预测模型,以更好地发挥两个模型的预测优势,削弱模型对于GNSS时间序列部分分解项预测能力不足的影响,进而实现更高精度的GNSS坐标时间序列预测。图 2为Prophet-XGBoost模型构建流程。
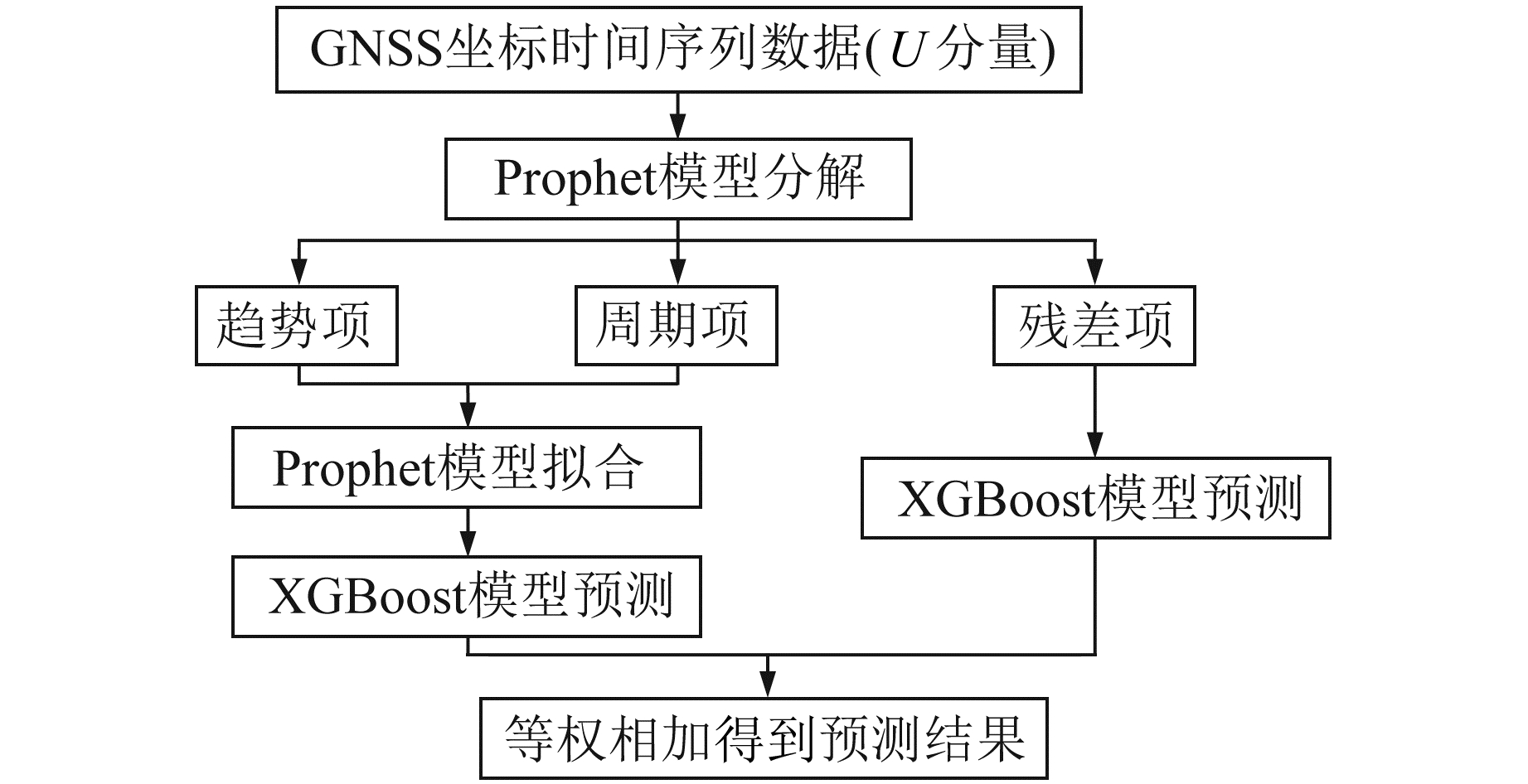
|
图 2 Prophet-XGBoost模型构建流程 Fig. 2 Construction process of Prophet-XGBoost model |
Prophet-XGBoost模型实现流程如下:
1) 通过Prophet模型对GNSS坐标时间序列U方向数据进行分解,将时间序列分解为趋势项、周期项和残差项,其中周期项由年周期项和周周期项等权相加构成。图 3为ALGO站Prophet模型分解结果。

|
图 3 ALGO站Prophet模型分解结果 Fig. 3 Decomposition results of Prophet model of ALGO station |
2) 通过Prophet模型对分解出的趋势项和周期项进行拟合,然后使用XGBoost模型对拟合时间序列进行预测,得到预测值yfit。图 4为ALGO站XGBoost模型拟合时间序列预测结果。

|
图 4 ALGO站XGBoost模型拟合时间序列预测结果 Fig. 4 Prediction results of fitting time series of XGBoost model of ALGO station |
3) 使用XGBoost模型对Prophet模型分解时间序列过程中遗留的残差项进行预测,得到预测值yresidual。
4) 将两个预测结果等权相加,得到预测值ypred:
| $ y_{\text {pred }}=y_{\text {fit }}+y_{\text {residual }} $ | (13) |
本文选用ALGO、ALRT、BRST三个IGS站U分量GNSS坐标时间序列作为实验数据,分别采用XGBoost模型、Prophet模型和Prophet-XGBoost模型进行预测。其中,ALGO和ALRT站纬度差异较大,ALGO和BRST站经度差异较大。预测精度对比结果如表 3所示。
|
|
表 3 预测精度对比 Tab. 3 Comparison of prediction accuracy |
由表 3可知,相较于XGBoost模型和Prophet模型,ALGO站Prophet-XGBoost模型的MAE值分别降低7.4%和11.5%,RMSE值分别降低16.6%和3.5%;ALRT站Prophet-XGBoost模型的MAE值分别降低7.1%和20.5%,RMSE值分别降低7.2%和6.5%;BRST站Prophet-XGBoost模型的MAE值分别降低10.5%和9.2%,RMSE值分别降低5.6%和3.5%。相较于Prophet模型,组合模型的RMSE值降低幅度较小,这是因为Prophet-XGBoost模型进行预测时的拟合数据是由Prophet模型拟合所得。对Prophet-XGBoost模型预测结果和原始数据值进行相关性检验,通过引入Pearson相关系数计算ALGO、ALRT和BRST三个站的ρ值分别为0.53、0.64和0.49,其中ALGO和BRST两个站预测结果和原始数据呈中等相关,ALRT站预测结果和原始数据呈强相关。
以ALGO站为例,对比分析XGBoost模型、Prophet模型和Prophet-XGBoost模型预测结果误差分布。图 5为各模型预测结果绝对误差分布情况。

|
图 5 各模型预测结果绝对误差分布 Fig. 5 Distribution of absolute error of prediction results of each model |
由图 5可知,Prophet-XGBoost组合模型的较高精度预测结果占比最高,即相较于Prophet和XGBoost单模型预测结果,组合模型准确率得到提升。图 6为模型预测结果误差对比。
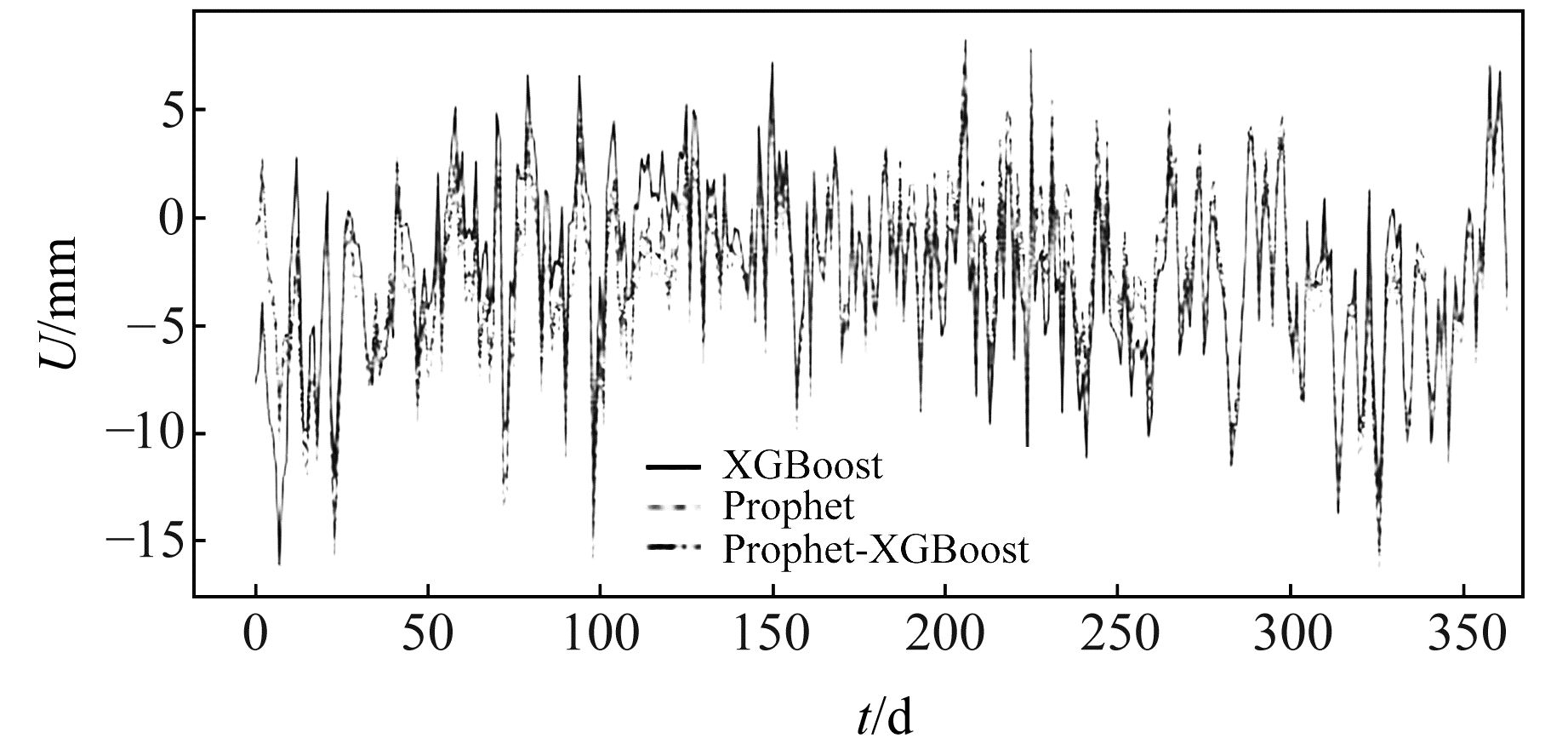
|
图 6 模型预测结果误差对比 Fig. 6 Error comparison of prediction results of each model |
由图 6可知,相较于XGBoost模型,Prophet-XGBoost组合模型的误差变化幅度和凸点值更小;Prophet模型和Prophet-XGBoost组合模型的误差变化趋势较为一致,但Prophet-XGBoost组合模型误差更小。结合图 4结果可知,Prophet模型对于时间序列的趋势变化较为敏感。
3 结语本文基于XGBoost模型和Prophet模型提出一种GNSS高程时间序列预测组合模型Prophet-XGBoost。在数据处理阶段,利用Prophet模型对时间序列进行分解,将时间序列分解成3个主要组成部分,有利于XGBoost模型在预测时提取时间序列中不同组成部分的特征,减弱预测模型提取特征时受到其他组成部分的影响。得益于此,XGBoost模型可以进行更高精度的GNSS坐标时间序列预测工作,也可弥补两个模型在单模型预测时存在的问题。此外,在计算预测结果时,也可依据XGBoost模型提供的特征分数进行定权相加。
XGBoost模型和Prophet模型在实验过程中也存在需要改进之处:XGBoost模型对于GNSS坐标时间序列的趋势变化不够敏感以及Prophet模型对于GNSS坐标时间序列非线性部分预测能力较弱。同时考虑到XGBoost模型的特征项构建具有很大灵活性,研究人员可以使用非GNSS坐标时间序列数据辅助进行特征构造,如水文载荷对GNSS坐标时间序列U方向振幅具有较为显著的影响[17]。因此,在以后研究中可以将水文载荷等因素纳入特征构造条件中,从而通过更多的特征子集进行模型构建和预测。基于该特性,Prophet-XGBoost模型可以作为通用预测模型,将其推广到其他研究领域,如海平面时间序列预测、天气预报和发病率预测,可极大增强该模型的适用性。
| [1] |
姜卫平, 王锴华, 李昭, 等. GNSS坐标时间序列分析理论与方法及展望[J]. 武汉大学学报: 信息科学版, 2018, 43(12): 2 112-2 123 (Jiang Weiping, Wang Kaihua, Li Zhao, et al. Prospect and Theory of GNSS Coordinate Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2018, 43(12): 2 112-2 123)
(  0) 0) |
| [2] |
Blewitt G, Lavallée D. Effect of Annual Signals on Geodetic Velocity[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B7)
(  0) 0) |
| [3] |
Deng L S, Jiang W P, Li Z, et al. Assessment of Second- and Third-Order Ionospheric Effects on Regional Networks: Case Study in China with Longer CMONOC GPS Coordinate Time Series[J]. Journal of Geodesy, 2017, 91(2): 207-227 DOI:10.1007/s00190-016-0957-y
(  0) 0) |
| [4] |
Wang J, Jiang W P, Li Z, et al. A New Multi-Scale Sliding Window LSTM Framework(MSSW-LSTM): A Case Study for GNSS Time-Series Prediction[J]. Remote Sensing, 2021, 13(16)
(  0) 0) |
| [5] |
Montillet J P, Williams S D P, Koulali A, et al. Estimation of Offsets in GPS Time-Series and Application to the Detection of Earthquake Deformation in the Far-Field[J]. Geophysical Journal International, 2015, 200(2): 1 207-1 221 DOI:10.1093/gji/ggu473
(  0) 0) |
| [6] |
Xi R J, Jiang W P, Meng X L, et al. Rapid Initialization Method in Real-Time Deformation Monitoring of Bridges with Triple-Frequency BDS and GPS Measurements[J]. Advances in Space Research, 2018, 62(5): 976-989 DOI:10.1016/j.asr.2018.06.018
(  0) 0) |
| [7] |
Chen Q S, Jiang W P, Meng X L, et al. Vertical Deformation Monitoring of the Suspension Bridge Tower Using GNSS: A Case Study of the Forth Road Bridge in the UK[J]. Remote Sensing, 2018, 10(3)
(  0) 0) |
| [8] |
Altamimi Z, Rebischung P, Métivier L, et al. ITRF2014: A New Release of the International Terrestrial Reference Frame Modeling Nonlinear Station Motions[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(8): 6 109-6 131 DOI:10.1002/2016JB013098
(  0) 0) |
| [9] |
Li Z, Chen W, Dam T, et al. Comparative Analysis of Different Atmospheric Surface Pressure Models and Their Impacts on Daily ITRF2014 GNSS Residual Time Series[J]. Journal of Geodesy, 2020, 94(4)
(  0) 0) |
| [10] |
贺小星, 花向红, 鲁铁定, 等. 时间跨度对GPS坐标序列噪声模型及速度估计影响分析[J]. 国防科技大学学报, 2017, 39(6): 12-18 (He Xiaoxing, Hua Xianghong, Lu Tieding, et al. Effect of Time Span on GPS Time Series Noise Model and Velocity Estimation[J]. Journal of National University of Defense Technology, 2017, 39(6): 12-18)
(  0) 0) |
| [11] |
李威, 鲁铁定, 贺小星, 等. 基于Prophet-RF模型的GNSS高程坐标时间序列预测分析[J]. 大地测量与地球动力学, 2021, 41(2): 116-121 (Li Wei, Lu Tieding, He Xiaoxing, et al. Prediction and Analysis of GNSS Vertical Coordinate Time Series Based on Prophet-RF Model[J]. Journal of Geodesy and Geodynamics, 2021, 41(2): 116-121)
(  0) 0) |
| [12] |
Tao R, Lu T D, Cheng Y M, et al. An Improved GNSS Vertical Time Series Prediction Model Using EWT[C]. China Satellite Navigation Conference, Nanchang, 2021
(  0) 0) |
| [13] |
Pan B Y. Application of XGBoost Algorithm in Hourly PM2.5 Concentration Prediction[J]. IOP Conference Series: Earth and Environmental Science, 2018, 113
(  0) 0) |
| [14] |
Taylor S J, Letham B. Forecasting at Scale[J]. The American Statistician, 2018, 72(1): 37-45 DOI:10.1080/00031305.2017.1380080
(  0) 0) |
| [15] |
翟笃林, 张学民, 熊攀, 等. Prophet时序预测模型在电离层TEC异常探测中的应用[J]. 地震, 2019, 39(2): 46-62 (Zhai Dulin, Zhang Xuemin, Xiong Pan, et al. Detection of Ionospheric TEC Anomalies Based on Prophet Time-Series Forecasting Model[J]. Earthquake, 2019, 39(2): 46-62)
(  0) 0) |
| [16] |
陈志方. 中国货币政策的有效性评估——基于皮尔森相关系数的分析[J]. 中国商论, 2020(6): 48-49 (Chen Zhifang. The Effectiveness Evaluation of China's Monetary Policy-Analysis Based on Pearson Correlation Coefficient[J]. China Journal of Commerce, 2020(6): 48-49)
(  0) 0) |
| [17] |
He Y F, Nie G G, Wu S G, et al. Analysis and Discussion on the Optimal Noise Model of Global GNSS Long-Term Coordinate Series Considering Hydrological Loading[J]. Remote Sensing, 2021, 13(3)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


