2. 中国矿业大学环境与测绘学院,江苏省徐州市大学路1号,221116
2000年Flores等[1]率先进行对流层三维大气水汽场的反演实验,随后国内外诸多学者基于对流层层析实验思路提出大量水汽层析技术的理论模型。目前层析方程组的解算方法主要有奇异值分解法、最小二乘法、卡尔曼滤波法和代数重构法[2],其中代数重构算法(ART)具有抗噪性强、稳定高效等优点,同时能够避免系数矩阵的求逆运算,在解算系数矩阵严重病态的层析方程组时具有巨大优势[3-4]。
ART通过投影的方式使迭代解逐步逼近层析方程组的解算域。层析方程组除了包含GNSS信号的观测方程外,通常还额外附加约束条件方程作为伪观测方程,以解决层析方程组的不适定性问题[5]。约束条件方程在ART迭代初期具有恢复无信号体素块内水汽参数的重要作用,但实际精度相对较低。随着迭代的进行,所有无信号体素块内的水汽参数逐渐恢复,此时迭代解若继续以相同的投影修正权重向低精度约束条件超平面投影,容易造成迭代解偏离GNSS信号观测方程组解算域的现象出现。为使ART的迭代解向精度更高的层析方程超平面投影,可引入高度角定权法控制GNSS信号观测方程组的投影修正量[4],而目前尚未提出控制附加约束条件方程组投影修正权重的方法。针对上述问题,本文提出一种约束条件变权的代数重构算法VWART,该算法以相邻2次迭代过程中约束条件方程观测值与重构值的残差为依据,对该约束条件方程的投影权重进行实时优化,以降低因迭代解偏离GNSS真观测方程组解算域而造成的误差,提高ART迭代结果的精度和可靠性。同时,利用香港地区CORS网GNSS观测数据进行水汽层析实验,对约束条件方程权重不变的传统ART和VWART进行对比验证,并对2种算法反演的层析结果进行精度评定。
1 GNSS水汽层析的基本原理GNSS水汽层析技术是根据层析区域内卫星信号传播路径上的斜路径水汽含量(SWV)来反演该区域内的三维水汽场[6],将对流层层析区域离散化,以每条信号的SWV为观测值建立层析区域内信号传播路径长度、水汽密度参数与SWV的函数关系,即
| $ \mathrm{SWV}_{i}=\sum\limits_{j=1}^{n} l_{i j} D_{j} $ | (1) |
式中,SWVi为第i条卫星信号传播路径上的斜路径水汽含量,lij为第i条信号穿过第j个体素块的直线长度,Dj为第j个体素块内的待求水汽密度,n为总体素块个数。式(1)模型构建的层析方程组的系数矩阵往往严重秩亏,因此一般通过附加约束条件的方法来解决层析方程组的不适定性问题[7]。常见的约束条件包括垂直约束和水平约束,其中垂直约束采用指数函数[8],水平约束采用高斯加权函数[9]。结合观测方程和约束条件方程的层析方程组可表示为:
| $ \underset{m\times 1}{\mathop{\left[ \begin{matrix} \underset{o\times 1}{\mathop{\bf{SW}{{\bf{V}}_{\text{Obs}}}}}\, \\ \underset{v\times 1}{\mathop{\bf{0}}}\, \\ \underset{h\times 1}{\mathop{\bf{0}}}\, \\ \end{matrix} \right]}}\, =\underset{m\times n}{\mathop{\left[ \begin{matrix} \underset{o\times n}{\mathop{{{\boldsymbol{A}}_{\text{Obs}}}}}\, \\ \underset{v\times n}{\mathop{{{\boldsymbol{A}}_{\text{V}}}}}\, \\ \underset{h\times n}{\mathop{{{\boldsymbol{A}}_{\text{H}}}}}\, \\ \end{matrix} \right]}}\, \underset{n\times 1}{\mathop{\boldsymbol{D}}}\, +\underset{m\times 1}{\mathop{\left[ \begin{matrix} \underset{o\times n}{\mathop{{{\boldsymbol{\varDelta} }_{\text{Obs}}}}}\, \\ \underset{v\times n}{\mathop{{{\boldsymbol{\varDelta} }_{\text{V}}}}}\, \\ \underset{h\times n}{\mathop{{{\boldsymbol{\varDelta} }_{\text{H}}}}}\, \\ \end{matrix} \right]}}\, $ | (2) |
式中,SWVObs为斜路径水汽含量的观测值向量;AObs、AV、AH分别为观测值系数矩阵、垂直约束系数矩阵和水平约束系数矩阵;D为水汽密度参数向量;n为水汽密度参数个数;Δ为观测噪声;m为方程总个数,其数值等于各部分方程个数o、v、h之和。
2 GNSS水汽层析的约束条件变权代数重构算法 2.1 代数重构算法ART运用迭代的方式获得方程组的迭代解,以迭代初值为起点,依次向各方程所代表的多维超平面投影,实现迭代解向超平面相交解算域的逐步逼近,在满足迭代终止条件时停止,便可输出方程组的迭代解。该算法在解算水汽层析方程组时避免系数矩阵的求逆运算,迭代速度快、解算效率高,具有较高的稳定性和较强的抗噪性,即使在观测方程较少、信号噪声较大的不利条件下,也能获得稳定且高精度的迭代解,因此被成功应用于电离层和对流层层析解算中[10]。GNSS水汽层析中传统ART迭代公式为:
| $ \boldsymbol{x}_{j}^{k}=\boldsymbol{x}_{j}^{k-1}+\lambda \frac{\boldsymbol{a}_{i, j}}{\sum\limits_{j=1}^{n} \boldsymbol{a}_{i, j}^{2}}\left(\boldsymbol{b}_{i}-\sum\limits_{j=1}^{n} \boldsymbol{a}_{i, j} \boldsymbol{x}_{j}^{k-1}\right) $ | (3) |
式中,xjk为第k次迭代中第j个体素块的水汽密度,当k=1时,x0为迭代的初值向量;n为总体素块数量;λ为松弛因子;ai, j为层析方程系数矩阵中第i行、第j列元素;bi为观测值列向量中第i行元素。ART每次迭代时将上次迭代解作为初值,逐次向第i个n维超平面投影,每次投影都会对待求参数向量xk进行修正。修正过程为:首先计算观测值bi与重构值〈ai,xk〉之间的残差;然后根据第j个待求参数xjk所对应的方程系数ai, j决定残差的分配量,实现对待求参数向量xk的修正;最后在所有n维超平面投影修正完成后得到第(k+1)次迭代结果。
2.2 约束条件变权的代数重构算法GNSS水汽层析的层析方程组一般由观测方程组和约束条件方程组2部分构成。由于受到卫星和测站的几何分布以及层析区域建模时格网划分等因素的影响,层析区域中存在许多无卫星信号穿过的体素块,约束条件方程组在ART迭代解算初期有助于恢复这些体素块内的水汽参数。随着迭代的进行,所有体素块逐渐恢复水汽参数,此时约束条件方程组的作用将大幅降低,过强的约束条件反而会使迭代解偏离真观测方程交会的解算域,进而造成较大误差。
考虑到上述问题,本文在传统ART的基础上对约束条件方程组引入一种随迭代实时变化的权重模型,提出一种新的约束条件变权代数重构算法VWART。VWART的迭代公式于观测方程组部分(1≤i≤o,o为观测方程组数量)见式(3),于约束条件方程组部分(o+1≤i≤m,m为层析方程组总个数)为:
| $ \boldsymbol{x}_{j}^{k}=\boldsymbol{x}_{j}^{k-1}+\lambda \frac{\boldsymbol{a}_{i, j}}{\sum\limits_{j=1}^{n} \boldsymbol{a}_{i, j}^{2}} \boldsymbol{P}_{i}^{k} \left(\boldsymbol{b}_{i}-\sum\limits_{j=1}^{n} \boldsymbol{a}_{i, j} \boldsymbol{x}_{j}^{k-1}\right) $ | (4) |
式中各参数和未知数的含义与式(3)相同。Pik为第k次迭代时约束条件方程组第i行的权重,其数值基于约束条件方程的观测值bi与重构值〈ai,xk-1〉之间的残差计算得到。当k=1时,P1为第1次迭代时使用的权重初值,其在每次迭代中的表达式为:
| $ \left\{\begin{array}{l} \boldsymbol{P}_{i}^{1}=1, k=1 \\ \boldsymbol{P}_{i}^{k}=\boldsymbol{P}_{i}^{k-1}\left|\frac{\boldsymbol{b}_{i}-\left\langle\boldsymbol{a}_{i}, \boldsymbol{x}^{k-2}\right\rangle}{\boldsymbol{b}_{i}-\left\langle\boldsymbol{a}_{i}, \boldsymbol{x}^{k-1}\right\rangle}\right|, k \geqslant 2 \end{array}\right. $ | (5) |
本文利用香港CORS网中19个测站的GNSS观测数据进行水汽层析实验,层析区域水平范围为113°50′38.4″~114°23′2.4″E、22°12′14.4″~22°33′50.4″N,水平分辨率为5′24″ ×5′24″[11];垂直范围以京士柏探空气象站(HKKP)的探空水汽密度为依据,将水汽密度为0.1 g/m3的高度作为对流层层顶。2009~2018年共计10 a的8月探空水汽密度统计结果表明,对流层层顶平均高度为10 560 m。采用上疏下密的非均匀分层方式对垂直方向建模[6, 12],建模后将层析区域在垂直方向上划分为13层,其中第1~6层的垂直分辨率为350 m,第7~13层的垂直分辨率分别为383 m、452 m、551 m、708 m、990 m、1 659 m、3 717 m。
研究时段为2019-08(共31 d),属于香港地区的夏季,气候炎热,受热带气旋“韦帕”及“白鹿”的影响,共发生3次大规模降雨。实验利用GAMIT10.7软件对19个测站的GNSS原始观测数据进行处理,解算策略如表 1所示。
|
|
表 1 GAMIT10.7解算策略 Tab. 1 Strategy of GAMIT10.7 |
本文分别基于约束条件方程权重不变的传统ART和本文提出的VWART方法设计2种方案进行层析实验,解算水汽密度参数。ART中初值的设置是影响迭代解算结果的重要因素,高精度的迭代初值可同时提高迭代速度和层析结果质量。本文以HKKP探空站2009~2018年每年8月高精度探空数据获得的水汽廓线信息作为迭代初值,利用原始探空数据精确计算出位于探空气球高度处的水汽密度,对分布于各分层高度区间内的探空水汽密度取平均值,即可获得各层水汽密度的迭代初值。利用HKKP探空站的原始探空数据计算HKKP站位置天顶方向的探空水汽密度ρRS,具体公式为:
| $ \rho_{\mathrm{RS}}=\frac{e}{R_{v} \cdot T} $ | (6) |
式中,Rv=461.5 J·kg-1·K-1;T为温度;e为水汽压,其数值可由世界气象组织推荐的Goff-Gratch公式计算得到[13]。
迭代终止的条件设置为:
| $ \left\|\boldsymbol{x}^{k+1}-\boldsymbol{x}^{k}\right\|_{2} < 10^{-5} $ | (7) |
式中,xk为第k次的迭代解,当相邻2次迭代解满足式(7)时,迭代终止。
4 GNSS水汽层析实验结果分析 4.1 层析解算结果的综合分析本文以原始探空数据计算获得的探空水汽密度为参考值,对层析反演结果进行验证。探空数据具有精度高、垂直分辨率高等特性,因此以探空数据作为参考标准对层析反演结果进行验证切实可行[14-15]。由于探空数据具有低时间分辨率的局限性,且HKKP探空站的探空数据仅UTC 00:00和UTC 12:00两个时刻可被获取,故本文仅利用探空水汽密度对实验时段内每日UTC 00:00~00:30及UTC 12:00~12:30两个时段的层析结果进行分析。除探空数据资料外,本文还以ECMWF数据资料为标准对层析反演结果进行验证。ECMWF的第4代产品ERA-Interim可提供全球再分析资料,其中包含温度、相对湿度等用于计算水汽密度的格网数据资料,最小空间分辨率可达7′30″ ×7′30″[7, 16]。表 2(单位g/m3)为分别以探空数据和ECMWF数据为参考,传统ART(方案A)和VWART(方案B)层析解算结果的RMSE(均方根误差)、MAE(平均绝对误差)和IQR(四分位区间)对比。
|
|
表 2 2种方案层析解算结果的RMSE、MAE和IQR对比 Tab. 2 RMSE, MAE and IQR of the tomography results for two projects |
由表 2可知,无论以哪种数据为参考标准,方案B的RMSE、MAE和IQR均小于方案A。以探空数据为参考时,VWART对RMSE、MAE和IQR的改进率分别为20.334%、18.126%和11.995%;以ECMWF数据为参考时,VWART的改进率分别为36.625%、29.096%和25.299%,说明相较于传统ART方法,VWART具有更高的层析解算精度。
图 1为2种实验方案解算获得的层析水汽密度与探空水汽密度对照散点图。由图可见,二者均呈橄榄形,其中方案B的散点相较于方案A表现出更强的聚集性。方案B散点的RMSE比方案A低19.558%,方案B的确定系数R2高于方案A,且方案B拟合曲线表达式的斜率也更接近于1。通过散点图的对比进一步表明,VWART解算结果的精度明显优于传统ART。

|
图 1 2种方案层析水汽密度与探空水汽密度对照散点图 Fig. 1 Scatter plots of tomogtaphy water vapor density versus sounding water vapor density for two projects |
图 2为2种方案层析解算结果残差的正态分布曲线。可以看出,方案B残差正态分布曲线的顶点位置高于方案A,说明方案B有更多的残差值位于0附近;方案B残差正态分布曲线具有更低的方差值和更接近于0的期望值,说明方案B的残差分布更加集中。方案A有相当一部分的残差分布于[-1,1]区间外,甚至有部分残差分布于[-4,4]区间外;而方案B的大部分残差分布于[-1,1]内。由此可知,方案B残差分布情况的集中性和稳定性整体优于方案A,说明相比于传统ART,VWART解算结果的整体稳定性和可靠性有十分显著的提高。
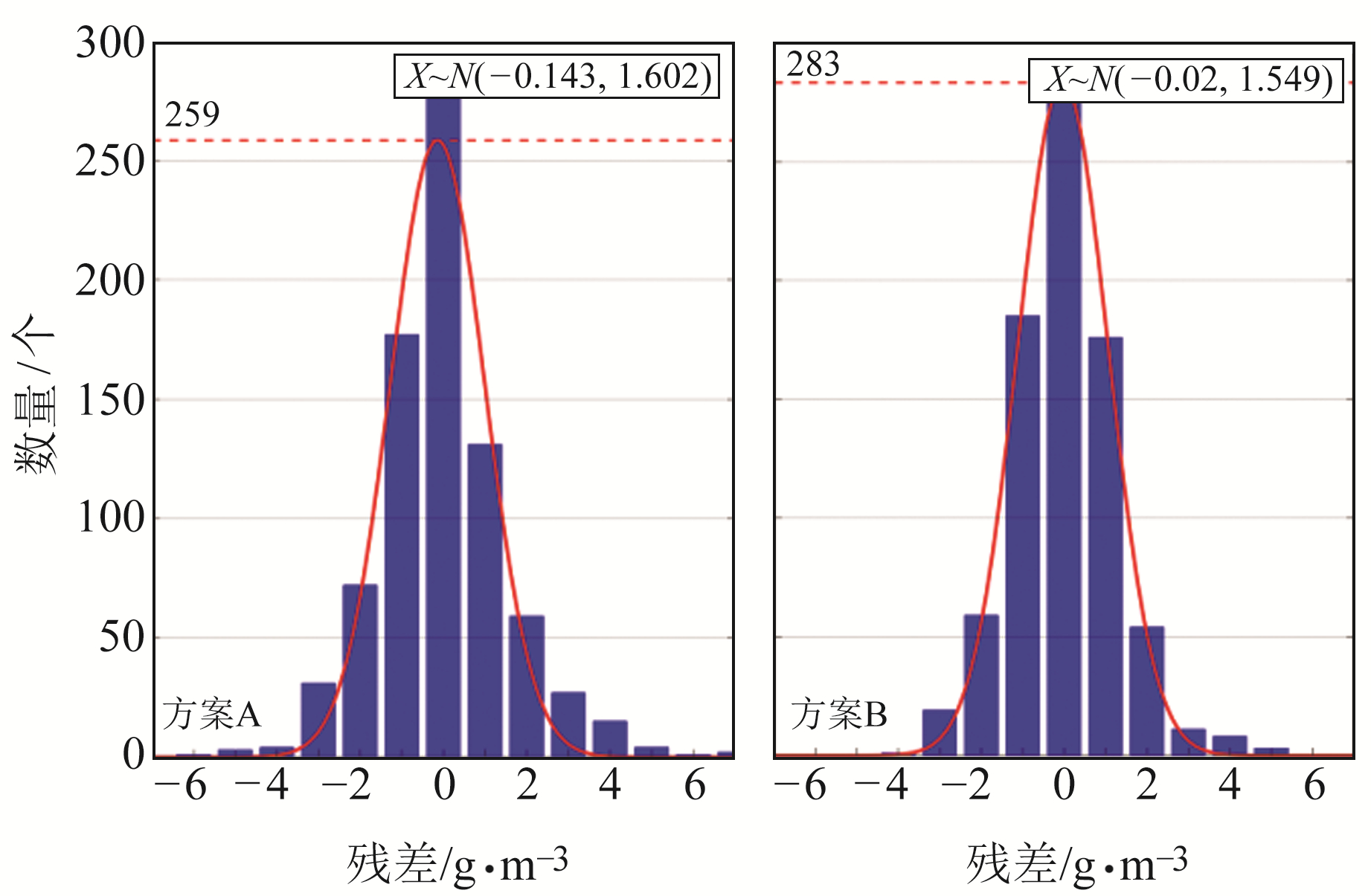
|
图 2 2种方案层析结果残差的正态分布曲线 Fig. 2 Gaussian distribution of the residuals of tomography results for two projects |
图 3为2种方案各层析历元解算结果的RMSE对比。实验时段内共进行62组层析实验,其中方案A的RMSE最大为3.074 g/m3,最小为0.501 g/m3;方案B的RMSE最大为2.473 g/m3,最小为0.410 g/m3。VWART层析解算结果的最大RMSE和最小RMSE相较于传统ART分别改进19.551%和18.164%。
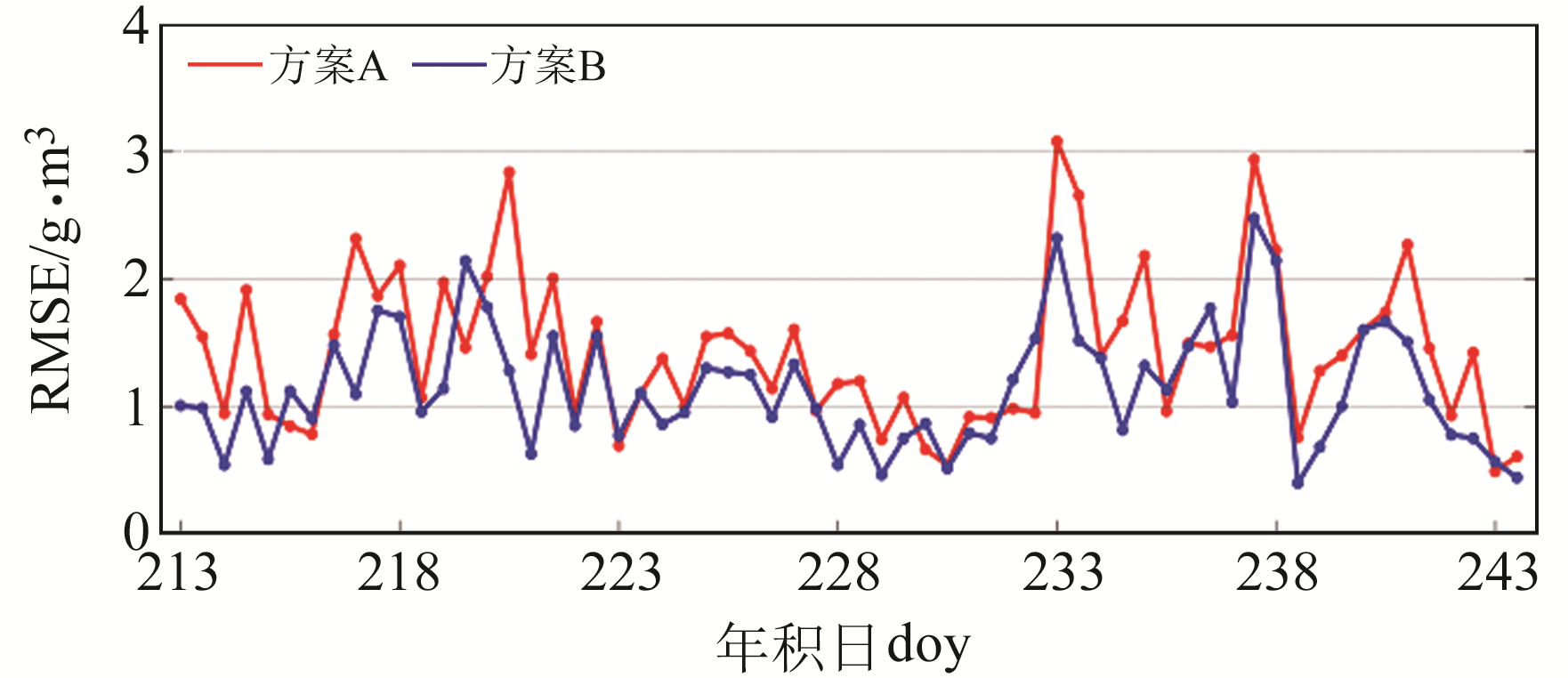
|
图 3 2种方案各层析历元解算结果的RMSE对比 Fig. 3 RMSE comparison at each epoch of the tomography results between two projects |
图 4和图 5进一步比较不同方案解算大气水汽密度的垂直精度。由图 4可见,以探空数据计算的垂直水汽廓线为参考,方案B反演的垂直水汽廓线的RMSE和相对误差在各高度层均低于方案A。在4 000 m以下的高度区间内,方案B对RMSE数值的降低尤为显著;而在地表附近的高度区间内,方案B对RMSE的优化接近50%,进一步证实VWART的优越性。由图 5可见,方案B各高度层残差分布的集中性优于方案A,仅第4、5、6三层出现较为明显的异常值;而方案A在第1~6层均出现明显的残差异常值,且异常值数量远多于方案B,其残差分布的总体情况相较于方案B也更加疏松。由此可见,VWART大幅提高了各垂直高度处层析解算结果的稳定性和精度。

|
图 4 2种方案层析结果的分层RMSE和相对误差 Fig. 4 RMSE and relative error at each layer of the tomography results for two projects |

|
图 5 2种方案层析结果残差的分层箱形图 Fig. 5 Box plots of the residuals at each layer of the tomography results for two projects |
对流层大气水汽含量与降水活动存在密切联系,为深入分析VWART方法在不同降水活动条件下的适用性,本文将3种天气条件下2种方案反演的层析水汽廓线与探空数据和ECMWF数据计算的水汽廓线进行对比分析。研究时段及天气条件分别为:2019-08-05(无雨)、2019-08-14(小雨)、2019-08-25(暴雨),反演水汽廓线所使用的数据由HKKP探空站位置、ECMWF格网点位置和体素块位置共同决定。由于HKKP探空站位于114°6′50.4″~114°12′14.4″E、22°17′38.4″~22°23′2.4″N范围内,故使用位于该区域的第1~13层体素块层析结果进行层析水汽廓线的反演。同时,该区域仅存在一处位于114°7′30″E、22°22′30″N的ECMWF格网点,因此使用该格网点处的ECMWF数据进行层析水汽廓线的对比分析。图 6为3种天气条件下层析水汽廓线与探空数据和ECMWF数据的对比。可以看出,不同天气条件下的大气水汽含量各不相同,整体表现为雨天大气水汽含量高、无雨天大气水汽含量低。2种方案均能正确反映出大气水汽的总体分布情况,反演的层析水汽廓线中方案B与探空数据和ECMWF数据表现出更强的一致性。在无雨的天气条件下,大气水汽含量较少,方案A的垂直水汽廓线在2 000~6 000 m处与探空水汽廓线的差异远大于方案B;在小雨的天气条件下,方案B反演的层析水汽廓线与探空水汽廓线在1 000 m以下的高度区间内具有更好的贴合度;在暴雨的天气条件下,方案A反演的层析水汽廓线与探空水汽廓线在3 000~6 000 m高度区间内存在较大差异,而方案B与探空水汽廓线的差异较小。综上所述,VWART在不同天气条件下均具有优秀的适用性,且相比于传统ART,其更能提高大气水汽的反演质量。
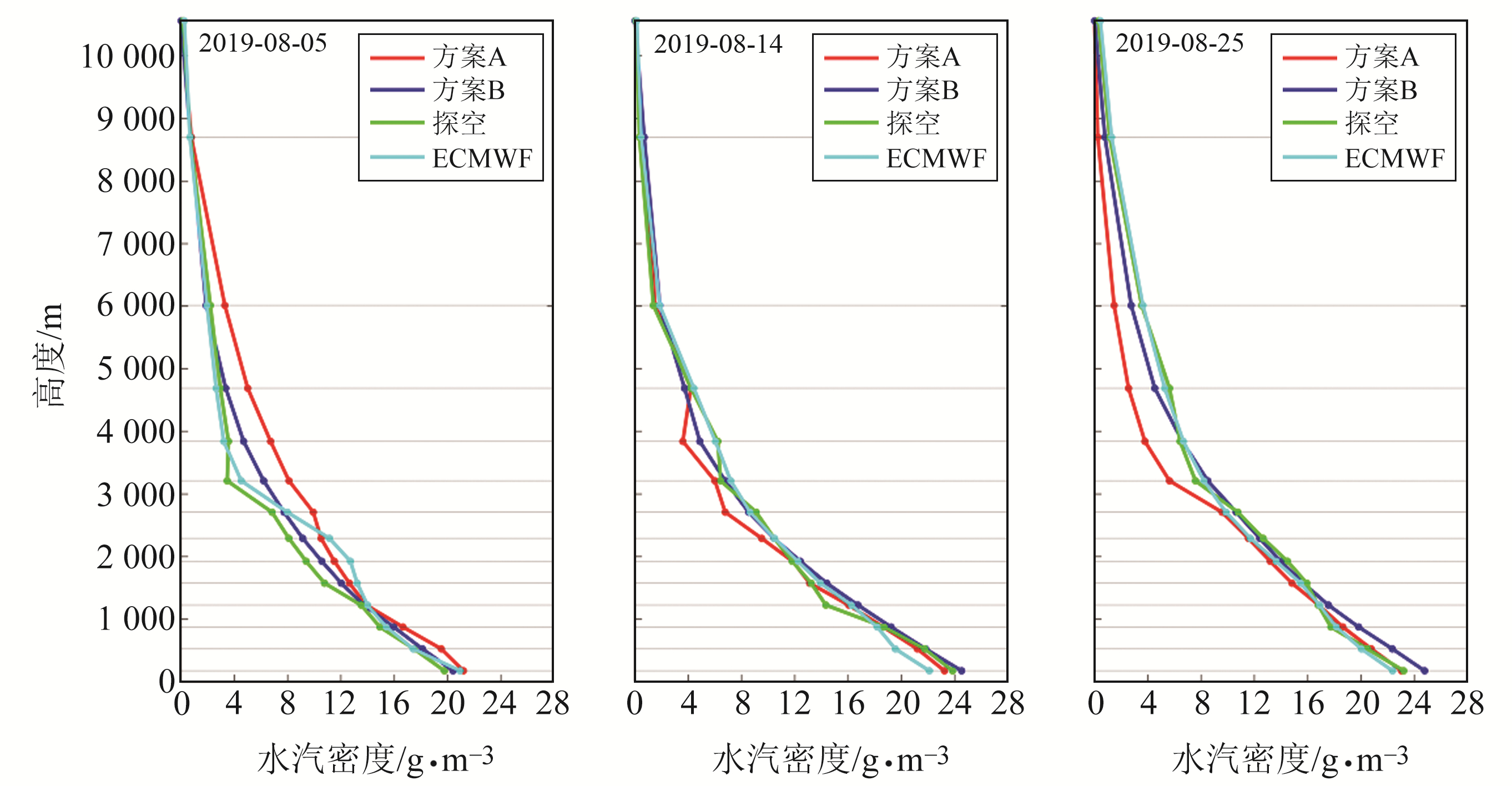
|
图 6 不同天气条件下2种方案反演的层析水汽廓线与探空数据和ECMWF数据对比 Fig. 6 Comparison of water vapor profiles between radiosonde, ECMWF and tomographic result for two projects under different weather conditions |
1) VWART解算结果的精度和稳定性均优于传统ART,在以探空数据为参考标准的情况下,其解算结果的RMSE、MAE和IQR相较于传统ART分别降低20.334%、18.126%和11.995%;在以ECMWF数据为参考标准的情况下其RMSE、MAE和IQR分别降低36.625%、29.096%和25.299%。VWART的散点图表明其具有更高的确定系数和更低的RMSE,解算结果的残差分布更集中,残差正态分布曲线拥有更低的方差和更接近于0的期望值。
2) VWART对各高度区间的层析解算质量均有所改进,对地表附近高度区间层析解算结果精度的提高尤为显著。在研究时段的所有层析历元中,VWART的RMSE最大值和最小值相较于传统ART分别改进19.551%和18.164%。
3) 与传统ART反演的水汽廓线进行对比发现,VWART反演的层析水汽廓线与探空水汽廓线具有更强的一致性,表现出优于传统ART的大气水汽反演效果,且VWART在无雨、小雨和暴雨等不同天气条件下均表现出优秀的大气水汽重构能力。
| [1] |
Flores A, Ruffini G, Rius A. 4D Tropospheric Tomography Using GPS Slant Wet Delays[J]. Annales Geophysicae, 2000, 18(2): 223-234 DOI:10.1007/s00585-000-0223-7
(  0) 0) |
| [2] |
Perler D, Geiger A, Hurter F. 4D GPS Water Vapor Tomography: New Parameterized Approaches[J]. Journal of Geodesy, 2011, 85(8): 539-550 DOI:10.1007/s00190-011-0454-2
(  0) 0) |
| [3] |
丁楠, 张书毕. 基于素数分解排序的水汽层析代数重构算法[J]. 地理与地理信息科学, 2017, 33(3): 42-47 (Ding Nan, Zhang Shubi. Water Vapor Tomography Algebraic Reconstruction Algorithm Based on the Prime Number Decomposition Access Order[J]. Geography and Geo-Information Science, 2017, 33(3): 42-47 DOI:10.3969/j.issn.1672-0504.2017.03.008)
(  0) 0) |
| [4] |
张文渊, 张书毕, 左都美, 等. GNSS水汽层析的自适应代数重构算法[J]. 武汉大学学报: 信息科学版, 2021, 46(9): 1 318-1 327 (Zhang Wenyuan, Zhang Shubi, Zuo Dumei, et al. Adaptive Algebraic Reconstruction Algorithms for GNSS Water Vapor Tomography[J]. Geomatics and Information Science of Wuhan University, 2021, 46(9): 1 318-1 327)
(  0) 0) |
| [5] |
于胜杰, 万蓉, 付志康. 代数重构算法在GNSS水汽层析解算中的应用[J]. 武汉大学学报: 信息科学版, 2016, 41(8): 1 113-1 117 (Yu Shengjie, Wan Rong, Fu Zhikang. Application of Algebraic Reconstruction Technique on the GNSS Water Vapor Tomography[J]. Geomatics and Information Science of Wuhan University, 2016, 41(8): 1 113-1 117)
(  0) 0) |
| [6] |
Ding N, Zhang S B, Wu S Q, et al. Adaptive Node Parameterization for Dynamic Determination of Boundaries and Nodes of GNSS Tomographic Models[J]. Journal of Geophysical Research: Atmospheres, 2018, 123(4): 1 990-2 003 DOI:10.1002/2017JD027748
(  0) 0) |
| [7] |
赵庆志, 姚宜斌, 姚顽强, 等. 利用ECMWF改善射线利用率的三维水汽层析算法[J]. 测绘学报, 2018, 47(9): 1 179-1 187 (Zhao Qingzhi, Yao Yibin, Yao Wanqiang, et al. A Method to Improve the Utilization Rate of Satellite Rays for Three-Dimensional Water Vapor Tomography Using the ECMWF Data[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(9): 1 179-1 187)
(  0) 0) |
| [8] |
张豹, 姚宜斌, 许超钤. 一种可用于估计全球水汽标高的经验模型[J]. 测绘学报, 2015, 44(10): 1 085-1 091 (Zhang Bao, Yao Yibin, Xu Chaoqian. Global Empirical Model for Estimating Water Vapor Scale Height[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1 085-1 091)
(  0) 0) |
| [9] |
万蓉, 郑国光, 于胜杰, 等. 基于观测约束的地基GPS三维水汽层析技术研究[J]. 气象学报, 2013, 71(2): 318-331 (Wan Rong, Zheng Guoguang, Yu Shengjie, et al. A Study of the Ground-Based GPS 3D Water Vapor Tomography with Radiosonde Vertical Constraining[J]. Acta Meteorologica Sinica, 2013, 71(2): 318-331)
(  0) 0) |
| [10] |
Wen D B, Yuan Y B, Ou J K, et al. Three-Dimensional Ionospheric Tomography by an Improved Algebraic Reconstruction Technique[J]. GPS Solutions, 2007, 11(4): 251-258 DOI:10.1007/s10291-007-0055-y
(  0) 0) |
| [11] |
马朋序, 丁楠, 张书毕. 加权距离排序的水汽层析算法[J]. 测绘科学, 2019, 44(10): 109-116 (Ma Pengxu, Ding Nan, Zhang Shubi. Water Vapor Tomography Algorithm Based on the Weighted Distance Scheme[J]. Science of Surveying and Mapping, 2019, 44(10): 109-116)
(  0) 0) |
| [12] |
陈宏斌, 熊永良, 陈志胜, 等. 垂直不均匀分层的地基GPS层析水汽研究[J]. 测绘工程, 2015, 24(5): 11-14 (Chen Hongbin, Xiong Yongliang, Chen Zhisheng, et al. Research on Tomography of Ground-Based GPS Water Vapor with Uneven Vertical Stratification[J]. Engineering of Surveying and Mapping, 2015, 24(5): 11-14 DOI:10.3969/j.issn.1006-7949.2015.05.003)
(  0) 0) |
| [13] |
Wexler A. Vapor Pressure Formulation for Water in Range 0 to 100 ℃. A Revision[J]. Journal of Research of the National Institute of Standards and Technology, 1976, 80A(5-6): 775-785
(  0) 0) |
| [14] |
Ha J, Park K D, Kim K, et al. Comparison of Atmospheric Water Vapor Profiles Obtained by GPS, MWR, and Radiosonde[J]. Asia-Pacific Journal of Atmospheric Sciences, 2010, 46(3): 233-241 DOI:10.1007/s13143-010-1012-1
(  0) 0) |
| [15] |
Adeyemi B, Joerg S. Analysis of Water Vapor over Nigeria Using Radiosonde and Satellite Data[J]. Journal of Applied Meteorology and Climatology, 2012, 51(10): 1 855-1 866 DOI:10.1175/JAMC-D-11-0119.1
(  0) 0) |
| [16] |
赵庆志, 姚宜斌, 辛林洋. 融合ECMWF格网数据的水汽层析精化方法[J]. 武汉大学学报: 信息科学版, 2021, 46(8): 1 131-1 138 (Zhao Qingzhi, Yao Yibin, Xin Linyang. A Method to Sophisticate the Water Vapor Tomography Model by Combining the ECMWF Grid Data[J]. Geomatics and Information Science of Wuhan University, 2021, 46(8): 1 131-1 138)
(  0) 0) |
2. School of Environment and Spatial Informatics, China University of Mining and Technology, 1 Daxue Road, Xuzhou 221116, China
 2022, Vol. 42
2022, Vol. 42

