全球导航卫星系统GNSS广泛应用于智慧城市和物联网建设中。但在城市环境中,GNSS信号易受建筑物、树木等影响,发生折射、衍射、遮挡等现象,产生严重的多路径效应和非视线信号(non-line-of-sight, NLOS),导致数十米的伪距和载波误差,严重影响复杂城市环境下的GNSS定位精度[1]。一般可通过接收机和天线的设计、数据处理和建模等方式削弱不同误差对定位精度的影响。其中,对接收机的硬件进行改良虽然可以在一定程度上抑制多路径效应、提高定位精度,但受限于接收机的成本和体积等因素,无法大面积推广[2],因此需要利用卫星和信号的相关信息进一步削弱多路径效应和NLOS信号对定位精度的影响。
目前,卫星高度角、信噪比模型是应用最广的数据处理模型,可有效提高复杂环境下的基线解算精度,但无法有效检测和分离多路径效应与NLOS信号[3]。相关学者将机器学习算法应用于GNSS信号的处理与建模中,采用支持向量机(SVM)分类器和神经网络模型将GNSS观测数据分为直射、多路径和NLOS三类,准确率可达85%以上,能有效提高定位精度[4]。此外,有学者将决策树算法与GNSS信号分类相结合,通过梯度下降树(GBDT)算法实现GNSS信号的修复和分类[5],并通过装袋(bagging)算法校正受树叶遮挡的GNSS信号,提升接收机在重叶区和轻叶区的定位精度[6]。虽然上述机器学习算法有效提高了接收机的定位精度,但需要提前对数据进行标记,无法兼顾成本和实时性的需求。
本文针对上述算法在成本、实时性上存在的问题,采用非监督分类算法对GNSS数据进行处理。非监督分类算法无需提前对数据进行标注、无需额外的硬件和人力成本,具有良好的适应性。但不同的非监督分类算法在分类效果上存在差异,需对其进行比较分析以确定最适合GNSS数据分类的算法。首先,在先验定权模型的基础上采用3种算法对数据进行分类,并比较3种算法分类后的定位精度;然后对分类效果最好的算法进行精度分析,并与传统的高度角、信噪比阈值法进行比较,以验证算法的有效性。
1 相关算法及模型介绍本文采用伪距单点定位(SPP)模型评估复杂观测环境下的GNSS定位精度,并在此基础上采用非监督分类(unsupervised)算法提高定位性能。
1.1 函数模型本文采用的伪距单点定位观测方程为[7]:
| $ \begin{gathered} P_{i, \mathrm{k}}^{\mathrm{s}}(t)=p_{\mathrm{k}}^{\mathrm{s}}(t)+c\left[\operatorname{dtr}_{\mathrm{k}}(t)-\operatorname{dts}^{\mathrm{s}}(t)\right]+ \\ T_{\mathrm{k}}^{\mathrm{s}}(t)+u_{i} I_{i, \mathrm{k}}^{\mathrm{s}}(t)+\varepsilon_{i, \mathrm{k}, p}^{\mathrm{s}}(t) \\ \varepsilon_{i, \mathrm{k}, p}^{\mathrm{s}}(t)=\operatorname{TGDR}_{i, r}^{\mathrm{s}}+\operatorname{TGDS}_{i, \mathrm{k}, p}+ \\ M_{i, \mathrm{k}, p}^{\mathrm{s}}+\Delta_{i, \mathrm{k}, p}^{\mathrm{s}}(t) \end{gathered} $ | (1) |
式中,上标s、k、i、p分别为卫星、接收机、频率和伪距观测值,Pi, ks(t)为接收机k的第i频率t时刻的伪距观测值,pks(t)为从卫星天线相位中心到接收机天线相位中心的几何距离,c为光在真空中的传播速度,dtrk(t)、dtss(t)分别为接收机和卫星钟差,Tks(t)、Ii, ks(t)分别为对流层和电离层延迟,
GNSS定位中采用的先验定权模型主要包括高度角定权模型和信噪比定权模型。其中高度角定权模型[8]根据卫星观测值噪声与高度角的相关性确定,通常高度角越高信号质量越好:
| $ {{\sigma }^{2}}={{f}^{2}}\left( {{a}^{2}}+\frac{{{b}^{2}}}{{{\sin }^{2}}E} \right) $ | (2) |
式中,f是与观测值类型相关的常系数,在伪距定位中取100,当采用无电离层组合时进一步放大3倍;E为卫星高度角;a、b根据经验均取为1 cm。
信噪比(signal-to-noise ratio, SNR)是指信号强度与噪声强度的比值,一般与观测值质量呈正相关。常用的信噪比定权模型为:
| $ {{\sigma }^{2}}={{C}_{n}}\times {{10}^{-\frac{C/{{N}_{0}}}{10}}} $ | (3) |
式中,C/N0为观测值的信噪比,可根据观测文件获取;Cn是与接收机性能和采用的定位系统相关的常系数,取值通常为1.61×104 mm2[9]。
1.3 非监督分类算法非监督分类算法无需提前对模型进行训练,可直接通过某种判别准则在源数据中进行搜寻和分类。本文采用的非监督分类算法为Kmeans++、ISODATA和DBSCAN三种[10]。Kmeans++算法与ISODATA算法都是从数据集中随机选择分类中心,通过判别样本到分类中心的距离进行样本的划分。2种算法的区别主要为:Kmeans++算法的分类中心数不变,而ISODATA算法在分类过程中会根据提前设置的阈值进行分类中心的分裂和合并。DBCAN算法的原理则较为简单:在数据样本中选择一个中心点不断向密度边界出发,直到样本点的数量低于预先指定的值,分类结束后得到一个包含核心点和边界点的最大区域[11]。相较于其他2种算法,DBSCAN算法不需要指定类别数即可完成数据集的分类,且对于异常点更不敏感。但当不同类别的数据间距很大且密度分布不均匀时,DBSCAN算法分类精度会受到影响,且耗时更长。
2 静态实验分析实验采用司南接收机进行数据采集,采样率为1 Hz,采样时间为2021-04-15 04:30~07:00,4个系统(GPS、BDS、Galileo、GLONASS)均采用双频定位,测站坐标均通过相对定位求平均获得。各系统卫星失锁较为严重,4个导航系统中BDS的观测数据质量最好,且在采集时段内始终存在4颗以上的可见卫星。接收机设置在南京信息工程大学藕舫楼边,其中E方向干扰源为种植在道路旁的树木,N方向干扰源为藕舫楼,是一种较为典型的多路径环境。
2.1 特征值选取和数据预处理GNSS数据的特征值是否合适决定了算法分类精度的好坏。SNR是衡量信号质量最直接的指标,在单一环境下能达到很好的分类效果。但在复杂环境下单个变量往往无法有效分离多路径效应和NLOS信号[12],尤其在信噪比较低时,若仅依靠SNR进行分类很容易造成信号误分,因此需要与其他特征值(伪距残差、高度角等)进行组合分类。伪距残差作为衡量卫星可视性的关键指标,可以用来剔除多路径效应和NLOS信号[4]。但由于复杂环境下的定位结果较差,伪距残差并不能清楚地体现出直射信号与NLOS的差异。由于在高仰角下信号不易被周围的建筑物遮挡,因此高度角也常用于剔除多路径效应和NLOS信号[12],但NLOS信号在高仰角和低仰角的情况下都有可能出现。由此可见,上述每一个分量都无法单独有效地检测多路径效应和NLOS信号,因此本文将高度角、信噪比、伪距残差3个指标进行组合,以提高分类精度。
确定特征向量后还需对数据进行归一化处理,以消除不同量纲对分类精度的影响。本文选用的归一化方法是z-score标准化,即利用原始数据的均值μ和标准差σ进行数据x的标准化,使经过处理的数据符合标准正态分布,即转化为均值为0、标准差为1的数据。具体的转化函数为:
| $ Z=\left( x-\mu \right)/\sigma $ | (4) |
本文将高度角阈值设为10°,在此基础上比较高度角定权法、信噪比定权法在E、N、U三个方向上的精度(表 1)。
|
|
表 1 先验定权模型精度比较 Tab. 1 Accuracy comparison of priori weighted models |
由表 1可知,E、N、U三个方向上高度角定权法的精度均优于信噪比定权法,但两者精度相差不大。由此可见,在复杂观测环境下,无论是高度角定权法还是信噪比定权法都无法有效提高接收机的定位精度。因此本文将在高度角定权法的基础上使用非监督分类算法剔除多路径效应和NLOS信号,进一步提升接收机的定位精度。
本文使用Kmeans++、ISODATA、DBSCAN算法对数据进行分类。其中,Kmeans++的信号类别为3、迭代次数为8 000;ISODATA的期望信号类别为3、迭代次数为14 000、最小样本数为120、样本间最大方差为0.5、不同类别间最小距离为0.3;DBSCAN的对象数为10、相邻样本距离阈值为0.119。Kmeans++和ISODATA算法将GNSS数据划分为3类,由于DBSCAN算法对离散点有较高的敏感度,因此将GNSS数据划分为25类。通过分类结果剔除多路径效应和NLOS信号后,各算法在E、N、U三个方向上的SPP定位精度如图 1所示,可以看出,相较于其他2种算法,Kmeans++算法的分类效果更好。

|
图 1 不同分类算法精度比较 Fig. 1 Comparison of accuracy of different classification algorithms |
在算法适宜性方面,由于接收机信号受时间、环境等多种因素影响,数据先验信息较难获取,因此数据先验信息的需求数量成为制约算法适宜性的关键因素。由表 2可见,相较于ISODATA、DBSCAN算法,Kmeans++算法对数据先验信息的需求更少,具有较好的算法适宜性,只需在分类前确定GNSS信号可能出现的类型,即可在不同的环境下快速得到最佳的分类精度。
|
|
表 2 不同分类算法比较 Tab. 2 Comparison of different classification algorithms |
由于Kmeans++算法在定位精度和算法适宜性方面有较大优势,因此本文将比较采用Kmeans++算法和未采用Kmeans++算法的定位精度,以验证该算法的有效性。
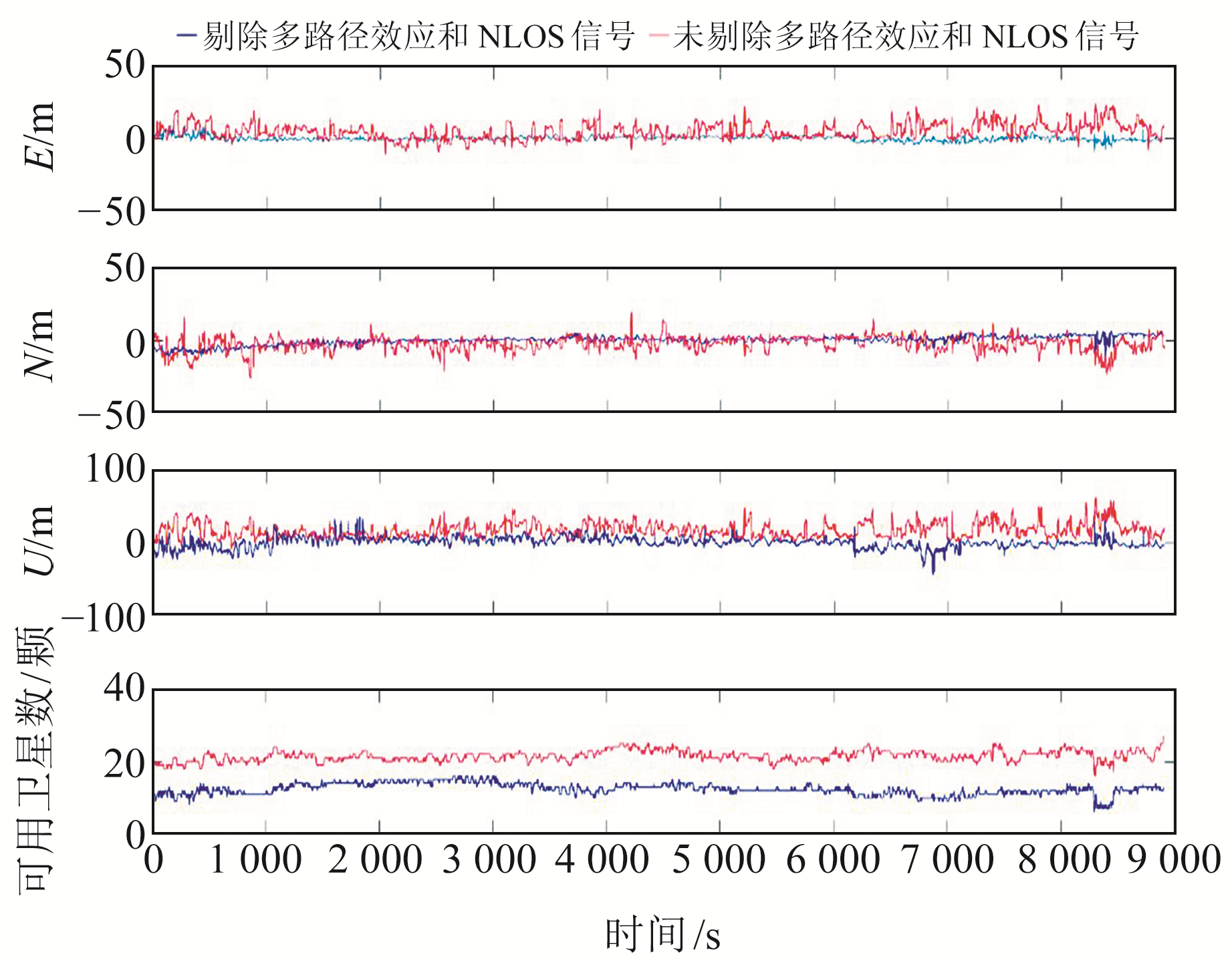
由图 2可见,采用Kmeans++算法剔除多路径效应和NLOS信号后有效卫星数量出现一定程度的下降,从而导致位置精度衰减因子PDOP增大,但PDOP的增大并没有过多地影响到定位精度。剔除多路径效应和NLOS信号后在E、N、U三个方向上的定位精度相较于剔除前分别提升57.86%、47.64%、60.98%。
|
图 2 3个方向上的定位精度和可用卫星数比较 Fig. 2 Comparison of three-way positioning accuracy and the number of available satellites |
由表 3可见,Kmeans++算法剔除多路径效应和NLOS信号后定位精度得到较大提升,其中E方向的提升效果强于N方向。接收机N方向主要的干扰源是因楼房遮挡而产生的NLOS信号,E方向的主要干扰源则是因树木遮挡而产生的多路径干涉信号,可见Kmeans++算法在该组特征向量下对多路径干涉信号具有更高的敏感性,由图 3也可以得到相同结论。并且除个别历元由于卫星剔除过多导致定位精度下降外,其他历元的定位精度都得到有效提升。
|
|
表 3 采用Kmeans++剔除多路径效应和NLOS信号前后定位误差比较 Tab. 3 Comparison of positioning errors before and after removing multipath effects and NLOS signals by Kmeans++ |

|
图 3 Kmeans++算法分类前后定位精度比较 Fig. 3 Comparison of positioning accuracy before and after the clustering of Kmeans++ |
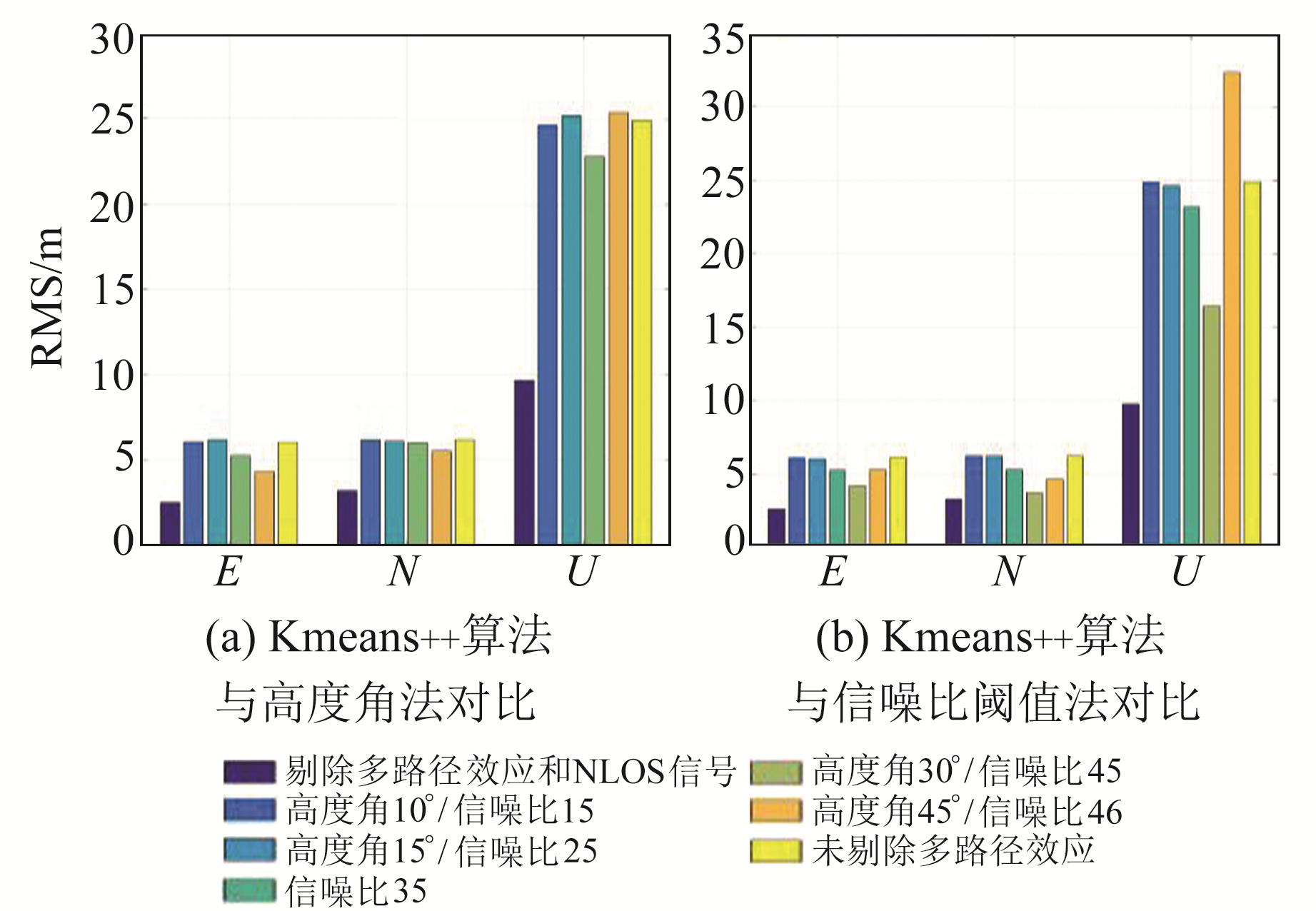
为进一步验证算法的有效性,将Kmeans++算法与传统阈值法进行比较。信噪比是衡量GNSS信号质量的关键指标,主要受天线的增益参数、接收机相关器状态及多路径误差的影响[13]。信噪比可以从观测文件中获得,数值越大代表信号质量越好。卫星高度角也能在一定程度上反映GNSS信号的质量,且高度角与多路径效应负相关,即高度角越高多路径效应越小。因此,本文采取高度角、信噪比阈值法与Kmeans++算法进行比较(图 4)。由图可见,GNSS数据经Kmeans++算法处理后,3个方向上的定位精度均优于传统方法,其中E方向的改善最为明显。说明仅通过信噪比、高度角阈值法无法有效剔除多路径效应和NLOS信号,且随着阈值的增大会出现卫星误剔现象。当信噪比阈值提升到46 dB时,E、N、U三个方向上的定位精度都出现明显下降。由于大多数情况下不可能对同一区间进行反复实验以获得高度角和信噪比的最佳阈值,因此阈值不适宜的情况难以避免。而Kmeans++算法不存在此类问题,具有较好的适应性。表 4比较了Kmeans++算法与高度角、信噪比阈值法在定位精度上的差异。
|
图 4 不同处理方法精度比较 Fig. 4 Comparison of precision of different processing methods |
|
|
表 4 不同处理方法的误差比较 Tab. 4 Comparison of errors of different processing methods |
1) 3种非监督分类算法中Kmeans++算法分类精度最高,适应性最好,在E、N、U三个方向上的RMSE分别为2.56 m、3.25 m和9.73 m。
2) 采用Kmeans++分类算法剔除多路径效应和NLOS信号数据后,在E、N、U三个方向上的接收机定位精度相较于剔除前分别提升了57.86%、47.64%和60.98%,三维精度提升了59.96%。
3) 相比于信噪比阈值法,Kmeans++算法的平面和三维定位精度分别提升24.87%、39.07%;相比于高度角阈值法,Kmeans++算法的平面和三维定位精度分别提升41.36%、59.91%。
| [1] |
Štern A, Kos A. Positioning Performance Assessment of Geodetic, Automotive, and Smartphone GNSS Receivers in Standardized Road Scenarios[J]. IEEE Access, 2018(6): 41 410-41 428
(  0) 0) |
| [2] |
李超. 北斗/GPS导航接收及抗干扰天线研究[D]. 西安: 西安电子科技大学, 2019 (Li Chao. Study on the Navigation Receiving and Anti-Jamming Antennas for BDS and GPS Applications[D]. Xi'an: Xidian University, 2019)
(  0) 0) |
| [3] |
刘志强, 黄张裕, 金建平. 利用卫星高度角和信噪比提高GPS定位精度的试验分析[J]. 测绘工程, 2008, 17(4): 54-58 (Liu Zhiqiang, Huang Zhangyu, Jin Jianping. An Experiment Study of Improving GPS Positioning Precision by Satellite Elevation and SNR[J]. Engineering of Surveying and Mapping, 2008, 17(4): 54-58)
(  0) 0) |
| [4] |
Suzuki T, Amano Y. NLOS Multipath Classification of GNSS Signal Correlation Output Using Machine Learning[J]. Sensors, 2021, 21(7): 2 503 DOI:10.3390/s21072503
(  0) 0) |
| [5] |
Sun R, Wang G Y, Zhang W Y, et al. A Gradient Boosting Decision Tree Based GPS Signal Reception Classification Algorithm[J]. Applied Soft Computing, 2020, 86: 105 942 DOI:10.1016/j.asoc.2019.105942
(  0) 0) |
| [6] |
Qin F, Fu L X, Wang Y Q, et al. A Bagging Tree-Based Pseudorange Correction Algorithm for Global Navigation Satellite System Positioning in Foliage Canyons[J]. International Journal of Distributed Sensor Networks, 2021, 17(5)
(  0) 0) |
| [7] |
周厚香. 基于单频低成本接收机的定位算法研究[D]. 北京: 中国地质大学, 2020 (Zhou Houxiang. Research on Positioning Algorithm Based on Single-Frequency Low-Cost Receiver[D]. Beijing: China University of Geosciences, 2020)
(  0) 0) |
| [8] |
刘亚, 何文涛, 张洁. 融合SISRE的卫星高度角定权模型及PPP应用性能分析[J]. 测绘科学技术学报, 2021, 38(3): 235-239 (Liu Ya, He Wentao, Zhang Jie. SISRE-Combined Satellite Elevation-Depending Weight Model and Its PPP Application Performance Analysis[J]. Journal of Geomatics Science and Technology, 2021, 38(3): 235-239)
(  0) 0) |
| [9] |
张玉爽, 黄张裕, 张文祥. 北斗伪距单点定位的随机模型影响评估[J]. 测绘工程, 2017, 26(8): 24-28 (Zhang Yushuang, Huang Zhangyu, Zhang Wenxiang. The Impact Assessment of Beidou Pseudo Range Point Positioning Stochastic Model[J]. Engineering of Surveying and Mapping, 2017, 26(8): 24-28)
(  0) 0) |
| [10] |
王俊. 面向大数据的DBSCAN聚类算法研究[D]. 郑州: 信息工程大学, 2017 (Wang Jun. Research on DBSCAN Clustering Algorithm Oriented Big Data[D]. Zhengzhou: Information Engineering University, 2017)
(  0) 0) |
| [11] |
荣秋生, 颜君彪, 郭国强. 基于DBSCAN聚类算法的研究与实现[J]. 计算机应用, 2004, 24(4): 45-46 (Rong Qiusheng, Yan Junbiao, Guo Guoqiang. Research and Implementation of Clustering Algorithm Based on DBSCAN[J]. Computer Applications, 2004, 24(4): 45-46)
(  0) 0) |
| [12] |
Yozevitch R, Moshe B B, Weissman A. A Robust GNSS LOS/NLOS Signal Classifier[J]. Navigation, 2016, 63(4): 429-442 DOI:10.1002/navi.166
(  0) 0) |
| [13] |
谭羽安, 袁本银, 鲍志雄. GPS/BDS/GLONASS多星座质量检核研究与实现[C]. 第四届中国卫星导航学术年会, 武汉, 2013 (Tan Yu'an, Yuan Benyin, Bao Zhixiong. Research and Implementation of the Quality Check of the GPS/BDS/GLONASS Multi-Constellation[C]. The 4th China Satellite Navigation Conference, Wuhan, 2013)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


