2. 安徽理工大学空间信息与测绘工程学院,安徽省淮南市泰丰大街168号,232001
与BDS-2相比,BDS-3不仅解决了BDS-2卫星观测值中的伪距偏差问题[1],并且在原有的B1I和B3I频率基础上新增B1C、B2a、B2b和B2等4种新频率,其中B1I和B3I信号的调制方式也有所不同。多频信号可用于电离层延迟消除、周跳探测和模糊度固定等,尤其在PPP的相关研究上存在许多潜在优势。由于前期BDS-3的建设不够完善,在轨卫星数量较少、能同时接收到B1C、B2a和B2b三种新频率的测站数量有限,因此针对BDS-3卫星播发新频率的PPP定位效果的研究较少。本文针对BDS-3卫星播发的新频率进行三频PPP相关研究,包括静态和仿动态2种模式。首先在原始观测方程的基础上推导出常用的三频PPP数学模型,即非差非组合模型、消电离层模型和无电离层组合模型,并对新频率组合模型中出现的偏差和改正进行详细分析[2];然后通过MGEX测站数据分别比较B1I和B3I的双频非差非组合模型(DU2)、B1C和B2a的双频非差非组合模型(DU3)、基于B1C、B2a、B2b的三频非差非组合模型(TU)、三频消电离层模型(TF)和三频无电离层两两组合模型(TDF)的定位性能;最后总结BDS-3新三频PPP定位性能,为未来的北斗多频定位相关研究提供参考依据。
1 三频PPP函数模型三频原始伪距和载波相位的基本观测方程为:
| $ \left\{ \begin{align} & P_{\text{r}, j}^{\text{s}}=\rho _{\text{r}}^{\text{s}}+c\cdot \text{d}{{t}_{\text{r}}}-c\cdot \text{d}{{t}^{\text{s}}}+{{T}_{\text{r}}}+ \\ & \ \ \ \ {{\gamma }_{j}}\cdot I_{\text{r}, 1}^{\text{s}}+c\left( d_{\text{r}, j}^{\text{s}}-d_{j}^{\text{s}} \right)+\varepsilon _{\text{r}, {{P}_{j}}}^{\text{s}, T} \\ & L_{\text{r}, j}^{\text{s}}=\rho _{\text{r}}^{\text{s}}+c\cdot \text{d}{{t}_{\text{r}}}-c\cdot \text{d}{{t}^{\text{s}}}+{{T}_{\text{r}}}- \\ & \ \ \ \ {{\gamma }_{j}}\cdot I_{\text{r}, 1}^{\text{s}}+\lambda _{j}^{\text{s}}\left( N_{\text{r}, j}^{\text{s}}+b_{\text{r}, j}^{\text{s}}-b_{j}^{\text{s}} \right)+\xi _{\text{r}, {{L}_{j}}}^{\text{s}} \\ \end{align} \right. $ | (1) |
式中,s、r分别为卫星PRN号和接收机;Pr, js和Lr, js分别为伪距和载波相位的原始观测值,j为频率(j=1, 2, 3);ρrs为接收机与卫星的几何距离;c为光速;dtr和dts分别为接收机钟差和卫星钟差;γj为电离层因子,γj=f12/fj2;Ir, 1s为f1信号上的斜电离层延迟;Tr为测站天顶对流层延迟;λjs为频率fj载波对应的波长;Nr, js为载波相位的整周模糊度;dr, js和djs分别为接收机端和卫星端的非校正伪距硬件延迟UCD;br, js和bjs分别为接收机端和卫星端的非校正相位硬件延迟UPD;εs, Tr, Pj和ξsr, Lj分别为伪距和载波相位的观测噪声、多路径效应以及其他未模型化的误差之和[3]。其他误差项(天线相位中心改正、地球潮汐改正以及相对论效应等)采用相应的模型进行改正[4]。
现定义:
| $ \left\{\begin{array}{l} \alpha_{m n}=\frac{f_{m}^{2}}{f_{m}^{2}-f_{n}^{2}}, \beta_{m n}=-\frac{f_{n}^{2}}{f_{m}^{2}-f_{n}^{2}} \\ \mathrm{DCB}_{P_{m} P_{n}}^{\mathrm{s}}=d_{m}^{\mathrm{s}}-d_{n}^{\mathrm{s}} \\ \mathrm{DCB}_{\mathrm{r}, P_{m} P_{n}}^{\mathrm{s}}=d_{\mathrm{r}, m}^{\mathrm{s}}-d_{\mathrm{r}, n}^{\mathrm{s}} \\ d_{\mathrm{IF}_{m n}}^{\mathrm{s}}=\alpha_{m n} \cdot d_{m}^{\mathrm{s}}+\beta_{m n} \cdot d_{n}^{\mathrm{s}}, d_{\mathrm{r}, \mathrm{F}_{m n}}^{\mathrm{s}}= \\ \;\;\;\; \alpha_{m n} \cdot d_{\mathrm{r}, m}^{\mathrm{s}}+\beta_{m n} \cdot d_{\mathrm{r}, n}^{\mathrm{s}} \end{array}\right. $ | (2) |
式中,fm和fn为不同的频率,αmn和βmn为无电离层组合因子,DCBPmPns和DCBr, PmPns为与频率有关的卫星端和接收机端的码间偏差DCB,dIFmns和dr, IFmns为卫星端和接收机端m、n频率原始的硬件延迟djs和dr, js经组合后的无电离层组合伪距硬件延迟。
由于卫星钟差dts与卫星端UCD线性相关,因此无法将两者直接分离,需要引入精密卫星轨道和钟差改正。一般采用IGS组织播发的基于B1I/B3I无电离层组合观测值估计的产品进行改正[5]:
| $ \begin{matrix} c\cdot \text{d}t_{\text{I}{{\text{F}}_{12}}}^{\text{s}}=c\left[ ~\text{d}{{t}^{\text{s}}}+\left( {{\alpha }_{12}}\cdot d_{1}^{\text{s}}+{{\beta }_{12}}\cdot d_{2}^{\text{s}} \right) \right]= \\ c\left( ~\text{d}{{t}^{\text{s}}}+d_{\text{I}{{\text{F}}_{12}}}^{\text{s}} \right) \\ \end{matrix} $ | (3) |
式中,dtIF12s为IGS提供的精密卫星钟差改正;dIF12s为卫星UCD,即dr, js和djs的无电离层组合。
引入精密卫星轨道和钟差改正,将式(3)代入式(1)并线性化得:
| $ \left\{\begin{array}{l} P_{\mathrm{r}, j}^{\mathrm{s}}=\rho_{\mathrm{r}}^{\mathrm{s}}+c \cdot \mathrm{d} t_{\mathrm{r}}-c \cdot \mathrm{d} t_{\mathrm{IF}_{12}}^{\mathrm{s}}+T_{\mathrm{r}}+\gamma_{j} \cdot \\ \;\;\;\; I_{\mathrm{r}, 1}^{\mathrm{s}}+c \cdot d_{\mathrm{r}, j}^{\mathrm{s}}+c\left(d_{\mathrm{IF}_{12}}^{\mathrm{s}}-d_{j}^{\mathrm{s}}\right)+\varepsilon_{\mathrm{r}, P_{j}}^{\mathrm{s}, T} \\ L_{\mathrm{r}, j}^{\mathrm{s}}=\rho_{\mathrm{r}}^{\mathrm{s}}+c \cdot \mathrm{d} t_{\mathrm{r}}-c \cdot \mathrm{d} t_{\mathrm{IF}_{12}}^{\mathrm{s}}+T_{\mathrm{r}}-\gamma_{j} \cdot \\ \;\;\;\; I_{\mathrm{r}, 1}^{\mathrm{s}}+\lambda_{j}^{\mathrm{s}}\left(N_{\mathrm{r}, j}^{\mathrm{s}}+b_{\mathrm{r}, j}^{\mathrm{s}}-b_{j}^{\mathrm{s}}\right)+c \cdot d_{\mathrm{IF}_{12}}^{\mathrm{s}}+\xi_{\mathrm{r}, L_{j}}^{\mathrm{s}} \end{array}\right. $ | (4) |
式中,dtIF12s直接使用精密钟差进行改正,伪距偏差项(dIF12s-djs)则通过卫星端DCB产品进行改正:
| $ \left\{ \begin{array}{*{35}{l}} d_{\text{I}{{\text{F}}_{12}}}^{\text{s}}-d_{1}^{\text{s}}={{\alpha }_{\text{B1B3}}}\cdot \text{DCB}_{\text{B1IB1C}}^{\text{s}}+{{\beta }_{\text{B1B3}}}\cdot \text{DCB}_{\text{B3IB1C}}^{\text{s}} \\ d_{\text{I}{{\text{F}}_{12}}}^{\text{s}}-d_{2}^{\text{s}}={{\alpha }_{\text{B1B3}}}\cdot \text{DCB}_{\text{B1IB2a}}^{\text{s}}+{{\beta }_{\text{B1B3}}}\cdot \text{DCB}_{\text{B3IB2a}}^{\text{s}} \\ d_{\text{I}{{\text{F}}_{12}}}^{\text{s}}-d_{3}^{\text{s}}={{\alpha }_{\text{B1B3}}}\cdot \text{DCB}_{\text{B1IB2b}}^{\text{s}}+{{\beta }_{\text{B1B3}}}\cdot \text{DCB}_{\text{B3IB2b}}^{\text{s}} \\ {{\alpha }_{\text{B1B3}}}=\frac{f_{\text{B}11}^{2}}{f_{\text{B}11}^{2}-f_{\text{B}31}^{2}}, {{\beta }_{\text{B1B3}}}=-\frac{f_{\text{B}31}^{2}}{f_{\text{B}11}^{2}-f_{\text{B}3\text{I}}^{2}} \\ \end{array} \right. $ | (5) |
与传统模型不同,由于三频PPP的前2个频率并不是B1I和B3I,因此DCB的值和无电离层组合因子也有所变化。改正后的观测方程为:
| $ \left\{ \begin{array}{*{35}{l}} P_{\text{r}, j}^{\text{s}}=\rho _{\text{r}}^{\text{s}}+c\cdot \text{d}{{t}_{\text{r}}}+{{T}_{\text{r}}}+{{\gamma }_{j}}\cdot I_{\text{r}, 1}^{\text{s}}+ \\ \quad c\cdot d_{\text{r}, j}^{\text{s}}+\varepsilon _{\text{r}, {{P}_{j}}}^{\text{s}, T} \\ L_{\text{r}, j}^{\text{s}}=\rho _{\text{r}}^{\text{s}}+c\cdot \text{d}{{t}_{\text{r}}}+{{T}_{\text{r}}}-{{\gamma }_{j}}\cdot I_{\text{r}, 1}^{\text{s}}+ \\ \quad \lambda _{j}^{\text{s}}\left( N_{\text{r}, j}^{\text{s}}+b_{\text{r}, j}^{\text{s}}-b_{j}^{\text{s}} \right)+c\cdot d_{\text{I}{{\text{F}}_{12}}}^{\text{s}}+\xi _{\text{r}, {{L}_{j}}}^{\text{s}} \\ \end{array} \right. $ | (6) |
TU模型不对三频数据作任何线性组合,而是直接使用原始伪距和相位观测方程,即
| $ \left\{\begin{array}{l} P_{\mathrm{r}, j}^{\mathrm{s}}=\rho_{\mathrm{r}}^{\mathrm{s}}+c \cdot \mathrm{d} t_{\mathrm{r}}+T_{\mathrm{r}}+ \\ \;\;\;\; \gamma_{j} \cdot I_{\mathrm{r}, 1}^{\mathrm{s}}+c \cdot d_{\mathrm{r}, j}^{\mathrm{s}}+ \varepsilon_{\mathrm{r}, P_{j}}^{\mathrm{s}, T} \\ L_{\mathrm{r}, j}^{\mathrm{s}}=\rho_{\mathrm{r}}^{\mathrm{s}}+c \cdot \mathrm{d} t_{\mathrm{r}}+T_{\mathrm{r}}-\gamma_{j} \cdot I_{\mathrm{r}, 1}^{\mathrm{s}}+ \\ \;\;\;\; \lambda_{j}^{\mathrm{s}}\left(N_{\mathrm{r}, j}^{\mathrm{s}}+b_{\mathrm{r}, j}^{\mathrm{s}}-b_{j}^{\mathrm{s}}\right)+c \cdot d_{\mathrm{IF}_{12}}^{\mathrm{s}}+\xi_{\mathrm{r}, L_{j}}^{\mathrm{s}} \end{array}\right. $ | (7) |
式中,接收机硬件延迟dr, js(j=1, 2)可以被接收机钟差和电离层延迟参数吸收,假设被两者吸收的部分分别为a和b,则有:
| $ \begin{array}{l} \left\{ {\begin{array}{*{20}{c}} {c \cdot d_{{\rm{r}}, 1}^{\rm{s}} = a + {\gamma _1} \cdot b}\\ {c \cdot d_{{\rm{r}}, 2}^{\rm{s}} = a + {\gamma _2} \cdot b} \end{array}} \right.\\ \qquad\qquad \Downarrow \\ \left\{ \begin{array}{l} a = {\alpha _{12}} \cdot c \cdot d_{{\rm{r}}, 1}^{\rm{s}} + {\beta _{12}} \cdot c \cdot d_{{\rm{r}}, 2}^{\rm{s}} = \\ \;\;\;\;c \cdot {d_{{\rm{r}}, {{\rm{F}}_{12}}}}\\ b = \frac{1}{{1 - {\gamma _2}}} \cdot c \cdot \left( {d_{{\rm{r}}, 1}^{\rm{s}} - d_{{\rm{r}}, 2}^{\rm{s}}} \right) = \\ \;\;\;\;{\beta _{12}} \cdot c \cdot {\rm{DC}}{{\rm{B}}_{{\rm{r}}, {P_1}{P_2}}} \end{array} \right. \end{array} $ | (8) |
将式(8)代入式(7)并重新规划参数:
| $ \left\{\begin{array}{l} P_{\mathrm{r}, j}^{\mathrm{s}}=\rho_{\mathrm{r}}^{\mathrm{s}}+c \cdot \overline{\mathrm{d} t_{\mathrm{r}}}+T_{\mathrm{r}}+\gamma_{j} \cdot \\ \;\;\;\; \bar{I}_{\mathrm{r}, 1}^{\mathrm{s}}+\mathrm{IFB}_{\mathrm{r}, j}+\varepsilon_{\mathrm{r}, P_{j}}^{\mathrm{s}, T} \\ L_{\mathrm{r}, j}^{\mathrm{s}}=\rho_{\mathrm{r}}^{\mathrm{s}}+c \cdot \overline{\mathrm{d} t_{\mathrm{r}}}+T_{\mathrm{r}}-\gamma_{j} \cdot \\ \;\;\;\; \bar{I}_{\mathrm{r}, 1}^{\mathrm{s}}+\bar{N}_{\mathrm{r}, j}^{\mathrm{s}}+\xi_{\mathrm{r}, L_{j}}^{\mathrm{s}} \end{array}\right. $ | (9) |
式中,IFBr, j为j频率上的伪距频间偏差,且
| $ \left\{ \begin{array}{l} \overline {{\rm{d}}{t_{\rm{r}}}} = {\rm{d}}{t_{\rm{r}}} + {d_{{\rm{r}}, {\rm{I}}{{\rm{F}}_{12}}}}\\ \bar I_{{\rm{r}}, 1}^{\rm{s}} = I_{{\rm{r}}, 1}^{\rm{s}} + c \cdot {\beta _{12}} \cdot {\rm{DC}}{{\rm{B}}_{{\rm{r}}, {P_1}{P_2}}}\\ \bar N_{{\rm{r}}, j}^{\rm{s}} = \lambda _j^{\rm{s}}\left( {N_{{\rm{r}}, j}^{\rm{s}} + b_{{\rm{r}}, j}^{\rm{s}} - b_j^{\rm{s}}} \right) + c\left( {d_{{\rm{I}}{{\rm{F}}_{12}}}^{\rm{s}} - } \right.\\ \left. {\;\;\;\;{d_{{\rm{r}}, {\rm{I}}{{\rm{F}}_{12}}}}} \right) + c \cdot {\gamma _j} \cdot {\beta _{12}} \cdot {\rm{DC}}{{\rm{B}}_{{\rm{r}}, {P_1}{P_2}}}\\ {\rm{IF}}{{\rm{B}}_{{\rm{r}}, 3}} = \left\{ {\begin{array}{*{20}{l}} {0, j < 3}\\ {c\left( {d_{{\rm{r}}, 3}^{\rm{s}} - {d_{{\rm{r}}, {\rm{I}}{{\rm{F}}_{12}}}}} \right) - c \cdot {\gamma _3} \cdot }\\ {\;\;\;{\beta _{12}} \cdot {\rm{DC}}{{\rm{B}}_{{\rm{r}}, {P_1}{P_2}}}, j = 3} \end{array}} \right. \end{array} \right. $ | (10) |
TF模型是将三频数据组合成消去电离层一阶项的观测值,即
| $ \left\{\begin{array}{l} P_{\mathrm{r}, \mathrm{IF}_{123}}^{\mathrm{s}} &=e_{1} \cdot P_{\mathrm{r}, 1}^{\mathrm{s}}+e_{2} \cdot P_{\mathrm{r}, 2}^{\mathrm{s}}+e_{3} \cdot \\ \;\;\;\; P_{\mathrm{r}, 3}^{\mathrm{s}} &=\rho_{\mathrm{r}}^{\mathrm{s}}+c \cdot \overline{\mathrm{d} t_{\mathrm{r}}}+T_{\mathrm{r}}+\varepsilon_{\mathrm{r}, \mathrm{IF}_{123}}^{\mathrm{s}} \\ L_{\mathrm{r}, \mathrm{IF}_{123}}^{\mathrm{s}}, &=e_{1} \cdot L_{\mathrm{r}, 1}^{\mathrm{s}}+e_{2} \cdot L_{\mathrm{r}, 2}^{\mathrm{s}}+e_{3} \\ \;\;\;\; L_{\mathrm{r}, 3}^{\mathrm{s}} &=\rho_{\mathrm{r}}^{\mathrm{s}}+c \cdot \overline{\mathrm{d} t_{\mathrm{r}}}+T_{\mathrm{r}}+\bar{N}_{\mathrm{r}, \mathrm{IF}_{123}}^{\mathrm{s}}+\xi_{\mathrm{r}, \mathrm{IF}_{123}}^{\mathrm{s}} \end{array}\right. $ | (11) |
式中,
| $ \left\{\begin{array}{l} \overline{\mathrm{d} t_{\mathrm{r}}}=\mathrm{d} t_{\mathrm{r}}+d_{\mathrm{r}, \mathrm{IF}_{123}}^{\mathrm{s}} \\ \bar{N}_{\mathrm{r}, \mathrm{IF}_{123}}^{\mathrm{s}}=e_{1} \cdot \lambda_{1}^{\mathrm{s}}\left(N_{\mathrm{r}, 1}^{\mathrm{s}}+b_{\mathrm{r}, 1}^{\mathrm{s}}-b_{1}^{\mathrm{s}}\right)+ \\ \;\;\; e_{2} \cdot \lambda_{2}^{\mathrm{s}}\left(N_{\mathrm{r}, 2}^{\mathrm{s}}+b_{\mathrm{r}, 2}^{\mathrm{s}}-b_{2}^{\mathrm{s}}\right)+e_{3} \cdot \lambda_{3}^{\mathrm{s}} \cdot \\ \;\;\; \left(N_{\mathrm{r}, 3}^{\mathrm{s}}+b_{\mathrm{r}, 3}^{\mathrm{s}}-b_{3}^{\mathrm{s}}\right)+c\left(d_{\mathrm{IF}_{12}}^{\mathrm{s}}-d_{\mathrm{r}, \mathrm{IF}_{123}}^{\mathrm{s}}\right) \end{array}\right. $ | (12) |
组合系数e1、e2、e3需满足[6]:
| $ \left\{\begin{array}{l} e_{1}=\frac{\gamma_{2}^{2}+\gamma_{3}^{2}-\gamma_{2}-\gamma_{3}}{2\left(\gamma_{2}^{2}+\gamma_{3}^{2}-\gamma_{2} \cdot \gamma_{3}-\gamma_{2}-\gamma_{3}+1\right)} \\ e_{2}=\frac{\gamma_{3}^{2}-\gamma_{2} \cdot \gamma_{3}-\gamma_{2}+1}{2\left(\gamma_{2}^{2}+\gamma_{3}^{2}-\gamma_{2} \cdot \gamma_{3}-\gamma_{2}-\gamma_{3}+1\right)} \\ e_{3}=\frac{\gamma_{2}^{2}-\gamma_{2} \cdot \gamma_{3}-\gamma_{3}+1}{2\left(\gamma_{2}^{2}+\gamma_{3}^{2}-\gamma_{2} \cdot \gamma_{3}-\gamma_{2}-\gamma_{3}+1\right)} \end{array}\right. $ | (13) |
BDS-3三频数据能够组合产生2个双频无电离层组合(B1C/B2a和B1C/B2b)[7],组合后的观测方程为:
| $ \left\{ \begin{array}{l} P_{{\rm{r}}, {\rm{I}}{{\rm{F}}_{12}}}^{\rm{s}} = {\alpha _{12}} \cdot P_{{\rm{r}}, 1}^{\rm{s}} + {\beta _{12}} \cdot P_{{\rm{r}}, 2}^{\rm{s}} = \\ \;\;\;\rho _{\rm{r}}^{\rm{s}} + c \cdot \overline {{\rm{d}}{t_{\rm{r}}}} + {T_{\rm{r}}} + \varepsilon _{{\rm{r}}, {\rm{I}}{{\rm{F}}_{12}}}^{\rm{s}}\\ P_{{\rm{r}}, {\rm{I}}{{\rm{F}}_{13}}}^{\rm{s}} = {\alpha _{13}} \cdot P_{{\rm{r}}, 1}^{\rm{s}} + {\beta _{13}} \cdot P_{{\rm{r}}, 3}^{\rm{s}} = \\ \;\;\;\rho _{\rm{r}}^{\rm{s}} + c \cdot \overline {{\rm{d}}{t_{\rm{r}}}} + {T_{\rm{r}}} + {\rm{IF}}{{\rm{B}}_{{\rm{r}}, {\rm{I}}{{\rm{F}}_{13}}}} + \varepsilon _{{\rm{r}}, {\rm{I}}{{\rm{F}}_{13}}}^{\rm{s}}\\ L_{{\rm{r}}, {\rm{I}}{{\rm{F}}_{12}}}^{\rm{s}} = {\alpha _{12}} \cdot L_{{\rm{r}}, 1}^{\rm{s}} + {\beta _{12}} \cdot L_{{\rm{r}}, 2}^{\rm{s}} = \\ \;\;\;\rho _{\rm{r}}^{\rm{s}} + c \cdot \overline {{\rm{d}}{t_{\rm{r}}}} + {T_{\rm{r}}} + \bar N_{{\rm{r}}, {\rm{I}}{{\rm{F}}_{12}}}^{{{\rm{s}}_{12}}} + \xi _{{\rm{r}}, {\rm{I}}{{\rm{F}}_{12}}}^{\rm{s}}\\ L_{{\rm{r}}, {\rm{I}}{{\rm{F}}_{13}}}^{\rm{s}} = {\alpha _{13}} \cdot L_{{\rm{r}}, 1}^{\rm{s}} + {\beta _{13}} \cdot L_{{\rm{r}}, 3}^{\rm{s}} = \\ \;\;\;\rho _{\rm{r}}^{\rm{s}} + c \cdot \overline {{\rm{d}}{t_{\rm{r}}}} + {T_{\rm{r}}} + \bar N_{{\rm{r}}, {\rm{I}}{{\rm{F}}_{13}}}^{\rm{s}} + \xi _{{\rm{r}}, {\rm{I}}{{\rm{F}}_{13}}}^{\rm{s}} \end{array} \right. $ | (14) |
式中,IFBr, IF13为无电离层两两组合的伪距频间偏差参数,且
| $ \begin{aligned} &\left\{\begin{array}{l} \overline{\mathrm{d} t_{\mathrm{r}}}=\mathrm{d} t_{\mathrm{r}}+d_{\mathrm{r}, \mathrm{IF}_{12}}^{\mathrm{s}} \\ \overline{N}_{\mathrm{r}, \mathrm{IF}_{12}}^{\mathrm{~s}}=\alpha_{12} \cdot \lambda_{1}^{\mathrm{s}}\left(N_{\mathrm{r}, 1}^{\mathrm{s}}+b_{\mathrm{r}, 1}^{\mathrm{s}}-b_{1}^{\mathrm{s}}\right)+\beta_{12} \cdot \\ \;\;\;\; \lambda_{2}^{\mathrm{s}}\left(N_{\mathrm{r}, 2}^{\mathrm{s}}+b_{\mathrm{r}, 2}^{\mathrm{s}}-b_{2}^{\mathrm{s}}\right)+c\left(d_{\mathrm{IF}_{12}}^{\mathrm{s}}-d_{\mathrm{r}, \mathrm{IF}_{12}}^{\mathrm{s}}\right) \\ \overline{N}_{\mathrm{r}, \mathrm{F}_{13}}^{\mathrm{~s}}=\alpha_{13} \cdot \lambda_{1}^{\mathrm{s}}\left(N_{\mathrm{r}, 1}^{\mathrm{s}}+b_{\mathrm{r}, 1}^{\mathrm{s}}-b_{1}^{\mathrm{s}}\right)+\beta_{13} \cdot \\ \;\;\;\; \lambda_{3}^{\mathrm{s}}\left(N_{\mathrm{r}, 3}^{\mathrm{s}}+b_{\mathrm{r}, 3}^{\mathrm{s}}-b_{3}^{\mathrm{s}}\right)+c\left(d_{\mathrm{IF}_{13}}^{\mathrm{s}}-d_{\mathrm{r}, \mathrm{IF}_{12}}^{\mathrm{s}}\right)\\ \mathrm{IFB}_{\mathrm{r}, \mathrm{IF}_{13}}=d_{\mathrm{r}, \mathrm{IF}_{13}}^{\mathrm{s}}-d_{\mathrm{r}, \mathrm{IF}_{12}}^{\mathrm{s}}=\left(1-\beta_{13}\right) d_{\mathrm{r}, 1}^{\mathrm{s}}+\\ \;\;\;\; \beta_{13} \cdot d_{\mathrm{r}, 3}^{\mathrm{s}}-\left(1-\beta_{12}\right) d_{\mathrm{r}, 1}^{\mathrm{s}}-\beta_{12} \cdot d_{\mathrm{r}, 2}^{\mathrm{s}}=\\ \;\;\;\; \beta_{12} \cdot \mathrm{DCB}_{\mathrm{r}, 12}^{\mathrm{s}}-\beta_{13} \cdot \mathrm{DCB}_{\mathrm{r}, 13}^{\mathrm{s}} \end{array}\right. \end{aligned} $ | (15) |
为研究BDS-3卫星新三频PPP的定位性能,采用BDS-3卫星2种双频非差非组合模型DU2和DU3进行对比。BDS-3卫星的双频、三频PPP模型特点见表 1,不同的模型采用不同的频率和组合系数,需要注意不同模型的卫星端DCB改正。
|
|
表 1 BDS-3双频、三频PPP模型特征 Tab. 1 Features of BDS-3 dual- and triple-frequency PPP models |
对于多个频率的观测值,通常将其方差量化为与卫星高度角、信噪比有关的函数形式[8]。本文基于卫星高度角的随机模型将观测值噪声σ模型化为卫星高度角E的函数[9],即
| $ \sigma =f\left( E \right)=\sqrt{{{a}^{2}}+{{b}^{2}}/{{\sin }^{2}}E} $ | (16) |
式中,a和b是常数。对于原始载波相位观测值噪声σL, a和b均设为0.003 m;原始伪距观测值σP设为载波相位观测值的100倍,即a和b取0.3 m。假设多个频率的观测值之间相互独立且伪距噪声值也相同,则载波相位观测值噪声与频率无关,因此σP1=σP2=σPn, σL1=σL2=σLn。
根据误差传播定律可得三频非差非组合模型(TU)、三频消电离层模型(TF)、三频无电离层组合模型(TDF)对应的方差协方差矩阵为:
| $ \left\{ \begin{array}{l} {\varSigma _{{\rm{TU}}}} = \left[ {\begin{array}{*{20}{c}} {{\sigma _P}}&{}&{}&{}&{}&{}\\ {}&{{\sigma _L}}&{}&{}&{}&{}\\ {}&{}&{{\sigma _P}}&{}&{}&{}\\ {}&{}&{}&{{\sigma _L}}&{}&{}\\ {}&{}&{}&{}&{{\sigma _P}}&{}\\ {}&{}&{}&{}&{}&{{\sigma _L}} \end{array}} \right], {\varSigma _{{\rm{TF}}}} = \left[ {\begin{array}{*{20}{c}} {\left( {e_1^2 + e_2^2 + e_3^2} \right){\sigma _P}}&0\\ 0&{\left( {e_1^2 + e_2^2 + e_3^2} \right){\sigma _L}} \end{array}} \right]\\ {\varSigma _{{\rm{TDF}}}} = \left[ {\begin{array}{*{20}{c}} {\left( {\alpha _{12}^2 + \beta _{12}^2} \right){\sigma _P}}&0&{{\alpha _{12}} \cdot {\alpha _{13}} \cdot {\sigma _P}}&0\\ 0&{\left( {\alpha _{12}^2 + \beta _{12}^2} \right){\sigma _L}}&0&{{\alpha _{12}} \cdot {\alpha _{13}} \cdot {\sigma _L}}\\ {{\alpha _{12}} \cdot {\alpha _{13}} \cdot {\sigma _P}}&0&{\left( {\alpha _{13}^2 + \beta _{13}^2} \right){\sigma _P}}&0\\ 0&{{\alpha _{12}} \cdot {\alpha _{13}} \cdot {\sigma _L}}&0&{\left( {\alpha _{12}^2 + \beta _{12}^2} \right){\sigma _L}} \end{array}} \right] \end{array} \right. $ | (17) |
选取14个MGEX测站2021-09-01~10的数据,采样间隔为30 s,所选测站均能接收到BDS-3卫星播发的新频率B1C、B2a、B2b信号。
分别以静态、仿动态2种定位模式从定位精度和收敛时间方面对比DU2、DU3、TU、TIF和TF等5种PPP模型的定位性能。以IGS提供的SINEX文件中的坐标为真值,当测站的E、N、U方向上的绝对定位误差连续60个历元(30 min)均小于0.1 m时判定为收敛。新频率B2b的卫星端DCB改正值采用MGEX提供的DCB文件中的C7Z类型,联合使用Geometry-Free和Melbourne-Wubben组合对周跳进行探测修复[10],具体PPP数据处理策略见表 2。
|
|
表 2 数据处理策略 Tab. 2 Data processing strategy |
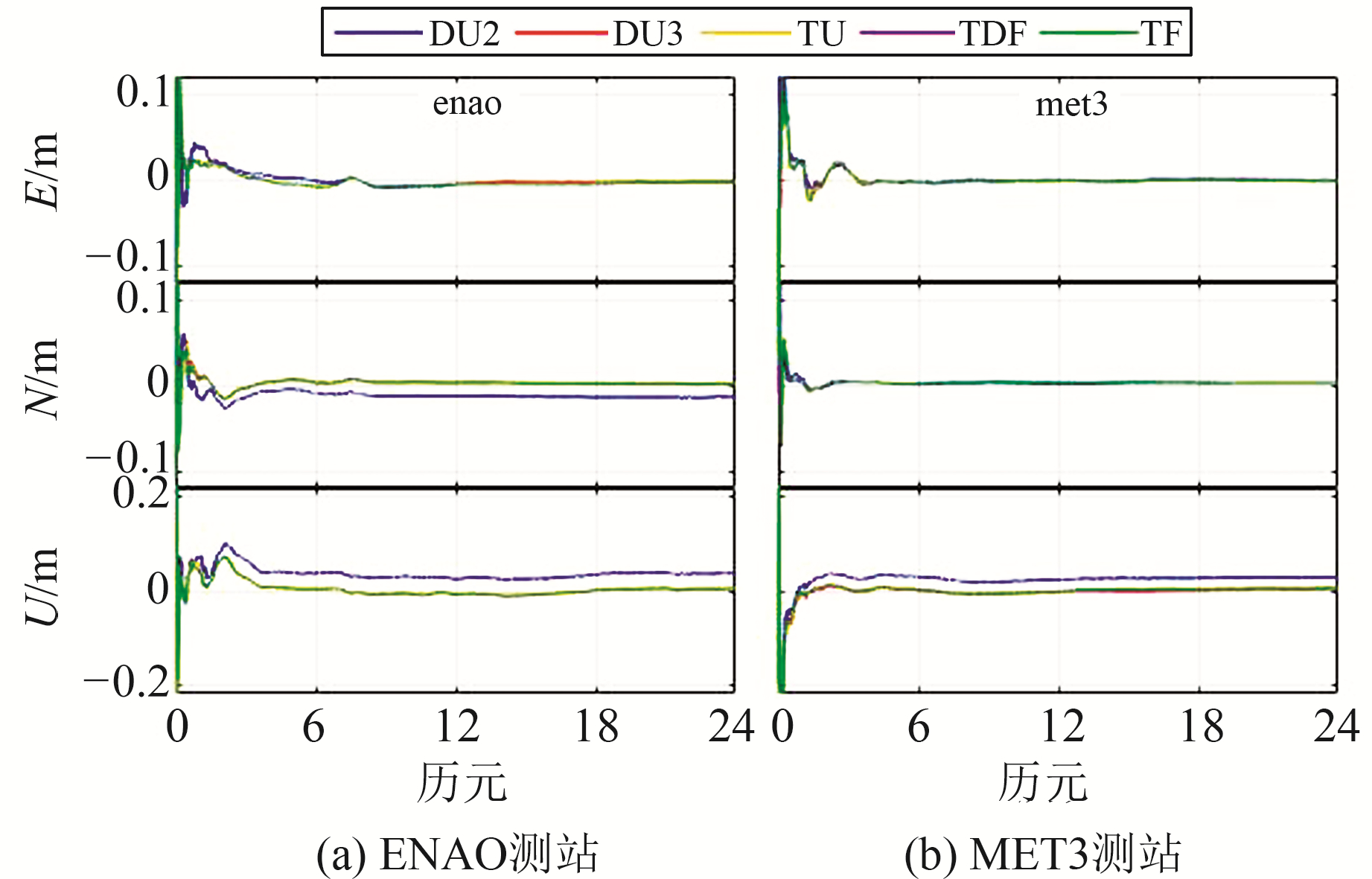
图 1为ENAO和MET3测站在doy244的5种PPP模型静态定位误差曲线。由图可见,DU2模型的定位效果最差,尤其是在U方向上。
|
图 1 5种PPP模型静态定位误差 Fig. 1 Static positioning error of five PPP models |
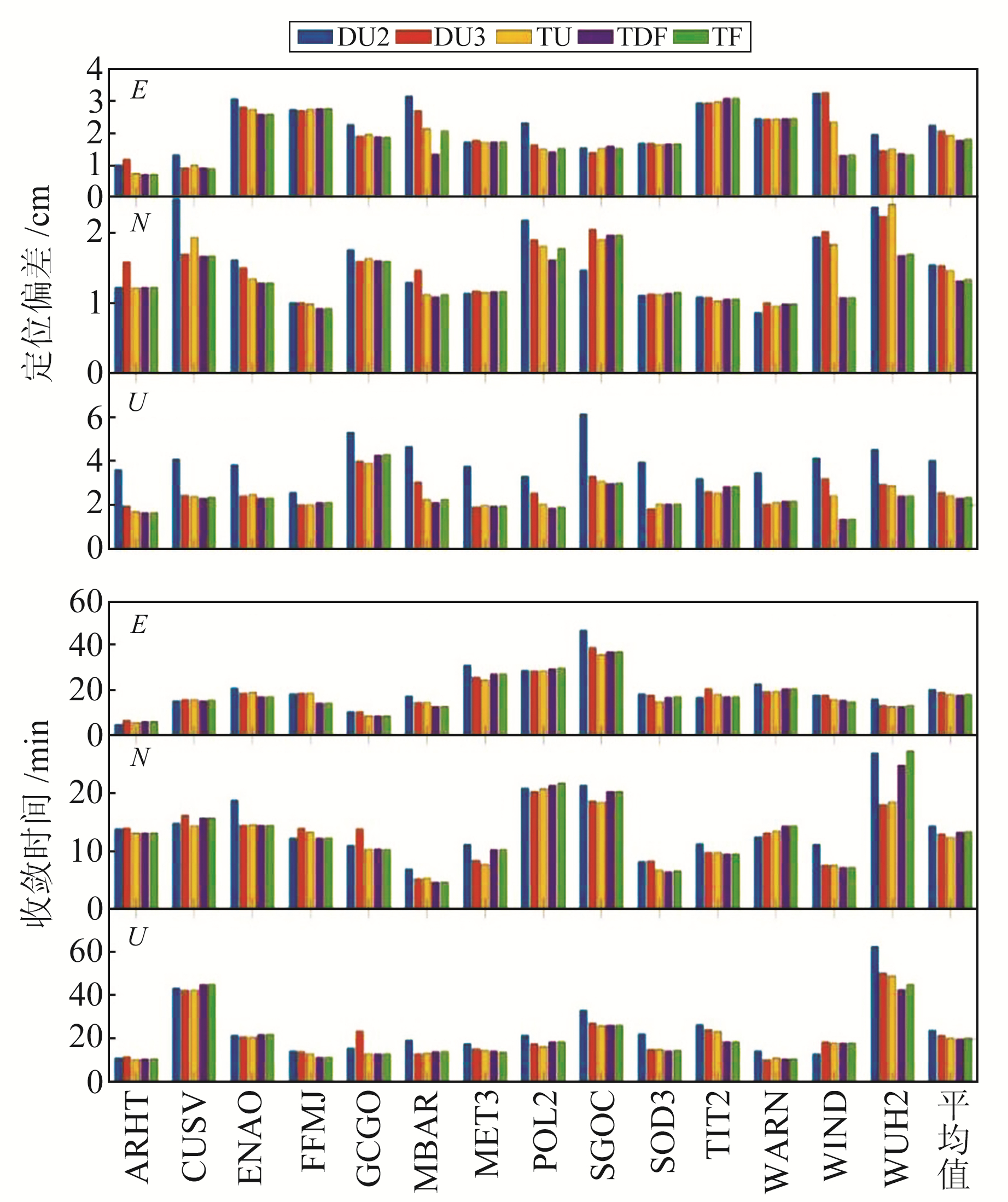
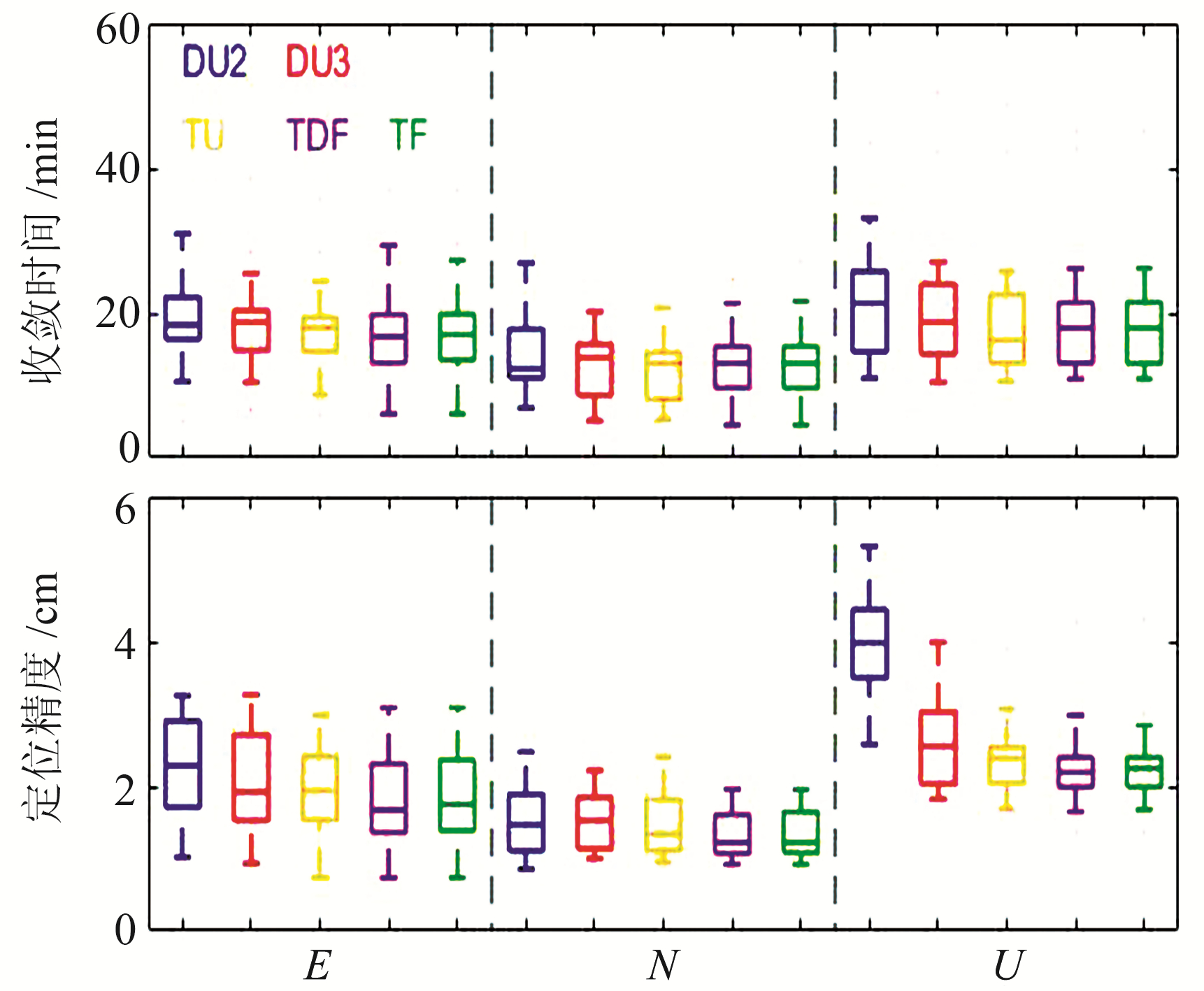
图 2为14个测站5种PPP模型doy244~253静态定位结果的平均偏差和收敛时间及其平均值,图 3为5种PPP模型三维收敛时间和定位精度。由图 2可见,除个别测站外,相对于DU2模型,新双频DU3模型和三频PPP模型在三维定位精度和收敛时间上均有所提升,其中U方向上的精度提升最大。5种模型的平均定位精度和收敛时间见表 3。由表可见,相比于传统的DU2模型,DU3模型在收敛时间和E、N、U方向上的定位精度分别提升9.4%和8.4%、0%、35.8%;TU模型分别提升14.9%和14.2%、4.6%、40.2%;TDF模型分别提升16.7%和21.2%、13.7%、42.7%;TF模型分别提升16.0%和18.6%、13.7%、42.2%。综上所述,三频PPP模型的定位效果略好于新双频DU3模型,其中TDF模型的精度最优。
|
图 2 14个测站5种PPP模型静态定位偏差和收敛时间平均值 Fig. 2 The average values of static positioning deviation and convergence time of five PPP models at fourteen stations |
|
图 3 5种PPP模型静态三维收敛时间和定位精度 Fig. 3 Static 3D convergence time and positioning accuracy of five PPP models |
|
|
表 3 5种PPP模型静态定位收敛时间和精度 Tab. 3 Static positioning convergence time and accuracy of five PPP models |
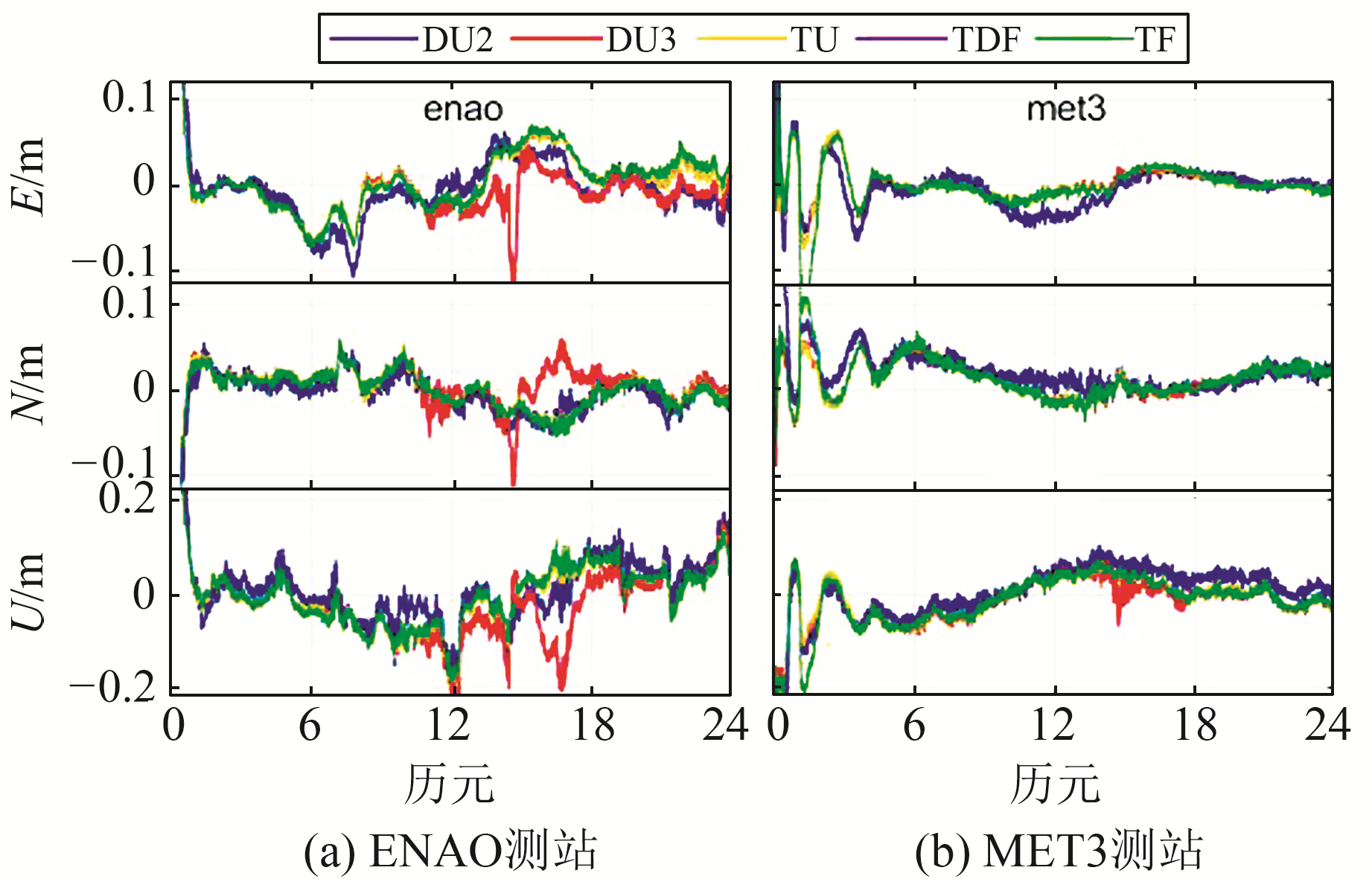
图 4是ENAO和MET3测站在doy244的5种PPP模型动态定位误差曲线。与静态定位相同,三频PPP模型和DU3模型在收敛时间和定位精度上均有所提升,但不同的是,动态定位中4种模型在收敛时间上的提升效果较为明显。
|
图 4 5种PPP模型动态定位误差 Fig. 4 Dynamic positioning error of five PPP models |
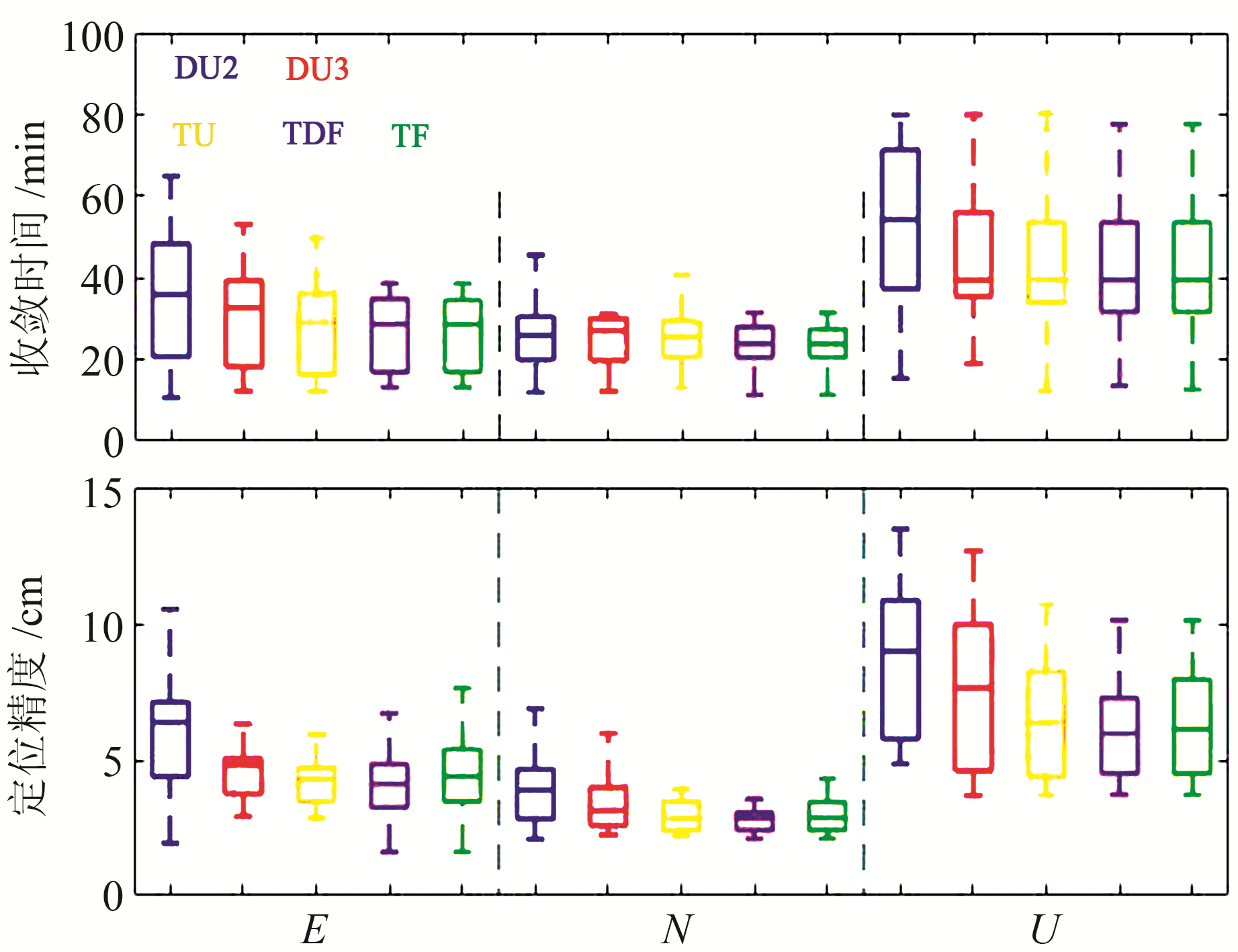
图 5为14个测站5种PPP模型连续10 d动态定位结果的平均偏差和收敛时间及其平均值,图 6为5种PPP模型三维收敛时间和定位精度,表 4为5种模型的平均定位精度和收敛时间。可以看出,相比于传统的DU2模型,DU3模型在收敛时间和E、N、U方向上的定位精度分别提升12.2%和20.1%、8.8%、13.5%;TU模型分别提升15.6%和32.6%、26.5%、27.7%;TDF模型分别提升16.9%和35.6%、30.4%、29.9%;TF模型分别提升17.2%和30.4%、25.8%、29.1%。综上所述,三频PPP模型的动态定位效果强于新双频DU3模型,其中TDF模型在定位精度上的提升效果最明显,TF模型对收敛时间的提升效果最好。

|
图 5 14个测站5种PPP模型动态定位偏差和收敛时间平均值 Fig. 5 The average values of dynamic positioning deviation and convergence time of five PPP models at fourteen stations |
|
图 6 5种PPP模型动态三维收敛时间和定位精度 Fig. 6 Dynamic 3D convergence time and positioning accuracy of five PPP models |
|
|
表 4 5种PPP模型动态定位收敛时间和精度统计 Tab. 4 Dynamic positioning convergence time and accuracy statistics of five PPP models |
1) BDS-3的DU2模型在静、动态定位中的收敛时间分别约为24 min和58 min;而B1C、B2a和B2b新频率组成的双频非差非组合模型和三频PPP模型在静、动态定位中的收敛时间可达约20 min和50 min,三维定位精度能达到2 cm和7 cm,提升较大。
2) 与传统B1I/B3I双频DU2模型相比,DU3、TU、TDF和TF模型的定位性能均有所提高。在收敛时间方面,TDF模型对静态定位的提升最大,略高于TF模型;TF模型对动态定位的提升最大,略高于TDF模型。在定位精度方面,TDF模型对静态和动态定位的提升最明显。
本文对于北斗三号卫星新三频PPP模型的性能分析仅限于模糊度浮点解,在北斗多频同时播发的条件下,PPP模糊度固定解具有更加广阔的应用前景。在后续研究中,笔者将着重研究北斗多频模糊度固定技术方法。
| [1] |
李昕, 张小红. BDS-2和BDS-3卫星伪距多路径偏差特性比较[J]. 大地测量与地球动力学, 2018, 38(2): 191-194 (Li Xin, Zhang Xiaohong. Comparison of Satellite-Induced Code Bias between BDS-2 and BDS-3 Satellites[J]. Journal of Geodesy and Geodynamics, 2018, 38(2): 191-194)
(  0) 0) |
| [2] |
苏珂, 金双根. BDS/Galileo四频精密单点定位模型性能分析与比较[J]. 测绘学报, 2020, 49(9): 1 189-1 201 (Su Ke, Jin Shuanggen. Analysis and Comparisons of the BDS/Galileo Quad-Frequency PPP Models Performances[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(09): 1 189-1 201)
(  0) 0) |
| [3] |
周锋. 多系统GNSS非差非组合精密单点定位相关理论和方法研究[J]. 测绘学报, 2020, 49(7): 938 (Zhou Feng. Theory and Methodology of Multi-GNSS Undifferenced and Uncombined Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(7): 938)
(  0) 0) |
| [4] |
魏子卿, 刘光明, 吴富梅. 2000中国大地坐标系: 中国大陆速度场[J]. 测绘学报, 2011, 40(4): 403-410 (Wei Ziqing, Liu Guangming, Wu Fumei. China Geodetic Coordinate System 2000: Velocity Field in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 403-410)
(  0) 0) |
| [5] |
Cao X Y, Shen F, Zhang S J, et al. Time Delay Bias between the Second and Third Generation of Beidou Navigation Satellite System and Its Effect on Precise Point Positioning[J]. Measurement, 2021, 168
(  0) 0) |
| [6] |
Deo M, El-Mowafy A. Triple-Frequency GNSS Models for PPP with Float Ambiguity Estimation: Performance Comparison Using GPS[J]. Survey Review, 2018, 50(360): 249-261 DOI:10.1080/00396265.2016.1263179
(  0) 0) |
| [7] |
李鹤峰, 党亚民, 秘金钟, 等. BDS/GPS/GLONASS融合定位模型及性能分析[J]. 测绘通报, 2014(9): 1-5 (Li Hefeng, Dang Yamin, Bei Jinzhong, et al. Research on Model and Performance of BDS/GPS/GLONASS Multi-Mode Fusion Positioning[J]. Bulletin of Surveying and Mapping, 2014(9): 1-5)
(  0) 0) |
| [8] |
Wang J L, Satirapod C, Rizos C. Stochastic Assessment of GPS Carrier Phase Measurements for Precise Static Relative Positioning[J]. Journal of Geodesy, 2002, 76(2): 95-104 DOI:10.1007/s00190-001-0225-6
(  0) 0) |
| [9] |
郭斐. GPS精密单点定位质量控制与分析的相关理论和方法研究[D]. 武汉: 武汉大学, 2013 (Guo Fei. Theory and Methodology of Quality Control and Quality Analysis for GPS Precise Point Positioning[D]. Wuhan: Wuhan University, 2013)
(  0) 0) |
| [10] |
Blewitt G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202 DOI:10.1029/GL017i003p00199
(  0) 0) |
2. School of Spatial Information and Geomatics Engineering, Anhui University of Science and Technology, 168 Taifeng Street, Huainan 232001, China
 2022, Vol. 42
2022, Vol. 42

