在卫星导航定位中,码观测值会因为硬件特性在卫星和接收机端产生硬件延迟,2个频率的码观测值硬件之差称为差分码偏差(differential code bias, DCB)[1-2],其在卫星端称为卫星差分码偏差,接收机端称为接收机差分码偏差。DCB是电离层建模和精密单点定位中重要的误差源,需要被精确计算。DCB分为频内DCB(同一频率的码观测值硬件延迟之差)和频间DCB(不同频率的码观测值硬件延迟之差)[3]。频内DCB一般可以通过码观测值的平均组合观测值求取,本文所指的DCB为频间DCB。
卫星和接收机DCB的估计方法一般有2种:一种是采用球谐函数进行全球电离层建模,同时估计卫星和接收机DCB[4-6]。首先需要联合全球的测站数据进行观测方程列立,然后估计球谐函数系数和卫星及接收机DCB。该方法估计DCB的效果依赖于建模的精度,并且有一定的计算量。另一种是使用已有的全球电离层图(global ionosphere map, GIM)。首先进行时间和空间上的内插来获取穿刺点的TEC,进而消除其参数,然后估计卫星和接收机的DCB值[7-9]。该方法可在一定程度上减少计算量、提高估计效率,但其估计DCB的效果主要依赖于GIM精度。
由于2种常规方法都需要进行电离层建模和使用已有的GIM信息,因此本文在原有方法的基础上提出一种差分码偏差估计的简化模型,将测站方向上各穿刺点的VTEC简化为一个参数,分时段进行直接估计。为验证该方法的有效性,采用球谐函数建模和基于GIM的估计方法进行比较分析。选用2016-01近200个IGS测站的GPS+GLONASS数据进行实验,并采用CODE提供的产品进行验证。实验结果验证了本文方法的有效性。
1 差分码偏差估计方法 1.1 电离层TEC观测值GPS和GLONASS的伪距和载波相位观测值可以表示为[10]:
| $ \begin{aligned} &P_{k, j}^{i}=\rho_{0, j}^{i}+d_{\text {ion }, k, j}^{i}+d_{\text {trop }, j}^{i}+ \\ &\quad c\left(\tau^{i}-\tau_{j}\right)+d_{k}^{i}+d_{k, j}+\varepsilon_{P, k, j}^{i} \\ &L_{k, j}^{i}=\rho_{0, j}^{i}-d_{\text {ion }, k, j}^{i}+d_{\text {trop }, j}^{i}+ \\ &\quad c\left(\tau^{i}-\tau_{j}\right)-\lambda\left(b_{k, j}^{i}+N_{k, j}^{i}\right)+\varepsilon_{L, k, j}^{i} \end{aligned} $ | (1) |
式中,Pk, ji和Lk, ji分别为测站j到卫星i、频率为k的伪距(码观测值)和载波相位观测值,ρ0, ji为测站到卫星的几何距离,dion, k, ji为电离层延迟,dtrop, ji为对流层延迟,c为真空中的光速,τi和τj分别为卫星和接收机钟差,dki和dk, j分别为频率为k的码观测值卫星和接收机的硬件延迟,λ为载波相位的波长,bk, ji为相位观测值的卫星和接收机相位偏差之和,Nk, ji为相位观测值的整周模糊度,εP, k, ji和εL, k, ji分别为伪距观测值和载波相位观测值的噪声。
一般情况下,采用载波相位平滑伪距法来提取电离层延迟:
| $ \begin{aligned} P_{4, s m}=& 40.3\left(\frac{1}{f_{1}^{2}}-\frac{1}{f_{2}^{2}}\right) \mathrm{STEC}+\\ & c \mathrm{DCB}^{i}+c \mathrm{DCB}_{j} \end{aligned} $ | (2) |
式中,P4, sm为采用双频载波相位平滑伪距的观测值;式(1)中的电离层延迟可以参数化为
| $ \begin{gathered} \mathrm{STEC}=M(z) \cdot \mathrm{VTEC}= \\ 1 / \cos \left(\arcsin \left(\frac{R}{R+H} \sin (\alpha z)\right)\right) \cdot \mathrm{VTEC} \end{gathered} $ | (3) |
式中,M(z)为电离层投影函数,R为地球平均半径,H为假设的电离层薄层高度,z为接收机到卫星方向上在假设电离层薄层处的天顶距,α为调节因子(一般取值为0.978 2)。因此,可以将式(2)进一步表示为:
| $ \begin{gathered} P_{4, s m}=F(f) \cdot M(z) \\ \mathrm{VTEC}+{c} \mathrm{DCB}^{i}+c \mathrm{DCB}_{j} \end{gathered} $ | (4) |
式中,
本文采用15阶球谐函数进行全球电离层TEC建模,结合式(4)可以将球谐函数建模的观测方程表示为[11]:
| $ \begin{array}{l} \sum\limits_{n = 0}^{{n_{\max }}} {\sum\limits_{m = 0}^n {{{\tilde P}_{nm}}} } (\sin \beta )\left( {{a_{nm}}\cos ms + {b_{nm}}\sin ms} \right)\\ F(f) \cdot M(z) + c{\rm{DC}}{{\rm{B}}_j} + c{\rm{DC}}{{\rm{B}}^i} = {P_{4, sm}} \end{array} $ | (5) |
式中,n和m分别为球谐函数的阶次,β和ms分别为穿刺点的地理纬度和日固经度,anm和bnm分别为模型的待求系数。采用分段线性方法进行球谐函数参数估计,每2 h估计一组参数,1 d共估计13组参数,则需要估计的球谐函数参数数量为13×256=3 328个。由于使用全球测站的GPS+GLONASS观测值共同建模,因此观测值的个数远大于待求参数的个数,可以直接使用最小二乘平差法求解。需要估计的参数为:
| $ \boldsymbol{X}=\left(\mathrm{DCB}_{\mathrm{r}}^{\mathrm{G}}, \mathrm{DCB}^{\mathrm{G}, \mathrm{i}}, \mathrm{DCB}_{\mathrm{r}}^{\mathrm{R}}, \mathrm{DCB}^{\mathrm{R}, \mathrm{i}}, a_{n m}, b_{n m}\right)^{\mathrm{T}} $ | (6) |
式中,G和R分别为GPS和GLONASS,r和i分别为测站和卫星。同时,为分离接收机DCB和卫星DCB,还需要在平差方程中分别对GPS和GLONASS进行卫星DCB零矩阵约束:
| $ \sum\limits_{j = 1}^{{N_{\rm{G}}}} {{\rm{DC}}{{\rm{B}}^{{\rm{G}}, {\rm{i}}}}} = 0, \sum\limits_{j = 1}^{{N_{\rm{R}}}} {{\rm{DC}}{{\rm{B}}^{{\rm{R}}, {\rm{i}}}}} = 0 $ | (7) |
不同于球谐函数建模,基于GIM建模可直接使用IGS提供的GIM。本文首先采用CODE的GIM产品进行时间和空间上的内插来获取穿刺点的VTEC值,然后直接消除VTEC参数,其观测方程可以表示为[7]:
| $ \begin{array}{*{20}{c}} {c{\rm{DC}}{{\rm{B}}_{\rm{r}}} + c{\rm{DC}}{{\rm{B}}^{\rm{i}}} = }\\ {\frac{1}{N}\sum\limits_{k = 1}^N {\left[ {{P_{4, sm}} - {\rm{VTEC}}_{\rm{r}}^{\rm{i}} \cdot F(f) \cdot M\left( {z_{\rm{r}}^{\rm{i}}} \right)} \right]} } \end{array} $ | (8) |
式中,N为观测值的总数,其他参数意义与前文相同。同时,为分离卫星和接收机DCB的参数,同样需要添加式(7)进行约束。因此,基于GIM建模求解DCB可以直接获取GPS和GLONASS的卫星及接收机DCB值。
1.4 简化模型建模求解DCB采用球谐函数建模在理论上比较严密,但待估参数较多,计算量较大。因此在求解DCB时,可以采用IGS的GIM产品直接获取VTEC,能减少估计参数、提高解算效率,但解算效果要依赖于GIM的精度。测站方向上的穿刺点在一定范围内的VTEC变化不大,对电离层TEC项进行平均(式(8))。根据这一特点,可以将穿刺点的VTEC在一个时段内简化为一个参数进行估计,从而获取卫星和接收机的DCB值。
根据球谐函数模型和基于GIM模型提出简化模型,假设一定空间范围内的测站穿刺点VTEC在一定时段内不变或变化很小,则可以将一个测站一段时间内(1 d可分为若干个时段,本文采用24个时段)的VTEC值设为一个参数,观测方程为:
| $ \begin{array}{l} F(f) \cdot F\left( {z_{\rm{r}}^{\rm{i}}} \right) \cdot {\rm{VTE}}{{\rm{C}}_{{\rm{r}}, t}} + \\ c{\rm{DC}}{{\rm{B}}^{\rm{i}}} + c{\rm{DC}}{{\rm{B}}_{\rm{r}}} = {P_{4, sm}} \end{array} $ | (9) |
式中,VTECr, t为测站r在t时段内的VTEC均值,即简化后的电离层TEC参数,其他参数意义与前文相同。该模型对穿刺点的VTEC参数进行简化,减少待估参数,可以直接求解DCB值。为分离卫星和接收机DCB参数,同样需要进行式(7)的卫星零均值约束。可以发现,TEC参数简化后模型的可行性决定了简化模型的有效性。但考虑到一定时段内测站方向上各穿刺点的TEC变化较为缓慢,而且简化过程相当于对各穿刺点的TEC进行平均,因此后续实验将进一步分析其估计DCB的效果。
2 实验数据为评估本文方法的有效性,选取IGS提供的2016-01(doy 001~031)近200个测站的观测值作为实验数据。这些测站在全球均匀分布,但陆地上的测站居多。测站都能接收到GPS信号,其中一部分还能接收到GLONASS信号。为更好地评估和分析本文方法的有效性,分别采用球谐函数建模(SHM)、基于GIM建模(DGM)和本文提出的简化模型建模(DSM)3种方法估计GPS和GLONASS的P1-P2卫星和接收机的DCB,同时采用CODE提供的GPS和GLONASS的P1-P2 DCB产品进行验证和分析。评估分析实验策略如表 1所示。
|
|
表 1 评估分析实验策略 Tab. 1 Evaluation and analysis of experimental strategy |
为更好地分析本文方法估计的DCB效果,选择CODE提供的GPS和GLONASS的DCB产品作为参考,比较分析3种方法估计的卫星DCB精度,分别如图 1(GPS卫星按照类型排列)和图 2(GLONASS卫星按照频率排列)所示。
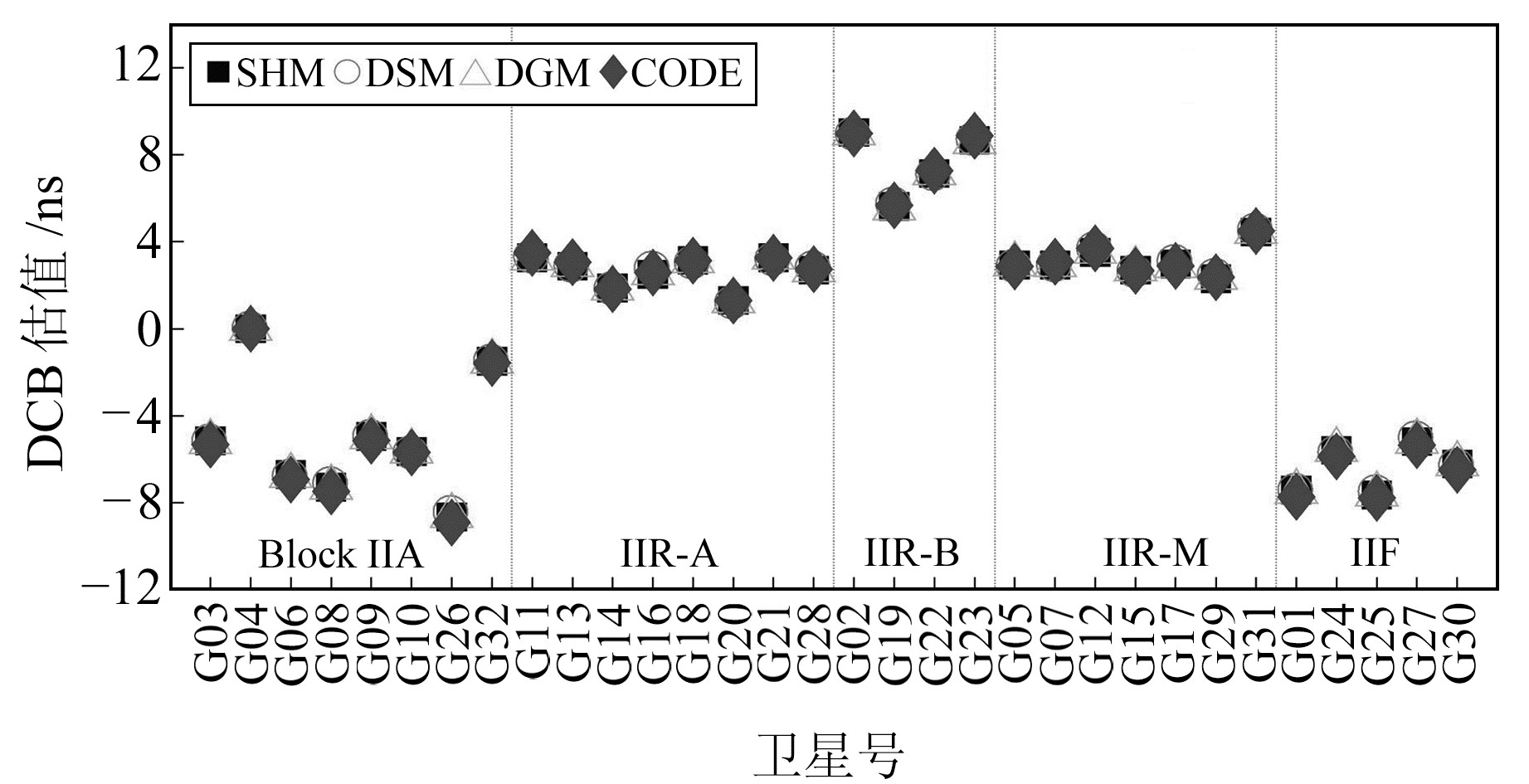
|
图 1 GPS卫星P1-P2 DCB估值 Fig. 1 The estimated P1-P2 DCB of GPS satellite |
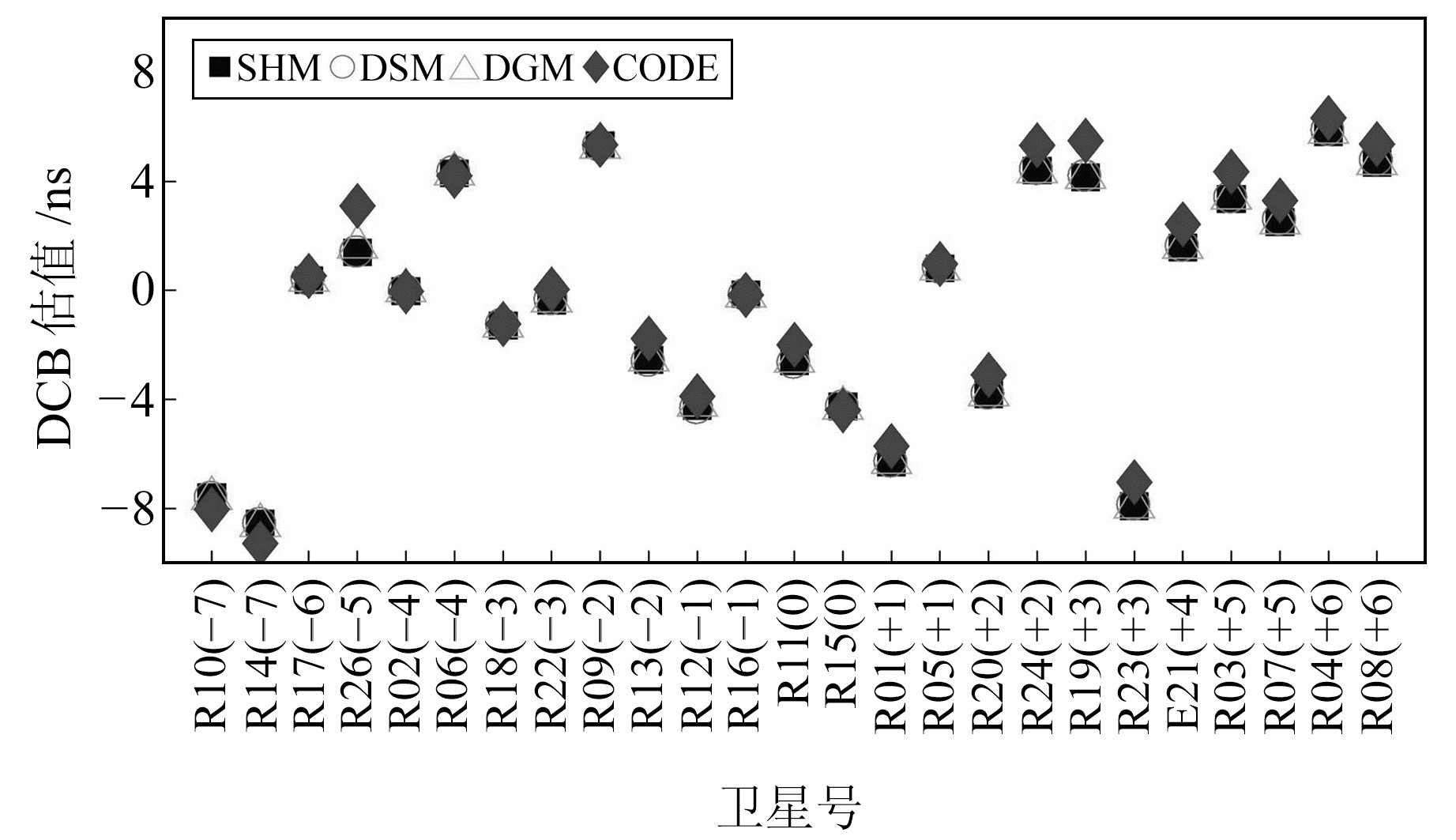
|
图 2 GLONASS卫星P1-P2 DCB估值 Fig. 2 The estimated P1-P2 DCB of GLONASS satellite |
由图 1可见,GPS卫星DCB月均值为-10~10 ns,3种方法估计的结果与CODE值非常接近,且相同类型卫星的DCB值较为接近,说明DCB主要与硬件设备有关。由图 2可见,GLNASS卫星的DCB估值为-10~7 ns,且比较分散。不同于GPS,各种方法的估计值在一些GLONASS卫星上有一定的差异,这是因为GLONASS卫星采用的是频分多址技术,该技术对其卫星DCB估值有一定的影响。
为进一步分析3种方法在估计GPS和GLONASS卫星DCB上的精度,以CODE提供的产品为参考,统计3种方法估计的卫星DCB值的平均偏差(bias)和标准差(STD),分别如图 3和图 4所示。
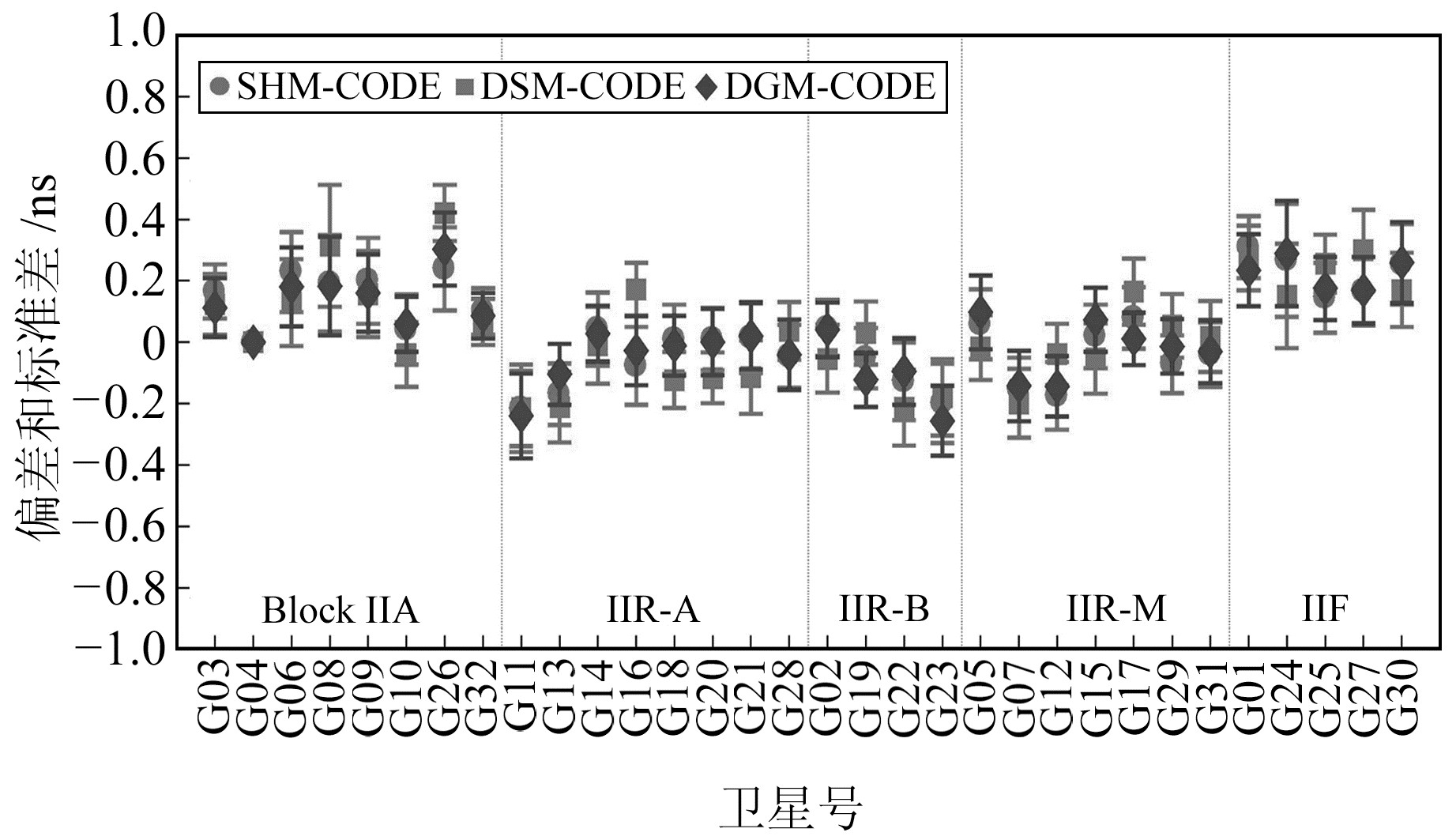
|
图 3 GPS卫星P1-P2 DCB偏差和标准差 Fig. 3 The bias and STD of GPS satellite P1-P2 DCB |
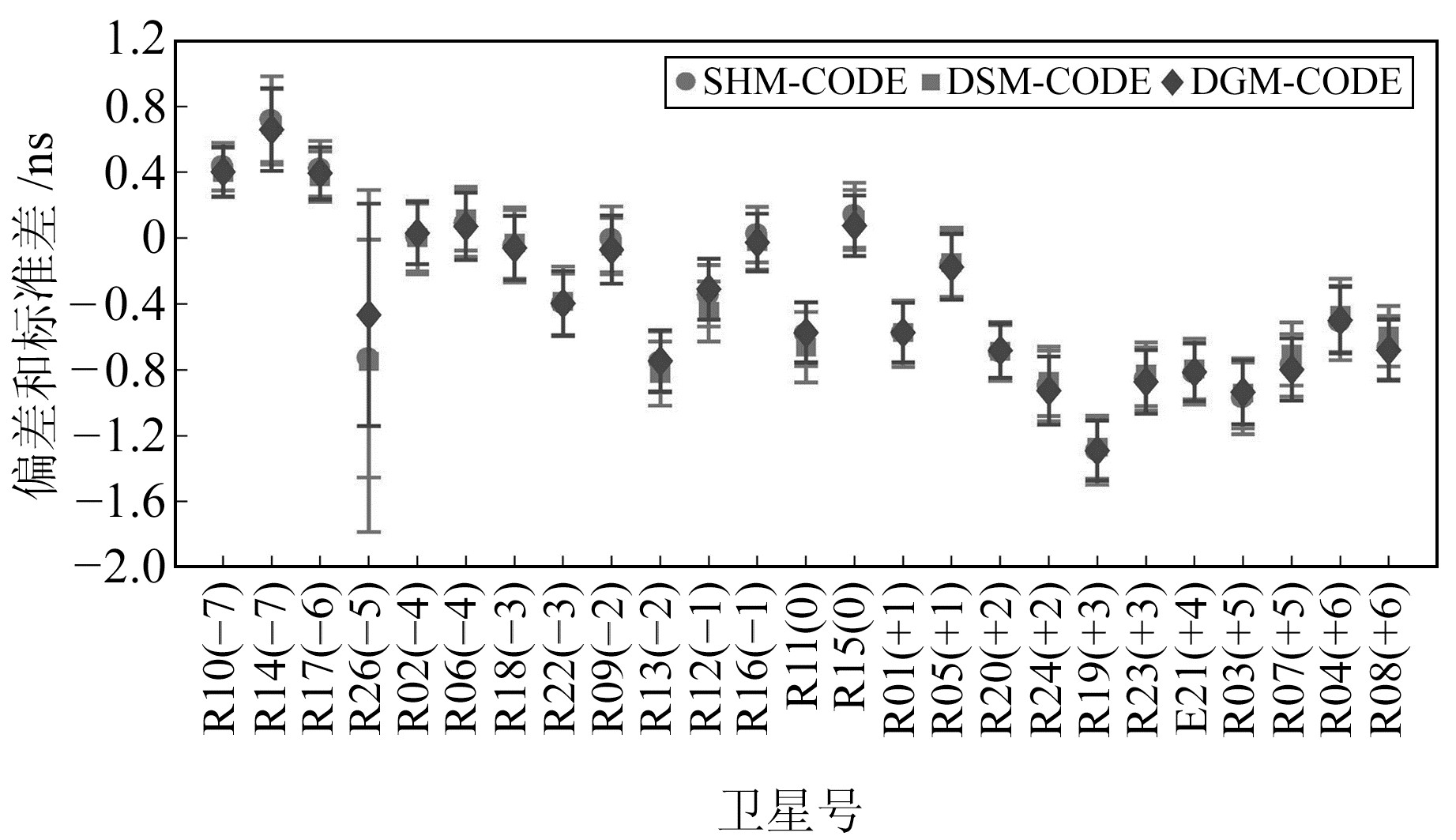
|
图 4 GLONASS卫星P1-P2 DCB偏差和标准差 Fig. 4 The bias and STD of GLONSSS satellite P1-P2 DCB |
由图 3可见,3种方法估计的GPS卫星DCB值与CODE产品相比,平均偏差为-0.3~0.5 ns,标准差为0.05~0.20 ns,说明3种方法的估计值与CODE产品有较好的一致性。相比于本文DSM方法,采用SHM和DGM方法估计的结果偏差更小,这是因为SHM与CODE都是采用球谐函数进行建模,DGM则直接使用CODE提供的GIM产品。而本文采用简化模型提高估计效率,观测数量较少的部分卫星可能影响其估值精度,但精度值也达到0.2 ns。由图 4可以看出,相比于GPS,GLONASS卫星3种方法的估计值与CODE产品的偏差比较分散,偏差为-1.3~0.7 ns,标准差为0.14~1.10 ns,这可能与GLONASS卫星采用的频分多址技术有关。其中,R26卫星的偏差最大,这可能与其较少的观测卫星数量有关。对比3种方法可知,本文方法相对于CODE的偏差和标准差还是比较接近的,说明本文方法能达到与SHM和DSM方法相同的估计效果。
3.2 接收机DCB估计结果与卫星DCB不同,接收机DCB除了与本身的硬件特性有关外,还与接收机类型、天线类型和接收机所处位置有关。为更好地比较分析GPS和GLONASS接收机DCB的估值效果,分别从观测数据中选择具有不同接收机类型的30个测站用于比较分析。表 2、表 3分别为30个GPS和GLONASS跟踪站的信息。图 5和图 6分别为3种方法和来自CODE产品的GPS和GLONASS 30个测站的接收机DCB值。图中测站按照不同的接收机类型排列,不同接收机类型用虚线划分。
|
|
表 2 GPS跟踪站信息 Tab. 2 The information of GPS stations |
|
|
表 3 GLONASS跟踪站信息 Tab. 3 The information of GLONASS stations |
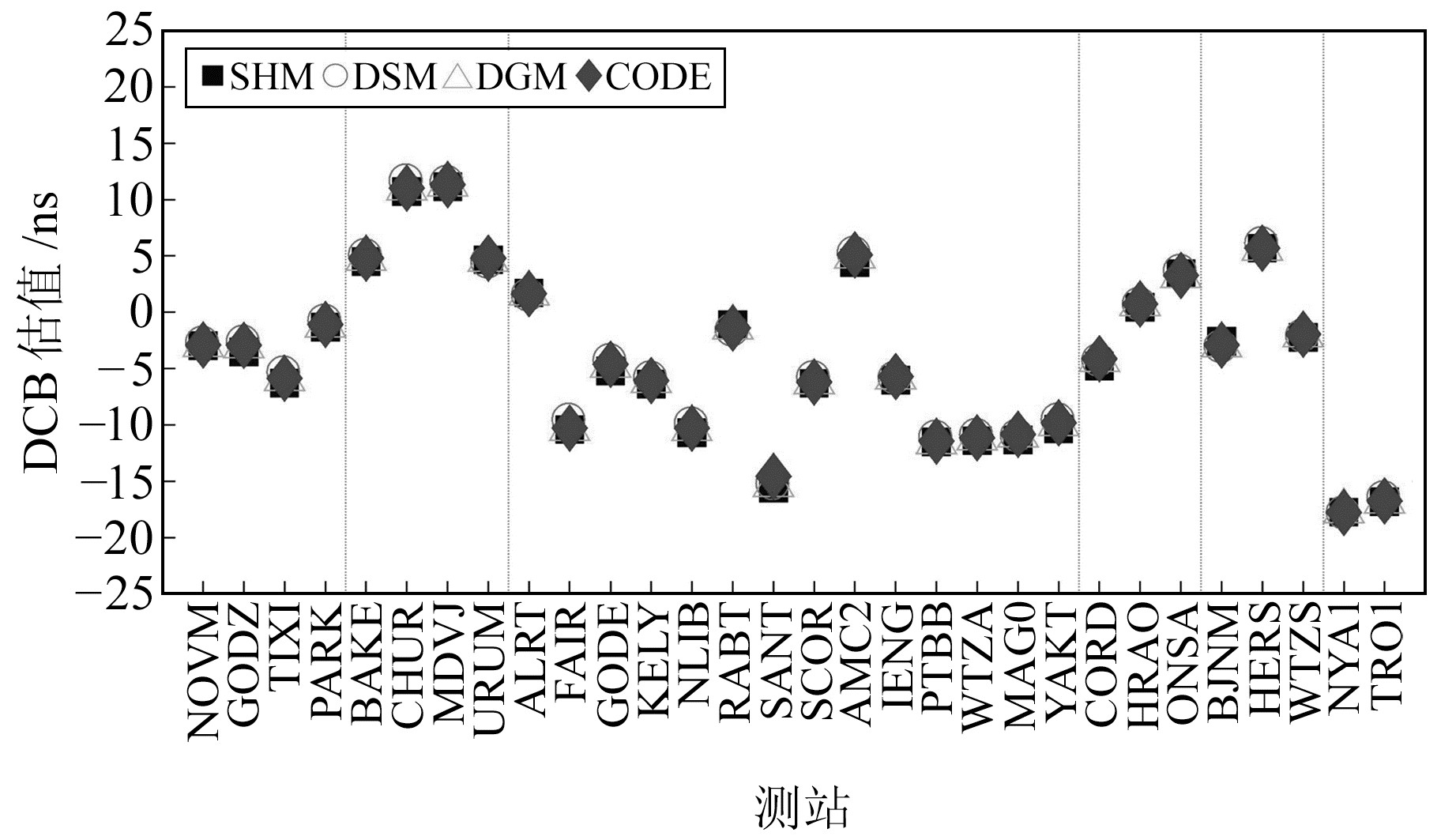
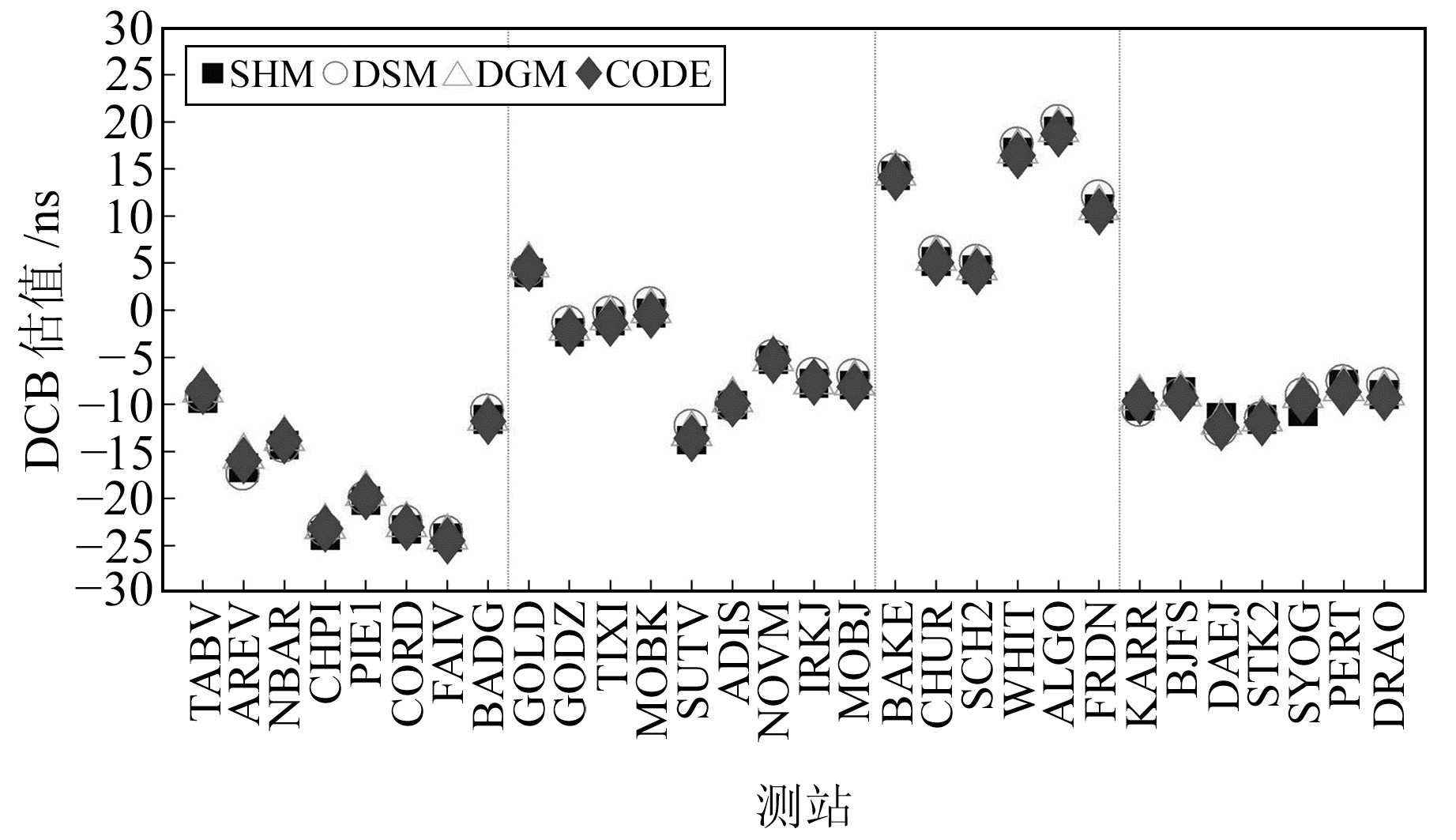
由图 5可见,GPS接收机DCB的月均值为-20~15 ns,3种方法解算的结果与CODE产品比较接近。同时,相同接收机类型的DCB月均值比较接近,但也会因天线类型的不同而产生波动,说明接收机DCB的值与接收机和天线类型均有关,但接收机DCB的稳定性还需要考虑地理纬度效应。图 6中GLONASS接收机DCB月均值为-30~20 ns,3种方法解算的结果比较接近。相同接收机类型的DCB月均值也比较接近,接收机类型、天线类型均相同的DCB值则更为接近。
|
图 5 GPS接收机P1-P2 DCB估值 Fig. 5 The estimated P1-P2 DCB of GPS receiver |
|
图 6 GLONASS接收机P1-P2 DCB估值 Fig. 6 The estimated P1-P2 DCB of GLONASS receiver |
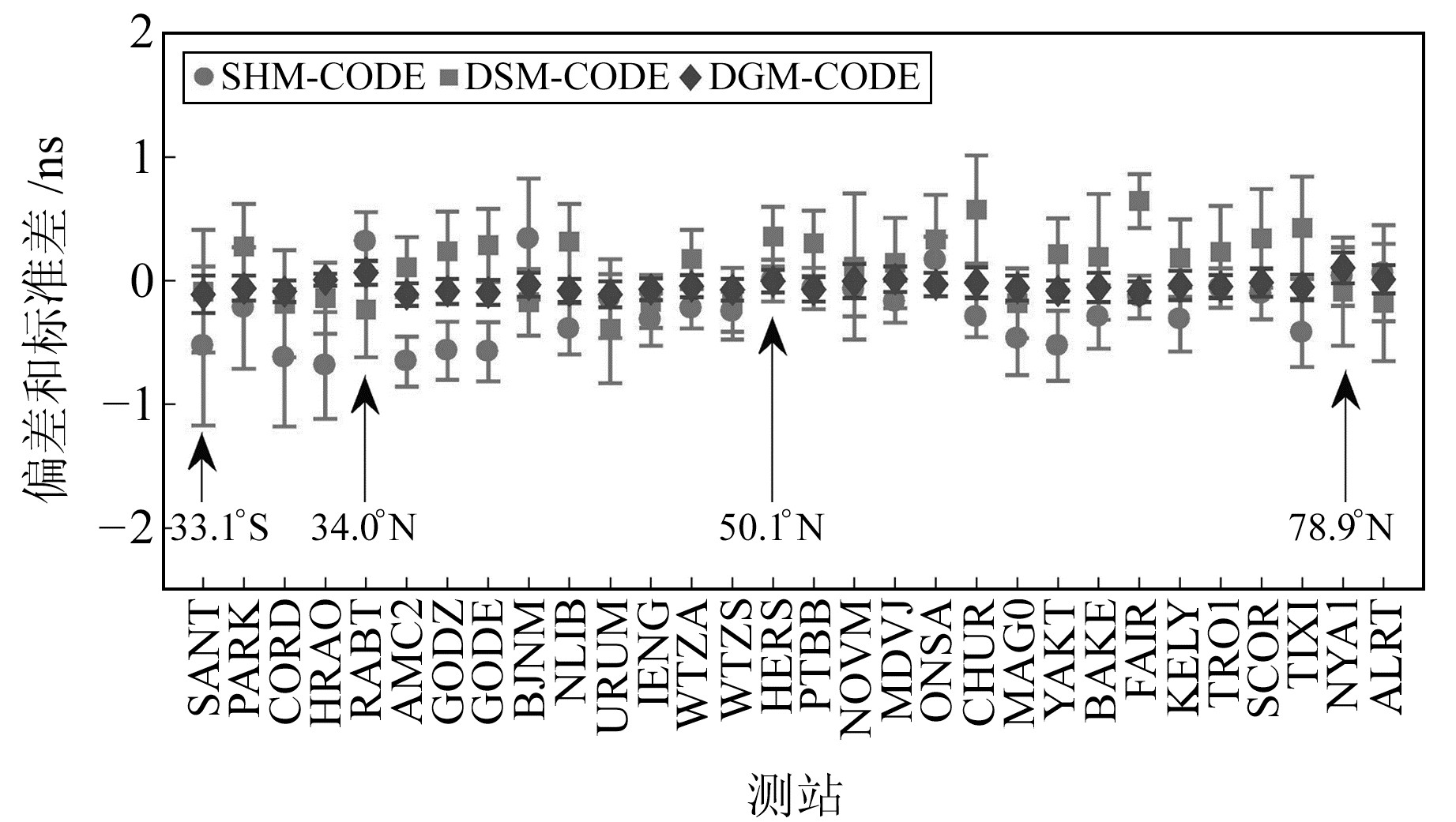
为进一步评估本文方法估计接收机DCB的效果,以CODE提供的DCB产品为参照,计算3种方法估计的接收机DCB值与CODE提供的DCB产品之间的平均偏差和标准差,如图 7和图 8所示,图中测站按照其所处的纬度位置排列。
|
图 7 GPS接收机P1-P2 DCB平均偏差和标准差 Fig. 7 The bias and STD of GPS receiver P1-P2 DCB |

|
图 8 GLONASS接收机P1-P2 DCB平均偏差和标准差 Fig. 8 The bias and STD of GLONASS receiver P1-P2 DCB |
由图 7可以看出,3种方法的结果与CODE的平均偏差为-0.6~0.7 ns,标准差为0.05~0.7 ns。其中DGM的偏差和标准差最小,说明电离层精度与接收机DCB的相关性最强。从测站纬度分布可以看出,电离层活跃程度与接收机DCB的估计结果有关。DSM简化模型偏差较大,说明简化估计VTEC带来的误差会影响接收机DCB的估计结果。
由图 8可见,3种方法的结果与CODE的平均偏差为-1.5~1.5 ns,标准差为0.16~1.2 ns。GLONASS接收机估计偏差较大,可能与其卫星采用的频率技术有关;简化模型的偏差较大,说明简化VTEC估计带来的电离层误差会影响接收机DCB;低纬度分布的接收机DCB偏差较大,说明其受到电离层纬度效应的影响。
4 结语1) 对于GPS和GLONASS卫星DCB,本文方法与其他2种方法的估计结果比较接近,且GPS和GLONASS卫星DCB与CODE产品相比的平均偏差分别为-0.3~0.5 ns、-1.3~0.7 ns,标准差分别为0.05~0.20 ns、0.14~1.10 ns。
2) 对于接收机DCB,3种方法与CODE产品的平均偏差分别为-0.6~0.7 ns (GPS)和-1.5~1.5 ns (GLONASS)。
实验结果验证了改进方法的有效性。需要说明的是,本文实验是在太阳活动相对平稳的条件下进行的,太阳活动剧烈条件下该方法的适应性还需进一步探讨分析。
| [1] |
王宁波. GNSS差分码偏差处理方法及全球广播电离层模型研究[J]. 测绘学报, 2017, 46(8): 1 069 (Wang Ningbo. Study on GNSS Differential Code Biases and Global Broadcast Ionospheric Models of GPS, Galileo and BDS[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(8): 1 069)
(  0) 0) |
| [2] |
章红平. 基于地基GPS的中国区域电离层监测与延迟改正研究[D]. 上海: 中国科学院上海天文台, 2006 (Zhang Hongping. Research on China Area Ionosphere Monitoring and Delay Correction Based on Ground-Based GPS[D]. Shanghai: Shanghai Astronomical Observatory, CAS, 2006)
(  0) 0) |
| [3] |
Zhao C B, Zhang B C, Odolinski R, et al. Combined Use of Single-Frequency Data and Global Ionosphere Maps to Estimate BDS and Galileo Satellite Differential Code Biases[J]. Measurement Science and Technology, 2020, 31(1)
(  0) 0) |
| [4] |
张强, 赵齐乐. 武汉大学IGS电离层分析中心全球电离层产品精度评估与分析[J]. 地球物理学报, 2019, 62(12): 4 493-4 505 (Zhang Qiang, Zhao Qile. Evaluation and Analysis of the Global Ionosphere Maps from Wuhan University IGS Ionosphere Associate Analysis Center[J]. Chinese Journal of Geophysics, 2019, 62(12): 4 493-4 505)
(  0) 0) |
| [5] |
王健, 党亚民, 王虎. 全球电离层延迟建模及精度分析[J]. 测绘工程, 2019, 28(2): 17-21 (Wang Jian, Dang Yamin, Wang Hu. Modeling Global Ionospheric Delay and Its Accuracy Analysis[J]. Engineering of Surveying and Mapping, 2019, 28(2): 17-21)
(  0) 0) |
| [6] |
Jin R, Jin S G, Feng G P. M_DCB: Matlab Code for Estimating GNSS Satellite and Receiver Differential Code Biases[J]. GPS Solutions, 2012, 16(4): 541-548 DOI:10.1007/s10291-012-0279-3
(  0) 0) |
| [7] |
Montenbruck O, Hauschild A, Steigenberger P. Differential Code Bias Estimation Using Multi-GNSS Observations and Global Ionosphere Maps[J]. Navigation, 2014, 61(3): 191-201
(  0) 0) |
| [8] |
Wang Q S, Jin S G, Yuan L L, et al. Estimation and Analysis of BDS-3 Differential Code Biases from MGEX Observations[J]. Remote Sensing, 2019, 12(1)
(  0) 0) |
| [9] |
Wang Q S, Jin S G, Hu Y J. Epoch-by-Epoch Estimation and Analysis of Beidou Navigation Satellite System(BDS) Receiver Differential Code Biases with the Additional BDS-3 Observations[J]. Annales Geophysicae, 2020, 38(5): 1 115-1 122 DOI:10.5194/angeo-38-1115-2020
(  0) 0) |
| [10] |
Schaer S. Mapping and Predicting the Earth's Ionosphere Using the Global Positioning System[D]. Berne: Astronomical Institute, University of Berne, 1999
(  0) 0) |
| [11] |
黄小东, 涂锐, 刘金海, 等. 基于不等式约束算法改善高纬度地区GNSS电离层建模精度[J]. 大地测量与地球动力学, 2019, 39(7): 722-727 (Huang Xiaodong, Tu Rui, Liu Jinhai, et al. Inequality Constraints Algorithm to Improve the High Latitudes GNSS Ionosphere Modeling Accuracy[J]. Journal of Geodesy and Geodynamics, 2019, 39(7): 722-727)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

