2. 内蒙古农业大学理学院,呼和浩特市昭乌达路306号,010018;
3. 内蒙古农业大学计算机与信息工程学院,呼和浩特市鄂尔多斯东街29号,010011
煤炭资源开采引起的地表沉降在附加荷载的影响下会导致地表、建(构)筑物荷载、地基等发生不均匀沉降,为确保建筑物安全、反馈设计参数,需对其进行变形监测[1]。依据监测数据,用模型表达变形时序与变化量之间的不确定性关系,对于施工质量监测和运行安全保障具有重要意义。邓聚龙[2]提出的灰色系统理论被广泛应用于变形监测领域。
建筑物形变量一般会随时间发生非线性变化,将GM(1, 1)模型中的灰作用量替换为幂指数形式,能够在样本数量较少的情况下灵活反映数据序列之间的非线性关系[3]。为提高幂模型的精度,相关学者从不同角度对其进行优化改进,常用的改进方法有:优化初始条件[4]、改进模型背景值构造方式[5]、优化参数估计方法[6]、构建无偏模型[7]等。但随着时间的推移,系统结构也在不断变化,若使用恒定参数会使模型拟合结果与预测结果之间的误差变大。王正新[8]在灰作用量中引入系统延迟时间和时间作用参数,构建适合分析小样本振荡序列的非线性优化模型,削弱了原始序列随机波动对建模的影响。但上述模型是基于等间隔的原始观测序列,而在实际变形监测中很难实现连续等间距观测。近年来,有学者建立非等间距GM(1, 1)幂模型[9],但未考虑到背景值等权构造的缺陷,导致优化模型对变形监测原始数据的拟合和预测精度不够理想。此外,现有的非等间距GM(1, 1)幂模型的研究忽略了参数随时间的动态变化特性,使得系统内部的相关变量无法随观测序列的变动而更新。
本文提出一种优化背景值的非等间距线性时变参数GM(1, 1)幂模型。根据GM(1, 1)幂模型的白化微分方程推导模型的时间响应序列,基于积分原理建立灰色微分方程,求解模型的线性参数,并使用粒子群算法优化选取非线性参数,避免出现参数选取时目标函数适应度局部最优的问题,从而有效提高模型的拟合与预测精度。
1 线性时变参数非等间距GM(1, 1)幂模型对同一序列而言,发展系数a保持不变,灰作用量b会随时间发生变化[10]。在非等间距GM(1, 1)幂模型中,若灰作用量保持不变,则估计误差会持续增大。由文献[11]可知,将b*=eμtb通过级数展开为(1+μt)b,用关于时间t的线性函数(μbt+b)代替原灰作用量b,能够改进非线性系统内部小样本数据序列建模精度不足的问题。由于μ为常数,为方便表示,下文用(bt+c)代替b建立线性时变参数非等间距GM(1, 1)幂模型。
定义1[12] 设原始非负光滑序列为X(0)={x(0)(t1), x(0)(t2), …, x(0)(tn)},时序间距Δti=ti-ti-1≠const, i=2, 3, …, n,Δt1=1, 称
| $ \frac{{{\rm{d}}{x^{(0)}}(t)}}{{{\rm{d}}t}} + a{x^{(0)}}(t) = (bt + c){\left[ {{x^{(0)}}(t)} \right]^\gamma } $ | (1) |
为线性时变参数非等间距GM(1, 1)幂模型的白化微分方程。
定理1 线性时变参数非等间距GM(1, 1)幂模型的时间响应序列为:
| $ {\hat x^{(0)}}\left( {{t_k}} \right) = \left\{ {\begin{array}{*{20}{l}} {{x^{(0)}}\left( {{t_1}} \right), k = 1}\\ {{{\left\{ {\left[ {{{\left[ {{x^{(0)}}} \right]}^{1 - \gamma }} - \frac{b}{a}{t_1} + \frac{b}{{{a^2}(1 - \gamma )}} - \frac{c}{a}} \right]{{\rm{e}}^{a(1 - \gamma )\left( {{t_1} - {t_k}} \right)}} + \frac{b}{a}{t_k} - \frac{b}{{{a^2}(1 - \gamma )}} + \frac{c}{a}} \right\}}^{\frac{1}{{1 - \gamma }}}}, k = 2, \cdots , n} \end{array}} \right. $ | (2) |
证明 根据伯努利微分方程求解法则,式(1)两端同时除以[x(0)(t)]γ得:
| $ {\left[ {{x^{(0)}}(t)} \right]^{ - \gamma }}\frac{{{\rm{d}}{x^{(0)}}(t)}}{{{\rm{d}}t}} + {\left[ {{x^{(0)}}(t)} \right]^{1 - \gamma }} = bt + c $ | (3) |
令y(0)(t)=[x(0)(t)]1-γ,求导有
| $ {y^{(0)}}(t) = {C_1}{{\rm{e}}^{ - a(1 - \gamma )t}} + \frac{b}{a}t - \frac{b}{{{a^2}(1 - \gamma )}} + \frac{c}{a} $ | (4) |
式中,C1为任意常数,由建模初始条件决定。
线性时变参数非等间距GM(1, 1)幂模型的时间响应函数可表示为:
| $ {x^{(0)}}(t) = {\left\{ {{C_1}{{\rm{e}}^{ - a(1 - \gamma )t}} + \frac{b}{a}t - \frac{b}{{{a^2}(1 - \gamma )}} + \frac{c}{a}} \right\}^{\frac{1}{{1 - \gamma }}}} $ | (5) |
时间响应序列为:
| $ \begin{array}{*{20}{c}} {{{\hat x}^{(0)}}\left( {{t_k}} \right) = }\\ {\left\{ {\left[ {{{\left[ {{x^{(0)}}\left( {{t_1}} \right)} \right]}^{1 - \gamma }} - \frac{b}{a}{t_1} + \frac{b}{{{a^2}(1 - \gamma )}} - \frac{c}{a}} \right] \cdot } \right.}\\ {{{\left. {{{\rm{e}}^{ - a(1 - \gamma )\left( {{t_k} - {t_1}} \right)}} + \frac{b}{a}{t_k} - \frac{b}{{{a^2}(1 - \gamma )}} + \frac{c}{a}} \right\}}^{\frac{1}{{1 - \gamma }}}}} \end{array} $ | (6) |
式中,t=tk, k=2, 3, …, n,定理1得证。
此外,由
| $ \begin{gathered} C_{1}= \\ \left\{\left[x^{(0)}\left(t_{1}\right)\right]^{1-\gamma}-\frac{b}{a} t_{1}+\frac{b}{a^{2}(1-\gamma)}-\frac{c}{a}\right\} \mathrm{e}^{-a(\gamma-1) t_{1}} \end{gathered} $ | (7) |
对于原始数据本身呈近似幂次增长的光滑序列,利用上述模型的时间响应序列即可求得模型拟合值。相比于传统GM(1, 1)幂模型,上述模型无需进行差分还原处理,可简化建模过程。
2 线性时变参数非等间距GM(1, 1)幂模型背景值优化 2.1 模型最优背景值构建传统GM(1, 1)幂模型背景值计算一般采用公式z(1)(tk)=0.5x(1)(tk-1)+0.5x(1)(tk),k=2, 3, …, n,即认为前后紧邻值等权,这与白化方程中对应的
改进后的背景值表达式为:
| $ z^{(1)}\left(t_{k}\right)=\lambda x^{(1)}\left(t_{k-1}\right)+(1-\lambda) x^{(1)}\left(t_{k}\right) $ | (8) |
式中,λ∈[0, 1], k=2, 3, …, n。
2.2 优化背景值的时变参数非等间距GM(1, 1)幂模型参数估计定义2 设非负原始光滑序列为:X(0)={x(0)(t1), x(0)(t2), …, x(0)(tn)},间距Δti=ti-ti-1≠const,Δt1=1;X(0)的(1-γ)次幂生成序列为y(0)(tk)=[x(0)(tk)]1-γ,y(0)(t1)=0,Y(0)的一阶累减生成序列为Y(-1)={y(-1)(t2), y(-1)(t3), …, y(-1)(tn)},其中y(-1)(tk)=y(0)(tk)-y(0)(tk-1)/Δtk;Z(0)={z(0)(t2), z(0)(t3), …, z(0)(tn)}为Y(0)的紧邻均值序列,z(0)(ti)=λx(0)(tk-1)+(1-λ)x(0)(tk),其中,λ∈[0, 1], k=2, 3, …, n。
定理2 线性时变参数非等间距GM(1, 1)幂模型的灰微分方程为:
| $ \begin{aligned} &y^{(-1)}\left(t_{k}\right) \Delta t_{k}+a(1-\gamma) z^{(0)}\left(t_{i}\right) \Delta t_{k}= \\ &\frac{1}{2} b(1-\gamma)\left(t_{k}^{2}-t_{k-1}^{2}\right)+c(1-\gamma) \Delta t_{k} \end{aligned} $ | (9) |
证明 式(1)两边同时乘以(1-γ)[x(0)]-γ得:
| $ \begin{gathered} (1-\gamma)\left[x^{(0)}(t)\right]^{-\gamma} \frac{\mathrm{d} x^{(0)}(t)}{\mathrm{d} t}+a(1-\gamma) \cdot \\ {\left[x^{(0)}(t)\right]^{1-\gamma}=(b t+c)(1-\gamma)} \end{gathered} $ | (10) |
令y(0)(t)=[x(0)]1-γ,则式(10)可简化为:
| $ \frac{\mathrm{d} y^{(0)}(t)}{\mathrm{d} t}+a(1-\gamma) y^{(0)}(t)=(b t+c)(1-\gamma) $ | (11) |
式(11)两边在区间[tk-1, tk]上积分得:
| $ \begin{aligned} &y^{(-1)}\left(t_{k}\right) \Delta t_{k}+a(1-\gamma) z^{(0)}\left(t_{i}\right) \Delta t_{k}= \\ &\frac{1}{2} b(1-\gamma)\left(t_{k}^{2}-t_{k-1}^{2}\right)+c(1-\gamma) \Delta t_{k} \end{aligned} $ | (12) |
即定理2得证。
确定幂指数γ与背景值权重λ后,同样采用最小二乘法估计灰微分方程参数,即
| $ {\left[ {\begin{array}{*{20}{l}} a&b&c \end{array}} \right]^{\rm{T}}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Y}} $ | (13) |
式中,
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {(\gamma - 1){z^{(0)}}\left( {{t_2}} \right)\Delta {t_2}}&{0.5(1 - \gamma )\left( {t_2^2 - t_1^2} \right)}&{(1 - \gamma )\Delta {t_2}}\\ {(\gamma - 1){z^{(0)}}\left( {{t_3}} \right)\Delta {t_3}}&{0.5(1 - \gamma )\left( {t_3^2 - t_2^2} \right)}&{(1 - \gamma )\Delta {t_3}}\\ \vdots & \vdots & \vdots \\ {(\gamma - 1){z^{(0)}}\left( {{t_n}} \right)\Delta {t_n}}&{0.5(1 - \gamma )\left( {t_n^2 - t_{n - 1}^2} \right)}&{(1 - \gamma )\Delta {t_n}} \end{array}} \right], \mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} {{y^{( - 1)}}\left( {{t_2}} \right)\Delta {t_2}}\\ {{y^{( - 1)}}\left( {{t_3}} \right)\Delta {t_3}}\\ \vdots \\ {{y^{( - 1)}}\left( {{t_n}} \right)\Delta {t_n}} \end{array}} \right] $ | (14) |
粒子群优化算法(particle swarm optimization,PSO)是一种全局优化算法。首先在搜索空间域内初始化一群随机粒子,然后经过不断迭代、调整得到最优解。PSO具有设置参数少、精度高、收敛速度快等优点,被广泛应用于函数优化、计算机大数据和神经网络等众多领域[13]。最优解的选择方式有目标函数小于给定限差和设定迭代次数2种,给定限差可能会导致粒子陷入局部最优,设定迭代次数可保证每个初始种群粒子调整位置与速度,再通过迭代次数与适应度的收敛关系调整迭代次数,确保粒子达到全局最优。因此,采用设定迭代次数的方式来选取优化背景值的线性时变参数非等间距GM(1, 1)幂模型的最优幂指数γ与背景值权重λ。
目标函数为最小平均绝对百分比误差(MAPE),即
| $ \begin{array}{*{20}{c}} {\min f(\gamma , \lambda ) = \frac{1}{{n - 1}}\sum\limits_{k = 2}^n {\left| {\frac{{{{\hat x}^{(0)}}\left( {{t_k}} \right) - {x^{(0)}}\left( {{t_k}} \right)}}{{{x^{(0)}}\left( {{t_k}} \right)}}} \right|} , }\\ {\gamma \in [ - 3, 3], \lambda \in [0, 1]} \end{array} $ | (15) |
首先根据PSO的常规参数设定方法设置实验运行参数;然后通过沉降观测序列适应度收敛趋势调整群体规模与迭代次数,加快计算速度;最后确定本文PSO的初始化参数。具体运行参数初始化设置如下:学习因子c1=2, c2=2;初始速度Vmin=-1, Vmax=1;动态惯性权重因子ω=0.8;粒子搜索域γ∈[-3, 3], λ∈[0, 1];群体规模size=100;进化迭代次数k=1 500;加权速度系数α1, α2∈[0, 1]。
模型非线性参数求解步骤如下:
1) 设置运行参数的初始化值,计算初始种群在搜索域内每个粒子的位置Xid1和速度Vid1。
2) 根据目标函数计算初始化粒子群各粒子的适应度fitness,寻找初始搜索域内参数γ与λ的个体最佳位置Pbest1、Pbest2和全局最佳位置Gbest1、Gbest2。
3) 在种群规模和进化次数的搜索条件下,通过迭代不断更新粒子速度Vid1和位置Xid1,即
| $ \begin{array}{l} V_{id}^{k + 1} = \omega V_{id}^k + {c_1}{\alpha _1}\left( {{P_{{\rm{best }}}} - X_{id}^k} \right) + \\ {c_2}{\alpha _2}\left( {{G_{{\rm{best }}}} - X_{id}^k} \right)\\ X_{id}^{k + 1} = X_{id}^k + V_{id}^{k + 1} \end{array} $ | (16) |
4) 若某粒子个体位置适应度优于Pbest1、Pbest2,则设置新位置为Pbest1、Pbest2;若粒子全局位置适应度优于Gbest1、Gbest2,则设置新位置为Gbest1、Gbest2。
5) 输出运行结果Gbest1为幂指数γ的最优解;参数Gbest2为背景值权重λ的最优解。此时优化背景值的线性时变非等间距GM(1, 1)幂模型的MAPE最小。
2.4 模型精度验证以MAPE为检验指标,比较不同优化角度下GM(1, 1)幂模型的拟合与预测精度。设原始序列观测值为X(0)={x(0)(t1), x(0)(t2), …, x(0)(tn)};模型求得原始序列的拟合值为
| $ \varepsilon\left(k_{k}\right)=x^{(0)}\left(k_{k}\right)-\hat{x}^{(0)}\left(k_{k}\right), k=2, 3, \cdots, n $ | (17) |
相对误差序列为:
| $ P\left(k_{k}\right)=\frac{\varepsilon\left(k_{k}\right)}{x^{(0)}\left(k_{k}\right)} \times 100 \%, k=2, 3, \cdots, n $ | (18) |
MAPE为:
| $ {\rm{MAPE}} = \frac{1}{{n - 1}}\sum\limits_{k = 2}^n {\left| {P\left( {{k_k}} \right)} \right|} $ | (19) |
为证明优化背景值的非等间距线性时变参数GM(1, 1)幂模型的适用性与优越性,利用2组矿区变形监测数据,分别建立非等间距幂指数优化模型[3](模型1)、初始值加权平均的非等间距GM(1, 1)幂模型[14](模型2)、线性时变参数GM (1, 1)幂模型[15] (模型3)与本文模型进行对比分析。
3.1 宁东矿区GNSS沉降监测工程以宁东矿区GNSS持续沉降监测数据为例,首先选取金凤20025监测站点前7期累积沉降量作为建模数据,然后利用第8期、第9期数据对模型进行预测结果验证,最后比较本文模型与其他3种幂模型的拟合精度和预测精度(表 1)。借助MATLAB软件得到模型参数:a=0.157 981、b=0.028 582、c=4.300 362、γ=-0.067 794、λ=0.777 521,非线性参数与MAPE的关系如图 1所示。对应的优化背景值的线性时变非等间距GM(1, 1)幂模型时间响应关系式为:
| $ \begin{array}{*{20}{c}} {{{\hat x}^{(0)}}\left( {{t_k}} \right) = \left\{ { - 13.642\;18{{\rm{e}}^{0.168691{t_k}}} + } \right.}\\ {{{\left. {0.180\;92{t_k} + 26.148\;27} \right\}}^{\frac{1}{{1.067794}}}}, k = 2, 3, \cdots , n} \end{array} $ | (20) |
|
|
表 1 4种模型预测精度对比 Tab. 1 Comparison of prediction results of four models |
宁东矿区GNSS沉降监测工程计算结果表明,模型1、模型2和模型3拟合数值的MAPE分别为3.31%、8.62%、4.18%;预测数值的MAPE分别为9.97%、4.70%、3.75%。优化背景值的非等间距线性时变参数GM(1, 1)幂模型拟合与预测的MAPE分别为2.33%、2.10%,相比于上述3种优化模型,本文模型的精度更高,拟合值和预测值与原始观测序列更加吻合。
图 1可反映PSO的寻优过程,由图可见,在该沉降监测工程中,随着幂指数γ在搜索区间内逐渐靠近0,背景值权重λ在搜索区间内不断接近0.7,MAPE持续减小。当幂指数为-0.067 794、背景值权重为0.777 521时,MAPE取得最小值2.33%。
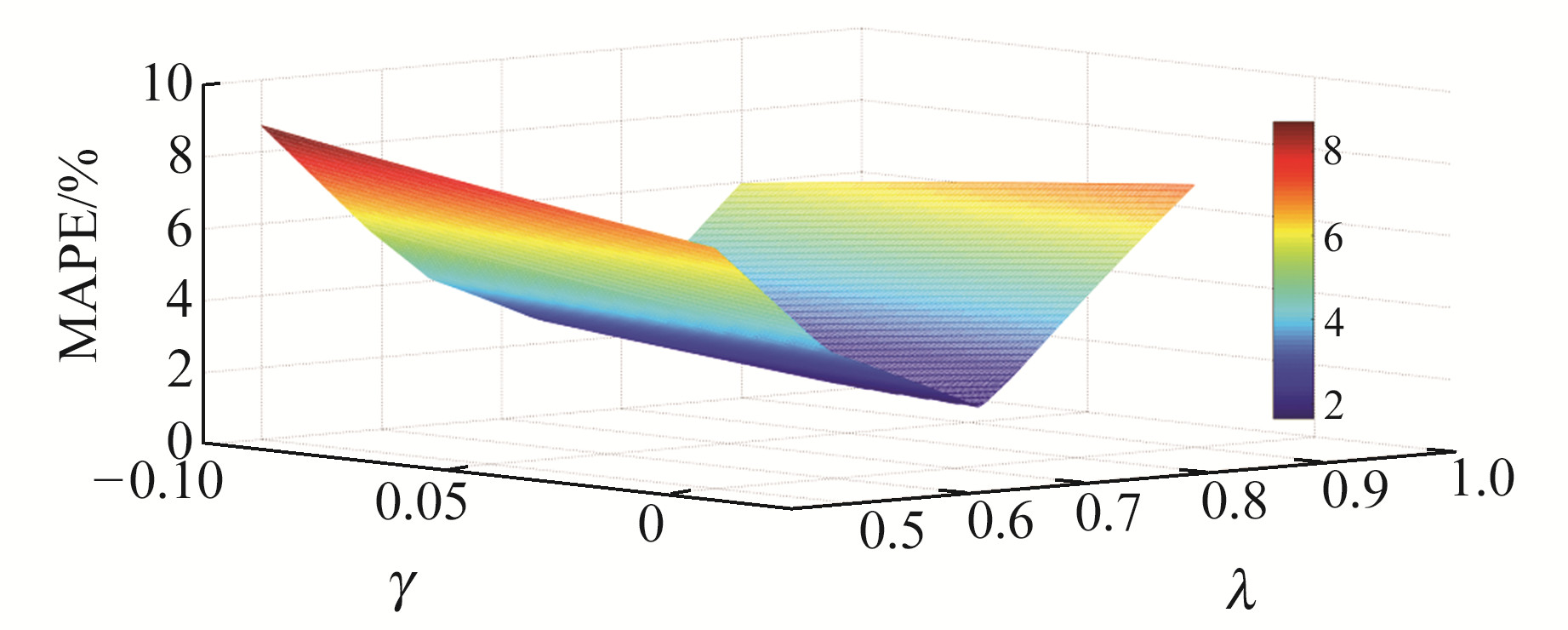
|
图 1 MAPE与非线性参数的关系 Fig. 1 Relationship between nonlinear parameters and MAPE |
以梁家矿4112回采工作面铁路岩移沉降数据为例,利用前8期原始沉降数据构建模型,后2期数据进行模型预测。4种模型的拟合值和预测值精度比较见表 2。本文模型参数分别为:a=0.327 970、b=0.006 893、c=1.681 693、γ=0.465 813、λ=0.792 941,非线性参数优化选取与MAPE的关系如图 2所示。对应的优化背景值的线性时变非等间距GM(1, 1)幂模型时间响应关系式为:
| $ \begin{array}{*{20}{c}} {{{\hat x}^{(0)}}\left( {{t_k}} \right) = \left\{ { - 2.438\;10{{\rm{e}}^{0.175198{t_k}}} + } \right.}\\ {{{\left. {0.021\;02{t_k} + 5.007\;57} \right\}}^{\frac{1}{{0.534187}}}}, k = 2, 3, \cdots , n} \end{array} $ | (21) |
|
|
表 2 4种模型预测结果比较 Tab. 2 Comparison of prediction results of four models |

|
图 2 MAPE与非线性参数关系 Fig. 2 Relationship between nonlinear parameters and MAPE |
由表 2可见,在梁家矿铁路岩移沉降监测工程中,优化背景值的非等间距线性时变参数GM(1, 1)幂模型拟合值与预测值的MAPE分别为4.70%和6.38%,拟合值精度较模型3提高6.37%,预测值精度提高2.63%,进一步体现出本文模型在沉降监测工程建模与分析中的优越性。
由图 2可知,在搜索阈γ∈[-3, 3], λ∈[0, 1]内,背景值权重λ的收敛速度较幂指数γ更快,当γ=0.465 813、λ=0.792 941时,MAPE取到最小值4.70%。
4 结语1) 针对沉降监测小样本非等间距原始数据序列建模问题,构建优化背景值的非等间距线性时变参数GM(1, 1)幂模型。基于粒子群算法,以最小MAPE为目标函数对非线性参数进行优化选取,可有效避免局部极小值陷阱,增强非线性参数选取的可靠性。
2) 以2组煤矿开采变形监测数据为例,对4种模型分别进行拟合与预测。计算结果表明,优化背景值的非等间距线性时变参数GM(1, 1) 幂模型在宁东矿区开采沉陷GNSS监测工程和梁家矿铁路岩移沉降监测工程的MAPE分别为2.33%、4.70%,预测误差分别为2.10%、6.38%,均优于其他3种常用的非等间距GM(1, 1)优化模型。
3) 相比于传统方法,优化背景值的非等间距线性时变参数GM(1, 1)幂模型可提升变形监测数据的拟合与预测精度,适用于短期沉降监测数据的预测分析,可拓宽GM(1, 1)幂模型在沉降监测数据处理中的应用范围。
| [1] |
郑渊茂, 王翠平, 王豪伟, 等. 厦门市地面沉降影响分析与风险评价[J]. 生态学报, 2021, 41(1): 388-400 (Zheng Yuanmao, Wang Cuiping, Wang Haowei, et al. Impact Analysis and Risk Assessment of Urban Land Subsidence in Xiamen City[J]. Acta Ecologica Sinica, 2021, 41(1): 388-400)
(  0) 0) |
| [2] |
邓聚龙. 灰预测与灰决策[M]. 武汉: 华中科技大学出版社, 2002 (Deng Julong. Grey Prediction and Grey Decision[M]. Wuhan: Huazhong University of Science and Technology Press, 2002)
(  0) 0) |
| [3] |
魏家猛, 刁建鹏, 姜华根. 非等间距GM(1, 1)幂指数优化模型在变形监测中的应用[J]. 辽东学院学报: 自然科学版, 2020, 27(4): 253-257 (Wei Jiameng, Diao Jianpeng, Jiang Huagen. Application of Non-Equidistant GM(1, 1) Power Exponent Optimization Model in Deformation Monitoring[J]. Journal of Eastern Liaoning University: Natural Science Edition, 2020, 27(4): 253-257)
(  0) 0) |
| [4] |
郭金海, 杨锦伟. GM(1, 1)模型初始条件和初始点的优化[J]. 系统工程理论与实践, 2015, 35(9): 2 333-2 338 (Guo Jinhai, Yang Jinwei. Optimizing the Initial Condition and the Initial Point of GM(1, 1)[J]. Systems Engineering-Theory and Practice, 2015, 35(9): 2 333-2 338)
(  0) 0) |
| [5] |
胡攀. 优化背景值的GM(1, 1)幂模型及其应用[J]. 数学的实践与认识, 2017, 47(19): 99-104 (Hu Pan. To Optimize the Background Value of GM(1, 1) Power Model and Its Application[J]. Mathematics in Practice and Theory, 2017, 47(19): 99-104)
(  0) 0) |
| [6] |
马光红, 魏勇. GM(1, 1)幂模型的幂指数计算新方法[J]. 统计与决策, 2021, 37(11): 16-20 (Ma Guanghong, Wei Yong. A New Method for Power Exponent Calculation of GM(1, 1) Power Model[J]. Statisticsand Decision, 2021, 37(11): 16-20)
(  0) 0) |
| [7] |
王正新, 党耀国, 练郑伟. 无偏GM(1, 1)幂模型其及应用[J]. 中国管理科学, 2011, 19(4): 144-151 (Wang Zhengxin, Dang Yaoguo, Lian Zhengwei. Unbiased GM(1, 1) Power Model and Its Application[J]. Chinese Journal of Management Science, 2011, 19(4): 144-151)
(  0) 0) |
| [8] |
王正新. 振荡型GM(1, 1)幂模型及其应用[J]. 控制与决策, 2013, 28(10): 1 459-1 464 (Wang Zhengxin. Oscillating GM(1, 1) Power Model and Its Application[J]. Control and Decision, 2013, 28(10): 1 459-1 464)
(  0) 0) |
| [9] |
陈鹏宇. GM(1, 1)幂模型的改进及其在沉降预测中的应用[J]. 大地测量与地球动力学, 2020, 40(5): 464-469 (Chen Pengyu. Improvement of GM(1, 1) Power Model and Its Application on Settlement Prediction[J]. Journal of Geodesy and Geodynamics, 2020, 40(5): 464-469)
(  0) 0) |
| [10] |
李希灿. 灰色系统GM(1, 1)模型适用范围拓广[J]. 系统工程理论与实践, 1999, 19(1): 97-101 (Li Xican. Widening of Suitable Limits of Grey System GM(1, 1) Model[J]. Systems Engineering-Theory and Practice, 1999, 19(1): 97-101)
(  0) 0) |
| [11] |
徐华锋, 刘思峰, 方志耕. GM(1, 1)模型灰色作用量的优化[J]. 数学的实践与认识, 2010, 40(2): 26-32 (Xu Huafeng, Liu Sifeng, Fang Zhigeng. Optimum Grey Action Quantity for GM(1, 1)[J]. Mathematics in Practice and Theory, 2010, 40(2): 26-32)
(  0) 0) |
| [12] |
王正新. 时变参数GM(1, 1)幂模型及其应用[J]. 控制与决策, 2014, 29(10): 1 828-1 832 (Wang Zhengxin. GM(1, 1) Power Model with Time-Varying Parameters and Its Application[J]. Control and Decision, 2014, 29(10): 1 828-1 832)
(  0) 0) |
| [13] |
袁德宝, 张振超, 张军. PSO优化的分数阶PFDGM(1, 1)模型在变形监测预报中的应用[J]. 测绘科学技术学报, 2019, 36(4): 340-345 (Yuan Debao, Zhang Zhenchao, Zhang Jun. Application of Fractional PFDGM(1, 1) Model Based on PSO in Deformation Monitoring and Forecasting[J]. Journal of Geomatics Science and Technology, 2019, 36(4): 340-345)
(  0) 0) |
| [14] |
熊萍萍, 党耀国, 姚天祥. 基于初始条件优化的一种非等间距GM(1, 1)建模方法[J]. 控制与决策, 2015, 30(11): 2 097-2 102 (Xiong Pingping, Dang Yaoguo, Yao Tianxiang. Modeling Method of Non-Equidistant GM(1, 1) Model Based on Optimization Initial Condition[J]. Control and Decision, 2015, 30(11): 2 097-2 102)
(  0) 0) |
| [15] |
罗友洪, 陈友军. 线性时变参数非等间距GM(1, 1)幂模型及其应用[J]. 系统工程, 2021, 39(5): 152-158 (Luo Youhong, Chen Youjun. Linear Time-Varying Parameter Non-Equidistant GM(1, 1) Power Model and Its Application[J]. Systems Engineering, 2021, 39(5): 152-158)
(  0) 0) |
2. College of Science, Inner Mongolia Agricultural University, 306 Zhaowuda Road, Hohhot 010018, China;
3. College of Computer and Information Engineering, Inner Mongolia Agricultural University, 29 East-Erdos Street, Hohhot 010011, China
 2022, Vol. 42
2022, Vol. 42


