2. 武汉大学卫星导航定位技术研究中心,武汉市珞喻路129号,430079
海潮负荷效应在垂直方向上引起的测站位移可达数cm[1],此误差在高精度GPS数据处理中不可忽略。诸多学者分析不同海潮模型引起的测站海潮负荷位移差异[2-3]以及不同模型的海潮负荷改正对GPS精密定位[4-5]和坐标时间序列的影响[6]。海潮负荷改正一般通过全球海潮模型和格林函数褶积积分计算得出,格林函数采用负荷勒夫数导出,其中一阶负荷勒夫数与选用的地球参考框架原点有关[7]。地球参考框架的原点可以定义为包括大气和海洋在内的整个地球系统的质心CM或者固体地球的质心CE[8]。海潮负荷改正可以基于CM框架或者CE框架进行计算,CM和CE框架下不同的一阶负荷勒夫数会得到不同的一阶形变,两者间的差异即为海潮负荷引起的地心运动。本文分别采用CM框架和CE框架的海潮负荷改正计算132个全球站2002~2019年长达18 a的GPS坐标时间序列,重点分析海潮负荷引起的地心运动对GPS坐标时间序列的影响,尤其是对异常周期信号的影响。
1 海潮负荷改正对于指定测站,海潮负荷位移可通过11个主潮波引起的位移进行叠加计算[9],即
| $ \Delta c=\sum\limits_{k=1}^{N} f_{k} A_{c k} \cos \left(\omega_{k} t+\chi_{k}\left(t_{0}\right)+\mu_{k}-\varphi_{c k}\right) $ | (1) |
式中,Δc为t时刻测站某一方向上(N、E、U)的海潮负荷位移;N为叠加的潮波数;ωk和χk(t0)分别为分潮波k的角频率和天文幅角初相;fk和μk分别为分潮波k的交点因子和交点订正角,与月球轨道升交点的经度有关;Ack和φck分别为分潮波k在测站相应方向上的振幅和相位,可根据具体的海潮模型计算得到。11个主潮波包括4个半日潮波M2、S2、N2、K2,4个全日潮波K1、O1、P1、Q1,以及3个长周期潮波Mf、Mm、Ssa。IERS采用一种更加严密的方法计算海潮负荷位移。首先利用Hans-Georg Scherneck网页工具计算得到11个主潮波在CM和CE框架下的振幅和相位;然后利用样条插值法将11个主潮波分量进行内插,得到共计342个分潮波的振幅和相位;最终计算得到总的海潮负荷位移。
2 数据处理策略 2.1 PPP坐标解算本文在IGS2014框架下选取132个全球站(如图 1所示,其中红色测站用于Helmert转换),利用武汉大学研发的PANDA软件,采用静态精密单点定位PPP模式解算测站坐标。测站总体观测时段为2002-01-01~2019-12-31。精密卫星轨道和钟差采用德国地学研究中心GFZ提供的第二次重处理产品和事后产品(均为SP3格式)。需要注意的是,自2017-01-29(GPS 1 934周)起,GFZ轨道采用IGS2014框架,而之前的轨道产品均采用IGb2008框架。

|
图 1 132个测站分布 Fig. 1 Distribution of 132 stations |
采用无电离层组合伪距/相位非差观测值进行数据处理,数据采样率为300 s,卫星截止高度角为7°。根据不同时期轨道产品的参考框架选用igs08.atx或igs14.atx绝对天线相位中心改正模型。利用双频无电离层组合观测值消除电离层延迟一阶项,忽略高阶项。采用GMF/GPT2模型改正对流层延迟[10-11],天顶对流层延迟每小时估计一次,将接收机钟差作为白噪声过程进行估计。采用文献[12]的方法,将模糊度参数固定为整数,固体潮、极潮引起的测站位移根据IERS 2010协议[9]进行改正。
为分析海潮负荷引起的地心运动对GPS精度定位和坐标时间序列的影响,采用3种处理策略对海潮负荷位移进行改正:1)不改正(NO-OTL);2)CM框架的海潮负荷改正(CM-OTL),在计算各潮波的振幅和相位时,需要考虑海潮负荷引起的地心运动;3)CE框架的海潮负荷改正(CE-OTL),在计算各潮波的振幅和相位时,不考虑海潮负荷引起的地心运动。针对CM框架和CE框架,采用FES2004海潮模型(GFZ轨道计算时亦采用)计算11个主潮波的振幅和相位[13]。在此基础上采用IERS 2010协议推荐的方法[9],将11个主潮汐分量应用样条插值法扩展为342个小潮波,以此计算总的海潮负荷位移改正。除海潮负荷位移改正的处理策略不同外,本文其他数据处理策略保持不变。
2.2 坐标时间序列分析为消除GFZ轨道产品解算PPP测站坐标时存在的框架差异,采用Helmert转换将52个核心站(图 1中红色测站)的PPP天解坐标对准到IGS2014框架中,最终获得框架一致的坐标时间序列,用于后续的时间序列分析。
本文采用Hector软件包进行时间序列分析[14]。首先对原始坐标时间序列进行预处理,在考虑跳变、周年项和半周年项的基础上,采用最小二乘拟合法得到时间序列的线性趋势;然后采用四分位距法探测去除趋势项后的坐标残差时间序列异常值[15],从而去除原始坐标时间序列中的粗差。在此基础上,基于闪烁噪声(FN)+白噪声(WN)模型,估计时间序列中的跳变、线性趋势、周年项和半周年项、GPS交点年信号[16]的第1~9个谐波。由地震、仪器变化等因素引起的跳变信息参考国际GNSS服务IGS提供的soln_IGS14.snx文件。
PPP解算的测站坐标时间序列大多是含噪声的非均匀采样序列,而快速傅立叶变换等常用的频谱分析方法要求序列均匀采样,因此常用的频谱分析方法在处理坐标时间序列时存在明显不足。Lomb-Scargle周期图[17]是一种适用于非均匀采样序列的频谱分析方法,常用于GNSS时间序列频谱分析领域[8, 16, 18-19]。基于此,本文采用Lomb-Scargle周期图对去除跳变、线性趋势的坐标残差序列进行频谱分析,提取坐标时间序列中的周期信号。由于坐标时间序列中的周期信号(特别是海潮负荷效应引起的周期信号)比较微弱,单个测站坐标时间序列的功率谱容易受噪声影响,因此本文首先计算单个测站坐标残差时间序列的功率谱,然后将所有测站的功率谱进行堆积处理[16],即按照N、E和U坐标分量将不同测站的功率谱聚合成单个功率谱,按频率排序后采用0.05 cpy的平滑窗口进行平滑处理,最终得到堆积功率谱。
3 结果与分析根据上述数据处理方法,采用NO-OTL、CM-OTL和CE-OTL三种处理策略计算得到3组测站坐标时间序列。
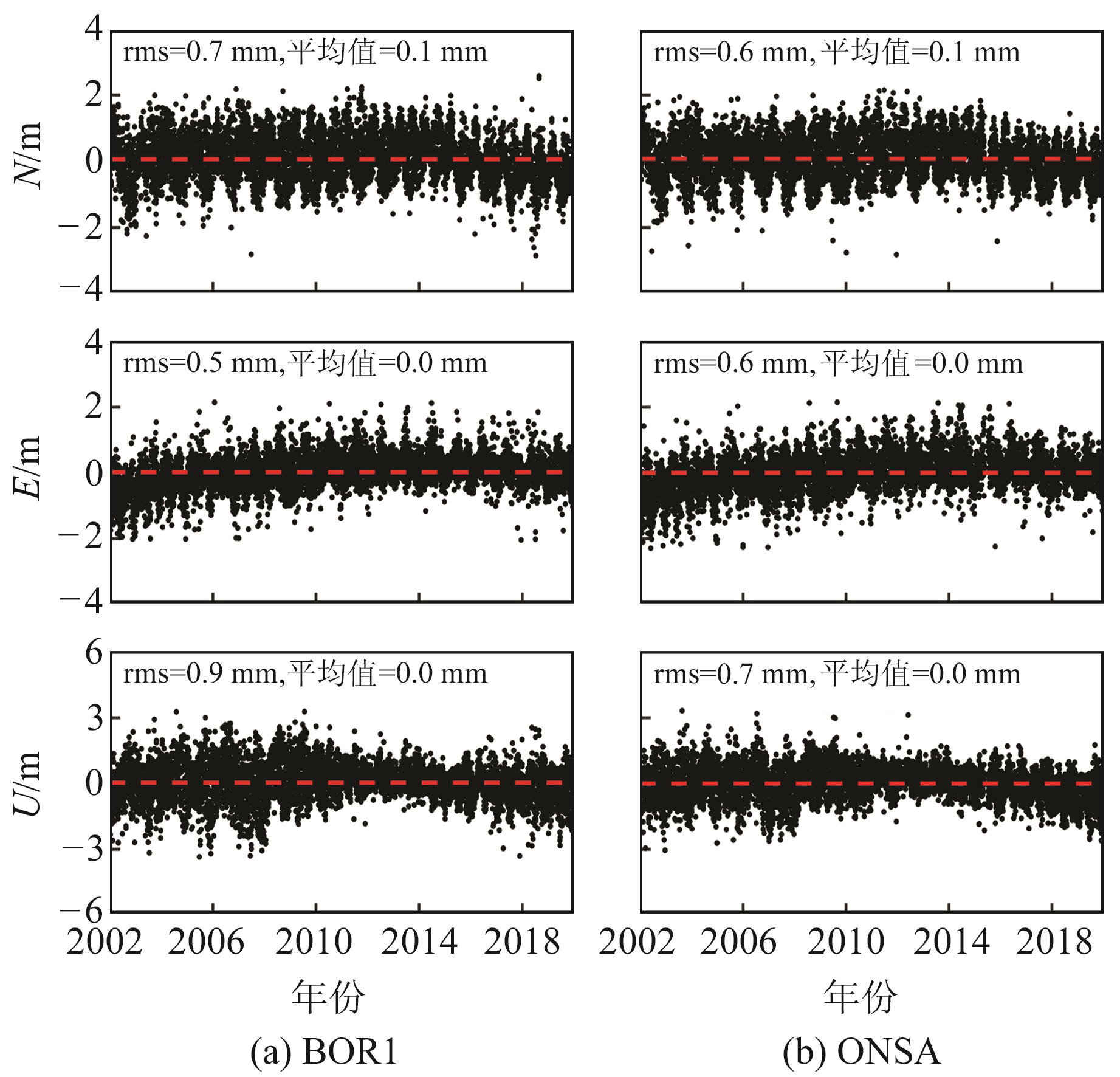
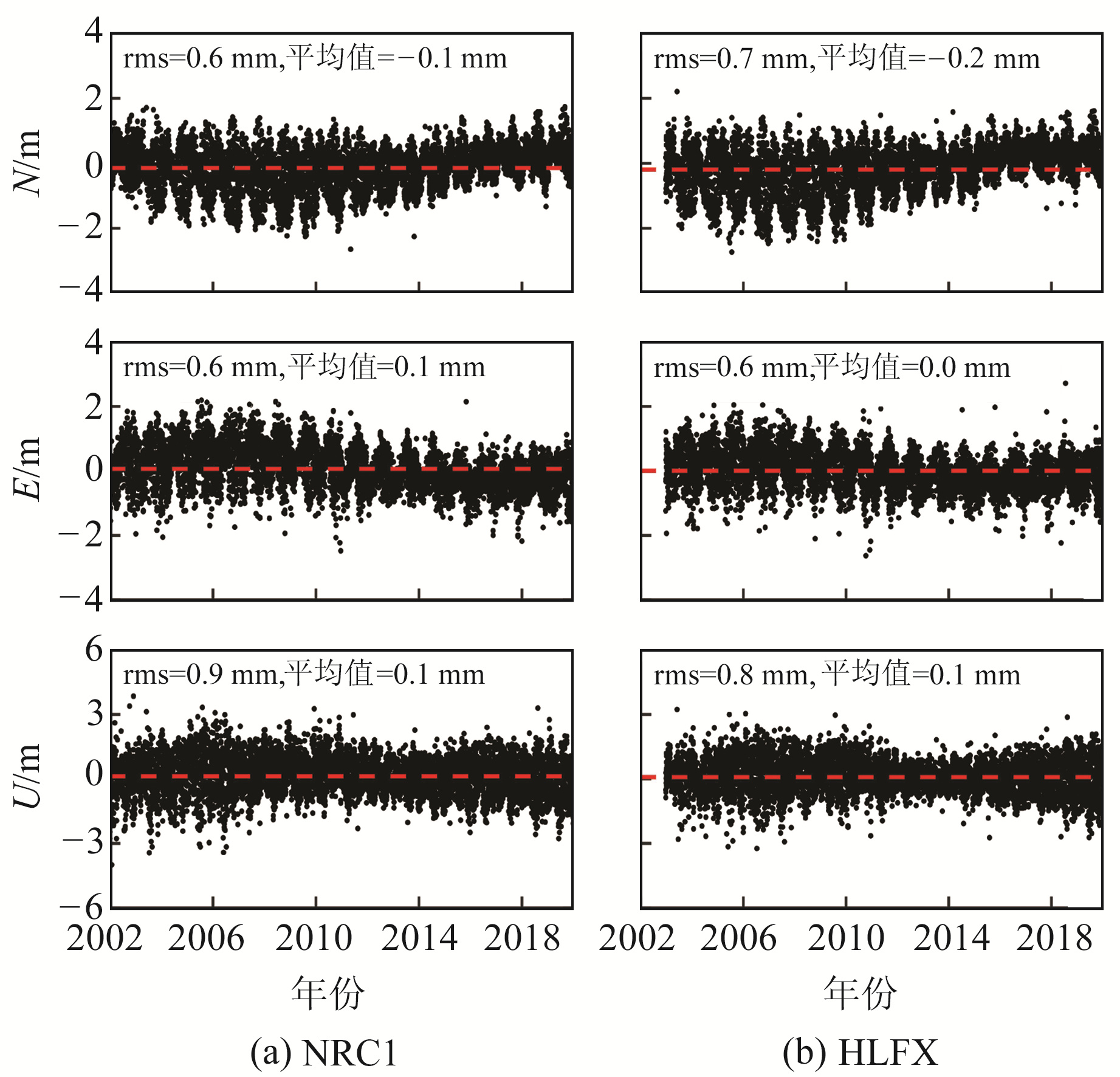
3.1 对测站坐标的影响为分析海潮负荷引起的地心运动对测站坐标的影响,对同一测站的CM-OTL和CE-OTL坐标时间序列作差,以IGS2014框架下2002.0历元的参考坐标为基准,提取N、E和U方向上的坐标差异时间序列。图 2为波兰的BOR1(17.07°E,52.38°N)和瑞典的ONSA(11.93°E,57.40°N)2个测站CM-OTL与CE-OTL之间的坐标差异时间序列,BOR1和ONSA测站分别距离海岸线约200 km和0.1 km。图 3为加拿大东南部地区NRC1(75.62°W,45.45°N)和HLFX(63.61°W,44.68°N)2个测站CM-OTL与CE-OTL之间的坐标差异时间序列,NRC1和HLFX测站分别距离海岸线约400 km和0.3 km。图中水平方向红色虚线表示坐标差异时间序列的平均值。由图 2和图 3可以看出,CM-OTL和CE-OTL之间的坐标差异没有明显的系统性偏差,但会随时间呈周期性变化。图 2的N方向和图 3的N、E方向均存在显著的周年信号,图 3的N、E方向还包含明显的长周期信号。对比图 2和图 3可以发现,不同地区测站坐标差异时间序列的变化趋势差别较大,但相同区域测站坐标差异时间序列的变化趋势较为一致。例如图 3中NRC1和HLFX测站在N、E方向上具有几乎相同的周期信号。由此可知,对同一地区的测站而言,海潮负荷地心运动引起的坐标差异具有相似的趋势特征,与测站至海岸线的距离无显著相关性。
|
图 2 CM-OTL与CE-OTL之间的坐标差异 Fig. 2 Position differences between CM-OTL and CE-OTL solutions |
|
图 3 CM-OTL与CE-OTL之间的坐标差异 Fig. 3 Position differences between CM-OTL and CE-OTL solutions |
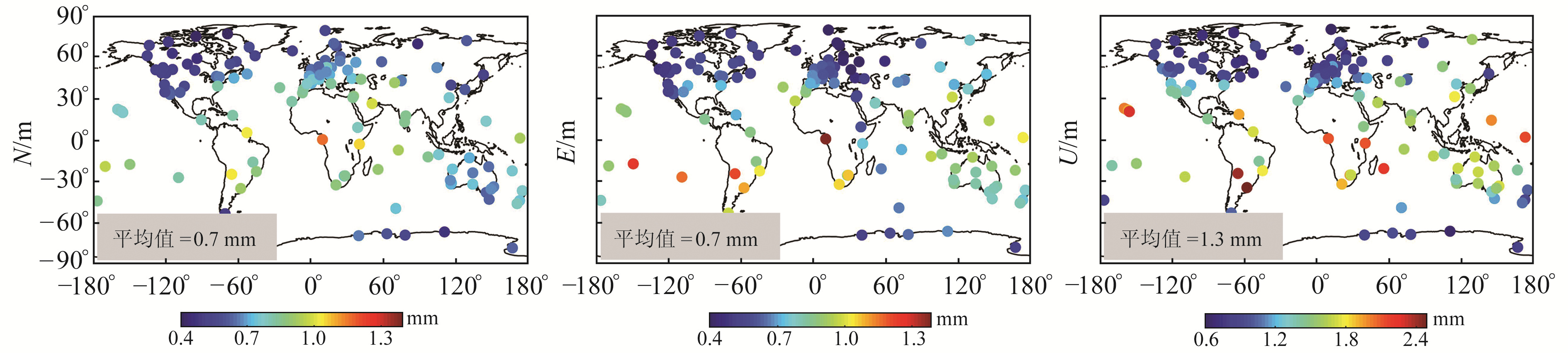
图 4为全球132个测站CM-OTL与CE-OTL之间坐标差异时间序列的RMS。由图可见,海潮负荷相关的地心运动引起的水平方向上(N、E)的坐标差异为0.4~1.4 mm,平均值为0.7 mm;垂直方向(U)上坐标差异为0.6~2.8 mm,平均值为1.3 mm。总体来看,海潮负荷地心运动引起的垂直方向坐标差异约为水平方向的2倍。结合图 2、图 3、图 4可以发现,海潮负荷地心运动引起的坐标差异量级与测站至海岸线的距离无显著相关性,但具有一定的区域分布特征。在北美洲北部、欧洲西北部和南极洲地区,测站坐标差异略低于平均水平;而在赤道附近,测站坐标差异略高于平均水平。
|
图 4 132个测站CM-OTL与CE-OTL之间坐标差异时间序列的RMS Fig. 4 RMS of position differences between the CM-OTL and CE-OTL solutions for 132 stations |
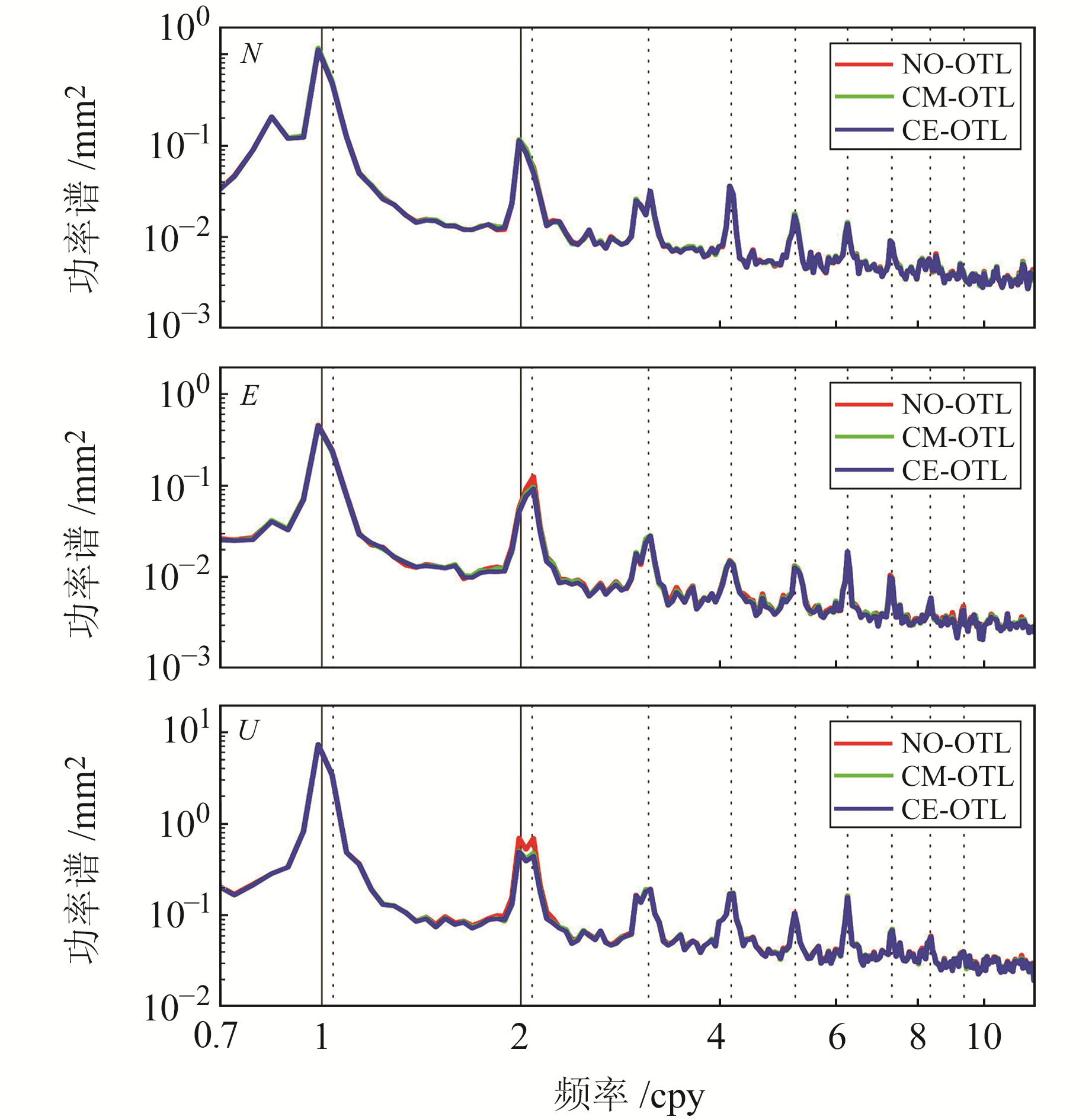
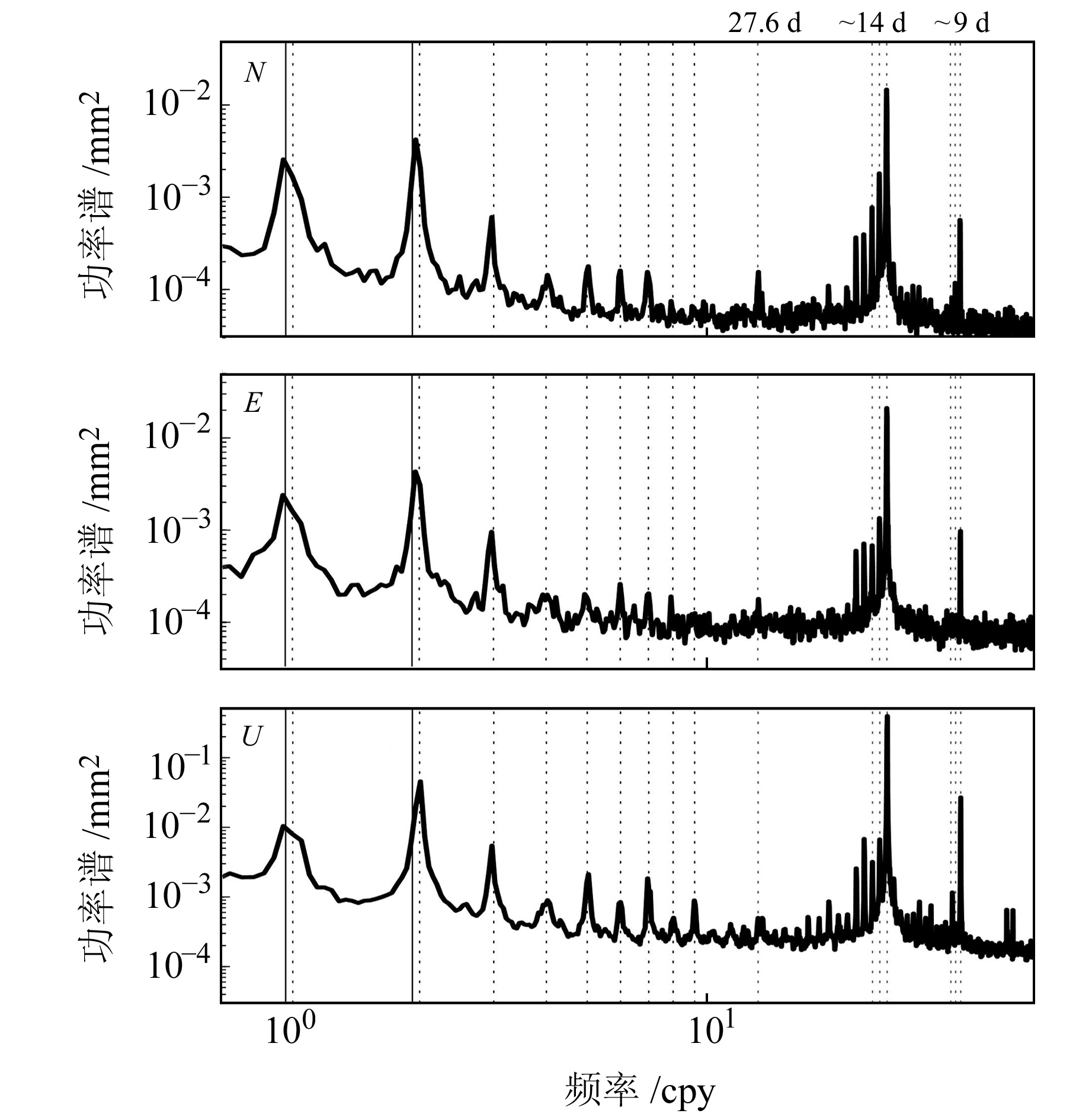
为分析坐标时间序列中的周期信号,采用Lomb-Scargle周期图计算所有测站的堆积功率谱。图 5和图 6分别为不同频率下NO-OTL、CM-OTL和CE-OTL坐标残差时间序列的堆积功率谱。图 5中垂直方向的实线表示周年和半周年信号,垂直方向的虚线表示GPS交点年信号的第1~9个谐波;图 6中垂直方向的虚线依次表示27.6 d、14.8 d、14.2 d、13.6 d、9.6 d、9.4 d、9.1 d信号。
|
图 5 不同海潮负荷改正策略解算的坐标时间序列堆积功率谱(0.7~10 cpy) Fig. 5 Stacked power spectra of position time series estimated using different OTL corrections(0.7~10 cpy) |

|
图 6 不同海潮负荷改正策略解算的坐标时间序列堆积功率谱(10~50 cpy) Fig. 6 Stacked power spectra of position time series estimated using different OTL corrections(10~50 cpy) |
由图 5和图 6可知,NO-OTL的功率谱在半周年、第2个GPS交点年谐波、27.6 d、14 d(14.8 d、14.2 d、13.6 d)、9 d(9.6 d、9.4 d、9.1 d)信号附近存在显著尖峰,说明若不改正海潮负荷位移,海潮负荷效应会引入周期信号。上述周期信号可以分为2类:1)周期信号来自海潮信号的直接传递,例如半周年、27.6 d、13.6 d的周期信号分别对应长周期潮波Ssa、Mm、Mf;2)周期信号与亚周日(接近24 h或12 h)信号的混叠有关[18],比如在24 h数据处理间隔下,M2、O1、N2、Q1的混叠周期分别为14.8 d、14.2 d、9.6 d、9.4 d;在卫星轨道重复周期(23.93 h)采样条件下,M2和O1的混叠周期接近13.6 d,N2和Q1的混叠周期接近9.1 d。与NO-OTL相比,CM-OTL和CE-OTL中海潮负荷效应引起的周期信号显著减小,其中半周年信号和第2个GPS交点年谐波信号轻微减弱,14 d和9 d的周期信号显著减弱,27.6 d信号消失。
由于CM-OTL和CE-OTL采用的海潮负荷改正框架不同,因此二者计算的坐标时间序列功率谱存在显著差异,主要表现为CM-OTL坐标时间序列的14 d和9.1 d信号更加明显。表 1(单位mm2)为采用CM-OTL和CE-OTL解算的14.8 d、14.2 d、13.6 d、9.1 d信号功率。统计结果表明,与CM-OTL相比,CE-OTL中14.8 d信号在N、E、U方向上分别减弱17.0%、17.1%、11.6%,14.2 d信号分别减弱47.9%、34.7%、19.7%,13.6 d信号分别减弱67.7%、83.5%、88.0%,9.1 d信号分别减弱24.0%、29.6%、55.4%。可以看出,海潮负荷地心改正对13.6 d、9.1 d信号的影响十分显著。
|
|
表 1 采用CM-OTL和CE-OTL解算的信号功率 Tab. 1 Power of the period signals estimated using CM-OTL and CE-OTL solutions |
为比较海潮负荷引起的地心运动对坐标时间序列周期信号的影响,对各测站CM-OTL与CE-OTL坐标时间序列作差,可消除公共的地球物理信号和其他模型误差,得到的差分时间序列将包含海潮负荷地心运动引起的坐标差异以及相应的周期信号。图 7为CM-OTL与CE-OTL坐标时间序列之差的堆积功率谱。由图可知,坐标差异时间序列存在明显的周年、GPS交点年、27.6 d、14 d以及9 d信号,说明海潮负荷地心运动可引入GPS交点年信号。由此推测,未完全模型化的海潮负荷效应或与海潮负荷效应周期类似的亚周日信号,可能是引入GPS交点年信号的原因之一。
|
图 7 CM-OTL与CE-OTL坐标时间序列之差的堆积功率谱 Fig. 7 Stacked power spectra of position difference time series between CM-OTL and CE-OTL solutions |
由于受到轨道动力学的约束,GPS卫星轨道的框架原点指向地心CM。根据IGS规定,卫星轨道从惯性坐标系转为地固坐标系时需要进行地心改正(center of mass correction, CMC),此时的框架原点指向测站网的中心(center of network, CN)。由于IGS及其分析中心提供的SP3轨道已经考虑了海潮负荷引起的地心改正[20],因此就海潮负荷而言,其框架原点指向CN。同样,采用SP3轨道解算的PPP坐标属于CN框架,CN可近似为CE,但是CN与CM之间的差异为CMC[21]。因此,CN框架的SP3轨道与CE框架的海潮负荷改正具有更好的框架一致性。本文研究结果表明,采用CN框架(针对海潮负荷)的SP3轨道和采用CM框架的海潮负荷改正将引入GPS交点年信号和14 d信号。利用IGS及其分析中心提供的精密轨道进行PPP解算时,推荐采用CE框架进行海潮负荷改正。
4 结语1) 在全球范围内,海潮负荷地心运动引起的坐标差异在N、E、U方向上的平均值分别为0.7 mm、0.7 mm和1.3 mm,垂直方向的坐标差异约为水平方向的2倍。海潮负荷地心运动引起的坐标差异具有显著的区域分布特征,邻近测站的坐标差异序列具有相似的变化趋势。
2) 当海潮负荷改正所属框架与GPS轨道所属框架不一致时,海潮负荷效应可混叠产生周期为GPS交点年信号、14 d、9 d的异常信号,与海潮负荷周期接近的亚周日误差可能是引入GPS交点年信号的原因之一。本文使用的GPS轨道考虑了海潮负荷效应引起的地心运动,与CM-OTL相比,CE-OTL中海潮负荷效应引入的周期信号显著减弱,其中14.8 d信号减弱11.6%~17.1%、14.2 d信号减弱19.7%~47.9%、13.6 d信号减弱67.7%~88.0%、9.1 d信号几乎消失。
3) IGS及其分析中心提供的SP3轨道从惯性坐标系转为地固坐标系时需要进行地心改正。对采用SP3轨道解算的PPP坐标而言,其框架原点近似为固体地球质心CE。采用IGS提供的SP3轨道计算PPP时,应采用CE框架进行海潮负荷改正。
| [1] |
Vey S, Calais E, Llubes M, et al. GPS Measurements of Ocean Loading and Its Impact on Zenith Tropospheric Delay Estimates: A Case Study in Brittany, France[J]. Journal of Geodesy, 2002, 76(8): 419-427 DOI:10.1007/s00190-002-0272-7
(  0) 0) |
| [2] |
赵大江, 郭春喜, 程传录, 等. 不同海潮模型对GNSS站负荷位移计算的影响[J]. 大地测量与地球动力学, 2016, 36(7): 654-658 (Zhao Dajiang, Guo Chunxi, Cheng Chuanlu, et al. The Load Effect of Ocean Tide Models on Displacement at the GNSS Station[J]. Journal of Geodesy and Geodynamics, 2016, 36(7): 654-658)
(  0) 0) |
| [3] |
范文蓝, 姜卫平, 袁林果, 等. 不同海潮模型对中国沿海区域海潮负荷位移改正影响分析[J]. 大地测量与地球动力学, 2018, 38(6): 598-602 (Fan Wenlan, Jiang Weiping, Yuan Linguo, et al. Effects of Different Ocean Tide Models on OTL Correction in China's Coastal Areas[J]. Journal of Geodesy and Geodynamics, 2018, 38(6): 598-602)
(  0) 0) |
| [4] |
赵红, 张勤, 黄观文, 等. 基于不同海潮模型研究海潮负荷对GPS精密定位的影响[J]. 大地测量与地球动力学, 2012, 32(5): 108-112 (Zhao Hong, Zhang Qin, Huang Guanwen, et al. Effect of Ocean Tide Loading on GPS Precise Positioning Based on Different Ocean Tide Models[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 108-112)
(  0) 0) |
| [5] |
何金鑫, 章浙涛, 何秀凤. FES2004和GOT4.7海潮模型改正对全球PPP的影响特征及差异分析[J]. 大地测量与地球动力学, 2021, 41(6): 612-617 (He Jinxin, Zhang Zhetao, He Xiufeng. Characteristics and Differences Analysis of the Effect of FES2004 and GOT4.7 Ocean Tide Model Corrections on Worldwide PPP[J]. Journal of Geodesy and Geodynamics, 2021, 41(6): 612-617)
(  0) 0) |
| [6] |
范文蓝, 姜卫平, 袁林果, 等. 海潮模型差异对GNSS坐标时间序列周期信号及噪声特性影响分析[J]. 大地测量与地球动力学, 2018, 38(9): 917-922 (Fan Wenlan, Jiang Weiping, Yuan Linguo, et al. Effects of Ocean Tide Model Discrepancies on Periodic Signal and Noise Characteristic of GNSS Coordinate Time Series[J]. Journal of Geodesy and Geodynamics, 2018, 38(9): 917-922)
(  0) 0) |
| [7] |
Goad C C. Gravimetric Tidal Loading Computed from Integrated Green's Functions[J]. Journal of Geophysical Research Atmospheres, 1980, 85(B5): 2679-2683 DOI:10.1029/JB085iB05p02679
(  0) 0) |
| [8] |
Blewitt G. Self-Consistency in Reference Frames, Geocenter Definition, and Surface Loading of the Solid Earth[J]. Journal of Geophysical Research: Solid Earth, 2003, 108(B2)
(  0) 0) |
| [9] |
Petit G, Luzum B. IERS Conventions(2010)[R]. Observatoire de Paris, Paris, 2010
(  0) 0) |
| [10] |
Boehm J, Niell A, Tregoning P, et al. Global Mapping Function(GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters, 2006, 33(7)
(  0) 0) |
| [11] |
Lagler K, Schindelegger M, Böhm J, et al. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1069-1073 DOI:10.1002/grl.50288
(  0) 0) |
| [12] |
Ge M, Gendt G, Dick G, et al. Improving Carrier-Phase Ambiguity Resolution in Global GPS Network Solutions[J]. Journal of Geodesy, 2005, 79(1-3): 103-110 DOI:10.1007/s00190-005-0447-0
(  0) 0) |
| [13] |
Lyard F, Lefevre F, Letellier T, et al. Modelling the Global Ocean Tides: Modern Insights from FES2004[J]. Ocean Dynamics, 2006, 56(5-6): 394-415 DOI:10.1007/s10236-006-0086-x
(  0) 0) |
| [14] |
Bos M S, Fernandes R M S, Williams S D P, et al. Fast Error Analysis of Continuous GNSS Observations with Missing Data[J]. Journal of Geodesy, 2013, 87(4): 351-360 DOI:10.1007/s00190-012-0605-0
(  0) 0) |
| [15] |
Langbein J, Bock Y. High-Rate Real-Time GPS Network at Parkfield: Utility for Detecting Fault Slip and Seismic Displacements[J]. Geophysical Research Letters, 2004, 31(15)
(  0) 0) |
| [16] |
Ray J, Altamimi Z, Collilieux X, et al. Anomalous Harmonics in the Spectra of GPS Position Estimates[J]. GPS Solutions, 2008, 12(1): 55-64 DOI:10.1007/s10291-007-0067-7
(  0) 0) |
| [17] |
Scargle J D. Studies in Astronomical Time Series Analysis. Ⅱ-Statistical Aspects of Spectral Analysis of Unevenly Spaced Data[J]. The Astrophysical Journal Letters, 1982, 263(2): 835-853
(  0) 0) |
| [18] |
Rebischung P, Altamimi Z, Ray J, et al. The IGS Contribution to ITRF2014[J]. Journal of Geodesy, 2016, 90(7): 611-630 DOI:10.1007/s00190-016-0897-6
(  0) 0) |
| [19] |
Penna N T, Stewart M P. Aliased Tidal Signatures in Continuous GPS Height Time Series[J]. Geophysical Research Letters, 2003, 30(23): 2184
(  0) 0) |
| [20] |
Weiss J, Steigenberger P, Springer T. Orbit and Clock Product Generation[M]. Berlin, Heidelberg: Springer, 2017
(  0) 0) |
| [21] |
Dong D, Yunck T, Heflin M. Origin of the International Terrestrial Reference Frame[J]. Journal of Geophysical Research: Solid Earth, 2003, 108(B4): 2200
(  0) 0) |
2. GNSS Research Centre, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2022, Vol. 42
2022, Vol. 42


