2. 湖北省地震局,武汉市洪山侧路40号,430071;
3. 中国地震局第二监测中心,西安市西影路316号,710054
地表重力场变化监测是我国开展地震预测研究的重要手段之一[1-2],目前主要采取绝对重力与相对重力联测的混合测量模式获取较大空间范围内的地表重力场变化[1]。在数据平差处理方面,20世纪80年代,我国地震重力监测人员采用基于最小二乘原理的经典平差法研制出流动重力数据平差处理软件[3],并一直沿用至今。但该软件在算法模型上存在隐含的假设条件,即在重力观测网单期观测的整个时段内,测点重力值保持不变,因此该方法也称为静态平差方法。然而地球系统动力学过程复杂,地表重力场会随时间发生变化,因此基于该方法的数据处理结果会存在因重力变化而产生的偏差[4],进而影响重力变化计算结果以及后续相关应用的研究。早期的重力监测网范围相对较小且分散独立[5-6],单个测网单期观测时间较短,影响相对较小。近年来,中国地震局建立范围覆盖中国大陆的地震重力监测网络,进行每年1期的整体观测,并在南北带、大华北、天山等地区实施1期加密观测(全年观测2期)。在观测组织实施上,重力网全网观测由近20家单位分测区共同完成,单期观测通常持续3~4个月,南北带等地区全年2期观测之间未出现明显间断,因此不可忽视重力网观测期间重力变化因素对计算结果的影响。
部分学者对基于动态平差模型的流动重力网复测数据处理方法进行研究,其基本思路是在平差观测方程中将重力值描述为与时间相关的变量,从而在数据处理模型上顾及重力值的时变因素[4, 7-8]。Pagiatakis等[7]利用重力随时间变化的线性速率模型对加拿大重力标准网超过40 a的观测数据进行动态平差处理,获得该地区的重力长期变化速率图;康开轩等[4]利用相同的平差模型对滇西区域重力网资料进行处理,获得该地区重力场长期变化趋势;隗寿春等[8]将一种分段线性动态平差模型引入我国地壳运动观测网络重力网资料中,认为相比于传统静态平差模型,分段线性动态平差模型能更有效地反映真实重力场的变化信息。
上述研究为利用动态平差方法进行流动重力网数据处理提供了良好基础,但静态和动态平差方法获得的重力变化处理结果的差异,尤其是不同时间尺度下重力变化结果的差异对比较为欠缺。基于上述分析,本文以我国南北地震带南段地区流动重力观测数据为例,分别采用传统静态平差和动态平差2种方法进行处理,对0.5~3 a时间尺度下的重力变化结果进行对比分析,探讨重力时变因素对静态平差方法不同时间尺度下重力变化结果的影响,进而为流动重力网数据处理提供参考。
1 平差模型 1.1 静态平差模型传统静态平差的基本观测方程为:
| $ \left\{\begin{array}{l} V_{i, j}=\bar{g}_{i}-\bar{g}_{j}-\Delta g_{i j} \\ V_{k}=\bar{g}_{k}-g_{k} \end{array}\right. $ | (1) |
式中,gi、gj分别为相对重力测段中i、j两测点的重力值未知数,Δgij为经过各项改正后的重力段差观测值,gk为第k个绝对重力测点的重力值未知数,gk为第k个绝对重力测点的观测值。式(1) 也可写为:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{A\bar X}} - \mathit{\boldsymbol{L}} $ | (2) |
式中,V为改正数向量,A为系数矩阵,X为未知数向量,L为观测值向量。
根据最小二乘准则,可求得各测点重力值:
| $ \left\{\begin{array}{l} \hat{\boldsymbol{X}}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{P L} \\ \boldsymbol{D}_{X X}=\hat{\sigma}_{0}^{2} \boldsymbol{Q}_{X X}=\hat{\sigma}_{0}^{2}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A}\right)^{-1} \\ \hat{\sigma}_{0}^{2}=\sqrt{\frac{\boldsymbol{V}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{V}}{r}} \end{array}\right. $ | (3) |
式中,P为权矩阵,
考虑到重力场在观测过程中的时变性,引入线性模型将gi、gj、gk表示成时间的函数,即
| $ \left\{\begin{array}{l} V_{i, j}=\bar{g}_{i}\left(t_{0}\right)+\left(t-t_{0}\right) \bar{g}_{i}-\bar{g}_{j}\left(t_{0}\right)- \\ \quad\left(t-t_{0}\right) \bar{g}_{j}-\Delta g_{i j} \\ V_{k}=\bar{g}_{k}\left(t_{0}\right)+\left(t-t_{0}\right) \bar{g}_{k}-g_{k} \end{array}\right. $ | (4) |
式中,t0为设置的基准时间,gi(t0)、gj(t0)分别为相对重力测段中i、j两测点在t0时刻的重力值未知数,gi、gj为相应的重力值时变速率未知数,gk(t0)、gk分别为第k个绝对重力测点在t0时刻的重力值未知数和相应的重力值时变速率未知数,其解算公式与式(3)相同。
2 数据与处理南北地震带南段是我国地震重力监测的重点区域之一。该区域自2014年起已形成常态化的整体观测模式,其中相对重力观测由四川省地震局(简称“四川局”,承担四川测区)、云南省地震局(简称“云南局”,承担云南测区)、中国地震局第一监测中心(简称“一测中心”,与湖北局共同承担贵州测区)、湖北省地震局(简称“湖北局”,承担重庆测区,与一测中心共同承担贵州测区)等4家单位分测区共同完成,绝对重力观测由湖北局、二测中心、一测中心、中国地震局地球物理研究所(简称“地球所”)等4家单位共同完成,图 1为绝对重力测点与各相对重力测区的测线分布。
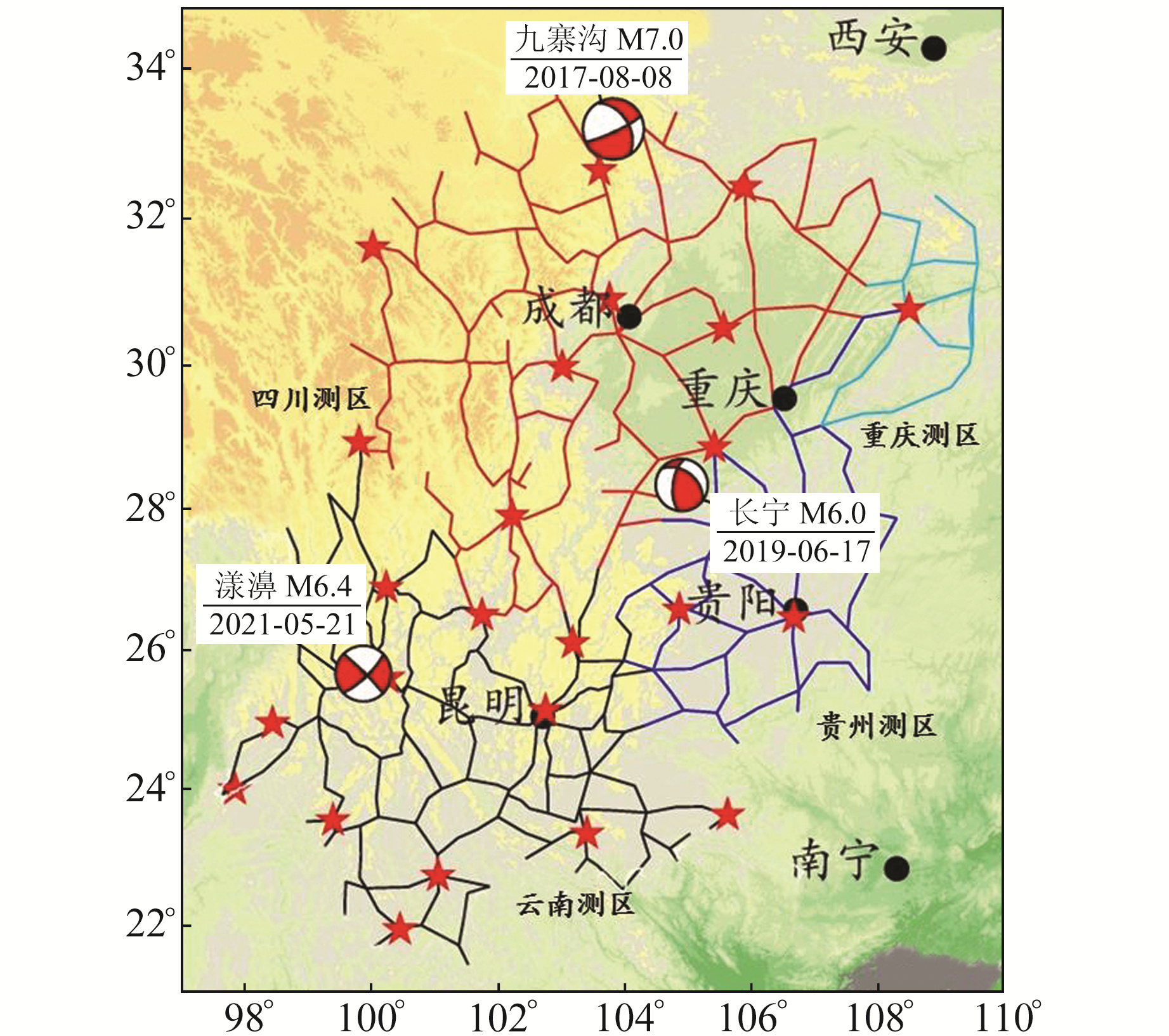
|
红色五角星为绝对重力测点, 线段为相对重力测线, 各测区以不同颜色区分 图 1 南北带南段地区重力观测网 Fig. 1 Gravity network in the southern segment of the north-south seismic belt |
在研究重力场变化特征时,通常会分析0.5~3 a时间尺度下的重力场变化图像[1, 9]。本文选取2015年第二期、2016年第二期、2017年第二期和2018年全年2期总计5期的观测资料,获取0.5~3 a时间尺度下的重力变化结果。表 1为5期观测资料概况,由表可见,每期观测的持续时间均为3个月左右,2018年全年2期观测中仅存在约1个月的空期。2015年以来,研究区内先后发生3次6级以上地震,分别为2017-08-08九寨沟7.0级地震、2019-06-17长宁6.0级地震和2021-05-21漾濞6.4级地震,上述地震均可作为震例分析研究区重力场变化特征与地震的关系。
|
|
表 1 相对重力观测数据概况 Tab. 1 Overview of relative gravity data |
采用传统静态平差和动态平差2种方法进行数据处理,分别获取0.5~3 a时间尺度下的重力变化结果,并分析2种方法所得重力变化结果的差异。首先对相对重力观测数据进行预处理,包括固体潮、气压、仪器高和零漂改正等,然后分别采用传统静态平差和动态平差方法进行平差计算。
静态平差计算时,首先采用线性拟合方法将多期绝对重力观测结果内插到相对重力观测的平均观测时间中获得起算基准值;然后与单期相对重力观测数据预处理结果进行联合解算,获得各期次各测点的重力值;最后采用2期差分结果获得重力变化。计算结果表明,各期次点值精度均值均优于±10 μGal,各时段重力变化精度均值均优于±15 μGal。
动态平差计算时,只需按照绝对重力观测的实际测量结果直接给出绝对值和观测时刻即可得到起算基准值;然后联合相应2期相对重力观测数据的预处理结果,计算重力时变速率和设定初始时刻的重力值。
动态平差方法的计算结果为时变速率,而静态平差方法的计算结果为2期观测的变化量。为进行对比分析,本文根据不同期次各测点的观测时间差,将动态平差计算的时变速率结果转换成重力变化量,再与静态平差获得的重力变化结果进行对比。由动态平差方法计算得到的各时段重力变化精度均值均优于±15 μGal,具体结果见表 2(单位μGal),其精度与静态平差方法基本相当。
|
|
表 2 静态和动态平差方法计算的各时段重力变化精度均值 Tab. 2 Average accuracy of gravity variation by static and dynamic adjustment methods |
图 2为动态平差和静态平差2种方法获得的不同时间尺度下重力变化结果的差异分布累积概率曲线。由图可见,随着时间尺度的增加,2种方法获得的重力变化结果差异逐步减小。在0.5 a时间尺度下,2种方法的最大差异约为19 μGal,平均约为2.9 μGal;在概率分布上,差异为2 μGal以内的占比约50%,差异为5 μGal以内的占比约85%,差异为10 μGal以内的占比约98%。在1 a时间尺度下,2种方法的差异明显减小,最大约为9.5 μGal,平均值为1.5 μGal;差异为2 μGal以内的占比约80%,差异为5 μGal以内的占比达95%。在2 a和3 a时间尺度下2种方法的差异进一步减小。2 a时间尺度下的最大差异约为5.5 μGal,均值为0.6 μGal;3 a时间尺度下的最大差异为4.0 μGal,均值为0.6 μGal,与2 a时间尺度下的结果相同。从概率分布结果来看,2 a和3 a时间尺度下的累积概率分布曲线基本重合,说明对于2 a以上时间尺度下的重力变化结果,单期观测期间重力测点时变因素的影响已趋于稳定,不会再随着时间尺度的增加发生快速衰减。
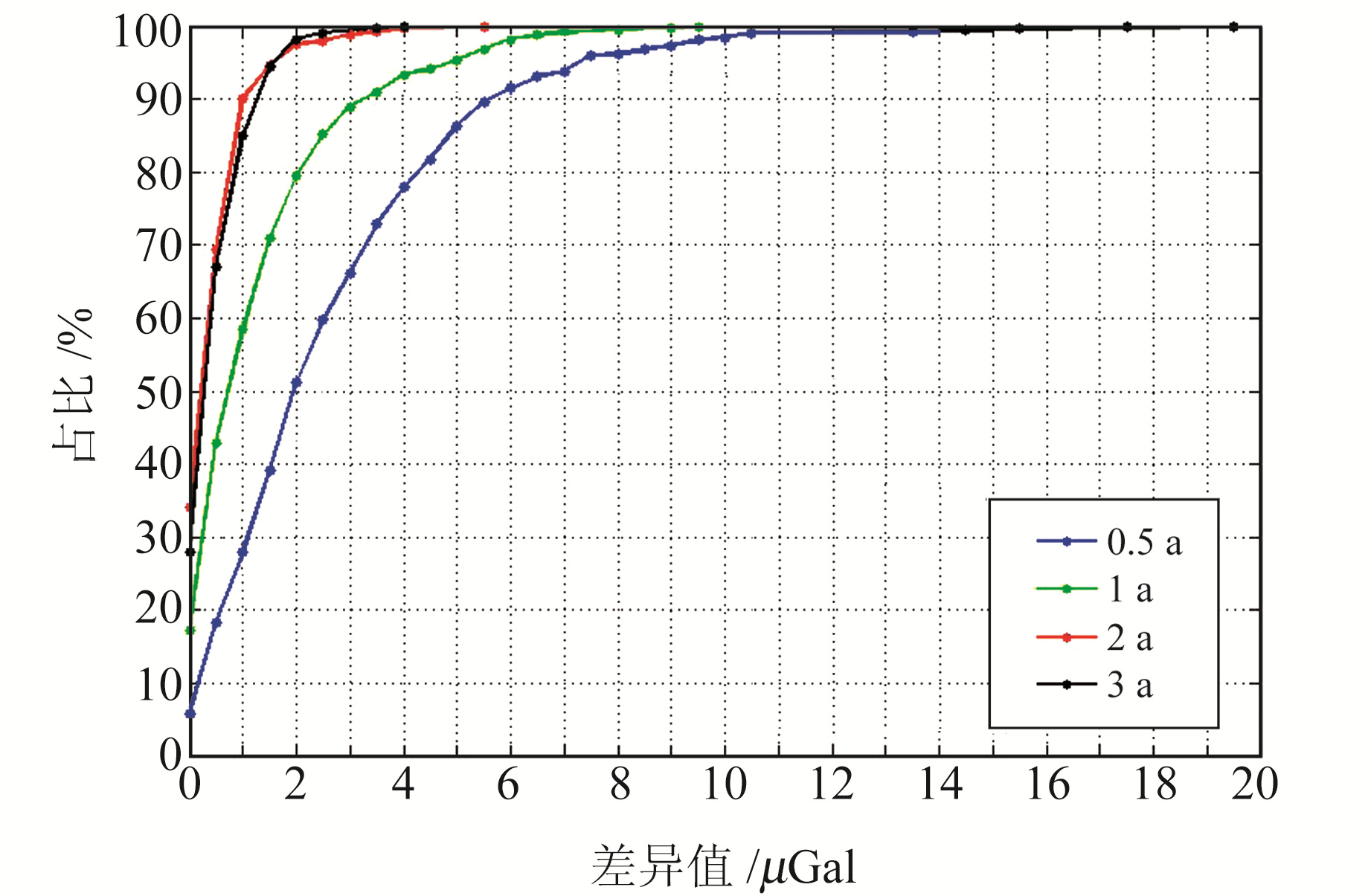
|
图 2 静态与动态平差方法重力变化结果的差异 Fig. 2 Difference between gravity variations by static and dynamic adjustment methods |
重力变化图像是分析重力变化特征的主要依据,图 3~6分别为基于2种方法获得的0.5~3 a时间尺度下的重力变化图像。
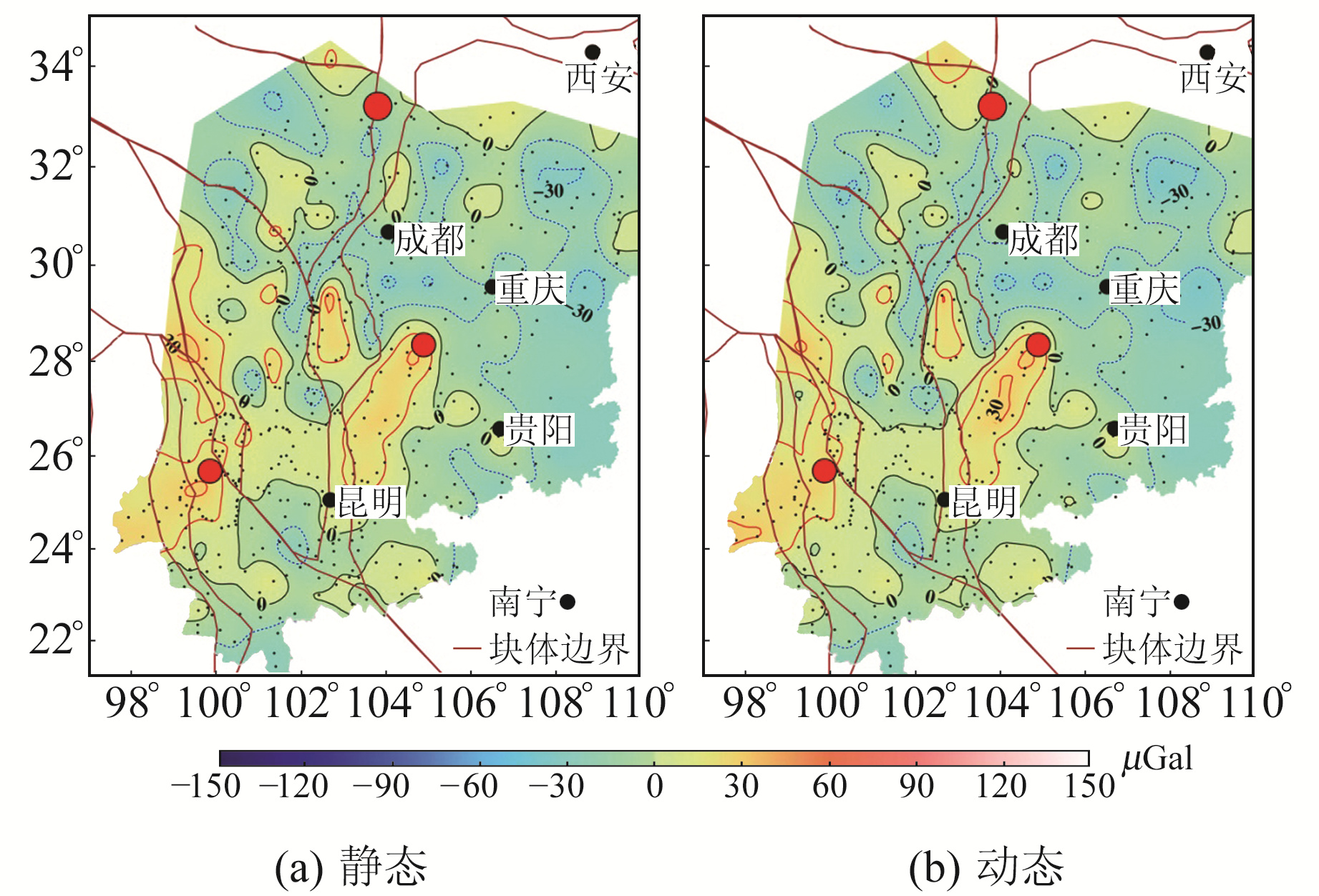
|
图 3 2018-04~08重力变化结果对比 Fig. 3 Gravity variation from April 2018 to August 2018 |
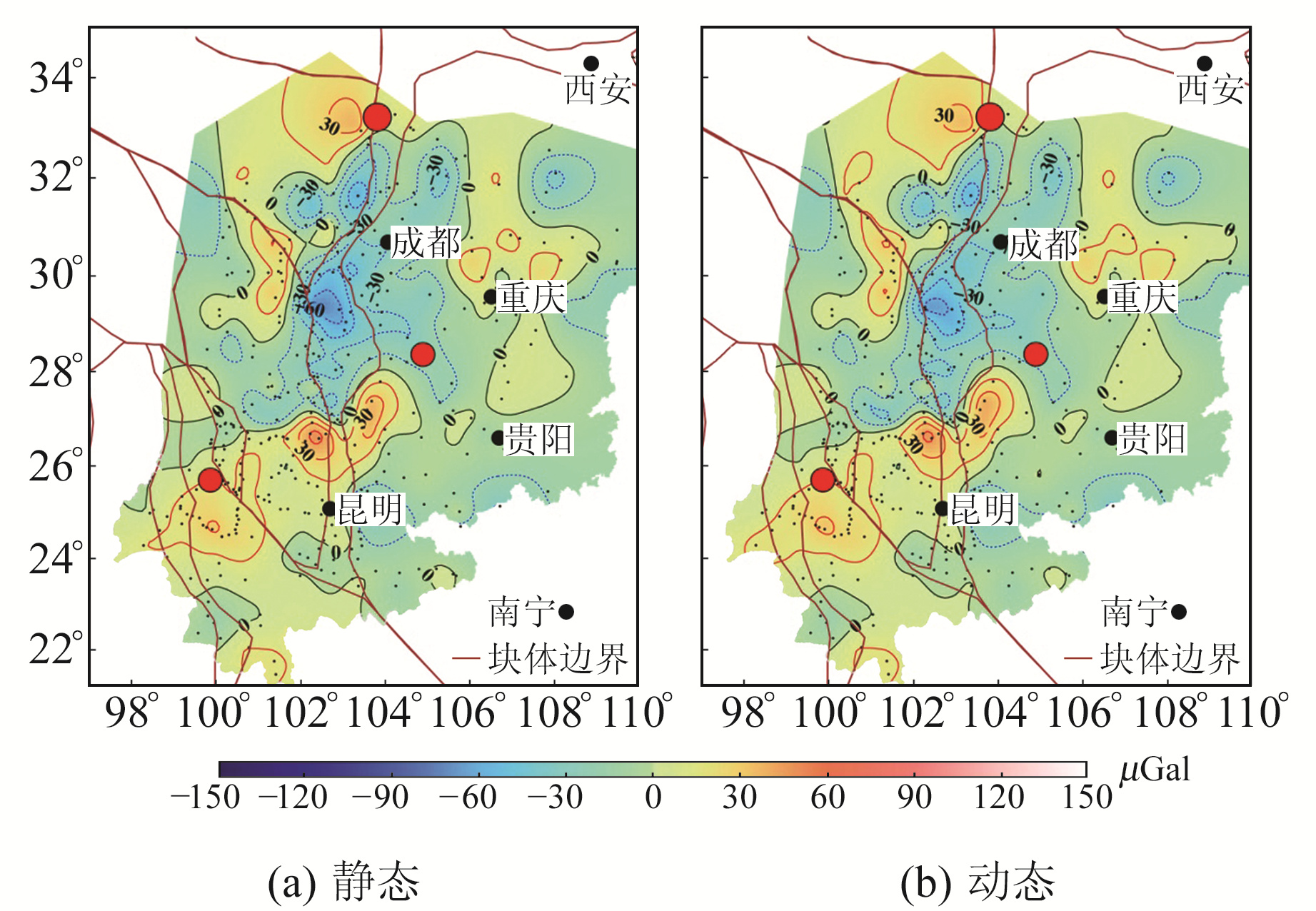
|
图 4 2017-09~2018-08重力变化结果对比 Fig. 4 Gravity variation from September 2017 to August 2018 |
|
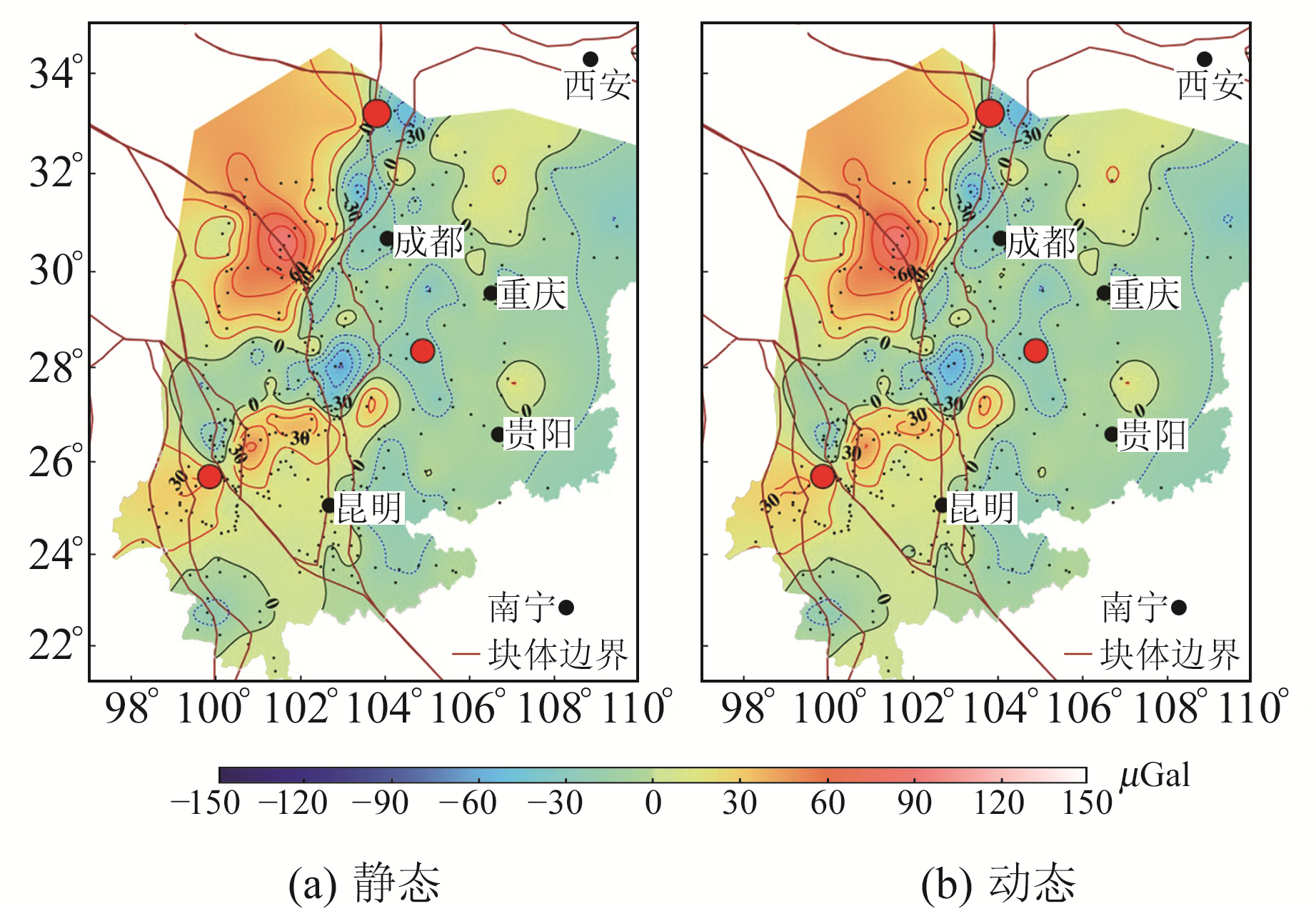
图 5 2016-09~2018-08重力变化结果对比 Fig. 5 Gravity variation from September 2016 to August 2018 |
|
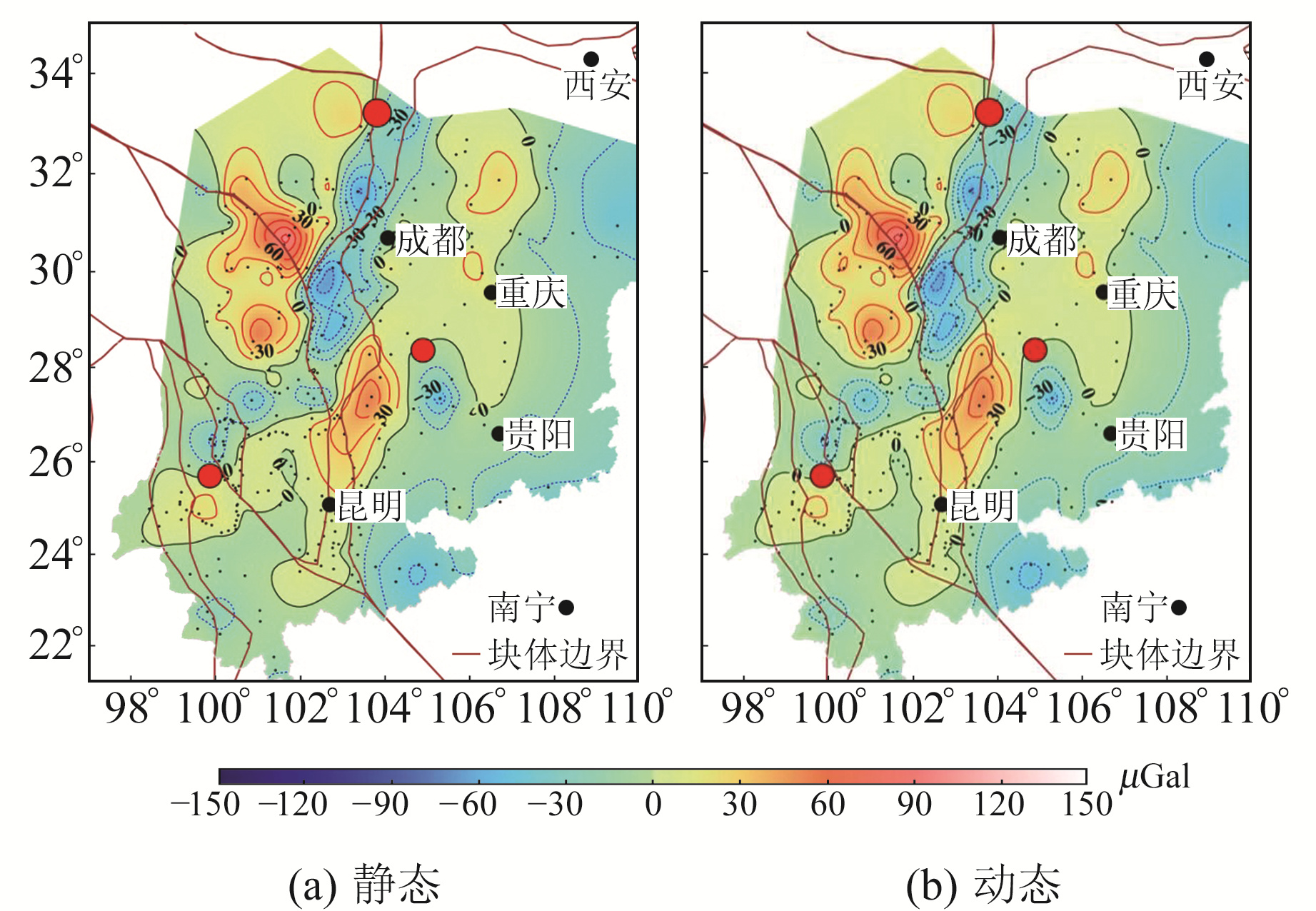
图 6 2015-08~2018-08重力变化结果对比 Fig. 6 Gravity variation from August 2015 to August 2018 |
由图 3可见,2种方法的重力变化并不显著,均在30 μGal以内。2种方法在空间分布态势上基本一致,主要区别在于部分地区的等值线分布细节和重力变化量级。研究区北部以大范围的负变化为主,在九寨沟震区西北部等地呈局部正变化。相比于静态平差结果,动态平差结果的正变化区域相对较大,且重力变化零值线穿过震中地区。在滇西南至川藏交界地区,2种方法的结果均为低值正变化,但等值线分布形态略有差异。在漾濞6.4级地震震区附近,动态平差结果正变化量级比静态平差结果略小,两者最大差异约为15 μGal。在大凉山次级块体东南侧的毗邻地区,动态平差结果正变化量级比静态平差大约15 μGal。2019-06-17在正变化区域东北缘近零值线地区发生长宁6.0级地震。
对于约0.5 a时间尺度下的重力变化而言,动态平差和静态平差2种方法的重力变化图像在整体空间分布态势上保持一致,但在具体的空间分布细节和重力变化量级上存在一定的差异。2种方法图像显示出的重力变化量级最大差异约为15 μGal,与上述重力变化数值的差异基本一致。
3.2.2 1 a尺度由图 4可见,相比于0.5 a尺度,1 a尺度下2种方法的差异明显减小,仅在重庆北部、大凉山次级块体西北部等地区等值线的分布细节上略有不同。在重力变化空间分布特征上,相比于0.5 a尺度,1 a尺度下巴颜喀拉块体内部的正变化区域发生扩展,块体东缘龙门山断裂一线地区负变化明显增强,与鲜水河断裂交会处的最大负变化可达60 μGal。九寨沟地震仍位于巴颜喀拉块体东北部正负变化分界的零值线上。莲峰-昭通断裂带南侧正变化区域向西收缩,最大量级增大至约45 μGal。滇西南地区仍维持低值正变化,但滇西北和川滇藏交界地区整体转为负变化,在漾濞6.4级地震北侧形成近东西向的零值线。整体而言,该时段相对显著的重力变化区基本沿巴颜喀拉块体东边界断裂和大凉山次级块体边界断裂展布,研究区东部和云南南部地区变化平缓。
3.2.3 2 a尺度由图 5可见,2种方法的差异进一步减小,仅在少数地区存在等值线分布上的细节差别。在重力变化空间分布态势上,巴颜喀拉块体东边界断裂、大凉山次级块体边界断裂和小江断裂带的控制作用更加明显,显著变化区均位于断裂带上或以西地区,东部地区变化平缓。相比于1 a尺度,2 a尺度下巴颜喀拉块体和川滇菱形块体北部的重力正变化进一步增强,龙门山断裂带一线负变化区域向东收缩,形成与断裂带大致平行的NNE向梯度带和零值线,九寨沟7.0级地震位于梯度带和零值线上。莲峰-昭通断裂带南侧至滇西南的NE向条带地区仍维持正变化,但滇西北地区负变化区域向南突刺,在漾濞6.4级地震震中地区形成近似四象限的中心特征。
3.2.4 3 a尺度由图 6可见,2种方法已基本无差异。显著变化区仍位于巴颜喀拉块体东边界断裂、大凉山次级块体边界断裂和小江断裂带上或以西地区,重力变化整体呈西强东弱态势。相比于2 a尺度,3 a尺度下巴颜喀拉块体和川滇菱形块体北部的重力正变化有所减弱,但鲜水河断裂南段地区的局部高值异常更加突出。龙门山断裂带一线地区负变化显著增强,九寨沟7.0级地震仍位于与断裂带大致平行的零值线上。莲峰-昭通断裂带南侧地区正变化明显增强,长宁6.0级地震位于正变化区东北侧的零值线上。滇西南地区正变化减弱,漾濞6.4级地震位于其零值线上。
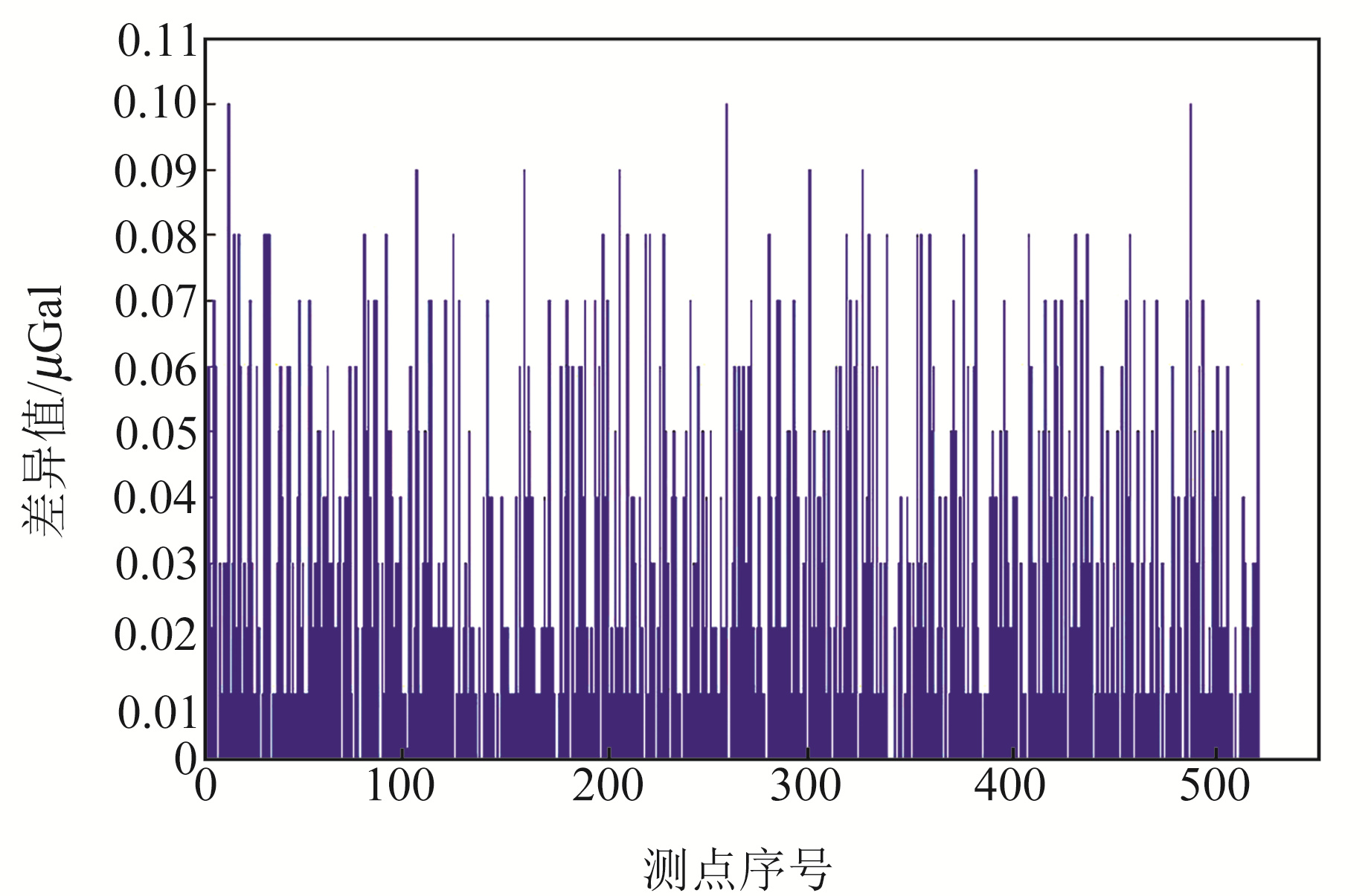
4 讨论动态平差与静态平差的主要区别在于动态平差模型可顾及单期观测期间测点的重力变化因素,当忽略单期内观测时间的差异时(即假设单期观测内各测点的观测时间相同),动态平差模型则等同于对多期观测数据同时进行静态平差,即同时计算多期观测期间的测点重力值,此时动态平差与静态平差2种方法获得的重力变化结果应该相同。为验证上述结论,本文将2018年2期观测数据的观测时间人为设定为相应期次的平均观测时间,分别采用动态和静态平差方法计算重力变化并进行对比分析。图 7为2种方法重力变化结果的数值差异,由图可见,最大差异仅约0.1 μGal,应为平差计算时观测方程不同所产生的计算误差。这也从另一方面证明了本文动态平差方法模型的正确性。
|
图 7 忽略单期内观测时间差异时2种方法获得的约0.5 a时间尺度下的重力变化结果差异 Fig. 7 Difference between gravity variations for 0.5 a time scale by two methods without considering observation time difference |
参与动态平差计算的不同期次观测资料时间跨度越大,动态平差模型越接近于静态平差。基于2种方法计算的0.5~3 a时间尺度下的重力变化结果也表明,随着时间尺度的增加,2种方法重力变化结果的差异也逐步减小。对于0.5 a尺度下的重力变化,2种方法在数值上的差异最大约20 μGal,2种方法在整体空间分布态势上能保持一致,但在具体的空间分布细节和重力变化量级上存在一定的差异。对于1 a尺度下的重力变化,2种方法在数值上的差异最大约10 μGal,部分地区的等值线分布存在细节差异。当重力变化时间尺度在2 a以上时,2种方法获得的重力变化结果在数值上的差异在5.5 μGal以内,同时重力变化图像基本不存在差异。上述结论表明,在0.5 a和1 a尺度下的重力变化结果中,单期观测期间测点的重力变化因素会对基于静态平差方法的重力图像造成一定的干扰,而在2 a以上时间尺度下的重力变化结果中单期观测期间测点重力变化因素的影响较小。
重力变化在空间分布上表现出西强东弱的整体态势,显著的重力变化区主要集中在巴颜喀拉块体、大凉山次级块体、川滇菱形块体中北部地区,东部扬子块体地区重力变化较小。从研究区构造背景来看,西部川滇地区位于青藏高原东南缘,新生代以来在青藏高原地壳物质向东侧运移和阿萨姆突刺的共同作用下,该地区新构造变形和地震活动十分强烈,是中国大陆最显著的强震活动区域[10-11]。研究区东部扬子块体在新构造运动中属于较为稳定的地块,地震活动性相对较弱[12]。由此可知,重力场变化的空间分布可大致反映研究区整体构造活动的强弱。
从重力场变化特征与地震发震地点的关系来看,近期研究区内3次6级以上地震的发震地点均与重力变化零值线具有较好的对应关系。动态平差方法图像显示,九寨沟7.0级地震在0.5~3 a尺度图像中均位于巴颜喀拉块体东边界断裂带与重力变化零值线的交会位置;长宁6.0级地震在0.5~3 a尺度图像中均位于零值线上;漾濞6.4级地震位于川滇菱形块体南边界断裂附近,在3 a尺度图像中位于零值线上,在2 a尺度图像中位于四象限中心和近零值线位置。重力场演化规律与构造活动关系的现有研究结果表明,活动地块的边界带在重力场演化过程中往往具有重要的控制作用,大地震一般发生在与主要活动断裂方向一致的重力场变化正负转换带上[13]。基于上述分析可以认为,本文基于动态平差方法获得的0.5~3 a尺度下的重力场变化图像可大致反映3次地震的发震背景。
5 结语1) 南北地震带南段地区流动重力网单期观测持续时间约3个月,观测期间的重力时变因素会导致静态平差方法计算的重力变化结果存在误差,但随着重力变化时间尺度的增加,其影响会逐步减小。对于0.5 a、1 a、2 a和3 a尺度下的重力变化结果,重力时变因素的最大影响分别约为19 μGal、9.5 μGal、5.5 μGal和4.0 μGal。
2) 动态平差和静态平差2种方法的重力变化图像在整体空间分布态势上保持一致,但0.5 a和1 a时间尺度图像在重力变化量级和等值线分布细节上存在一定的差异,2 a和3 a时间尺度下的重力变化图像则基本相同。因此对于计算0.5 a和1 a时间尺度下的重力变化宜采用动态平差方法。
3) 近期研究区内3次6级以上地震的发震地点均与重力变化零值线具有较好的对应关系,基于动态平差方法获得的0.5~3 a时间尺度下的重力场变化图像可反映3次地震的发震背景。
| [1] |
申重阳, 祝意青, 胡敏章, 等. 中国大陆重力场时变监测与强震预测[J]. 中国地震, 2020, 36(4): 729-743 (Shen Chongyang, Zhu Yiqing, Hu Minzhang, et al. Time-Varying Gravity Field Monitoring and Strong Earthquake Prediction on the Chinese Mainland[J]. Earthquake Research in China, 2020, 36(4): 729-743)
(  0) 0) |
| [2] |
祝意青, 申重阳, 刘芳, 等. 重力观测地震预测应用研究[J]. 中国地震, 2020, 36(4): 708-717 (Zhu Yiqing, Shen Chongyang, Liu Fang, et al. Application of Earthquake Prediction Based on Gravity Observation[J]. Earthquake Research in China, 2020, 36(4): 708-717)
(  0) 0) |
| [3] |
刘绍府, 刘冬至, 李辉. 高精度重力测量平差及其软件[J]. 地震, 1991, 11(4): 57-66 (Liu Shaofu, Liu Dongzhi, Li Hui. Adjustment of High Precision Gravity Measurements and Its Software[J]. Earthquake, 1991, 11(4): 57-66)
(  0) 0) |
| [4] |
康开轩, 李辉, 申重阳, 等. 基于绝对重力基准控制的流动重力观测资料动态平差方法研究[J]. 大地测量与地球动力学, 2015, 35(3): 508-511 (Kang Kaixuan, Li Hui, Shen Chongyang, et al. Method of Dynamic Adjustment on Repeated Gravity Measurements under the Constraint of Absolute Gravity Observations[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 508-511)
(  0) 0) |
| [5] |
贾民育, 詹洁晖. 中国地震重力监测体系的结构与能力[J]. 地震学报, 2000, 22(4): 360-367 (Jia Minyu, Zhan Jiehui. The Structure and Ability of the China Seismological Gravity Monitoring System[J]. Acta Seismologica Sinica, 2000, 22(4): 360-367 DOI:10.3321/j.issn:0253-3782.2000.04.004)
(  0) 0) |
| [6] |
祝意青, 王庆良, 徐云马. 我国流动重力监测预报发展的思考[J]. 国际地震动态, 2008, 38(9): 19-25 (Zhu Yiqing, Wang Qingliang, Xu Yunma. Thoughts on the Development of Earthquake Monitoring and Prediction in Mobile Gravity[J]. Recent Developments in World Seismology, 2008, 38(9): 19-25 DOI:10.3969/j.issn.0253-4975.2008.09.004)
(  0) 0) |
| [7] |
Pagiatakis S D, Salib P. Historical Relative Gravity Observations and the Time Rate of Change of Gravity Due to Postglacial Rebound and other Tectonic Movements in Canada[J]. Journal of Geophysical Research: Solid Earth, 2003, 108(B9)
(  0) 0) |
| [8] |
隗寿春, 徐建桥, 周江存. 重力网的分段线性动态平差[J]. 测绘学报, 2016, 45(5): 511-520 (Wei Shouchun, Xu Jianqiao, Zhou Jiangcun. Piece-Wise Linear Dynamic Adjustment for Gravity Network[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 511-520)
(  0) 0) |
| [9] |
胡敏章, 郝洪涛, 李辉, 等. 地震分析预报的重力变化异常指标分析[J]. 中国地震, 2019, 35(3): 417-430 (Hu Minzhang, Hao Hongtao, Li Hui, et al. Quantitative Analysis of Gravity Changes for Earthquake Prediction[J]. Earthquake Research in China, 2019, 35(3): 417-430 DOI:10.3969/j.issn.1001-4683.2019.03.001)
(  0) 0) |
| [10] |
阚荣举, 张四昌, 晏凤桐, 等. 我国西南地区现代构造应力场与现代构造活动特征的探讨[J]. 地球物理学报, 1977, 20(2): 96-109 (Kan Rongju, Zhang Sichang, Yan Fengtong, et al. Present Tectonic Stress Field and Its Relation to the Characteristics of Recent Tectonic Activity in Southwestern China[J]. Chinese Journal of Sinica, 1977, 20(2): 96-109)
(  0) 0) |
| [11] |
苏有锦, 秦嘉政. 川滇地区强地震活动与区域新构造运动的关系[J]. 中国地震, 2001, 17(1): 24-34 (Su Youjin, Qin Jiazheng. Strong Earthquake Activity and Relation to Regional Neotectonic Movement in Sichuan-Yunnan Region[J]. Earthquake Research in China, 2001, 17(1): 24-34 DOI:10.3969/j.issn.1001-4683.2001.01.004)
(  0) 0) |
| [12] |
张培震, 邓起东, 张国民, 等. 中国大陆的强震活动与活动地块[J]. 中国科学: 地球科学, 2003, 33(增1): 12-20 (Zhang Peizhen, Deng Qidong, Zhang Guomin, et al. Active Tectonic Blocks and Strong Earthquakes on the Chinese Mainland[J]. Science China: Earth Sciences, 2003, 33(S1): 12-20)
(  0) 0) |
| [13] |
祝意青, 梁伟锋, 湛飞并, 等. 中国大陆重力场动态变化研究[J]. 地球物理学报, 2012, 55(3): 804-813 (Zhu Yiqing, Liang Weifeng, Zhan Feibing, et al. Study on Dynamic Change of Gravity Field in China Continent[J]. Chinese Journal of Geophysics, 2012, 55(3): 804-813 DOI:10.6038/j.issn.0001-5733.2012.03.010)
(  0) 0) |
2. Hubei Earthquake Agency, 40 Hongshance Road, Wuhan 430071, China;
3. The Second Monitoring and Application Center, CEA, 316 Xiying Road, Xi'an 710054, China
 2022, Vol. 42
2022, Vol. 42


