地磁转换函数可以表达地磁水平分量和垂直分量之间的线性转换关系,能够反映地下电性结构的横向不均匀性。地震地磁研究中转换函数的时序变化可以反映孕震区的电性结构变化[1],用于震前微观异常信息的提取。诸多学者对转换函数进行深入研究[2-5],获取了丰富的震例经验。感应矢量最早用于分析海岸效应和低阻异常体的影响[6],Schmucker[7]最先确立感应矢量的计算公式,明确地磁水平分量和垂直分量之间的关系。由于不受局部异常体的影响,感应矢量可更加直观地展现地下结构的电性差异,被广泛应用于在电磁测深中对宏观电性结构的研究[8-9]。但在地震地磁观测中,感应矢量和区域电性结构的研究较少,王桥等[10]和龚绍京等[11]对部分地磁台站资料进行感应矢量计算,并对其时序特征和构造指示意义进行研究。
本文计算山东省地磁台阵15个台站的转换函数和感应矢量,并对其时序变化特征进行多台站对比分析,对区域电性结构和构造指示关系等进行研究。所选台站均为固定连续观测且数量较多,其数据质量和稳定性明显优于传统的大地电磁测深(MT)数据,适合开展感应矢量的背景特征分析。本文研究可以为区域磁场变化、构造活动性和地震危险性研究提供背景数据,后续可在该基础上开展时移动态监测,为地震活动趋势判定提供地球物理依据。
1 数据来源与计算方法 1.1 数据来源2016年山东省建成地磁台阵,采用GM4磁通门磁力仪进行秒值观测,台站分布较为均匀,2017年开始多数台站数据趋于稳定。本文基于数据有效率、背景噪声等评价指标选取数据质量较好的15个台站,台站分布如图 1所示。其中沂沭断裂带(F2)附近分布有莱州、安丘、留山、玉皇山、陵阳、郯城6个台站,济南、长清、泰安、嘉祥、邹城5个台站分布于鲁西隆起西侧,莱州、北长山、文登、平度4个台站分布于胶东隆起附近且距离海域较近。为保证结果的稳定性,选取分钟值预处理数据进行转换函数和感应矢量的计算。

|
F1:五莲-即墨-牟平断裂带; F2:沂术断裂带(F2-1:昌邑-大店断裂; F2-2:安丘-莒县断裂; F2-3:沂水-汤头断裂; F2-4:鄌郚-葛沟断裂); F3:聊城-兰考断裂; F4:齐河-广饶断裂; Ⅰ1: 苏鲁造山带﹔Ⅱ1: 胶辽陆块; Ⅱ2: 鲁西隆起; Ⅱ3: 华北坳陷 图 1 地磁观测台站分布 Fig. 1 Distribution of geomagnetic observations |
地磁场垂直分量与2个水平分量之间的关系可表示为[7]:
| $ Z(\omega)=A(\omega) X(\omega)+B(\omega) Y(\omega) $ | (1) |
式中,所有量均为复数;Z(ω)、X(ω)、Y(ω)分别为地磁垂直分量、南北分量和东西分量在某频率ω上的频谱;A、B为地磁转换函数,其表现形式与MT中阻抗张量的估算方式一致。可使用最小二乘法使残差趋于最小值,其残差ε可表示为:
| $ \begin{gathered} \varepsilon=\sum\limits_{k=1}^{N} e_{k} \bar{e}_{k}= \\ \sum\limits_{k=1}^{N}\left(Z_{k}-A X_{k}-B Y_{k}\right)\left(\bar{Z}_{k}-\overline{A X}_{k}-\bar{B}_{k}\right) \end{gathered} $ | (2) |
式中,k为事件序号;N为事件总数;Z、X、Y为各分量的复数频谱;A、B为复数转换函数,其中A=Ar+iAi, B=Br+iBi。由于地磁连续观测可能会受到较多干扰,导致计算结果出现较大偏差,因此可采用加权最小二乘法对强干扰数据进行加权,降低其参与计算的比重,减小对计算结果的影响。
基于转换函数可计算得到实感应矢量Gr和虚感应矢量Gi,具体表示为:
| $ \boldsymbol{G}_{r}=A_{r} \boldsymbol{i}+B_{r} \boldsymbol{j}, \boldsymbol{G}_{i}=A_{i} \boldsymbol{i}+B_{i} \boldsymbol{j} $ | (3) |
式中,i和j分别为指向正北和正东方向的单位矢量。在实际应用时,为使实感应矢量指向电流聚集方向,应对实感应矢量取反向。文中感应矢量均指帕金森矢量,其大小和方向为:
| $ \begin{gathered} \alpha=\arctan \left(B_{r} / A_{r}\right), \\ I=\arctan \left(\sqrt{A_{r}^{2}+B_{r}^{2}}\right), L=\sin I \end{gathered} $ | (4) |
式中α、L分别为帕金森矢量的方位角和大小,I为地磁变化矢量优势平面倾角。
首先对数据进行预处理,剔除有效率低于20%的数据,对超过5倍均方差的数据作删除处理;然后将每天的预处理分钟数据分4段进行离散傅里叶变换;最后对每个频点数据进行整合,单独计算各频点的转换函数。其中,频谱基于地磁分析预报软件进行计算,其他操作均用Python语言编程实现。
2 结果分析 2.1 转换函数时频分析基于加权最小二乘法对山东省地磁台阵数据进行转换函数计算。为保证结果的稳定性、减小计算误差、便于开展背景特征研究,选取2019-05~2020-05共1 a的数据参与计算。分别以Ar和Br表示转换函数A和B的实部,15个台站的计算结果如图 2所示,图中大部分台站的转换函数曲线比较光滑、计算误差较小,各频点结果的连续性较好,说明计算结果具有稳定性。
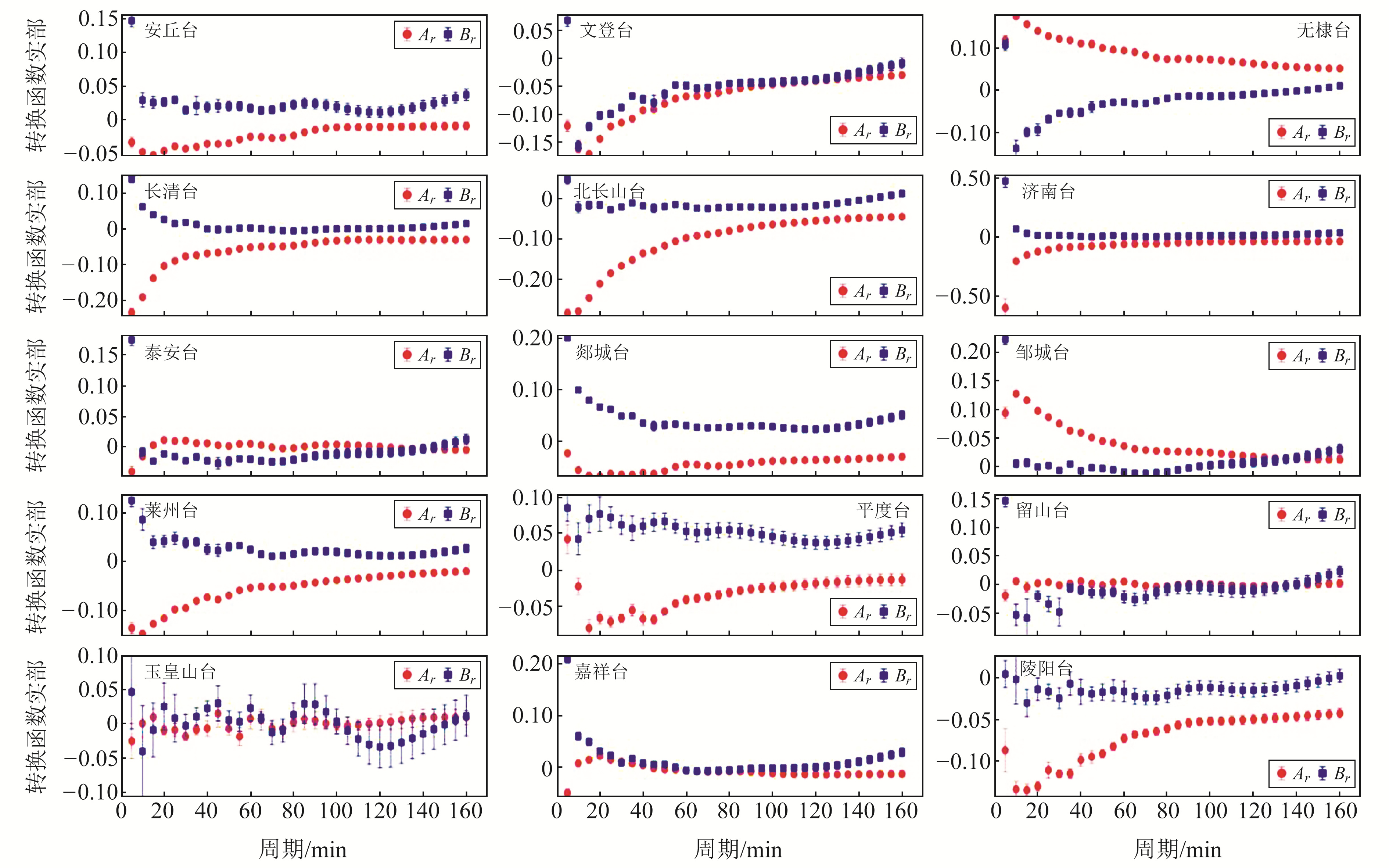
|
图 2 转换函数Ar和Br周期变化曲线 Fig. 2 The curves of transfer function Ar and Br with period |
从转换函数曲线可以看出,20 min周期内转换函数的数值波动较大,误差也相对较大,Ar和Br之间没有明显的趋势性变化,说明转换函数对于浅层电性结构的表现力较弱。原因主要有2点:一是地磁观测在浅层受到的外部干扰较多,导致高频数据计算误差较大;二是由于山东省区域地表多为第四系覆盖,没有明确的构造特征,转换函数特征不明显。沂沭断裂带附近的安丘、留山、玉皇山、陵阳4个台站的转换函数随周期呈波动性变化,没有趋势性特征。相比于鲁西地区,上述4个台站的变化更加复杂,其中玉皇山台和陵阳台相距19 km,安丘台和留山台相距23 km,2组台站转换函数的相关系数分别为-0.25和0.45,相关性较低,说明2组台站的地下电性结构和构造特征存在较大差异。沂沭断裂带是由4条分支断裂组成的深大断裂,其内部可能为深度破碎带,结构复杂。而鲁西地区的泰安、长清、济南等台站的转换函数随周期变化较为平稳,说明该地区地下电性结构随深度变化较小。
基于转换函数研究地下电性结构的长期缓慢变化,从而提取与孕震有关的磁异常信息,是地震地磁转换函数研究的主要目的。为对长期变化趋势和背景特征进行分析,本文基于逐日滑动算法对泰安台和郯城台2011~2020年共10 a的数据进行逐日滑动计算。以N为窗长(windows length, WL)计算得到第1 d的值,其后窗长不变,逐日向后滑动计算每天的转换函数。为得到最优的计算参数,分别以10 d、30 d、60 d、180 d为窗长对40 min周期的转换函数及频谱进行对比分析,计算结果如图 3、4所示。可以看出,10 d窗长的结果波动较大,难以进行长趋势分析;30 d窗长的转换函数具有一定的年变趋势,数据波动相对较小。窗长为10 d和30 d的频谱曲线中含有较多的短周期成分,说明滑动计算并没有将短周期信号滤掉。窗长为60 d和180 d的频谱曲线以年周期变化为主,短周期成分较少,60 d窗长显示出0.5 a周期变化。由于长期背景成分主要来自空间磁场变化,与地下电性结构关系不大,因此本文分别计算泰安台和郯城台Ar、Br的相关系数(表 1)。由表可知,窗长为30 d和60 d时2个台站的相关系数最高,说明此时计算结果中长周期背景最突出。王桥等[10]选取10 d窗长计算得到泰安台和郯城台长期变化趋势具有较大差异,与本文结论不一致,可能与窗长的选取有关。综合时频曲线变化特征和相关性分析结果可知,选取60 d窗长计算山东地区逐日滑动转换函数更加合适。不同窗长的时频分析均证实了转换函数的年变特征,因此如果要从转换函数时间序列中提取震磁异常信息或构造活动信息,需对长周期背景成分进行分析、提取和滤波,才能从强大的背景场中提取出微弱、可靠的异常信息。
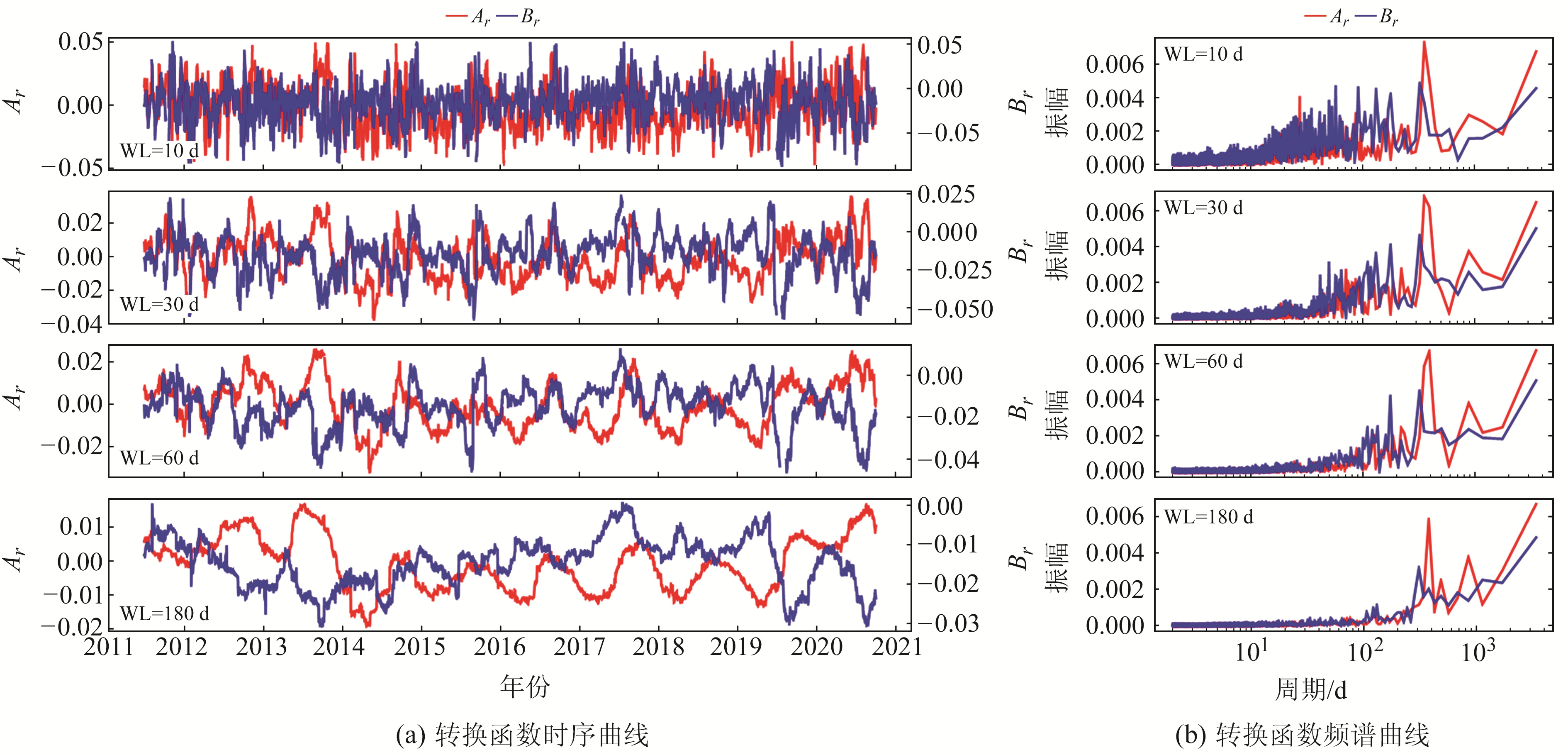
|
图 3 泰安台转换函数时间变化曲线及频谱分析 Fig. 3 The time curves of transfer function and the frequency spectrum analysis of Tai'an station |
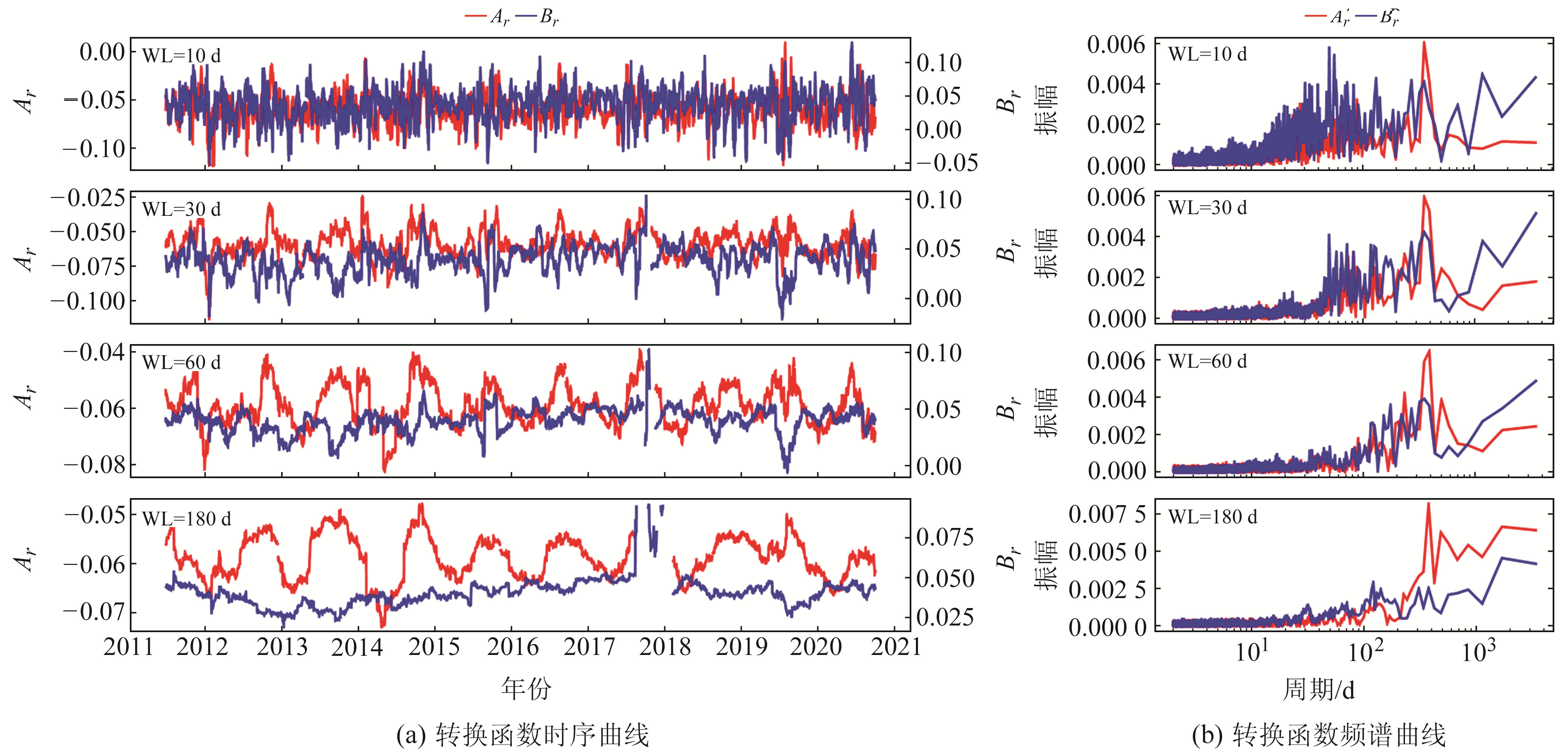
|
图 4 郯城台转换函数时间变化曲线及频谱分析 Fig. 4 The time curves of transfer function and the frequency spectrum analysis of Tancheng station |
|
|
表 1 不同窗长计算的泰安台和郯城台Ar、Br的相关系数 Tab. 1 Correlation coefficients of Ar and Br between Tai'an station and Tancheng station calculated with different window lengths |
分析60 d窗长的时序曲线发现,转换函数的峰谷值出现的时间大约为1月和7月,呈明显的季节性变化特征,Ar和Br呈反向变化,即Ar的峰值对应Br的谷值。对比Ar和Br的曲线可以看出,Ar的年变特征较Br更加明显,数据稳定性更好;Br随时间变化波动较大,年变特征被压制,数据毛刺较多。由此可知,选取Ar结果参与异常分析更加可靠。该结论对后续时序分析和震前转换函数异常信息的提取具有一定的指导意义。
2.2 感应矢量特征分析基于转换函数计算1 a尺度下(2019-05~2020-05)的感应矢量。为保证曲线的连续性,矢量方向角度范围设置为-360°~360°,15个台站的计算结果如图 5所示。各频点的感应矢量指向电流聚集方向(高导体),其大小可反映该深度下的横向不均匀程度,矢量越大说明其电性结构差异越大。不同周期的感应矢量可反映不同深度下的电性结构差异,感应矢量随周期的变化能够反映出地下电性结构的垂向变化。从各台站感应矢量曲线可以看出,矢量大小随周期变化稳定,矢量方向随周期变化波动。大部分台站矢量方位角在高频(80 min以下)部分存在波动变化,在低频部分主要呈趋势性变化,整个频段的方位角变化小于30°,说明山东省区域地下电性结构的横向相对差异随深度变化不明显,没有较大的电性反转或构造转折。各台站大部分频点矢量绝对值小于0.2,且随频率降低呈趋势性减小,说明整体电性横向不均匀性较小,横向差异随深度增加而减小,而浅层电性差异相对更加明显。

|
图 5 帕金森矢量周期变化曲线 Fig. 5 The curves of Parkinson vector with period |
为了更加直观地体现地下电性结构的变化情况,以15°为区间对矢量方向进行统计并绘制玫瑰图(图 6)。图中玫瑰花瓣的长度代表该方向区间的频点在所有频点中的占比,花瓣数则表示方向区间数量,花瓣越多说明该观测点的电性方向越分散,主花瓣越长且其他花瓣越少则说明该点的垂向电性越均匀。结合感应矢量曲线和玫瑰图综合分析可知,文登、长清、郯城、莱州、北长山、陵阳6个台站的矢量方位角最集中,其主要方向占比均超过50%,说明其地下电性结构随深度变化较小,构造指示单一且明确。其中北长山、莱州、文登3个台站沿海,其感应矢量均指向海洋,呈现出明显的海岸效应。位于沂沭断裂带东侧的郯城、安丘、平度3个台站的矢量主要指向NW向,位于断层内部的留山台矢量主要指向NEE向。上述4个台站矢量均近似垂直指向断裂带方向,说明沂沭断裂带是一个显著的电性分界面,其两侧的胶东隆起和鲁西隆起电性结构差异较大。结合矢量大小可知,浅层矢量越大,说明断层两侧浅层的电性结构差异越明显,距离深部越近电性结构差异越小。泰安台感应矢量主要指向SEE向,大小在0.05以下且变化较小,该结果与龚绍京等[11]的结论基本一致,说明该区域电性结构相对比较简单,电性横向差异较小。长清台和济南台相距38 km,二者矢量指向一致且各频段明确指向NNW向的齐广断裂,周期曲线高度相似,相关系数为0.9,说明其地下电性结构基本一致,均处于同一构造活动区。嘉祥台和邹城台相距60 km,二者相关系数为0.68,2个台站感应矢量在40~80 min周期频段内具有明显的方向转折,尤其是嘉祥台的矢量方向变化较大,高导体由SW向往NE向转换,60 min周期后又向W转换,说明该区域在整个研究频率所对应深度下的SW向为高导区。40~80 min周期对应深度下的NE向存在较大范围的高导异常体,使电流聚集方向发生反转,可能对应较大的高导构造区,但由于感应矢量较小,该高导区与邻区的电性差异并不明显。
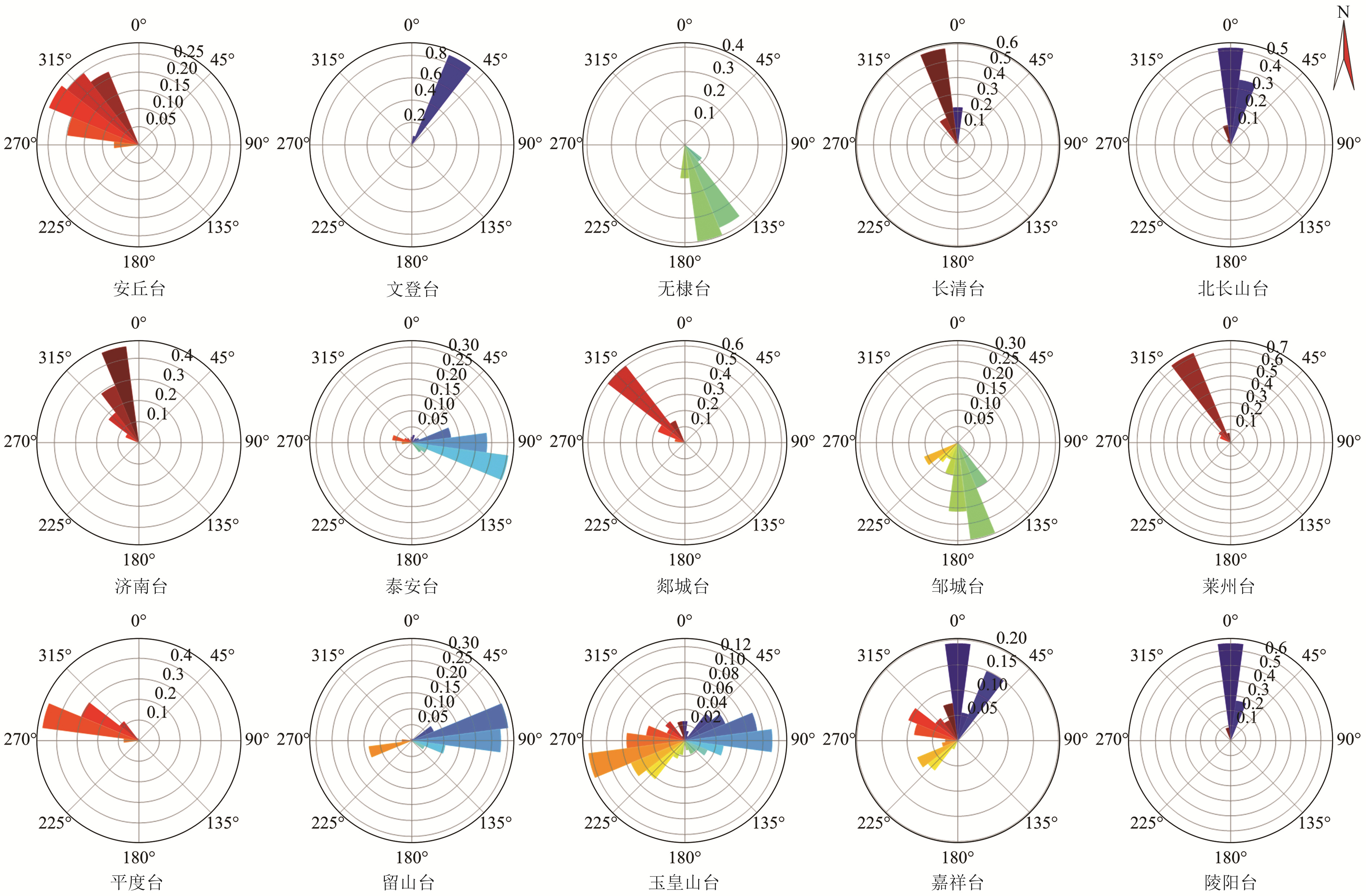
|
图 6 帕金森矢量方向统计 Fig. 6 The statistical graph of Parkinson vector direction |
1) 山东地区的地磁转换函数对浅层的表现特征不明显,在断裂带等构造复杂地区的变化较大。
2) 利用逐日滑动算法进行转换函数时序分析,并确立最优计算参数。分析显示,转换函数具有长周期变化背景,呈明显的季节性波动,周期为1 a,转换函数A的稳定性优于B,更适合进行时移分析。
3) 感应矢量结果显示,沂沭断裂带是一个显著的电性分界面,其两侧的胶东隆起和鲁西隆起具有明显的电性结构差异,鲁西隆起区内部的横向电性结构差异较小。山东省地下电性结构整体横向不均匀性未随深度发生变化,浅层不均匀性较强。处于鲁西隆起的济宁地区在40~80 min周期内电流聚集方向发生近180°转换,说明在该深度下的NE向存在较大范围的高导构造区。
本文对山东省地磁转换函数和感应矢量开展背景分析和时序特征分析,由于山东地区震例较少,因此未开展震前异常信息的提取分析。后续可结合川滇等地区的资料进行震前异常信息提取,从逐日滑动转换函数的时移变化中挖掘孕震区电性结构变化信息,加强对震前区域电性结构变化的研究,为地震危险性评价提供依据。
致谢: 本文频谱计算使用的是冯志生研究员、朱培育高工编写的软件,在此表示感谢!
| [1] |
Yanagihara K, Nagano T. Time Change of Transfer Function in the Central Japan Anomaly of Conductivity with Special Reference to Earthquake Occurrences[J]. Journal of Geomagnetism and Geoelectricity, 1976, 28(2): 157-163 DOI:10.5636/jgg.28.157
(  0) 0) |
| [2] |
陈伯舫, 冯戬云. 转换函数和磁场振幅比的水平源场效应的数值计算研究[J]. 地震学报, 1988, 10(2): 192-205 (Chen Bofang, Feng Jiyun. A Numerical Study of Some Horizontal Source Field Effects on the Transfer Functions and the Amplitude Ratios in Geomagnetic Induction Investigation[J]. Acta Seismologica Sinica, 1988, 10(2): 192-205)
(  0) 0) |
| [3] |
陈伯舫. 水平磁场台际转换函数Cu的大小: 有限差分法模型计算研究[J]. 地震地磁观测与研究, 2004, 25(1): 48-51 (Chen Bofang. On the Magnitude of the Interstation Transfer Functions Cu of the Horizontal Magnetism Field—A Study on the Numerical Modeling of Finite Difference[J]. Seismological and Geomagnetic Observation and Research, 2004, 25(1): 48-51)
(  0) 0) |
| [4] |
龚绍京, 刘双庆, 张明东. 2007年5月~2013年12月成都、西昌和重庆台地磁转换函数的时间变化[J]. 地震学报, 2015, 37(1): 144-159 (Gong Shaojing, Liu Shuangqing, Zhang Mingdong. Time Changes in the Geomagnetic Transfer Functions at Chengdu, Xichang and Chongqing Stations from May 2007 to December 2013[J]. Acta Seismologica Sinica, 2015, 37(1): 144-159)
(  0) 0) |
| [5] |
杨杰, 李琪, 袁伊人. 2013年3月3日洱源MS5.5地震前地磁转换函数异常研究[J]. 地震学报, 2021, 43(2): 215-226 (Yang Jie, Li Qi, Yuan Yiren. Geomagnetic Transform Function Anomaly before the MS5.5 Eryuan Earthquake on March 3, 2013[J]. Acta Seismologica Sinica, 2021, 43(2): 215-226)
(  0) 0) |
| [6] |
Parkinson W D. Directions of Rapid Geomagnetic Fluctuations[J]. Geophysical Journal International, 1959, 2(1): 1-14 DOI:10.1111/j.1365-246X.1959.tb05776.x
(  0) 0) |
| [7] |
Schmucker U. Anomalies of Geomagnetic Variations in the Southwestern United States[J]. Journal of Geomagnetism and Geoelectricity, 1964, 15(4): 193-221 DOI:10.5636/jgg.15.193
(  0) 0) |
| [8] |
余年, 胡祥云, 王绪本, 等. 大地电磁二维倾子和视倾子模拟及其应用研究[J]. 西南交通大学学报, 2014, 49(2): 268-275 (Yu Nian, Hu Xiangyun, Wang Xuben, et al. Two-Dimensional Magnetotelluric Tipper and Apparent Tipper: Simulation and Application[J]. Journal of Southwest Jiaotong University, 2014, 49(2): 268-275)
(  0) 0) |
| [9] |
林昌洪, 谭捍东, 佟拓. 倾子资料三维共轭梯度反演研究[J]. 地球物理学报, 2011, 54(4): 1106-1113 (Lin Changhong, Tan Handong, Tong Tuo. Three-Dimensional Conjugate Gradient Inversion of Tipper Data[J]. Chinese Journal of Geophysics, 2011, 54(4): 1106-1113)
(  0) 0) |
| [10] |
王桥, 黄清华. 华北地磁感应矢量时空特征分析[J]. 地球物理学报, 2016, 59(1): 215-228 (Wang Qiao, Huang Qinghua. The Spatio-Temporal Characteristics of Geomagnetic Induction Vectors in North China[J]. Chinese Journal of Geophysics, 2016, 59(1): 215-228)
(  0) 0) |
| [11] |
龚绍京, 刘双庆, 梁明剑. 中国大陆地磁帕金森矢量特征及其与主要构造关系[J]. 地震学报, 2017, 39(1): 47-63 (Gong Shaojing, Liu Shuangqing, Liang Mingjian. Characteristics of Geomagnetic Parkinson Vector in Chinese Mainland and Their Tectonic Implication[J]. Acta Seismologica Sinica, 2017, 39(1): 47-63)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


