钻孔应变观测是研究地壳运动的手段之一,主要分为体积式和分量式(包括RZB-2和YRY-4分量式钻孔应变)两种,观测分辨率达10-10,可以记录到各种应变潮汐信息。钻孔应变观测是通过测量钻孔孔径变化来直接或间接计算地壳应力-应变状态相对变化的,可记录到与地震的孕育及发生直接相关的应力-应变信息。目前,国内许多专家已在相关领域开展了研究工作[1-2],部分学者对客观评定钻孔应变四分量观测资料质量的方法进行了分析[3-5],为科学应用四分量钻孔应变观测资料奠定了基础。本文选取邹城地震台RZB-2分量式钻孔应变2020-01~2021-07更换探头前后的数据资料,利用相对标定、四分量自检分析、M2波潮汐因子相对中误差计算及与同台站TJ-2体应变观测资料进行相关性对比等方法,计算更换探头前后仪器的内精度、自检情况及M2波潮汐因子精度,以综合分析分量式钻孔应变观测系统的稳定性和观测数据的可靠性。
1 台站及仪器概况邹城地震台位于邹城市吉玉山东南麓,海拔138 m,地处尼山断裂与峄山断裂之间,地势北高南低,地表出露岩性为花岗岩,地下水埋深4~5 m。台站周围无大型工业厂房施工,周边有几处作坊使用地下水,对台站仪器产生一定影响。RZB-2分量式钻孔应变安装于2017-11-29,钻孔开口孔径为146 mm,终孔孔径为130 mm,孔井基岩完整,探头深度81 m,应变探头内应变传感器由上到下依次呈顺时针45°排列,NS分量方位角为NW5°,EW分量方位角为SW5°,NE分量方位角为NE40°,NW分量方位角为NW40°,于2019-06接入前兆数据库。因EW分量故障,2020-10-29更换探头并重新安装,新探头深度73 m,方位角不变,采样率均为秒采样。自运行以来,仪器观测数据固体潮清晰,有年变趋势。TJ-2体应变安装于2015-12-12,钻孔深度71 m,探头在井下68 m处,水位探头在水下8 m处,2017-02正式加入中国地震局前兆台网管理系统,观测数据质量较好,2台仪器相距5 m。
2 评价指标 2.1 相对标定自检内精度四分量应变自洽好坏关系到观测数据的可信度。仪器探头安装最重要的条件是孔井基岩要完整,当孔井基岩完整时,仪器观测系统基本符合自洽方程。而在有完整基岩的孔井中,也可能因为元件灵敏度发生变化,造成与实验室灵敏度不同,导致观测偏离自洽。邱泽华等[3]根据四分量钻孔应变观测的特点,提出四分量钻孔应变观测的实地相对标定方法,唐磊等[4-5]则在此基础上改进了相对标定自检内精度法,进一步保证客观地评价数据质量。相对标定自检内精度法的具体计算原理见文献[4]。
根据月数据,选用整点值计算得到2020-01~2021-07邹城台RZB-2分量式钻孔应变观测资料的相对标定结果及年平均相对标定结果,具体见表 1。通过对比探头更换前(2020-01~09)和更换后(2020-12~2021-07,因2020-11仪器零漂较大不参与计算)的结果发现,更换探头后钻孔应变各分量每月K值明显增大,偏差S明显减小,自检内精度指标α数值大幅度降低,表明更换探头后观测数据的内精度明显增高。
|
|
表 1 邹城台RZB-2钻孔应变2020-01~2021-07观测资料相对标定结果 Tab. 1 Relative calibration results of RZB-2 borehole strain at Zoucheng station from January 2020 to July 2021 |
钻孔施工方、仪器安装专家及台站技术人员对更换探头前观测数据内精度较低的情况共同进行了分析。首先,由于钻井工艺问题,在探头安装并灌注水泥后,泥浆无法完全固结,导致探头与围岩耦合效果不好[2, 6]。而更换探头时,泥浆已经过长时间沉淀,探头与围岩耦合效果较好,因此内精度较高。由于台站周边存在抽水干扰,需结合四分量自检和M2潮汐因子相对中误差对数据质量进行进一步分析。
2.2 数据自检分析钻孔应变各观测时刻满足双衬套模型观测方程组[7]:
| $ \left\{\begin{array}{l} S_{1}=A\left(\varepsilon_{1}+\varepsilon_{2}\right)+B\left(\varepsilon_{1}-\varepsilon_{2}\right) \cos 2(\theta-\varphi) \\ S_{2}=A\left(\varepsilon_{1}+\varepsilon_{2}\right)-B\left(\varepsilon_{1}-\varepsilon_{2}\right) \sin 2(\theta-\varphi) \\ S_{3}=A\left(\varepsilon_{1}+\varepsilon_{2}\right)-B\left(\varepsilon_{1}-\varepsilon_{2}\right) \cos 2(\theta-\varphi) \\ S_{4}=A\left(\varepsilon_{1}+\varepsilon_{2}\right)+B\left(\varepsilon_{1}-\varepsilon_{2}\right) \sin 2(\theta-\varphi) \end{array}\right. $ | (1) |
式中,Si(i=1, 2, 3, 4)为分量式钻孔应变的4个观测分量,ε1为最大主应变,ε2为最小主应变,φ为最大主应变方向,θ为第1个分量的方位角,A、B为与钻孔各层材料的弹性参数和半径相关的耦合系数。据此方程组可以得到:
| $ S_{1}+S_{3}=S_{2}+S_{4}=2 A\left(\varepsilon_{1}+\varepsilon_{2}\right) $ | (2) |
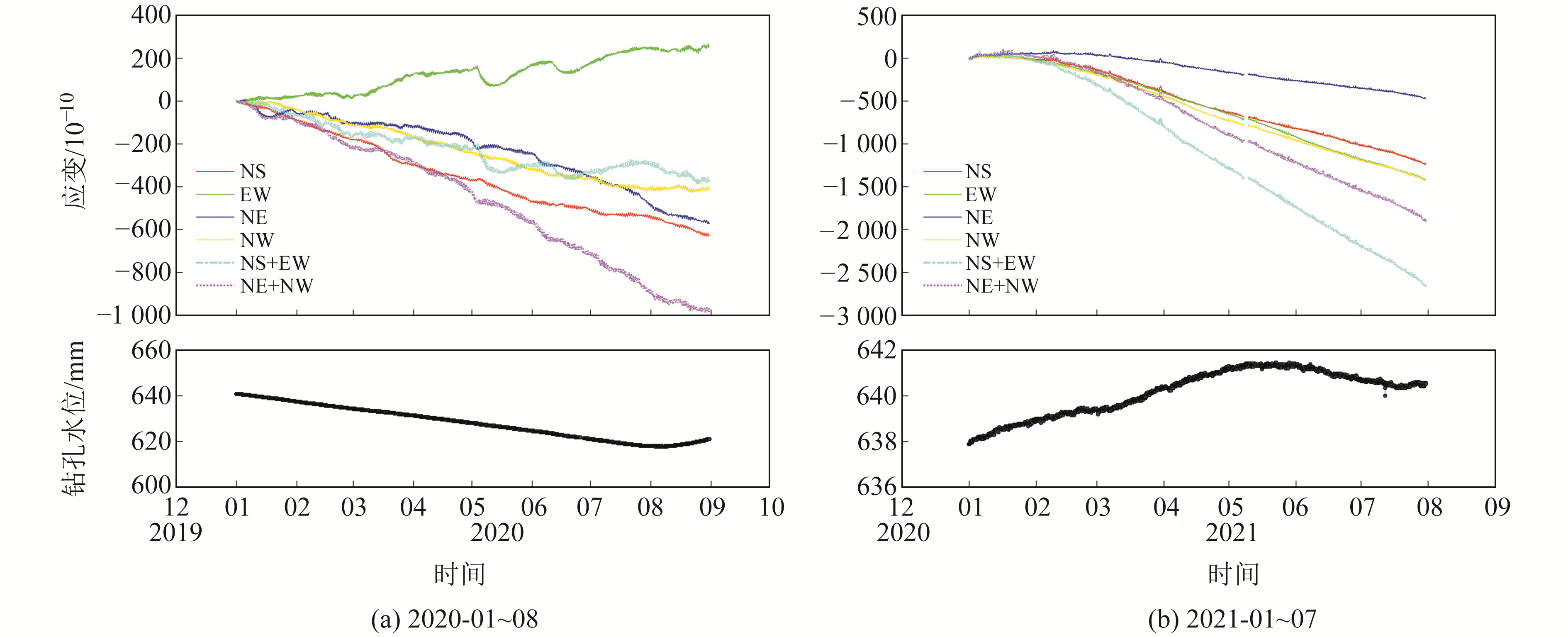
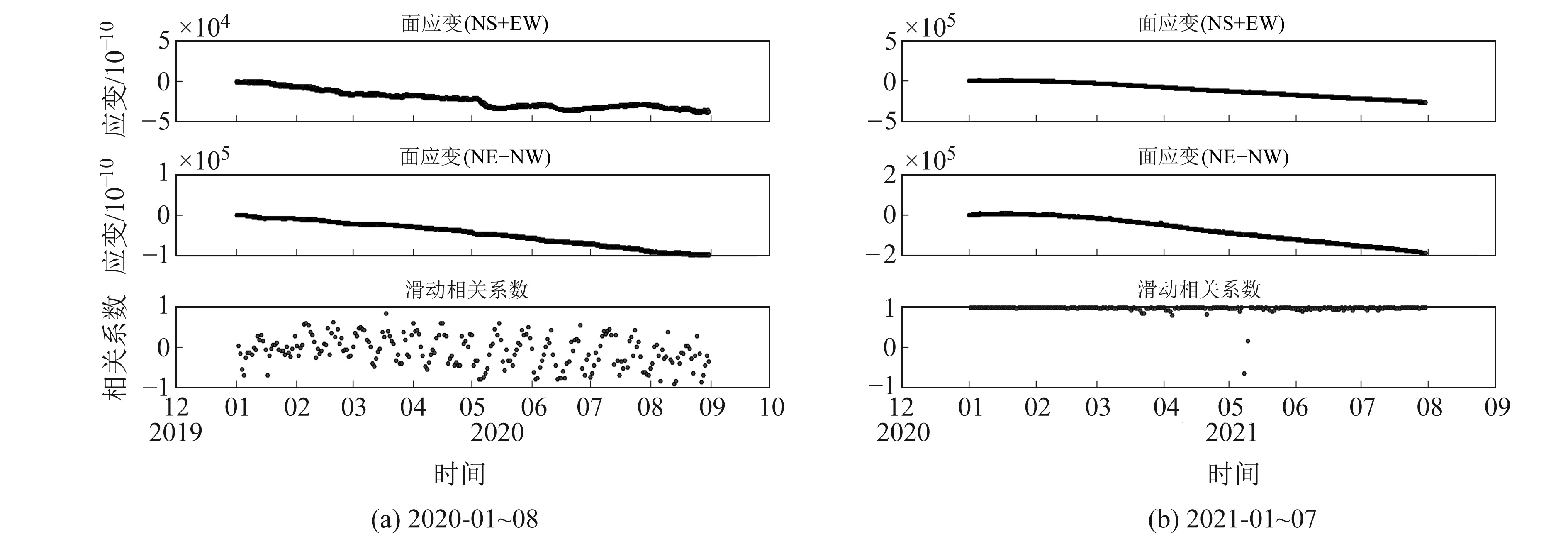
式(2)即为四分量钻孔应变观测特有的自恰方程,可以计算面应变,从而验证钻孔应变观测结果的可靠性和仪器数据的稳定性[8]。采用整点值计算2组面应变的相关系数,相关系数越接近1表明观测系统越稳定。为对比降雨的影响,采用钻孔水位数据进行对比分析(图 1),计算结果表明,RZB-2钻孔应变在更换探头前2组面应变相关性较低(图 2(a)),更换探头后2组面应变相关系数较高,接近1,具有很好的同步特征(图 2(b)),说明邹城台RZB-2分量式钻孔应变在更换探头后观测系统稳定,数据符合四分量钻孔应变观测原理。
|
图 1 邹城台RZB-2钻孔应变数据自检分析 Fig. 1 Surface strain sliding correlation analysis of RZB-2 borehole strain at Zoucheng station |
|
图 2 邹城台RZB-2钻孔应变2组面应变滑动相关性分析 Fig. 2 Observation system self-checking analysis of RZB-2 borehole strain at Zoucheng station |
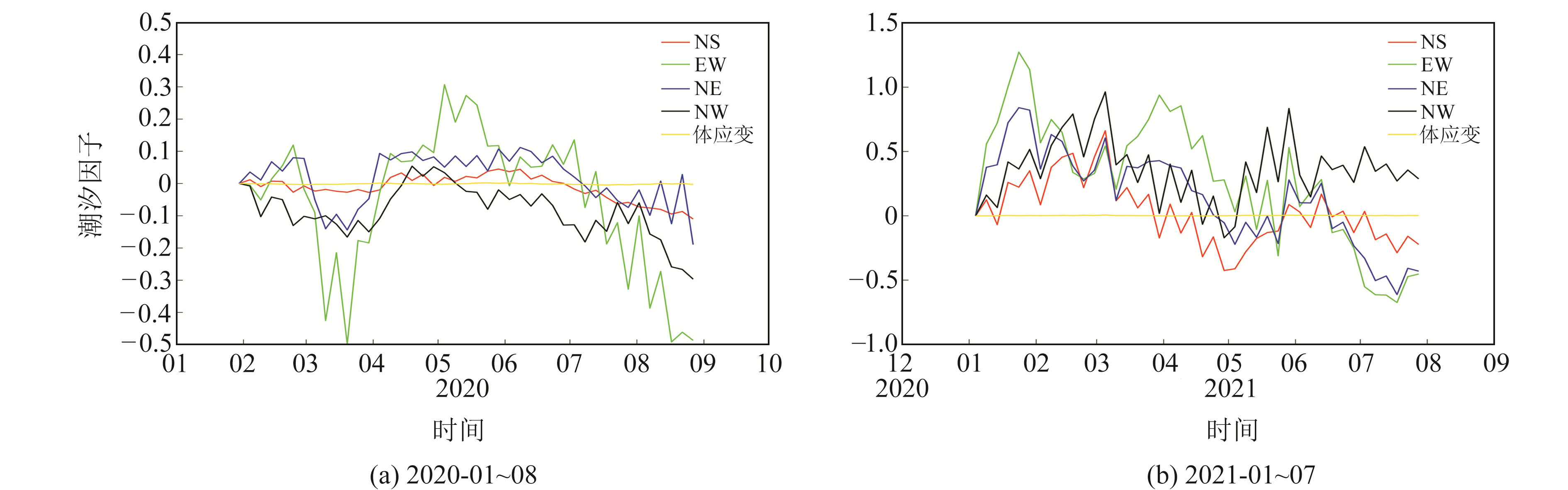
应变固体潮M2波潮汐因子的内精度是指M2波潮汐因子与M2波潮汐因子中误差的比值,即潮汐因子相对中误差[6]。可用该指标数值大小来说明观测固体潮数据的可靠性,相对中误差(内精度)数值越小,说明观测值越可靠。选取邹城台RZB-2分量式钻孔应变和TJ-2体应变2020-01~2021-07整点值观测资料,利用维尼迪柯夫调和分析方法进行逐月分析,计算2套钻孔应变M2波潮汐因子相对中误差。由图 3可以看出,邹城台RZB-2钻孔应变潮汐因子内精度在2020-01~08较差,平均为0.016 7,TJ-2体应变内精度较高,平均为0.008 2;2021-01以来,钻孔应变各分量数据内精度较差,平均为0.073 7,体应变平均内精度为0.008 4。经现场核实发现,2020-12在距离台站东侧约200 m处新增一作坊,不定时通过30 m深抽水井进行抽水,导致干扰明显,在2021-01及春季3~5月尤其严重,EW分量曲线干扰显著。根据TJ-2体应变和RZB-2钻孔应变面应变相关性分析(图 4)可知,虽然钻孔应变潮汐因子的内精度较差,但2套仪器的面应变相关性较高,说明观测系统的运行是稳定可靠的;而TJ-2体应变几乎不受抽水干扰,RZB-2钻孔应变受抽水干扰严重,可能由于TJ-2体应变与RZB-2钻孔应变观测的分辨率相差2个量级,且RZB-2钻孔应变在体应变东侧5 m处,距离抽水井更近。另外,钻井之间可能存在一定的裂隙,导致仪器对干扰的响应程度不一致。
|
图 3 邹城台RZB-2钻孔应变更换探头前后观测精度曲线 Fig. 3 Observation precision curves before and after change sensor probe of RZB-2 borehole strain at Zoucheng station |

|
图 4 邹城台RZB-2钻孔应变更换探头前后与TJ-2体应变面应变滑动相关性分析 Fig. 4 The sliding correlation analysis of surface strain before and after change sensor probe of RZB-2 borehole strain with TJ-2 volumetric strain at Zoucheng station |
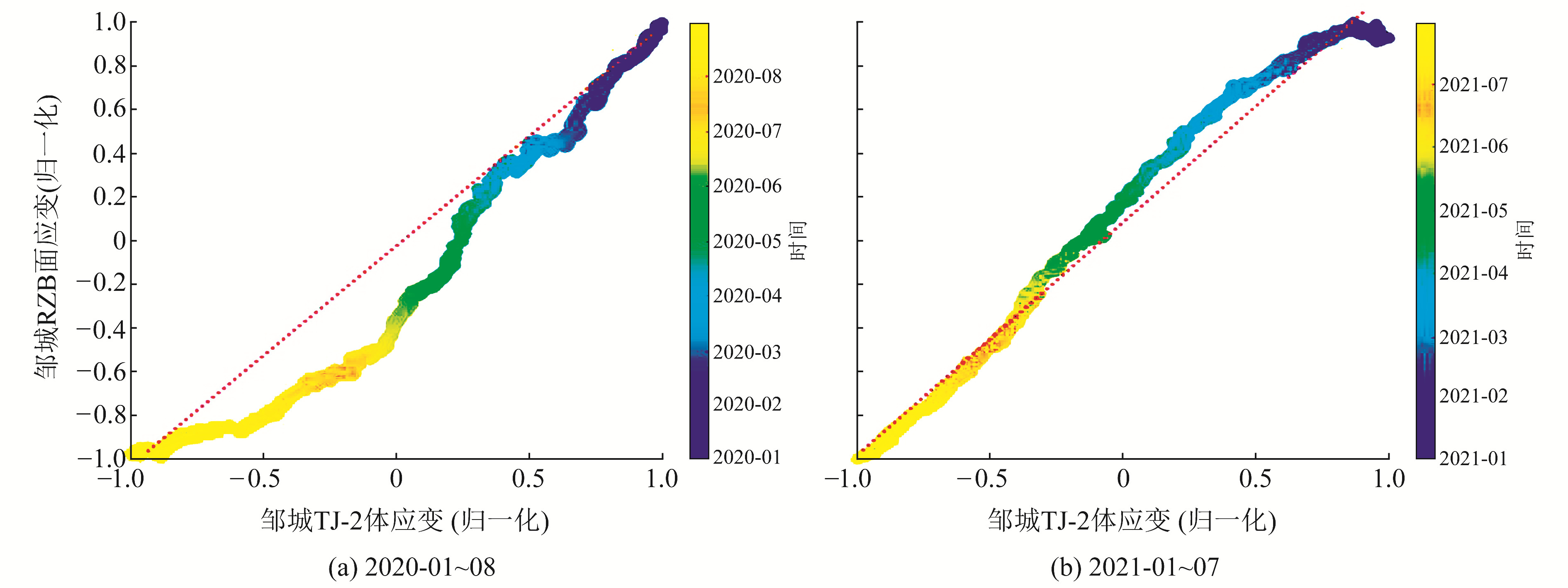
邹城台TJ-2体应变2017年正式加入中国地震前兆台网以来,观测资料精度较高。RZB-2分量式钻孔应变和TJ-2体应变的探头安装在同一深度,相距仅5 m。利用窗长为20 d的整点值进行日相关性滑动分析,为方便比较,将2套仪器数据均换算至10-8量级。更换探头前,RZB-2钻孔应变的2组面应变和TJ-2体应变的面应变日相关系数相对较低且不稳定,多集中在0.8~0.95范围内(图 4(a));更换探头后,2套仪器的面应变日相关系数接近1(图 4(b))。将2套仪器的整点值时间序列进行归一化处理,图 5中红色虚线为同步变化产生的线性相关性,可以看出,更换探头前仪器的面应变一致性较差,更换探头后面应变的一致性较好。综合分析发现,更换探头前仪器观测结果的一致性、内精度及自检情况均较差,说明RZB-2分量式钻孔应变的观测系统不稳定,观测数据可靠性较差;更换探头后仪器的观测系统正常,2套仪器的观测结果一致性好,数据可靠性高。
|
图 5 邹城台RZB-2钻孔应变更换探头前后与TJ-2体应变散点分布 Fig. 5 Scatter distribution of correlated time series of surface strain before and after change sensor probe of RZB-2 borehole strain with TJ-2 volumetric strain at Zoucheng station |
邹城台RZB-2分量式钻孔应变第1次安装后内精度较差,2组面应变不符合四分量自检方程,面应变相关性较差,主要原因是探头与围岩耦合不好;第2次更换探头后,RZB-2钻孔应变的内精度较高,2组面应变符合四分量自检方程,面应变相关系数接近1,自检曲线非常好,与体应变面应变的相关性也接近1,说明RZB-2钻孔应变的观测系统正常稳定,数据可靠。2021年台站周边新增一工厂导致抽水干扰增多,数据潮汐因子内精度较差,平均值为0.07左右,严重影响观测数据质量,建议尽快采取相关环境保护措施,减小干扰。根据分析结果可知,日常工作中仅凭潮汐因子内精度或相对标定自检内精度来评价仪器的工作情况及数据质量是不全面的,应综合考虑各种参数。
| [1] |
邱泽华. 钻孔应变观测理论和应用[M]. 北京: 地震出版社, 2017 (Qiu Zehua. Theory and Application of Borehole Strain Observation[M]. Beijing: Seismological Press, 2017)
(  0) 0) |
| [2] |
苏恺之, 李海亮, 张钧, 等. 钻孔地应变观测新进展[M]. 北京: 地震出版社, 2003 (Su Kaizhi, Li Hailiang, Zhang Jun, et al. Borehole Strain Observation New Progress[M]. Beijing: Seismological Press, 2003)
(  0) 0) |
| [3] |
邱泽华, 石耀霖, 欧阳祖熙. 四分量钻孔应变观测的实地相对标定[J]. 大地测量与地球动力学, 2005, 25(1): 118-122 (Qiu Zehua, Shi Yaolin, Ouyang Zuxi. Relative in-Situ Calibration of 4-Component Borehole Strain Observation[J]. Journal of Geodesy and Geodynamics, 2005, 25(1): 118-122)
(  0) 0) |
| [4] |
唐磊, 邱泽华, 宋茉. 钻孔四分量应变观测自检内精度分析[J]. 大地测量与地球动力学, 2010, 30((增2)): 36-39 (Tang Lei, Qiu Zehua, Song Mo. Self-Test Accuracy of 4-Component Borehole Strain Observation[J]. Journal of Geodesy and Geodynamics, 2010, 30(S2): 36-39)
(  0) 0) |
| [5] |
唐磊, 吕品姬. 钻孔四分量应变观测数据不同时间尺度的自检分析[J]. 大地测量与地球动力学, 2015, 35(3): 525-528 (Tang Lei, Lü Pinji. The Self-Test of 4-Component Borehole Strain Observation Data in Different Time Scales[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 525-528)
(  0) 0) |
| [6] |
刘春国, 李正媛, 吕品姬, 等. 数字化地震前兆台网观测数据质量评价方法[J]. 中国地震, 2017, 33(1): 112-121 (Liu Chunguo, Li Zhengyuan, Lü Pinji, et al. The Quality Evaluation Method of the Digital Observation Data from the Earthquake Precursory Observation Networks[J]. Earthquake Research in China, 2017, 33(1): 112-121)
(  0) 0) |
| [7] |
张凌空, 牛安福. 分量式钻孔应变观测耦合系数的计算[J]. 地球物理学报, 2013, 56(9): 3 029-3 037 (Zhang Lingkong, Niu Anfu. Component Borehole Strain Observations Coupling Coefficients Calculation[J]. Chinese Journal of Geophysics, 2013, 56(9): 3 029-3 037)
(  0) 0) |
| [8] |
贾媛, 甘卫军, 李杰, 等. 抽水对泰安地震台钻孔分量应变的影响及其机制[J]. 地震地质, 2019, 41(6): 1 429-1 443 (Jia Yuan, Gan Weijun, Li Jie, et al. Influence of Pumping on Four-Component Borehole Strain at Tai'an Seismic Station and Its Interference Mechanism[J]. Seismology and Geology, 2019, 41(6): 1 429-1 443)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


