2. 苏州科技大学北斗导航与环境感知研究中心,江苏省苏州市学府路99号,215009
近年来,利用由GNSS技术获取的PWV时空变化趋势来预测降雨的方法成为国内外学者关注的重点[1-3]。传统的获取PWV的方法是利用由GNSS技术得到的对流层延迟(ZTD)减去干延迟(ZHD),得到湿延迟(ZWD),再利用ZWD推算得到PWV。计算ZHD需要的参数有测站处地面大气压(Ps)、测站纬度(θ)、测站大地高(H),ZWD与PWV之间的转换系数也要用到加权平均温度(Tm)、地面气温(Ts)等参数,参数越多,计算过程越复杂,会导致数据量大、计算效率低,且易产生误差累积等问题。因此,建立ZTD与GNSS-PWV之间的直接转换模型,以计算特定时段的PWV时序信息十分必要[4-6]。
本文基于2017年东南沿海地区18个GNSS站的观测数据,采用多元函数线性回归法建立该地区GNSS-PWV与ZTD、地面气温(Ts)、地面大气压(Ps)之间的直接转换模型,并利用模型预报2018年GNSS-PWV,以各站实测PWV为参考值,验证本文模型的预报精度。
1 数据来源及其相关性分析 1.1 数据来源选取由江苏省气象局和中国地震局GNSS数据产品服务平台(http://www.cgps.ac.cn)提供的2017~2018年东南沿海地区18个GNSS站资料,主要包括PWV、ZTD、地面大气压(Ps) 和地面气温(Ts)等,其中常州、黄山、蚌埠、武夷山4个气象站用于精度检验,其余14个测站用于建模,测站空间位置信息见表 1,选取的18个GNSS站均匀分布于108°~122°E、19°~33°N区域,涵盖了东南沿海大部分地区。
|
|
表 1 GNSS测站空间位置信息 Tab. 1 Spatial location information of GNSS stations |
中国地震局GNSS数据产品服务平台采用Saastamoinen模型计算ZHD[7],其表达式为:
| $ \left\{\begin{array}{l} \mathrm{ZTD}=(2.2678 \pm 0.0024) \times \frac{P_{s}}{f(\theta, H)} \\ f(\theta, H)=1-0.00266 \times \cos 2 \theta+0.00028 H \end{array}\right. $ | (1) |
用ZTD减去ZHD获得ZWD,ZWD乘以转换系数Ⅱ便可得到GNSS-PWV:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{PWV}} = \mathit{\Pi } \times {\rm{ZWD}}}\\ {\mathit{\Pi } = \frac{{1 \times {{10}^6}}}{{{\rho _w}\left( {{k_3}/{T_m} + k_2^\prime } \right){R_v}}}}\\ {{T_m} = 70.2 + 0.72{T_s}} \end{array}} \right. $ | (2) |
式中,ρw为液态水密度,k′2、k3为大气折射常数,Rv为水汽气体常数,Tm为加权平均温度。
1.2 影响因子相关性验证皮尔森(Pearson)相关系数R可用来描述2个变量之间的线性相关程度,R的绝对值越大,表明其相关性越强,在0.8~1.0之间表示极强相关,0.6~0.8之间为强相关,0.4~0.6之间为中等程度相关,0.2~0.4之间为弱相关,0.0~0.2则无相关性[8]。
PWV与ZTD、Ts、Ps之间的相关程度如图 1所示,可以看出,ZTD与PWV的相关系数为0.98,为极强相关,表明ZTD对PWV值有极大影响;PWV与Ts的相关系数为0.78,为强相关;PWV与Ps的相关系数为-0.65,为负强相关。
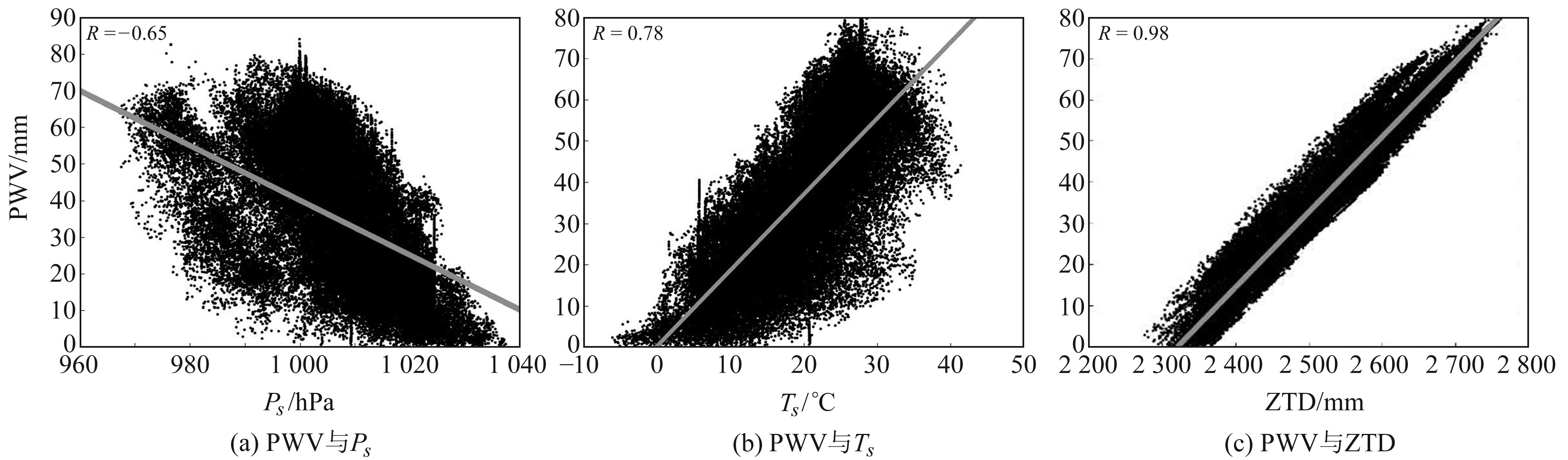
|
图 1 相关性分析 Fig. 1 Correlation analysis |
表 2为各变量间相关性统计结果,可以看出,各自变量之间也存在一定的线性关系。若建模选取的样本自变量之间本身就存在高度共线性关系,会导致线性回归模型不稳定,难以区分各自变量对模型结果的影响,因此需要对自变量进行共线性分析。
|
|
表 2 相关性分析统计 Tab. 2 Statistical table of correlation analysis |
本文利用方差膨胀因子(variance inflation factor,VIF)分析各自变量之间的共线性,其表达式为:
| $ \mathrm{VIF}_{i}=1 /\left(1-R^{2}\right) $ | (3) |
式中,R为自变量x与其余自变量作回归分析的复相关系数。通常认为,当0 < VIF < 10时,不存在多重共线性;当10≤VIF < 100时,存在较强的多重共线性;当VIF≥100时,存在严重多重共线性[9]。
由表 2可知,ZTD与Ps的相关系数积的平方
利用多元函数线性拟合方法建立PWV直接转换模型。设多元线性回归模型为:
| $ y=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{m} x_{m}+\varepsilon, \varepsilon \sim N\left(0, \sigma^{2}\right) $ | (4) |
式中,y为因变量;x1、x2、…、xm为自变量;β0为常数项;β1、…、βm为回归系数,是与自变量无关的未知参数;ε为误差项[10],是均值为0、方差σ2>0的不可观测随机变量。若有n个独立观测数据,则可列出n个关于未知参数x1、x2、…、xm的方程:
| $ \begin{gathered} y_{i}=\beta_{0}+\beta_{1} x_{i 1}+\cdots+\beta_{m} x_{i m}+\varepsilon_{i} \\ \varepsilon_{i} \sim N\left(0, \sigma^{2}\right), i=1, \cdots, n \end{gathered} $ | (5) |
则有:
| $ \begin{gathered} \boldsymbol{X}=\left[\begin{array}{cccc} 1 & x_{11} & \cdots & x_{1 m} \\ \vdots & \vdots & \cdots & \vdots \\ 1 & x_{n 1} & \cdots & x_{n m} \end{array}\right], \boldsymbol{Y}=\left[\begin{array}{c} y_{1} \\ \vdots \\ y_{n} \end{array}\right] \\ \boldsymbol{\varepsilon}=\left[\begin{array}{ccc} \varepsilon_{1} & \cdots & \varepsilon_{n} \end{array}\right]^{\mathrm{T}}, \boldsymbol{\beta}=\left[\begin{array}{llll} \beta_{0} & \beta_{1} & \cdots & \beta_{m} \end{array}\right]^{\mathrm{T}} \end{gathered} $ |
PWV转换模型可表示为:
| $ \boldsymbol{Y}=\boldsymbol{X} \boldsymbol{\beta}+\boldsymbol{\varepsilon}, \boldsymbol{\varepsilon} \sim \boldsymbol{N}\left(0, \sigma^{2} \boldsymbol{E}_{n}\right) $ | (6) |
式中,En为n阶单位矩阵。该线性回归模型可用最小二乘法原理求解,其中自变量的系数βi为最小二乘估计值。
2.1.1 多因子模型基于PWV与ZTD、Ts、Ps的线性关系,PWV与其他参数函数的关系为:
| $ \mathrm{PWV}=\beta_{0}+\beta_{1} \mathrm{ZTD}+\beta_{2} T_{s}+\beta_{3} P_{s} $ | (7) |
将2017年14个测站的PWV与ZTD、Ts、Ps代入式(7),利用最小二乘法可得到多因子PWV的直接转换模型为:
| $ \begin{aligned} \mathrm{PWV}=&-13.3805+0.1629 \mathrm{ZTD}+\\ & 0.0741 T_{s}-0.3597 P_{s} \end{aligned} $ | (8) |
将2017年14个测站的PWV与ZTD、Ts代入式(7),得到基于ZTD和Ts的双因子PWV直接转换模型:
| $ \begin{gathered} \mathrm{PWV}=-377.3157+0.1610 \mathrm{ZTD}+ \\ 0.4157 T_{s} \end{gathered} $ | (9) |
将PWV与ZTD、Ps代入式(7),得到基于ZTD和Ps的双因子PWV直接转换模型:
| $ \mathrm{PWV}=3.3354+0.1658 \mathrm{ZTD}-0.3821 P_{s} $ | (10) |
假设PWV和ZTD之间的线性关系为:
| $ \mathrm{PWV}=\beta_{0}+\beta_{1} \mathrm{ZTD} $ | (11) |
将2017年14个测站的PWV和ZTD代入式(11),得到基于ZTD的单因子PWV直接转换模型:
| $ \mathrm{PWV}=-423.9912+0.1827 \mathrm{ZTD} $ | (12) |
利用2017年14个测站的数据建立PWV模型,分别将2017~2018年的数据代入所建模型中,计算得到PWV模型预测值,并与原始数据中的PWV实测值(作为真值)进行比较,验证模型的精度。
本文将PWV实测值减去PWV模型预测值,计算得到真值与预测值之间的偏差(bias),通过统计分析平均bias与RMS值来验证PWV模型的精度。图 2为各PWV模型的bias变化趋势,可以看出,单因子PWV模型预测值与真值的bias基本在15 mm以内;双因子(无Ps)PWV模型预测值与真值的bias在10 mm以内;双因子(无Ts)PWV模型预测值与真值的bias在2 mm以内;多因子PWV模型预测值与真值的bias在1 mm以内,精度最高。2018年的数据未参与建模,PWV模型预测值及bias的变化趋势与2017年情况基本一致。

|
图 2 2017~2018年不同PWV模型预测值偏差 Fig. 2 Bias of different PWV model estimate during 2017 to 2018 |
图 3为未参与建模的常州、黄山、蚌埠和武夷山等4个测站2017~2018年各PWV模型预测值bias。由图可知,常州站和蚌埠站基于双因子(无Ps)模型和单因子模型的预测值大部分大于真值,而基于双因子(无Ts)模型的预测值大部分小于真值,基于多因子模型的预测值则均匀分布于真值两侧;黄山站和武夷山站基于双因子(无Ps)模型和单因子模型的预测值均小于真值,基于双因子(无Ts)模型的预测值均大于真值,而基于多因子模型的预测值同样均匀分布于真值两侧。从bias的变化范围来看,4个测站的PWV偏差值与参与建模的PWV偏差值分布基本一致,各类模型的bias变化范围也与图 2非常接近。
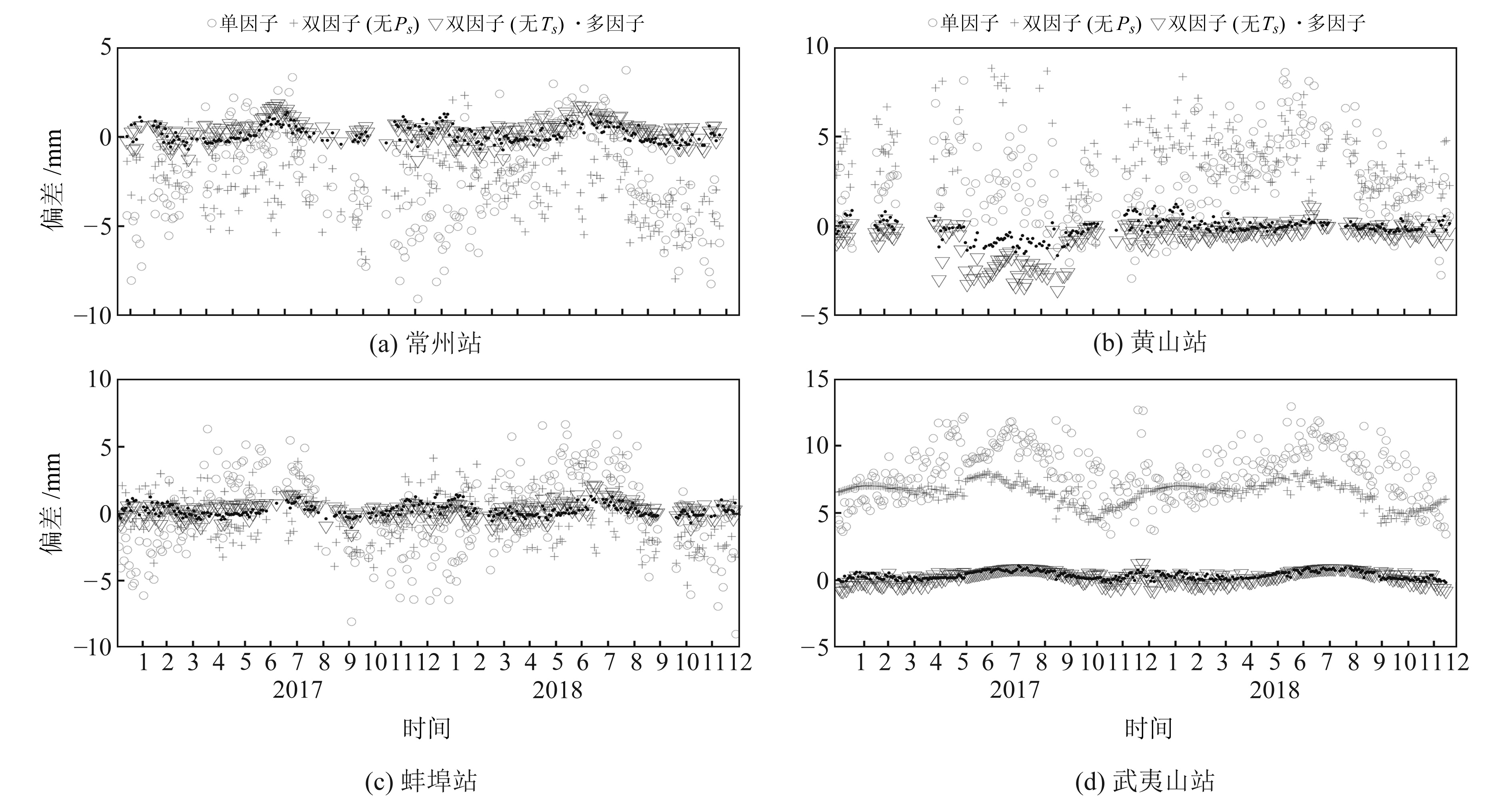
|
图 3 2017~2018年各测站PWV模型预测值偏差 Fig. 3 Bias of PWV model estimate at differentstations during 2017 to 2018 |
表 3(单位mm)为各PWV模型预测值的平均bias和RMS统计结果,可以看出,基于单因子模型的RMS值为4.66 mm,平均bias为3.73 mm;加入Ts的双因子模型RMS值降至3.94 mm,平均bias为3.13 mm,精度有小幅提升;加入Ps的双因子模型RMS值降至0.50 mm,平均bias为0.40 mm,精度大幅提高;同时加入Ps和Ts的多因子模型RMS值降至0.33 mm,平均bias降为0.24 mm,精度达到最高。
|
|
表 3 全年PWV模型精度统计 Tab. 3 Precision statistics of yearly PWV model |
由式(1)和式(2)可知,ZHD主要通过Ps计算得到,ZWD主要通过Ts及Tm计算得到,而Tm也由Ts计算得出。由于ZHD约占对流层延迟的80%~90%,加入Ps的双因子模型能提升ZHD的计算精度,而ZWD在ZTD中的占比较小,因此基于ZTD与Ps的双因子PWV模型的精度明显比基于ZTD和Ts的双因子PWV模型的精度高。
与基于ZTD、Ts和Ps的多因子PWV模型相比,基于ZTD和Ps的双因子PWV模型的精度稍低,但其RMS值有0.50 mm,可满足绝大部分GNSS气象学研究的需求,且其计算参数较少,转换效率较高。
3 结语本文利用2017~2018年东南沿海地区18个GNSS站的数据,通过分析PWV与ZTD、地面气温(Ts)、地面大气压(Ps)等参数的相关性,基于多元线性拟合方法构建东南沿海地区的多因子PWV直接转换模型,得出以下结论:
1) PWV与ZTD之间的相关性最强,相关系数达到0.98;PWV与Ps、Ts之间也具有较强的相关性,相关系数分别为-0.65和0.78。
2) 基于ZTD的单因子PWV模型平均bias为3.73 mm,RMS为4.66 mm;基于ZTD和Ts的双因子PWV模型平均bias为3.13 mm,RMS为3.94 mm;基于ZTD和Ps的双因子PWV模型平均bias为0.40 mm,RMS为0.50 mm;基于ZTD、Ts和Ps的多因子PWV模型平均bias为0.24 mm,RMS为0.33 mm。多因子PWV直接转换模型的精度最高,基于ZTD和Ps的双因子模型次之,这两种模型均可获得精度优于1 mm的PWV结果。
3) 东南沿海地区的PWV直接转换模型不仅可应对传统PWV计算过程数据量大、效率低且易产生误差累积的问题,也可在基本地面气象数据缺失时,基于ZTD直接计算特定时段的PWV时序信息,以用于GNSS气象学研究。
| [1] |
杨露华, 叶其欣, 邬锐, 等. 基于GPS/PWV资料的上海地区2004年一次夏末暴雨的水汽输送分析[J]. 气象科学, 2006, 26(5): 502-508 (Yang Luhua, Ye Qixin, Wu Rui, et al. Analyses of Water Vapor Transport in a Heavy Rain in the Late Summer of 2004 in Shanghai Based on GPS/PWV Data[J]. Scientia Meteorologica Sinica, 2006, 26(5): 502-508)
(  0) 0) |
| [2] |
Zhao Q Z, Yao Y B, Yao W Q. GPS-Based PWV for Precipitation Forecasting and Its Application to a Typhoon Event[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2018, 167: 124-133 DOI:10.1016/j.jastp.2017.11.013
(  0) 0) |
| [3] |
易正晖, 王帅民, 王勇, 等. GNSS对流层延迟推算可降水量的季节转换模型研究[J]. 大地测量与地球动力学, 2017, 37(8): 830-834 (Yi Zhenghui, Wang Shuaimin, Wang Yong, et al. Research on Seasonal Transition Model of GNSS Zenith Tropospheric Delay Calculating Precipitable Water Vapor[J]. Journal of Geodesy and Geodynamics, 2017, 37(8): 830-834)
(  0) 0) |
| [4] |
于胜杰, 柳林涛. 无地面温压数据的可降水量研究[J]. 大地测量与地球动力学, 2008, 28(5): 34-38 (Yu Shengjie, Liu Lintao. Study on Precipitable Water Vapor without Meteorological Data[J]. Journal of Geodesy and Geodynamics, 2008, 28(5): 34-38)
(  0) 0) |
| [5] |
李黎, 宋越, 易金花, 等. 对流层延迟与可降水量直接转换模型研究[J]. 大地测量与地球动力学, 2019, 39(5): 492-495 (Li Li, Song Yue, Yi Jinhua, et al. Study on the Direct Conversion Model between Tropospheric Delay and Precipitable Water Vapor[J]. Journal of Geodesy and Geodynamics, 2019, 39(5): 492-495)
(  0) 0) |
| [6] |
范頔, 李黎, 刘彦, 等. 长三角地区GNSS可降水量直接转换模型研究[J]. 大地测量与地球动力学, 2021, 41(6): 628-632 (Fan Di, Li Li, Liu Yan, et al. Research on Direct Conversion Model of GNSS Precipitable Water Vapor in Yangtze River Delta Region[J]. Journal of Geodesy and Geodynamics, 2021, 41(6): 628-632)
(  0) 0) |
| [7] |
李国平. 地基GPS遥感大气可降水量及其在气象中的应用研究[D]. 成都: 西南交通大学, 2007 (Li Guoping. On the Remote Sensing of Precipitable Water Vapor Using Ground-Based GPS Technique and Applications in Meteorology[D]. Chengdu: Southwest Jiaotong University, 2007)
(  0) 0) |
| [8] |
杜爱军, 张强, 杨世琦, 等. 北斗CORS探测的大气可降水量与重庆降雨的关系[J]. 大地测量与地球动力学, 2020, 40(2): 134-139 (Du Aijun, Zhang Qiang, Yang Shiqi, et al. Relations between Precipitable Water Vapor Measured by Beidou CORS and Chongqing Precipitation Processes[J]. Journal of Geodesy and Geodynamics, 2020, 40(2): 134-139)
(  0) 0) |
| [9] |
魏红燕. 回归分析中多重共线性的诊断与处理[J]. 周口师范学院学报, 2019, 36(2): 11-15 (Wei Hongyan. Diagnosis and Treatment of Multicollinearity in Regression Analysis[J]. Journal of Zhoukou Normal University, 2019, 36(2): 11-15)
(  0) 0) |
| [10] |
冷建飞, 高旭, 朱嘉平. 多元线性回归统计预测模型的应用[J]. 统计与决策, 2016(7): 82-85 (Leng Jianfei, Gao Xu, Zhu Jiaping. Application of Multivariate Linear Regression Statistical Prediction Model[J]. Statistics and Decision, 2016(7): 82-85)
(  0) 0) |
2. Research Center of Beidou Navigation and Environmental Remote Sensing, Suzhou University of Science and Technology, 99 Xuefu Road, Suzhou 215009, China
 2022, Vol. 42
2022, Vol. 42


