2. 中国三峡建工(集团)有限公司,成都市府城大道东段288号,610023
大气可降水量PWV作为数值天气预报的初始值,可提高预报结果的精度[1-2]。PWV的估算方法大致分为3种:第1种是利用无线探空产品、无线掩星产品、水汽辐射计产品及数值天气预报产品,采用数值积分的方法计算得到;第2种是基于GNSS精密单点定位、气象遥感卫星等技术获取;第3种是构建精确的PWV模型实时估算得到。通过第1种和第2种方法得到的PWV值可作为真值检验第3种方法[3-9],但由于前2种方法存在一定的局限性,建立高精度的PWV模型是进行水汽监测的重要环节。目前的PWV模型均以高精度、长序列的PWV产品作为背景值,利用数学函数拟合出PWV与地面大气元素之间的函数关系,缺少实际的物理意义。因此,本文基于理想气体状态方程和静水力平衡条件,提出一种顾及水汽衰减因子的PWV模型,并分别利用探空产品和GNSS-PPP估算的PWV作为真值,验证新模型的可行性。
1 PWV建模 1.1 利用地面水汽压与PWV相关性构建的大气可降水量估算模型大气可降水量与地面水汽压之间关系密切,常利用区域PWV和地面水汽压进行建模,构建基于地面水汽压的大气可降水量回归估算模型。部分研究采用一次、二次多项式模型和幂函数模型构建区域GPS大气可降水量模型,且验证精度高于Cole模型等[5, 10]。
一次多项式模型为:
| $ \mathrm{PWV}=a_{0}+a_{1} e $ | (1) |
二次多项式模型为:
| $ \mathrm{PWV}=a_{0}+a_{1} e+a_{2} e^{2} $ | (2) |
幂函数模型为:
| $ \mathrm{PWV}=c e^{\gamma} $ | (3) |
式中,PWV为模型计算的大气可降水量,e为地表水汽压,ai(i=0, 1, 2)、c、γ均为模型系数。
1.2 基于水汽物理特性构建新的PWV模型大气可降水量是指从地表至对流层顶部单位截面积空气柱中包含的总水汽含量,利用积分的形式可表示为[11-13]:
| $ \mathrm{PWV}=\frac{1}{\rho_{v}} \int_{P_{s}\left(h_{s}\right)}^{P_{s}\left(h_{\infty}\right)} \frac{q}{g} \mathrm{~d} P=\frac{1}{\rho_{v} R_{w}} \int_{h_{s}}^{\infty} \frac{e}{T} \mathrm{~d} h $ | (4) |
式中,ρv为液态水密度,Ps为地表处大气压强,h为海平面高程,q为比湿,g为重力加速度,Rw为湿大气常数。
根据比湿和大气压强在垂直分布上的函数关系及比湿表示的大气压强与大气水汽压的函数关系可以得到[14-16]:
| $ \frac{e}{e_{s}}=\left(\frac{P}{P_{s}}\right)^{\lambda+1} $ | (5) |
式中,e为水汽压,es为地表处的水汽压,P为大气压强,Ps为地表处大气压强,λ为水汽衰减因子。大气压强和大气温度在垂直分布上的函数关系可表示为:
| $ \frac{P}{P_{s}}=\left(\frac{T}{T_{s}}\right)^{\frac{-g_{s}}{\beta R_{d}}} $ | (6) |
式中,T为大气温度,Ts为地表处大气温度,Rd为干大气常数,β为温度递减率。
联合式(5)和式(6)可以得到:
| $ \frac{e}{T}=\frac{e_{s}}{T_{s}}\left(\frac{T}{T_{s}}\right)^{\frac{-(\lambda+1) g_{s}}{\beta R_{d}}-1} $ | (7) |
将式(7)代入式(4)可以得到:
| $ \mathrm{PWV}=\frac{R_{d} e_{s}}{\rho_{v} R_{w}(\lambda+1) g_{s}} $ | (8) |
根据式(8)可知,若已知水汽衰减因子λ,则只需输入地表大气水汽压即可估算出大气可降水量PWV。
2 水汽衰减因子获取方法 2.1 通过当日水汽压与气压垂直剖面拟合基于式(5)水汽压与气压的指数关系,可使用最小二乘拟合得到当日的水汽衰减因子λ(图 1)。该方法需要当日水汽压和气压的垂直剖面数据,虽然难以实时获得,但计算结果精度较高。
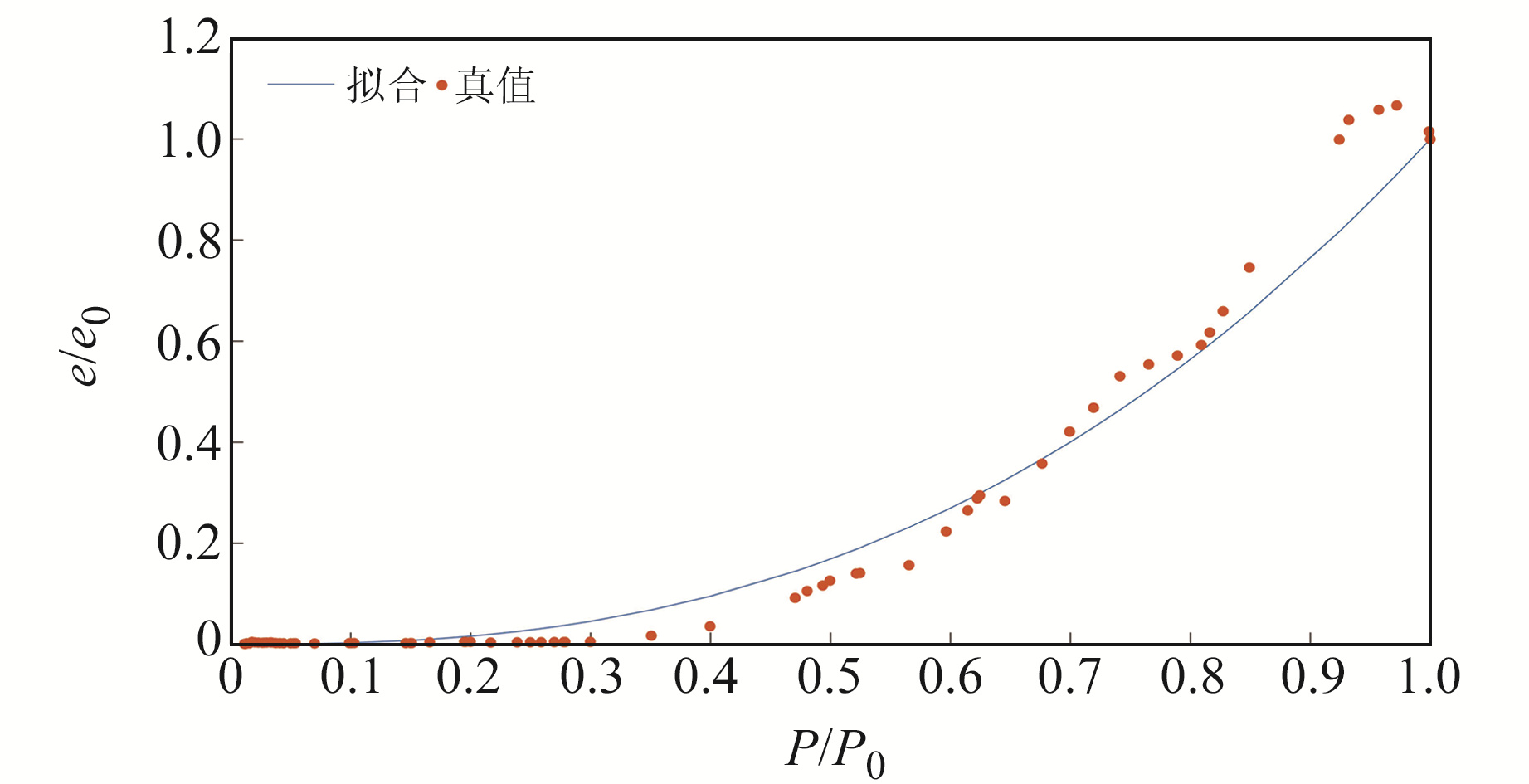
|
图 1 最小二乘拟合λ Fig. 1 Least squares fitting λ |
为进一步探究水汽衰减因子λ的时空特性,选取2015~2018年中国区域探空数据,绘制不同纬度的λ时间序列(图 2)。
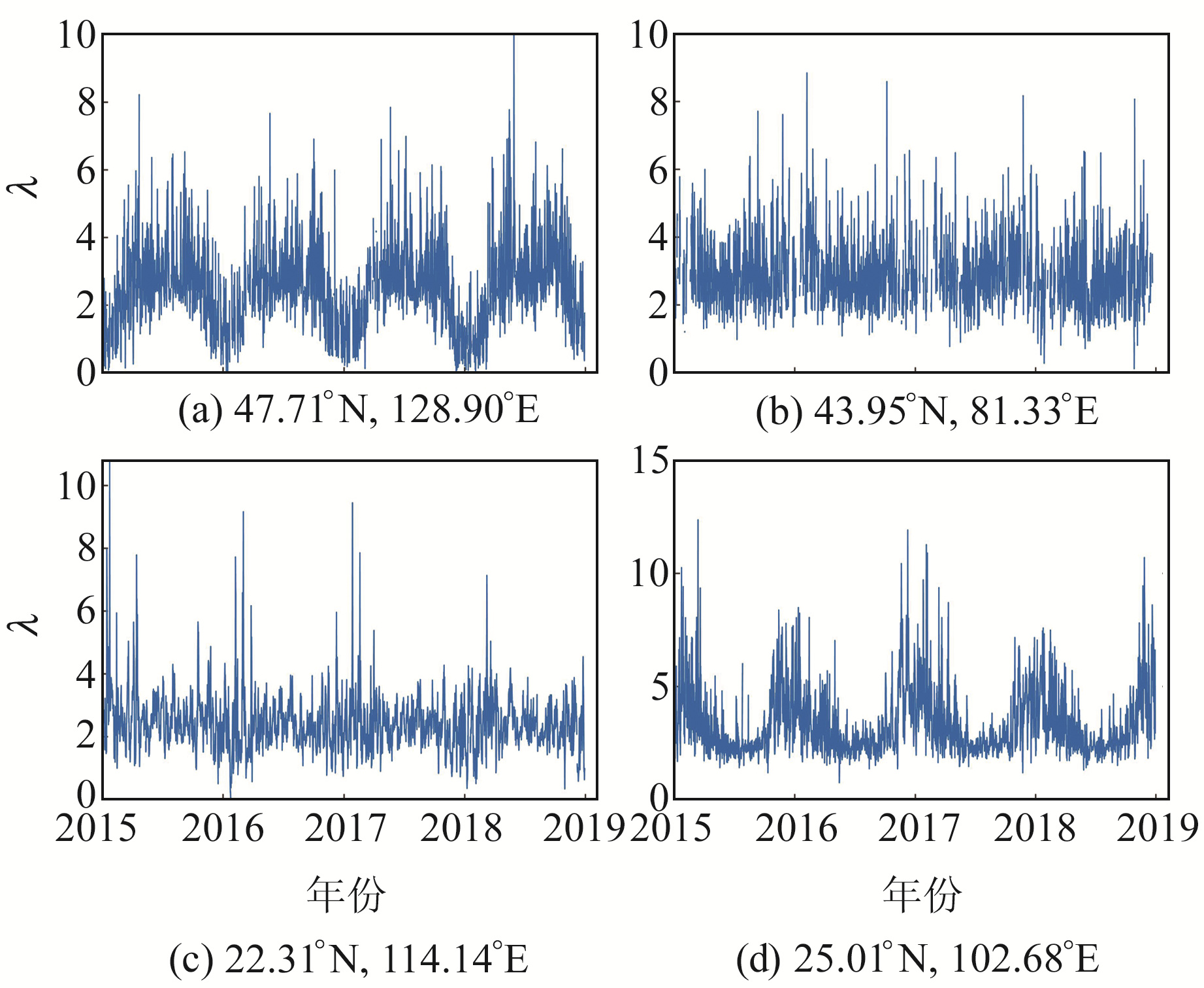
|
图 2 2015~2018年不同纬度的λ时间序列 Fig. 2 λ time series at different latitudes from 2015 to 2018 |
水汽衰减因子λ在一定程度上可反映该地区水汽压在垂直方向上的变化,λ增大表明水汽压在垂直方向上快速衰减,此时水汽压主要集中在地表附近;λ减小则表明水汽压在垂直方向上衰减缓慢,其垂直分布较为均匀。
由图 2(a)可见,水汽衰减因子λ在高纬度地区表现出春季逐渐增大、夏季保持高值振荡、秋冬季逐渐减小的明显年周期变化趋势。由图 2(c)可见,低纬度地区的λ全年都在均值上下振荡,周期性变化并不显著。同纬度的内陆和沿海地区的λ变化也不尽相同,如图 2(b)的高纬度地区,其λ并没有出现季节性波动,而图 2(d)低纬度地区的λ仍表现出明显的季节性波动。由此可知,λ受地理位置和季节性气候的影响,时空变化情况复杂,难以用统一函数表示,可通过构建格网模型来表达。
2.2 基于GPT2w的格网数据内插GPT2w是目前精度较高的经验对流层模型,以1°×1°和5°×5°两种分辨率格网形式存储气压、水汽压、温度、水汽衰减因子等多种气象元素模型系数,具体公式为:
| $ \begin{gathered} r(t)=A_{0}+ \\ A_{1} \cos \left(\frac{\text { doy }}{365.25} 2 \pi\right)+A_{2} \sin \left(\frac{\text { doy }}{365.25} 2 \pi\right)+ \\ A_{3} \cos \left(\frac{\text { doy }}{365.25} 4 \pi\right)+A_{4} \sin \left(\frac{\text { doy }}{365.25} 4 \pi\right) \end{gathered} $ | (9) |
式中,r为气象元素,A0为均值,A1、A2为年周期振幅,A3、A4为半年周期振幅。
图 3为GPT2w模型1°×1°和5°×5°两种格网采用双线性内插得到的水汽衰减因子λ与真值的比较。由图可见,两种格网表现相当,但仅能表示真实λ的变化趋势,无法准确描述其波动情况。

|
图 3 GPT2W模型两种格网得到的λ与真值比较 Fig. 3 Comparison of the λ obtained by the two grids of the GPT2W model with the true value |
选取中国区域85个探空测站及7个IGS测站数据作为真值,检验传统基于地表水汽压的大气可降水量估算模型和本文构建的顾及水汽衰减因子的大气可降水量估算模型的精度。
3.2 与探空产品的比较基于地表水汽压拟合的大气可降水量估算模型利用了地表水汽压与大气可降水量之间的相关关系,因此首先分析两者之间的相关性:
| $ \rho(e, \mathrm{PWV})=\frac{\operatorname{cov}(e, \mathrm{PWV})}{\sigma_{e} \sigma_{\mathrm{PWV}}} $ | (10) |
式中,e、PWV分别为地表水汽压和大气可降水量,cov为协方差,σ为标准差。选取85个探空站2015~2017年3 a的地表水汽压和大气可降水量序列进行分析,结果如图 4所示。
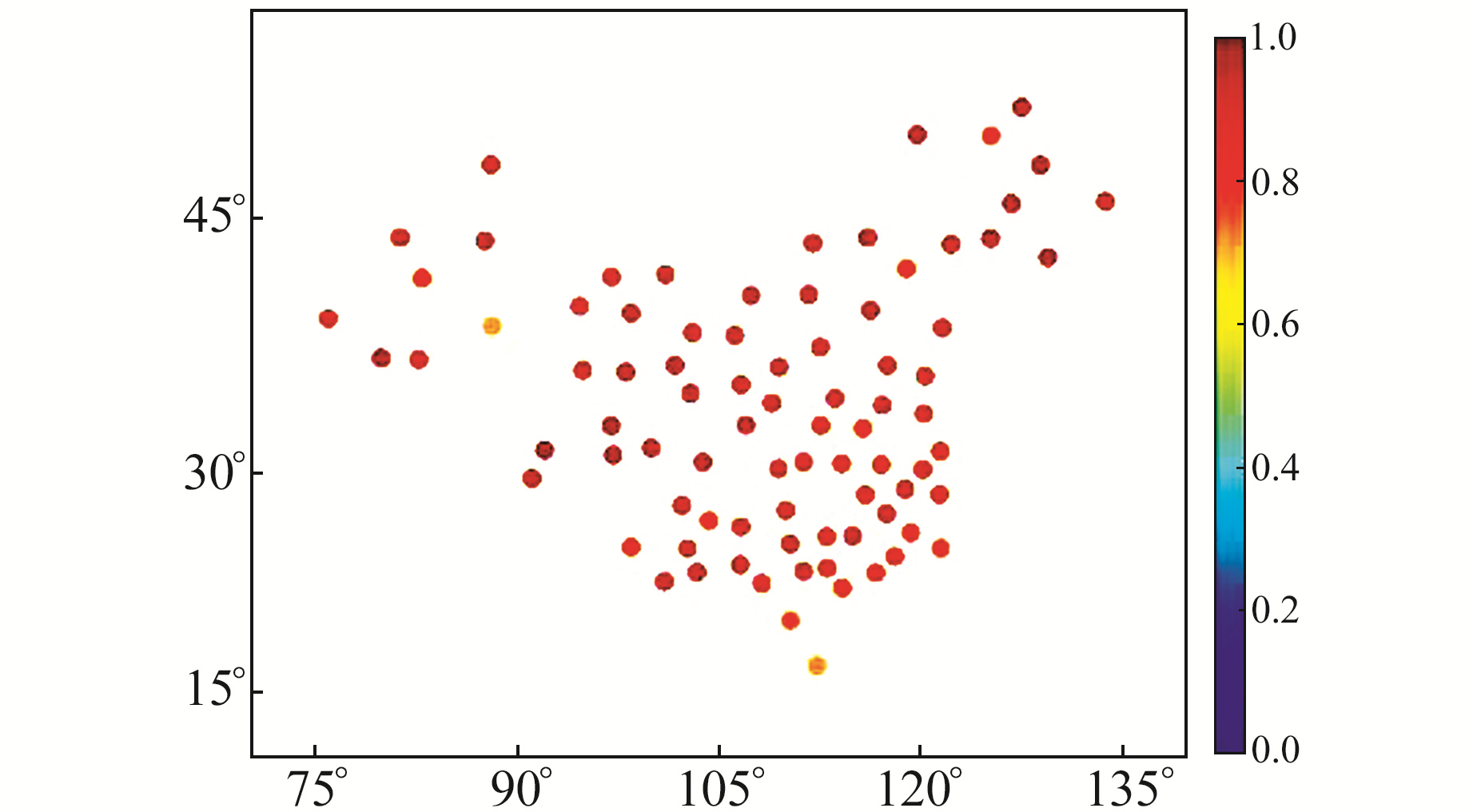
|
图 4 2015~2017年中国区域探空站地表水汽压与PWV的相关性 Fig. 4 The correlation between surface water vapor pressure and PWV of radiosonde stations in China from 2015 to 2017 |
统计结果显示,两者的平均相关性为0.91,最大为0.97,最小为0.72。由统计结果可知,水汽压与大气可降水量之间有较强的正相关性,大气可降水量会随着水汽压的增大而增大。
鉴于水汽压与大气可降水量的强相关性,选择一次多项式模型与本文构建的顾及水汽衰减因子的大气可降水量模型进行比较。设计以下几组实验:
1) 利用2015~2017年的水汽压和大气可降水量序列进行一次多项式拟合,得到拟合系数,并计算得到2018年的PWV_LP。
2) 利用GPT2w模型1°×1°和5°×5°两种格网内插得到的水汽衰减因子,结合2018年水汽压数据,使用新模型计算得到PWV_GRID1和PWV_GRID5。
3) 以2018年当日水汽压与气压的指数关系,拟合得到水汽衰减因子,使用新模型计算得到PWV_E/P。
将上述实验计算得到的大气可降水量与探空数据大气可降水量进行比较,计算其RMSE和bias,结果如图 5和表 1(单位mm)所示。

|
图 5 种模型得到的PWV与探空PWV的RMSE和bias Fig. 5 RMSE and bias of PWV obtained by 4 models and sounding PWV |
|
|
表 1 4种模型与探空数据比较的统计 Tab. 1 Statistical results of the comparison between the four models and radiosonde data |
由实验结果可知,各模型在我国西部和北部地区的RMSE和bias均较小,在东南部地区普遍较大,尤其是在东部沿海地区。主要原因可能是东南部气候湿润,水汽波动的随机性更明显,经验模型难以准确描述大气可降水量的变化。比较PWV_LP和PWV_GRID1及PWV_GRID5可知,一次多项式拟合模型的精度略高于另外2个模型,主要原因是水汽压与大气可降水量具有强相关性,且PWV_GRID1和PWV_GRID5中的水汽衰减因子来自全球数据计算的格网,并不是局部区域内的最优解。由图 3可见,格网内插的水汽衰减因子仅能表示真实水汽衰减因子的变化趋势,无法反映其真实波动情况,因此新模型退化成为近似的线性模型。4种模型中,PWV_E/P模型利用当日水汽压和气压拟合出的水汽衰减因子精度最高,更能表现出水汽的波动,也验证了本文构建模型的可行性。
3.3 与GNSS-PPP估算的PWV比较选取中国区域7个IGS测站(BJFS、CHAN、LHAZ、SHAO、TNML、URUM和JFNG)数据,以GNSS-PPP处理得到的PWV作为真值,比较各模型计算的PWV精度,结果如表 2(单位mm)和图 6所示。
|
|
表 2 4种模型与IGS测站比较的统计 Tab. 2 Statistical results of the comparison between the four models and IGS stations |
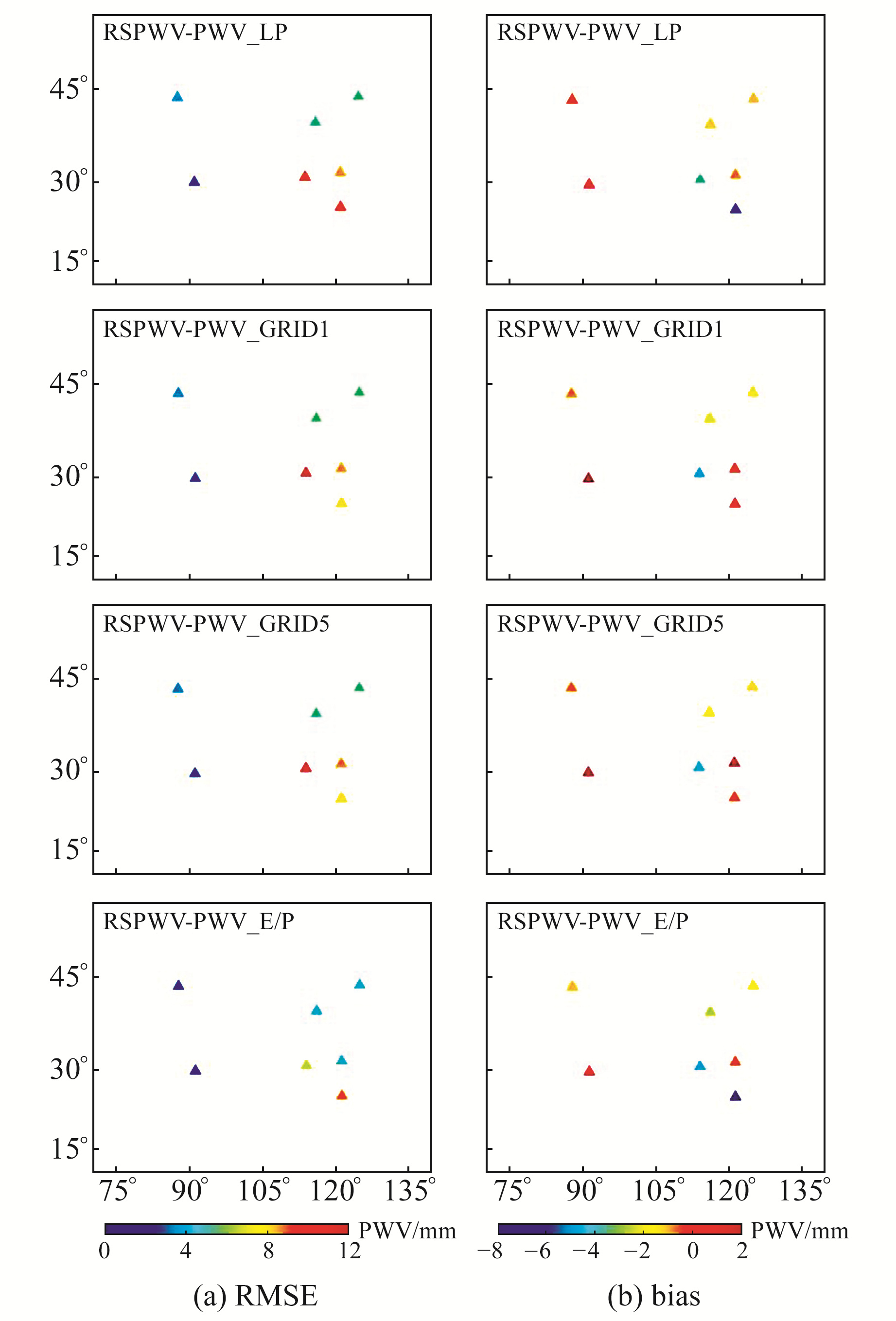
|
图 6 4种模型计算得到的PWV与GNSS-PWV的RMSE和bias Fig. 6 RMSE and bias of PWV obtained by 4 models and GNSS-PWV |
由实验结果可知,4种模型计算的PWV与IGS测站提取的PWV在我国东南部地区均表现出较大差异,且此差异与4种模型和探空数据PWV比较得到的差异趋势较为一致。但从总体上看,模型计算的PWV与IGS测站提取的PWV的差异大于与探空测站PWV的差异,主要原因是IGS测站提取的PWV存在一定误差。一次多项式模型与GPT2w格网内插的水汽衰减因子模型精度相当,利用当日水汽压和气压序列拟合的水汽衰减因子模型具有最高的精度,证实本文顾及水汽衰减因子的大气可降水量估算模型在已知高精度水汽衰减因子的情况下能达到较高的精度。
4 结语本文构建了一种顾及水汽衰减因子的大气可降水量估算模型,并通过中国区域85个探空站和7个IGS测站2018年的数据检验其与传统模型的精度。结果表明,本文构建的估算模型在已知高精度水汽因子的情况下,精度约为2 mm。另外,也可使用GPT2w格网内插得到水汽衰减因子,但其结果精度低于本文构建的估算模型。与一次多项式模型相比,格网内插法无需基于区域长时间序列的水汽压和PWV进行拟合,可获取任意位置的水汽衰减因子,有更好的适用性。与地基GNSS提取PWV方法相比,格网内插法仅需水汽衰减因子和地表水汽压,计算方便,可作为地表水汽监测的重要补充,但受限于格网精度,计算结果无法达到较高的精度。
| [1] |
翟树峰, 吕志平, 李林阳, 等. 基于GPT2w模型化加权平均温度反演可降水量[J]. 大地测量与地球动力学, 2019, 39(7): 733-737 (Zhai Shufeng, Lü Zhiping, Li Linyang, et al. Precipitable Water Vapor Retrieval Based on Weighted Mean Temperature from GPT2w[J]. Journal of Geodesy and Geodynamics, 2019, 39(7): 733-737)
(  0) 0) |
| [2] |
Xia P F, Ye S R, Jiang P, et al. Assessing Water Vapor Tomography in Hong Kong with Improved Vertical and Horizontal Constraints[J]. Annales Geophysicae, 2018, 36(4): 969-978 DOI:10.5194/angeo-36-969-2018
(  0) 0) |
| [3] |
Smith W L. Note on the Relationship between Total Precipitable Water and Surface Dew Point[J]. Journal of Applied Meteorology, 1966, 5(5): 726-727 DOI:10.1175/1520-0450(1966)005<0726:NOTRBT>2.0.CO;2
(  0) 0) |
| [4] |
Cole R J. Direct Solar Radiation Data as Input into Mathematical Models Describing the Thermal Performance of Buildings—Ⅱ. Development of Relationships[J]. Building and Environment, 1976, 11(3): 181-186 DOI:10.1016/0360-1323(76)90004-4
(  0) 0) |
| [5] |
李超, 魏合理, 刘厚通, 等. 整层大气水汽含量与地面水汽压相关性的统计研究[J]. 武汉大学学报: 信息科学版, 2008, 33(11): 1 170-1 173 (Li Chao, Wei Heli, Liu Houtong, et al. Statistics of Correlation of Integrated Water Vapor and Surface Vapor Pressure[J]. Geomatics and Information Science of Wuhan University, 2008, 33(11): 1 170-1 173)
(  0) 0) |
| [6] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15 787-15 801 DOI:10.1029/92JD01517
(  0) 0) |
| [7] |
李颖, 张俊东, 罗鹏. 大气可降水量估算模型研究[J]. 气象与环境科学, 2013, 36(2): 21-25 (Li Ying, Zhang Jundong, Luo Peng. Research on Estimation Model of Atmospheric Precipitable Water Vapor[J]. Meteorological and Environmental Sciences, 2013, 36(2): 21-25)
(  0) 0) |
| [8] |
杨景梅, 邱金桓. 我国可降水量同地面水汽压关系的经验表达式[J]. 大气科学, 1996, 20(5): 620-626 (Yang Jingmei, Qiu Jinhuan. The Empirical Expressions of the Relation between Precipitable Water and Ground Water Vapor Pressure for Some Areas in China[J]. Scientia Atmospherica Sinica, 1996, 20(5): 620-626 DOI:10.3878/j.issn.1006-9895.1996.05.14)
(  0) 0) |
| [9] |
Elgered G, Davis J L, Herring T A, et al. Geodesy by Radio Interferometry: Water Vapor Radiometry for Estimation of the Wet Delay[J]. Journal of Geophysical Research: Solid Earth, 1991, 96(B4): 6 541-6 555 DOI:10.1029/90JB00834
(  0) 0) |
| [10] |
张学文. 可降水量与地面水汽压力的关系[J]. 气象, 2004, 30(2): 9-11 (Zhang Xuewen. A Relationship between Precipitable Water and Surface Vapor Pressure[J]. Meteorological Monthly, 2004, 30(2): 9-11)
(  0) 0) |
| [11] |
Liu Z Z, Wong M S, Nichol J, et al. A Multi-Sensor Study of Water Vapour from Radiosonde, MODIS and AERONET: A Case Study of Hong Kong[J]. International Journal of Climatology, 2013, 33(1): 109-120 DOI:10.1002/joc.3412
(  0) 0) |
| [12] |
Zhang W X, Lou Y D, Cao Y C, et al. Corrections of Radiosonde-Based Precipitable Water Using Ground-Based GPS and Applications on Historical Radiosonde Data over China[J]. Journal of Geophysical Research: Atmospheres, 2019, 124(6): 3 208-3 222 DOI:10.1029/2018JD029662
(  0) 0) |
| [13] |
Askne J, Nordius H. Estimation of Tropospheric Delay for Microwaves from Surface Weather Data[J]. Radio Science, 1987, 22(3): 379-386 DOI:10.1029/RS022i003p00379
(  0) 0) |
| [14] |
Saastamoinen J. The Use of Artificial Satellites for Geodesy[M]. Washington DC: American Geophysical Union, 1972
(  0) 0) |
| [15] |
Dousa J, Elias M. An Improved Model for Calculating Tropospheric Wet Delay[J]. Geophysical Research Letters, 2014, 41(12): 4 389-4 397 DOI:10.1002/2014GL060271
(  0) 0) |
| [16] |
Chen B Y, Liu Z Z. A Comprehensive Evaluation and Analysis of the Performance of Multiple Tropospheric Models in China Region[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 663-678 DOI:10.1109/TGRS.2015.2456099
(  0) 0) |
2. China Three Gorges Construction Engineering Corporation, 288 East-Fucheng Road, Chengdu 610023, China
 2022, Vol. 42
2022, Vol. 42

