目前,在利用北斗卫星导航系统进行动态相对定位时,大多利用载波相位观测值获得高精度的定位结果。但由于定位过程中经常因观测环境复杂等造成卫星信号被遮挡,从而引起信号失锁,使得相位测量需重新进行。该现象会使相邻历元间的观测值跳过整周的倍数,这种整周计数出现系统偏差而不足1整周的部分仍然保持正确的现象,简称周跳[1-3]。无论在静态还是动态观测环境中,周跳现象都会影响定位精度。
最常用的周跳探测方法有卡尔曼滤波法、电离层残差法和TurboEdit探测法,其中TurboEdit探测法结合无几何距离GF组合及窄巷伪距与宽巷相位之差MW组合进行探测,具有单站探测、高效探测等优点,得到广泛应用[4]。但由于在探测过程中引入噪声较大的伪距观测值及设定的阈值模型单一等因素影响,在观测环境复杂及采样率较低时,TurboEdit探测法也经常发生误判及漏判。许多学者对其进行了改进[5-8],但这些改进大多围绕GPS的MEO卫星展开,未对北斗3种不同轨道类型卫星的探测及其在静态和动态环境下的差异进行研究。本文针对北斗不同轨道卫星在不同场景下的相位历元差与卫星高度角和数据采样率之间的关系,提出一种新的阈值模型,对不同类型轨道的卫星及各种环境状态下发生的周跳特点展开研究。
1 常见的GF组合探测及改进方法 1.1 GF组合探测周跳在动态相对定位中,伪距观测量和载波相位观测量是测量卫星与地面距离的基本观测数据,在不同的频率间对伪距和载波相位观测量作差,可以消除几何距离项。以北斗两个频段为例,求差结果如式(1)所示:
| $ \begin{gathered} L_{\mathrm{GF}}=L_{1}-L_{2}=\frac{f_{1}^{2}-f_{2}^{2}}{f_{1}^{2}} I_{1}+\lambda_{1} N_{1}- \\ \lambda_{2} N_{2}=\Delta I+\lambda_{1} N_{1}-\lambda_{2} N_{2}+e_{\mathrm{GF}} \\ P_{\mathrm{GF}}=P_{1}-P_{2}=\frac{f_{1}^{2}-f_{2}^{2}}{f^{2}} I_{1}+e_{\mathrm{GF}}=\Delta I+E_{\mathrm{GF}} \end{gathered} $ | (1) |
式中,i为两个频段,Li和Pi分别为北斗两个频段上以m为单位的相位观测值和伪距观测值;λi为两个频段上的频率;LGF和PGF为无几何距离的相位和伪距观测值;Ni为相位整周模糊度;ΔI为两个频段上的电离层延迟之差;EGF及eGF为伪距和载波相位上的残余误差,包括多路径误差及噪声等。由式(1)可以看出,在不同频率间作差可以消除对流层误差及卫星轨道误差,同时也能削弱电离层误差的影响,仅剩模糊度参数、削弱后的电离层误差及多路径效应和噪声等。而模糊度参数在未发生周跳时保持不变,短时间内电离层的变化趋近于0,因此在历元间作差,可用于周跳检测,这就是无几何探测法,具体的算法如式(2)所示:
| $ \Delta \mathrm{GF}=L_{\mathrm{GF}}-Q_{\mathrm{GF}}=\lambda_{1} N_{1}-\lambda_{2} N_{2} $ | (2) |
式中,QGF为伪距频率之差拟合后的结果。由于在伪距观测值中大约存在0.3 m的噪声,需要对无几何距离的伪距观测值PGF进行拟合,以保证周跳探测的准确性。多项式拟合的类型可自由选择,但拟合的阶数一般满足n=min [6, N/100+1],其中N为参与计算的历元总数。对于GF组合来说,满足以下条件则证明在该历元中有周跳产生:
| $ \begin{array}{l} 条件1):\left| {\Delta {\rm{GF}}(i + 1) - \Delta {\rm{GF}}(i)} \right|<\left( {{\lambda _1} - {\lambda _2}} \right)\\ 条件2):\left| {\Delta {\rm{GF}}(i) - \Delta {\rm{GF}}(i - 1)} \right|<6\left( {{\lambda _1} - {\lambda _2}} \right) \end{array} $ | (3) |
该方法对于数据采样率要求较高,采样率越高,历元之间的电离层变化越缓慢;采样率越低,电离层之间变化越快,越容易造成周跳误判。同时,由于在计算过程中对伪距差值进行了拟合,而多项式拟合的类型及阶数未考虑观测数据环境等变量的影响,会人为降低原始观测数据的准确性,所以该方法具有很大的局限性。
1.2 相邻相位历元求差法为减少伪距观测值中噪声带来的影响,相邻相位历元求差法仅将两个相邻历元GF组合的相位观测值作差,具体的表达式为:
| $ \begin{gathered} \Delta L_{\mathrm{GF}}=L_{\mathrm{GF}}(i)-L_{\mathrm{GF}}(i-1)= \\ \Delta \nabla I+\lambda_{1} \Delta N_{1}-\lambda_{2} \Delta N_{2} \end{gathered} $ | (4) |
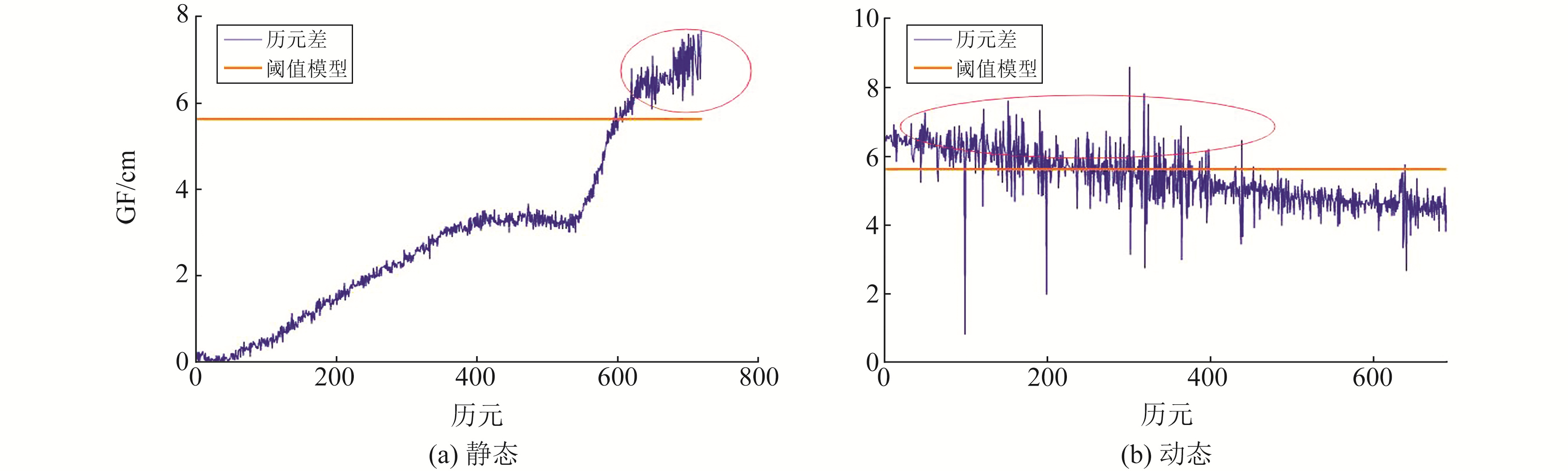
从式(4)可以看出,求差之后的观测值仅剩两个相邻历元之间电离层误差的差值,未涉及到噪声较大的伪距观测值。由于载波相位的精度很高,在高采样率的情况下,GF组合的序列观测值一般在2.5 cm以下波动。以λ2和λ7为例,对于较难探测的小周跳组合(1,1)来说,λ2=19.20 cm,λ7=24.83 cm,此时λ7-λ2=5.63 cm。因此,该方法的阈值一般选定为5~6 cm, 当大于该阈值范围时,说明发生了周跳现象。但当采样率较低或多路径误差较为严重时,也容易造成周跳的误判。图 1为电离层较活跃时采样率为15 s的静态测站和动态测站数据,经GF组合及MW联合探测检验后发现,该时间段内未发生周跳,但按照此判断条件,许多历元都被误判为发生了周跳。这是因为在电离层活跃的静态环境中,采样率过大会使得相邻历元之间的电离层变化过快,引起周跳的误判;在动态环境中,多路径误差比较严重,使得相位历元差波动较大,也会引起误判。
|
图 1 GF相位历元差 Fig. 1 GF phase epoch difference |
GF组合的加权阈值模型是利用数据采样率与高度角之间的关系建立的,但是该阈值模型仅针对GPS的MEO卫星,对北斗3种不同轨道类型的卫星及静态和动态等不同场景下的阈值模型未加区别,因此在对北斗实时观测数据进行探测时容易造成周跳的误判及漏判。
2 北斗不同轨道GF组合相位历元差为探究北斗不同轨道卫星在不同场景下的相位历元差与卫星高度角及数据采样率之间的关系,设计多组实验来确定适合不同轨道的阈值模型。动态数据采集自2020-09-26船载动态实验,地点为威海市葡萄滩附近海域(37°35′8.88″N,122°6′41.67″E),动态站接收机型号分别为Septentrio PolaRx5和Trimble R9。静态数据采集自2018-08-27的IGS测站、赤道附近的SGDC测站及香港卫星定位参考站中的HKCL测站,当天发生了磁暴现象,电离层比较活跃。
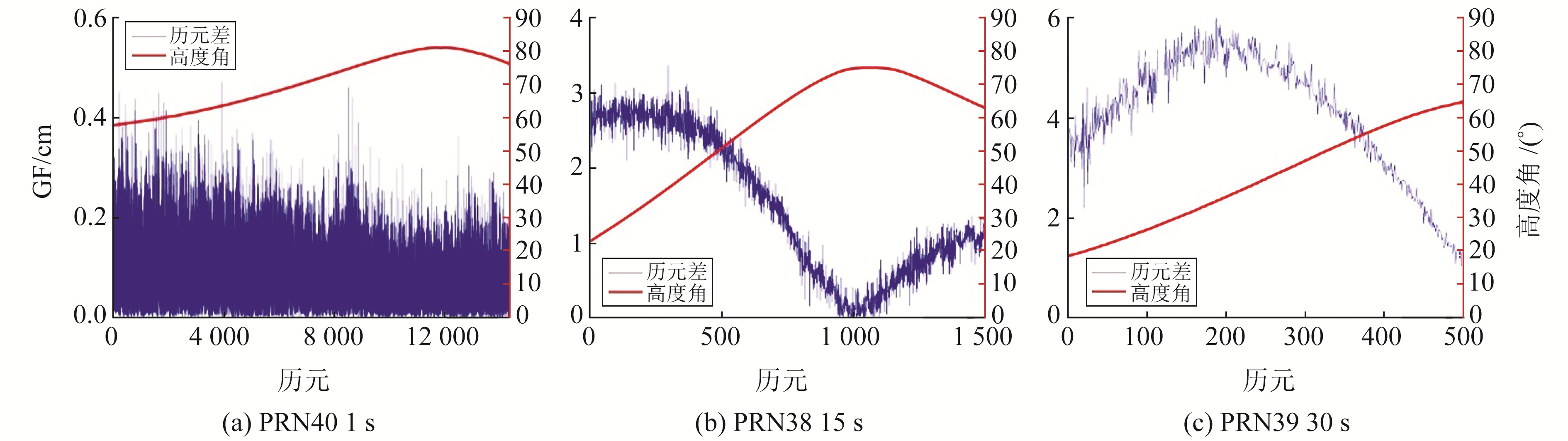
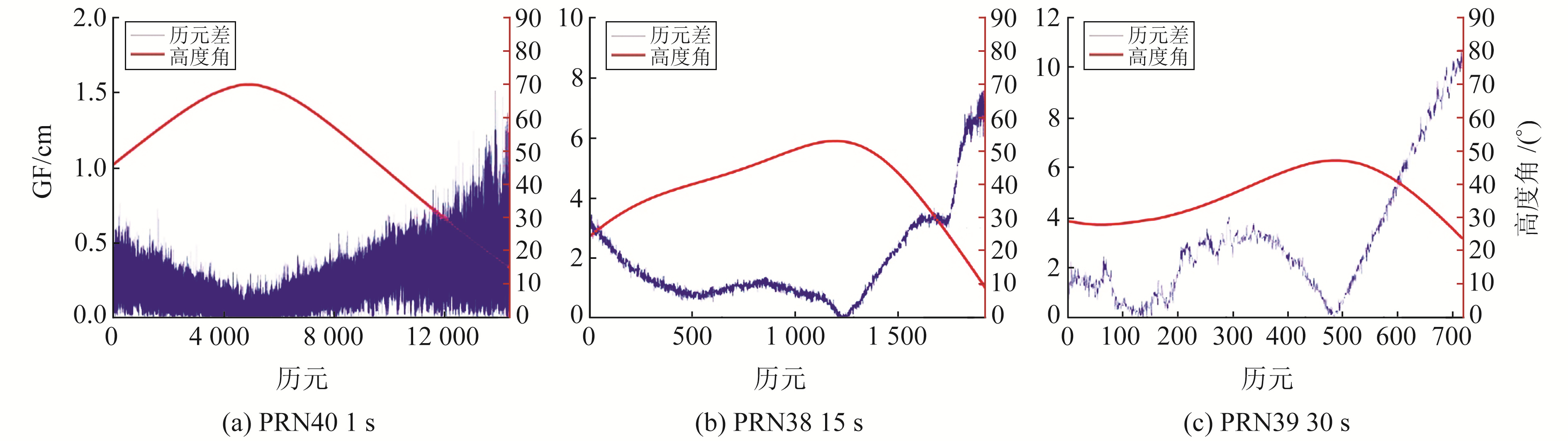
图 2和3分别为无周跳发生的情况下,采样率为1 s、15 s、30 s的IGSO与MEO卫星静态观测数据的相位历元差时间序列及高度角随时间的变化情况(以B1I和B3I为例)。由图 2和3可见,随着采样间隔的增加,IGSO和MEO卫星相位历元之间的差值越来越大,这是因为此时电离层变化比较活跃。若此时对不同采样率的卫星采用统一的阈值进行周跳探测,很容易造成多历元误判。而对于固定的采样率,其相位历元差与高度角呈现出较大的相关性:卫星高度角越高,相位历元差的变化越小;卫星高度角越低,相位历元差的变化越大。这是因为卫星刚进入和即将离开观测视线时,多路径效应和噪声对其的影响程度较大,此时影响IGSO和MEO卫星相位历元差进行周跳探测的因素主要为数据采样率和卫星高度角。
|
图 2 IGSO静态测站各采样率相位历元差 Fig. 2 Phase epoch difference of each sampling rate of IGSO static station |
|
图 3 MEO静态测站各采样率相位历元差 Fig. 3 Phase epoch difference of each sampling rate of MEO static station |
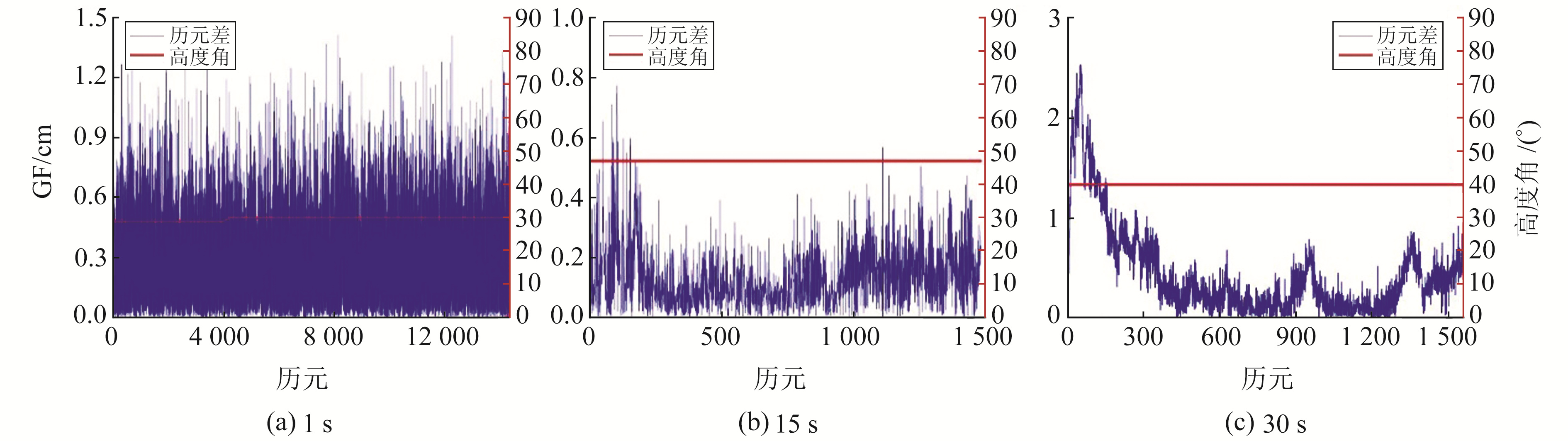
图 4为无周跳发生的情况下,随机选取采样率为1 s、15 s、30 s的GEO卫星静态观测数据相位历元差的时间序列及高度角随时间的变化情况。对于GEO卫星而言,卫星绕地球的运行周期与地球自转周期同步,卫星与地球之间处于相对静止的状态,因此卫星高度角基本保持不变。在卫星高度角一定的情况下,GF组合的影响因素仅为数据采样率。实验证明,在电离层活跃期和低高度角的情况下,GEO卫星相位观测值之间的历元差都远小于IGSO及MEO卫星,波动范围均在3 cm以下。
|
图 4 GEO静态测站各采样率相位历元差 Fig. 4 Phase epoch difference of each sampling rate of GEO static station |
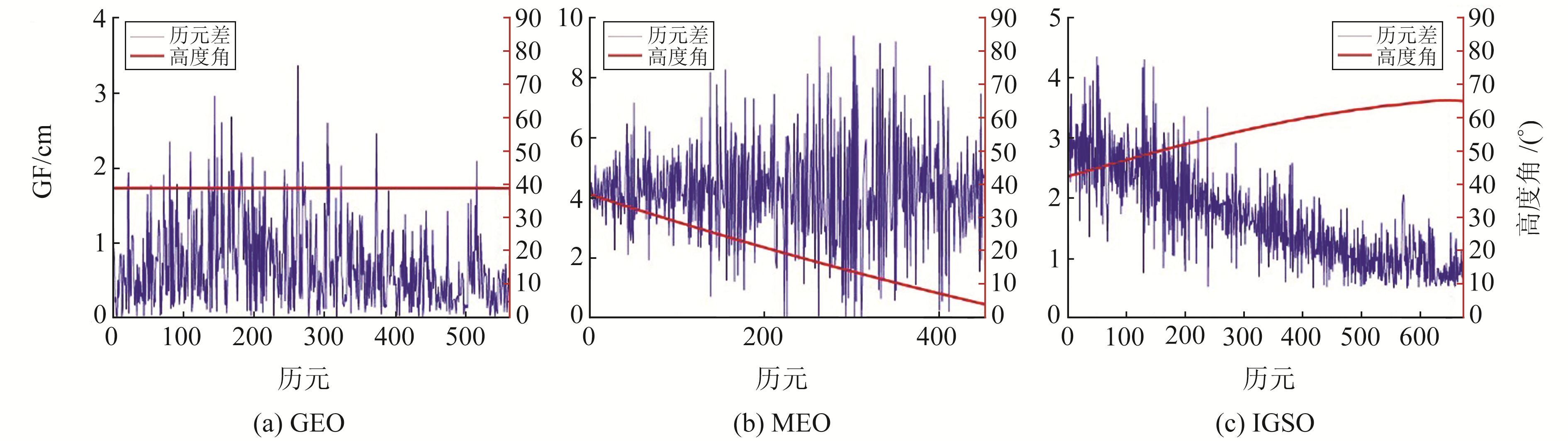
为研究动态环境和静态环境下相位历元差的差异,选取3种不同类型轨道的卫星同一测站同日采样率为15 s的动态观测数据,3种卫星的相位历元差与高度角关系如图 5所示。
|
图 5 动态测站15 s采样率各类型轨道相位历元差 Fig. 5 Phase ephemeris difference for each type of orbit at 15 s sampling rate for dynamic stations |
由图 4和5可知,与静态测站相比,动态环境下相位历元差之间的波动更大,MEO卫星与IGSO卫星的历元差虽然与高度角呈现出反比例关系,但当高度角较高时,历元差也呈现出较大波动。这是因为动态环境下多路径效应较为严重,致使误差增大。此外,GEO卫星在卫星高度角较低、多路径效应较大的情况下仍能保持较小的波动。
3 阈值建立为使建立的阈值模型适用于北斗数据测量过程中的各种场景,选取各种环境下的北斗观测数据进行处理与分析。阈值模型以卫星高度角和采样率为自变量,经大量实验证明,MEO与IGSO卫星的采样率与相位历元差的最值及均值呈比例函数关系。采样率函数模型是以观测环境复杂时观测数据的采样率为自变量,对应的相位历元差最大值为因变量建立的函数关系。高度角采用苗赢等[9]提出的高度角加权模型,并根据实际观测情况进行选择。在静态观测环境下,IGSO及MEO卫星的高度角函数模型如式(5)所示:
| $ k_{1}=\sqrt{\sin E / \sin e} $ | (5) |
式中,k为高度角加权因子,e为当前历元的观测高度角,E为根据实际情况选取的一个临界高度角。静态数据中临界高度角选为15°;动态环境中因多路径误差较为严重,临界高度角选为30°。当观测高度角小于30°时,高度角阈值模型才适用;大于30°时,仅根据采样率模型建立相关函数模型。动态环境下的高度角模型如式(6)所示:
| $ k_{2}=\left\{\begin{array}{l} 1, e \gg 30^{\circ} \\ \sqrt{\sin E / \sin e}, e<30^{\circ} \end{array}\right. $ | (6) |
采样率函数模型如式(7)所示:
| $ M=\left\{\begin{array}{l} 5, 0<S_{a} \ll 8 \mathrm{~s} \\ 0.51 S_{a}+0.92, 8 \mathrm{~s}<S_{a} \ll 30 \mathrm{~s} \\ 16.22, 30 \mathrm{~s}<S_{a} \ll 60 \mathrm{~s} \end{array}\right. $ | (7) |
式中,M为采样率函数模型,Sa为数据的采样率。在静态环境下,GEO卫星因相位历元差与IGSO及MEO卫星相比波动极小,因此可将采样率为30 s以内的观测数据阈值统一设置为5 cm;在动态环境下,考虑到多路径误差的影响,采用k2的阈值模型。当采样率大于5 s时,IGSO及MEO卫星的阈值模型如式(8)所示,GEO卫星的阈值模型如式(9)所示:
| $ \mathrm{THR}=\left\{\begin{array}{l} M \cdot k_{1}, \text { 静态数据 } \\ M \cdot k_{2}, \text { 动态数据 } \end{array}\right. $ | (8) |
| $ \mathrm{THR}=\left\{\begin{array}{l} 5, \text { 静态数据 } \\ 5 k_{2}, \text { 动态数据 } \end{array}\right. $ | (9) |
为更好地验证阈值模型的适用性,选择9组观测数据,其中包括电离层较为活跃时的静态及动态数据,进行周跳探测。随机选取各类型卫星数据,人为地在每组数据中加入7组周跳,其中包括较难探测的小周跳、敏感周跳和连续周跳,也包括比较容易探测的粗差等,实验结果如表 1和图 6所示。
|
|
表 1 加入的周跳位置和大小 Tab. 1 The values and positioning of cycle slips |
|
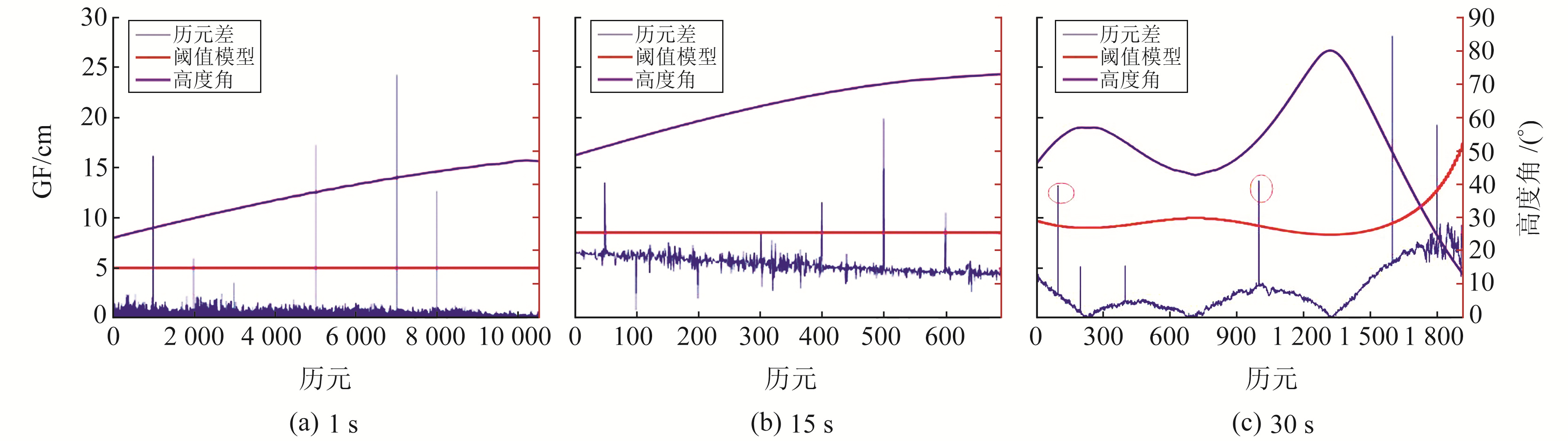
图 6 IGSO卫星各采样率下的相位历元差 Fig. 6 Phase epoch difference at each sampling rate of IGSO satellite |
图 6(a)为1 s采样率的静态数据,在刚开始的历元,IGSO卫星高度角在较低的范围内变化,但相位历元差并未有太大波动,基本都在2.5 cm以下,此时的阈值模型可以探测出0.5周的周跳,但未能探测出加入的两组敏感周跳(5,4)和(9,7)。图 6(b)和6(c)分别为15 s和30 s采样率的动态及静态环境数据,从动态数据变化可以看出,即使在高度角较高的情况下,相位历元差也呈现出在一定范围的波动,且动态数据随高度角变化的趋势不如静态数据明显,这是由海面上的多路径效应引起的,若此时高度角超过30°,则高度角所参与计算的权值全部设置为1。对于30 s采样率的静态数据,阈值模型与相位历元差之间呈现出一致的波动趋势,此时可以减少因设定固定阈值带来的误判,还可以最大程度地减少漏判。若按照GPS的阈值模型进行判断,此时阈值设定为15 cm,会因为两组敏感周跳之比接近北斗两个波段的频率之比,使图 6(c)中红色圆圈所示位置的周跳不能被探测到。
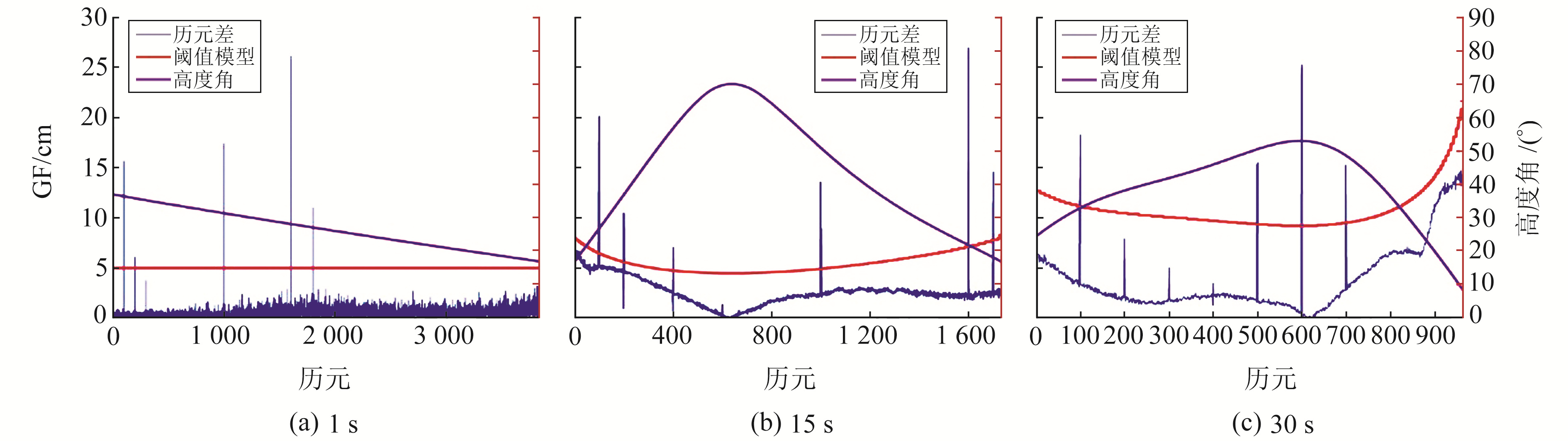
对于MEO卫星,其相位历元差与高度角及采样率的变化趋势与IGSO卫星基本保持一致,因此采用与IGSO卫星相同的阈值模型。图 7(a)选择了卫星即将离开观测视线时的动态数据,由图可见,尽管此时卫星高度角较低,但相位历元差的变化基本在2.5 cm左右,即使在动态环境高度角较低的情况下,5 cm的阈值范围也同样适用于1 s的观测数据,不会发生误判,但敏感周跳未被探测出。图 7(b)和7(c)均采用静态环境下电离层比较活跃时的观测数据进行验证,可以发现,阈值模型也能很好地贴合历元差的变化趋势,除敏感周跳及30 s观测数据时(1,1)等难以探测的小周跳未被探测出外,其他周跳均可被探测到。
|
图 7 MEO卫星各采样率下的相位历元差 Fig. 7 Phase epoch difference at each sampling rate of MEO satellite |
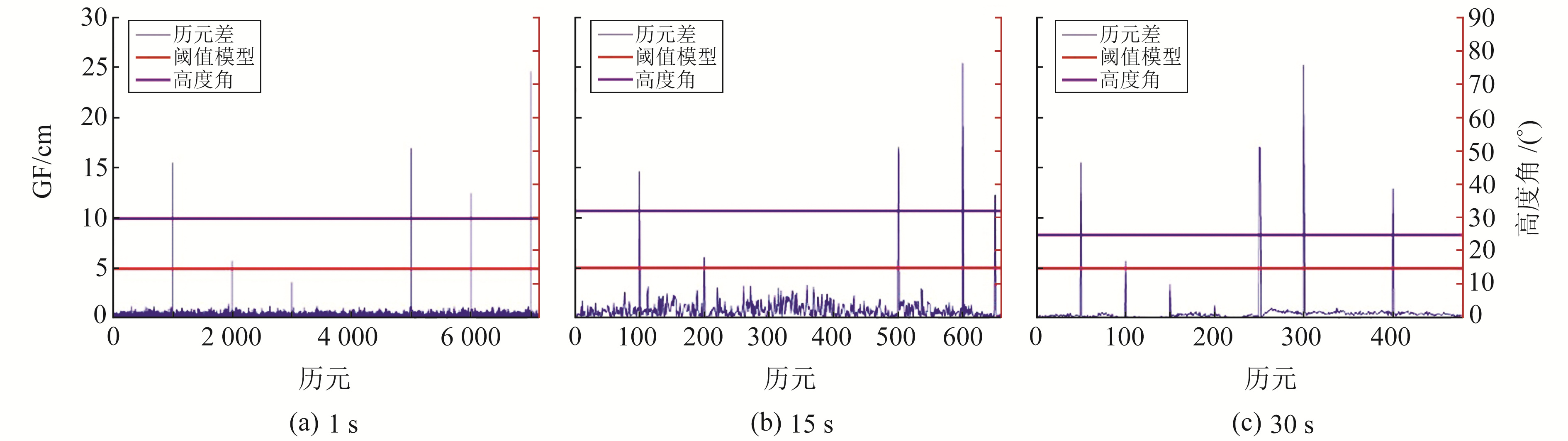
为验证GEO卫星设置的阈值范围是否合理,选择不利的观测环境进行实验。图 8(a)为采样率为1 s、低高度角、电离层活跃期的静态观测数据,图 8(b)为采样率为15 s、较低高度角的动态观测数据,图 8(c)为采样率为30 s、低高度角、电离层活跃期的静态观测数据。由图可见,除动态数据外,GEO卫星的相位历元差基本都在1~2 cm范围内波动,由此可知,在环境复杂的情况下,设置此阈值范围依旧可以探测出除敏感周跳以外的其他周跳。
|
图 8 GEO卫星各采样率下的相位历元差 Fig. 8 Phase epoch difference at each sampling rate of GEO satellite |
本文针对北斗不同轨道类型卫星提出了适合的周跳探测阈值模型,同时针对相位历元差在静态及动态观测环境下的不同特点,对GF组合阈值模型进行了改进。结果表明:
1) IGSO与MEO卫星的相位历元差与高度角存在明显的反比例关系,且相位历元差随采样率的增大而逐渐增大;对于GEO卫星,在卫星高度角一定的情况下,相位历元差与采样率的关系并不明显,GEO卫星的波动比IGSO和MEO卫星的波动小很多。
2) 在动态观测环境下,多路径效应较为严重,GF组合的残差也较大,在卫星高度角较高的情况下会受到多路径效应的影响,此时的高度角加权模型应根据实际观测条件进行设置。
3) 改进后的GF组合阈值模型能够探测出绝大多数的周跳,同时尽可能地减少各采样率下的周跳错判、漏判现象。但由于GF组合在两个不同频率的相位观测值之间作差,使得敏感周跳无法被探测出来,此时可利用MW组合的周跳探测方法进行联合探测。
| [1] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2010 (Li Zhenghang, Huang Jinsong. GPS Measurement and Data Processing[M]. Wuhan: Wuhan University Press, 2010)
(  0) 0) |
| [2] |
许国昌. GPS理论、算法与应用[M]. 北京: 科学出版社, 2017 (Xu Guochang. GPS: Theory, Algorithms and Applications[M]. Beijing: Science Press, 2017)
(  0) 0) |
| [3] |
杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6 (Yang Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6)
(  0) 0) |
| [4] |
曾琪. BDS/GPS组合动态相对定位及其质量控制方法研究[D]. 武汉: 武汉大学, 2017 (Zeng Qi. Research on Method and Quality Control for BDS/GPS Combined Kinematic Relative Positioning[D]. Wuhan: Wuhan University, 2017)
(  0) 0) |
| [5] |
王振杰, 聂志喜, 欧吉坤. 一种基于TurboEdit改进的GPS双频观测值周跳探测方法[J]. 武汉大学学报: 信息科学版, 2014, 39(9): 1 017-1 021 (Wang Zhenjie, Nie Zhixi, Ou Jikun. An Improved Cycle Slip Detection Based on Turbo-Edit Method for Dual-Frequency GPS Receiver[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9): 1 017-1 021)
(  0) 0) |
| [6] |
Li B F, Qin Y N, Liu T X. Geometry-Based Cycle Slip and Data Gap Repair for Multi-GNSS and Multi-Frequency Observations[J]. Journal of Geodesy, 2019, 93(3): 399-417 DOI:10.1007/s00190-018-1168-5
(  0) 0) |
| [7] |
张小红, 曾琪, 何俊, 等. 构建阈值模型改善TurboEdit实时周跳探测[J]. 武汉大学学报: 信息科学版, 2017, 42(3): 285-292 (Zhang Xiaohong, Zeng Qi, He Jun, et al. Improving TurboEdit Real-Time Cycle Slip Detection by the Construction of Threshold Model[J]. Geomatics and Information Science of Wuhan University, 2017, 42(3): 285-292)
(  0) 0) |
| [8] |
方荣新, 施闯, 魏娜, 等. GPS数据质量控制中实时周跳探测研究[J]. 武汉大学学报: 信息科学版, 2009, 34(9): 1 094-1 097 (Fang Rongxin, Shi Chuang, Wei Na, et al. Real-Time Cycle-Slip Detection for Quality Control of GPS Measurements[J]. Geomatics and Information Science of Wuhan University, 2009, 34(9): 1 094-1 097)
(  0) 0) |
| [9] |
苗赢, 孙兆伟. 星载GPS测量数据周跳探测方法研究[J]. 宇航学报, 2009, 30(2): 521-525 (Miao Ying, Sun Zhaowei. A Cycle-Slip Detection Method for Satellite-Borne GPS Observation[J]. Journal of Astronautics, 2009, 30(2): 521-525 DOI:10.3873/j.issn.1000-1328.2009.02.021)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


