载波相位观测是GNSS高精度定位及应用的关键[1]。由于接收机自身原因或GNSS信号受物理遮蔽等因素的影响,载波相位观测可能发生周跳,因此当载波相位观测量参与GNSS高精度定位及相关应用时,需要进行有效的周跳探测和修复[2]。目前常用的GNSS双频观测值周跳探测方法有TurboEdit方法、卡尔曼滤波法、多普勒积分法等,其中TurboEdit方法具有探测精度高、程序容易实现等优点,应用最为广泛[3]。随着三频GNSS的发展,相关学者针对三频周跳探测与修复的特性及方法展开了大量研究[4-6]。
如今中国北斗三号全球卫星导航系统BDS-3和欧盟Galileo系统已经可以播发4个频率的信号[7-8],四频周跳处理方法相较于GNSS双频和三频具有更广阔的应用前景[9],而目前针对GNSS四频周跳探测与修复特性及方法的研究较少。限于篇幅,本文仅利用BDS-3提供的四频信号研究周跳探测与修复的新方法,选用B1C、B1I、B2a、B3I四个频率信号,根据电离层延迟最小和组合观测值噪声最小原则对组合系数进行优选,联合四频无几何相位组合和四频无几何无电离层组合两种方法进行周跳探测,然后基于最小二乘法估计周跳浮点解,最后利用MGEX提供的BDS-3四频数据验证本文算法的有效性和可靠性。
1 四频组合观测值系数选择 1.1 四频无几何相位组合观测值特性分析GNSS原始伪距和载波相位观测值的观测方程可以写为[9]:
| $ P_{i}=\rho+c\left(\mathrm{~d} t_{\mathrm{r}}-\mathrm{d} t^{\mathrm{s}}\right)+T+\eta_{i} I_{1}+\varepsilon_{P_{i}} $ | (1) |
| $ \lambda_{i} \varphi_{i}=\rho+c\left(\mathrm{~d} t_{\mathrm{r}}-\mathrm{d} t^{s}\right)+T-\eta_{i} I_{1}+\lambda_{i} N_{i}+\lambda_{i} \varepsilon_{\varphi_{i}} $ | (2) |
式中,Pi和φi分别为第i频点的伪距和载波相位观测值;λi为第i频点的波长;ρ为站星几何距离;c为真空中的光速;dtr和dts分别为接收机和卫星钟差;T为对流层延迟;ηi=f12/fi2为电离层延迟系数,其中fi为第i频点的频率;I1为频率f1对应的电离层延迟误差;εPi和εφi分别为伪距和载波相位的观测噪声。
对式(2)进行组合[10],可以得到四频无几何GF相位组合:
| $ \begin{gathered} \varphi_{\mathrm{GF}}=\alpha \lambda_{1} \varphi_{1}+\beta \lambda_{2} \varphi_{2}+\gamma \lambda_{3} \varphi_{3}+\delta \lambda_{4} \varphi_{4}= \\ -\eta_{\mathrm{GF}} I_{1}+N_{\mathrm{GF}}+\varepsilon_{\mathrm{GF}} \end{gathered} $ | (3) |
式中,α、β、γ、δ为GF组合系数,
为满足无几何条件[10],提高周跳探测的灵敏度,令
| $ \left\{\begin{array}{l} \alpha+\beta+\gamma+\delta=0 \\ \left(\alpha \lambda_{1}\right)^{2}+\left(\beta \lambda_{2}\right)^{2}+\left(\gamma \lambda_{3}\right)^{2}+\left(\delta \lambda_{4}\right)^{2}=\min \end{array}\right. $ | (4) |
对相邻历元的GF组合观测值进行历间差分可得:
| $ \begin{gathered} \Delta N_{\mathrm{GF}}=N_{\mathrm{GF}}(k)-N_{\mathrm{GF}}(k-1)= \\ \Delta \varphi_{\mathrm{GF}}-\eta_{\mathrm{GF}} \Delta I_{1}+\Delta \varepsilon_{\mathrm{GF}} \end{gathered} $ | (5) |
式中,ΔφGF为相邻历元差分后的GF相位组合,ΔNGF为GF相位组合周跳探测量,k和k-1为当前历元和前一历元。
由式(5)可知,ΔNGF会受到ηGFΔI1和ΔεGF的影响,因此在选择组合系数时应尽量选择ηGFΔI1和ΔεGF较小的组合。在高采样率条件下,ΔI1的值极小,当ηGF也极小时,ηGFΔI1可忽略不计。根据误差传播定律,ΔNGF的标准差可表示为式(6),此处σφ取0.01周:
| $ \begin{array}{c} {\sigma _{\Delta {\mathit{N}_{{\rm{GF}}}}}} = \\ \sqrt {2\left( {{{\left( {\alpha {\lambda _1}} \right)}^2} + {{\left( {\beta {\lambda _2}} \right)}^2} + {{\left( {\gamma {\lambda _3}} \right)}^2} + {{\left( {\delta {\lambda _4}} \right)}^2}} \right)\sigma _\varphi ^2} \end{array} $ | (6) |
以4倍周跳探测量标准差(对应正态分布假设下99.9%的置信水平)作为周跳探测阈值,GF相位组合探测出周跳的条件为:
| $ \left|\Delta N_{\mathrm{GF}}\right| \geqslant 4 \sigma_{\Delta N_{\mathrm{GF}}} $ | (7) |
上述公式中的4个频点分别对应BDS-3的B1C(1 575.420 mHz)、B1I(1 561.098 mHz)、B2a(1 176.450 mHz)和B3I(1 268.520 mHz)。在[-10, 10]范围内BDS-3较优的GF相位组合系数及10周以内不敏感周跳个数如表 1所示,由表可见,对于任一GF相位组合均存在不敏感周跳,但不同组合的不敏感周跳是不同的。为此,从表 1中选取3个GF相位组合同时进行周跳探测,以减少不敏感周跳的组合数并提高周跳探测的灵敏度。以式(4)作为组合系数选择条件,同时保证联合使用3个GF相位组合时不存在10周以内的不敏感周跳。通过筛选,BDS-3组合[1, -1, 0, 0]、[0, 1, 0, -1]和[0, 0, -1, 1]满足条件,因此本文选择上述3个GF相位组合作为设定条件下的最优组合。由于四频GF相位组合中的任意4个都是线性相关的,因此无论使用多少个GF相位组合,总存在不敏感周跳。为解决这一问题,本文选择四频无几何无电离层GIF组合联合四频GF相位组合进行周跳探测。
|
|
表 1 BDS-3四频无几何相位组合及不敏感周跳个数 Tab. 1 BDS-3 four-frequency geometry-free phase combination andthe number of insensitive cycle-clip |
根据式(1)和式(2)可知,四频GIF组合可以表示为:
| $ \begin{gathered} \varphi_{\mathrm{GIF}}=i \varphi_{1}+j \varphi_{2}+k \varphi_{3}+l \varphi_{4}- \\ \frac{a P_{1}+b P_{2}+c P_{3}+d P_{4}}{\lambda_{\mathrm{GIF}}}= \\ i N_{1}+j N_{2}+k N_{3}+l N_{4}+\varepsilon_{\mathrm{GIF}} \end{gathered} $ | (8) |
式中,i、j、k、l为GIF组合载波相位组合观测值系数,a、b、c、d为GIF组合伪距组合观测值系数,
为消除几何误差项和电离层误差一阶项,尽可能降低伪距噪声的影响[4],需满足:
| $ \left\{\begin{array}{l} a+b+c+d=1 \\ a+b \frac{f_{1}^{2}}{f_{2}^{2}}+c \frac{f_{1}^{2}}{f_{3}^{2}}+d \frac{f_{1}^{2}}{f_{4}^{2}}= \\ \quad-\frac{\lambda_{\mathrm{GIF}}}{\lambda_{1}}\left(i+j \frac{f_{1}}{f_{2}}+k \frac{f_{1}}{f_{3}}+l \frac{f_{1}}{f_{4}}\right) \\ a^{2}+b^{2}+c^{2}+d^{2}=\min \end{array}\right. $ | (9) |
当发生周跳时,通过历元间差分可构造周跳探测方程:
| $ \Delta N_{\mathrm{GIF}}=N_{\mathrm{GIF}}(k)-N_{\mathrm{GIF}}(k-1)=\Delta \varphi_{\mathrm{GIF}}+\Delta \varepsilon_{\mathrm{GIF}} $ | (10) |
式中,ΔφGIF为相邻历元差分后的GIF组合,ΔNGIF为GIF组合周跳探测量,k和k-1为当前历元和前一历元。
根据误差传播定律,ΔNGIF的标准差可表示为式(11),此处σφ取0.01周,σP取0.1 m:
| $ \begin{array}{c} {\sigma _{\Delta {\mathit{N}_{{\rm{GIF}}}}}} = \\ \sqrt {2\left[ {\left( {{i^2} + {j^2} + {k^2} + {l^2}} \right)\sigma _\varphi ^2 + \frac{{\left( {{a^2} + {b^2} + {c^2} + {d^2}} \right)\sigma _P^2}}{{\lambda _{{\rm{GIF}}}^2}}} \right]} \end{array} $ | (11) |
同样以4倍周跳探测量标准差作为周跳探测阈值,GIF组合探测出周跳的条件为:
| $ \left|\Delta N_{\mathrm{GIF}}\right| \geqslant 4 \sigma_{\Delta N_{\mathrm{GIF}}} $ | (12) |
在GIF组合系数筛选过程中,首先要确定载波相位组合系数[i, j, k, l],然后在满足式(9)前两式的条件下在[-1, 1]范围内对伪距组合系数a、b、c、d进行搜索,最后将满足a2+b2+c2+d2=min的伪距组合系数a、b、c、d及对应的载波相位组合系数[i, j, k, l]作为该设定条件下的最优GIF组合。通过筛选,BDS-3四频较优的GIF组合如表 2所示,由表可知,观测噪声σΔNGIF越小,周跳探测灵敏度越高,因此为了减小σΔNGIF,应选择λGIF更长的超宽巷或宽巷组合。以4σΔNGIF作为探测阈值时,周跳探测组合均可实现对1周小周跳的探测,为了表达简便,以载波相位组合系数[i, j, k, l]表示GIF组合。当BDS-3组合[1 , -1 , 0,0]具有较长的波长时,观测噪声达到最小,且周跳探测阈值均不超过0.1周,因此选择组合[1 ,-1 ,0,0]作为BDS-3四频GIF组合的周跳探测组合。针对3个GF相位组合中存在不敏感周跳的问题,采用一个GIF组合构成4个线性无关的组合,可以保证无公共不敏感周跳组合,从而实现对各类周跳的探测。
|
|
表 2 BDS-3四频无几何无电离层组合 Tab. 2 BDS-3 four-frequency geometry-free and ionosphere-free combination |
本文采用3个四频GF相位组合和1个四频GIF组合构造4个线性无关的周跳探测组合,以4倍周跳探测量标准差作为周跳探测阈值。当满足周跳探测量大于探测阈值时,表明相应历元发生了周跳。通过对GF相位组合系数和GIF组合系数进行优选,得到3个GF相位组合和1个GIF组合,其中BDS-3组合系数对应[1, -1,0,0]、[0,1, 0, -1]、[0,0, -1,1] 和[1, -1,0,0],周跳探测阈值分别为0.015 3、0.017 2、0.019 7和0.081 1。
当载波相位观测值中的周跳被成功探测后,需要对周跳进行修复。在每个历元下,通过联立3个GF相位组合观测值和1个GIF组合观测值得到组合观测值L,这里L表示为[LGF1, LGF2, LGF3, LGIF]T,其中LGF1、LGF2、LGF3为3个不同的GF相位组合观测值,LGIF为GIF组合观测值;然后在相邻历元间对 L进行求差,可得历元间差分后的组合观测值ΔL。当ΔL探测出周跳后,根据式(13)即可得到单个频点上的待估周跳值ΔX:
| $ \boldsymbol{A} \Delta \boldsymbol{X}+\boldsymbol{\varepsilon}=\Delta \boldsymbol{L} $ | (13) |
式中,ε 为观测噪声,ΔX =[ΔN1, ΔN2, ΔN3, ΔN4]T为4个不同频点上的待估周跳浮点解,A为其系数矩阵,此处表示为:
| $ \boldsymbol{A}=\left[\begin{array}{cccc} \lambda_{1} & -\lambda_{2} & 0 & 0 \\ 0 & \lambda_{2} & 0 & -\lambda_{4} \\ 0 & 0 & -\lambda_{3} & -\lambda_{4} \\ 1 & -1 & 0 & 0 \end{array}\right] $ | (14) |
利用最小二乘法对式(13)进行参数估计,可得ΔX的估计值
|
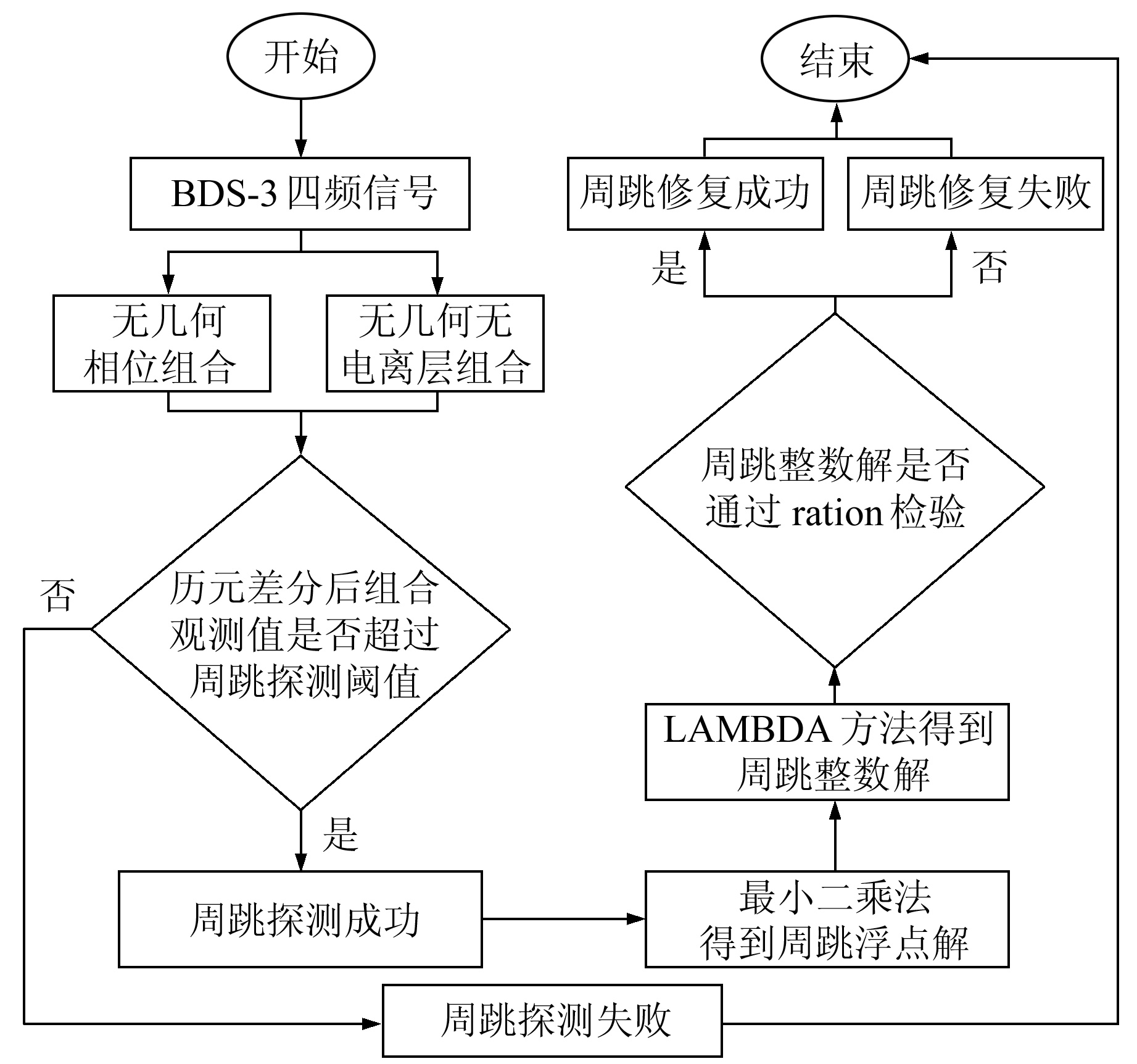
图 1 BDS-3四频周跳探测与修复算法流程 Fig. 1 Procedure of quad-frequency cycle-slip detection and repair algorithm for BDS-3 |
选取MGEX提供的WUH2测站(30.53°N,114.36°E)2020-10-26的观测数据,采样间隔为1 s,卫星截止高度角为10°。其中,BDS-3系统选择C39和C40两颗卫星,每颗卫星选择连续500个没有周跳和粗差的历元作为本次实验的观测时间序列。
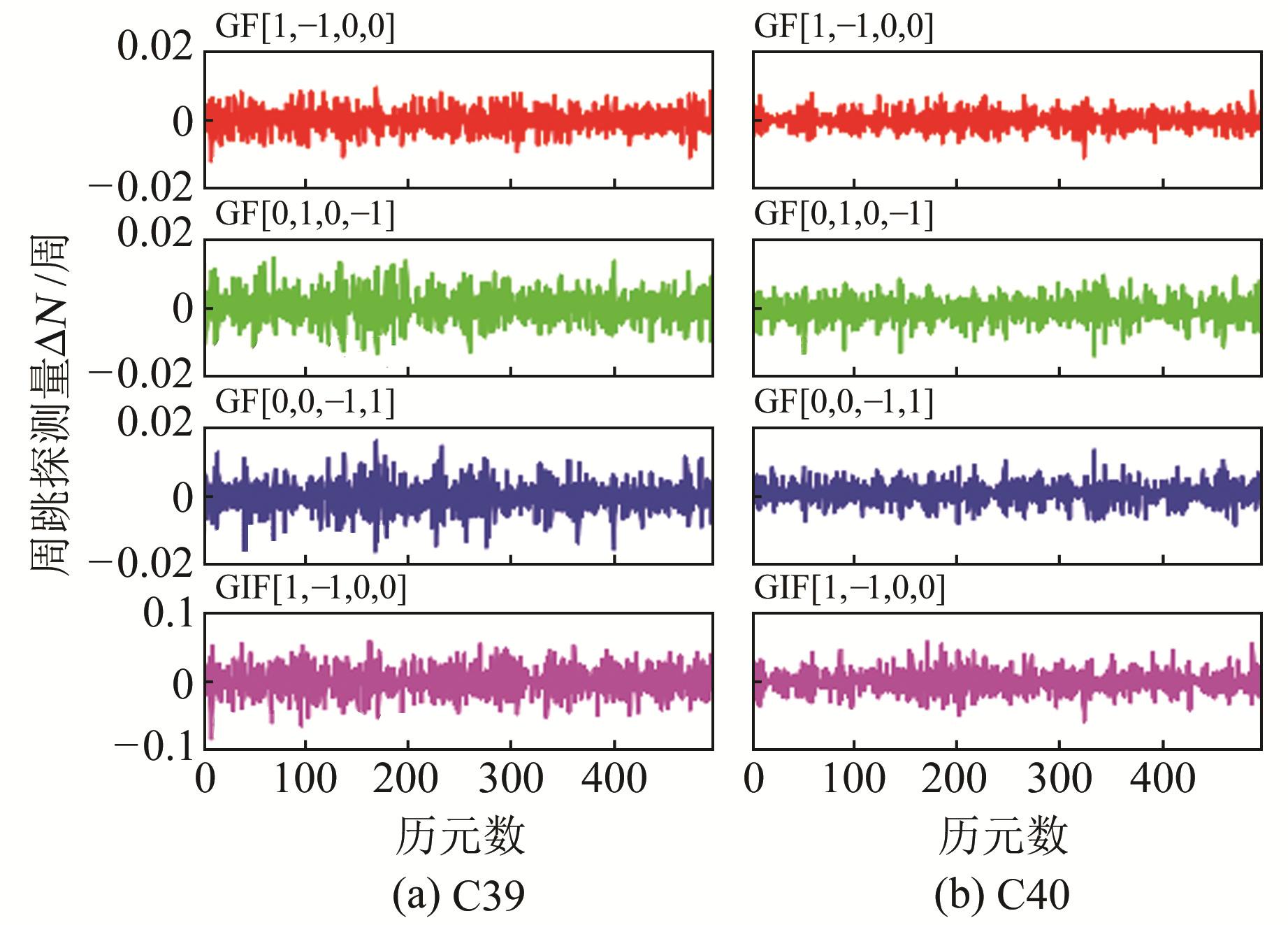
由图 2可见,3个GF载波相位组合探测量的波动均保持在[-0.02, 0.02]范围内,而GIF组合周跳探测量在[-0.1, 0.1]范围内。由此可知,相较于GIF组合,GF相位组合的周跳探测能力更高,这是因为GF相位组合比GIF组合受到的噪声影响更小。
|
图 2 BDS-3无周跳组合探测值 Fig. 2 Combination detection values without cycle-slip for BDS-3 |
由于原始测站非差观测值中无周跳,因此本文在不同历元时刻加入一般周跳和特殊周跳(一般周跳指4个组合均可以探测出的1~10周的周跳,特殊周跳指单个频率上发生1~2周的小周跳或者在不同频率发生相同跳变的小周跳),以验证本文所选线性组合的周跳探测能力及修复效果。
3.1 一般周跳的探测与修复分别在BDS-3 C39和C40卫星每隔100个历元加入不同的10周以内一般小周跳(3, 1, 2, 1)、(6, 7, 4, 3)、(1, 4, 3, 2)、(5, 7, 4, 7),探测结果如图 3所示。由图可见,4个组合均可同时检测到一般周跳,BDS-3具体周跳探测与修复结果列于表 3。由表可知,所有一般周跳的ratio值均大于阈值,同时利用LAMBDA算法得到的周跳计算值与周跳模拟值均保持一致,从而验证了采用LAMBDA算法对一般周跳进行修复的正确性。

|
图 3 BDS-3一般周跳组合探测值 Fig. 3 Normal cycle-slip combination detection values for BDS-3 |
|
|
表 3 BDS-3一般周跳的周跳探测与修复结果 Tab. 3 The general cycle-slip detect and repair result of BDS-3 |
为进一步验证本文方法的周跳探测与修复效果,分别在BDS-3 C39和C40卫星不同历元时刻加入特殊周跳,探测结果如图 4所示。

|
图 4 BDS-3特殊周跳组合探测值 Fig. 4 Particular cycle-slip combination detection values for BDS-3 |
首先考虑当4个频率信号中某一单独频点发生周跳的情况,分别在第100、200、300、400历元中加入周跳(1, 0, 0, 0)、(0, 1, 0, 0)、(0, 0, 1, 0)、(0, 0, 0, 1)。由图 4(a)和4(b)可见,GF相位组合[1 , -1 ,0,0] 和GIF组合均可探测出周跳(1, 0, 0, 0);对于周跳(0, 1, 0, 0),仅有GF相位组合[0, 0,1 , -1 ] 对其不敏感;采用GF相位组合[0,0, -1 ,1]可探测出周跳(0, 0, 1, 0)和(0, 0, 0, 1)。考虑其他特殊的不敏感周跳,在第100和200历元加入4个频点发生相同周跳的周跳组合(1, 1, 1, 1)和(5, 5, 5, 5),在第300历元加入频点2和频点3发生相同周跳的周跳组合(0, 2, 2, 0),在第400历元加入频点1、频点3、频点4同时发生相同周跳的周跳组合(3, 3, 0, 3)。由图 4(c)和4(d)可见,对于周跳组合(1, 1, 1, 1),C39和C40卫星的GF相位组合[0,1 ,0, -1 ] 的探测量均超过探测阈值;对于周跳(5, 5, 5, 5)、(0, 2, 2, 0)和(3, 3, 0, 3),C39和C40卫星的GF相位组合[0,1 ,0, -1 ]和[0,0, -1 ,1]均可将其探测出。
通过分析可知,特殊的不敏感周跳可能对部分探测组合不敏感,但4个组合联合后均能很好地探测出周跳,极大地减少了探测盲区。BDS-3四个组合特殊周跳的周跳探测及修复具体信息列于表 4,由表可知,所有特殊周跳的ratio值均大于阈值,且计算值均与模拟值相同,表明采用LAMBDA方法同样可以对特殊周跳进行准确修复。
|
|
表 4 BDS-3特殊周跳的周跳探测与修复结果 Tab. 4 The particular cycle-slip detect and repair result of BDS-3 |
本文对BDS-3四频数据的周跳探测与修复方法进行研究,首先基于无几何条件下的观测噪声最小准则优选出3个GF相位组合,再基于无几何无电离层条件下的观测噪声最小准则优选出1个GIF组合,并联合4个组合观测值进行周跳探测。在探测出周跳后,将4个周跳探测组合进行方程组联立,采用最小二乘法确定周跳浮点解,基于LAMBDA降相关搜索法获得周跳整数解,并采用ratio检验进一步对周跳整数解进行验证。最后采用MGEX提供的BDS-3四频观测数据进行实验验证,结果表明,本文提出的方法可以实现对单站非差观测值中各类周跳的准确探测及快速高效修复。值得说明的是,本文提出的方法同样可以用于Galileo四频数据的周跳探测与修复,限于篇幅,本文不进行具体介绍。
| [1] |
Feng W, Zhao Y H, Zhou L T, et al. Fast Cycle Slip Determination for High-Rate Multi-GNSS RTK Using Modified Geometry-Free Phase Combination[J]. GPS Solutions, 2020, 24(2): 1-11
(  0) 0) |
| [2] |
Zhang W H, Wang J L. A Real-Time Cycle Slip Repair Method Using the Multi-Epoch Geometry-Based Model[J]. GPS Solutions, 2021, 25(2): 1-12
(  0) 0) |
| [3] |
Banville S, Langley R B. Mitigating the Impact of Ionospheric Cycle Slips in GNSS Observations[J]. Journal of Geodesy, 2013, 87(2): 179-193 DOI:10.1007/s00190-012-0604-1
(  0) 0) |
| [4] |
Zhao Q L, Sun B Z, Dai Z Q, et al. Real-Time Detection and Repair of Cycle Slips in Triple-Frequency GNSS Measurements[J]. GPS Solutions, 2015, 19(3): 381-391 DOI:10.1007/s10291-014-0396-2
(  0) 0) |
| [5] |
Gao X, Yang Z Q, Liu Y, et al. Real-Time Cycle Slip Correction for a Single Triple-Frequency BDS Receiver Based on Ionosphere-Reduced Virtual Signals[J]. Advances in Space Research, 2018, 62(9): 2 381-2 392 DOI:10.1016/j.asr.2018.06.044
(  0) 0) |
| [6] |
张晨晰, 党亚民, 薛树强, 等. BDS三频GIF组合非显著周跳探测与修复[J]. 测绘学报, 2018, 47(S1): 38-44 (Zhang Chenxi, Dang Yamin, Xue Shuqiang, et al. Detection and Repair of the Non-Significant Cycle Slip in BDS Triple-Frequencies GIF Combination[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(S1): 38-44)
(  0) 0) |
| [7] |
Yang Y X, Mao Y, Sun B J. Basic Performance and Future Developments of Beidou Global Navigation Satellite System[J]. Satellite Navigation, 2020, 1(1): 1-8 DOI:10.1186/s43020-019-0006-0
(  0) 0) |
| [8] |
Tu R, Liu J H, Zhang R, et al. RTK Model and Positioning Performance Analysis Using Galileo Four-Frequency Observations[J]. Advances in Space Research, 2019, 63(2): 913-926 DOI:10.1016/j.asr.2018.10.011
(  0) 0) |
| [9] |
Wu Y, Jin S G, Wang Z M, et al. Cycle Slip Detection Using Multi-Frequency GPS Carrier Phase Observations: A Simulation Study[J]. Advances in Space Research, 2010, 46(2): 144-149 DOI:10.1016/j.asr.2009.11.007
(  0) 0) |
| [10] |
黄令勇, 宋力杰, 王琰, 等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报, 2012, 41(5): 763-768 (Huang Lingyong, Song Lijie, Wang Yan, et al. Beidou Triple-Frequency Geometry-Free Phase Combination for Cycle-Slip Detection and Correction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 763-768)
(  0) 0) |
| [11] |
Dai Z, Knedlik S, Loffeld O. Real-Time Cycle-Slip Detection and Determination for Multiple Frequency GNSS[C]. Workshop on Positioning, Navigation and Communication, Germany, 2008
(  0) 0) |
| [12] |
Li B F, Liu T, X Nie L W, et al. Single-Frequency GNSS Cycle Slip Estimation with Positional Polynomial Constraint[J]. Journal of Geodesy, 2019, 93(9): 1 781-1 803 DOI:10.1007/s00190-019-01281-7
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


