北斗卫星导航系统(BDS)是我国自主建设、独立运行的卫星导航系统[1]。2020-07-31北斗三号全球卫星导航系统(BDS-3)正式开通,并为全球用户提供导航、定位、授时服务。北斗三号系统在北斗二号系统基础上新增加了B1C、B2a和B2b信号,进一步提升了定位性能[2]。实时动态定位(real-time kinematic,RTK)是高精度相对定位的常用手段之一,一般利用基准站和流动站的载波相位观测值组成双差模型进行,可以得到cm级的实时定位精度,目前已经被广泛应用于工程测量等领域[3]。官方文件显示[4],GNSS接收机已经可以接收到BDS-3的B1C和B2a新信号,且接收机观测数据质量与定位的可靠性、稳定性有直接关系。因此,对BDS-3新信号进行数据质量分析和RTK定位性能分析,对BDS-3走向实际应用具有重要参考价值。
很多学者对BDS-3的B1C和B2a新信号进行了数据质量和定位性能分析[5-8],但有关BDS-3新信号RTK定位的研究较少,尤其是中长基线RTK定位。鉴于此,本文利用4组中长基线实测数据,采用GPS的L1+L2、BDS-3的B1I+B3I和BDS-3的B1C+B2a三种无电离层组合方式,对BDS-3新信号进行数据质量分析和中长基线RTK定位精度分析。
1 北斗三号系统介绍北斗三号系统是北斗系统“三步走”战略建设发展的最后一步,于2009年启动建设,2020年投入使用[2]。BDS-3由3颗地球静止轨道(GEO)卫星、3颗倾斜地球同步轨道(IGSO)卫星和24颗中圆地球轨道(MEO)卫星组成[9]。BDS-3在BDS-2基础上,新增加了B1C、B2a和B2b信号,其中B1C和B2a信号只在MEO卫星和IGSO卫星上播发,并提供公开服务。B1C信号与GPS的L1信号和Galileo的E1信号形成兼容互操作,B2a信号与GPS的L5信号和Galileo的E5a信号形成兼容互操作,具体信号频率见表 1。BDS-3的坐标系统采用2000国家大地坐标系(CGCS2000),时间系统采用北斗时(BDT)[10]。
|
|
表 1 BDS-3、GPS和Galileo的信号频率 Tab. 1 Signal frequency of BDS-3, GPS, Galileo |
RTK定位通常采用双差观测方程,即在基准站和流动站之间求一次差后再在卫星之间求二次差。该模型可以消除接收机钟差、卫星钟差,削弱电离层延迟误差、对流层延迟误差、多路径效应和星历误差等误差项的影响。假设基准站为B,流动站为R,参考星为k,非参考星为s,则伪距和载波相位双差观测方程为:
| $ \begin{array}{*{20}{c}} {{\lambda _i}\Delta \nabla \varphi _{{\rm{BR}}}^{{\rm{ks}}} = \Delta \nabla \rho _{{\rm{BR}}}^{{\rm{ks}}} + \Delta \nabla O_{{\rm{BR}}}^{{\rm{ks}}} + \Delta \nabla T_{{\rm{BR}}}^{{\rm{ks}}} - }\\ {\Delta \nabla I_{{\rm{BR}}}^{{\rm{ks}}} + {\lambda _i}\Delta \nabla N_{{\rm{BR}}}^{{\rm{ks}}} + {\xi _{\Delta \nabla \varphi _{{\rm{BR}}}^{{\rm{ks}}}}}} \end{array} $ | (1) |
| $ \begin{array}{l} \Delta \nabla P_{{\rm{BR}}}^{{\rm{ks}}} = \Delta \nabla \rho _{{\rm{BR}}}^{{\rm{ks}}} + \Delta \nabla O_{{\rm{BR}}}^{{\rm{ks}}} + \\ \Delta \nabla T_{{\rm{BR}}}^{{\rm{ks}}} + \Delta \nabla I_{{\rm{BR}}}^{{\rm{ks}}} + {\xi _{\Delta \nabla P_{{\rm{BR}}}^{{\rm{ks}}}}} \end{array} $ | (2) |
式中,Δ∇为双差算子,i为频率,λ为频率i下的波长,P为伪距观测值,φ为载波相位观测值,ρ为接收机与卫星之间的几何距离,O为卫星轨道误差,T为对流层延迟误差,I为电离层延迟误差,N为整周模糊度,ξφ和ξP分别为含多路径误差及观测噪声的载波相位观测值误差及伪距观测值误差。
中长基线定位通常采用“三步走”策略进行整周模糊度解算,首先利用载波相位的宽巷组合和伪距的窄巷组合解算宽巷模糊度;然后利用卡尔曼滤波求解无电离层组合的浮点解,并将其转换为宽巷模糊度和窄巷模糊度两个部分;最后利用LAMBDA算法对窄巷模糊度进行搜索固定[11],将正确固定的窄巷模糊度回代从而得到三维基线分量。根据基准站的已知坐标和基线分量便可以得到流动站的三维坐标,即RTK的最终定位结果。
2.2 附加模糊度参数的卡尔曼滤波中长基线RTK定位采用附加模糊度参数的卡尔曼滤波模型,该模型的状态方程和观测方程如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{X}}_e} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{e, e - 1}}{\mathit{\boldsymbol{X}}_{e - 1}} + {w_e}}\\ {{\mathit{\boldsymbol{L}}_e} = {\mathit{\boldsymbol{A}}_e}{\mathit{\boldsymbol{X}}_e} + {\mathit{\boldsymbol{V}}_e}} \end{array}} \right. $ | (3) |
| $ \begin{array}{l} {\mathit{\boldsymbol{X}}_e} = \left[ {{x_e}{y_e}{z_e}x_e^\prime y_e^\prime z_e^\prime x_e^{\prime \prime }y_e^{\prime \prime }{z^{\prime \prime }}_e} \right.\\ \left. {\;\;\;\;\;\;\;\;\Delta \nabla {N_1}\;\Delta \nabla {N_2}\; \cdots \;\Delta \nabla {N_n}} \right] \end{array} $ | (4) |
式中,Xe、Xe-1为te与te-1时刻的状态向量参数;Φe, e-1为te到te-1时刻的状态转移矩阵;we为高斯白噪声过程输入噪声向量;Le为te时刻的观测向量;Ae为观测方程的系数矩阵;Ve为观测值的噪声向量;xe、ye、ze为坐标未知参数,初值采用伪距单点定位结果;x′e、y′e、z′e为速度未知参数,初值根据多普勒观测值求解;x″e、y″e、z″e为加速度未知参数,初值设为0 m/s2;Δ∇Ni(i=1, 2, …n)为n个模糊度未知参数,初值如下:
| $ \Delta \nabla N = \left( {\frac{{\Delta \nabla P - \Delta \nabla \varphi }}{\lambda }} \right) $ | (5) |
式中,P为伪距观测值,φ为载波相位观测值,λ为波长。
卡尔曼滤波的具体计算过程主要分3步:
1) 状态预测。计算下一个历元的状态向量Xe, e-1及其协方差阵Pe, e-1:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{X}}_{e, e - 1}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{e, e - 1}}{\mathit{\boldsymbol{X}}_{e - 1}}}\\ {{\mathit{\boldsymbol{P}}_{e, e - 1}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{e, e - 1}}{\mathit{\boldsymbol{P}}_{e - 1, e - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{e, e - 1}^{\rm{T}} + {\mathit{\boldsymbol{Q}}_{e - 1}}} \end{array}} \right. $ | (6) |
2) 滤波增益。计算增益矩阵Ke:
| $ \boldsymbol{K}_{e}=\boldsymbol{P}_{e, e-1} \boldsymbol{A}_{e}^{\mathrm{T}}\left(\boldsymbol{A}_{e} \boldsymbol{P}_{e, e-1} \boldsymbol{A}_{e}^{\mathrm{T}}+\boldsymbol{R}_{e}\right)^{-1} $ | (7) |
3) 滤波更新。计算当前时刻的滤波估值Xe, e和协方差矩阵Pe, e:
| $ \left\{\begin{array}{l} \boldsymbol{X}_{e, e}=\boldsymbol{X}_{e, e-1}+\boldsymbol{K}_{e} \boldsymbol{v}_{e} \\ \boldsymbol{P}_{e, e}=\left(\boldsymbol{I}-\boldsymbol{K}_{e} \boldsymbol{A}_{e}^{\mathrm{T}}\right) \boldsymbol{Q}_{e, e-1} \end{array}\right. $ | (8) |
上述公式中的系统噪声阵Qe-1、观测误差方差阵Re和观测方程残差项ve的具体设置见文献[12]。需要注意的是,相邻历元间会存在卫星的上升与下降和参考星的变换,使模糊度参数的维数发生改变,滤波过程中要构建合适的转换矩阵来解决卫星升降和参考星变换的问题。
3 实验结果与分析本文使用陕西省和广东省某区域参考站的实测数据,选取其中HZLB、HZNZ、HZXX、GDYT和GDJN五个测站,组成4组中长基线进行实验(表 2)。陕西省3个测站数据观测时间为2020-05-27,广东省2个测站数据观测时间为2021-08-21,5个测站均能接收到BDS-3新信号B1C和B2a的观测值,数据采样间隔为30 s,采样时长为24 h,历元数为2 880个。
|
|
表 2 基线具体信息 Tab. 2 Baseline specific information |
利用自编软件进行实验时,截止高度角为10°,选用高度角模型作为随机模型,采用卡尔曼滤波进行参数估计,采用LAMBDA算法进行模糊度搜索固定,采用UNB3模型改正对流层延迟误差,采用无电离层组合观测值改正电离层延迟误差,利用经验模型改正相对论效应和地球自转带来的误差。为分析BDS-3新信号的数据质量和中长基线RTK的定位性能,分别对GPS的L1、GPS的L2、BDS-3的B1I、BDS-3的B3I、BDS-3的B1C和BDS-3的B2a信号进行数据质量分析,对GPS的L1+L2、BDS-3的B1I+B3I和BDS-3的B1C+B2a无电离层组合进行中长基线RTK定位精度分析。
3.1 数据质量分析 3.1.1 可见卫星数与PDOP值在RTK定位中,可见卫星数越多,空中卫星分布越稳定,几何图形强度越强。图 1统计了HZXX测站可视卫星数目和定位精度因子(PDOP),可以看出,能接收GPS的L1、L2信号的卫星数目为7~12颗,能接收BDS-3的B1I、B3I信号的卫星数目为10~15颗,能接收BDS-3的B1C、B2a信号的卫星数目为8~13颗。接收BDS-3新信号的观测卫星数少于B1I、B3I信号的观测卫星数,原因是BDS-3的GEO卫星不播发新信号。两个系统的可视卫星数存在一定波动,但均满足RTK定位所需的卫星数。BDS-3的PDOP值在2以内,GPS的PDOP值在4以内,说明BDS-3系统卫星的空间几何结构稳定,具有较好的定位观测结构。

|
图 1 HZXX测站可视卫星数和PDOP值 Fig. 1 The visible satellite number and PDOP values of HZXX station |
信噪比(SNR)是信号功率与噪声功率的比值,单位为dB-Hz。信噪比能反映载波相位观测值的质量,数值越大,观测质量就越好。除了反映观测质量,信噪比还可以反映接收机性能和卫星状态,因此观测数据文件中会记录当前历元每颗卫星各信号的信噪比。图 2是5个测站相应信号所有卫星信噪比的平均值,可以看出,各信号之间具有差异性。BDS-3的B2a信号信噪比最高,GPS的L2信号信噪比最低,但也大于35 dB-Hz;GPS的2个信号信噪比差异较大,最大可达5 dB-Hz;BDS-3的4个信号信噪比相当,均大于40 dB-Hz,高于适宜跟踪的信号强度,体现了BDS-3各颗卫星在建设上的统一性。

|
图 2 各测站信噪比平均值 Fig. 2 Average SNR ratio of each station |
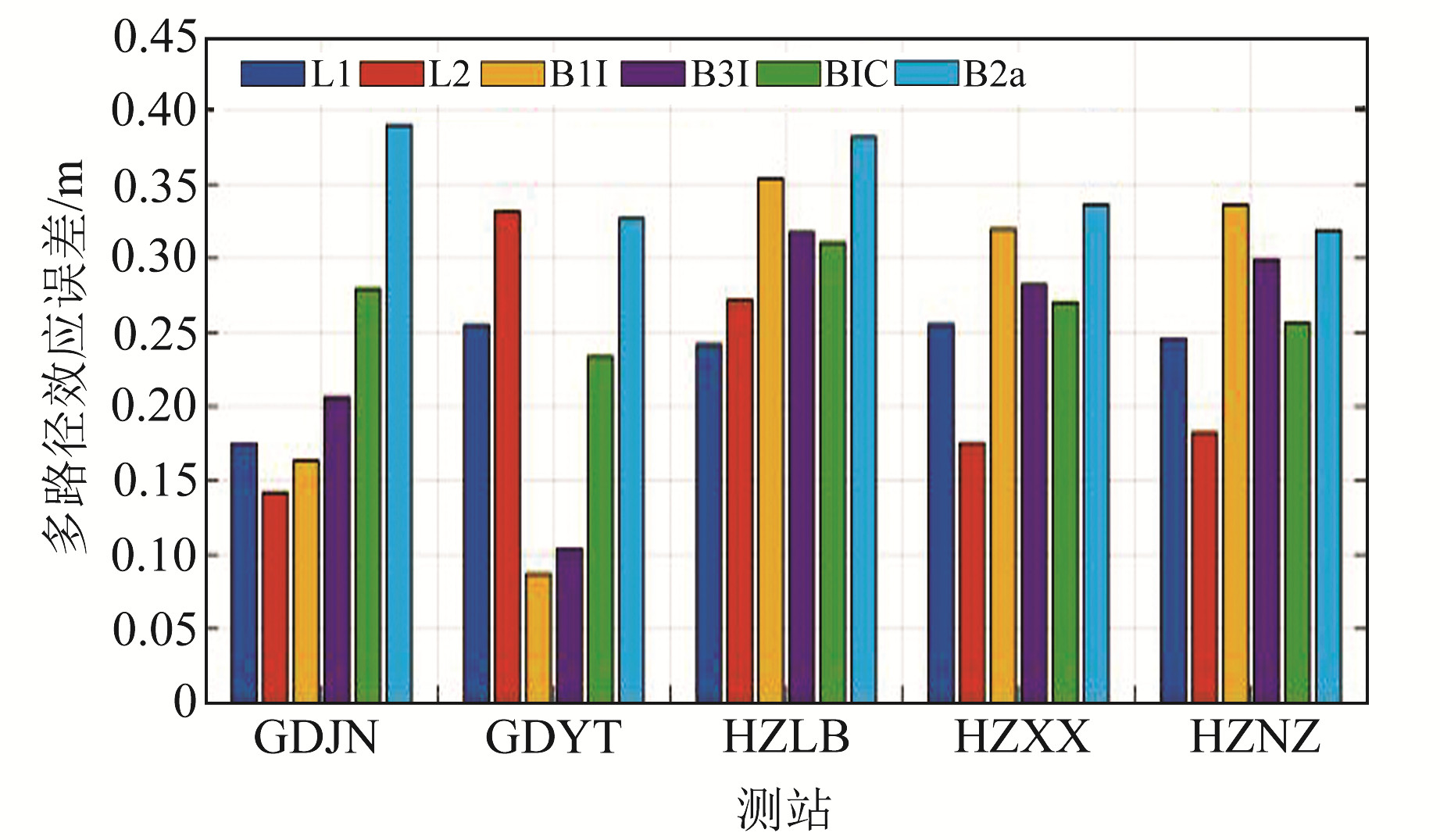
卫星信号传播过程中产生的反射波进入接收机天线时,与直接来自卫星的信号产生干涉,从而使观测值与真值之间产生偏差,这种偏差称为多路径误差。多路径误差会影响定位的精度,严重时还会造成卫星失锁。图 3为5个测站相应信号所有卫星伪距多路径误差的平均值,可以看出,由于各测站外部观测环境不同,同一信号之间存在差异,但在同一测站内,GPS和BDS-3不同信号的多路径误差相对大小关系一致。GPS的L1和L2信号在不同环境下的多路径误差相差不大,均优于0.3 m;BDS-3的B1C新信号的多路径误差略优于B2a信号,但差距不大。两个系统所有信号的伪距多路径误差均小于0.4 m,说明5个测站的外部观测环境较优,数据质量较好。
|
图 3 各测站多路径误差平均值 Fig. 3 Average values of multipath error of each station |
ratio值是模糊度整数解的最优单位权方差与次优单位权方差的比值,在一定程度上可以反映确定的整周模糊度的可靠性,即模糊度固定是否成功。当ratio值大于2或3时,模糊度固定成功[13]。表 3统计了4组基线的模糊度首次固定时间,其中模糊度首次固定的标志为:1)ratio≥2;2)固定后水平方向定位误差小于0.1 m,高程方向定位误差小于0.2 m。由表 3可知,BDS-3新信号的模糊度首次固定时间略低于B1I+B3I组合,高于L1+L2组合,且随着基线长度的增加,3种组合方式的模糊度首次固定时间均会增加。此外,由于实验数据观测时间较长,模糊度首次固定后,会出现固定失败的情况。本文将ratio值的阈值设为2后,4组基线3种组合方式的模糊度固定成功率均大于80%。
|
|
表 3 模糊度首次固定时间 Tab. 3 Time to the first fix of ambiguity |
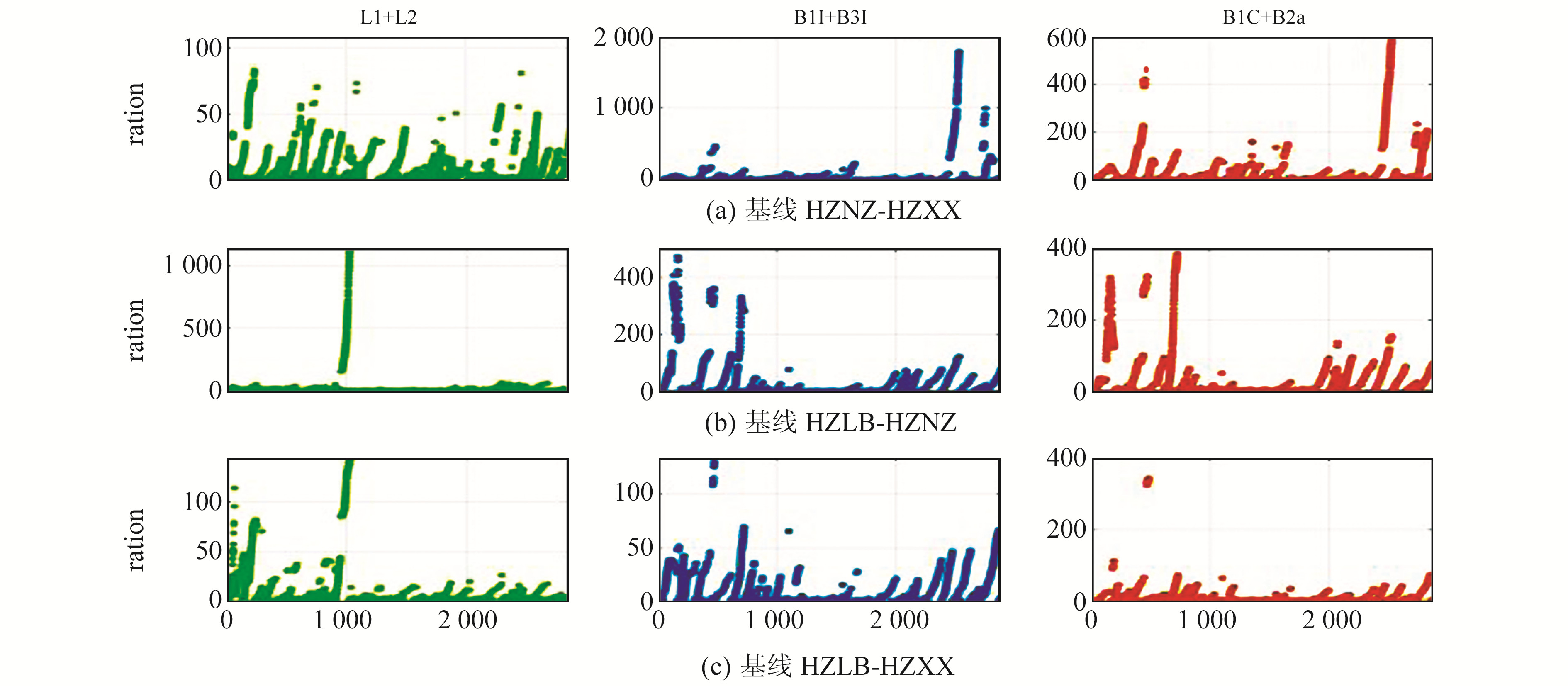
陕西省3组基线3种组合方式每个历元的ratio值如图 4所示,可以看出,由于使用LAMBDA算法对模糊度浮点解进行搜索固定时,不同组合参与搜索的模糊度数量不同,3组基线3种组合方式的ratio值互有高低,BDS-3的B1C+B2a组合与B1I+B3I组合总体水平相当。
|
图 4 陕西省3组基线ratio值变化 Fig. 4 Changes of ratio values of three baselines in Shaanxi |
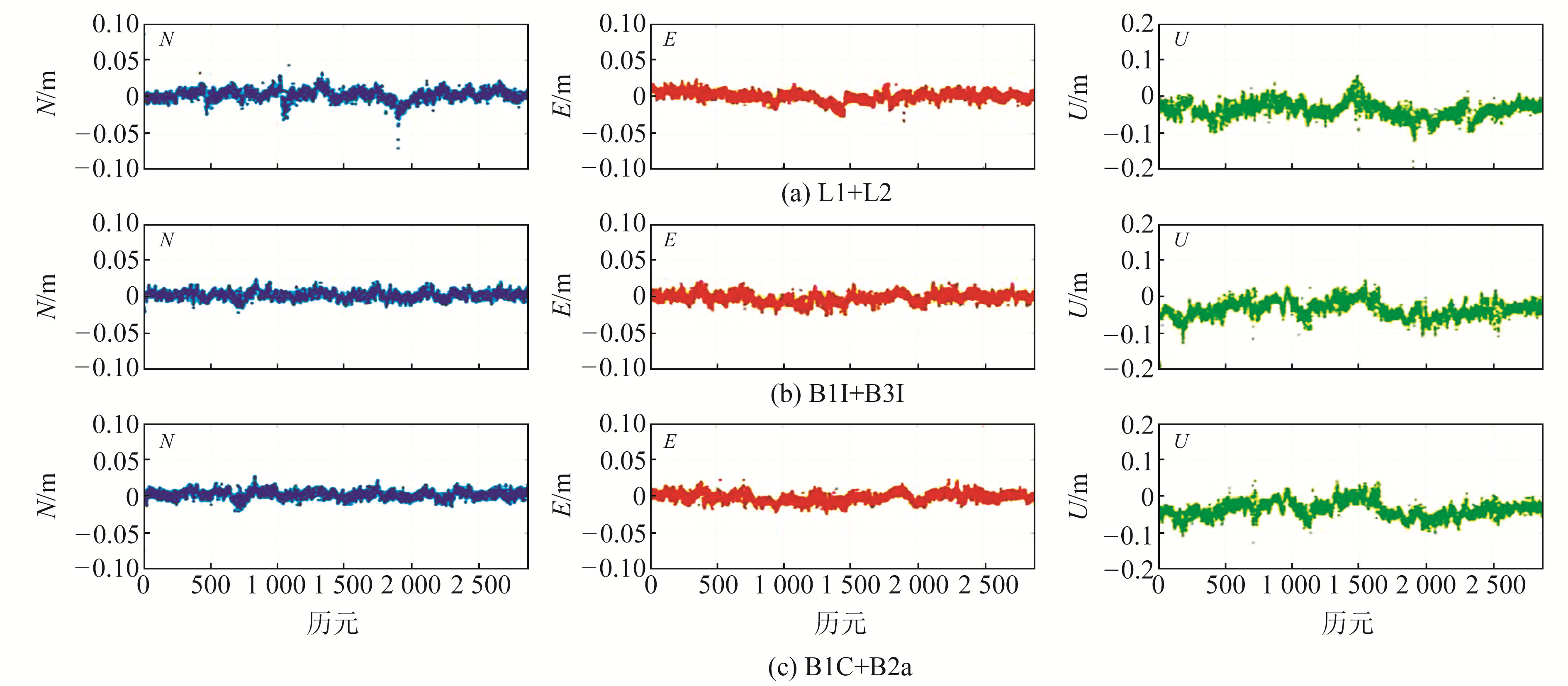
计算4组基线3种无电离层组合方式的RTK定位结果,将每个历元的定位结果与流动站真实坐标作差,并利用转换矩阵将差值转换到北(N)、东(E)、天(U)3个方向。图 5统计了基线HZNZ-HZXX的定位误差,其中包含浮点解和固定解,可以看出,在3种组合方式下,基线HZNZ-HZXX水平方向定位误差在-5.0~5.0 cm范围内波动,高程方向定位误差在-10.0~10.0 cm范围内波动。
|
图 5 基线HZNZ-HZXX在3种组合方式下N、E、U方向误差 Fig. 5 Error of N, E and U directions under three combinations of baseline HZNZ-HZXX |
表 4统计了固定解情况下4组基线3种组合方式在N、E和U三方向的RMS值,同时统计了水平和高程方向的定位精度。可以看出,GPS的L1+L2组合水平定位精度优于3.0 cm,高程定位精度优于6.0 cm;BDS-3的B1I+B3I组合水平定位精度优于3.0 cm,高程定位精度优于5.0 cm;BDS-3的B1C+B2a组合水平定位精度优于2.0 cm,高程定位精度优于5.0 cm。随着基线长度的增加,位于同一区域的3组基线测站之间大气延迟误差相关性下降,从而导致定位精度降低。基线1的定位精度低于基线2和基线3,原因是基线1位于低纬度地区,基线2和基线3位于中纬度地区,低纬度地区电离层活跃程度较强,电离层残余误差会对基线1的定位结果造成影响。GPS的L1+L2组合定位精度低于BDS-3的两种组合;BDS-3的B1C+B2a组合定位精度略优于其他两种组合,验证了BDS-3新信号中长基线双频RTK定位具有更优的定位精度。
|
|
表 4 4组基线RTK定位的RMS值 Tab. 4 RMS of RTK positioning error of four baselines |
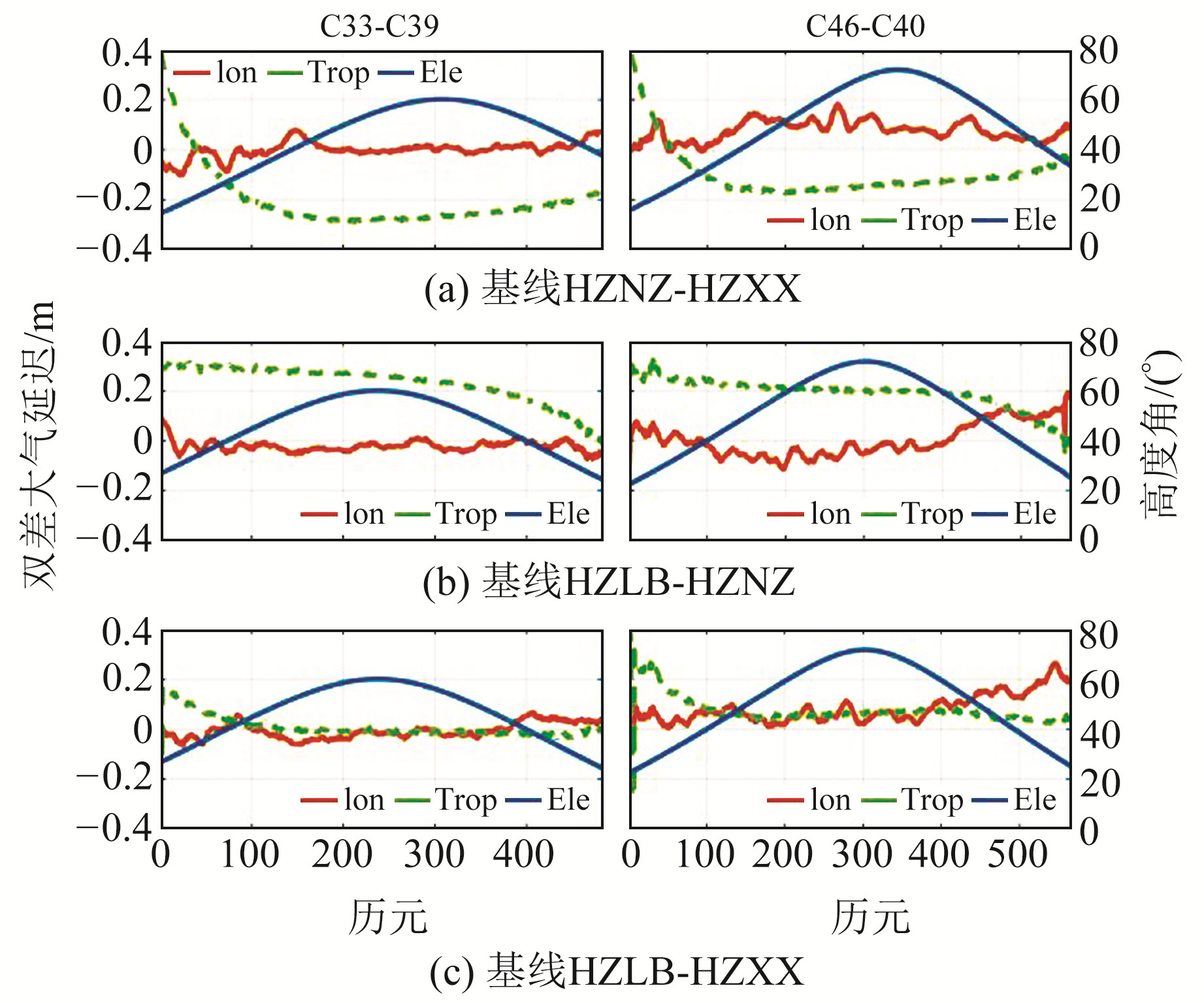
在模糊度固定后,将模糊度参数回代,可以计算出基线的双差大气延迟误差。图 6统计了陕西省3组基线在B1C+B2a组合下C33卫星(参考星为C39)和C46卫星(参考星为C40)的双差大气延迟,可以看出,双差电离层延迟在-0.25~0.25 m范围波动,双差对流层延迟在-0.40~0.40 m范围波动。大气延迟与卫星高度角之间存在相关性,高度角低的卫星电离层延迟较大,对流层延迟随卫星高度角变化比较明显。3组基线的双差电离层延迟最大值接近0.25 m,双差对流层延迟最大值接近0.40 m,因此在中长基线RTK定位时需顾及大气延迟误差的影响。
|
图 6 陕西省3组基线双差大气延迟 Fig. 6 Double difference atmospheric delay of three baselines in Shaanxi province |
针对北斗三号卫星B1C和B2a新信号中长基线RTK定位精度仍未确定的问题,本文利用4组中长基线实测数据,对BDS-3的B1C和B2a新信号进行数据质量分析和中长基线双频RTK定位精度分析,得出如下结论:
1) BDS-3接收新信号的卫星数目多于接收GPS的2个信号的卫星数目,BDS-3空中卫星的几何强度优于GPS,具有较好的定位观测结构。
2) BDS-3的B1C和B2a新信号的信噪比均大于40 dB-Hz,高于良好信噪比阈值,与B1I、B3I、L1、L2信号相差不大;新信号的多路径误差与B1I、B3I、L1、L2信号相当,均小于0.4 m,总体反映出BDS-3卫星工作性能一致、观测数据质量较高。
3) BDS-3的B1C和B2a新信号的中长基线RTK定位模糊度首次固定时间略低于BDS-3的B1I+B3I组合,高于GPS的L1+L2组合;定位精度略优于GPS的L1+L2组合和BDS-3的B1I+B3I组合,水平定位精度优于2.0 cm,高程定位精度优于5.0 cm,可以为用户提供cm级定位精度。
本文中长基线RTK定位实验中,大气延迟误差采用模型进行改正,高程方向定位结果明显受未完全修正的大气延迟误差影响,后续将从以大气延迟误差作为未知参数估计、区域大气延迟误差建模等方面尝试削弱大气延迟误差的影响,以获得更优的中长基线RTK定位性能。
| [1] |
杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6 (Yang Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6)
(  0) 0) |
| [2] |
中国卫星导航系统管理办公室. 北斗卫星导航系统公开服务性能规范(3.0版)[EB/OL]. http://www.beidou.gov.cn/xt/gfxz/202105/P020210526215541444683.pdf, 2021-05-26 (China Satellite Navigation Office. Beidou Navigation Satellite System Open Service Performance Standard(Version 3.0)[EB/OL]. http://www.beidou.gov.cn/xt/gfxz/202105/P020210526215541444683.pdf, 2021-05-26)
(  0) 0) |
| [3] |
王世进. BDS/GPS-RTK算法研究及软件实现[D]. 阜新: 辽宁工程技术大学, 2014 (Wang Shijin. Research on Real-Time Kinematic Algorithm of BDS/GPS and Its Implement of Software[D]. Fuxin: Liaoning Technical University, 2014)
(  0) 0) |
| [4] |
国家市场监督管理总局, 国家标准化管理委员会. GB/T 27606-2020 GNSS接收机数据自主交换格式[S]. 北京: 中国标准出版社, 2020 (State Administration for Market Regulation, Standardization Administration of the People's Republic of China. GB/T 27606-2020 GNSS Receiver Independent Exchange Format[S]. Beijing: Standards Press of China, 2020)
(  0) 0) |
| [5] |
张明远, 周星宇, 陈华. 北斗三号新信号B2a和B2(B2a+b)质量分析及星座几何性能评估[J]. 大地测量与地球动力学, 2020, 40(6): 629-633 (Zhang Mingyuan, Zhou Xingyu, Chen Hua. Quality Analysis and Constellation Geometric Performance Evaluation of New Signals B2a and B2(B2a+b) of BDS-3[J]. Journal of Geodesy and Geodynamics, 2020, 40(6): 629-633)
(  0) 0) |
| [6] |
Zhang Q H, Zhu Y X, Chen Z S. An In-Depth Assessment of the New BDS-3 B1C and B2a Signals[J]. Remote Sensing, 2021, 13(4): 788 DOI:10.3390/rs13040788
(  0) 0) |
| [7] |
慕仁海, 党亚民, 许长辉. BDS-3新频点单点定位研究[J]. 测绘通报, 2021(3): 12-17 (Mu Renhai, Dang Yamin, Xu Changhui. Research on Single Point Positioning of BDS-3 New Signal[J]. Bulletin of Surveying and Mapping, 2021(3): 12-17)
(  0) 0) |
| [8] |
吴仁攀, 刘万科, 吴风波, 等. 北斗中长基线动态定位首次固定时间和定位精度分析[J]. 大地测量与地球动力学, 2018, 38(7): 668-672 (Wu Renpan, Liu Wanke, Wu Fengbo, et al. Analysis of TTFF and Accuracy of BDS Medium-Long Baseline Kinematic Relative Positioning[J]. Journal of Geodesy and Geodynamics, 2018, 38(7): 668-672)
(  0) 0) |
| [9] |
刘健, 曹冲. 全球卫星导航系统发展现状与趋势[J]. 导航定位学报, 2020, 8(1): 1-8 (Liu Jian, Cao Chong. Development Status and Trend of Global Navigation Satellite System[J]. Journal of Navigation and Positioning, 2020, 8(1): 1-8)
(  0) 0) |
| [10] |
高成发, 胡伍生. 卫星导航定位原理与应用[M]. 北京: 人民交通出版社, 2011 (Gao Chengfa, Hu Wusheng. The Principle and Application of Satellite Navigation and Positioning[M]. Beijing: China Communications Press, 2011)
(  0) 0) |
| [11] |
乔龙雷. 多星座多频组合高精度基线解算算法研究及软件开发[D]. 南京: 东南大学, 2017 (Qiao Longlei. Research on Multi-Constellation and Multi-Frequency Combined High-Precision Baseline Resolution and Software Development[D]. Nanjing: Southeast University, 2017)
(  0) 0) |
| [12] |
王世进, 秘金钟, 李得海, 等. GPS/BDS的RTK定位算法研究[J]. 武汉大学学报: 信息科学版, 2014, 39(5): 621-625 (Wang Shijin, Bei Jinzhong, Li Dehai, et al. Real-Time Kinematic Positioning Algorithm of GPS/BDS[J]. Geomatics and Information Science of Wuhan University, 2014, 39(5): 621-625)
(  0) 0) |
| [13] |
鄢子平, 丁乐乐, 黄恩兴, 等. 网络RTK参考站间模糊度固定新方法[J]. 武汉大学学报: 信息科学版, 2013, 38(3): 295-298 (Yan Ziping, Ding Lele, Huang Enxing, et al. A New Method of Ambiguity Resolution in Network RTK between Reference Stations[J]. Geomatics and Information Science of Wuhan University, 2013, 38(3): 295-298)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


