2. 地震预警湖北省重点实验室, 武汉市洪山侧路48号, 430071;
3. 湖北省地震局, 武汉市洪山侧路48号, 430071;
4. 运城学院数学与信息技术学院, 山西省运城市复旦西街1155号, 044031;
5. 南华大学计算机学院, 湖南省衡阳市常胜西路28号, 421001
随着人类生产活动的急剧增加,距离地震台站较近或震感强烈的人工爆破事件有一定概率被地震观测仪器视作天然地震事件所记录,产生的误记录操作将会污染已有的地震目录甚至产生地震灾害应急误判。天然地震事件与人工爆破事件性质辨识是当下地震学研究及地震观测技术应用的重要内容,结合机器学习或深度学习的分类决策方法在其中占据重要地位[1]。
地震事件性质辨识的主要手段是寻找合适的地震波形特征及特征识别方法。在地震特征提取领域,已有学者基于时域或频域特征深入研究,如香农熵小波系数[2]、波形对称度[3]、HHT提取IMF特征[4]等;在地震特征识别领域,常见的识别方法有决策树[5]、支持向量机[6]、Boosting[7]、线性判别分析[8]等,但这些方法存在易过拟合、分类错误率较高或对多重共线性特征敏感等弊端。
本文首先对原始记录进行归一化处理,提取排列熵、近似熵及香农熵等特征值形成实验数据集,利用基于SVM改进的LSSVM二分类方法对天然地震、非天然地震事件进行性质分类,采用机器学习混淆矩阵中的准确率、召回率及F-measure指标对分类结果进行有效性评价,结合其他机器学习方法的辨识效果对比分析LSSVM算法的优劣性能。
1 事件性质分类方法最小二乘支持向量机(least square SVM,LSSVM)擅长处理大规模非线性问题,数据训练速度较快,属于支持向量机的改进型方法[9],其变化有3点:1)优化目标函数采用2NF(第2范式);2)将不等式约束条件转化为等式约束条件,进而求解线性方程组,加快了求解速度,更有利于处理较大规模问题;3)对排序后的Lagrange乘子进行裁剪处理,增强解的稀疏性和决策函数的适用性。
LVSVM的分类过程为:
1) 对于LSSVM分类问题,约束条件是不等式约束:
| $ \begin{gathered} \min \nolimits_{\omega, b, e} J(\boldsymbol{\omega}, e)=\frac{1}{2} \boldsymbol{\omega}^{\mathrm{T}} \boldsymbol{\omega}+\frac{1}{2} \gamma \sum\limits_{k=1}^{N} e_{k}^{2}, \\ y_{k}\left[\boldsymbol{\omega}^{\mathrm{T}} \varphi\left(x_{k}\right)+b\right]=1-e_{k}, k=1,2, \cdots, N \end{gathered} $ | (1) |
式中,γ为权重参数;ω为超平面法向量;ek为偏离超平面的松弛变量;φ(xk)为核函数定义的非线性映射;b为超平面的截距;yk表示线性分类一般模型{yk|yk=ω·xk+b}的分类类别,xk为训练样本数据。
2) 采用Lagrange乘数法转换为求解α的极大值问题:
| $ \begin{gathered} \boldsymbol{L}(\boldsymbol{\omega}, b, e ; \boldsymbol{\alpha})=J(\boldsymbol{\omega}, e)- \\ \sum\limits_{k=1}^{N} \alpha_{k}\left\{y_{k}\left[\boldsymbol{\omega}^{\mathrm{T}} \varphi\left(x_{k}\right)+b\right]-1+e_{k}\right\} \end{gathered} $ | (2) |
式中,αk为Lagrange乘子。分别对ω、αk、b、ek求导,使其等于0:
| $ \left\{\begin{array}{l} \frac{\partial \boldsymbol{L}}{\partial \boldsymbol{\omega}}=0 \rightarrow \boldsymbol{\omega}=\sum\limits_{k=1}^{N} \alpha_{k} y_{k} \varphi\left(x_{k}\right) \\ \frac{\partial \boldsymbol{L}}{\partial b}=0 \rightarrow \sum\limits_{k=1}^{N} \alpha_{k} y_{k}=0 \\ \frac{\partial \boldsymbol{L}}{\partial e_{k}}=0 \rightarrow \alpha_{k}=\gamma e_{k}, k=1,2, \cdots, N \\ \frac{\partial \boldsymbol{L}}{\partial \alpha_{k}}=0 \rightarrow y_{k}\left[\boldsymbol{\omega}^{\mathrm{T}} \varphi\left(x_{k}\right)+b\right]-1+e_{k}=0, \\ \ \ \ \ k=1,2, \cdots, N \end{array}\right. $ | (3) |
根据式(3)列出关于α和b的线性方程组:
| $ \left[\begin{array}{cc} 0 & \boldsymbol{y}^{\mathrm{T}} \\ \boldsymbol{y} & \boldsymbol{\varOmega}+I / \gamma \end{array}\right]\left[\begin{array}{l} b \\ \boldsymbol{\alpha} \end{array}\right]=\left[\begin{array}{c} 0 \\ 1_{v} \end{array}\right] $ | (4) |
定义核矩阵Ωkl:
| $ \begin{gathered} \boldsymbol{\varOmega}_{k l}=y_{k} y_{l} \varphi\left(x_{k}\right)^{\mathrm{T}} \varphi\left(x_{l}\right)=y_{k} y_{l} K\left(x_{k}, x_{l}\right), \\ k, l=1,2, \cdots, N \end{gathered} $ | (5) |
3) 解以上方程组可以得到α和b,最终得到LSSVM的分类表达式为:
| $ f(x)=\operatorname{sign}\left[\sum\limits_{k=1}^{N} \alpha_{k} y_{k} K\left(x, x_{k}\right)+b\right] $ | (6) |
特征提取是展开地震事件属性识别的重要基础工作,提取的特征参数直接关系到事件性质判断的准确性和辨识模型的合理性。本文利用信息论中的熵来表征地震事件记录的特征。熵(entropy)是一种描述系统内部混乱状态的度量值,由克劳修斯于1865年在解决热力学问题时提出。常见的熵值类型包括香农熵、交叉熵、条件熵、相对熵等,已在应用物理、生命科学、应用数学及人工智能等学科领域得到应用。地震仪器记录到的震级较大的地震记录具有明显的波形统计特征和不规则性(局部混乱),采用熵概念中的排列熵[10]、近似熵[11]、香农熵[12]等表征地震事件性质是一种新的尝试和探讨。
2.1 排列熵排列熵(permutation entropy,Hp)是2002年由Bandt等[10]提出的,其值的大小表示时间序列的复杂程度或随机性,值越小,信号的复杂性越低;值越大,信号的不规则性越严重。
设信号时间序列为{X(i), i=1, 2, …, n},进行相空间重构后得到如下矩阵:
| $ \left[\begin{array}{cccc} x(1) & x(1+\tau) & \cdots & x(1+(m-1) \tau) \\ x(2) & x(2+\tau) & \cdots & x(2+(m-1) \tau) \\ \vdots & \vdots & \ddots & \vdots \\ x(k) & x(k+\tau) & \cdots & x(k+(m-1) \tau) \end{array}\right] $ | (7) |
其中,m为嵌入维数,τ为延时因子,k=n-(m-1)τ, j=1, 2, …, k。矩阵共有k个重构分量,每个重构分量有m维嵌入元素。
将式(7)中的第j个分量按数值大小升序排列,得到:
| $ \begin{gathered} x\left(i+\left(j_{1}-1\right) \tau\right) \leqslant x\left(i+\left(j_{2}-1\right) \tau\right) \leqslant \cdots \\ \leqslant x\left(i+\left(j_{m}-1\right) \tau\right) \end{gathered} $ | (8) |
每个重构分量都可以得到一个重构符号序列:
| $ S(l)=\left(j_{1}, j_{2}, \cdots, j_{m}\right) $ | (9) |
其中,l=1, 2, …, k,满足k≤m!。每个重构分量是m维空间映射到m维的符号序列,共有m!种排列方式。
计算每种m维符号序列的概率P1, P2, …, Pk,根据香浓熵的定义,信号时间序列X(i)的排列熵定义为:
| $ H_{p}(m)=-\left(\sum\limits_{j=1}^{k} P_{j} \ln P_{j}\right) $ | (10) |
当Pj=1/m!时,排列熵达到最大值ln(m!)。
2.2 近似熵近似熵(approximate entropy,ApEn)是1991年由Pincus[11]提出的,描述m维向量扩展至m+1维向量时的相似性或周期性度量值。作为一个非负值,ApEn的值越大,表示时序数据具有越强的随机性或非周期性,可用来描述信号的复杂程度。近似熵的计算步骤为:
1) 按照式(11)构建m维向量,用y(i)表示,即{y(i), i=1, 2, …, M, M=N-m+1},其中y(i)={x(i), x(i+1), …, x(i+m-1)},m为嵌入维数,是重构序列的长度。计算y(i)与y(j)任意分量之间的欧氏距离d{y(i), y(j)},并将各分量之间最大的距离定义为最大贡献成分距离D{y(i), y(j)},得到:
| $ D\{\boldsymbol{y}(i), \boldsymbol{y}(j)\}=\max \{|\boldsymbol{y}(i+k)-\boldsymbol{y}(j+k)|\} $ | (11) |
其中,j, i=1, 2, …, N-m+1;k=0, 1, …, m-1。
2) 给定阈值r(r>0),给定嵌入维数m,计算代表序列{y(i)}规律性的概率大小量度Cim(r),即统计D{y(i), y(j)} < r的个数Nm(i)与总数N-m+1的比例,也叫概率大小,即
| $ C_{i}^{m}(r)=N^{m}(i) /(N-M+1), i \leqslant N-m+1 $ | (12) |
对每个求得的Cim(r)计算对数值,并计算对数的平均值φm(i),即
| $ \varphi^{m}(i)=\left(\sum\limits_{i=1}^{N-m+1} \ln C_{i}^{m}(r)\right) /(N-m+1) $ | (13) |
3) 将嵌入维数变为m+1,重复上述步骤,得到Cim(r)和φm(i)。该序列的近似熵(ApEn)表示为:
| $ \operatorname{ApEn}(m, r)=\varphi^{m}(i)-\varphi^{m+1}(i) $ | (14) |
其中,当嵌入维数m选取2或3时,有效阈值可设定为0.15倍或0.2倍的时序标准差值。
2.3 香农熵香农熵H是包含平均信息量多少的度量指标,熵值越大,说明数据中的信息量越多[12]。其定义为:
| $ H=-\sum\limits_{i=0}^{l-1} p(i) \log _{2} p(i) $ | (15) |
本文实验数据来源于中国地震局工程力学研究所记录的2021年青海玛多MS7.4地震事件与云南漾濞MS6.4、MS5.6地震事件及人工爆破事件,其中源于地震事件的三分量波形数目为158,源自人工爆破干扰事件的波形数目为342,共500份波形数据。事件及数据描述如下:
1) 根据中国地震台网中心测定,2021-05-21 21:21云南省大理州漾濞县发生MS5.6地震,震源深度10 km,共有28个台站(表 1)记录到此次强震动事件,其中漾濞台震中距最小,为5.4 km,东西、南北及垂直向加速度峰值分别为-339.2 cm/s2、267.2 cm/s2、-220.1 cm/s2,计算仪器地震烈度为7.7度。
|
|
表 1 云南漾濞地震事件台站信息 Tab. 1 Information of Yunnan Yangbi seismic event station |
2) 2021-05-21 21:48云南省大理州漾濞县(25.67°N,99.87°E)发生MS6.4地震,震源深度8 km,其中漾濞台震中距最小,为7.9 km,东西、南北、垂直向加速度峰值分别为-379.9 cm/s2、720.3 cm/s2、-448.4 cm/s2,速度峰值分别为30.4 cm/s、-29.8 cm/s、-7.2 cm/s,计算仪器地震烈度为8.3度。
3) 2021-05-22 02:04青海省果洛州玛多县(34.59°N,98.34°E)发生MS7.4地震,震源深度17 km,共有16个台站(表 2)记录到此次强震动事件,其中大武台震中距175.6 km,东西、南北、垂直向加速度峰值分别为46.0 cm/s2、40.6 cm/s2、-19.1 cm/s2,计算仪器地震烈度为6.0度。
|
|
表 2 青海玛多地震事件台站信息 Tab. 2 Information of Maduo seismic event station in Qinghai |
4) 人工爆破事件数据来自中国水利水电科学研究院岩土工程研究所,使用PCB 350B01型加速度计和PCB 350D02型加速度计进行采集,频率响应为1 Hz~10 kHz,得到共计342条加速度波形记录,记录长度皆为40 000 m/s2。
由于每条记录的长度(或采样时间)及采样频率并不一致且差异较大,为消除幅值大小对特征工程的影响,本文统一取全波段数据进行归一化处理,并按照排列熵、近似熵、香农熵的公式计算得到地震辨识实验的机器学习特征集,其中熵值计算的嵌入维数设定为2,时间延迟为1,容忍度(标准差std)为0.15,计算结果如图 1所示,统计结果见表 3。设计多个辨识子实验,其中训练集比例分别为10%、20%、40%、60%、80%,皆为完全随机抽取。
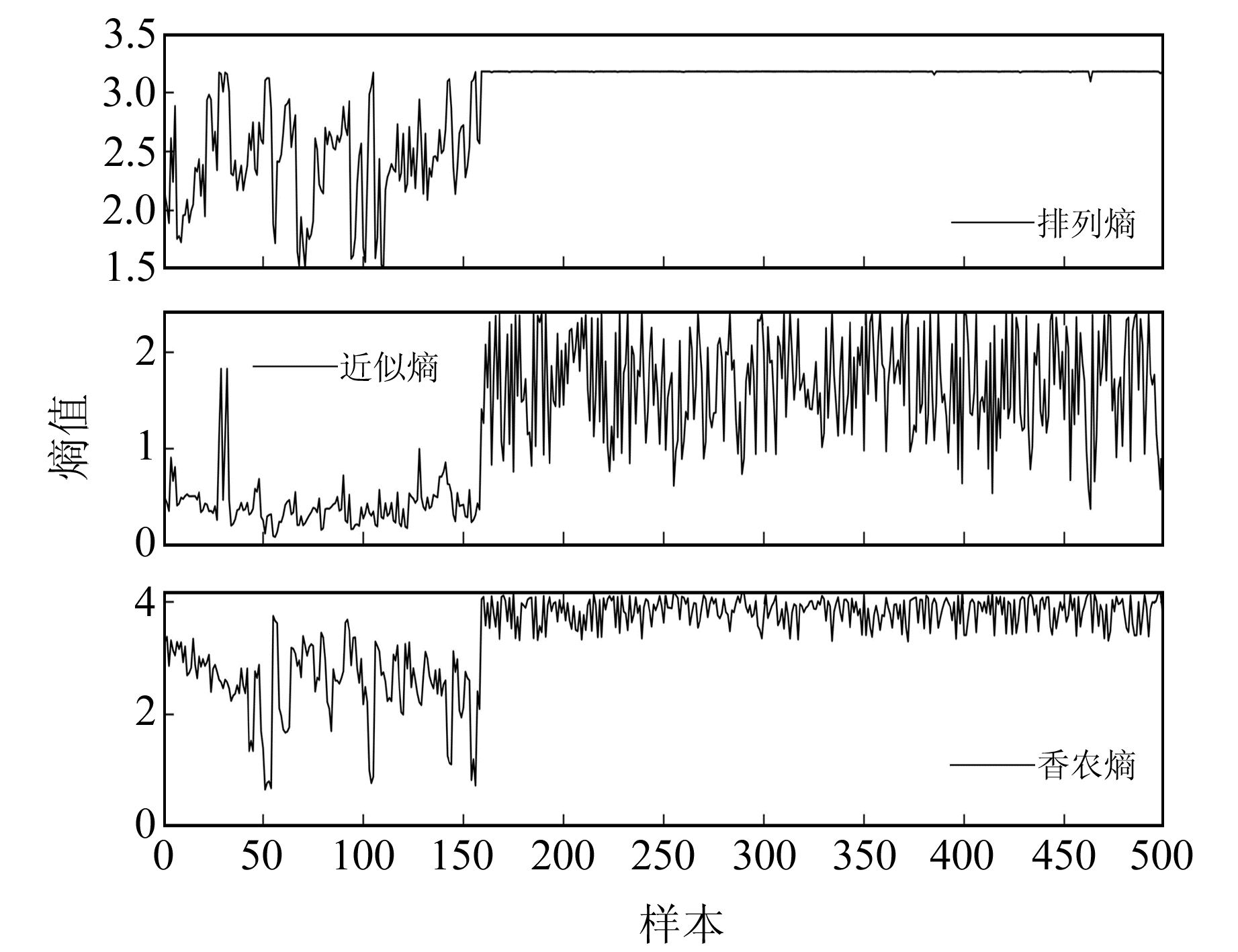
|
图 1 熵值计算结果 Fig. 1 Calculation results of entropy |
|
|
表 3 样本特征集统计结果 Tab. 3 Statistical results of sample characteristics |
结合图 1和表 3可知,排列熵、近似熵、香农熵等指标均具有明显的特征区分效果:在排列熵指标上,非天然地震信号的熵值分布具有明显的平稳特性,标准差为0.004 9;而天然地震信号熵值则有较大的起伏变化,较不规律,标准差为0.424 6;在近似熵与香农熵指标上,非天然地震信号与天然地震的熵值都具有振荡现象,标准差均超过0.2,但非天然地震信号的熵值期望皆比天然地震信号的大,证明该熵可用于区分二者波形。
采用机器学习混淆矩阵中的准确率(accuracy)、召回率(recall)、特效度(specificity)、精确度(precision)及F-measure等评价指标,衡量LS-SVM模型分类的有效性,核函数采用RBF函数,分类子实验相关结果如表 4所示。
|
|
表 4 LSSVM辨识实验结果 Tab. 4 LSSVM identification results |
以训练集与测试集数据分别占比总数据量80%和20%为例,地震事件LSSVM模型二分类结果如图 2所示,计算得到的核函数参数为2.071 1,惩罚因子为2.307,并得到一条划分事件波形类别较明显的非线性超平面。LSSVM模型的输入往往只需要二维特征矩阵即可,若为多维输入矩阵,可由模型选择2条特征向量绘制二分类平面结果,并自动添加与核函数类型相匹配的超平面(如采用线性核函数得到的超平面多为直线,采用多项式核函数得到的超平面多为光滑曲线,基于RBF核函数得到的超平面多为封闭曲线)。如图 2所示,横坐标和纵坐标分别为测试集的排列熵与香农熵,由超平面分割开的浅灰色地带代表LSSVM超平面划分的非天然地震分类区,深灰色地带为LSSVM超平面划分的天然地震分类区。超平面近似为凹曲线,这与非天然地震事件在分类平面上的特征映射散点在凹曲线上侧且较为聚集的现象保持一致,说明模型对二者的辨识较为合理。
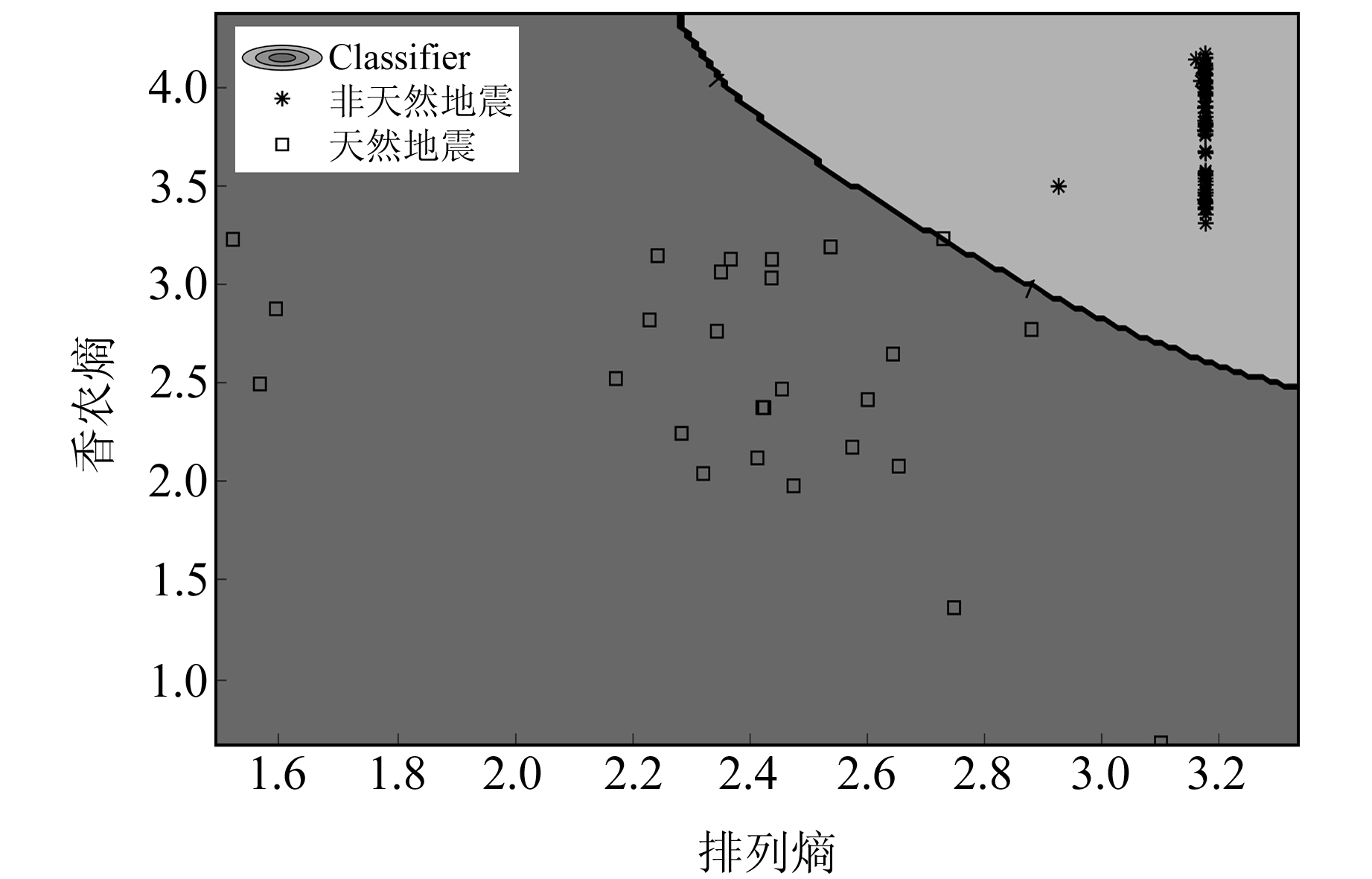
|
图 2 LSSVM模型二分类结果 Fig. 2 Two-class results of LSSVM model |
为获悉LSSVM模型在同类机器学习模型中的优势,选取决策树、朴素贝叶斯、二次判别分析(QDA)、线性判别分析(LDA)及集成学习中的LogitBoost与RobustBoost等作为辨识实验对照方法,其中训练集与测试集的数据量比例均设定为4 ∶1,具体结果见表 5。
|
|
表 5 机器学习模型辨识效果对比 Tab. 5 Comparison of identification effects of machine learning methods |
由表 5可知,在相同的训练集与测试集比例设置情况下,QDA、LDA、朴素贝叶斯、决策树、LogitBoost、RobustBoost等6种机器方法的准确率、召回率、特效度、精确度及F-measure值均小于或等于本文方法,证明3种熵结合最小二乘向量机的地震辨识方法具有较好的分类效果,对天然地震事件与非天然地震事件波形的区分皆达到预期,在同类方法中也有一定的先进性。
4 结语本文通过对预处理后的全波段波形信号提取排列熵、近似熵、香农熵等熵值,组建三维样本特征矩阵,并采用最小二乘支持向量分类机方法进行地震辨识,从而实现对地震事件的有效识别,得到以下结论:
1) 将排列熵、近似熵、香农熵引入地震识别中,具有一定新颖性,其特征提取结果也具有明显的事件区分效果。
2) LSSVM模型收敛速度较快,在训练量较少的情况下依然可以保持较理想的识别效果,且整体识别效果要优于QDA、LDA、朴素贝叶斯、决策树、LogitBoost及RobustBoost等经典机器学习方法,基于准确率、召回率、特效度、精确度、F-measure等指标的多重评价结果也证明LSSVM模型在地震识别领域具有一定的优越性。
3) 基于RBF核函数的LSSVM模型性能会受惩罚因子、RBF等参数的影响,在样本学习和目标泛化方面仍有一定的改进空间,下一步将结合智能优化算法对其正则化超参数进行寻优,增强LSSVM模型的稳健性,并提高其对含噪地震样本的非线性求解能力。另外,本文研究仅限于识别地震波形,若用于地震预警等,需要考虑辨识模型的运算速度与预警时效,将在后续研究中对此进行补充。
致谢: 中国地震局工程力学研究所为本文提供数据支持,中国水利水电科学研究院岩土工程研究所提供爆破数据,在此一并表示感谢!
| [1] |
李健, 王晓明, 张英海, 等. 基于深度卷积神经网络的地震震相拾取方法研究[J]. 地球物理学报, 2020, 63(4): 1 591-1 606 (Li Jian, Wang Xiaoming, Zhang Yinghai, et al. Research on the Seismic Phase Picking Method Based on the Deep Convolution Neural Network[J]. Chinese Journal of Geophysics, 2020, 63(4): 1 591-1 606)
(  0) 0) |
| [2] |
范晓易, 曲均浩, 曲保安, 等. 支持向量分类机LIBSVM方法识别天然地震、爆破与塌陷[J]. 大地测量与地球动力学, 2019, 39(9): 916-918 (Fan Xiaoyi, Qu Junhao, Qu Bao'an, et al. Support Vector Machine LIBSVM Method for Identifying Natural Earthquakes, Blasting and Collapse[J]. Journal of Geodesy and Geodynamics, 2019, 39(9): 916-918)
(  0) 0) |
| [3] |
江汶乡, 于海英, 赵晓芬, 等. 用于地震预警系统的单台站防误触发算法研究[J]. 自然灾害学报, 2015, 24(2): 23-31 (Jiang Wenxiang, Yu Haiying, Zhao Xiaofen, et al. Research on Anti-False Triggering Algorithm of Single Station for Earthquake Early Warning System[J]. Journal of Natural Disasters, 2015, 24(2): 23-31)
(  0) 0) |
| [4] |
周海军, 李磊. 地震波形的HHT特征提取和GMM识别研究[J]. 黑龙江工业学院学报: 综合版, 2018, 18(4): 69-73 (Zhou Haijun, Li Lei. Feature Extraction of HHT and GMM Recognition of Seismic Waveform[J]. Journal of Heilongjiang University of Technology: Comprehensive Edition, 2018, 18(4): 69-73 DOI:10.3969/j.issn.1672-6758.2018.04.015)
(  0) 0) |
| [5] |
庞聪, 江勇, 廖成旺, 等. 基于机器学习的强震动监测环境抗干扰方法对比研究[J]. 内陆地震, 2020, 34(2): 119-124 (Pang Cong, Jiang Yong, Liao Chengwang, et al. Research on Anti-Jamming Technology of Strong Motion Based on Machine Learning[J]. Inland Earthquake, 2020, 34(2): 119-124)
(  0) 0) |
| [6] |
范晓易, 曲均浩, 刘方斌, 等. 使用支持向量机识别地震类型的影响因素分析[J]. 大地测量与地球动力学, 2020, 40(10): 1034-1038 (Fan Xiaoyi, Qu Junhao, Liu Fangbin, et al. Analysis of Influencing Factors in Use of Support Vector Machine Method to Identify Earthquake Types[J]. Journal of Geodesy and Geodynamics, 2020, 40(10): 1034-1038)
(  0) 0) |
| [7] |
庞聪, 江勇, 廖成旺, 等. 基于AdaBoost集成学习的强震动观测抗干扰技术研究[J]. 四川地震, 2020(4): 14-18 (Pang Cong, Jiang Yong, Liao Chengwang, et al. Research on Anti-Jamming Technology of Strong Seismograph Based on Machine Learning[J]. Earthquake Research in Sichuan, 2020(4): 14-18)
(  0) 0) |
| [8] |
韩绍卿, 宋仔标, 伍海军. 改进的波形复杂度算法在核爆炸监测中的应用[J]. 振动与冲击, 2011, 30(2): 205-209 (Han Shaoqing, Song Zibiao, Wu Haijun. Application of Improved Algorithms of P-Wave Complexity in Nuclear Explosion Monitoring[J]. Journal of Vibration and Shock, 2011, 30(2): 205-209 DOI:10.3969/j.issn.1000-3835.2011.02.041)
(  0) 0) |
| [9] |
宋晋东, 余聪, 李山有. 地震预警现地PGV连续预测的最小二乘支持向量机模型[J]. 地球物理学报, 2021, 64(2): 555-568 (Song Jindong, Yu Cong, Li Shanyou. Continuous Prediction of Onsite PGV for Earthquake Early Warning Based on Least Squares Support Vector Machine[J]. Chinese Journal of Geophysics, 2021, 64(2): 555-568)
(  0) 0) |
| [10] |
许康生, 李英. 汶川MS8.0地震前的地面运动排列熵变化[J]. 大地测量与地球动力学, 2019, 39(6): 573-576 (Xu Kangsheng, Li Ying. The Permutation Entropy Change of Ground Motion before the MS8.0 Wenchuan Earthquake[J]. Journal of Geodesy and Geodynamics, 2019, 39(6): 573-576)
(  0) 0) |
| [11] |
许康生, 辛长江. 汶川大地震前后地磁Z分量的近似熵变化[J]. 大地测量与地球动力学, 2015, 35(1): 154-157 (Xu Kangsheng, Xin Changjiang. Variation of Approximate Entropy of Geomagnetic Z-Component of the 2008 Wenchuan Earthquake[J]. Journal of Geodesy and Geodynamics, 2015, 35(1): 154-157)
(  0) 0) |
| [12] |
卢世军. 天然地震与人工爆破波形特征提取与识别算法研究[D]. 桂林: 广西师范大学, 2009 (Lu Shijun. Research of Seismic Wave Features Extraction and Recognition Algorithm of Earthquake and Explosion[D]. Guilin: Guangxi Normal University, 2009)
(  0) 0) |
2. Hubei Key Laboratory of Early Warning, 48 Hongshance Road, Wuhan 430071, China;
3. Hubei Earthquake Agency, 48 Hongshance Road, Wuhan 430071, China;
4. School of Mathematics and Information Technology, Yuncheng University, 1155 West-Fudan Street, Yuncheng 044031, China;
5. School of Computer Science, Nanhua University, 28 West-Changsheng Road, Hengyang 421001, China
 2022, Vol. 42
2022, Vol. 42

