钻孔应变仪观测的准确性检验分为2个部分:1)钢筒内壁应变状态观测的准确性检验,其实质是检验应变测量单元格值标定的准确性;2)区域应变状态观测的准确性检验,其实质是检验钢筒内壁与区域应变状态之间关系标定的准确性。
我国四分量钻孔应变仪具有钢筒内壁应变状态观测准确性的自检验功能,与其4个分量的等间隔布局有关[1-4]。随着四分量钻孔应变仪的垂向安装方式由堆叠式[5](stack)改进为平面式[6],其观测面应变的准确性得到大幅提高[7],已达到科学观测仪器的基本要求。但由于钢筒内壁的应变状态可分解为面应变和剪应变2个部分,完整的自检应该包括面应变和剪应变的准确性自检,而面应变观测的准确性自检并不能替代剪应变观测的准确性自检。因此,目前四分量钻孔应变仪观测钢筒内壁应变状态的准确性自检是不完整的。
本文针对现有四分量钻孔应变仪观测准确性检验的不完整性问题,着眼于钻孔应变仪的未来发展,在理论上推导出n≥3分量钻孔应变观测的一般化公式,再定性地评价其对钢筒内壁面应变和剪应变观测的准确性自检能力,以期对钻孔应变观测的最佳方案作出预测。
1 钻孔应变观测的一般化公式在钢筒内水平等间隔布设n≥3个应变测量单元,设第1个应变测量单元的方位角为θ1,则第i个测量单元的方位角为:
| $ \theta_{i}=\theta_{1}+\frac{\pi}{n}(i-1), i=1,2,3, \cdots, n $ | (1) |
第i个测量单元的观测值为Si(i=1, 2, 3, …, n),钻孔应变仪钢筒内壁的水平应变状态用N向正应变εN、E向正应变εE和N向剪应变γNE表示。根据平面应变转换方程[8],第i个应变分量的理论值为:
| $ \begin{gathered} \varepsilon_{i}=\frac{\varepsilon_{\mathrm{N}}+\varepsilon_{\mathrm{E}}}{2}+\frac{\varepsilon_{\mathrm{N}}-\varepsilon_{\mathrm{E}}}{2} \cos 2 \theta_{i}+\frac{\gamma_{\mathrm{NE}}}{2} \sin 2 \theta_{i}, \\ i=1,2,3, \cdots, n \end{gathered} $ | (2) |
令εa=εN+εE(即水平面应变),λNE=εN-εE (即N向差应变),则式(2)可简化为:
| $ \begin{gathered} \varepsilon_{i}=\frac{\varepsilon_{a}}{2}+\frac{\lambda_{\mathrm{NE}}}{2} \cos 2 \theta_{i}+\frac{\gamma_{\mathrm{NE}}}{2} \sin 2 \theta_{i}, \\ i=1,2,3, \cdots, n \end{gathered} $ | (3) |
理论值与观测值的误差平方和为:
| $ \begin{gathered} Q=\sum\limits_{i=1}^{n}\left(\varepsilon_{i}-S_{i}\right)^{2}= \\ \sum\limits_{i=1}^{n}\left(\frac{\varepsilon_{a}}{2}+\frac{\lambda_{\mathrm{NE}}}{2} \cos 2 \theta_{i}+\frac{\gamma_{\mathrm{NE}}}{2} \sin 2 \theta_{i}-S_{i}\right)^{2} \end{gathered} $ | (4) |
由最小二乘法得:
| $ \begin{gathered} \frac{\partial Q}{\partial \varepsilon_{a}}=\frac{n}{2} \varepsilon_{a}+\frac{\lambda_{\mathrm{NE}}}{2} \sum\limits_{i=1}^{n} \cos 2 \theta_{i}+ \\ \frac{\gamma_{\mathrm{NE}}}{2} \sum\limits_{i=1}^{n} \sin 2 \theta_{i}-\sum\limits_{i=1}^{n} S_{i}=0 \end{gathered} $ | (5) |
式中,cos2θi和sin2θi为周期序列。由周期序列的傅里叶级数展开式不难推得
| $ \frac{\partial Q}{\partial \varepsilon_{a}}=\frac{n}{2} \varepsilon_{a}-\sum\limits_{i=1}^{n} S_{i}=0 $ | (6) |
于是有:
| $ \varepsilon_{a}=\frac{2}{n} \sum\limits_{i=1}^{n} S_{i} $ | (7) |
由最小二乘法得:
| $ \begin{gathered} \frac{\partial Q}{\partial \lambda_{\mathrm{NE}}}=\frac{\varepsilon_{a}}{2} \sum\limits_{i=1}^{n} \cos 2 \theta_{i}+\frac{\lambda_{\mathrm{NE}}}{2} \sum\limits_{i=1}^{n} \cos ^{2} 2 \theta_{i}+ \\ \frac{\gamma_{\mathrm{NE}}}{2} \sum\limits_{i=1}^{n} \sin 2 \theta_{i} \cos 2 \theta_{i}-\sum\limits_{i=1}^{n} S_{i} \cos 2 \theta_{i}= \end{gathered} $ | (8) |
式中,cos2θi、cos22θi和sin2θicos2θi为周期序列。由周期序列的傅里叶级数展开式可得
| $ \frac{\partial Q}{\partial \lambda_{\mathrm{NE}}}=\frac{n \lambda_{\mathrm{NE}}}{4}-\sum\limits_{i=1}^{n} S_{i} \cos 2 \theta_{i}=0 $ | (9) |
于是有:
| $ \lambda_{\mathrm{NE}}=\frac{4}{n} \sum\limits_{i=1}^{n} S_{i} \cos 2 \theta_{i} $ | (10) |
由最小二乘法得:
| $ \begin{gathered} \frac{\partial Q}{\partial \gamma_{\mathrm{NE}}}=\frac{\varepsilon_{a}}{2} \sum\limits_{i=1}^{n} \sin 2 \theta_{i}+\frac{\lambda_{\mathrm{NE}}}{2} \sum\limits_{i=1}^{n} \sin 2 \theta_{i} \cos 2 \theta_{i}+ \\ \frac{\gamma_{\mathrm{NE}}}{2} \sum\limits_{i=1}^{n} \sin ^{2} 2 \theta_{i}-\sum\limits_{i=1}^{n} S_{i} \sin 2 \theta_{i}=0 \end{gathered} $ | (11) |
式中,sin2θi、sin22θi和sin2θicos2θi为周期序列。由周期序列的傅里叶级数展开式可得
| $ \frac{\partial Q}{\partial \gamma_{\mathrm{NE}}}=\frac{n}{4} \gamma_{\mathrm{NE}}-\sum\limits_{i=1}^{n} S_{i} \sin 2 \theta_{i}=0 $ | (12) |
于是有:
| $ \gamma_{\mathrm{NE}}=\frac{4}{n} \sum\limits_{i=1}^{n} S_{i} \sin 2 \theta_{i} $ | (13) |
钢筒内壁的水平应变状态可由水平面应变εa、N向差应变λNE和N向剪应变γNE表示。对于任意分量数n≥3的钻孔应变观测方案,式(7)、式(10)和式(13)为求取这3个应变的一般化公式。
根据式(10)和式(13)可得,最大剪应变γmax(即最大差应变)的平方为:
| $ \begin{gathered} \left(\gamma_{\max }\right)^{2}=\lambda_{\mathrm{NE}}^{2}+\gamma_{\mathrm{NE}}^{2}= \\ \left(\frac{4}{n}\right)^{2}\left[\left(\sum\limits_{i=1}^{n} S_{i} \cos 2 \theta_{i}\right)^{2}+\left(\sum\limits_{i=1}^{n} S_{i} \sin 2 \theta_{i}\right)^{2}\right]= \\ \left(\frac{4}{n}\right)^{2} \sum\limits_{i, j=1}^{n}\left(S_{i} S_{j} \cos 2 \theta_{i} \cos 2 \theta_{j}+S_{i} S_{j} \sin 2 \theta_{i} \sin 2 \theta_{j}\right)= \\ \left(\frac{4}{n}\right)^{2} \sum\limits_{i, j=1}^{n} S_{i} S_{j} \cos 2\left(\theta_{i}-\theta_{j}\right) \end{gathered} $ | (14) |
于是有:
| $ \gamma_{\max }=\frac{4}{n} \sqrt{\sum\limits_{i, j=1}^{n} S_{i} S_{j} \cos 2\left(\theta_{i}-\theta_{j}\right)} $ | (15) |
对于任意分量数n≥3的钻孔应变观测方案,式(15)为求取钢筒内壁最大剪应变的一般化公式。
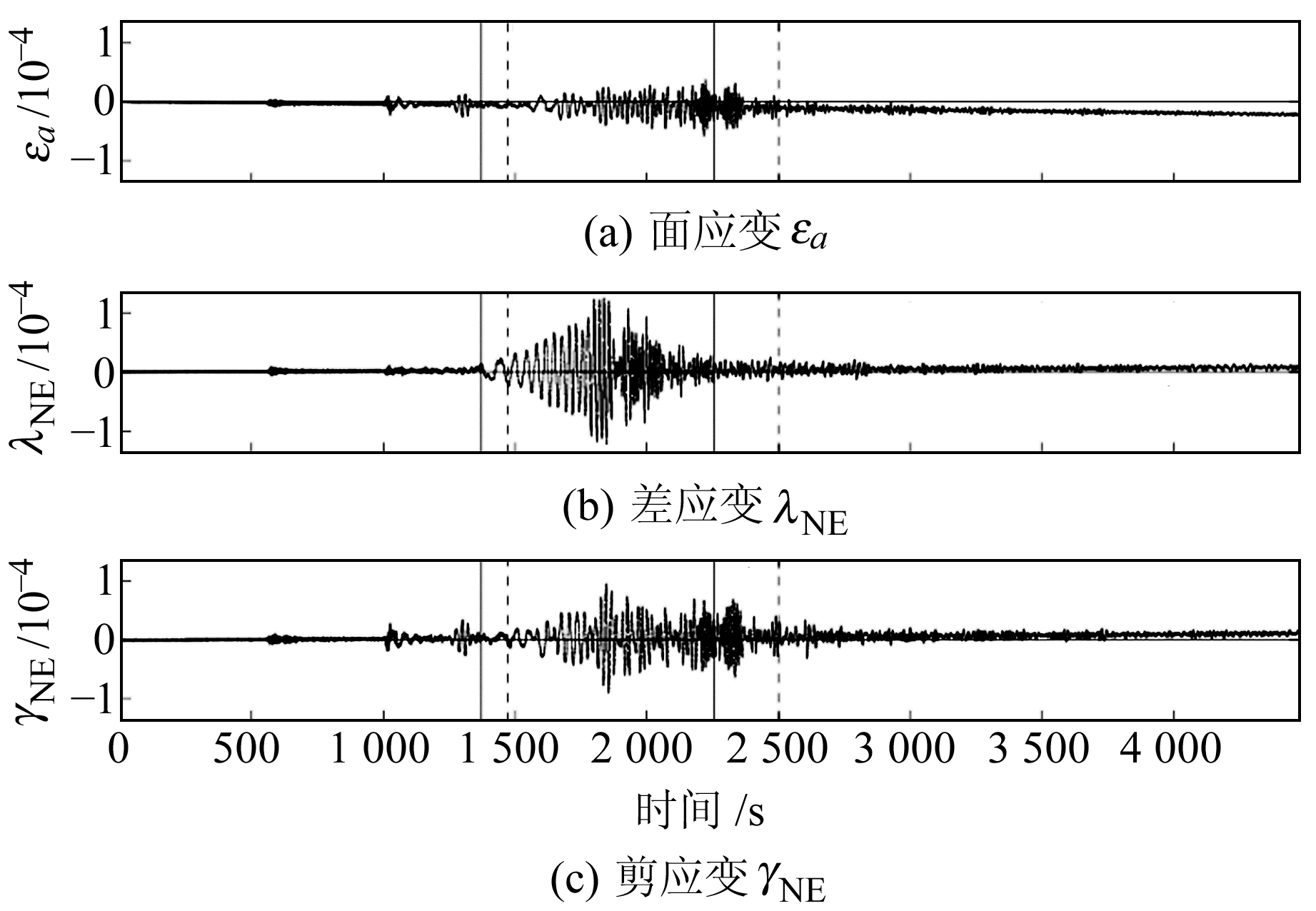
表 1为四川省仁和地震台YRY-4型钻孔应变仪观测到的一个远震,根据其四分量观测数据(S1,S2,S3,S4),应用式(7)、式(10)和式(13)计算钢筒内壁面应变εa、差应变λNE和剪应变γNE,结果见图 1,图中竖虚线区间为瑞利波显著的起始-终止时段,竖实线区间为勒夫波显著的起始-终止时段。
|
|
表 1 地震信息表(据GCMT) Tab. 1 Some information on the earthquake used in this article (from GCMT) |
|
图 1 仁和台钻孔应变仪钢筒内壁各应变曲线 Fig. 1 The curves of the inner wall of the steel cylinder of the borehole strainmeter at Renhe station |
面应变(剪应变)自检的条件是,可从钻孔应变观测分量中独立地解算出可对比的2个或2个以上的面应变(剪应变)。当2个分量垂直时,可解算出1个面应变;当2个分量不垂直时,需要增加1个分量,即3个分量才能解算出1个面应变。因此,可以首先找出分量中全部的垂直分量对,再找出剩下的全部三分量组,统计解算出的独立面应变数,如果独立面应变数大于或等于2,那么就可进行面应变自检。3个分量可解算出1个剪应变,如果分量数是3的2倍或大于2倍,那么就可进行剪应变自检。
表 2列出三分量到九分量钻孔应变观测方案解算出的面应变数和剪应变数及面应变和剪应变的自检能力,表中“√”表示可进行自检,“□”表示不可进行自检。可以看出,在能进行面应变自检的钻孔应变观测方案中,分量数最少的是四分量方案;在能同时进行面应变和剪应变自检(能进行观测全面自检)的钻孔应变观测方案中,分量数最少的是六分量方案。由此可知,四分量方案是只进行面应变自检的最佳方案,六分量方案是进行钻孔应变观测全面自检的最佳方案。
|
|
表 2 钻孔应变观测方案的自检能力 Tab. 2 Self-verification capacities of different borehole strain observation solutions |
在六分量方案中有3对互相垂直的分量(S1和S4,S2和S5,S3和S6),S1+S4、S2+S5、S3+S6为3个独立观测的面应变值,可用于面应变的自检。
在六分量方案中有2组等间隔分布的三分量组:(S1,S3,S5)、(S2,S4,S6),根据(S1,S3,S5)应用式(15)计算得到的最大剪应变
由于观测的是同一最大剪应变,应有γmax135=γmax246,则:
| $ \begin{gathered} S_{1}^{2}+S_{3}^{2}+S_{5}^{2}-S_{1} S_{3}-S_{1} S_{5}-S_{3} S_{5}= \\ S_{2}^{2}+S_{4}^{2}+S_{6}^{2}-S_{2} S_{4}-S_{2} S_{6}-S_{4} S_{6} \end{gathered} $ | (16) |
式(16)为六分量钻孔应变观测方案的剪应变自检公式。
由式(7)和式(10)可知,六分量应变观测方案的计算公式是建立在应变分量的理论值与观测值之差平方和最小这一基础上的。另外,(γmax)2=λNE2+γNE2,而γmax135=γmax246是公理,那么反之,如果6个应变测量单元的观测值与γmax135=γmax246的偏离程度很小,说明上述应变分量的应变理论值与观测值之差值平方和最小。这从另一个角度说明了六分量观测方案相对于四分量的优越性。
由此可见,六分量钻孔应变观测方案的剪应变自检公式,同时也是其应变分量的应变理论值与观测值之差的平方和是否最小的检验公式。若检验通过,则说明观测值最逼近理论值。表 3列出四分量和六分量钻孔应变观测方案的观测公式和自检公式。
|
|
表 3 四分量和六分量钻孔应变观测方案的观测公式和自检公式 Tab. 3 Observation equations and self-verification equations for four-and six-component borehole strain observation schemes |
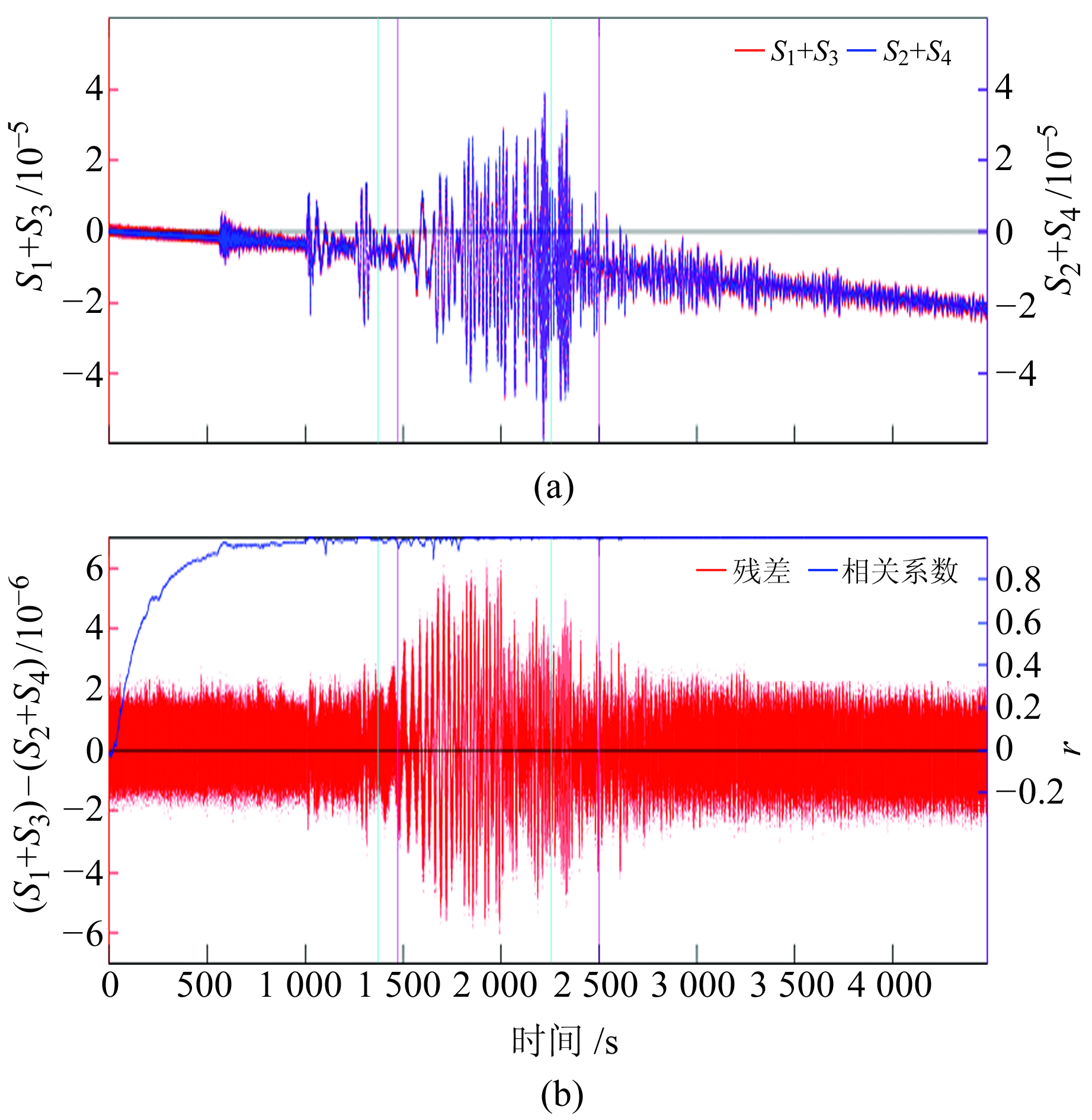
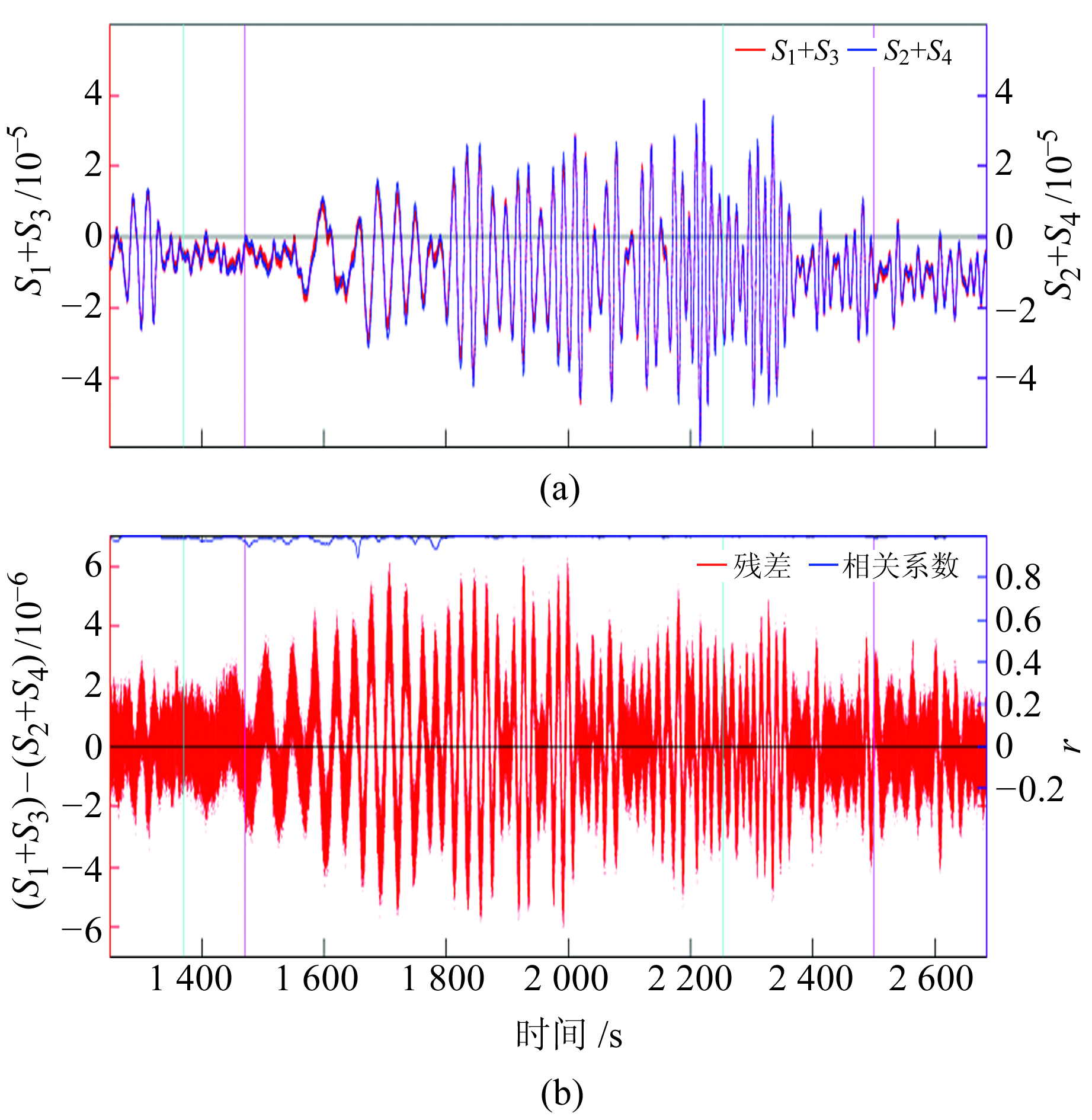
图 2(a)为四川省仁和地震台YRY-4型钻孔应变仪观测的2个面应变S1+S3和S2+S4曲线,可以看出,二者几乎重合;图 2(b)为2个面应变的残差及相关系数(滑动窗口长度为20 s),可以看出,远震信号的残差范围为(-6.0~6.2)×10-6,其中噪声残差的范围为(-2.0~2.0)×10-6。图 3为图 2中瑞利波显著区域的放大结果,可以看出,在瑞利波显著区域,2个面应变S1+S3和S2+S4的相关系数为0.994 9,说明YRY-4型钻孔应变仪对面应变的观测是准确的。
|
青色竖线内区域为勒夫波显著的区域,红色竖线内区域为瑞利波显著的区域 图 2 S1+S3与S2+S4观测曲线、残差和相关系数曲线 Fig. 2 S1+S3 versus S2+S4 observation curves, residuals and correlation coefficient curves |
|
图 3 瑞利波显著区域放大图 Fig. 3 Enlarged view of the significant region of Rayleigh waves |
所谓的钻孔应变仪观测自检,指的是对应变测量单元格值标定的准确性进行自检,也是对由应变测量单元观测值解算出来的钢筒内壁水平应变状态的准确性进行自检。钢筒内壁的水平应变状态可由水平面应变εa、N向差应变λNE和N向剪应变γNE表示,本文推导出了n≥3分量水平等间隔钻孔应变观测方案的εa、λNE和γNE一般化公式。
理论分析表明,若仅考虑进行面应变观测的准确性自检,我国现有的四分量钻孔应变仪是最佳方案;若考虑观测的准确性全面自检,即可同时进行面应变和剪应变的准确性自检,并考虑对观测值是否最逼近理论值的检验,那么六分量是最佳方案。针对六分量方案,本文给出面应变和剪应变的准确性自检公式。通过对远震面波数据进行面应变的准确性自检发现,2个面应变(S1+S3与S2+S4)的相关系数达到了0.99以上,说明YRY-4型钻孔应变仪对面应变的观测是准确的。
准确性对于仪器的重要性是不言而喻的,四分量的垂向布局由堆叠式改为平面式,极大地提高了钻孔应变仪面应变观测的准确性,但四分量方案不能进行剪应变准确性自检。如果再增加2个分量,达到六分量,就可实现观测的全面自检,同时还可实现对观测值是否最逼近理论值的检验。因此认为,六分量钻孔应变仪是未来的发展方向。
致谢: 应急管理部国家自然灾害防治研究院的苏恺之研究员在钻孔应变观测基础理论等方面给予悉心指导,在此表示衷心感谢。
| [1] |
和泰名, 李世愚. 地震的应变张量观测与应用前景[J]. 地球物理学报, 2017, 60(11): 4 327-4 340 (He Taiming, Li Shiyu. The Seismological Application Prospect of Strain Tensor Meters[J]. Chinese Journal of Geophysics, 2017, 60(11): 4 327-4 340)
(  0) 0) |
| [2] |
苏恺之. 中国四分量钻孔应变仪风雨历程四十年[J]. 地震地磁观测与研究, 2020, 41(2): 172-180 (Su Kaizhi. Forty Years of Four-Component Borehole Strain Gauge in China[J]. Seismological and Geomagnetic Observation and Research, 2020, 41(2): 172-180 DOI:10.3969/j.issn.1003-3246.2020.02.020)
(  0) 0) |
| [3] |
邱泽华. 钻孔应变观测理论与应用[M]. 北京: 地震出版社, 2017 (Qiu Zehua. Borehole Strain Observation: Theory and Application[M]. Beijing: Seismological Press, 2017)
(  0) 0) |
| [4] |
池顺良. 钻孔应变观测能够告诉我们些什么?[J]. 山西地震, 2019(1): 17-29 (Chi Shunliang. What can Borehole Strain Observations Tell Us?[J]. Earthquake Research in Shanxi, 2019(1): 17-29)
(  0) 0) |
| [5] |
GTSM Technologies. GTSM Technologies: Frequently Asked Questions[EB/OL]. http://www.gtsmtechnologies.com/index_files/faqs.htm, 2021
(  0) 0) |
| [6] |
池顺良. 小型分量钻孔应变仪探头: CN201420763236.6[P]. 2015-06-10 (Chi Shunliang. Small Component Borehole Strain Gauge Probe: CN201420763236.6[P]. 2015-06-10)
(  0) 0) |
| [7] |
Kong X Y, Su K Z, Fujinawa Y. Application Prospects of SKZ-1 4-Component Borehole Strain Meter[C]. Geoscience Union Meting, Japan, 2015
(  0) 0) |
| [8] |
盖尔, 古德诺. 材料力学[M]. 北京: 机械工业出版社, 2017 (James M Gere, Barry J Goodno. Mechanics of Materials[M]. Beijing: China Machine Press, 2017)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


