2. 武汉地震科学仪器研究院有限公司, 武汉市洪山侧路40号, 430071;
3. 湖北省重大工程地震监测与预警处置工程技术研究中心, 湖北省咸宁市青龙路11号, 437000
地球重力场的精准测量对计量科学、防震减灾、大地测量、地球物理等领域具有十分重要的科学意义。我国一直对重力相关领域投入巨大,也取得众多研究成果。尤其是高精密重力仪器的开发,如超导重力仪、小型绝对重力仪和海空重力仪等均取得突破性进展[1]。高精密重力仪器的发展对重力数据处理方法提出更高的精度需求。
DZW重力仪是我国自行研发的第一台高精度重力仪,分辨率可达到μGal级。由于其采用的是垂直悬挂弹性系统,弹簧张力的衰减以及未被补偿或屏蔽的外界作用会产生零漂[2]。DZW重力仪1 d的零漂有时可高达40 μGal,直接影响到重力仪的观测精度与准确性。
经典的线性零漂处理方法认为,零漂率在观测过程中为恒值,在1个月以上的长期实际外业测量中呈非线性[2]。因此,线性零漂处理方法在重力观测过程中的应用方案是以24 h作为时间节点进行分段线性拟合,得到各段的零漂率[3]。然而对于处理几个月以上的长期重力观测数据,该方法会耗费较多时间和物力。如果1 d数据中有温度、气压等其他非线性因素,也会导致经过线性零漂校正后观测值的精度难以保证。
文献[4-5]通过建立贝叶斯平差模型来解决非线性漂移观测误差,从而为提高数据精度提供新的解决方案。本文在其基础上进行优化尝试,贝叶斯平差模型中的研究对象为零漂率,本文贝叶斯模型将其变为零漂。这是由于零漂与重力观测值之间只涉及到加减运算,不涉及与时间的乘法运算,所需要的参量只有重力观测值以及理想的重力仪读数,因此可以简化运算并增加算法的计算效率。
为将本文算法运用到实际重力观测中,我们设计一套关于该算法的应用方案,使得该算法可以在每次获得新观测数据后自动进行计算,增加算法的实用性。该方案将算法运用到重力观测数据的实时处理中,在采样重力观测值的同时进行零漂计算,可以减少后期数据处理中消除零漂所消耗的人力和物力[6]。
1 模型构建零漂的贝叶斯估计模型需要先定义与算法相关的矩阵以及基本公式,模型的核心公式为贝叶斯公式,需要分别确定先验分布形式、似然函数以及边缘密度函数。
1.1 矩阵定义将经过潮汐校正的相对重力观测数据表示为:
| $ \boldsymbol{x}=\left[x_{1}, x_{2}, \cdots, x_{n}\right]^{\mathrm{T}} $ |
将每个样本点对应的零漂表示为:
| $ \boldsymbol{v}=\left[v_{1}, v_{2}, \cdots, v_{n}\right]^{\mathrm{T}} $ |
将每个样本点的重力仪读数(理想值)表示为:
| $ \boldsymbol{g}=\left[g_{1}, g_{2}, \cdots, g_{n}\right]^{\mathrm{T}} $ |
将用于得到一组数据的梯度变化量的矩阵A(A∈Rn×n)表示为:
| $ \boldsymbol{A}=\left[\begin{array}{cccccc} 1 & -2 & 1 & & & \\ & 1 & -2 & 1 & & \\ & & \ddots & \ddots & \ddots & \\ & & & 1 & -2 & 1 \\ & & & & \zeta & \\ & & & & & \zeta \end{array}\right] $ |
式中,ζ为方阵的补充值,取值趋近于0。
1.2 基本公式对于经过潮汐校正后的相对重力观测数据,其与零漂之间的关系式可表示为[7]:
| $ \boldsymbol{x}-\boldsymbol{v}-\boldsymbol{g}=\boldsymbol{\delta} $ | (1) |
式中,δ为公式计算产生的误差,满足以下分布:
| $ \boldsymbol{\delta} \sim N\left(0, \boldsymbol{\varSigma}_{1}\right) $ | (2) |
式中,Σ1为高斯分布的协方差矩阵。
由式(1)可推出以下分布:
| $ \boldsymbol{x} \sim N\left(\boldsymbol{v}+\boldsymbol{g}, \boldsymbol{\varSigma}_{1}\right) $ | (3) |
对零漂的先验分布形式进行确认,每个时刻的零漂是未知的,因此存在随机性[8-9],可用随机变量表示:
| $ \boldsymbol{v}_{i} \sim N\left(\boldsymbol{v}_{i}^{\prime}, \sigma_{i}^{2}\right) $ | (4) |
式中,v′i为传统算法所认定的真实值,σi2为估计值和真实值之间的偏差。整个测量时间段的零漂服从高斯过程[10],该过程的均值矩阵和协方差矩阵可通过以下推算求得。
假设零漂在连续时间中具有连续性[11],则需要满足:
| $ \boldsymbol{A v}=\boldsymbol{\xi} $ | (5) |
式中,ξ为趋向于0的数组,满足以下分布:
| $ \boldsymbol{\xi} \sim N\left(0, \boldsymbol{\varSigma}_{2}\right) $ | (6) |
式中,Σ2为高斯分布的协方差矩阵。
由式(5)可推出以下分布:
| $ \boldsymbol{A} \boldsymbol{v} \sim N\left(0, \boldsymbol{\varSigma}_{2}\right) $ | (7) |
已知v为高斯过程,根据高斯过程的线性性质,由式(7)可推算出v的具体分布为:
| $ \begin{gathered} \boldsymbol{v} \sim N\left(\boldsymbol{A}^{-1} \cdot {\bf{0}}, \boldsymbol{A}^{-1} \boldsymbol{\varSigma}_{2}\left(\boldsymbol{A}^{\mathrm{T}}\right)^{-1}\right) \Rightarrow \\ \boldsymbol{v} \sim N\left({\bf{0}}, \boldsymbol{A}^{-1} \boldsymbol{\varSigma}_{2}\left(\boldsymbol{A}^{\mathrm{T}}\right)^{-1}\right) \end{gathered} $ | (8) |
先验分布的概率密度函数为:
| $ \begin{gathered} {\rm{ \mathsf{ π} }}(\boldsymbol{v})=(2 {\rm{ \mathsf{ π} }})^{-\frac{n}{2}} \frac{1}{\operatorname{det}\left(\boldsymbol{A}^{-1} \boldsymbol{\varSigma}_{2}\left(\boldsymbol{A}^{\mathrm{T}}\right)^{-1}\right)^{\frac{1}{2}}} \cdot\\ \exp \left\{-\frac{1}{2}(\boldsymbol{v})^{\mathrm{T}}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{\varSigma}_{2}^{-1} \boldsymbol{A}\right)(\boldsymbol{v})\right\} \end{gathered} $ | (9) |
似然函数是样本信息的集中体现,由式(3)可推出其表达式为:
| $ \begin{gathered} {\rm{ \mathsf{ π} }}(\boldsymbol{x} \mid \boldsymbol{v})=(2 {\rm{ \mathsf{ π} }})^{-\frac{n}{2}} \frac{1}{\operatorname{det}\left(\boldsymbol{\varSigma}_{1}\right)^{\frac{1}{2}}} \cdot \\ \exp \left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{v}-\boldsymbol{g})^{\mathrm{T}} \boldsymbol{\varSigma}_{1}^{-1}(\boldsymbol{x}-\boldsymbol{v}-\boldsymbol{g})\right\} \end{gathered} $ | (10) |
边缘密度函数本身并不会影响后验分布的分布形式,但会影响后验分布的幅值变化[12],可通过式(9)、(10)推出边缘密度函数的表达式为:
| $ \begin{gathered} \boldsymbol{m}(\boldsymbol{x})=\int_{-\infty}^{+\infty} \boldsymbol{\cdots} \int_{-\infty}^{+\infty} {\rm{ \mathsf{ π} }}(\boldsymbol{x} \mid \boldsymbol{v}) {\rm{ \mathsf{ π} }}(\boldsymbol{v}) \mathrm{d} v_{1} \mathrm{~d} v_{2} \cdots \mathrm{d} v_{n}=\\ \int_{-\infty}^{+\infty} \cdots \int_{-\infty}^{+\infty}(2 {\rm{ \mathsf{ π} }})^{-\frac{n}{2}} \frac{1}{\operatorname{det}\left(\boldsymbol{\varSigma}_{1}\right)^{\frac{1}{2}}} \exp \left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{v}-\boldsymbol{g})^{\mathrm{T}} \boldsymbol{\varSigma}_{1}^{-1}(\boldsymbol{x}-\boldsymbol{v}-\boldsymbol{g})\right\}\cdot\\ (2 {\rm{ \mathsf{ π} }})^{-\frac{n}{2}} \frac{1}{\operatorname{det}\left(\boldsymbol{A}^{-1} \boldsymbol{\varSigma}_{2}\left(\boldsymbol{A}^{\mathrm{T}}\right)^{-1}\right)^{\frac{1}{2}}} \exp \left\{-\frac{1}{2}(\boldsymbol{v})^{\mathrm{T}}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{\varSigma}_{2}^{-1} \boldsymbol{A}\right)(\boldsymbol{v})\right\} \mathrm{d} v_{1} \mathrm{~d} v_{2} \cdots \mathrm{d} v_{n}=\\ \int_{-\infty}^{+\infty} \cdots \int_{-\infty}^{+\infty}(2 {\rm{ \mathsf{ π} }})^{-n} \frac{1}{\operatorname{det}\left(\boldsymbol{\varSigma}_{1}\right)^{\frac{1}{2}} \operatorname{det}\left(\boldsymbol{A}^{-1} \boldsymbol{\varSigma}_{2}\left(\boldsymbol{A}^{\mathrm{T}}\right)^{-1}\right)^{\frac{1}{2}}} \cdot\\ \exp \left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{v}-\boldsymbol{g})^{\mathrm{T}} \boldsymbol{\varSigma}_{1}^{-1}(\boldsymbol{x}-\boldsymbol{v}-\boldsymbol{g})-\frac{1}{2}(\boldsymbol{v})^{\mathrm{T}}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{\boldsymbol { \varSigma }}_{2}^{-1} \boldsymbol{A}\right)(\boldsymbol{v})\right\} \mathrm{d} v_{1} \mathrm{~d} v_{2} \cdots \mathrm{d} v_{n}=\\ (2 {\rm{ \mathsf{ π} }})^{-\frac{n}{2}} \frac{1}{\operatorname{det}\left(\boldsymbol{\varSigma}_{1}+\boldsymbol{A}^{-1} \boldsymbol{\varSigma}_{2}\left(\boldsymbol{A}^{\mathrm{T}}\right)^{-1}\right)^{\frac{1}{2}}} \exp \left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{g})^{\mathrm{T}}\left(\boldsymbol{\varSigma}_{1}+\boldsymbol{A}^{-1} \boldsymbol{\boldsymbol { \varSigma }}_{2}\left(\boldsymbol{A}^{\mathrm{T}}\right)^{-1}\right)^{-1}(\boldsymbol{x}-\boldsymbol{g})\right\} \end{gathered} $ | (11) |
将先验分布的概率密度函数、似然函数和边缘密度函数代入贝叶斯公式,推出后验分布的概率密度函数:
| $ {\rm{ \mathsf{ π} }}(v \mid \boldsymbol{x})=\frac{{\rm{ \mathsf{ π} }}(\boldsymbol{x} \mid \boldsymbol{v}) {\rm{ \mathsf{ π} }}(\boldsymbol{v})}{\boldsymbol{m}(\boldsymbol{x})} $ | (12) |
正态均值(方差已知)的共轭先验分布为正态分布。后验分布满足以下分布形式:
| $ \begin{gathered} {{\rm{ \mathsf{ π} }}}(\boldsymbol{v} \mid \boldsymbol{x}) \sim N\left(\left(\left(\boldsymbol{x}^{\mathrm{T}} \boldsymbol{\varSigma}_{1}^{-1}+\boldsymbol{g}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{\varSigma}_{2}^{-1} \boldsymbol{A}\right) \cdot\right.\right. \\ \left.\left.\left(\boldsymbol{\varSigma}_{1}^{-1}+\boldsymbol{A}^{\mathrm{T}} \boldsymbol{\varSigma}_{2}^{-1} \boldsymbol{A}\right)^{-1}-\boldsymbol{g}^{\mathrm{T}}\right)^{\mathrm{T}},\left(\boldsymbol{\varSigma}_{1}^{-1}+\boldsymbol{A}^{\mathrm{T}} \boldsymbol{\varSigma}_{2}^{-1} \boldsymbol{A}\right)^{-1}\right) \end{gathered} $ | (13) |
由式(13)可知,要得到确定的后验分布,需要确定两组超参数值,分别是Σ1和Σ2。其中,Σ1为样本所产生的方差,代表重力仪的属性,视为恒定值[13],可以取其中1 d的数据进行线性拟合得到零漂率,从而得到零漂校正后的数据方差;Σ2为零漂先验分布的超参数,可通过增加计算次数得到收敛极限进行确定,初始值可以取与Σ1同一量级的数值。
对于零漂后验分布均值和方差的确定,方法如下:
收敛性证明。为方便表示,将Σ1和ATΣ2-1A转化为只有1个元素的1×1矩阵σ12和σ22,则式(13)可表示为:
| $ \begin{gathered} {\rm{ \mathsf{ π} }}(\boldsymbol{v} \mid \boldsymbol{x}) \sim N\left(\left(\boldsymbol{x} \boldsymbol{\sigma}_{1}^{-2}+\boldsymbol{g}^{-2} \boldsymbol{\sigma}_{2}^{2}\right)\cdot\right. \\ \left.\left(\boldsymbol{\sigma}_{1}^{-2}+\boldsymbol{\sigma}_{2}^{-2}\right)^{-1}-\boldsymbol{g},\left(\boldsymbol{\sigma}_{1}^{-2}+\boldsymbol{\sigma}_{2}^{-2}\right)^{-1}\right) \end{gathered} $ | (14) |
经过贝叶斯公式计算得到的零漂后验分布方差是两者的综合体现。将该后验分布作为下一次贝叶斯公式的先验分布,则得到的第二次后验分布的方差可表示为:
| $ \boldsymbol{\sigma}_{3}^{2}=\left(\boldsymbol{\sigma}_{1}^{-2}+\left(\boldsymbol{\sigma}_{1}^{-2}+\boldsymbol{\sigma}_{2}^{-2}\right)\right)^{-1} $ | (15) |
第n次后验分布的方差为:
| $ \boldsymbol{\sigma}_{n+1}^{2}=\left(n \boldsymbol{\sigma}_{1}^{-2}+\boldsymbol{\sigma}_{2}^{-2}\right)^{-1} $ | (16) |
由式(16)可知,后验分布方差会随着计算层数的增加而不断减小并趋向于零,表明后验分布具有收敛性,并且收敛极限为0。
后验分布的均值经过化简可表示为:
| $ \begin{gathered} \boldsymbol{\mu}_{n}=\left(\boldsymbol{\sigma}_{1}^{-2} \boldsymbol{x}+\boldsymbol{\sigma}_{n}^{-2}\left(\boldsymbol{\mu}_{n-1}+\boldsymbol{g}\right)\right)\left(\boldsymbol{\sigma}_{1}^{-2}+\boldsymbol{\sigma}_{n}^{-2}\right)^{-1}- \\ \boldsymbol{g}=\frac{\boldsymbol{\sigma}_{1}^{-2}(\boldsymbol{x}-\boldsymbol{g})+\boldsymbol{\mu}_{n-1} \boldsymbol{\sigma}_{n}^{-2}}{\boldsymbol{\sigma}_{1}^{-2}+\boldsymbol{\sigma}_{n}^{-2}}= \\ \frac{\boldsymbol{\sigma}_{1}^{-2}(\boldsymbol{x}-\boldsymbol{g}) \boldsymbol{\sigma}_{n}^{2}+\boldsymbol{\mu}_{n-1}}{\boldsymbol{\sigma}_{1}^{2} \boldsymbol{\sigma}_{n}^{2}+1} \end{gathered} $ | (17) |
从式(17)可以看出,随着计算层数不断增加,σn2逐渐趋向于0,则μn→μn-1。说明随着计算层数的增加,在后验分布方差收敛的同时,零漂均值也具有收敛性。零漂均值的收敛极限是否为零漂的最终估计,还需要进一步的数据验证。
2 算法数据验证本文算法在经过前文数学逻辑推导后,需要通过实际重力数据来进一步验证。首先,对算法中超参数进行初步估计,通过数据进一步验证零漂超参数的收敛性;然后,通过数据来确认均值的收敛极限性质。在算法本身逻辑性得到证明的基础上,需要确定应用方案来模拟测量过程,对所得结果的可用性和准确性进行分析;最后,通过与传统线性拟合去零漂方案进行对比分析,探讨算法是否实现去非线性零漂的目标。
2.1 超参数初步估计将九峰台站DZW重力仪在2019年的连续观测数据作为算法的验证数据源。该数据已经过精度为10-5 μGal的固体潮校正,可不考虑温度、气压等因素的影响。通过线性拟合,得到图 1中表示线性零漂的直线,与潮汐校正后的数据点进行对比。拟合直线斜率即为估计的零漂率,为0.014 25 μGal/min=0.855 μGal/h,由给出的均方根误差RMSE(root mean squared error)推出样本的数据方差Σ1=RMSE2=0.184 92 μGal2=0.034 19 μGal2,Σ1即为0.034 19的对角矩阵。由于零漂的先验分布的协方差矩阵Σ2为未知参数,但在多层运算后将会趋近于0,因此不妨设其为与Σ1同数量级的矩阵,令其为0.01的对角矩阵。

|
图 1 对1 d重力观测数据进行线性拟合所得结果 Fig. 1 The results obtained by linear fitting of one-day gravity observation data |
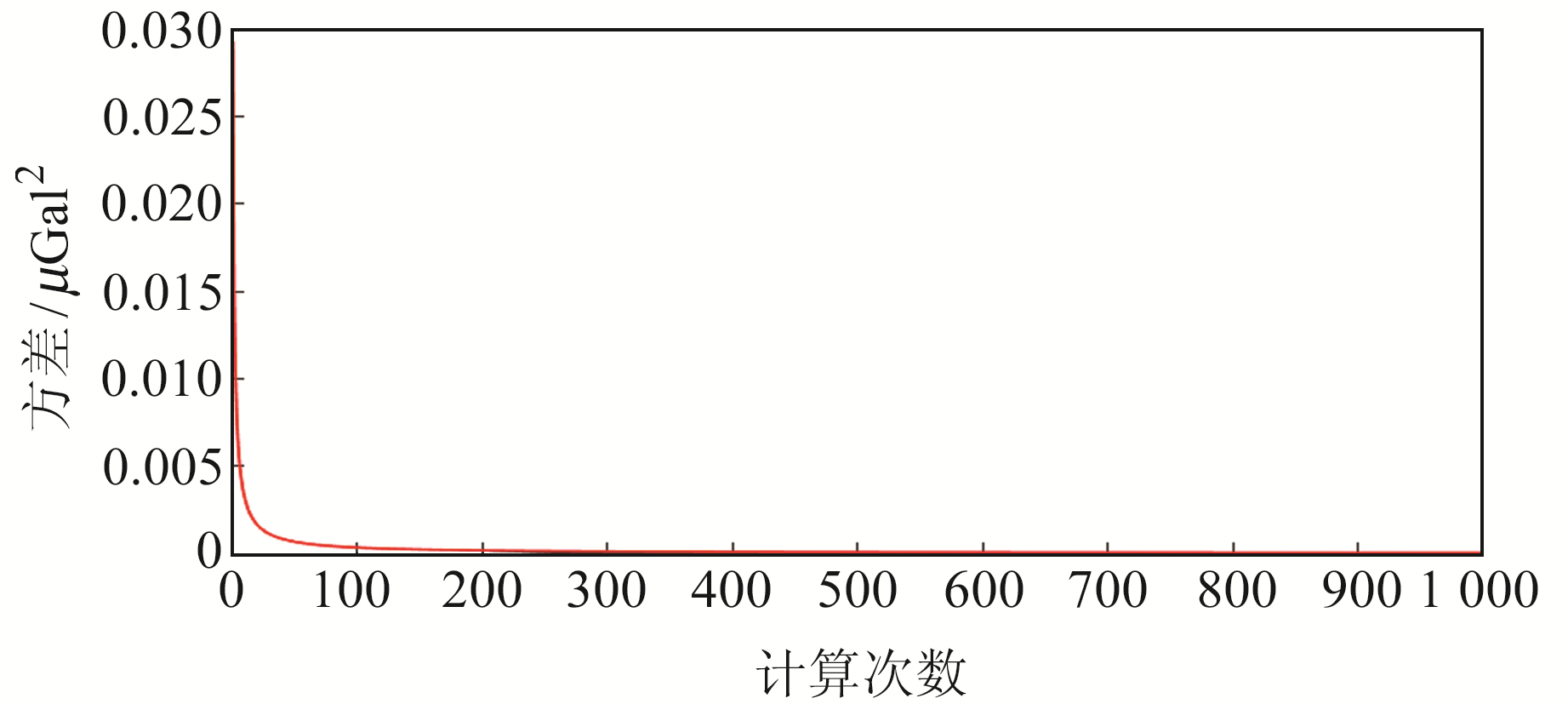
为确保计算次数足够多,将计算次数设置为1 000。1 000次计算中后验分布的方差变化如图 2所示。
|
图 2 后验分布方差变化 Fig. 2 Variance variation of posteriori distribution |
在前100次计算中,方差下降速度较快;在后900次计算中,下降速度趋于平缓,总体呈收敛态势。为进一步验证均值的收敛性,需要研究均值的收敛方向和收敛极限。为遍历所有点的均值收敛情况,将计算次数减少至100。经过研究发现,每个样本点的收敛方向不同,收敛极限也存在差异。以第11个和第1 003个样本点的均值变化为例,结果见图 3(a)和3(b)。

|
图 3 样本点均值变化 Fig. 3 Meanvalues change of sample points |
通过上述分析可知,随着计算次数不断增加,后验分布的方差趋近于0,各样本点的均值沿着各自方向趋近于不同的收敛极限。但收敛极限是否为零漂的真实值需进一步确认。
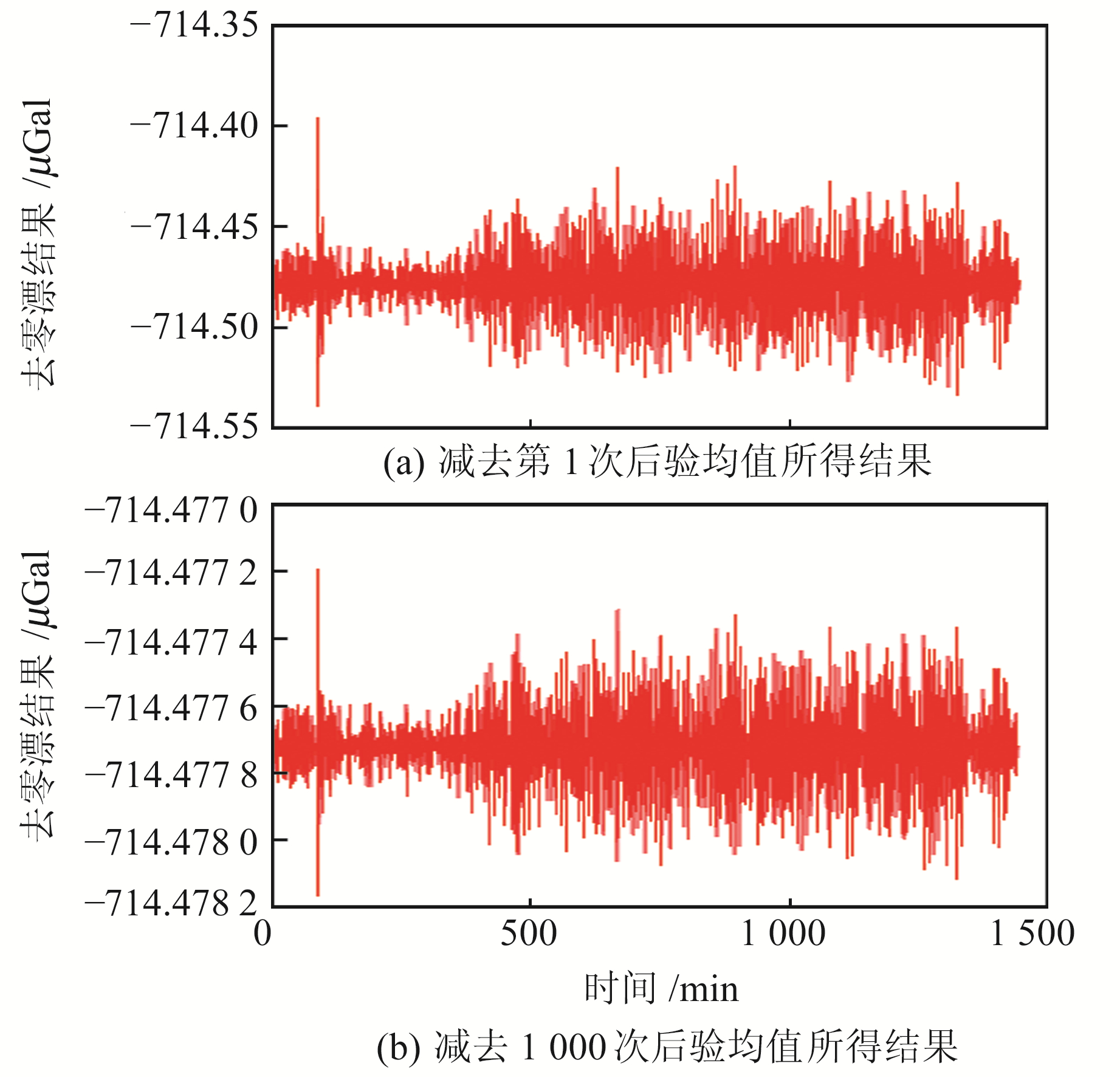
2.3 均值收敛极限性质确认将重力观测值与后验分布均值作差,理论结果为真实重力观测值,是一个恒值,结果如图 4所示。
|
图 4 观测数据在去除不同计算次数所得零漂结果 Fig. 4 Drift results of observed data after removing different calculation times |
图 4(a)中方差为0.000 343 μGal2,图 4(b)中方差为1.803 78×10-8 μGal2,后者方差明显小于前者,说明随着计算次数的增加,均值不断逼近,使去零漂结果为常数数值,均值的收敛极限即为真实的零漂值。
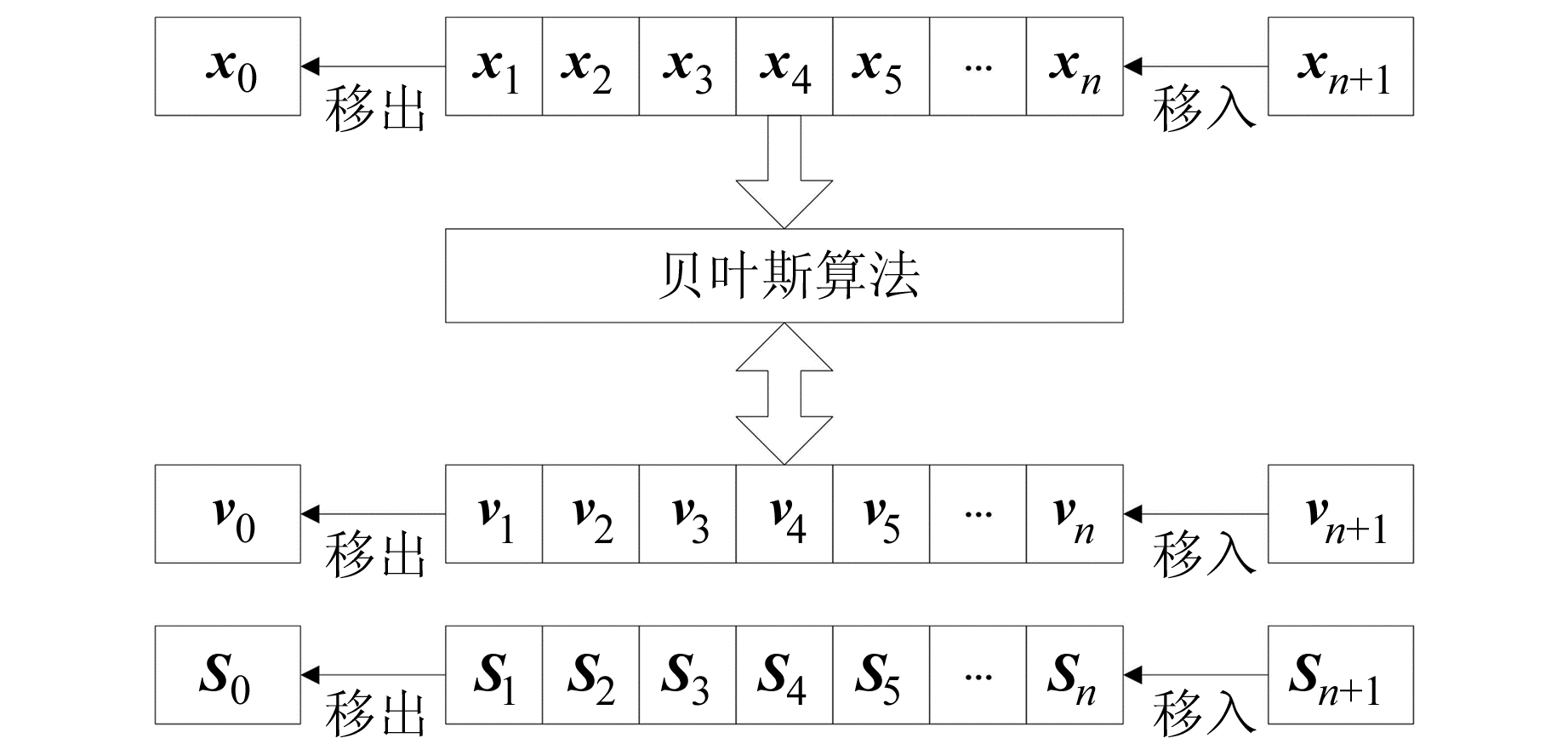
2.4 算法应用方案确定第1天的1 440个样本点采用贝叶斯模型进行预处理,通过对其进行1 000次重复计算,得到精准的1 440个零漂值。对于新样本数据,通过左移操作实现样本数组的更新,为确保样本点与零漂值一一对应,零漂的均值矩阵与协方差矩阵中的对角元素数组同时进行左移操作(图 5)。
|
图 5 算法应用方案 Fig. 5 Scheme of algorithm application |
图 5中v0作为零漂数组的输出数据按序存放,形成的数据组即为精准的零漂数组。xn+1为新样本值,vn+1代表与新样本值对应的均值,是需要预测的参数。Sn+1代表与新样本值对应的方差,等于先验分布的方差。该方案的优点是对于新移入的样本值,其均值由移入至最后输出会经历1 440次贝叶斯算法计算,可保证结果的高精度。
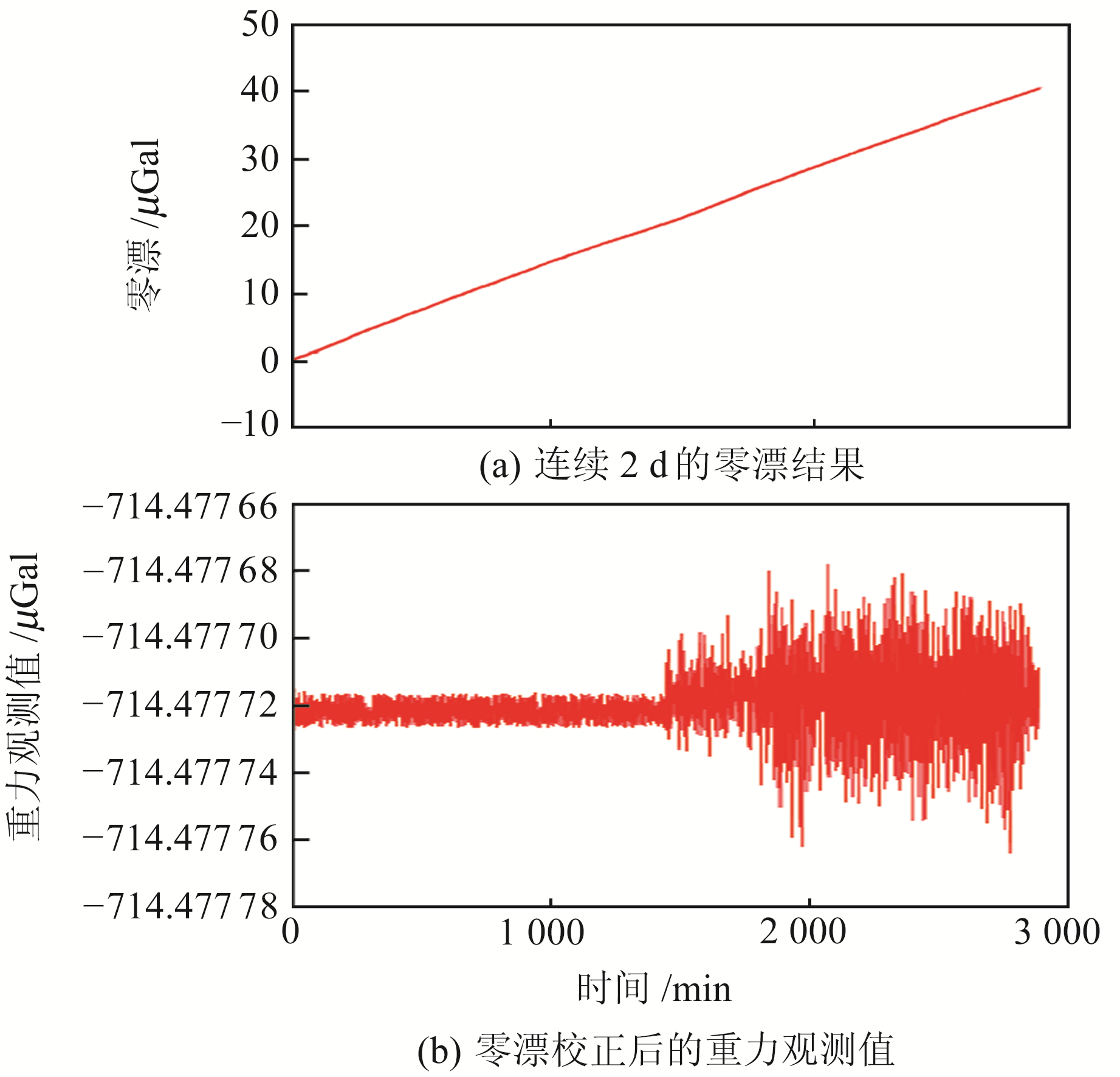
2.5 贝叶斯算法结果分析贝叶斯算法得到连续2 d的零漂以及零漂校正后的重力观测值如图 6所示。
|
图 6 贝叶斯算法所得结果 Fig. 6 Bayesian algorithm results |
由图 6(b)可知,样本矩阵、零漂矩阵、协方差矩阵的不断变化,会使第2天的重力观测值方差更大,第1天重力观测值方差为8.458 01×10-12 μGal2,而第2天为1.595 53×10-10 μGal2,方差数量级已符合高精度的要求。
2.6 干扰作用下的结果分析人为添加白噪声作为干扰信号加入到重力观测值中,模拟在观测过程中遇到外部干扰的情况。通过算法得到连续2 d的零漂结果以及零漂校正后的重力观测值如图 7所示。

|
图 7 加入干扰后的算法结果 Fig. 7 Algorithm results after adding interference |
由图 7(a)可知,干扰信号会对零漂结果造成一定影响,影响在可控范围内的原因在于先验分布的协方差矩阵会约束零漂的变动幅度。由图 7(b)可知,经过零漂校正后的重力观测值仍会将干扰信号特征体现出来,同时也说明算法具有一定的抗干扰能力,在干扰结束后仍然可以精准地计算零漂值。
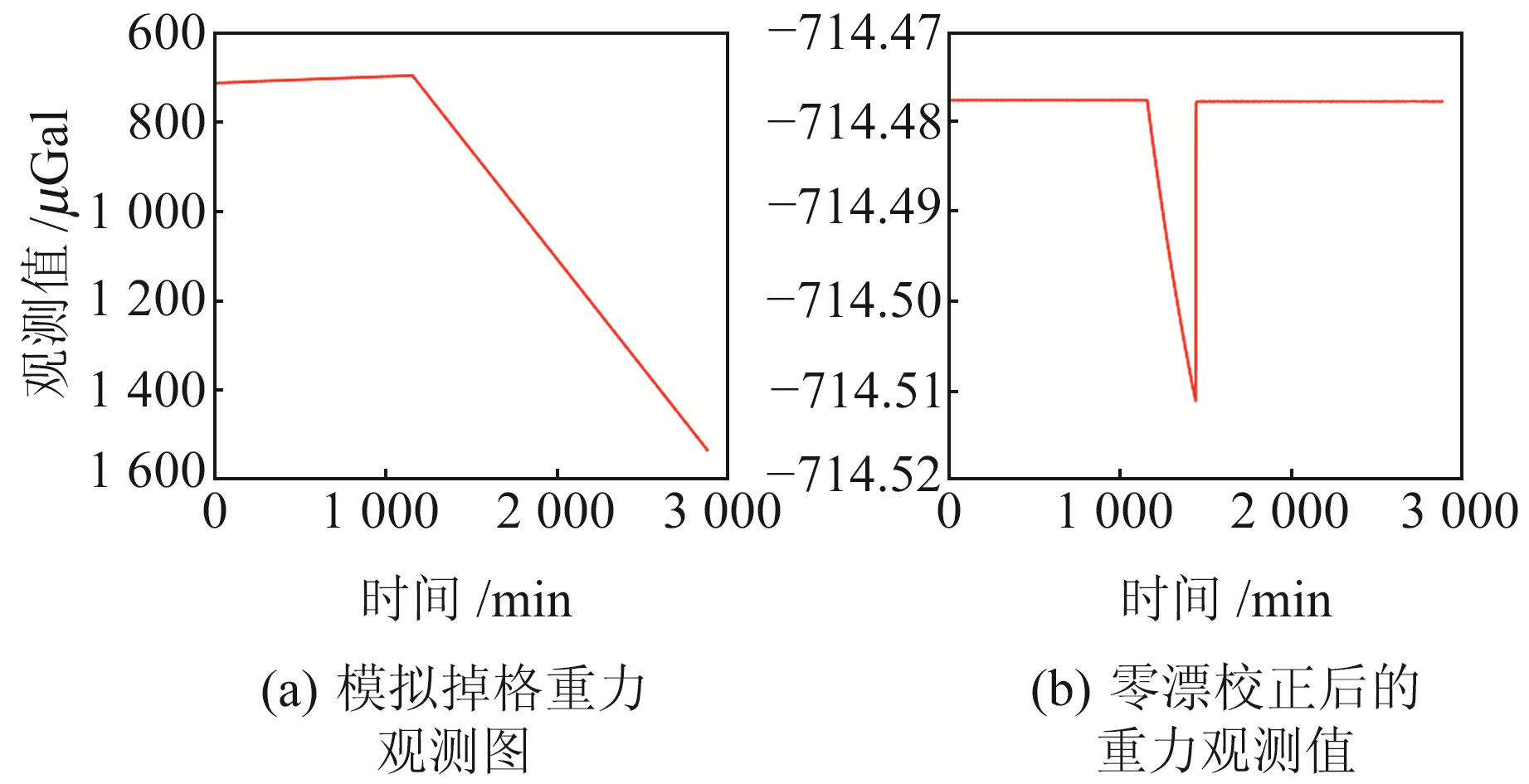
2.7 线性掉格下的结果分析人为在重力观测数据中添加线性参数,模拟重力仪由于人员操作或温度骤变等外界因素而使仪器出现线性掉格的情况,结果如图 8(a)所示。
|
图 8 线性掉格情况下算法结果 Fig. 8 Algorithm results in case of linear drifting |
由图 8(b)可知,重力仪出现掉格后,该算法的去零漂结果会出现微小跳变,经过300个数据点后零漂校正结果回归正常,说明该算法需要300个数据点进行恢复零漂计算,但由于跳动较小,因此可以视为在出现线性掉格时,该算法仍然可以正常工作并保持准确度。
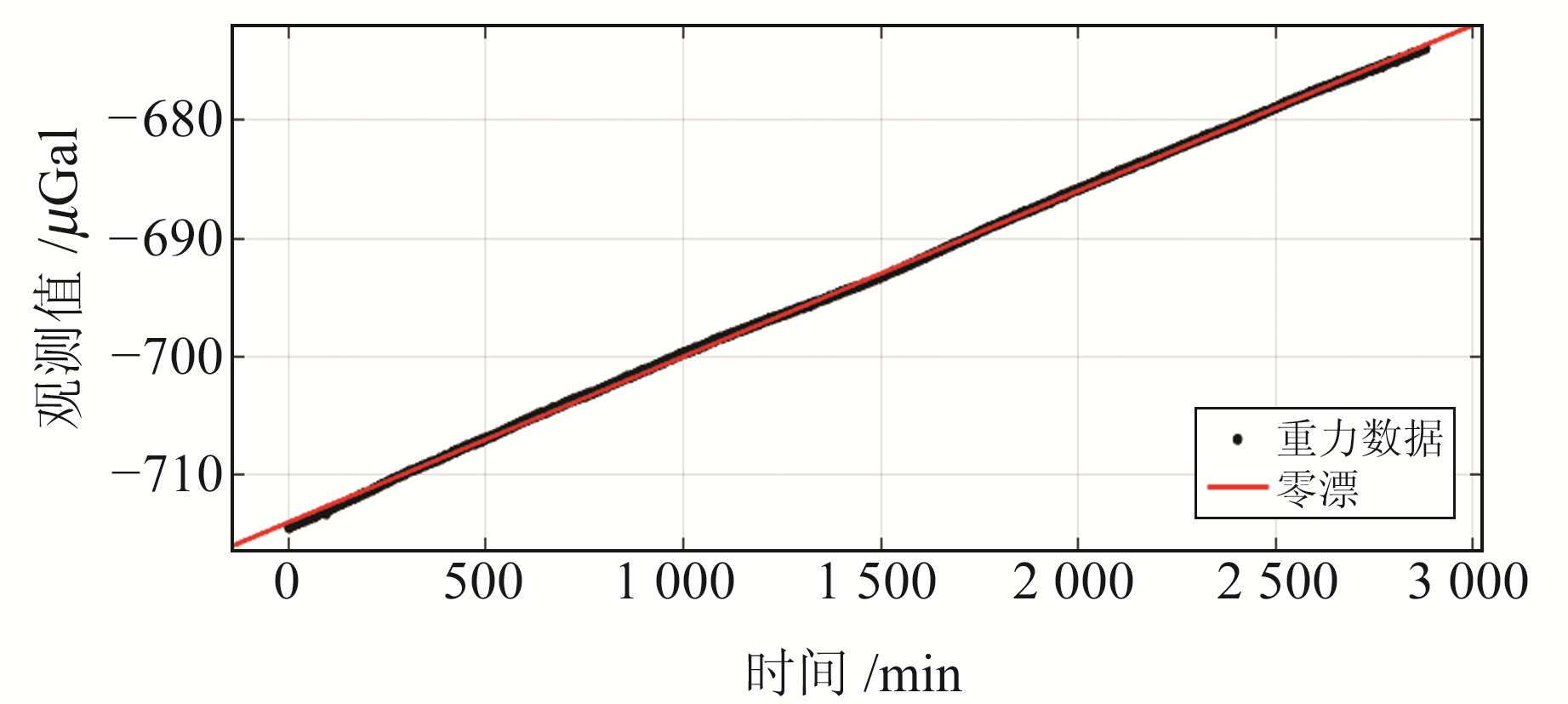
2.8 经典算法结果对比通过线性拟合对同样2 d的连续重力观测值进行零漂估计,拟合结果如图 9所示。
|
图 9 连续2 d重力观测值线性拟合结果 Fig. 9 Linear fitting results of gravity observations for two consecutive days |
线性拟合的零漂率为0.014 02 μGal/min,由此得到去除零漂的重力观测值如图 10所示。
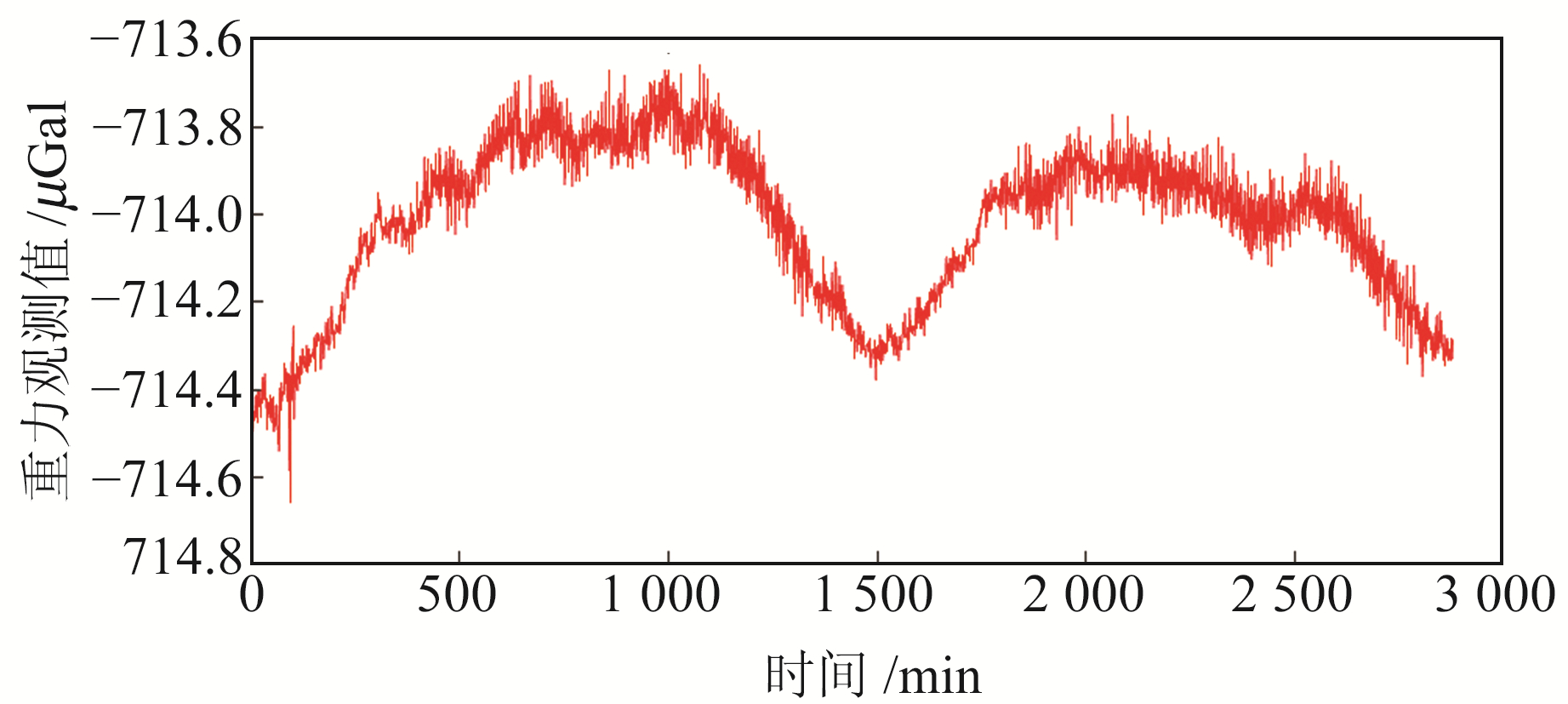
|
图 10 线性拟合算法零漂校正 Fig. 10 Drift correction of linear fitting algorithm |
对比图 10与图 6(b)发现,贝叶斯算法可将重力观测值中的非线性零漂去除,实现对非线性零漂的精准估计。
3 结语本文提出一种基于贝叶斯公式,以零漂的连续性作为先验约束条件,考虑重力观测数据浮动产生的偏差,将每个采样点零漂的均值和方差作为超参数进行求解,从而获得零漂估计值的算法。通过零漂与重力观测数据的关系式以及零漂的连续性得到零漂的分布规律,采用逻辑推导和数据验证证明,贝叶斯算法得到零漂后验分布的均值会随着计算次数的增加而向零漂真实值收敛。在模拟的数据采样过程中,通过贝叶斯算法得到零漂校正结果的方差为1.595 53×10-10 μGal2,符合DZW重力仪的精度需求。在添加人为干扰后得到的零漂校正结果表明,该算法可以在保留重力信号特征的前提下精准去除零漂值。
本文提出的非线性零漂贝叶斯估计方法能有效地去除重力观测值中的非线性零漂,可以在重力分采样过程中实时对重力观测值进行预处理,从而为重力观测精度提供保障。
| [1] |
孙和平, 孙文科, 申文斌, 等. 地球重力场及其地学应用研究进展——2020中国地球科学联合学术年会专题综述[J]. 地球科学进展, 2021, 36(5): 445-460 (Sun Heping, Sun Wenke, Shen Wenbin, et al. Research Progress of Earth's Gravity Field and Its Application in Geosciences: A Summary of Annual Meeting of Chinese Geoscience Union in 2020[J]. Advances in Earth Science, 2021, 36(5): 445-460)
(  0) 0) |
| [2] |
隗寿春, 徐建桥, 郝洪涛, 等. 零漂改正对中国地壳运动观测网络重力数据处理的影响[J]. 大地测量与地球动力学, 2017, 37(4): 403-406 (Wei Shouchun, Xu Jianqiao, Hao Hongtao, et al. Impacts of Zero Drift Correction in CMONOC Data Processing[J]. Journal of Geodesy and Geodynamics, 2017, 37(4): 403-406)
(  0) 0) |
| [3] |
郝洪涛, 刘少明, 韦进, 等. CG-6型重力仪零漂特性研究[J]. 大地测量与地球动力学, 2019, 39(10): 1 086-1 090 (Hao Hongtao, Liu Shaoming, Wei Jin, et al. Study on Zero Drift Characteristics of CG-6 Gravimeter[J]. Journal of Geodesy and Geodynamics, 2019, 39(10): 1 086-1 090)
(  0) 0) |
| [4] |
王林海, 陈石, 庄建仓, 等. 精密重力测量中相对重力仪格值系数的贝叶斯估计方法[J]. 测绘学报, 2020, 49(12): 1 543-1 553 (Wang Linhai, Chen Shi, Zhuang Jiancang, et al. Bayesian Estimation of the Scale Factor of Relative Gravimeter in Precise Gravity Survey[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(12): 1 543-1 553)
(  0) 0) |
| [5] |
杨锦玲, 陈石, 王林海, 等. 华南陆地时变重力观测数据质量评估[J]. 测绘学报, 2021, 50(3): 333-342 (Yang Jinling, Chen Shi, Wang Linhai, et al. Data Quality Assessment of Time-Varying Terrestrial Gravity Observation in South China[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(3): 333-342)
(  0) 0) |
| [6] |
郝洪涛, 李辉, 孙和平, 等. CG-5重力仪零漂改正及格值系数检测应用研究[J]. 武汉大学学报: 信息科学版, 2016, 41(9): 1 265-1 271 (Hao Hongtao, Li Hui, Sun Heping, et al. Application of Zero Drift Correct and Detection of Scale Parameters of CG-5 Gravimeter[J]. Geomatics and Information Science of Wuhan University, 2016, 41(9): 1 265-1 271)
(  0) 0) |
| [7] |
李瑞浩. 重力学引论[M]. 北京: 地震出版社, 1988 (Li Ruihao. Introduction to Gravity[M]. Beijing: Seismological Press, 1988)
(  0) 0) |
| [8] |
茆诗松, 汤银才. 贝叶斯统计[M]. 北京: 中国统计出版社, 2012 (Mao Shisong, Tang Yincai. Bayesian Statistics[M]. Beijing: China Statistics Press, 2012)
(  0) 0) |
| [9] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2019 (Li Hang. Statistical Learning Method[M]. Beijing: Tsinghua University Press, 2019)
(  0) 0) |
| [10] |
Sakamoto Y, Ishiguro M. A Bayesian Approach to Nonparametric Test Problems[J]. Annals of the Institute of Statistical Mathematics, 1988, 40(3): 587-602 DOI:10.1007/BF00053067
(  0) 0) |
| [11] |
Chen S, Zhuang J C, Li X Y, et al. Bayesian Approach for Network Adjustment for Gravity Survey Campaign: Methodology and Model Test[J]. Journal of Geodesy, 2019, 93(5): 681-700 DOI:10.1007/s00190-018-1190-7
(  0) 0) |
| [12] |
Xia M. Bayesian Adjustment for Insurance Misrepresentation in Heavy-Tailed Loss Regression[J]. Risks, 2018, 6(3)
(  0) 0) |
| [13] |
郝洪涛, 刘少明, 韦进, 等. CG-6型重力仪零漂特性研究[J]. 大地测量与地球动力学, 2019, 39(10): 1 086-1 090 (Hao Hongtao, Liu Shaoming, Wei Jin, et al. Study on Zero Drift Characteristics of CG-6 Gravimeter[J]. Journal of Geodesy and Geodynamics, 2019, 39(10): 1 086-1 090)
(  0) 0) |
2. Wuhan Institute of Seismic Scientific Instruments Co Ltd, 40 Hongshance Road, Wuhan 430071, China;
3. Engineering Technology Research Center for Earthquake Monitoring and Early Warning Disposal of Major Projects in Hubei Province, 11 Qinglong Road, Xianning 437000, China
 2022, Vol. 42
2022, Vol. 42


