2. 中国测绘科学研究院, 北京市莲花池西路28号, 100830;
3. 甘肃省地理国情监测工程实验室, 兰州市安宁西路88号, 730070;
4. 地理国情监测技术应用国家地方联合工程研究中心, 兰州市安宁西路88号, 730070
地球表层系统中的环境变化会引起固体地球发生形变,表现在地面垂直形变、地面重力、地倾斜与大地水准面变化[1-2]等方面。大气负荷是地表环境负荷的主要影响因素之一,是研究GNSS时间序列周期信号特征及地表负荷形变场不可忽略的因素。近年来,许多学者在研究固体地球形变和GNSS站时间序列分析中均已考虑大气压变化的负荷影响。Martens等[3]分析GPS基站位置的大气压力负荷表明,季节性变形存在差异;Yue等[4]结合GNSS基准站分析不同地区大气变化与地壳形变的相关性;安旭伟等[5]对祁连山南麓区域的大气负荷动力学效应进行研究;王海涛等[6]结合地表温度变化与大气压变化,综合分析温度变化与大气压变化对基准站垂向形变的影响规律;刘宇等[7]计算浙江地区的负荷形变场和重力场变化发现,该区域的大气负荷影响达cm级,该研究虽然结合了区域内部气象站数据,但气象站分布离散且稀疏,内插格网化时会引入噪声。上述研究表明,在高精度高分辨率区域进行大气负荷形变场解算时,结合区域高分辨率大气压格网数据的相关研究较少,因此本文利用中国气象网滇西地区高分辨率的大气压数据进一步精化该区域的大气负荷影响,提高大地测量精度。
本文以滇西地区为例,引入局部重力场逼近的移去-恢复思想,基于负荷球谐系数和区域负荷格林函数,结合滇西地区的全球大气压变化数据和区域高分辨率大气压变化数据,分析大气压变化对滇西地区的负荷影响。
1 理论与方法大气压变化引起的负荷形变场和时变重力场变化由负荷位和负荷附加位两个部分组成[8],常用的计算方法有球谐系数法和格林函数积分法等。
1.1 全球负荷形变场的球谐分析地球表层大气压变化为非潮汐运动,可用地面等效水高表示,地面上任意一点(R, θ, λ)处的等效水高hw可表示为规格化负荷球谐级数[8]:
| $ \begin{array}{*{20}{c}} {{h_{\rm{w}}}(R, \theta , \lambda ) = }\\ {R\sum\limits_{n = 1}^N {\sum\limits_{m = 0}^n {\left[ {\Delta {C_{nm}}\cos m\lambda + \Delta {S_{nm}}\sin m\lambda } \right]} } {{\bar P}_{nm}}(\sin \varphi )} \end{array} $ | (1) |
式中,R为地球平均半径,θ、λ分别为地面点的地心纬度和经度,ΔCnm、ΔSnm为n阶m次规格化负荷球谐系数,Pnm(sinφ)为完全规格化缔合Legendre函数,N为球谐展开的最大阶数。
由负荷形变理论[1]可知,地面及地球外部的高程异常负荷影响可表示为:
| $ \begin{array}{*{20}{c}} {\zeta = \frac{{GM}}{{\gamma r}}\sum\limits_{n = 2}^\infty {{{\left( {\frac{a}{r}} \right)}^n}} \left( {1 + k_n^\prime } \right) \cdot }\\ {\sum\limits_{m = 0}^n {\left( {\Delta {{\bar C}_{nm}}\cos m\lambda + \Delta {{\bar S}_{nm}}\sin m\lambda } \right)} {{\bar P}_{nm}}} \end{array} $ | (2) |
地面重力负荷影响计算公式为:
| $ \begin{array}{*{20}{c}} {{g_t} = \frac{{GM}}{{{r^2}}}\sum\limits_{n = 2}^\infty {(n + 1)} \left( {1 + \frac{2}{n}h_n^\prime - \frac{{n + 1}}{n}k_n^\prime } \right) \cdot }\\ {{{\left( {\frac{a}{r}} \right)}^n}\sum\limits_{m = 0}^n {\left( {\Delta {{\bar C}_{nm}}\cos m\lambda + \Delta {{\bar S}_{nm}}\sin m\lambda } \right)} {{\bar P}_{nm}}} \end{array} $ | (3) |
大地高负荷影响计算公式为:
| $ \begin{array}{*{20}{c}} {{H_t} = \frac{{GM}}{{\gamma r}}\sum\limits_{n = 2}^\infty {{{\left( {\frac{a}{r}} \right)}^n}} h_n^\prime \cdot }\\ {\sum\limits_{m = 0}^n {\left( {\Delta {{\bar C}_{nm}}\cos m\lambda + \Delta {{\bar S}_{nm}}\sin m\lambda } \right)} {{\bar P}_{nm}}} \end{array} $ | (4) |
式(2)~(4)中,G为万有引力常数,M为地球总质量,r为地面计算点的地心距,γ为地面计算点的正常重力,h′n为n阶径向负荷勒夫数,k′n为n阶位负荷勒夫数,Pnm为n阶Legendre函数。
1.2 区域负荷影响的格林函数积分公式地面测站位置的变化也可用负荷数(负荷格林函数)进行表示[9]:
| $ \Delta \mathit{\Theta }(\varphi , \lambda ) = G{\rho _{\rm{w}}}\iint_s {\frac{{\Delta {h_{\rm{w}}}\left( {{\varphi ^\prime }, {\lambda ^\prime }} \right)}}{L}} G(\psi ){\rm{d}}S $ | (5) |
式中,ΔΘ(φ, λ)为地面测站位置的变化量,ψ为地面测站点和流动点(φ′, λ′)之间的球面角距,G(ψ)为负荷格林函数,ρw为水的密度,S为地球表面积。
格林函数积分法计算的负荷位[10]为:
| $ \begin{array}{*{20}{c}} {G_i^V(\psi ) = \frac{{\gamma R}}{M} \cdot }\\ {\sum\limits_{n = 0}^\infty {\left( {\frac{{k_\infty ^\prime }}{{2\sin (\psi /2)}} + \sum\limits_{n = 0}^\infty {\left( {k_n^\prime + k_\infty ^\prime } \right)} {P_n}(\cos \psi )} \right)} } \end{array} $ | (6) |
格林函数积分法计算的负荷附加位为:
| $ G_d^V(\psi ) = \frac{{\gamma R}}{M}\frac{1}{{2\sin (\psi /2)}} $ | (7) |
式(6)、(7)中,G为地球平均半径,M为地球总质量,k′n为n阶位负荷数。
地面重力的负荷格林函数总影响[10]可表示为:
| $ \begin{array}{l} \begin{array}{*{20}{c}} {G(\psi ) = - \frac{\gamma }{M}\left( {\frac{{k_\infty ^\prime - 2h_\infty ^\prime }}{{2\sin (\psi /2)}} + } \right.}\\ {\left. {\sum\limits_{n = 0}^\infty {\left( {(n + 1)k_n^\prime - k_\infty ^\prime - 2\left( {h_n^\prime - h_\infty ^\prime } \right){P_n}(\cos \psi )} \right)} } \right) + } \end{array}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{\gamma }{M}\frac{1}{{4\sin (\psi /2)}} \end{array} $ | (8) |
大地高的负荷格林函数总影响计算公式为:
| $ \begin{array}{c} G_{i}^{r}(\psi)= \\ \frac{R}{M}\left(\frac{h_{\infty}^{\prime}}{2 \sin (\psi / 2)}+\sum\limits_{n=0}^{\infty}\left(h_{n}^{\prime}+h_{\infty}^{\prime}\right) P_{n}(\cos \psi)\right) \end{array} $ | (9) |
式(8)、(9)中,当ΔΘ(φ, λ)为地面重力的变化量时,G(ψ)为重力格林函数;当ΔΘ(φ, λ)为地面大地高的变化量时,G(ψ)为径向格林函数;Pn(cosψ)为n阶Legendre函数。
2 研究区与实验数据处理 2.1 研究区概况本文将滇西地区作为研究区,包括保山、大理两个地级市及周边区域(97.5°~101.5°E,23.5°~27°N)。该区地貌以高山为主,怒江、澜沧江、金沙江等河流流经该区。受地形地貌多样性影响,雨季局部地区暴雨频发。
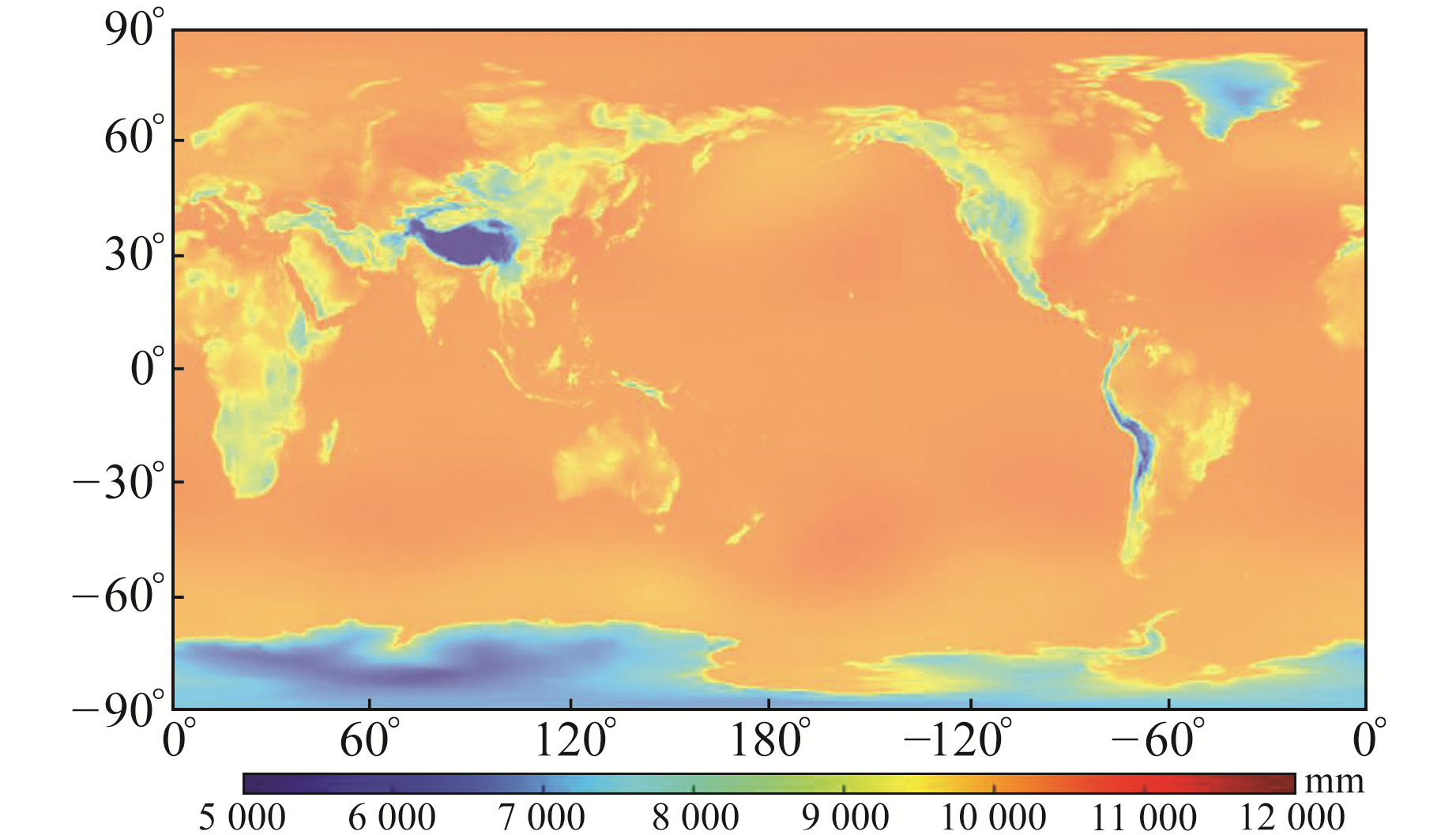
2.2 实验数据 2.2.1 全球大气压变化数据全球大气压数据采用欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts)的全球气候和天气第五代再分析产品(http://cds.climate.copernicus.eu),该产品在其前身基础上采用先进的数据同化和模式系统,可用来估计更为准确的大气状况。本次实验下载全球范围数据,空间分辨率为0.25°× 0.25°,时间分辨率为h,时间跨度为2018-01-01 00:00~2020-12-31 23:00。利用MATLAB程序提取原始NC文件中的surface press(表面压力),将每天24 h数据取平均值作为日值数据。图 1为2018-01-01全球大气压数据分布图。
|
图 1 全球大气压数据分布 Fig. 1 Distribution of global atmospheric pressure data |
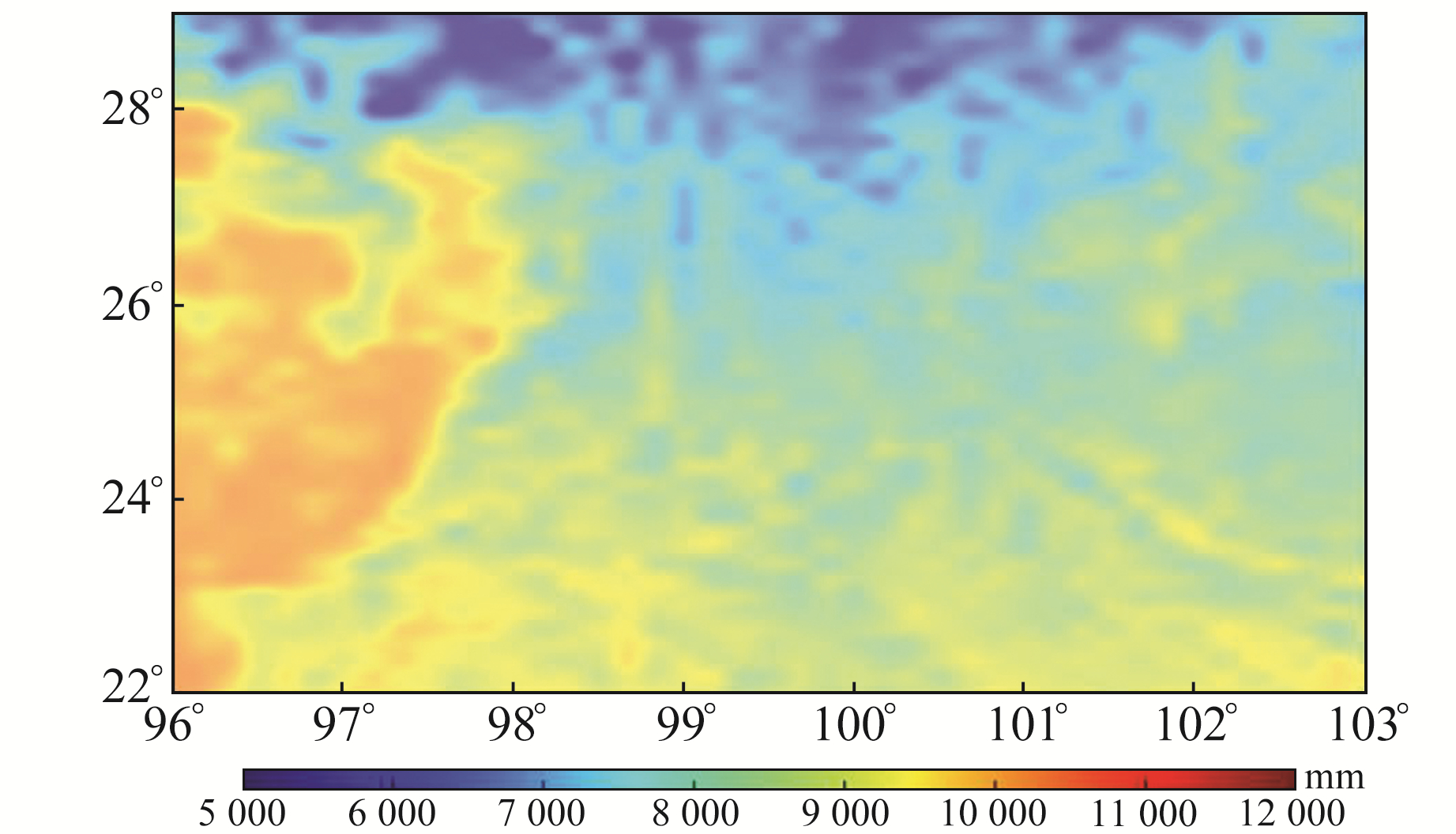
区域高分辨率大气压数据采用国家气象科学数据中心中国气象局陆面数据同化系统(CLDAS-V2.0)近实时产品数据集(http://data.cma.cn),范围为96°~103°E、22°~29°N,空间分辨率为0.062 5°×0.062 5°,时间分辨率为d,时间跨度为2018-01-01~2020-12-31。CLDAS-V2.0产品利用多种来源于地面、卫星的观测资料,范围覆盖亚洲区域,在中国区域质量优于国际同类产品,且时空分辨率更高。考虑到格林积分函数计算负荷形变时是对区域进行卷积积分,在选择区域高分辨率大气压变化数据范围时适当扩展区域范围。图 2为2018-01-01区域高分辨率大气压变数据分布。
|
图 2 区域高分辨率大气压数据分布 Fig. 2 Distribution of regional high resolution atmospheric pressure data |
通过解算滇西地区内72个CORS站每天的观测数据,并扣除固体潮、海潮等潮汐影响,得到CORS站大地高变化时间序列,时间跨度为2018-01-01~2020-12-31,时间分辨率为d。
2.3 数据处理流程本文将全球大气压数据和区域高分辨率大气压数据转换为数字格网模型,然后将其转换为等效水高格网模型(地表大气负荷质量变化),再采用距离反比插值方法将全球大气等效水高格网的空间分辨率由0.25°转为0.5°,区域高分辨率等效水高格网的空间分辨率由0.062 5°转为30″。由区域高分辨率大气压变化数据,采用基于全球负荷形变场球谐系数模型的移去-恢复法,计算区域高精度大气负荷形变场和时变重力场。计算流程为:
1) 对全球等效水高变化格网进行球谐分析展开,得到360阶次负荷变化球谐系数模型,并通过球谐综合计算得到滇西地区参考等效水高和负荷影响模型值格网;
2) 将区域等效水高变化格网数据移去参考等效水高,获得区域等效水高变化残差格网数据,并利用负荷格林函数积分理论计算区域残余负荷影响模型值格网;
3) 将全球负荷影响模型值格网与区域残余负荷影响模型值格网结合,恢复为滇西地区区域高精度负荷影响格网模型。
3 实验结果与分析为了统一基准,本文将全球大气压变化格网和区域高分辨率大气压变化格网的日值数据按照GPS周进行周平均,得到周值文件,并将2018年52个周值文件的平均值作为基准扣除,得到大气压周变化格网。然后根据移去-恢复法计算大气压变化对滇西地区高精度负荷形变场及时变重力场的影响,计算得到空间分辨率为30″、时间分辨率为周。高精度负荷形变场和时变重力场可以更好地反映大气压变化对滇西地区的影响。
3.1 地壳形变地壳垂直形变是地壳在高程方向的变化量,即大地高变化。表 1为大气压变化对滇西地区高程异常、大地高等大地测量参数的统计信息。可以看出,大气压变化对地壳高程方向的影响较大,年变化幅度达cm级;而对地壳水平方向的影响较小,年变化幅度最大仅为0.944 mm。其中,大气负荷对高程异常的影响等于其对正常高影响与大地高影响之差。
|
|
表 1 大气负荷地壳形变信息统计 Tab. 1 Statistical information of crustal deformation caused by atmospheric load |
由于不同时间内大气压变化存在差异,因此本文选取年变化幅度最大的2019年中每个月第1周的大气压变化对大地高的影响进行分析。图 3为2019年大气压变化对滇西地区大地高的影响,可以看出,大气压变化对大地高的影响具有十分明显的季节性变化规律。由春入夏过程中,滇西地区大地高变化缓慢抬升,6月份大地高变化量达到最大值;而从秋到冬,大地高变化又逐渐下降,12月份大地高变化量达到最小值。

|
图 3 大气压变化对滇西地区大地高的影响 Fig. 3 The influence of atmospheric pressure change on the geodetic height in western Yunnan |
为更好地分析大气压负荷对滇西地区的影响,选取滇西区域内YNLC(临沧)、YNLJ(丽江)、YNRL(瑞丽)、YNSD(施甸)、YNYA(姚安)、YAYS(永善)6个CORS站进行分析。从原始大地高时间序列中扣除均值并进行粗差探测,移去线性项和常数项,得到非线性大地高时间序列,并按照GPS周进行周平均,得到周值数据,结果如图 4所示。可以看出,滇西地区CORS站大地高变化具有十分明显的年、半年周期规律,变化幅度达到-30~30 mm。

|
图 4 CORS站大地高变化时间序列 Fig. 4 Time series of geodetic height variation at CORS stations |
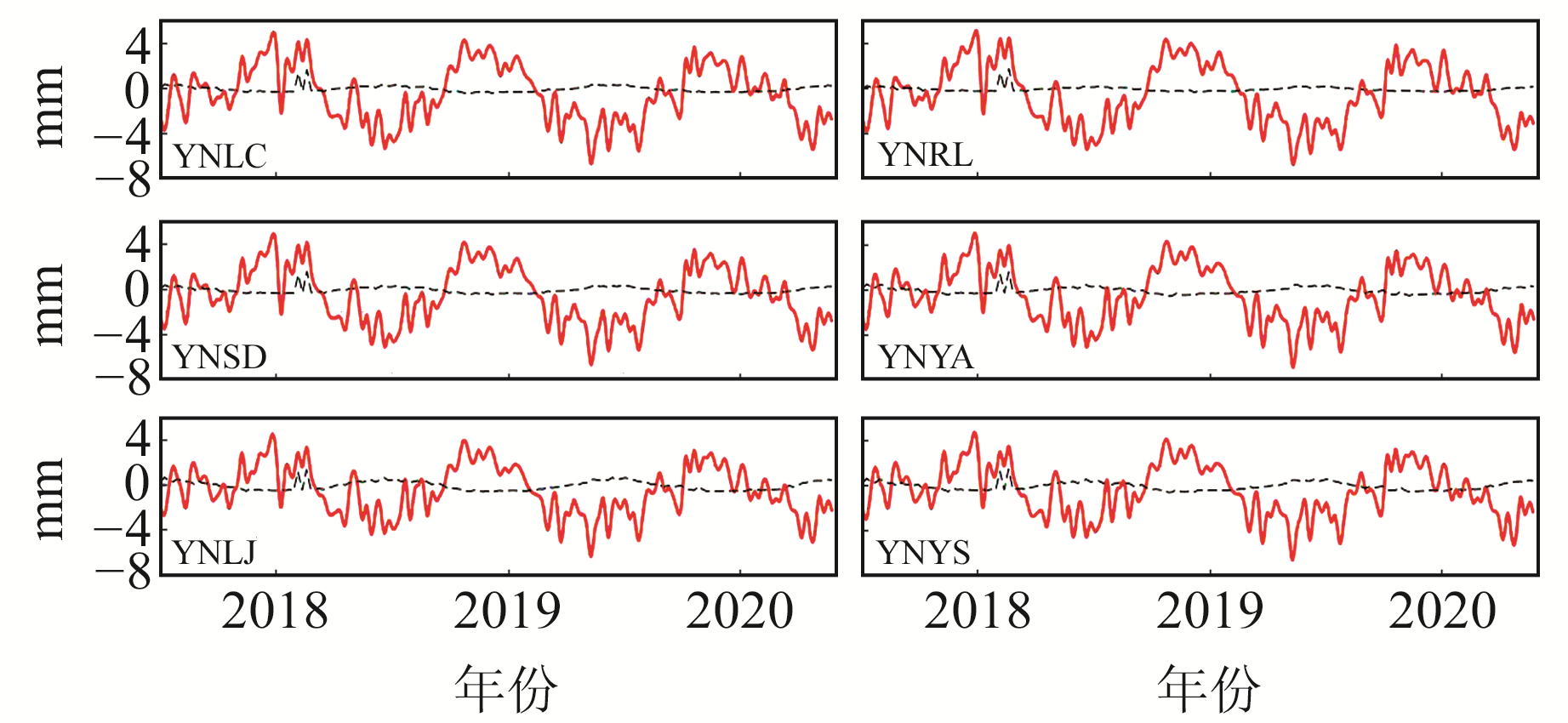
将利用移去-恢复法计算的大地高负荷影响采用距离反比插值方法,得到6个CORS站点处大气压变化对大地高的负荷影响,结果如图 5所示。对比图 4与图 5可知,大气负荷对CORS站大地高的影响与CORS站大地高变化的趋势一致,且变化幅度为-8~6 mm。图 5中黑色虚线为区域高分辨率大气压数据与全球大气压模型数据计算的大地高负荷影响的差值,可以看出,两者差异较小,这可能与研究区地理位置有关。由于大气压变化与海拔相关,我国大气压变化引起的负荷影响,南方比北方小,西部比东部小,本文研究区位于西南地区,因此计算的负荷影响较小。
|
图 5 CORS站大气负荷时间序列 Fig. 5 Time series of atmospheric load at CORS stations |
为进一步说明在分析GNSS时间序列周期信号特征及地表环境负荷形变场时大气负荷改正的重要性,本文通过分析扣除大气负荷前后CORS站大地高时间序列的均方根(RMS)来反映大气负荷影响对CORS站大地高的贡献。表 2为计算结果,在扣除大气负荷后,CORS站非线性大地高时间序列的RMS值减小,大气负荷的贡献可达8.62%。这一方面明确了大气压变化引起的大地高变化在CORS站大地高时间序列中的贡献率,不同CORS站的大地高变化对大气负荷的敏感性有所不同;另一方面也说明,在研究CORS站非线性运动中,大气负荷改正具有必要性。
|
|
表 2 大气负荷对CORS站大地高时间序列的贡献 Tab. 2 Contribution of atmospheric load to geodetic height time series of CORS stations |
本文主要从地面重力、扰动重力等方面来说明大气压变化对时变重力场的影响。大气压变化对地面重力与扰动重力的影响包括负荷位引起的直接影响和负荷附加位引起的间接影响。计算过程中将地面重力和扰动重力的直接影响与间接影响相加,得到大气压变化对地面重力和扰动重力的总负荷影响;垂线偏差为垂线偏差南向与垂线偏差西向的矢量和。为了解大气负荷对滇西地区时变重力场的影响,对时变重力场参数进行统计分析,通过计算其年变化振幅来了解其影响的量级规律(表 3)。由表 3可知,大气压变化对地面重力的影响较大,年变化振幅约为8 μGal;对垂线偏差的影响较小,年变化振幅最大仅为2.4 ms。
|
|
表 3 大气负荷时变重力场信息统计 Tab. 3 Statistical information of time-varying gravity field of atmospheric load |
图 6为2019-01~12第1周大气压变化对滇西地区地面重力的影响分布。可以看出,地面重力与大气压成反比,大气压越大,所引起的地面重力影响越小,且大气负荷对地面重力的影响同样具有年周期规律。规律显示,大气负荷对地面重力的影响在春、夏季具有增大趋势,在秋、冬季则表现为减小趋势。滇西地区雨季暴雨频发,主要集中在6~8月,该段时间大气压较小,对地面重力的影响较大,最大可达3.8 μGal。

|
图 6 大气压变化对滇西地区地面重力的影响 Fig. 6 Influence of atmospheric pressure change on surface gravity in western Yunnan |
本文以滇西地区为研究区,根据地球重力场理论,引入移去-恢复思想,结合全球大气压变化数据和区域高分辨率大气压变化数据,基于负荷球谐系数和区域负荷格林函数方法,得到大气压变化对滇西地区高精度负荷形变场及时变重力场的影响。结果表明,大气压变化引起的负荷影响具有十分明显的年周期规律。大气压变化对地壳形变中垂直形变的影响在1 a内大于10 mm,且大气压变化引起的大地高变化在CORS站大地高时间序列中的贡献率占8%左右;对水平方向的负荷影响较小。大气压变化对时变重力场中地面重力的影响约为8 μGal,且与大气变化呈现明显的负相关性。本文研究结果对负荷形变场的精化具有一定的参考意义。
| [1] |
章传银, 李爱勤, 党亚民, 等. CORS网区域重力场变化与地面稳定性跟踪监测方法[J]. 测绘科学, 2019, 44(6): 29-36 (Zhang Chuanyin, Li Aiqin, Dang Yamin, et al. A Method of Tracking and Monitoring of Regional Time-Varying Gravity Field and Ground Stability Based on CORS Network[J]. Science of Surveying and Mapping, 2019, 44(6): 29-36)
(  0) 0) |
| [2] |
王伟, 章传银, 杨强, 等. 大气负荷对区域地壳形变和重力变化的影响分析[J]. 武汉大学学报: 信息科学版, 2018, 43(9): 1 302-1 308 (Wang Wei, Zhang Chuanyin, Yang Qiang, et al. Impact of Atmospheric Pressure Loading on Regional Crustal Deformation and Gravity Change[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1 302-1 308)
(  0) 0) |
| [3] |
Martens H R, Argus D F, Norberg C, et al. Atmospheric Pressure Loading in GPS Positions: Dependency on GPS Processing Methods and Effect on Assessment of Seasonal Deformation in the Contiguous USA and Alaska[J]. Journal of Geodesy, 2020, 94(12): 155
(  0) 0) |
| [4] |
Yue C Y, Dang Y M, Xu C H, et al. Effects and Correction of Atmospheric Pressure Loading Deformation on GNSS Reference Stations in Chinese Mainland[J]. Mathematical Problems in Engineering, 2020(2): 1-10
(  0) 0) |
| [5] |
安旭伟, 杨国林, 孙学先, 等. 祁连山南麓区域的大气负荷动力学效应研究[J]. 导航定位学报, 2021, 9(2): 90-95 (An Xuwei, Yang Guolin, Sun Xuexian, et al. Study on the Dynamical Effects of Atmospheric Load on the Southern Foot of Qilian Mountains[J]. Journal of Navigation and Positioning, 2021, 9(2): 90-95)
(  0) 0) |
| [6] |
王海涛, 聂建亮, 田婕, 等. 地表温度变化对GNSS连续运行基准站垂向形变影响研究[J]. 大地测量与地球动力学, 2020, 40(11): 1 170-1 174 (Wang Haitao, Nie Jianliang, Tian Jie, et al. Research on Influence of Surface Temperature Change on Vertical Deformation of GNSS Continuously Operating Reference Station[J]. Journal of Geodesy and Geodynamics, 2020, 40(11): 1 170-1 174)
(  0) 0) |
| [7] |
刘宇, 李爱勤, 俞志强, 等. 大气负荷效应对浙江地区的影响分析[J]. 大地测量与地球动力学, 2020, 40(6): 591-595 (Liu Yu, Li Aiqin, Yu Zhiqiang, et al. Analysis of the Impact of Atmospheric Load Effect on Zhejiang Province[J]. Journal of Geodesy and Geodynamics, 2020, 40(6): 591-595)
(  0) 0) |
| [8] |
党亚民, 章传银, 陈俊勇, 等. 现代大地测量基准[M]. 北京: 测绘出版社, 2015 (Dang Yamin, Zhang Chuanyin, Chen Junyong, et al. Modern Geodetic Datum[J]. Beijing: Surveying and Mapping Press, 2015)
(  0) 0) |
| [9] |
章传银, 王伟, 甘卫军, 等. 利用CORS站网监测三峡地区环境负荷引起的地壳形变与重力场时空变化[J]. 武汉大学学报: 信息科学版, 2018, 43(9): 1 287-1 294 (Zhang Chuanyin, Wang Wei, Gan Weijun, et al. Monitoring Temporal and Spatial Changes of Crustal Deformation and Gravity Filed Caused by Environment Loading in the Three Gorges Reservoir Region Based on CORS Network[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1 287-1 294)
(  0) 0) |
| [10] |
何迎东. 基于CORS站网的丽水温州地质灾害监测预警研究[D]. 兰州: 兰州交通大学, 2019 (He Yingdong. The Study of Monitoring and Early Warning for Geological Disaster on Lishui and Wenzhou City Based on CORS Network[D]. Lanzhou: Lanzhou Jiatong University, 2019)
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100830, China;
3. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, 88 West-Anning Road, Lanzhou 730070, China;
4. National-Local Joint Engineering Research Center of Technologies and Applications for National Geographic State Monitoring, 88 West-Anning Road, Lanzhou 730070, China
 2022, Vol. 42
2022, Vol. 42


