2. 广西空间信息与测绘重点实验室, 桂林市雁山街319号, 541006;
3. 武汉大学卫星导航定位技术研究中心, 武汉市珞喻路129号, 430079
奇异谱分析(singular spectrum analysis,SSA)是一种处理非线性时间序列数据且与经验正交函数相联系的主成分分析,适合于研究周期振荡行为。SSA分解的空间结构与时间尺度密切相关,在细节分量分析方面具有优势,可以较好地提取TEC序列中的趋势项、周期项、噪声残差项信息,从而对TEC时间序列进行分析或去噪[1-2]。长短期记忆(long-short term memory,LSTM)神经网络模型是一种特殊的递归神经网络(recursive neural network,RNN),解决了神经网络在反向传播过程中出现梯度爆炸、消失等缺点,可以更好地学习电离层TEC长期时序信息。但单一LSTM模型易受冗余信息等因素影响,难以完全利用时间信息,无法很好地表现TEC时间序列的动态变化规律,导致电离层TEC预报精度较低[3-5]。本文采用SSA法对电离层TEC原始序列数据进行预处理,与LSTM神经网络组合构建SSA-LSTM短期电离层TEC预报模型,并分析其在磁暴期和磁平静期的TEC预报精度。
1 模型算法原理 1.1 奇异谱分析理论奇异谱分析处理过程主要为构造轨迹矩阵X(嵌入)、对轨迹矩阵X进行奇异值分解(singular value decomposition,SVD)、分组、对角平均化(重构)。详细过程如下[6-8]:
1) 构建轨迹矩阵X(嵌入)。
电离层TEC时间序列可表示为s=(s1, s2, s3, …, sN),N为时间序列长度。轨迹矩阵XM×K可以表示为:
| $ \begin{array}{c} \boldsymbol{X}=\left[\boldsymbol{X}_{1}, \boldsymbol{X}_{2}, \boldsymbol{X}_{3}, \cdots, \boldsymbol{X}_{K}\right]=\left(x_{i j}\right)_{i, j=1}^{M, K}= \\ {\left[\begin{array}{cccc} s_{0} & s_{1} & \cdots & s_{K} \\ s_{1} & s_{2} & \cdots & s_{K+1} \\ \vdots & \vdots & \ddots & \vdots \\ s_{M} & s_{M+1} & \cdots & s_{N} \end{array}\right]} \end{array} $ | (1) |
式中,X为M×K维Hankel矩阵,K=N-M+1,M为窗口长度,是取值范围为2≤M≤N/2的整数,窗口长度设置为时序数据周期的整数倍,一般不超过N/3。
2) 奇异值分解(SVD)。
X可形成M阶矩阵A=XXT,$\sqrt{\lambda_{i}}$为矩阵X的奇异值, i=1, 2, 3, …, d, d=rank(X)。Ui为矩阵X的左奇异向量。设向量Vi为矩阵X的右奇异向量,$\boldsymbol{V}_{i}=\frac{\boldsymbol{X}^{\mathrm{T}} \boldsymbol{U}_{i}}{\sqrt{\lambda}}$。轨迹矩阵X可分解为若干个与其结构相同的初等矩阵$\boldsymbol{E}_{i}=\sqrt{\lambda} \boldsymbol{U}_{i} \boldsymbol{V}_{i}^{\mathrm{T}}$。
3) 分组。
根据分析目标结合特征值贡献率$p = \frac{{{\lambda _i}}}{{\sum\limits_{i = 1}^d {{\lambda _i}} }}$将初等矩阵划分为k个不相交的子集。
4) 对角平均化(重构)。
定义Z=XIk, z1, z2, …, zN为Z经过对角平均化所得到的序列,设M*=min(N, K),K*=max(M, K)且N=M+K-1,若M<K,则zij*=zij;反之zij*=zji。重构公式为:
| $ {z_i} = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{i}\sum\limits_{m = 1}^i {z_{m, i - m + 1}^*} , 1 \le i \le {M^*}}\\ {\frac{1}{{{M^*}}}\sum\limits_{m = 1}^{{L^*}} {z_{m, i - m + 1}^*} , {M^*} < i \le {K^*}}\\ {\frac{1}{{N - i + 1}}\sum\limits_{m = i - {K^*} + 1}^{N - {K^*} + 1} {z_{m, i - m + 1}^*} , {K^*} < i \le N} \end{array}} \right. $ | (2) |
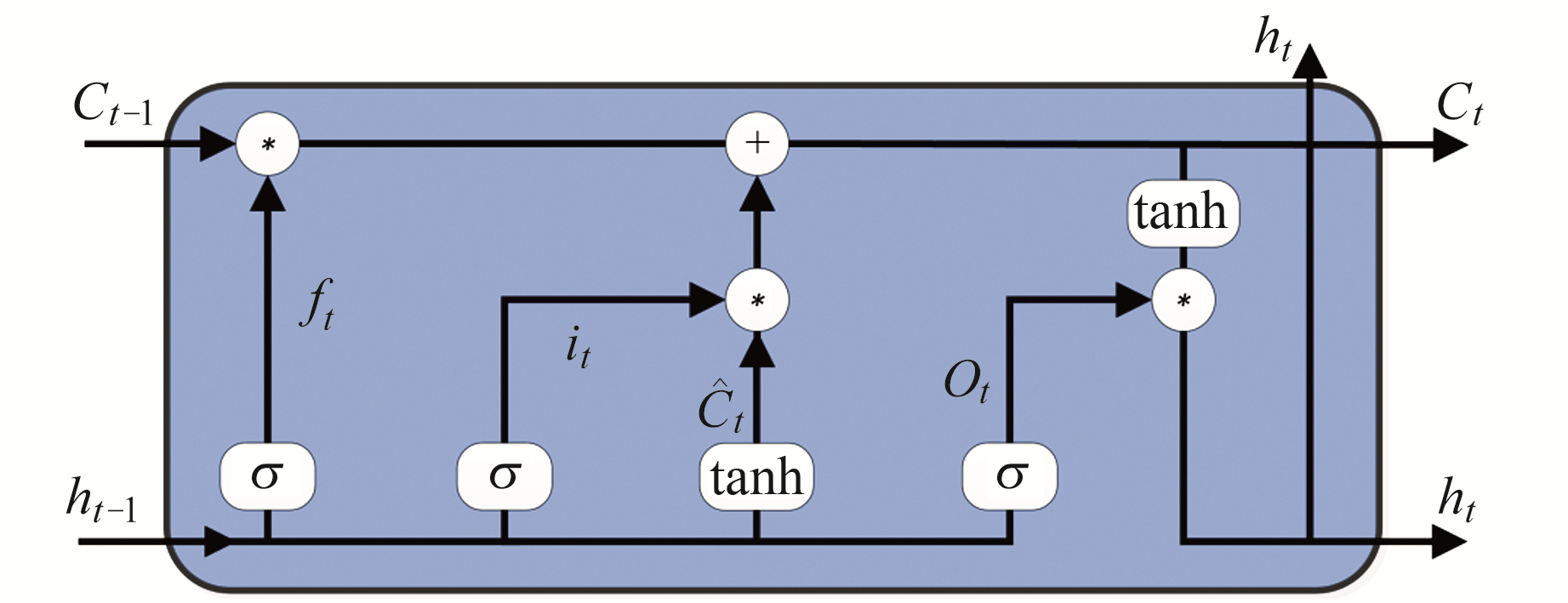
LSTM模型神经元通过添加3个“门”(输入门、遗忘门、输出门)的结构来替换RNN神经元,以改进长期序列的预测:输入门通过确定在单元格状态中需要记住的新信息来处理输入;遗忘门从单元格状态中删除不重要的信息;输出门提取存储在单元格状态中的信息,实现选择记忆反馈的误差函数随梯度下降的修正参数,从而实现时间上的记忆功能,并防止梯度消失[9-10]。其网络神经元结构如图 1所示,Ot和t分别为t时刻神经元经过输出门的输出结果和当前输入的单元状态;ht-1为隐藏层状态;Ct-1为上一时刻的单元状态;Ct为更新后的神经元状态信息;σ为sigmoid激活函数,值域(0, 1);tanh为双曲正切激活函数。
|
图 1 LSTM模型神经元网络结构 Fig. 1 Neural network structure of LSTM model |
本文SSA-LSTM短期电离层TEC预报模型思路如下:首先对电离层TEC数据进行SSA分解,重构为趋势项、周期项和噪声残差项3个分量;然后各分量分别使用LSTM模型进行预测;最后叠加各分量预测结果,得到TEC预报值。SSA-LSTM模型示意图如图 2所示。在磁平静期时,神经元层数为8,初始学习率为0.02,迭代次数为50,学习率衰减周期为20,衰减因子为0.2;在磁暴期时,由于TEC非平稳性与非线性特征明显增强,将学习率衰减周期调整为30。

|
图 2 SSA-LSTM模型示意图 Fig. 2 Schematic diagram of SSA-LSTM model |
本文采用EUREF(ftp://gnss.oma.be/gnss/products/IONEX/)提供的P1(35.5°N,10°W)、P2(35.5°N,0°)、P3(35.5°N,10°E)、P4(35.5°N,20°E)、P5(61.5°N,10°W)、P6(61.5°N,0°)、P7(61.5°N,10°E)、P8(61.5°N,20°E)8个格网点2015年doy050~079(磁暴期)、2020年doy173~202(磁平静期)的电离层TEC数据,时间分辨率为15 min,空间范围为15°W~25°E、35°~62°N,空间分辨率为0.5°。用前27 d的TEC值预报后3 d的TEC值,实验数据和预报结果数据的时间分辨率均为15 min。
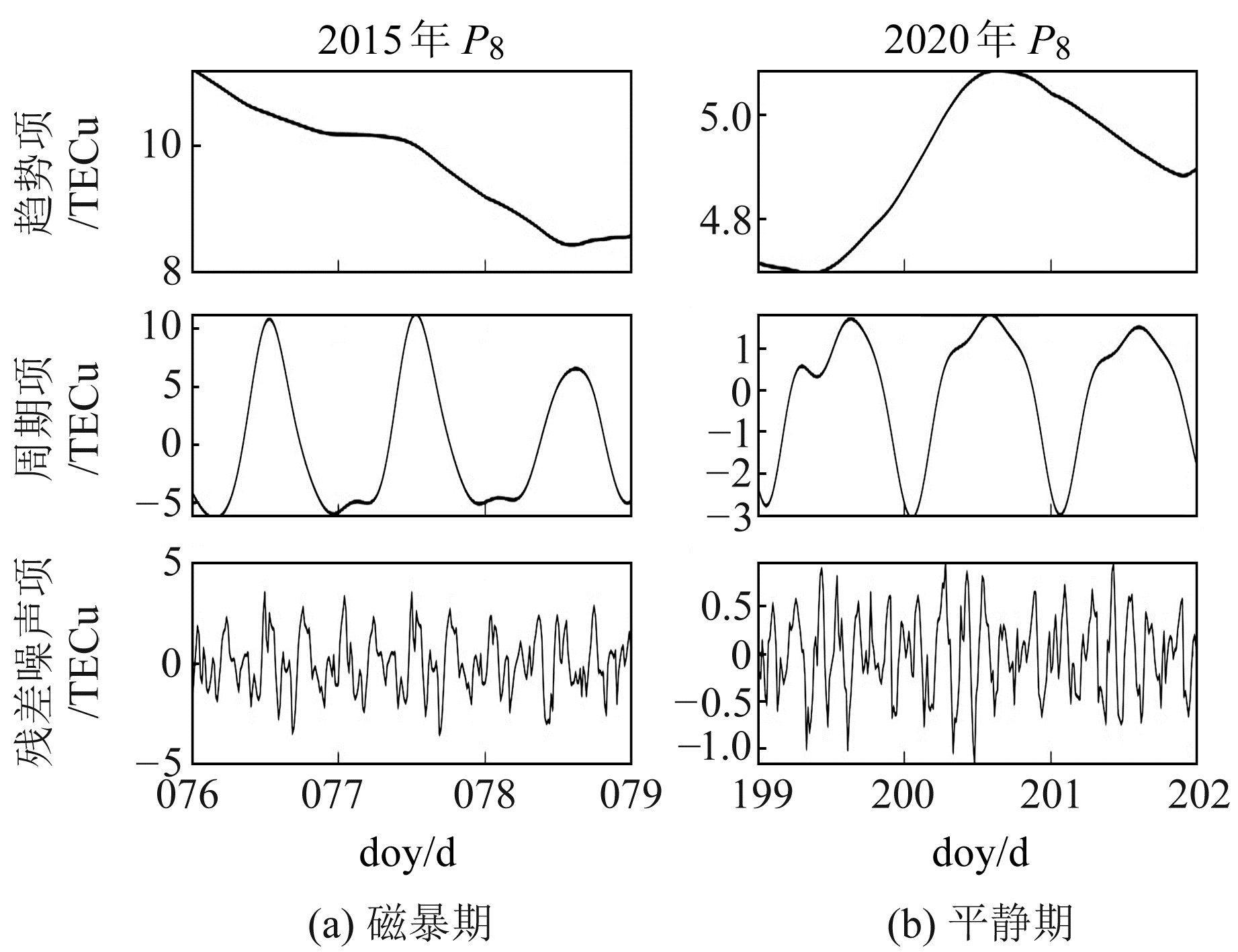
根据电离层TEC时间序列(取窗口长度M=96)经奇异值分解(SVD)降序排列得到奇异值的贡献率,第1项成分贡献率最大,将其作为趋势项;周期项重构成分与噪声残差项重构成分的选取以贡献率变化速率突变拐点为界线,突变拐点之前(含拐点)的作为周期项重构成分,突变拐点之后的作为噪声残差项重构成分。因此选取第1奇异值对应的矩阵重构为趋势项,第2~8奇异值对应的组合矩阵重构为周期项,其余的组合矩阵重构为噪声残差项。P8(61.5°N,20°E)格网点在磁暴期和磁平静期的重构分量如图 3所示。
|
图 3 SSA重构分量 Fig. 3 Component reconstructed with SSA |
Dst(disturbance storm time)是研究地磁暴及其相关现象的重要指标。本文采用ICSU-WDS数据中心(http://wdc.kugi.kyoto-u.ac.jp/wdc/Sec3.html)提供的地磁指数Dst,参考地磁暴强度等级标准文件(GB/T 31160-2014)和NOAA空间天气预报中心等级标准,得到Dst值与磁暴等级如表 1所示。
|
|
表 1 磁暴等级划分 Tab. 1 Magnetic explosion classification |
表 2为2个预报时段的Dst指数日均值,数据来自ICSU-WDS数据中心(http://wdc.kugi.kyoto-u.ac.jp/wdc/Sec3.html)。从表 1可知,2015年doy077~079为地磁磁暴期;2020年doy200~202为地磁平静期。
|
|
表 2 预报时段的Dst指数 Tab. 2 Dst index of forecast periods |
本文采用相对精度P和均方根误差RMSE作为预报模型精度的评估指标:
| $ P = 1 - \frac{{\left| {{\rm{te}}{{\rm{c}}_p} - {\rm{te}}{{\rm{c}}_r}} \right|}}{{{{{\mathop{\rm tec}\nolimits} }_r}}} $ | (3) |
| $ {\rm{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{{{\mathop{\rm tec}\nolimits} }_p} - {\rm{te}}{{\rm{c}}_r}} \right)}^2}} } $ | (4) |
式中,tecp为模型预测值,tecr为EUREF提供的参考值,n为预报TEC数据长度。
图 4为地磁平静期2种模型在P4、P6格网点的TEC预报结果与参考值对比,图 5为2种模型的预报结果误差。结合图 4、图 5可知,SSA-LSTM模型的预报结果与参考值更为接近。在低纬度格网点P4(35.5°N,20°E),SSA-LSTM模型预报结果与EUREF参考值最大残差为0.85 TECu,比单一LSTM模型预报结果降低0.03 TECu。其3 d预报相对精度为97.10%,比单一LSTM模型提高1.20百分点;RMSE为0.27 TECu,比单一LSTM模型提高0.06 TECu。在高纬度格网点P6(61.5°N,0°),SSA-LSTM模型预报结果与EUREF参考值最大残差为0.77 TECu,比单一LSTM模型结果降低0.25 TECu。其3 d预报相对精度为94.60%,比单一LSTM模型提高1.00百分点;RMSE为0.20 TECu,比单一LSTM模型提高0.02 TECu。

|
图 4 地磁平静期2种模型在P4、P6格网点的TEC预报结果对比 Fig. 4 Comparison of the prediction results of the two models during the geomagnetic calm period at P4 and P6 grid networks |

|
图 5 地磁平静期2种模型在P4、P6格网点的预报结果误差 Fig. 5 Errors of the prediction results of the two models during the geomagnetic calm period at P4 and P6 grid networks |
图 6为地磁磁暴期2种模型在P3、P5格网点的TEC预报结果与参考值对比,图 7为2种模型的预报结果误差。结合图 6、图 7可知,在地磁磁暴期,电离层处于极不稳定状态,SSA-LSTM模型和单一LSTM模型预报结果精度都低于地磁平静期,但SSA-LSTM模型预报效果更优。在低纬度格网点P3(35.5°N,10°E),SSA-LSTM模型预报结果与EUREF参考值最大残差为3.88 TECu,比单一LSTM模型预报结果降低2.70 TECu。其3 d预报相对精度为92.40%,比单一LSTM模型提高5.60百分点;RMSE为1.19 TECu,比单一LSTM模型提高0.27 TECu。在高纬度格网点P5(61.5°N,10°W),SSA-LSTM模型预报结果与EUREF参考值最大残差为1.62 TECu,比单一LSTM模型预报结果降低0.75 TECu。其3 d预报相对精度为94.60%,比单一LSTM模型提高4.20百分点;RMSE为0.48 TECu,比单一LSTM模型提高0.19 TECu。

|
图 6 地磁活跃期2种模型在P3、P5格网点的TEC预报结果对比 Fig. 6 Comparison of the prediction results of the two models during the geomagnetic explosion period at P3 and P5 grid networks |

|
图 7 地磁活跃期2种模型在P3、P5格网点的预报结果误差 Fig. 7 Errors of the prediction results of the two models during the geomagnetic explosion period at P3 and P5 grid networks |
根据2种模型在不同地磁活动情况下8个格网点3 d TEC预报结果的RMSE百分比统计结果(见表 3,单位%)可知,在地磁平静期,SSA-LSTM模型预报结果的RMSE均在1.0 TECu之内,RMSE≤0.5 TECu的占比94.10%,比单一LSTM模型提高20.49百分点;在地磁磁暴期,SSA-LSTM模型预报结果RMSE≤2.0 TECu的占比98.61%,比单一LSTM提高12.85百分点。
|
|
表 3 2种模型3 d预报结果RMSE百分比统计 Tab. 3 Statistics of RMSE percentage of 3-day prediction results of the two models |
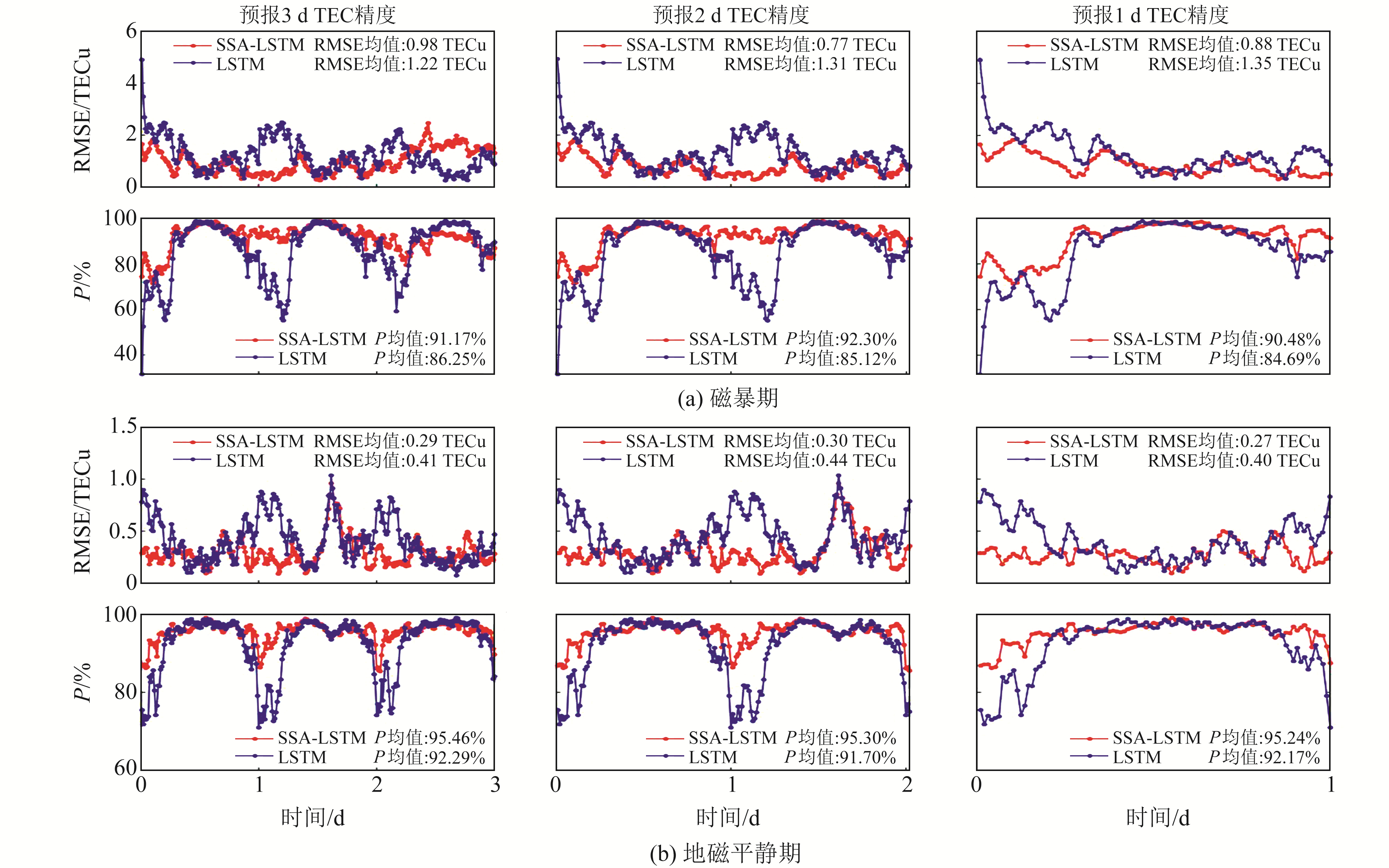
图 8为2种模型在不同地磁活动情况下所有实验格网点的TEC预报结果的相对精度P和RMSE均值统计结果。由图 8可知,在磁暴期,SSA-LSTM模型预报3 d、2 d、1 d TEC的相对精度分别为91.17%、92.30%、90.48%,比单一LSTM模型分别提高4.92百分点、7.18百分点、5.79百分点;SSA-LSTM模型预报结果的RMSE分别为0.98 TECu、0.77 TECu、0.85 TECu,比单一LSTM模型分别提高0.24 TECu、0.54 TECu、0.50 TECu。在地磁平静期,SSA-LSTM模型预报3 d、2 d、1 d TEC的相对精度分别为95.46%、95.30%、95.24%,比单一LSTM模型分别提高3.17百分点、3.60百分点、3.07百分点;SSA-LSTM模型预报结果的RMSE分别为0.29 TECu、0.30 TECu、0.27 TECu,比单一LSTM模型分别提高0.12 TECu、0.14 TECu、0.13 TECu。由此得出,SSA-LSTM模型比单一LSTM模型能够更好地利用电离层TEC时序数据的时间信息,反映TEC动态变化趋势。
|
图 8 2种模型在不同地磁活动情况下TEC预报结果的相对精度P和RMSE均值 Fig. 8 Results of the relative accuracy P and RMSE of TEC forecast results of the two models for different geomagnetic periods |
本文提出一种新的电离层TEC预报模型SSA-LSTM,该模型对电离层TEC时间序列数据进行SSA分解,根据每个初等矩阵的贡献率确定合适的矩阵分组并重构为趋势项、周期项、噪声残差项,用LSTM预测结果叠加各分量得到最终的TEC预报值。实验分析表明,在磁暴期,SSA-LSTM模型3 d预报结果相对精度为91.17%,比单一LSTM模型提高4.92百分点;RMSE为0.98 TECu,精度比单一LSTM模型提高0.24 TECu。在地磁平静期,SSA-LSTM模型3 d预报结果相对精度为95.46%,比单一LSTM模型提高3.17百分点;RMSE为0.29 TECu,精度比单一LSTM模型提高0.12 TECu。
| [1] |
Vautard R, Ghil M. Singular Spectrum Analysis in Nonlinear Dynamics, with Applications to Paleoclimatic Time Series[J]. Physica D: Nonlinear Phenomena, 1989, 35(3): 395-424 DOI:10.1016/0167-2789(89)90077-8
(  0) 0) |
| [2] |
徐克红, 程鹏飞, 文汉江. 太阳黑子数时间序列的奇异谱分析和小波分析[J]. 测绘科学, 2007, 32(6): 35-38 (Xu Kehong, Cheng Pengfei, Wen Hanjiang. Singular Spectrum Analysis and Wavelet Analysis on Time Series of Sunspot[J]. Science of Surveying and Mapping, 2007, 32(6): 35-38)
(  0) 0) |
| [3] |
Zhou S K, Reuckert D, Fichtinger G. Handbook of Medical Image Computing and Computer Assisted Intervention[M]. Salt Lake: Academic Press, 2020
(  0) 0) |
| [4] |
Al-Jabery K K, Obafemi-Ajayi T, Olbricht G R, et al. Computational Learning Approaches to Data Analytics in Biomedical Applications[M]. Salt Lake: Academic Press, 2020
(  0) 0) |
| [5] |
吉长东, 王强, 王贵朋, 等. 深度学习LSTM模型的电离层总电子含量预报[J]. 导航定位学报, 2019, 7(3): 76-81 (Ji Changdong, Wang Qiang, Wang Guipeng, et al. TEC Prediction of Ionosphere Based on Deep Dearning LSTM Model[J]. Journal of Navigation and Positioning, 2019, 7(3): 76-81)
(  0) 0) |
| [6] |
王鹏程, 郭金运, 王方建, 等. 基于奇异谱分析的汶川地震震前地倾斜数据分析[J]. 地球物理学进展, 2020, 35(2): 467-474 (Wang Pengcheng, Guo Jinyun, Wang Fangjian, et al. Singular Spectrum Analysis on Ground Tilt Data before Wenchuan Earthquake[J]. Progress in Geophysics, 2020, 35(2): 467-474)
(  0) 0) |
| [7] |
卢辰龙, 匡翠林, 张晋升, 等. 组合SSA与ARMA模型预报电离层TEC[J]. 大地测量与地球动力学, 2014, 34(6): 44-49 (Lu Chenlong, Kuang Cuilin, Zhang Jinsheng, et al. Predicting Ionosphere TEC with the Combination of Singular Spectrum Analysis and ARMA Model[J]. Journal of Geodesy and Geodynamics, 2014, 34(6): 44-49)
(  0) 0) |
| [8] |
Vautard R, Yiou P, Ghil M. Singular-Spectrum Analysis: A Toolkit for Short, Noisy Chaotic Signals[J]. Physica D: Nonlinear Phenomena, 1992, 58(1-4): 95-126 DOI:10.1016/0167-2789(92)90103-T
(  0) 0) |
| [9] |
Chimsuwan P, Supnithi P, Phakphisut W, et al. Construction of LSTM Model for Total Electron Content(TEC) Prediction in Thailand[C]. International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology(ECTI-CON), Chiang Mai, 2021
(  0) 0) |
| [10] |
Cheng N, Kuo A. Using Long Short-Term Memory(LSTM) Neural Networks to Predict Emergency Department Wait Time[J]. Studies in Health Technology and Informatics, 2020, 270: 1 425-1 426
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China;
3. GNSS Research Centre, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2022, Vol. 42
2022, Vol. 42


