2. 昆明理工大学民航与航空学院, 昆明市景明南路727号, 650504
大气延迟是全球导航卫星系统GNSS的主要误差源之一,在卫星定位中对流层延迟一般可近似为天顶对流层延迟ZTD和映射函数的乘积,因此精确的ZTD模型对提高卫星定位精度十分重要[1]。随着GNSS技术的发展,许多地区建立了连续运行的参考站CORS。利用参数估计法将ZTD作为未知参数参与GNSS定位解算,将经验模型作为先验值,可获得改正后的高精度ZTD[2]。基于参考站提供的ZTD,可采用线性组合、反距离加权内插、最小二乘配置等方法得到流动站处的大气信息模型。张小红等[3]利用区域CORS网基站上解算的高精度ZTD内插得到流动站ZTD,对空间回归模型的适用性和内插效果进行研究;姚宜斌等[4]通过指数经验公式对参考站天顶对流层湿延迟进行高程归算,采用反距离加权法内插得到流动站处的天顶对流层湿延迟内插值;Li等[5]分析ZTD水平和垂直方向的相关性,对垂直和水平相关分量分别建模。上述文献均基于ZTD日变化特征进行建模研究,未考虑ZTD存在实时变化的特性。杨旭[6]对比四参数法、BP神经网络、支持向量机3种方法在实时ZTD估计中的建模效果,结果表明,3种模型的拟合精度与测站高程相关,但后两种方法的模型参数和计算量较大,不适用于实时建模。考虑到ZTD模型的建立与区域地形气候具有较强的相关性,石鑫等[7]采用克里金插值法对ZTD进行估计,但忽略了地形起伏较大时测站高程与ZTD直接相关的问题。
本文利用中国香港地学中心CORS网的GPS观测数据,采用双差观测模型解算各CORS站的天顶对流层延迟。基于对流层与观测站高程相关这一特性,在克里金插值模型的基础上加入高程归算,将建模结果分别与反距离加权插值和四参数法进行对比分析,进一步探究模型的内插和外插精度以及建模测站数对精度的影响。该模型为建立区域实时无气象参数天顶对流层延迟改正模型提供了参考依据。
1 基于高程归算的克里金插值法建模 1.1 克里金插值算法克里金插值法充分考虑要素的空间相关性,通过对已知样本进行加权平均来估计平面上的未知点,使得估计值与真实值的数学期望相同且方差最小[8]:
| $ \hat Z\left( {{x_0}} \right) = \sum\limits_{i = 1}^n {{\lambda _i}} Z\left( {{x_i}} \right) $ | (1) |
式中,
大量研究表明测站高程与天顶对流层延迟强相关,ZTD与测站高程的关系常用指数模型或者线性模型来表示[9]。指数模型可表示为:
| $ {\rm{ZT}}{{\rm{D}}_h} = {\rm{ZT}}{{\rm{D}}_{{h_1}}} \cdot {{\rm{e}}^{ - \frac{{h - {h_1}}}{\alpha }}} $ | (2) |
式中,h为归算高程,h1为测站实际高程,α为高程改正系数,ZTDh为高程归算后的对流层延迟。将归算后的ZTD用于克里金插值建模,可得到基于高程归算的克里金改进模型:
| $ {\rm{ZT}}{{\rm{D}}_{{\rm{rover }}}} = \sum\limits_{i = 1}^n {{\lambda _i}} Z\left( {{L_i},{B_i}} \right) \cdot {{\rm{e}}^{ - \frac{{{H_i}}}{\alpha }}} $ | (3) |
式中,Li、Bi、Hi分别为第i个测站的经度、纬度和高程信息。首先计算所有测站在高程为0处的ZTD,再利用克里金插值计算流动站所在位置的ZTD,最后将高程归算至流动站高程对应的ZTDrover。
2 区域ZTD建模 2.1 数据来源及处理为分析基于高程归算的克里金插值模型(以下简称为KH)在区域ZTD的插值效果,将插值结果与反距离加权插值法(IDW)和四参数法(FP)进行对比。选取中国香港地区2019年doy196~201的18个CORS站观测数据,测站分布如图 1所示。其中高程最小的测站为5.17 m的hkqt站,高程最大的测站为350.67 m的hknp站。hksl站与hkws站为IGS测站,IGS发布的全球ZTD产品以天顶延迟作为待定参数,由全球7个分析中心采用6套不同的软件计算得到,产品精度达4 mm,可作为其他ZTD产品的标准[10]。利用GAMIT解算hksl和hkws两个测站的ZTD,并与IGS对流层延迟产品进行比较,验证解算精度。结果表明,GAMIT解算结果与IGS对流层产品误差小于6 mm。本文最终采用GAMIT解算结果作为真值,利用均方根误差RMSE和偏差bias两个指标来评判建模效果。

|
图 1 香港CORS网测站分布 Fig. 1 Distribution of CORS network stations in Hong Kong |
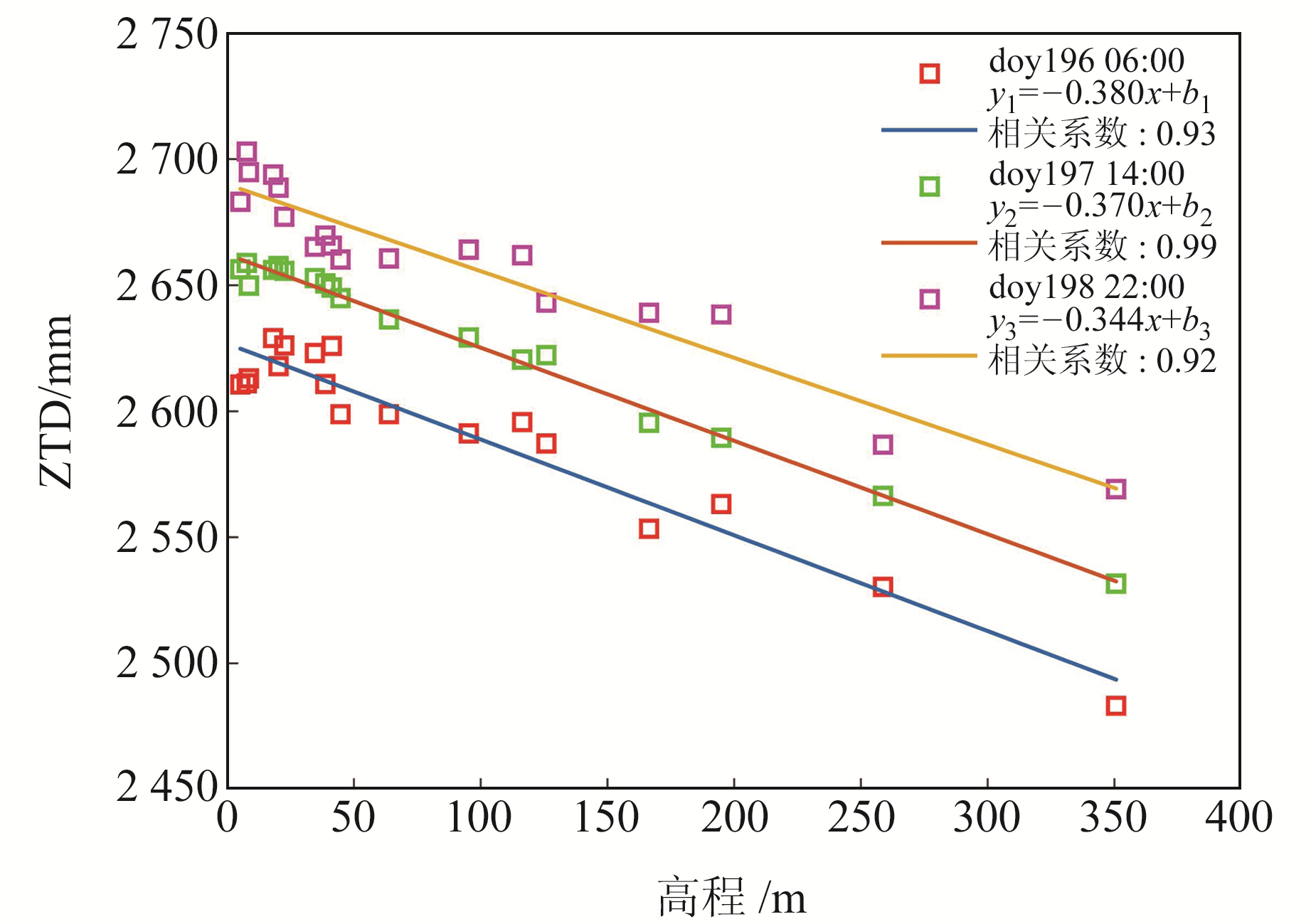
首先利用doy196~198的观测数据来分析测站高程与ZTD的关系。对香港地区18个CORS站3 d中不同时段的ZTD与测站高程进行拟合,结果如图 2所示。由图可知,线性拟合相关系数均大于0.9,高程变化范围较小时指数拟合和线性拟合结果保持一致。根据拟合结果,本文采用线性模型对香港地区进行高程归算。
|
图 2 天顶对流层延迟与测站高程拟合结果 Fig. 2 Fitting results of ZTD and station elevation |
选取doy199~201期间采样间隔为1 h共72历元的ZTD作为观测数据用于建模分析。选取图 1中红色标记的11个测站用于插值建模,蓝色标记的4个测站hkst、hknp、kyc1和hkws用于分析实时建模内插和外插精度。为验证hknp和hkws测站外插效果,减小测站几何位置分布对外插结果的影响,未选取绿色标记的3个测站参与建模。4个测站的插值结果如图 3所示,蓝色线段为采用GAMIT解算的ZTD,并将其作为参考值。可以看出,3种方法在kyc1和hkws测站的插值结果相似,在hkst和hknp测站插值结果中KH模型精度优于IDW和FP模型。

|
图 3 3种插值法在流动站插值结果对比 Fig. 3 Comparison of interpolation results of three interpolation methods in moving station |
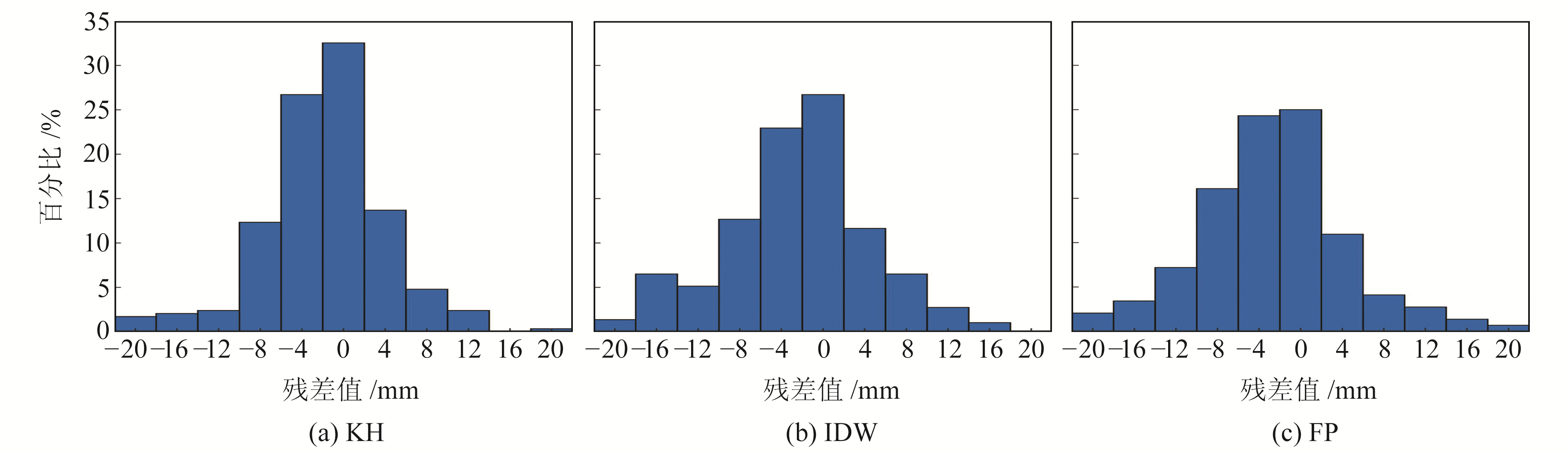
表 1分别给出4个测站72个历元ZTD的真值与KH、IDW和FP模型之间的RMSE和bias值(单位mm)。可以看出,kyc1站在3种插值模型中均有较高的精度。hkst站和kyc1站属于内插估计,KH模型的RMSE与bias均小于其他两种方法,其中高程为116.38 m的kyc1站KH插值结果与IDW和FP模型接近,高程为258.70 m的hkst站KH模型精度明显优于其他两种方法。在外插精度上,高程为63.79 m的hkws测站3种方法精度保持一致,高程较高的khnp与hkst测站的KH内插效果优于IDW和FP模型。综上可知,KH模型在内插精度上优于IDW和FP模型,且对高程较高测站的精度提升明显。图 4给出3种模型的插值估计与实际观测值之间的残差分布,在±10 mm以内的残差情况下3种插值模型中FP占比为81.85%、IDW占比为81.64%、KH占比为90.07%。结果表明,区域对流层延迟估计的KH模型建模精度优于IDW和FP模型。
|
|
表 1 流动站ZTD插值精度结果统计 Tab. 1 Statistics of ZTD interpolation accuracy results of moving station |
|
图 4 3种模型插值残差分布 Fig. 4 Interpolation residual distribution of three models |
进一步研究表明,随着参与建模测站数量的增加,3种模型的插值精度将趋于一致。为验证KH模型在参与建模测站数较少时的模型效果,选取hkkt、hkqt、hkks、hklm和hkmw共5个测站参与建模。由表 2(单位mm)可知,在参与建模测站数为5个时,除kyc1站外KH模型的RMSE和bias最小,IDW和FP模型精度相似。进一步分析可知,由于kyc1站与参与建模的hkwm站高程相似、距离最小,且ZTD变化相似,因此在反距离加权方法中kyc1站估计值受hkwm站影响较大,使得kyc1站的IDW插值有较高精度。对比表 1与表 2可知,在参与建模测站数较少的情况下,KH模型精度有所下降,但插值精度仍优于10 mm,相较于IDW和FP模型依然存在精度优势。
|
|
表 2 流动站ZTD插值精度结果统计 Tab. 2 Statistics of ZTD interpolation accuracy results of moving station |
针对天顶对流层延迟与高程线性相关的特性,结合克里金插值法能有效反映空间相关性这一特点,提出基于高程归算的克里金插值模型用于区域ZTD建模。此模型基于CORS网观测数据,无需考虑气象参数,不仅可以估计空间任意点的ZTD,还可以对空间区域进行建模。结果表明,基于高程归算的克里金插值法相对于传统对流层延迟估计插值算法具有明显优势,内插和外插精度均高于反距离加权和四参数算法,且在参与建模测站数较少的情况下依旧可以维持较高的插值精度。由于本文并未涉及特殊气候条件或特殊局部环境区域下的内插效果,因此未来需要作进一步分析验证。
| [1] |
易正晖, 王帅民, 王勇, 等. GNSS对流层延迟推算可降水量的季节转换模型研究[J]. 大地测量与地球动力学, 2017, 37(8): 830-834 (Yi Zhenghui, Wang Shuaimin, Wang Yong, et al. Research on Seasonal Transition Model of GNSS Zenith Tropospheric Delay Calculating Precipitable Water Vapor[J]. Journal of Geodesy and Geodynamics, 2017, 37(8): 830-834)
(  0) 0) |
| [2] |
张小红, 胡家欢, 任晓东. PPP/PPP-RTK新进展与北斗/GNSS PPP定位性能比较[J]. 测绘学报, 2020, 49(9): 1 084-1 100 (Zhang Xiaohong, Hu Jiahuan, Ren Xiaodong. New Progress of PPP/PPP-RTK and Positioning Performance Comparison of BDS/GNSS PPP[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1 084-1 100)
(  0) 0) |
| [3] |
张小红, 朱锋, 李盼, 等. 区域CORS网络增强PPP天顶对流层延迟内插建模[J]. 武汉大学学报: 信息科学版, 2013, 38(6): 679-683 (Zhang Xiaohong, Zhu Feng, Li Pan, et al. Zenith Troposphere Delay Interpolation Model for Regional CORS Network Augmented PPP[J]. Geomatics and Information Science of Wuhan University, 2013, 38(6): 679-683)
(  0) 0) |
| [4] |
姚宜斌, 徐星宇, 胡羽丰. GGOS对流层延迟产品精度分析及在PPP中的应用[J]. 测绘学报, 2017, 46(3): 278-287 (Yao Yibin, Xu Xingyu, Hu Yufeng. Precision Analysis of GGOS Tropospheric Delay Product and Its Application in PPP[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 278-287)
(  0) 0) |
| [5] |
Li Y Y, Zou X, Tang W M, et al. Regional Modeling of Tropospheric Delay Considering Vertically and Horizontally Separation of Station for Regional Augmented PPP[J]. Advances in Space Research, 2020, 66(10): 2 338-2 348 DOI:10.1016/j.asr.2020.08.003
(  0) 0) |
| [6] |
杨旭. 多卫星导航系统实时精密单点定位数据处理模型与方法[D]. 徐州: 中国矿业大学, 2019 (Yang Xu. Models and Methods of Data Processing for Multi-GNSS Real-time Precise Point Positioning[D]. Xuzhou: China University of Mining and Technology, 2019)
(  0) 0) |
| [7] |
石鑫, 吕志伟, 杨川, 等. 基于克里金插值法的NRTK误差改正[J]. 导航定位学报, 2016, 4(2): 102-107 (Shi Xin, Lü Zhiwei, Yang Chuan, et al. Errors Correction of NRTK Based on Kriging Interpolation Method[J]. Journal of Navigation and Positioning, 2016, 4(2): 102-107)
(  0) 0) |
| [8] |
毛田, 万卫星, 孙凌峰. 用Kriging方法构建中纬度区域电离层TEC地图[J]. 空间科学学报, 2007, 27(4): 279-285 (Mao Tian, Wan Weixing, Sun Lingfeng. Central and Northern China TEC Map Using the Kriging Method[J]. Chinese Journal of Space Science, 2007, 27(4): 279-285 DOI:10.3969/j.issn.0254-6124.2007.04.003)
(  0) 0) |
| [9] |
丁君生, 陈俊平, 王君刚. GNSS观测数据ZTD建模的质量控制方法[J]. 宇航学报, 2020, 41(9): 1 195-1 203 (Ding Junsheng, Chen Junping, Wang Jungang. Quality Control Method for ZTD Modeling Based on GNSS Observation Data[J]. Journal of Astronautics, 2020, 41(9): 1 195-1 203)
(  0) 0) |
| [10] |
Wielgosz P, Grejner-Brzezinska D, Kashani I. Regional Ionosphere Mapping with Kriging and Multiquadric Methods[J]. Journal of Global Positioning Systems, 2003, 2(1): 48-55 DOI:10.5081/jgps.2.1.48
(  0) 0) |
2. Faculty of Civil Aviation and Aeronautics, Kunming University of Science and Technology, 727 South-Jingming Road, Kunming 650504, China
 2022, Vol. 42
2022, Vol. 42


