2. 中国科学院大学,北京市玉泉路19号甲,100049
随着BDS-3系统以及Galileo系统的建成,全球导航卫星系统即将进入一个新的发展阶段[1-2]。与此同时,用户对导航定位精度的需求也在日益增加,为进一步满足用户对导航系统服务性能的需求,广大学者及相关机构都开展了针对各导航星座产品精度以及服务性能的研究[3-5]。其中针对卫星星座状态的研究主要围绕对精度衰减因子PDOP的监测与评估展开,PDOP既能反映观测未知数在精度评定过程中系数阵的大小,也能体现观测卫星同用户接收机之间几何空间构型所带来的误差大小,因此PDOP成为反映用户定位精度的重要指标[6-7]。国内外已有相关机构及学者开展了对PDOP的监测评估研究,主要评估方式是在全球范围内构建等经纬度间隔格网模型GRID_ELL[8],利用格网点来计算各个区域的PDOP,并以此来为该区域范围内的用户提供参考。目前随着GNSS实时监测评估研究工作的进一步开展,对监测评估算法的效率和可靠性又有了更高要求。在PDOP实时监测方面,先前使用的GRID_ELL模型存在大量冗余格网点,降低计算效率的同时也增加了监测评估产品对于存储的需求,不利于PDOP长周期实时监测的开展。此外由于GRID_ELL模型受到投影畸变的影响[9-10],高纬度地区格网点分布过于密集,一方面有悖于真实用户位置的分布,另一方面也使各导航星座全球PDOP监测评估的统计结果存在一定偏差。
为进一步提升PDOP监测评估的实效性与可靠性,推进实时监测评估研究工作的开展,本文引入等弧长格网模型GRID_EAL和正二十面体球面格网模型GRID_IB两种等面积格网模型[11],应用到PDOP的监测评估研究中。
1 GRID_EAL模型及GRID_IB模型概述相较于先前PDOP监测评估中所使用的GRID_ELL模型,本文引入的两种等面积格网模型均是从控制单位格网面积的角度出发,将地球表面分割成若干个面积近似相等的格网单元。此类格网模型能有效避免由于地球球面效应所引起的格网点分布不均匀的问题,使格网点参照真实的区域面积在全球均匀分布。
1.1 GRID_EAL模型概述及其划分方法GRID_EAL模型通过设置单位格网弧长所对应的弧度大小来控制格网模型的疏密程度,并通过确定的弧长大小来确定划分格网的经纬度间隔。其具体划分步骤如下:
1) 选取单位球以模拟真实地球,确定间隔弧度大小d以控制格网模型疏密程度;
2) 确定格网模型在纬度上的划分数Nθ=round(π/d),近似纬度间隔dθ=π/Nθ,近似经度间隔dφ=d2/dθ;
3) 选取划分的任意纬圈θ=π·(i+0.5)/Nθ,i∈[0, Nθ-1]且i∈Z,则该纬圈上的经度划分数Nφ=round(2π·sinθ/dφ),其上格网点对应经度φ=2jπ/Nφ,j∈[0, Nφ-1]且j∈Z。
1.2 GRID_IB模型概述及其划分方法GRID_IB初始格网点由正二十面体的12个顶点定义(表 1),通过将相邻点所构成的球面三角形进一步细分,可以使格网点进一步加密[12]。因此该模型的格网点数N与细分次数k间有如下函数关系:N=2+10×4k,且k∈N。其具体划分步骤如下:
|
|
表 1 正二十面体初始顶点 Tab. 1 Initial vertices of regular icosahedron |
1) 定义中心为原点的正二十面体,并对其每个顶点进行定义;
2) 利用已有顶点构建Delaunay三角网;
3) 逐一将每个三角形边长进行二等分,其等分点构成新的顶点,此过程中每个初始三角形都能被分割成4个新的三角形;
4) 剔除重复顶点,并重复3)中的二等分操作直至将顶点数加密至所需数量;
5) 将每个自原点指向顶点的矢量归一化即可将每个顶点投影至模拟地球的单位球球面上,此过程可确保投影后的任意两点间弧度相等;
6) 将顶点坐标除以
GRID_ELL模型与两种等面积格网模型在不同纬度地区的格网点分布存在明显差异。相较于GRID_ELL模型,两种等面积格网模型均可显著改善高纬度地区以及极地地区格网点过密的问题。
2.1 不同格网模型格网点分布情况为分析3种格网模型之间的差异,选取5°×5°的GRID_ELL模型(共计2 664个格网点)、4°间隔的GRID_EAL模型(共计2 664个格网点)以及进行4次细分后构建的GRID_IB模型(共计2 562个格网点)进行研究,对3种格网模型格网点在全球范围内的分布规律进行分析和统计。结果表明,不同纬度地区格网点密度呈现出明显的差异,GRID_ELL模型相较于两种等面积格网模型在高纬度地区至极区范围格网点密度过大(图 1),而赤道附近的低纬度地区格网点较稀疏(图 2),格网整体分布不均匀。
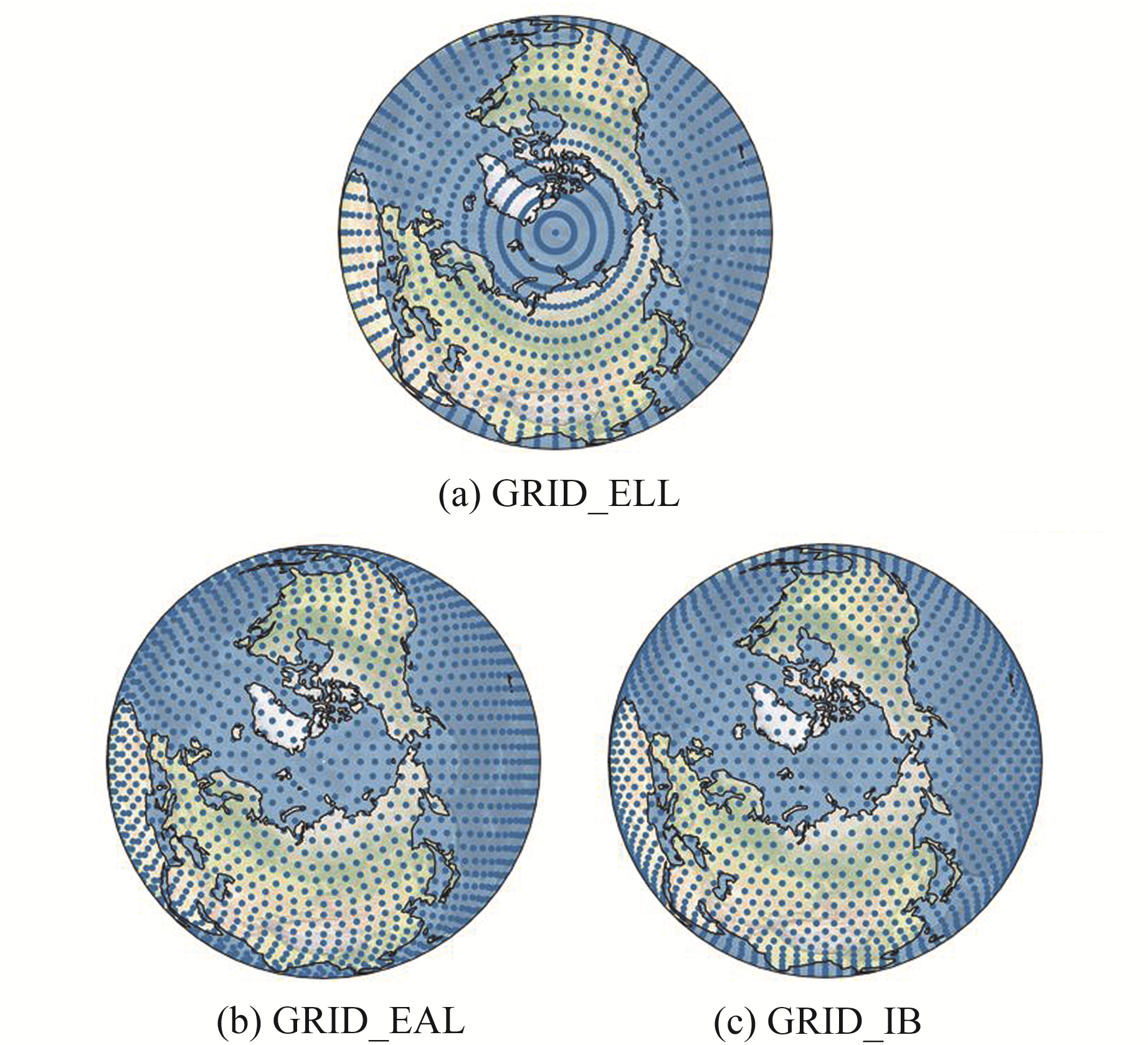
|
图 1 3种格网模型极地地区格网点分布 Fig. 1 Grid points distribution of three grid models in polar regions |
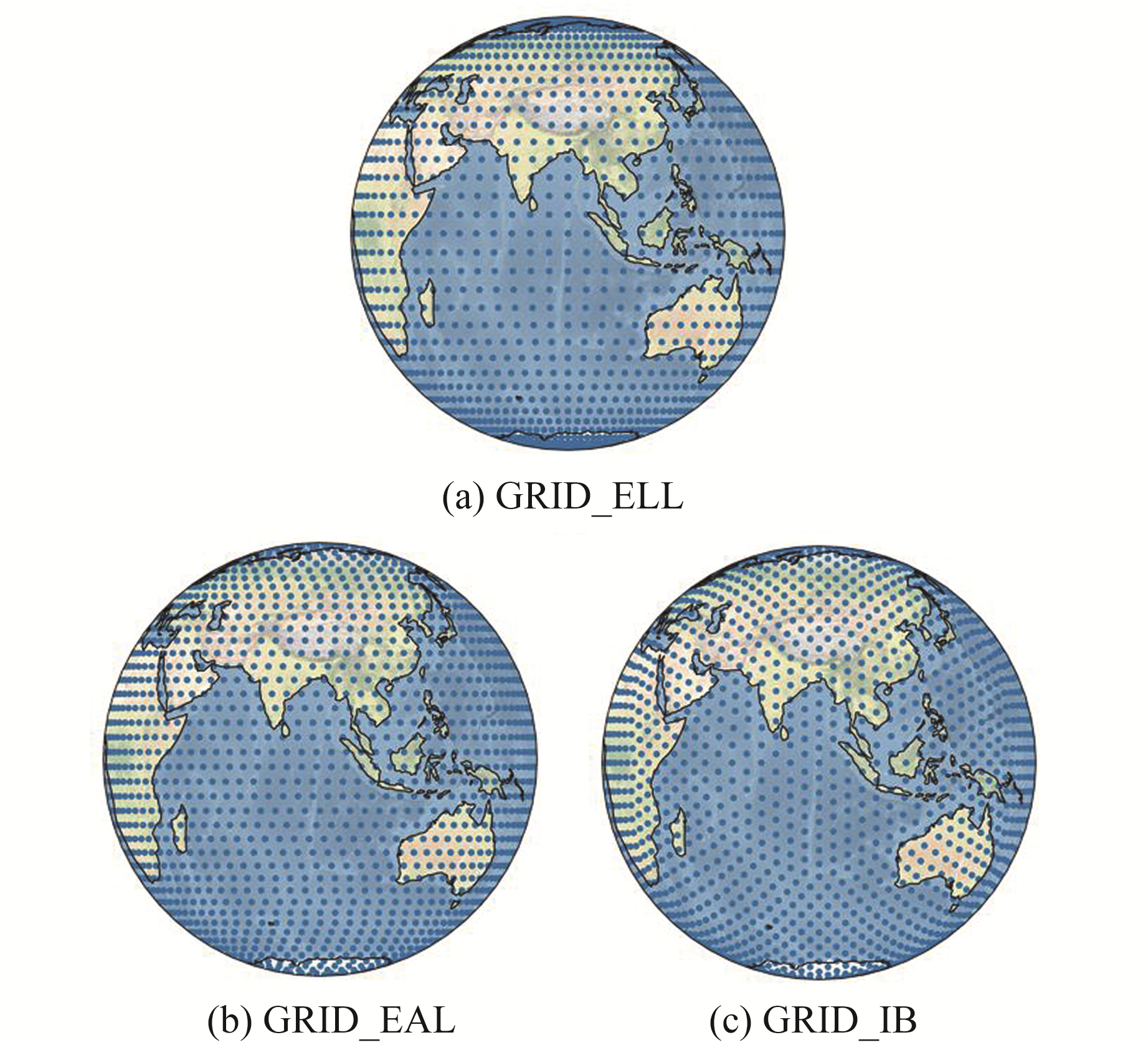
|
图 2 3种格网模型赤道地区格网点分布 Fig. 2 Grid points distribution of three grid models in equatorial regions |
为进一步分析3类格网模型在不同纬度地区的格网点数差异,本文按照低纬度地区(南北纬0°~30°)、中纬度地区(南北纬30°~60°)和高纬度地区(南北纬60°~90°)进行区域划分,得到各区域内格网点数统计结果(图 3)。结果表明,在高纬度地区,GRID_ELL模型格网点数分别约为GRID_EAL模型和GRID_IB模型的2.59倍和3.05倍;在中纬度地区,GRID_ELL模型格网点数分别约为GRID_EAL模型和GRID_IB模型的0.96倍和0.90倍;在低纬度地区,GRID_ELL模型格网点数分别约为GRID_EAL模型和GRID_IB模型的0.57倍和0.62倍。
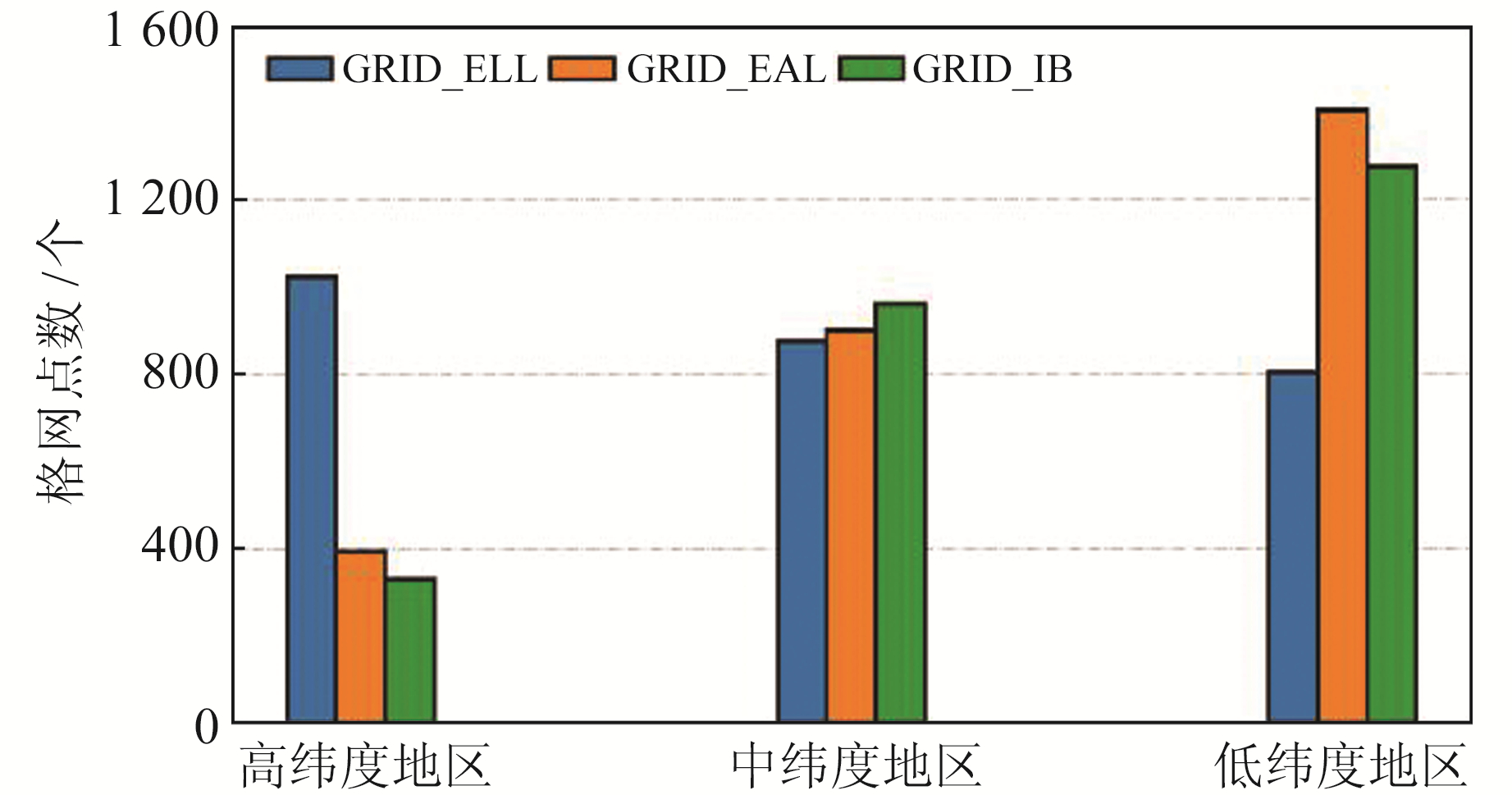
|
图 3 3种格网模型不同纬度地区格网点数 Fig. 3 Grid points volume in different latitude regions among three grid models |
对各格网模型不同纬度带上格网点数进行拟合,得到3种格网模型格网点数随纬度变化的相关函数曲线(图 4),图中各曲线的积分面积与各格网模型格网点总数成正比。通过平移GRID_ELL模型的蓝色线条可以看出,若GRID_ELL模型要在0°~30°范围内任意纬度带上实现格网点数密度与其他两种格网模型点数密度相同,则需要大幅度加密格网,提高格网点总数,而这将进一步增加其在高纬度地区的冗余格网点数。

|
图 4 3种格网模型格网点数随纬度变化趋势 Fig. 4 The trend of grid point volume with latitude among three grid models |
在上述实验的基础上,利用2020-11-23~11-29共7 d的广播星历对基于3种格网模型计算得到的全球PDOP评估结果及区域PDOP可用性评估结果进行分析,实验过程中采用的格网密度同先前实验一致,采样间隔为300 s,卫星截止高度角为15°。
3.1 全球PDOP图 5(a)~(c)为3种格网模型利用GPS(共33颗星)得到的全球PDOP评估结果,(d)~(f)为3种格网模型利用BDS(更新至C59,共45颗星)得到的全球PDOP评估结果(截止高度角为15°)。由图可见,3种格网模型的评估结果在图像上呈现出一致性,两种等面积格网模型在南北纬0°~50°范围内格网点更为密集,更好地反映了该区域由于导航卫星星座构型所引起的PDOP变化。在南北纬50°~90°范围内,两种等面积格网模型去除了大量冗余格网点,但由于该范围内相同经度间隔所对应的实际距离大幅度缩短,因此少量格网点也能较为真实地反映出该区域的PDOP变化。

|
图 5 3种格网模型全球PDOP Fig. 5 Global PDOP of three grid models |
PDOP可用性计算公式如下[1]:
| $ \mathrm{ava}_{i}=\frac{\sum\limits_{t=t_{\text {start }}, \Delta t=T}^{t_{\text {end }}} \operatorname{bool}\left\{\operatorname{PDOP}_{t} \leqslant f_{\text {Acc }}\right\}}{1+\frac{t_{\text {end }}-t_{\text {start }}}{T}} $ | (1) |
式中,i为格网点标识;T为采样间隔;tstart、tend为开始时间段与结束时间段;PDOPt为t时刻该格网点的PDOP值;fAcc为设置的PDOP阈值;bool{ }为布尔函数,当满足判断条件时取值为1,否则为0。
由于在卫星截止高度角为15°的情况下,四系统所计算出的全球PDOP可用性无法明显反映出各区域PDOP可用性变化情况,因此本文主要针对GPS和BDS的PDOP可用性作进一步分析。当阈值为6时,各格网模型计算的PDOP可用性结果如图 6所示。由图可见,3种格网模型所计算出的PDOP可用性结果同样具有一致性,尤其是BDS,其可用性变化较为明显的区域均集中在中低纬度地区,两种等面积格网模型均能很好地反映全球PDOP的可用性分布情况。

|
图 6 3种格网模型计算的全球PDOP可用性结果 Fig. 6 Global PDOP availability from three grid models |
此外,各系统基于3种格网模型计算出的全球PDOP可用性统计结果如表 2所示(截止高度角为15°, PDOP≤6),其中GPS与BDS卫星数同先前实验一致,GLONASS共22颗星,Galileo共24颗星。由表可知,GLONASS的全球PDOP可用性统计结果在GRID_ELL模型和两种等面积格网模型之间存在明显差异,这是其卫星构型不同所致。GLONASS在高纬度地区的PDOP值明显小于低纬度地区的PDOP值,呈现为带状分布。但结合真实情况下的高纬度地区面积、实际用户数量和可见卫星数变化可知,传统的GRID_ELL模型给该区域附加了一个过高的权重,进而提升了GLONASS在全球范围内的PDOP可用性统计值。因此结合实际情况考虑,两种等面积格网模型所反映的统计结果更为真实准确。
|
|
表 2 3种格网模型全球PDOP可用性统计 Tab. 2 Statistical global PDOP availability of three grid models |
从上述实验结果可以看出,等面积格网模型在与GRID_ELL模型拥有近似相同的格网点总数情况下可以对全球PDOP及PDOP可用性实现有效、一致甚至更为真实准确的监测评估。在PDOP的监测评估过程当中,格网模型的最低分辨率会在很大程度上影响监测评估结果的精度。由于两种等面积格网模型的单位格网边长近似相等,因此在全球范围内的最低分辨率始终近似为常数;但GRID_ELL模型会受到投影畸变的影响,其最低分辨率等于其在赤道上2个相邻格网点之间的距离。在格网点数量近似相同的情况下,先前实验中的两种等面积格网模型的最低分辨率实际上要远高于GRID_ELL模型的最低分辨率。因此在PDOP监测评估过程中,若使用与GRID_ELL模型最低分辨率相同的等面积格网模型,即维持现有的监测评估精度时,其格网点总数将大幅度减少,这将使PDOP监测评估算法效率进一步提升。
4.1 运算效率优化由于GRID_IB模型最低分辨率的确定与其剖分次数相关,无法灵活设置最低分辨率,不利于实际应用,因此本文主要针对GRID_EAL模型作进一步研究。表 3为不同最低分辨率下GRID_EAL模型和GRID_ELL模型应用于BDS全球PDOP监测评估算法时的表现。
|
|
表 3 格网性能差异 Tab. 3 Performance between different grid models |
由表可见,与目前PDOP监测评估研究中常使用的5°×5°的GRID_ELL模型相比,4°、5°、6°、7°间隔的GRID_EAL模型在运算效率上分别提升了2.8%、36.3%、55.1%、65.2%,在存储空间需求上分别优化了0.2%、34.1%、52.9%、64.3%。
4.2 可靠性验证为确保利用GRID_EAL模型的PDOP监测评估优化算法能够对全球范围内的PDOP剧烈变化或是异常区域实现有效的监测与评估,进一步针对不同分辨率的GRID_EAL模型评估结果的准确性进行比较与分析。实验将1°×1°高密度的GRID_ELL模型全球PDOP评估结果视为参考值,将4°、5°、6°、7°间隔的GRID_EAL模型全球PDOP评估结果根据找寻最小二范数的格网点数据原则,同样栅格化为1°×1°的高密度结果,并与参考值作差,设定差值小于等于1则将该格网点监测评估结果视为准确。在此基础上对四系统24 h内的全球PDOP评估结果准确性进行统计,结果如图 7所示(截止高度角为15°,PDOP≤6, ABS≤1)。由图可见,4°与5°间隔的GRID_EAL模型对四系统的全球PDOP评估结果准确性基本都能维持在90%以上,6°与7°间隔的GRID_EAL模型结果准确性则在85%以上。对于目前全球PDOP指标性能较好的系统(如GPS和BDS)而言,其准确性也要明显高于其他系统。

|
图 7 GRID_EAL模型全球PDOP评估准确性 Fig. 7 Global PDOP assessment accuracy rate of GRID_EAL |
通过上述实验可知,5°间隔的GRID_EAL模型能够在满足全球PDOP监测评估准确性的同时,在运算效率及存储上带来36.3%和34.1%的提升与优化。
5 结语本文介绍GRID_EAL和GRID_IB两种等面积格网模型,并对其与GRID_ELL模型之间的差异进行分析。将两种等面积格网模型应用到全球PDOP监测评估算法研究中,能够显著改善GRID_ELL全球格网点分布不均匀给全球PDOP统计结果带来的偏差。对于不同格网间隔的GRID_EAL模型应用到全球PDOP监测评估的适用性进行实验验证,结果表明,同目前基于GRID_ELL模型的全球PDOP监测评估方法相比,利用5°间隔的GRID_EAL模型能在保持全球PDOP监测评估准确性的同时,在运算效率和存储上带来36.3%和34.1%的提升与优化,这有助于进一步推动全球PDOP长周期实时监测的开展。
致谢: 上海天文台iGMAS分析中心给予帮助和支持,IGS提供数据,在此一并表示感谢。
| [1] |
国家市场监督管理总局, 国家标准化管理委员会. 北斗卫星导航系统公开服务性能规范GB/T 39473-2020[S]. 北京: 中国标准出版社, 2020 (State Administration for Market Regulation, Standardization Administration of China. Specifications for Open Service Performance of Beidou Navigation Satellite System GB/T 39473-2020[S]. Beijing: Standards Press of China, 2020)
(  0) 0) |
| [2] |
Hein G W. Status, Perspectives and Trends of Satellite Navigation[J]. Satellite Navigation, 2020, 1(1): 1-12 DOI:10.1186/s43020-019-0006-0
(  0) 0) |
| [3] |
Jiao G Q, Song S L, Liu Y Y, et al. Analysis and Assessment of BDS-2 and BDS-3 Broadcast Ephemeris: Accuracy, the Datum of Broadcast Clocks and Its Impact on Single Point Positioning[J]. Remote Sensing, 2020, 12(13): 2 081 DOI:10.3390/rs12132081
(  0) 0) |
| [4] |
郭树人, 蔡洪亮, 孟轶男, 等. 北斗三号导航定位技术体制与服务性能[J]. 测绘学报, 2019, 48(7): 810-821 (Guo Shuren, Cai Hongliang, Meng Yinan, et al. BDS-3 RNSS Technical Characteristics and Service Performance[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(7): 810-821)
(  0) 0) |
| [5] |
Wang M H, Wang J X, Dong D N, et al. Performance of BDS-3: Satellite Visibility and Dilution of Precision[J]. GPS Solutions, 2019, 23(2): 1-14
(  0) 0) |
| [6] |
Dempster A G. Dilution of Precision in Angle-of-Arrival Positioning Systems[J]. Electronics Letters, 2006, 42(5): 291 DOI:10.1049/el:20064410
(  0) 0) |
| [7] |
Xue S Q, Yang Y X. Positioning Configurations with the Lowest GDOP and Their Classification[J]. Journal of Geodesy, 2015, 89(1): 49-71 DOI:10.1007/s00190-014-0760-6
(  0) 0) |
| [8] |
He H B, Li J L, Yang Y X, et al. Performance Assessment of Single- and Dual-Frequency Beidou/GPS Single-Epoch Kinematic Positioning[J]. GPS Solutions, 2014, 18(3): 393-403 DOI:10.1007/s10291-013-0339-3
(  0) 0) |
| [9] |
景一帆, 杨元喜, 曾安敏, 等. 北斗区域卫星导航系统定位性能的纬度效应[J]. 武汉大学学报: 信息科学版, 2017, 42(9): 1 243-1 248 (Jing Yifan, Yang Yuanxi, Zeng Anmin. Latitude Effect in Positioning Performance by Using Beidou Regional Satellite Navigation System[J]. Geomatics and Information Science of Wuhan University, 2017, 42(9): 1 243-1 248)
(  0) 0) |
| [10] |
杨元喜, 徐君毅. 北斗在极区导航定位性能分析[J]. 武汉大学学报: 信息科学版, 2016, 41(1): 15-20 (Yang Yuanxi, Xu Junyi. Navigation Performance of Beidou in Polar Area[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 15-20)
(  0) 0) |
| [11] |
Teanby N A. An Icosahedron-Based Method for Even Binning of Globally Distributed Remote Sensing Data[J]. Computers and Geosciences, 2006, 32(9): 1 442-1 450 DOI:10.1016/j.cageo.2006.01.007
(  0) 0) |
| [12] |
林冰仙, 许德朋, 盛业华, 等. 正二十面体球面菱形离散格网的编码模型及其映射方法[J]. 测绘学报, 2016, 45(增1): 23-31 (Lin Bingxian, Xu Deming, Sheng Yehua, et al. Coding Model and Mapping Method of Spherical Diamond Discrete Grids Based on Icosahedron[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1): 23-31 DOI:10.11947/j.AGCS.2016.F003)
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2022, Vol. 42
2022, Vol. 42


