滑坡在我国已成为一种严重危害社会经济可持续发展及威胁人民生命财产安全的主要地质灾害之一。开展滑坡灾害研究尤其是对滑坡位移的高精度预测研究,对滑坡灾害的防灾预警具有重要的理论与现实意义。
造成滑坡灾害频发原因十分复杂,会受多种外部环境因素的影响,如强降雨、农业灌溉等;受人类活动的影响,如塬边人工削方等;也会受滑坡内部自身地质条件影响,如自身重力与岩层岩性变化等。为解决滑坡灾害预测预警难题,近些年许多学者利用神经网络在滑坡时序位移预测方面展开相关研究。而相较于神经网络,循环神经网络可克服传统神经网络模型存在的模型简单、预测稳定性差、未充分挖掘形变数据中蕴含的时间信息特征等局限性,已在机器翻译和图像注释等数据分析领域得到成功应用[1],并结合主成分分析法与随机森林法等应用于滑坡位移预测[2-3]、结合重标方差法为滑坡变形综合评价提供决策支撑[4]及应用到滑坡长时序位移的预测分析[5]。但上述研究在利用循环神经网络对滑坡位移进行预测分析时,对循环神经网络参数的选取仍采用网格搜索法或传统手动调参法,会造成算法计算量大,并且构建的循环神经网络适应性较差。因此,探索一种有效改进循环神经网络参数自动化最优选取的方法,将更好地服务于循环神经网络在滑坡位移的实际预测应用。
为此,本文选取我国黄土滑坡最为典型的黑方台党川6#滑坡体为示范实验区,主要基于滑坡体北斗与位移计时序监测数据[6],分别建立简单循环神经网络(SimpleRNN)、长短期记忆网络(LSTM)、门控循环单元(GRU)3种循环神经网络预测模型。在此基础上进一步利用遗传算法(GA)对循环神经网络层数及每层网络记忆体数量进行随机搜索,并以均方误差最小为目标函数,自动确定循环神经网络最佳参数组合,分别构建出3种基于遗传算法改进的循环神经网络高精度位移预测模型(GA-SimpleRNN、GA-LSTM、GA-GRU),通过计算对比验证改进后的循环神经网络预测模型在滑坡时序位移预测中的突出优势。
1 循环神经网络及其优化模型 1.1 简单循环神经网络(SimpleRNN)SimpleRNN是深度学习中重要的一种神经网络模型,具有可循环递归地处理滑坡历史形变数据及可对历史记忆进行建模的特殊性能,适用于解决滑坡位移时间序列预测问题[7]。循环核中记忆体内存储着每个时刻的滑坡位移状态信息ht可表示为:
| $ {h_t} = \tanh \left( {{x_t}{\mathit{\boldsymbol{w}}_{xh}} + {h_{t - 1}}{\mathit{\boldsymbol{w}}_{hh}} + {b_h}} \right) $ | (1) |
式中,wxh、whh为权重矩阵,bh为偏置,xt为当前时刻的滑坡位移输入特征,ht-1为记忆体上一时刻存储的滑坡位移状态信息,tanh为激活函数。滑坡位移输出特征yt计算公式为:
| $ {y_t} = {\mathop{\rm softmax}\nolimits} \left( {{h_t}{\mathit{\boldsymbol{w}}_{hy}} + {b_y}} \right) $ | (2) |
式中,why为权重矩阵,by为偏置,softmax为激活函数,相当于一层全连接层。可通过设定记忆体数量改变记忆容量,当记忆体个数及xt、yt被指定时,待训练参数的维度即被限定。在前向传播时,记忆体内存储的滑坡位移状态信息ht在每个时刻均被刷新,而3个参数矩阵wxh、whh、why和2个偏置项bh、by均固定不变;在反向传播时,3个参数矩阵和两个偏置项则可利用梯度下降法进行更新确定[8]。
1.2 长短期记忆网络(LSTM)LSTM算法通过门控单元较好地解决了SimpleRNN长时间序列预测精度低的问题。LSTM的门机制可以对滑坡位移信息的流通和损失进行控制,使网络更适合于滑坡时序位移预测[9]。LSTM算法中引入了输入门it、遗忘门ft、输出门ot、细胞态Ct、记忆体ht及候选态
| $ {输入门}:{i_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_i} \cdot \left[ {{h_{t - 1}}, {x_t}} \right] + {b_i}} \right) $ | (3) |
| $ {遗忘门}:{f_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_f}} \right. \cdot \left. {\left[ {{h_{t - 1}}, {x_t}} \right] + {b_f}} \right) $ | (4) |
| $ {{输出门}}:{o_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_o}.\left[ {{h_{t - 1}}, {x_t}} \right) + {b_o}} \right) $ | (5) |
| $ {细胞态}:{C_t} = {f_t} \cdot {C_{t - 1}} + {i_t} \cdot {\tilde C_t} $ | (6) |
| $ {记忆体}:{h_t} = {o_t} \cdot \tanh \left( {{C_t}} \right) $ | (7) |
| $ {候选态}:{\tilde C_t} = \tanh \left( {{\mathit{\boldsymbol{W}}_c} \cdot \left[ {{h_{t - 1}}, {x_t}} \right) + {b_c}} \right. $ | (8) |
式中,3个门限的取值范围为0~1,σ代表Sigmoid激活函数,Wi·、Wf·、Wo·、Wc·分别为待训练参数矩阵,bi、bf、bo、bc分别为待训练偏置项,tanh为激活函数[10]。输入门决定新输入的滑坡位移特征是否容许被更新, 是否被保存至记忆体; 遗忘门控制着记忆体记住或遗忘之前的滑坡位移状态; 输出门决定滑坡位移信息是否容许被输出; 细胞态存储长期滑坡位移信息; 记忆体存储短期滑坡位移信息; 候选态则代表循环神经网络归纳出的滑坡新位移信息。
1.3 门控循环单元(GRU)GRU算法将LSTM中的遗忘门与输入门合二为一,形成“更新门”。相比于LSTM模型,GRU模型更加精简。GRU使记忆体ht融合了长期滑坡位移信息和短期滑坡位移信息,其中ht包含过去滑坡位移信息ht-1和现在滑坡位移信息
| $ {更新门}:{z_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_z} \cdot \left[ {{h_{t - 1}}, {x_t}} \right]} \right) $ | (9) |
| $ {重置门}:{r_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_r} \cdot \left[ {{h_{t - 1}}, {x_t}} \right]} \right) $ | (10) |
| $ {记忆体}:{h_t} = \left( {1 - {z_t}} \right) \cdot {h_{t - 1}} + {z_t} \cdot {\tilde h_t} $ | (11) |
| $ {候选隐藏层}:{\tilde h_t} = \tanh \left( {\mathit{\boldsymbol{W}}.\left[ {{r_t}*{h_{t - 1}}, {x_t}} \right]} \right) $ | (12) |
式中,σ代表Sigmoid激活函数,Wz·、Wr·、W·代表待训练参数矩阵,其余参数含义同LSTM。更新门决定当前时间步t的滑坡位移输入特征xt是否对网络产生影响;重置门决定新的滑坡位移输入特征与历史滑坡位移信息相结合的方式;记忆体则通过更新门将长期滑坡位移信息与短期滑坡位移信息相结合;候选隐藏层代表现在的滑坡位移信息,其由过去滑坡位移信息通过重置门和当前滑坡位移输入特征xt共同决定。
1.4 遗传算法(GA)及其优化的循环神经网络遗传算法是一种通过模拟自然进化过程搜索最优解的方法。该算法利用计算机进行仿真运算,将问题求解过程转换成染色体基因的交叉、变异等过程,适合求解较复杂优化问题。鉴于遗传算法的良好拓展性且易与其他算法相结合的特性[12],适用于循环神经网络参数寻优,可避免人工设置循环神经网络参数的盲目性,提高循环神经网络预测的运行效率和准确度。
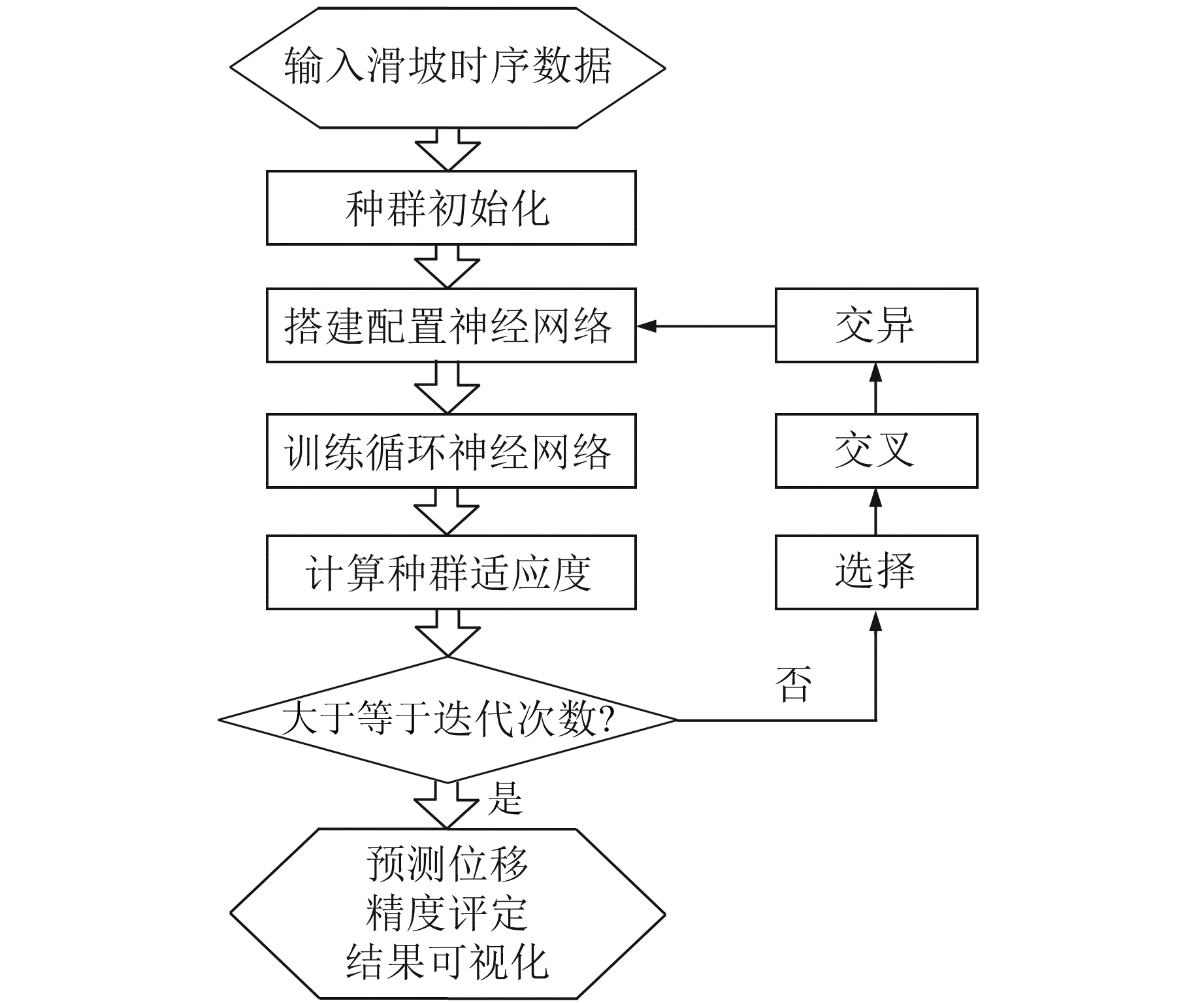
基于遗传算法优化循环神经网络预测模型技术路线主要可分为以下6个步骤(图 1):
|
图 1 基于遗传算法优化循环神经网络技术路线 Fig. 1 Technology road map of recurrent neural network optimized by genetic algorithm |
1) 产生初始种群。设置种群规模、交叉概率、变异概率与进化代数。随机产生初始种群,每个个体基因编码为[P,N1,N2,N3],其中P表示神经网络层数,范围为1~3;N1、N2、N3分别代表第1层、第2层和第3层记忆体数量。
2) 计算适应度。适应度函数设计为均方误差的倒数乘以常系数k,这样就将寻求均方误差最小的目标转化为搜索适应度最高的个体,即最佳网络结构参数。根据个体基因编码配置循环神经网络的网络结构参数,训练模型并进行预测。根据预测结果计算第i组网络结构参数的适应度fi:
| $ f_{i}=k m / \sum\limits_{i=1}^{m}\left(y_{i}-\tilde{y}_{i}\right)^{2} $ | (13) |
式中,常数k取值6 000,这只是为便于观察适应度的变化情况,并不影响寻参的结果;m代表预测期数;yi表示预测位移值;
3) 选择。该运算利用每组网络结构参数的适应度占种群适应度总和的比重决定其遗传到下一代的可能性。若设种群数为n,第i组网络结构参数的适应度为fi,该组参数在进化中遗传的概率pi可表示为:
| $ p_{i}=f_{i} / \sum\limits_{j=1}^{n} f_{j} $ | (14) |
4) 交叉。以2组网络结构参数为一对,将种群中所有网络结构参数组合随机分成若干对。每对参数组合给定一个0~1的随机数p0,在给定交叉概率pc的情况下,若p0 < pc,则单点交叉产生新的网络结构参数组合,否则按照之前的网络结构参数遗传到子代。
5) 变异。如果只进行交叉操作,适应度较高的某组网络结构参数可能会造成算法过早收敛而陷入局部最优解。因此,需要对少量参数组合进行变异操作从而产生新的网络结构参数组合。每组网络结构参数给定一个0~1的随机数p1,在给定变异概率pm的条件下,如果p1 < pm则进行变异操作。
6) 逐代进化。循环计算适应度,由交叉和变异操作产生新的网络结构参数组合,返回到步骤2)。进化结束时,种群中适应度最大的参数组合即为循环神经网络的最佳参数组合。
2 滑坡时序位移预测实例 2.1 示范实验区滑坡概况与监测信息黑方台位于甘肃省永靖县盐锅峡镇,是我国典型且近年最为频发的黄土滑坡灾害域之一。黑方台为典型黄土塬地貌,其上堆积有离石黄土和马兰黄土。离石黄土在台塬北部堆积而在台塬南部则无大量堆积。马兰黄土在研究区内分布广泛,堆积厚度约为25~50 m。粘土层(4~17 m)结构致密,具有弱透水性,其下为卵砾石层(2~5 m),透水性较好,最下层为单斜构造的砂质泥岩[13]。本文所选典型滑坡体党川6#位于永靖县西北向约25 km的黑方台台塬南侧,黑方台曾发生过多起滑坡灾害事件,本次滑塌事件发生于2019-03-26。
为精细刻画出滑坡体运动变形过程,依据切线角判别法作为滑坡阶段演变的划分依据。对HF08北斗监测偏移量进行分析发现,党川6#滑坡体是一个较典型的渐变破坏型滑坡体。滑坡体从2018-11-03~2019-01-24为等速变形阶段(α≈45°),2019-01-25~03-12为初加速变形阶段(45° < α < 80°),2019-03-13~03-24为中加速变形阶段(α≥80°),2019-03-25起滑坡则进入临滑阶段[14]。
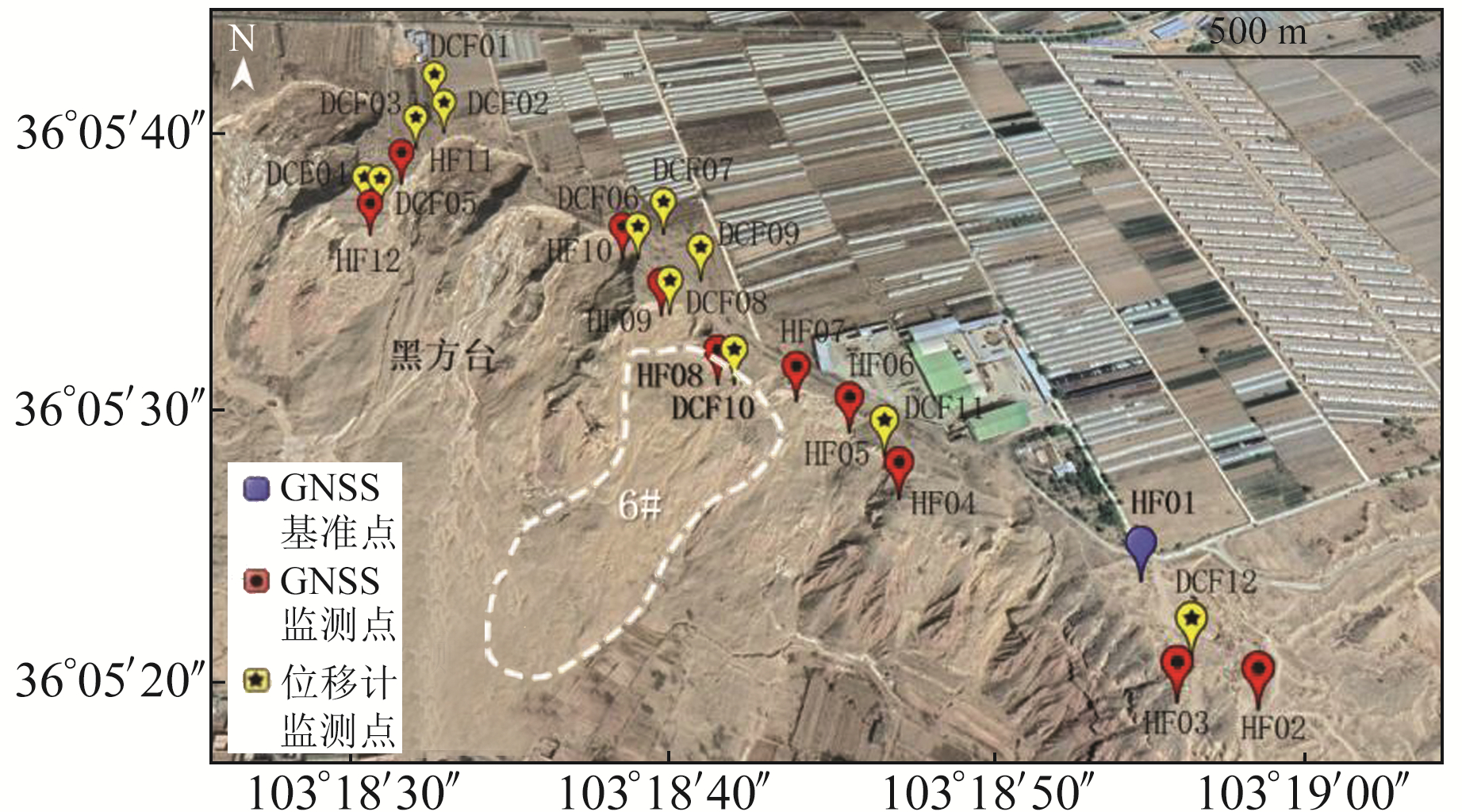
鉴于研究区域滑坡灾害具有多发性,长安大学空间定位与灾害监测研究所在该区域建设了由12个北斗监测站组成的滑坡位移实时监测网络(基准点为HF01),此外还布设了12个位移计监测点(图 2)。
|
HF**为北斗监测站,DCF**为位移计监测站, 白色虚线框代表党川6 # 典型滑坡体 图 2 黑方台党川6#典型滑坡区域监测站点分布 Fig. 2 Distribution of monitoring stations of 6# typical landslide in Dangchuan, Heifangtai |
本文以党川6#滑坡体2019-03-26滑塌事件为例,选取该滑坡体上HF08北斗监测站和DCF10位移计监测数据,数据段均为2018-10-25~2019-03-25,数据采样间隔为1 h,经聚合运算后转换为间隔1 d的时间序列,最终获得的位移计与北斗监测数据均为152期。需要说明的是,DCF10位移计监测的是滑坡体的后缘裂缝宽度变化,位移计累积位移的量值在2019-01-14为11.43 mm,2019-03-25为85.79 mm,2个时段位移计的累积位移变化了74.36 mm。HF08北斗监测站监测的是滑坡体E、N、U三个方向的位移,其中E方向累积位移量值在2019-01-14为-29.86 mm,2019-03-25为-94.67 mm,2个时间段累积位移变化了-64.81 mm;N方向累积位移量值在2019-01-14为-62.63 mm,2019-03-25为-190.91 mm,累积位移变化了-128.28 mm;U方向累积位移量值在2019-01-14为-97.86 mm,2019-03-25为-357.69 mm,累积位移变化了-259.83 mm。为同时对两类滑坡时序监测数据进行高精度预测分析,将北斗三维监测数据归算至偏移量,并联合位移计监测获得的滑坡后缘裂缝累积位移形成位移时间序列。位移时间序列进行归一化处理后,取前5 d的累积位移和偏移量作为训练输入特征,第6 d的数据作为训练输出结果。训练数据构建成三维结构,第1个维度为样本数量(147个),第2个维度为样本长度(5 d),第3个维度为输入特征维度(2类);测试数据构建成二维结构,第1个维度为样本数量(71个),第2个维度为输出特征维度(2 d);采用测试集作为验证集,每迭代一次使用验证集验证一次结果。
实验采用Keras-Sequential方法分别搭建SimpleRNN、LSTM、GRU三种循环神经网络预测模型,配置均方误差作为损失函数,配置训练方法为自适应矩估计(加速神经网络的训练),配置自动保存网络权重参数。循环神经网络一般很少超过3层。记忆体数量太少或太多均会导致模型的预测精度降低,而记忆体数量越多则网络规模越大,网络权重参数越多,模型训练时间也就越长。因此,基于实测数据经多次测试后,本文构建3种循环神经网络模型时网络结构参数(神经网络的层数及记忆体数量)均设置为[2, 10, 10, 0]。
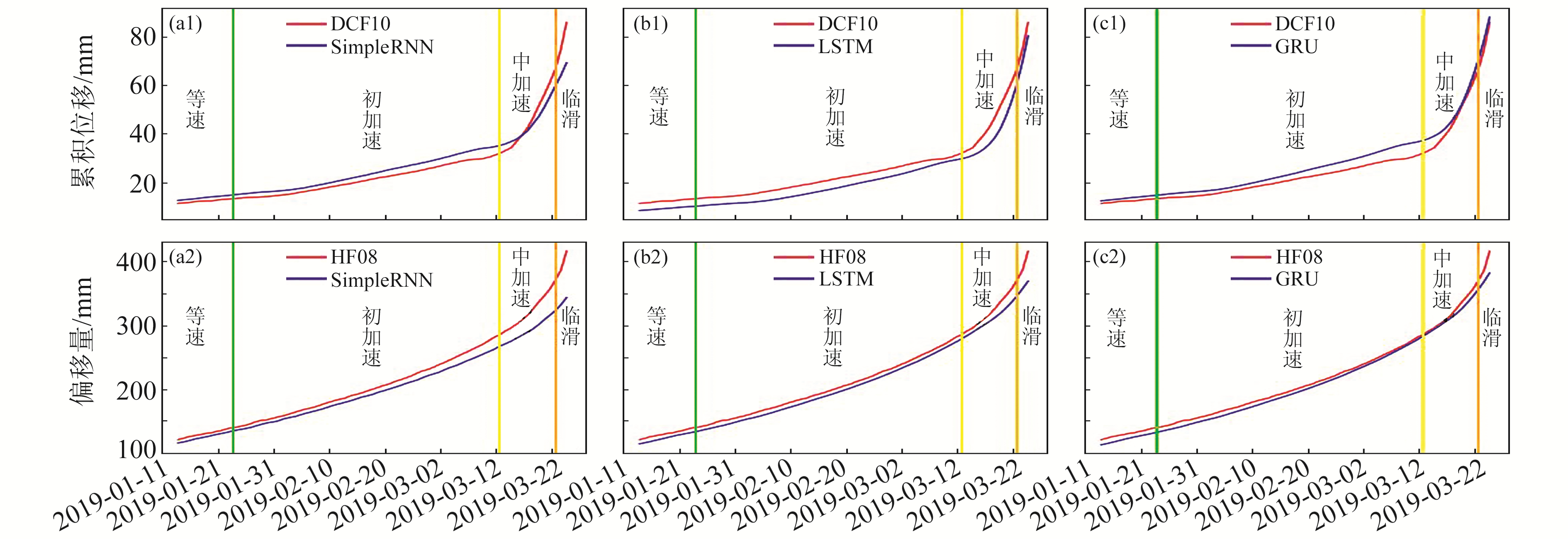
基于党川6#滑坡体的HF08北斗监测偏移量和DCF10位移计监测累积位移,首先采用SimpleRNN、LSTM、GRU三种循环神经网络分别进行训练和预测,训练过程中,循环核按时间步展开,记忆体根据更新公式进行刷新,最后循环核提取滑坡位移数据的时间特征后将其送入全连接网络。经30次迭代后,3种神经网络均收敛,模型预测结果与实测结果对比如图 3所示。
|
图 3 3种循环神经网络预测模型预测值与观测值对比 Fig. 3 Comparison of prediction and observation results of the three kinds of recurrent neural network models |
从图 3可看出,3种循环神经网络对滑坡的等速和大部分初加速变形趋势整体上能进行较好的预测,但在部分滑坡初加速、中加速和临滑变形阶段则相差较大,GRU整体的预测效果相比SimpleRNN与LSTM略好。
由表 1可定量看出,SimpleRNN(HF08)、SimpleRNN(DCF10)预测均方根误差分别为18.2 mm、5.3 mm;LSTM(HF08)、LSTM(DCF10)预测均方根误差分别为10.6 mm、4.4 mm,可见LSTM在解决长时序预测问题上较SimpleRNN具有优势;而GRU(HF08)、GRU(DCF10)预测均方根误差仅分别为7.9 mm、3.2 mm。此外,计算得到LSTM网络权重参数总量为1 371,而GRU网络权重参数总量则为1 091,表明GRU网络中的参数较LSTM少,这也与GRU网络模型复杂度较LSTM更低、训练速度更快、收敛时间更短且预测精度更高的优异性能相符。
|
|
表 1 3种循环神经网络对HF08北斗与DCF10位移计位移时序预测精度对比 Tab. 1 Comparison of prediction accuracy of the three kinds of recurrent neural networks in HF08 BDS and DCF10 displacement meters |
当前对循环神经网络中参数的选取多是凭经验进行手动调参或是采用效率低下的网格搜索法,这些做法主要有两点弊端:一是计算效率低下,二是建立的网络鲁棒性差。因此,本文进一步基于§1.4优化策略引入遗传算法改进循环神经网络,使其具有自动调参功能。
在执行遗传算法时有4个参数需提前设定,这些参数一般在以下区间内进行设置:群体大小为20~100,交叉概率为0.4~0.99,变异概率为0.000 1~0.1,进化代数为10~500。上述4个参数的设置均会影响到网络结构参数以及计算效率等,如种群规模太小进行交叉操作时会产生低效的网络结构参数,规模太大则难以收敛;交叉概率太小也不能有效更新参数库且易导致有效参数迅速丢失,交叉概率太大则易破坏现有参数库且会破坏已找到的较优解;进化代数太小会导致算法不易收敛,进化代数太大又会浪费计算资源。因此,本文基于实测数据经多次测试,应用遗传算法进行参数寻优时最终设置如下:种群个体为40,交叉概率为0.5,变异概率为0.1,进化代数为20,记忆体数量搜索范围为10~50,变异范围为50~100[15]。
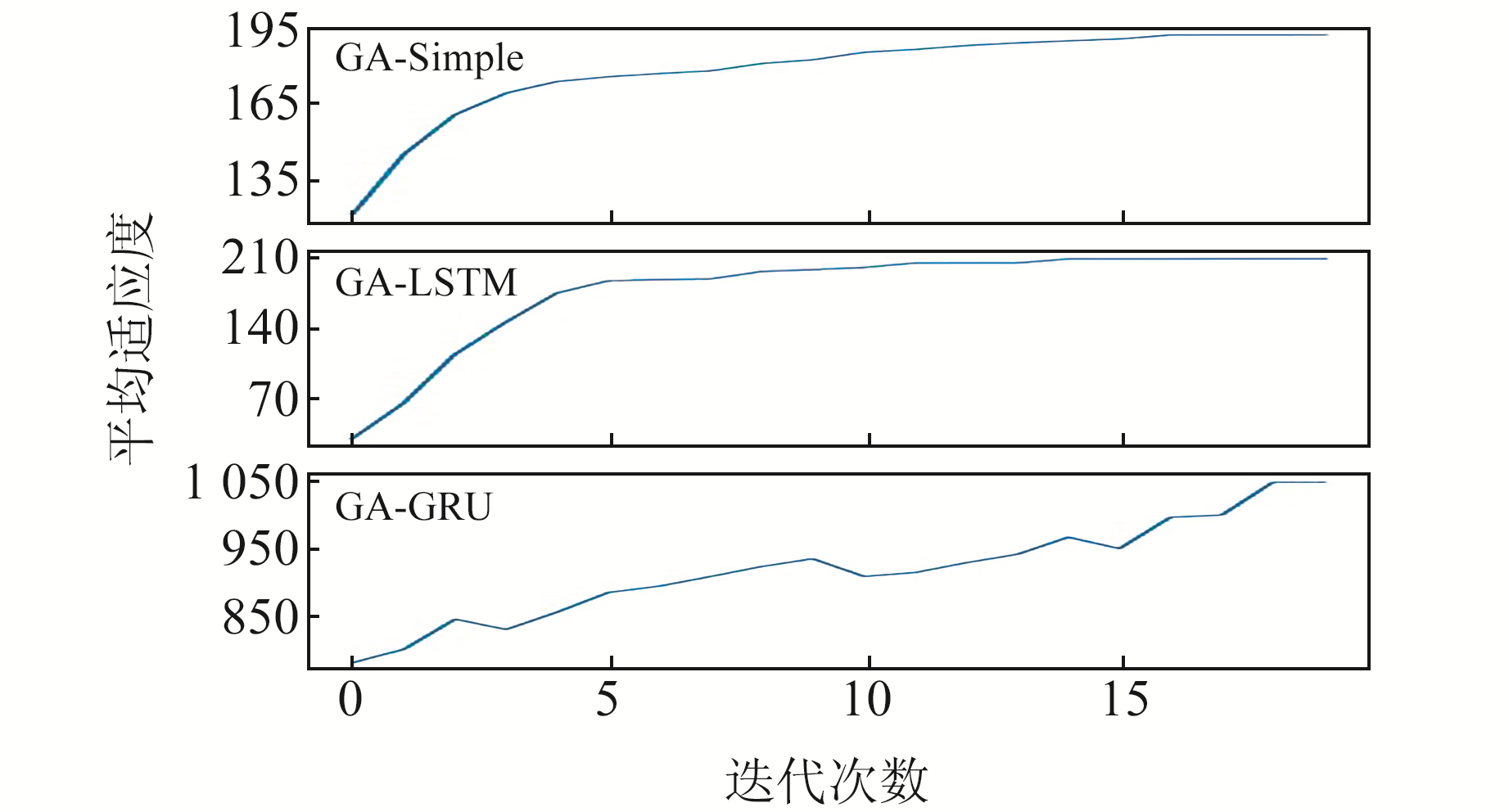
经遗传算法优化循环神经网络调参,仅在20次种群进化后3种循环神经网络算法在搜索空间即能快速找到最优解(对应神经网络的层数及最佳记忆体数量):遗传算法对SimpleRNN、LSTM与GRU分别进行优化后得到的最优网络结构参数分别为[2, 24, 10, 0]、[3, 19, 24, 47]与[3, 21, 18, 36]。图 4显示,GA-SimpleRNN的种群平均适应度在进化中从121.71逐渐上升至191.92,GA-LSTM从28.34逐渐上升至209.05,GA-GRU则从780.86逐渐上升至1 048.04。基于遗传算法改进的3种循环神经网络种群平均适应度变化曲线整体均呈现上升趋势,这种特性体现了种群在进化中经过了优胜劣汰(轮盘赌法)、交叉、变异的算法优化过程。
|
图 4 基于遗传算法改进的3种循环神经网络预测模型种群平均适应度变化曲线 Fig. 4 Variation curves of population average fitness based on the three types of recurrent neural network models optimized by genetic algorithm |
利用遗传算法搜索得到的最优参数分别重新训练3种循环神经网络,优化后3种模型的预测结果与监测结果对比如图 5所示。
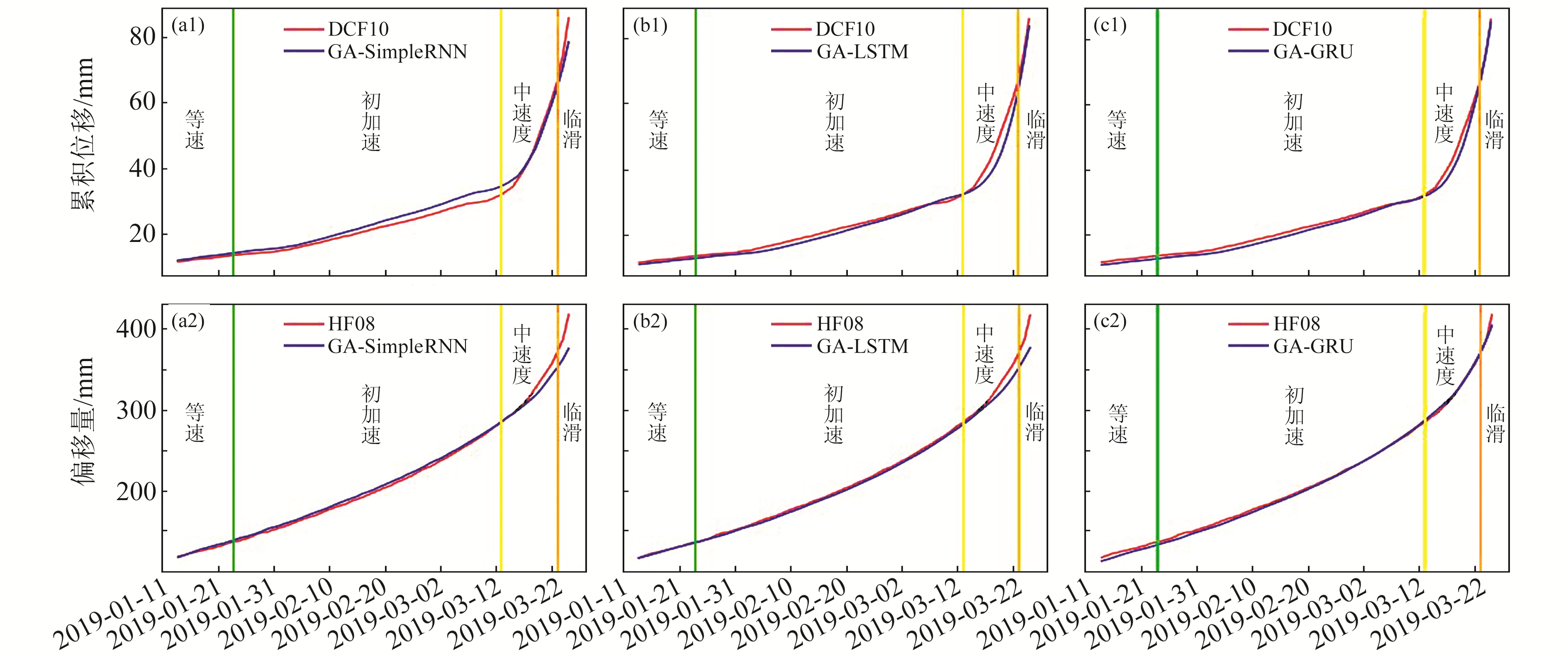
|
图 5 基于遗传算法优化后3种循环神经网络预测模型预测值与观测值对比 Fig. 5 Comparison of prediction and observation results of the three kinds of recurrent neural network models optimized by genetic algorithm |
对比图 3和图 5可明显看出,基于遗传算法优化后的3种循环神经网络较优化前对滑坡变形趋势无论在滑坡初加速与中加速变形,还是加速变形阶段均表现出更优的预测性能,特别是GA-GRU模型预测值与观测值相关系数达到0.99。
对比表 1和表 2可以直观定量地看出,遗传算法优化后的3种循环神经网络整体预测性能均较优化前有显著提升,其中GA-SimpleRNN(HF08)、GA-SimpleRNN(DCF10)预测的均方根误差分别为7.2 mm、3.0 mm,较优化前的SimpleRNN(HF08)与SimpleRNN(DCF10)分别减少11.0 mm与2.3 mm;GA-LSTM(HF08)、GA-LSTM(DCF10)预测的均方根误差分别为6.9 mm、2.3 mm,较优化前的LSTM(HF08)与LSTM(DCF10)分别减少3.7 mm与2.1 mm;GA-GRU(HF08)、GA-GRU(DCF10)预测的均方根误差仅分别为3.1 mm、1.7 mm,较优化前的GRU(HF08)与GRU(DCF10)分别减少4.8 mm与1.5 mm。
|
|
表 2 基于遗传算法优化后3种循环神经网络模型对时间序列的预测精度对比 Tab. 2 Comparison of prediction accuracy of the three kinds of recurrent neural networks optimized by genetic algorithm in HF08 BDS and DCF10 displacement meters |
为进一步展示遗传算法优化后的3种循环神经网络在位移计与北斗监测时序位移预测中的突出优势,综合给出神经网络优化前后模型预测精度对比柱状图(图 6)。由图可见,优化后的3种循环神经网络无论在位移计还是在北斗监测时序位移的预测中其预测性能均有显著提升,其中GA-GRU相较于GA-SimpleRNN与GA-LSTM在滑坡位移时间序列预测中表现出更优的预测性能。
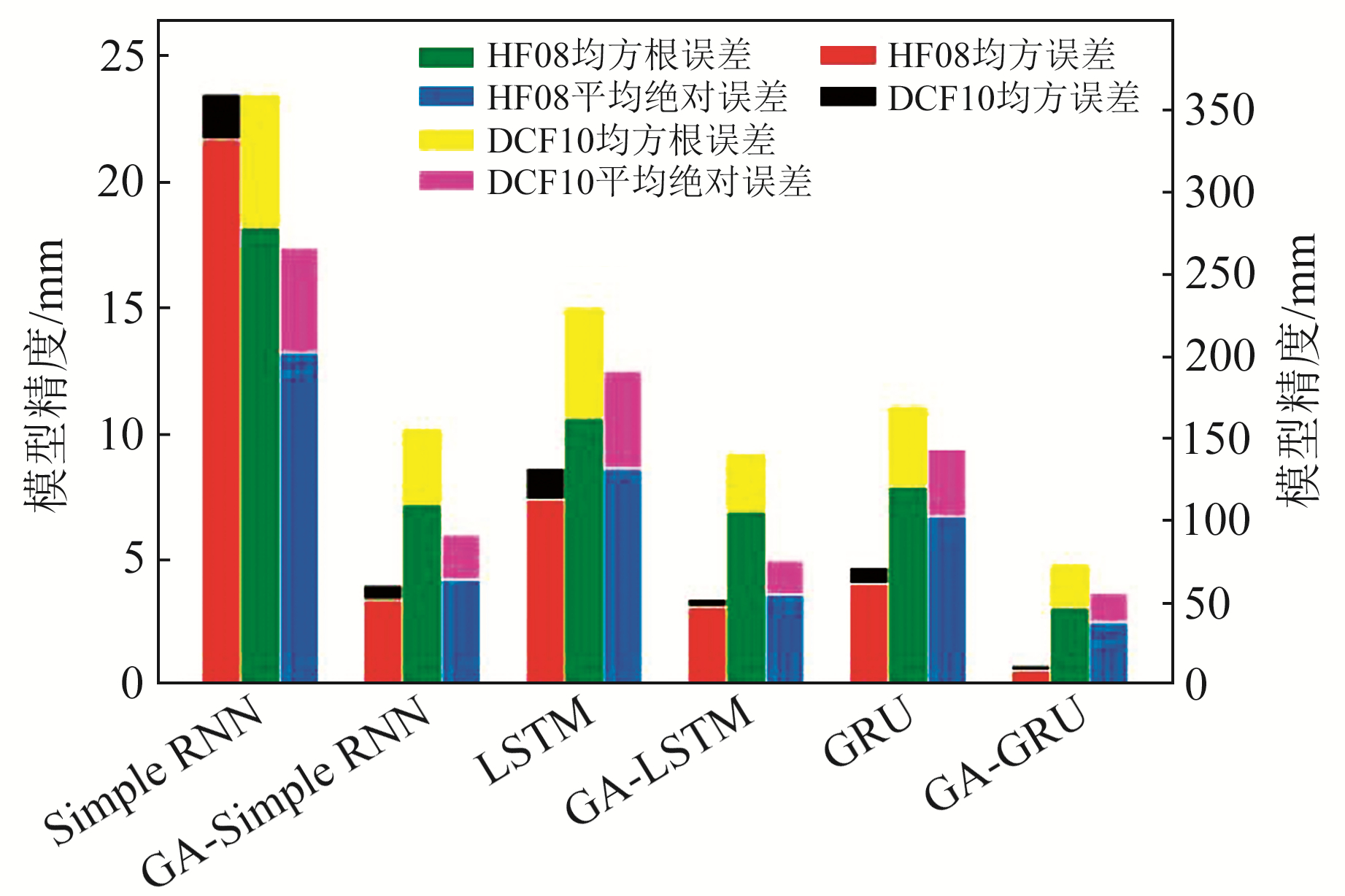
|
图 6 遗传算法优化前后的循环神经网络预测模型对比 Fig. 6 Comparison chart of recurrent neural network prediction models before and after genetic algorithm optimization |
本文针对循环神经网络预测模型存在的预测精度低,特别是调参困难的突出问题,通过引入遗传算法用于改进循环神经网络参数的自动化最优选取,构建出GA-SimpleRNN、GA-LSTM和GA-GRU三种改进循环神经网络预测模型,并将其成功应用于我国典型黄土滑坡区域黑方台党川6#滑坡体形变时间序列高精度预测研究,取得主要结论如下:
1) 遗传算法可对循环神经网络层数及每层网络记忆体数量进行随机搜索且自动确定出最佳参数组合,从而优化循环神经网络结构,显著提高网络预测性能。
2) 3种基于遗传算法改进后的循环神经网络预测模型的预测均方误差、均方根误差、平均绝对误差均较改进前循环神经网络预测精度更高,特别是GA-GRU模型预测精度最优,更加适用于滑坡长时间时序位移的高精度预测。
本文构建出一种主要针对滑坡时序监测位移的改进循环神经网络预测模型,但在实际中影响滑坡高精度预测的因素极为繁杂。随着深度学习算法研究的不断发展,结合滑坡多源监测数据、先进深度学习算法、滑坡外部多环境影响因素及滑坡自身地质条件的滑坡灾害综合高精度预测模型将是本文下一步重点研究方向。
| [1] |
佘雅文, 付广裕. 基于循环神经网络的重力异常数据推估研究[J]. 大地测量与地球动力学, 2021, 41(3): 234-237 (She Yawen, Fu Guangyu. Estimation of Gravity Anomaly Data Based on Recurrent Neural Network[J]. Journal of Geodesy and Geodynamics, 2021, 41(3): 234-237)
(  0) 0) |
| [2] |
曹国清, 张晓明, 陈亚峰. 基于PCA-LSTM的多变量矿山排土场滑坡预警研究[J]. 计算机系统应用, 2018, 27(11): 252-258 (Cao Guoqing, Zhang Xiaoming, Chen Yafeng. Early Warning of Landslide in Mined Mine Dumping Site Based on PCA-LSTM[J]. Computer Systems and Applications, 2018, 27(11): 252-258)
(  0) 0) |
| [3] |
Liu Z Q, Guo D, Lacasse S, et al. Algorithms for Intelligent Prediction of Landslide Displacements[J]. Journal of Zhejiang University-Science A: Applied Physics and Engineering, 2020, 21(6): 412-429
(  0) 0) |
| [4] |
冯非凡, 武雪玲, 牛瑞卿, 等. 一种V/S和LSTM结合的滑坡变形分析方法[J]. 武汉大学学报: 信息科学版, 2019, 44(5): 784-790 (Feng Feifan, Wu Xueling, Niu Ruiqing, et al. A Landslide Deformation Analysis Method Using V/S and LSTM[J]. Geomatics and Information Science of Wuhan University, 2019, 44(5): 784-790)
(  0) 0) |
| [5] |
梁阳, 肖婷, 胡程, 等. 基于长期监测数据与LSTM网络的滑坡位移预测[EB/OL]. http://kns.cnki.net/kcms/detail/11.2406.TN.20210512.1045.032.html, 2021-09-21 (Liang Yang, Xiao Ting, Hu Cheng, et al. Prediction of Landslide Displacement Based on Long Term Monitoring Data and LSTM Network[EB/OL]. http://kns.cnki.net/kcms/detail/11.2406.TN.20210512.1045.032.html, 2021-09-21)
(  0) 0) |
| [6] |
王智伟, 王利, 韩清清, 等. 一种位移传感器数据解码方法及其在滑坡监测中的应用[J]. 大地测量与地球动力学, 2020, 40(4): 436-440 (Wang Zhiwei, Wang Li, Han Qingqing, et al. Data Decoding Method of the Displacement Sensor and Its Application in Landslide Monitoring[J]. Journal of Geodesy and Geodynamics, 2020, 40(4): 436-440)
(  0) 0) |
| [7] |
Pearlmutter B A. Learning State Space Trajectories in Recurrent Neural Networks[J]. Neural Computation, 1989, 1(2): 263-269 DOI:10.1162/neco.1989.1.2.263
(  0) 0) |
| [8] |
Kim D S, Chae Y S, Kim Y S, et al. A Comparative Study between BPNN and RNN on the Settlement Prediction during Soft Ground Embankment[J]. Journal of the Society of Disaster Information, 2007, 3(1): 37-53
(  0) 0) |
| [9] |
Hochreiter S, Schmidhuber J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8): 1 735-1 780 DOI:10.1162/neco.1997.9.8.1735
(  0) 0) |
| [10] |
杨背背, 殷坤龙, 杜娟. 基于时间序列与长短时记忆网络的滑坡位移动态预测模型[J]. 岩石力学与工程学报, 2018, 37(10): 2 334-2 343 (Yang Beibei, Yin Kunlong, Du Juan. A Model for Predicting Landslide Displacement Based on Time Series and Long and Short Term Memory Neural Network[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(10): 2 334-2 343)
(  0) 0) |
| [11] |
Kurochkin I I, Volkov S S. Using GRU Based Deep Neural Network for Intrusion Detection in Software-Defined Networks[C]. IOP Conference Series: Materials Science and Engineering, Russia, 2020
(  0) 0) |
| [12] |
栾晓东, 底青云, 雷达. 基于牛顿迭代法和遗传算法的CSAMT近场校正[J]. 地球物理学报, 2018, 61(10): 4 148-4 159 (Luan Xiaodong, Di Qingyun, Lei Da. Near-Field Correction of CSAMT Data Based on Newton Iteration Method and GA Method[J]. Chinese Journal of Geophysics, 2018, 61(10): 4 148-4 159)
(  0) 0) |
| [13] |
李天磊. 地下水诱发黄土滑坡机理及其稳定性分析[D]. 北京: 中国地质大学, 2018 (Li Tianlei. Mechanism and Stability Analysis of Loess Landslide Induced by Groundwater[D]. Beijing: China University of Geosciences, 2018)
(  0) 0) |
| [14] |
白正伟, 张勤, 黄观文, 等. "轻终端+行业云"的实时北斗滑坡监测技术[J]. 测绘学报, 2019, 48(11): 1 424-1 429 (Bai Zhengwei, Zhang Qin, Huang Guanwen, et al. Real-Time Beidou Landslide Monitoring Technology of "Light Terminal Plus Industry Cloud"[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(11): 1 424-1 429)
(  0) 0) |
| [15] |
陈玉萍, 袁志强, 周博, 等. 遗传算法优化BP网络在滑坡灾害预测中的应用研究[J]. 水文地质工程地质, 2012, 39(1): 114-119 (Chen Yuping, Yuan Zhiqiang, Zhou Bo, et al. Application of Back Propagation Neural Networks with Optimization of Genetic Algorithms to Landslide Hazard Prediction[J]. Hydrogeology and Engineering Geology, 2012, 39(1): 114-119)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


