2. 武汉引力与固体潮国家野外观测研究站, 武汉市洪山侧路40号, 430071;
3. 地震预警湖北省重点实验室, 武汉市洪山侧路40号, 430071
地倾斜测量是研究地壳形变和固体潮的重要手段,对地球动力学研究和地震前兆观测具有重要意义[1-3]。高精度垂直摆倾斜仪由于体积小、自动化程度高、维护方便等优点,在我国地震前兆观测台网中得到广泛应用[4-6]。由于垂直摆倾斜仪是基于高精度平面电容进行微位移检测的,限定了其只有1个敏感轴方向。若要同时测量2个正交方向(东西向和南北向)的倾斜量,常用的方法是在同一底板上安装2个单分向的垂直摆倾斜仪传感器,分别获取东西向和南北向的地倾斜信号。但这种方式不仅需要保证2个传感器的一致性,还存在成本高、工作量大等问题。而采用圆弧柱面电容极板的二维倾斜仪,通过合理布置电容极板,即可实现采用单个倾斜仪传感器同时测量2个方向的倾斜量[7-8]。本文对应用于倾斜仪中的圆弧柱面电容器进行分析,为基于圆弧柱面电容极板的二维倾斜仪的研制提供理论依据。
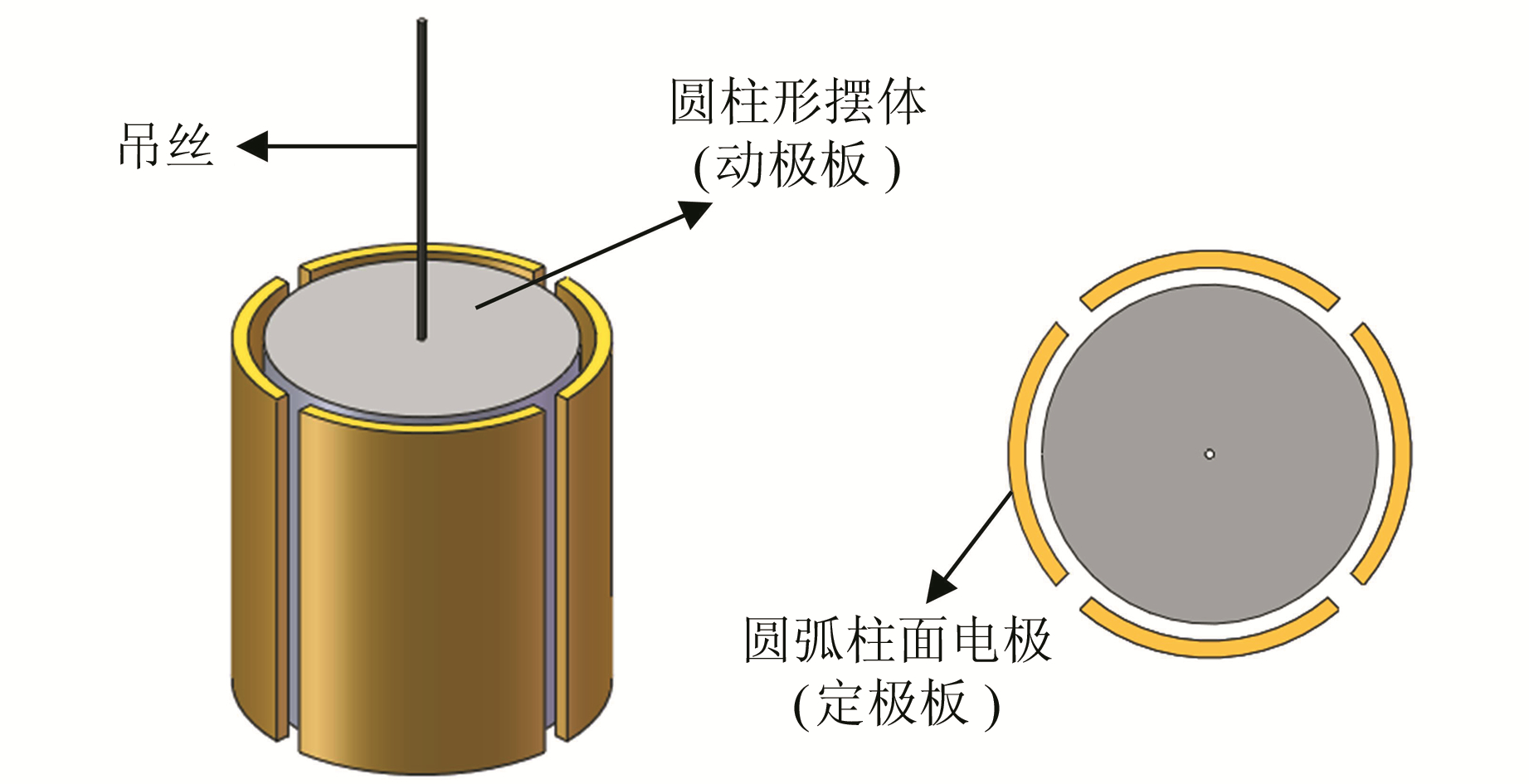
1 基于圆弧柱面电容极板的二维倾斜仪模型图 1为基于圆弧柱面电容极板的二维倾斜仪模型,主要由吊丝、圆柱形摆体和4片均匀分布的圆弧柱面极板构成。圆柱形摆体通过吊丝悬挂作为电容动极,与4块圆弧柱面电容定极板构成2对敏感轴相互正交的差动电容器,在每对圆弧柱面定极板上施加幅度相等、相位相反的激励信号,再由摆体动极板引出输出信号,通过解耦电路就可同时测量2个敏感轴方向的倾斜位移量。
|
图 1 基于圆弧柱面电容极板的二维倾斜仪模型 Fig. 1 Two-dimensional tiltmeter model based on arc cylindrical capacitor plate |
差动电容方法已广泛应用于高精度位移测量中,以提高测量信号输出的线性度。垂直摆倾斜仪中的平板差动电容结构如图 2所示,中间为动极板,两侧为定极板。若在2个定极板上施加幅度相等、相位相反的激励信号u和-u,可在动极板上检测得到输出信号u0。由基尔霍夫定律公式计算极板间电容C1、C2,得到动极板偏移两定极板中心零位的距离x,如已知悬挂吊丝折合摆长h,可计算得到倾斜位移量。

|
图 2 平面差动电容示意图 Fig. 2 Schematic diagram of planar differential capacitor |
|
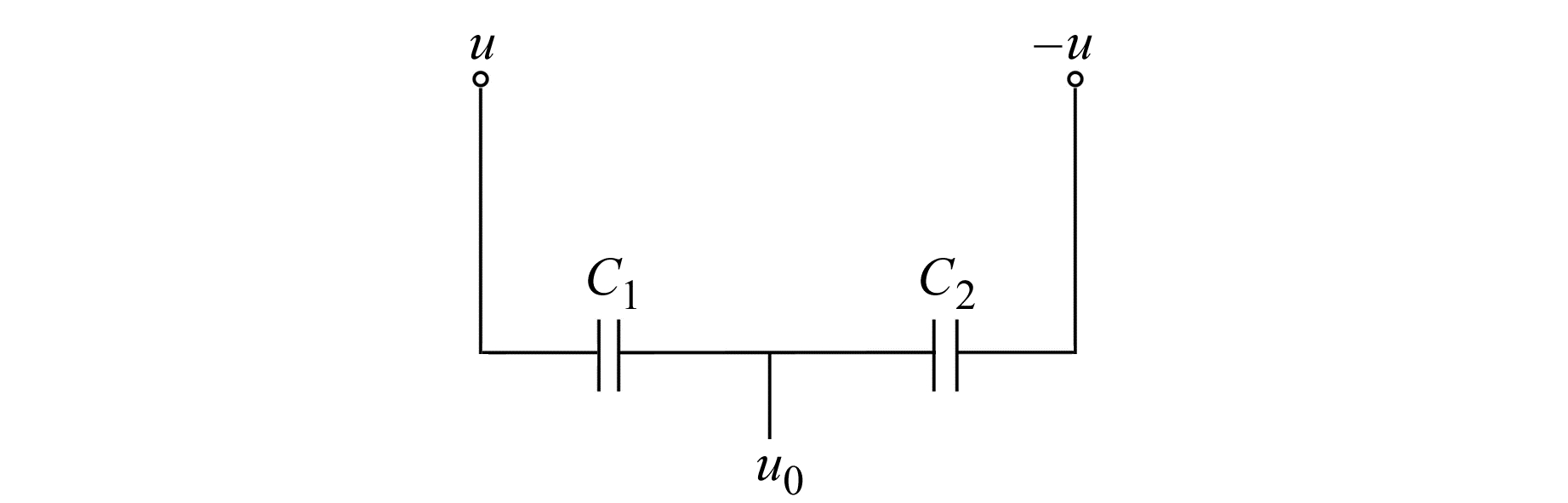
图 3 差动电容等效电路 Fig. 3 Equivalent circuit of differential capacitor |
由基尔霍夫定律可得:
| $ \frac{u-u_{0}}{\frac{1}{\omega C_{1}}}=\frac{u_{0}-(-u)}{\frac{1}{\omega C_{2}}} $ | (1) |
变换得到电路中输出电压与激励电压的关系为:
| $ u_{0}=\frac{C_{1}-C_{2}}{C_{1}+C_{2}} u $ | (2) |
以垂直倾斜仪中圆柱形动极板与一块圆弧柱面定极板为例进行分析,其几何分布如图 4所示。

|
图 4 同轴圆弧柱面极板电容器模型 Fig. 4 Coaxial arc cylindrical plate capacitor model |
为计算动极板与定极板间的电容量,构建一个包含圆弧柱面的密闭曲面。根据高斯定理,通过该闭合曲面的电通量ΦE为[1]:
| $ \varPhi_{E}=\int E \cdot \mathrm{d} S=\frac{Q}{\varepsilon_{0}} $ | (3) |
电容极板之间的电场强度E为:
| $ E=\frac{Q}{\varepsilon_{r} \cdot \varepsilon_{0} \cdot S}=\frac{Q}{\varepsilon_{r} \cdot \varepsilon_{0}(r \cdot \theta \cdot L)} $ | (4) |
式中,Q为极板上电荷,εr为相对介电常数,r为动极板半径,θ为圆弧柱面极板的圆心角,L为极板高度。极板两端的电压U为:
| $ U=\int_{R_{1}}^{R_{2}} E \mathrm{d} r=\frac{Q}{\varepsilon_{r} \cdot \varepsilon_{0} \cdot \theta \cdot L} \ln \left(\frac{R_{2}}{R_{1}}\right) $ | (5) |
定极板与动极板之间的电容C为:
| $ C=\frac{Q}{U}=\frac{\varepsilon_{r} \cdot \varepsilon_{0} \cdot \theta \cdot L}{\ln \left(\frac{R_{2}}{R_{1}}\right)} $ | (6) |
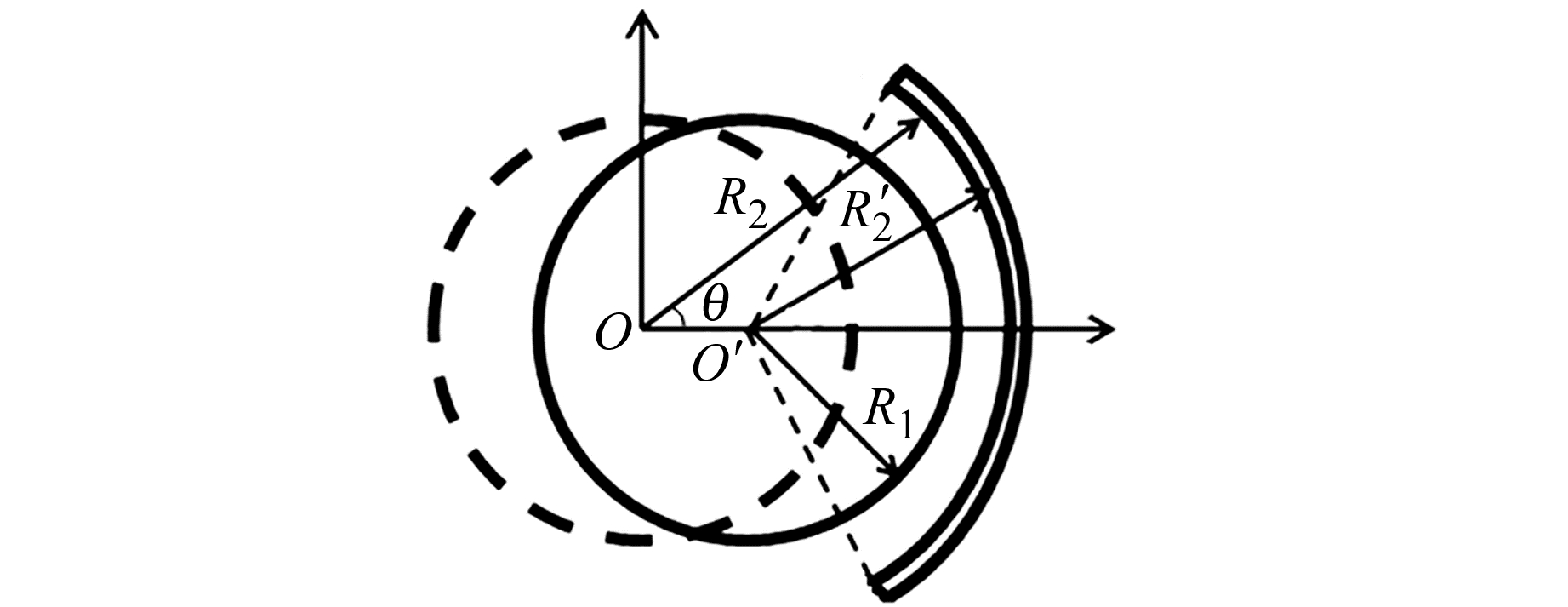
式(6)反映了同轴圆弧柱面极板电容器的电容。而作为动极板的圆柱形摆体,实际应用在倾斜仪电路中的电容器敏感到外界发生倾斜时就会出现位移变化,其位移变化的平面几何分布如图 5所示。显然,产生位移后2个极板不再同轴,此时定极板和动极板的间距随定极板圆心角的变化而变化。采用有限元方法分析,将圆弧柱面电容极板分割成若干个圆心角为dθ的动极板,每个小动极板dθ对应电容为dC。由式(6)可得到:
| $ \mathrm{d} C=\frac{\varepsilon_{r} \cdot \varepsilon_{0} \cdot L}{\ln \left(\frac{R_{2}}{R_{1}}\right)} \mathrm{d} \theta $ | (7) |
|
图 5 非同轴圆弧柱面极板电容器模型 Fig. 5 Non-coaxial arc cylindrical plate capacitor model |
图 5为圆柱形摆体变化出现位移时动极板的运动情况,动极板的摆体轴线从O移动至O′,因而得到位移x,此时R1不变,R2变为R′2。根据余弦定理可得:
| $ R_{2}^{\prime}=\sqrt{\left(x^{2}+R_{2}^{2}\right)-2 x R_{2} \cos \theta} $ | (8) |
式(8)代入式(7)得非同轴圆弧柱面极板电容为:
| $ \begin{gathered} C=\int_{\alpha}^{\beta} \frac{\varepsilon_{r} \cdot \varepsilon_{0} \cdot L}{\ln \left(\frac{R_{2}^{\prime}}{R_{1}}\right)} \mathrm{d} \theta= \\ \int_{\alpha}^{\beta} \frac{\varepsilon_{r} \cdot \varepsilon_{0} \cdot L}{\ln \sqrt{\left(R_{2}^{2}+x^{2}\right)+2 x R_{2} \cos \theta}-\ln R_{1}} \mathrm{~d} \theta \end{gathered} $ | (9) |
将式(9)代入式(2),可计算出圆弧柱面极板倾斜仪的输出信号u0与摆动距离x之间的关系:
| $ u_{0}=\frac{\int_{\alpha}^{\beta} \frac{\varepsilon_{r} \cdot \varepsilon_{0} \cdot L}{\ln \sqrt{\left(R_{2}^{2}+x^{2}\right)-2 x R_{2} \cos \theta}-\ln R_{1}} \mathrm{~d} \theta-\int_{\alpha}^{\beta} \frac{\varepsilon_{r} \cdot \varepsilon_{0} \cdot L}{\ln \sqrt{\left(R_{2}^{2}+x^{2}\right)+2 x R_{2} \cos \theta}-\ln R_{1}} \mathrm{~d} \theta}{\int_{\alpha}^{\beta} \frac{\varepsilon_{r} \cdot \varepsilon_{0} \cdot L}{\ln \sqrt{\left(R_{2}^{2}+x^{2}\right)-2 x R_{2} \cos \theta}-\ln R_{1}} \mathrm{~d} \theta+\int_{\alpha}^{\beta} \frac{\varepsilon_{r} \cdot\varepsilon_{0} \cdot L}{\ln \sqrt{\left(R_{2}^{2}+x^{2}\right)+2 x R_{2} \cos \theta}-\ln R_{1}} \mathrm{~d} \theta} \cdot u $ | (10) |
通过输出信号u0检测得到动极板的位移量x,根据已知吊丝折合摆长计算倾斜角度,实现对地倾斜位移的测量。
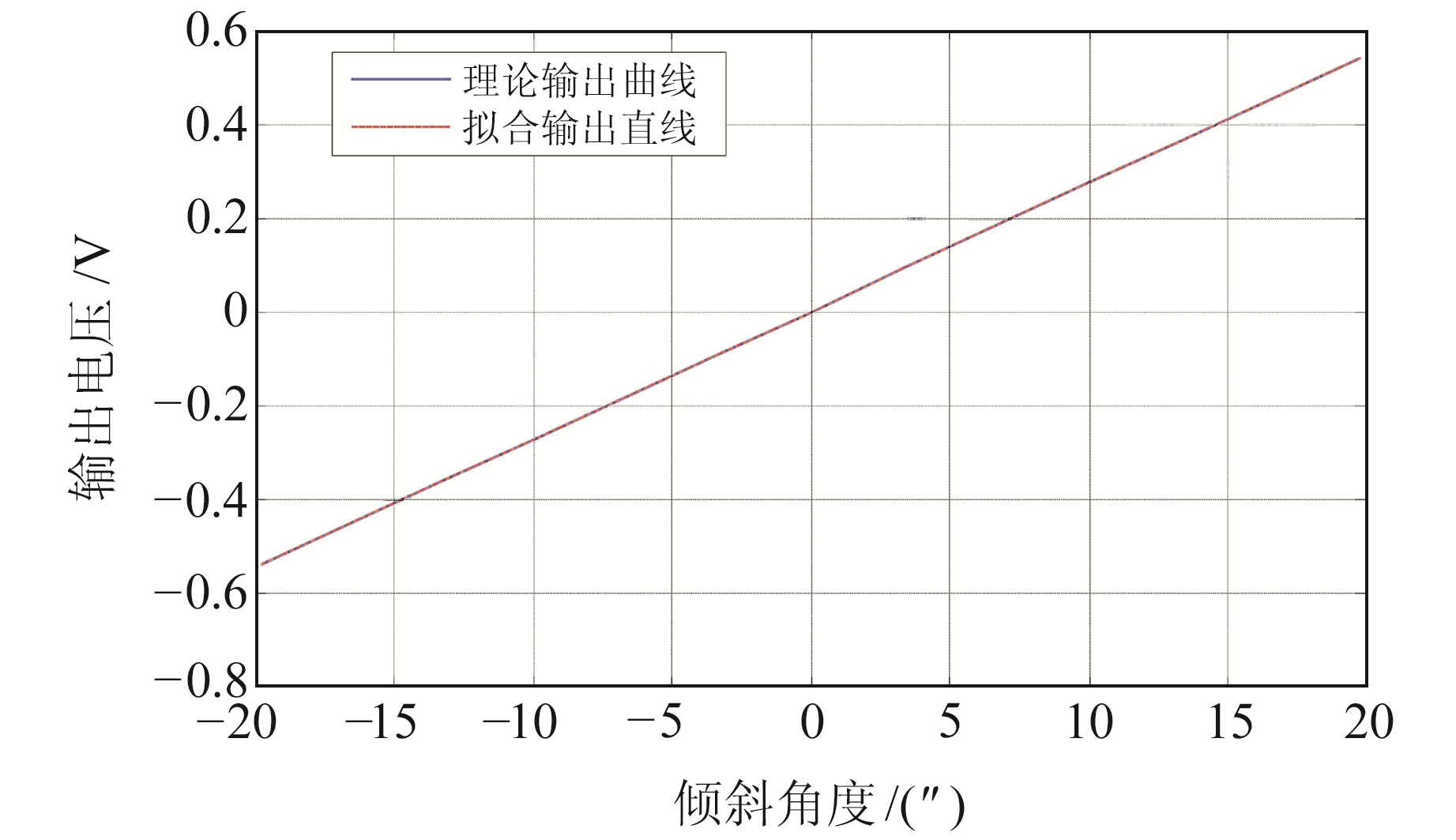
3 圆弧柱面电容参数对倾斜仪影响为进一步分析圆弧柱面极板差动电容倾斜仪的输出信号,设置摆体的摆动角度范围为φ=±20″,对应的摆动距离为x=φ(h+L/2)。根据式(10)可知,圆弧柱面极板差动电容倾斜仪的输出信号u0与摆动距离x呈非线性关系。将表 1中参数代入式(10),结合摆动距离与摆动角度之间的关系,即可绘制出输出信号u0随摆动角度φ变化的理论输出曲线。再采用最小二乘法对理论输出曲线进行一阶拟合,得到拟合输出直线u0=kφ+b,绘制的理论输出曲线和线性拟合直线如图 6所示。为计算圆弧柱面极板差动电容输出的非线性度,将理论输出值与拟合值相减,结果如图 7所示。
|
|
表 1 圆弧柱面极板差动电容器的典型参数 Tab. 1 Typical parameters of arc cylindrical plate differential capacitor |
|
图 6 输出信号随倾角变化 Fig. 6 Output signal varies with tilt angle |

|
图 7 理论输出与拟合直线的差值 Fig. 7 Differences between theoretical and fitted lines |
图 6中计算的拟合直线斜率(k=0.028 5V/(″))即为倾斜仪的灵敏度。再根据图 7计算出圆弧柱面差动电容的非线性度:
| $ \begin{gathered} \delta=\frac{\Delta Y_{\max }}{k \times\left(x_{\max }-x_{\min }\right)} \times 100 \%= \\ \frac{1.427\ 3 \times 10^{-5}}{0.028\ 5 \times[20-(-20)]} \times 100 \% \approx 0.001\ 2 \% \end{gathered} $ |
为研究圆弧柱面极板差动电容中各项参数对倾斜仪输出的影响,采用控制变量法对表 1中的参数进行分析。
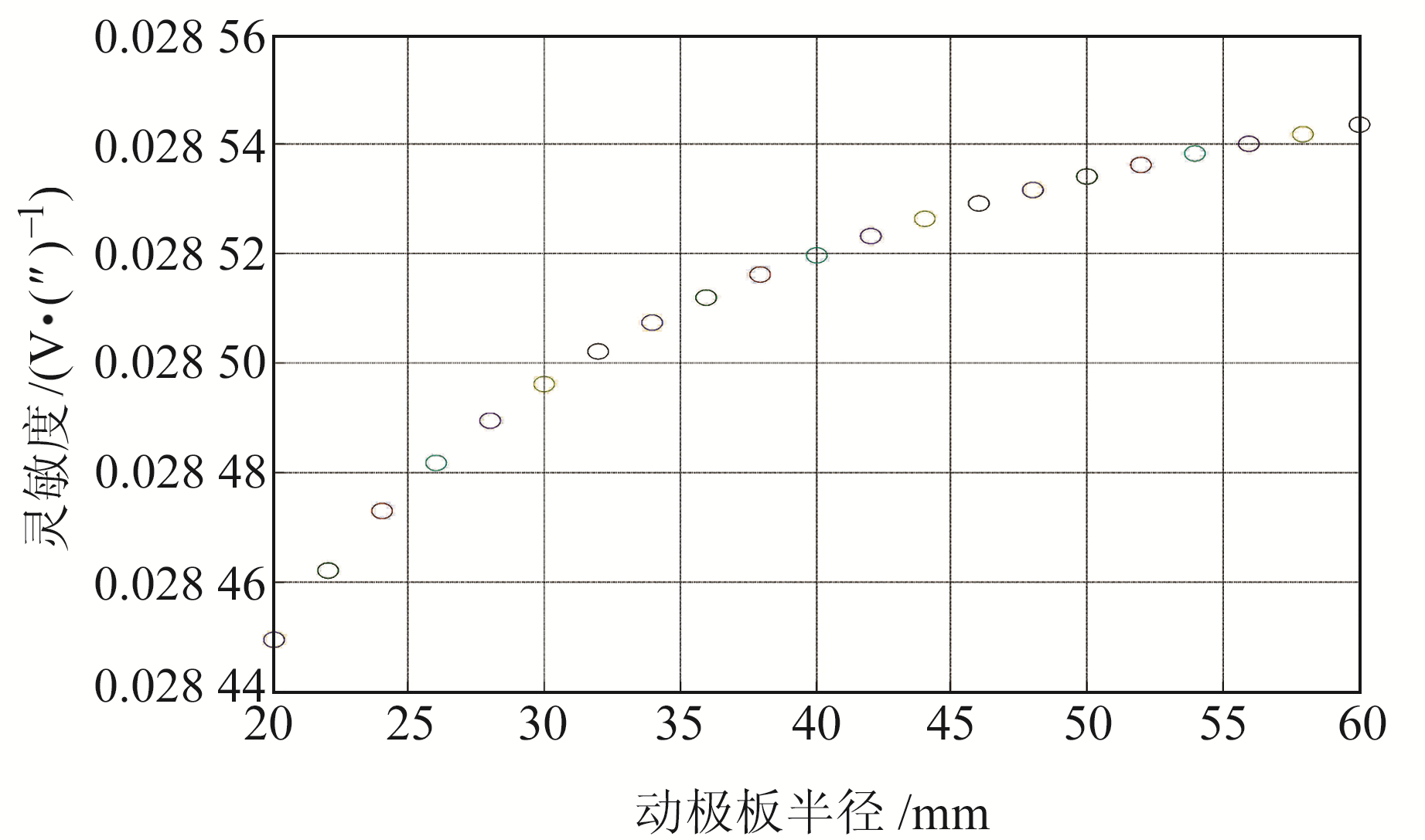
3.1 动极板半径变化对倾斜仪输出影响将表 1中圆柱形摆体(动极板)半径R1由20 mm变为60 mm,其他参数不变,采用最小二乘法进行拟合计算,得到倾斜仪灵敏度和非线性度随动极板半径变化曲线,结果如图 8和9所示。由图可知,圆弧柱面极板差动电容输出的灵敏度随动极板半径增大而增大,非线性度随动极板半径增大而减小。
|
图 8 灵敏度随动极板半径变化曲线 Fig. 8 Sensitivity varies with the radius of the moving plate |

|
图 9 非线性度随动极板半径变化曲线 Fig. 9 Nonlinearity varies with the radius of the moving plate |
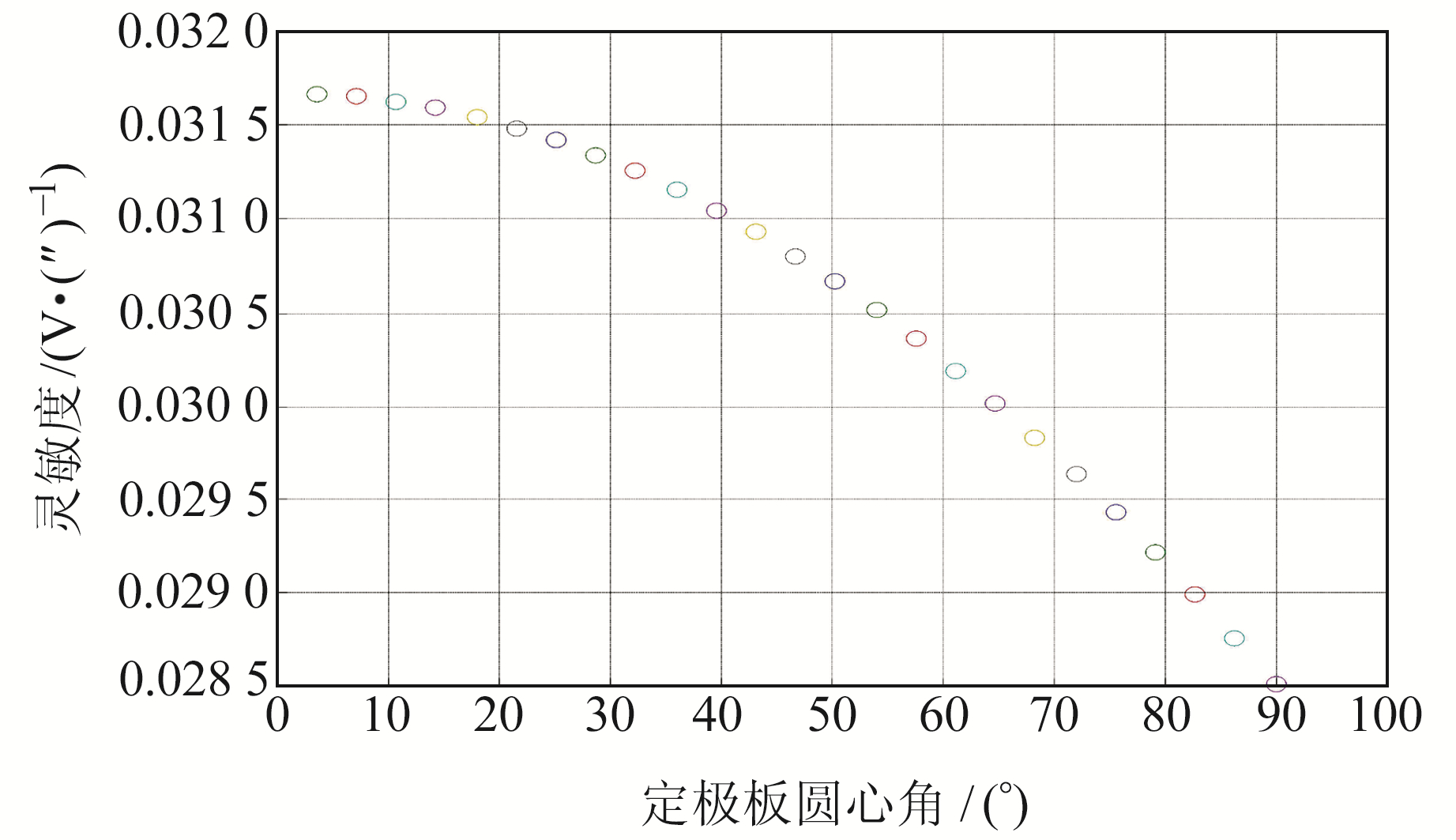
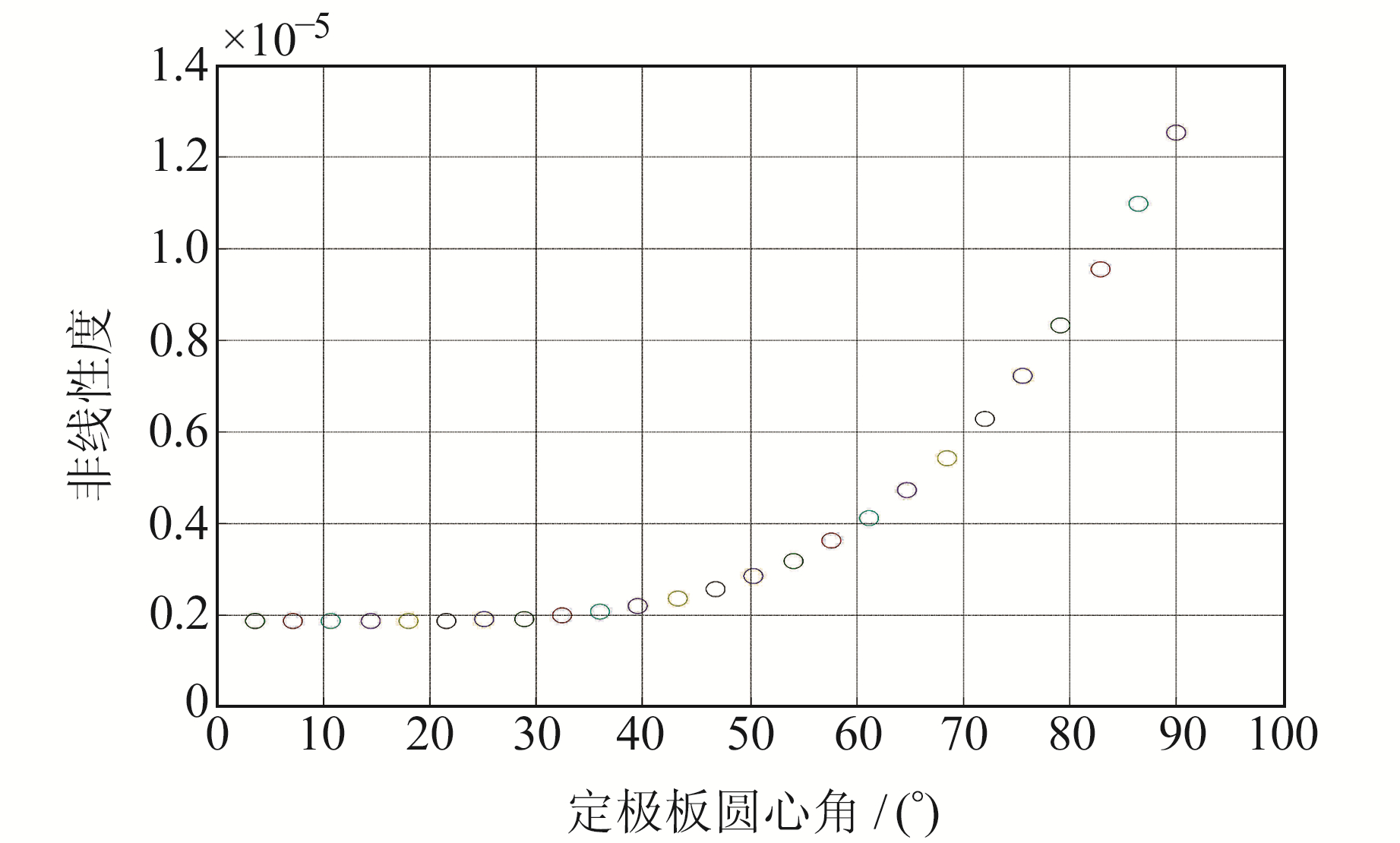
将表 1中圆弧柱面极板圆心角θ由0°变为90°,其他参数不变,得到倾斜仪输出灵敏度和非线性度随圆弧柱面定极板圆心角变化曲线,结果如图 10和11所示。由图可知,圆弧柱面极板差动电容输出的灵敏度随定极板圆心角增大而减小,非线性度随定极板圆心角增大而变大。
|
图 10 灵敏度随定极板圆心角变化曲线 Fig. 10 Sensitivity varies with central angle of the fixed plate |
|
图 11 非线性度随定极板圆心角变化曲线 Fig. 11 Nonlinearity varies with central angle of the fixed plate |
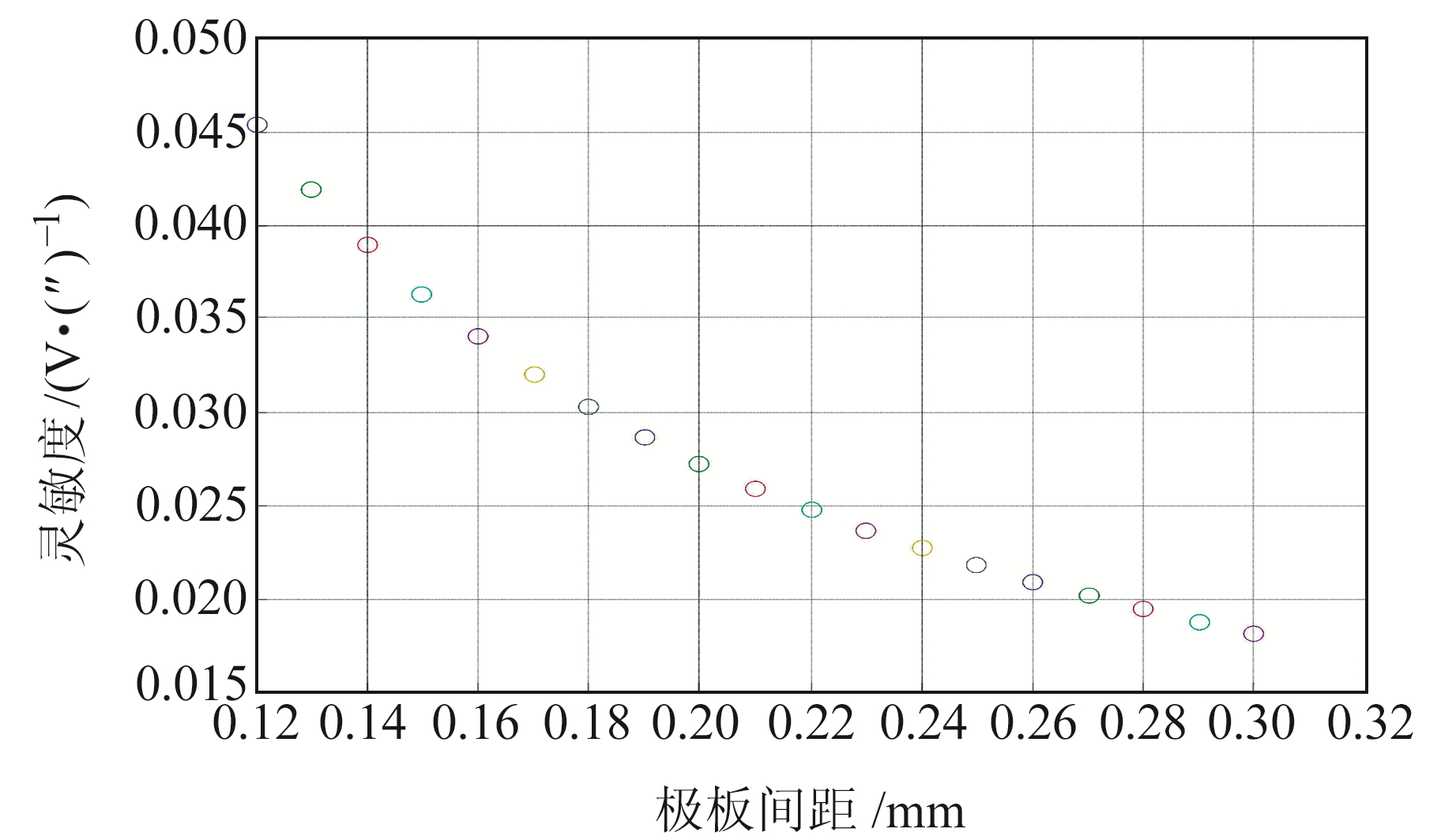
将表 1中动极板与定极板间距d由0.12 mm变为0.32 mm,其他参数不变,得到输出灵敏度和非线性度随吊丝长度变化曲线,结果如图 12和13所示。由图可知,圆弧柱面极板差动电容输出的灵敏度和非线性度均随极板间距增大而减小。
|
图 12 灵敏度随极板间距变化曲线 Fig. 12 Sensitivity varies with the gap between capacitor plates |

|
图 13 非线性度随极板间距变化曲线 Fig. 13 Nonlinearity varies with the gap between capacitor plates |
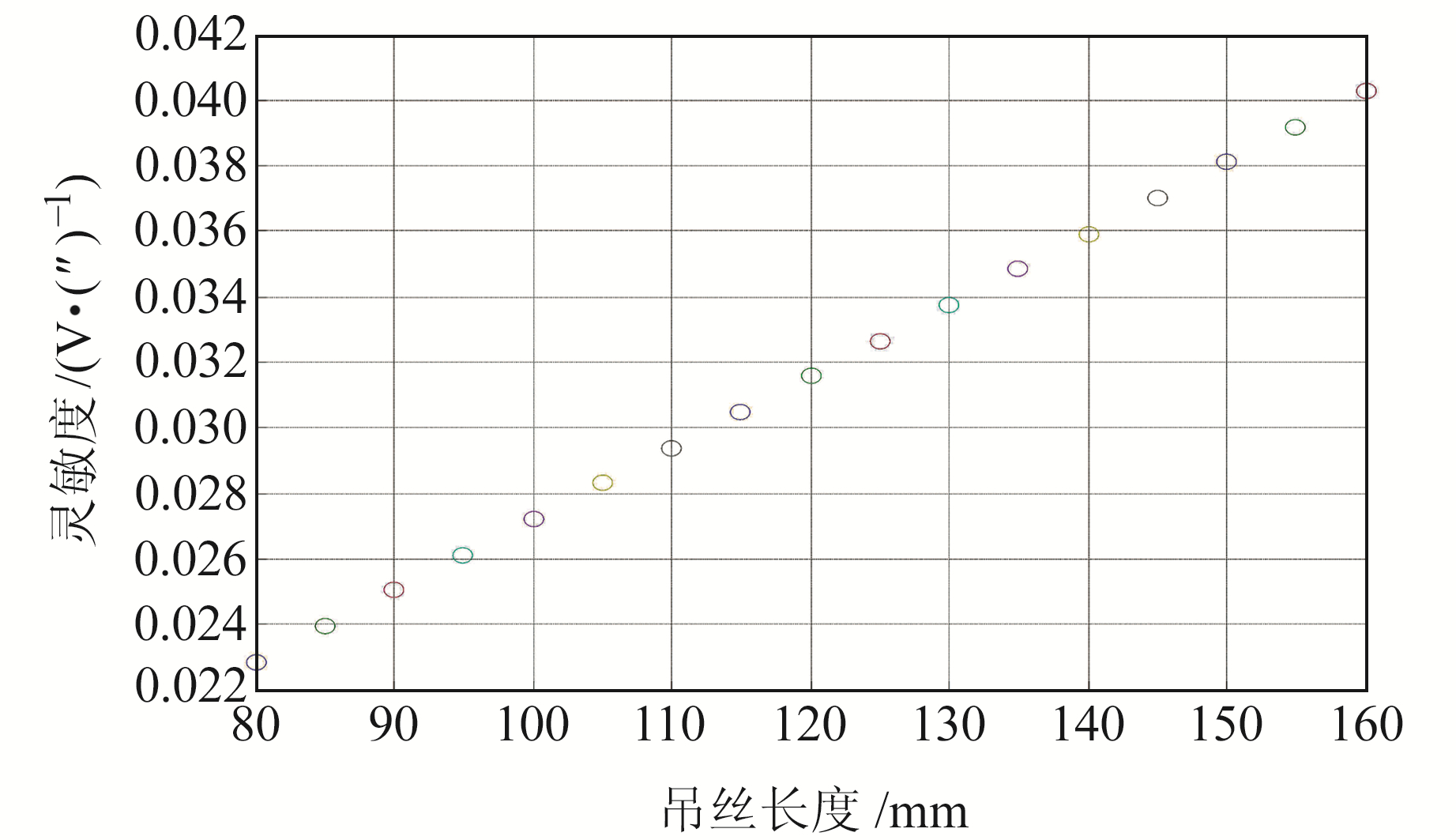
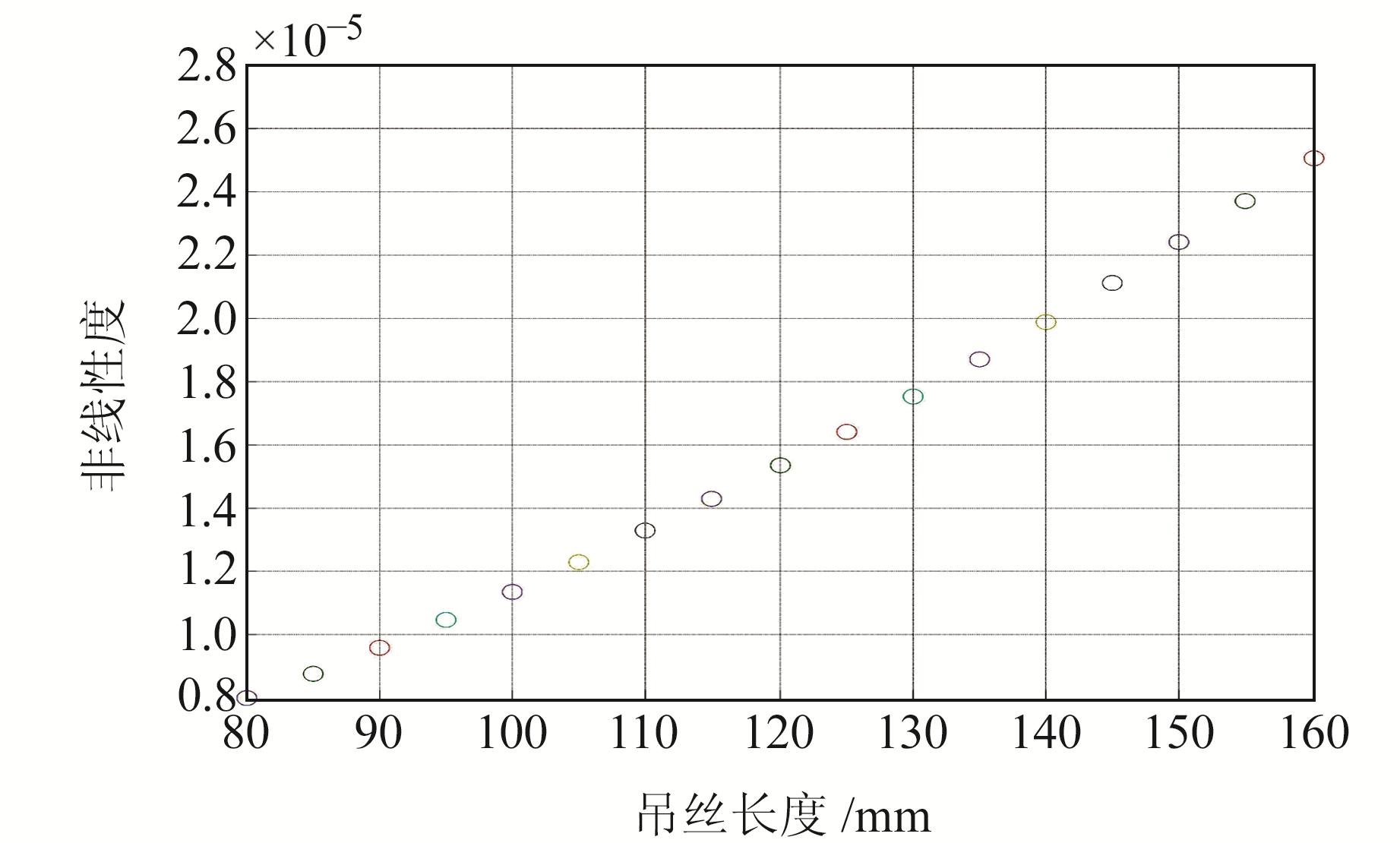
将表 1中吊丝长度h由80 mm变为160 mm,其他参数不变,获得输出灵敏度和非线性度随吊丝长度变化曲线,结果如图 14和15所示。由图可知,圆弧柱面极板差动电容输出的灵敏度和非线性度都随吊丝长度增大而增大。
|
图 14 灵敏度随吊丝长度变化曲线 Fig. 14 Sensitivity varies with the length of the hanger wire |
|
图 15 非线性度随吊丝长度变化曲线 Fig. 15 Nonlinearity varies with the length of the hanger wire |
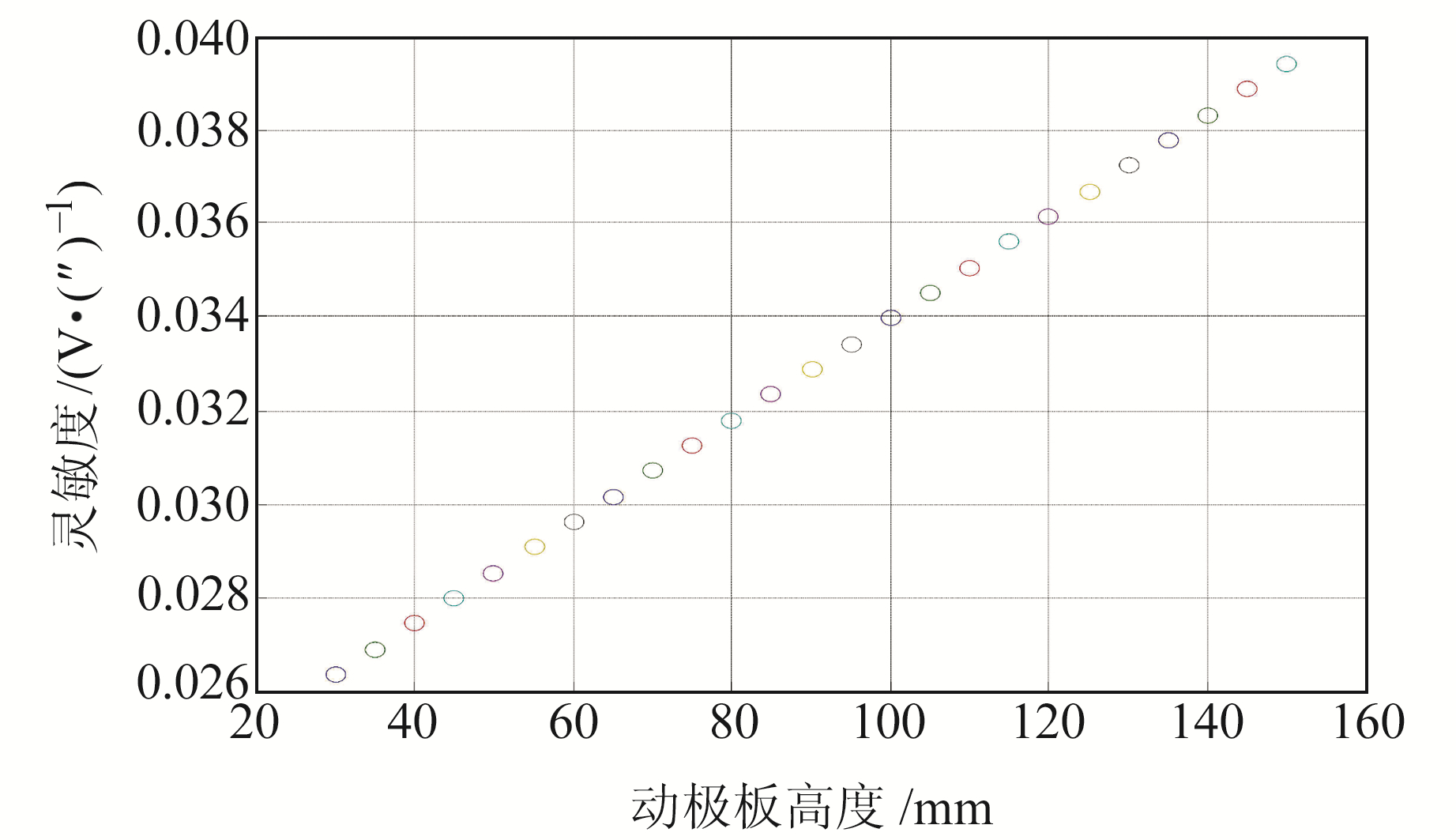
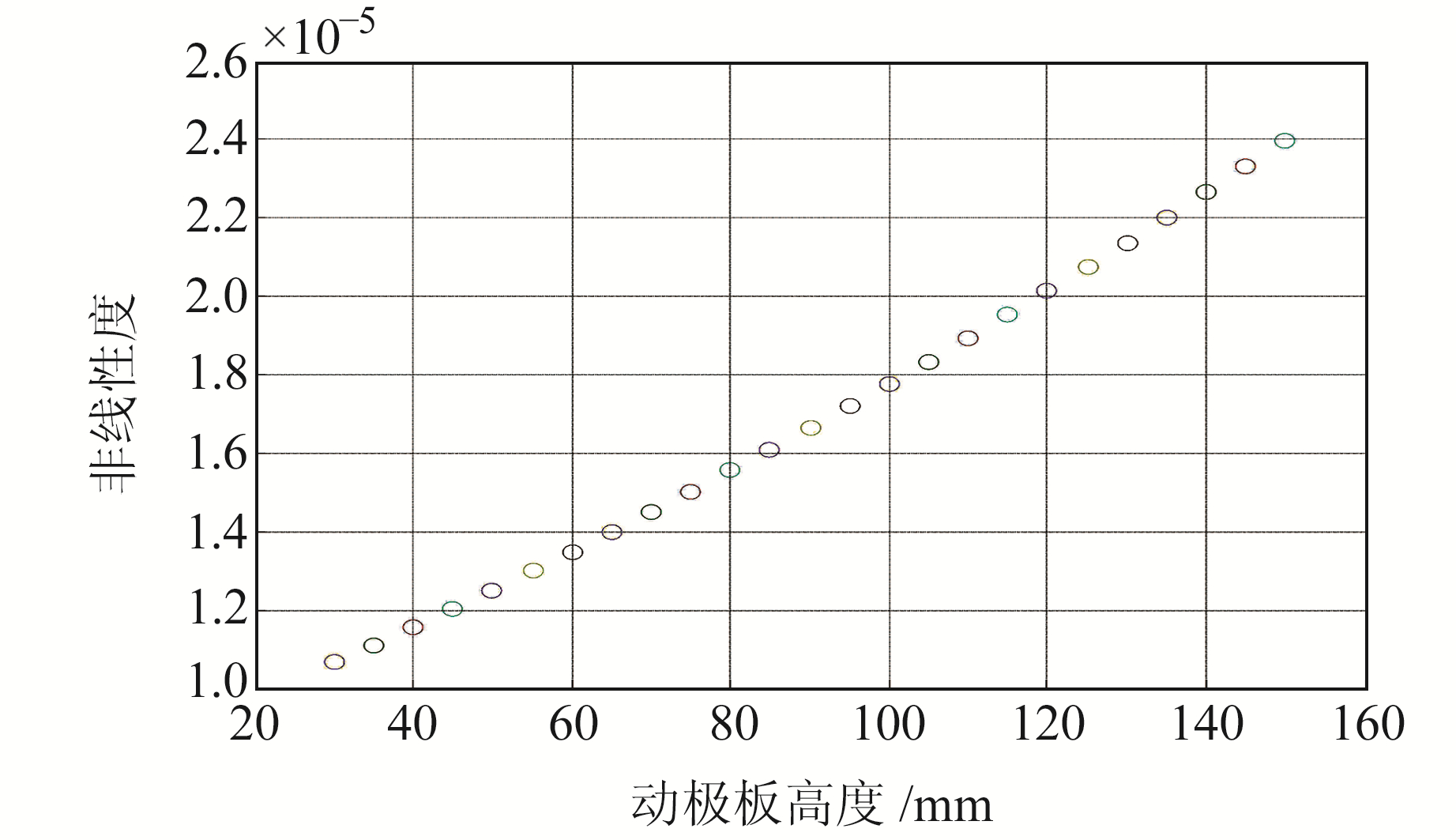
将表 1中动极板高度L由30 mm变为150 mm,其他参数不变,获得输出灵敏度和非线性度随动极板高度变化曲线,结果如图 16和17所示。由图可知,圆弧柱面极板差动电容输出的灵敏度和非线性度都随动极板高度增大而增大。
|
图 16 灵敏度随动极板高度变化曲线 Fig. 16 Sensitivity varies with the height of the moving plate |
|
图 17 非线性度随动极板高度变化曲线 Fig. 17 Nonlinearity varies with the height of the moving plate |
本文通过对二维倾斜仪中的圆弧柱面差动电容理论模型的参数变化进行分析,探讨圆弧柱面差动电容器各个构件结构参数对仪器输出灵敏度、非线性度的影响。结果发现,对于应用于倾斜仪中的圆柱形电容器,增大动极板摆体半径时,输出灵敏度增大,非线性度减小;增大定极板圆心角时,输出灵敏度减小,非线性度增大;增大极板间距时,输出灵敏度减小,非线性度减小;增大吊丝长度和动极板高度时,输出灵敏度和非线性度都增大。
对倾斜仪中圆柱形电容器各构件结构参数的增加或缩小不能是无限制的,如吊丝增长、圆柱体增高等,虽然会提高倾斜仪的灵敏度、减小非线性度,但同时也会使倾斜仪体积增大,动态范围变小,仪器噪声急剧增加。因此,对电容器各构件结构参数进行适度选择和合理设计,使倾斜仪能够满足应用场景才是最重要的。
| [1] |
肖峻. 高精度垂直摆倾斜仪及其应用研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2002 (Xiao Jun. High Precision Vertical Pendulum Tiltmeter and Its Application[D]. Wuhan: Institute of Geodesy and Geophysics, CAS, 2002)
(  0) 0) |
| [2] |
肖峻, 莫易敏, 胡国庆. 基于固体潮观测的高精度垂直摆倾斜仪[J]. 武汉大学学报: 信息科学版, 2004, 29(11): 973-976 (Xiao Jun, Mo Yimin, Hu Guoqing. High Precision Vertical Pendulum Tiltmeter for Measuring Earth Tide[J]. Geomatics and Information Science of Wuhan University, 2004, 29(11): 973-976)
(  0) 0) |
| [3] |
施志龙, 吴书朝. 垂直摆倾斜仪灵敏度标定方法研究[J]. 测绘科学, 2007, 32(4): 63-64 (Shi Zhilong, Wu Shuchao. Research on Calibration of Vertical Pendulum Tiltmeter[J]. Science of Surveying and Mapping, 2007, 32(4): 63-64 DOI:10.3771/j.issn.1009-2307.2007.04.022)
(  0) 0) |
| [4] |
马武刚, 吴艳霞, 胡国庆. VP型宽频带潮汐观测仪的研制[J]. 地震工程学报, 2015, 37(3): 873-877 (Ma Wugang, Wu Yanxia, Hu Guoqing. Development of VP-Type Broadband Tide Meter[J]. China Earthquake Engineering Journal, 2015, 37(3): 873-877 DOI:10.3969/j.issn.1000-0844.2015.03.0873)
(  0) 0) |
| [5] |
马武刚, 卢海燕, 胡国庆, 等. VP型垂直摆倾斜仪校准装置的设计[J]. 大地测量与地球动力学, 2012, 32(4): 152-155 (Ma Wugang, Lu Haiyan, Hu Guoqing, et al. Design of Calibration Device for VP Vertical Pendulum Tiltmeter[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 152-155)
(  0) 0) |
| [6] |
马武刚, 胡国庆, 谭业春, 等. 新型宽频带垂直摆倾斜仪的设计及应用[J]. 测绘信息与工程, 2010, 35(5): 28-30 (Ma Wugang, Hu Guoqing, Tan Yechun, et al. Design and Application of New Wide Frequency Band Vertical Pendulum Tiltmeter[J]. Journal of Geomatics, 2010, 35(5): 28-30)
(  0) 0) |
| [7] |
黄玉, 武立华. 二维垂直摆倾斜仪对地倾斜的测量[J]. 仪器仪表学报, 2007, 28(8): 1 514-1 517 (Huang Yu, Wu Lihua. Crustal Tilt Measurement with Two-Dimension Vertical Pendulum Tiltmeter[J]. Chinese Journal of Scientific Instrument, 2007, 28(8): 1 514-1 517)
(  0) 0) |
| [8] |
黄玉, 武立华. 二维垂直摆倾斜仪对地倾斜的响应[J]. 哈尔滨工程大学学报, 2006, 27(3): 469-473 (Huang Yu, Wu Lihua. Response of Two-Dimensional Vertical Pendulum Tilt Meter to Crustal Tilt[J]. Journal of Harbin Engineering University, 2006, 27(3): 469-473 DOI:10.3969/j.issn.1006-7043.2006.03.033)
(  0) 0) |
2. Wuhan Gravitation and Solid Earth Tides, National Observation and Research Station, 40 Hongshance Road, Wuhan 430071, China;
3. Hubei Key Laboratory of Earthquake Early Warning, 40 Hongshance Road, Wuhan 430071, China
 2022, Vol. 42
2022, Vol. 42


