2. 国家遥感中心绵阳科技城分部, 四川省绵阳市青龙大道中段59号, 621010;
3. 四川航遥智测科技有限公司, 四川省绵阳市涪金路389号, 621010
随着测绘技术的不断更新,矿区地表形变监测方法取得了很大进展[1-2]。传统GNSS测量方法可得到高精度的单点三维形变数据,但仅依靠单点测量无法客观反映地表真实形变情况[3]。合成孔径雷达干涉测量(InSAR)技术具有高空间分辨率、高自动化和广域监测等优点,为形变监测领域提供了前所未有的机遇[4-5]。然而,InSAR仅能监测沿卫星视距方向的形变,且由于合成孔径雷达(SAR)卫星近南北向飞行,导致其对南北向形变不敏感[6]。将GNSS与InSAR数据融合解算三维形变场是目前国内外众多学者关注和研究的热点[7-9]。目前的融合方法主要分为2种:1)将GNSS南北向形变插值后代入解算InSAR在东西向和垂直向的形变场[10],但该方法过于依赖GNSS在南北向的形变精度,忽略了InSAR在南北向形变的贡献;2)通过建立合适的融合模型解算三维形变场[11],但会遇到先验方差不准确及迭代负方差的情况,导致不能完整地表达真实地表三维变化。
本文以金昌市金川西二采矿区为研究对象,提出一种融合赫尔默特方差分量估计(Helmert variance component estimation, HVCE)和径向基函数神经网络(radial basis function neural network, RBFNN)的三维形变计算法HVCE-RBFNN。利用该方法对同期的GNSS和InSAR数据进行迭代定权,解算出地表三维形变场,并与地下采空区进行对比分析,以期为矿区地表三维形变监测提供新方法。
1 HVCE-RBFNN模型建立 1.1 InSAR三维几何分解原理传统InSAR技术仅能获取沿卫星视线(LOS)向的一维形变,然而真实地表形变通常是三维的,因此需要将InSAR单一方向的形变分解为三维方向的形变。根据卫星侧视观测几何,沿卫星LOS向的形变可分解为地表某一点在东西向、南北向和垂直向的位移[12],如图 1所示。InSAR的累积形变DLOS可以表示为:
| $ D_{\mathrm{LOS}}=-D_{E} \sin \theta \cos \alpha+D_{N} \sin \theta \sin \alpha+D_{U} \cos \theta $ | (1) |

|
图 1 InSAR三维几何分解原理 Fig. 1 3D geometric decomposition schematic of InSAR |
式中,DE、DN和DU分别为地面点P沿东西向、南北向和垂直向的位移;θ为卫星入射角;α为卫星方位角,以顺时针方向为正。令S=[SE SN SU]T、SE=-sinθcosα、SN=sinθsinα、SU=cosθ分别为卫星LOS向形变在三维方向的投影。
1.2 HVCE-RBFNN模型假设有n组观测数据,且各组数据之间互不相关,根据间接平差的数学模型有:
| $ \boldsymbol{V}_{i}=\boldsymbol{B}_{i} \hat{\boldsymbol{x}}-\boldsymbol{l}_{i}, i=1,2, \cdots, n $ | (2) |
式中,Vi为改正数矢量;Bi为系数矩阵;li为观测数据。法方程表达式为:
| $ \hat{\boldsymbol{x}}=\boldsymbol{N}^{-1} \boldsymbol{W} $ | (3) |
| $ \boldsymbol{N}=\sum\limits_{i=1}^{n} \boldsymbol{B}_{i}^{\mathrm{T}} \boldsymbol{P}_{i} \boldsymbol{B}_{i}=\sum\limits_{i=1}^{n} \boldsymbol{N}_{i} $ | (4) |
| $ \boldsymbol{W}=\sum\limits_{i=1}^{3} \boldsymbol{B}_{i}^{\mathrm{T}} \boldsymbol{P}_{i} \boldsymbol{l}_{i}=\sum\limits_{i=1}^{3} \boldsymbol{W}_{i} $ | (5) |
式中,Pi为权重矩阵,在第1次最小二乘平差中可定义为任意矩阵[13]。
通常情况下,由于很难准确计算观测数据的先验方差,因此在第1次平差中给定的权阵Pi也是不合理的。为此引入HVCE法,设各组观测数据的单位权方差为
| $ \hat{\boldsymbol{\theta}}=\boldsymbol{A}^{-1} \boldsymbol{W}_{\theta} $ | (6) |
| $ \hat{\boldsymbol{\theta}}=\left[\begin{array}{llll} \hat{\sigma}_{01}^{2} & \hat{\sigma}_{02}^{2} & \cdots & \hat{\sigma}_{0 n}^{2} \end{array}\right]^{\mathrm{T}} $ | (7) |
| $ \boldsymbol{W}_{\theta}=\left[\begin{array}{llll} \boldsymbol{V}_{1}^{\mathrm{T}} \boldsymbol{P}_{1} \boldsymbol{V}_{1} & \boldsymbol{V}_{2}^{\mathrm{T}} \boldsymbol{P}_{2} \boldsymbol{V}_{2} & \cdots & \boldsymbol{V}_{n}^{\mathrm{T}} \boldsymbol{P}_{n} \boldsymbol{V}_{n} \end{array}\right]^{\mathrm{T}} $ | (8) |
| $ \boldsymbol{A}=\left[\begin{array}{ccc} a_{1}-2 \operatorname{tr}\left(\boldsymbol{N}^{-1} \boldsymbol{N}_{1}\right)+\operatorname{tr}\left(\boldsymbol{N}^{-1} \boldsymbol{N}_{1}\right)^{2} & \cdots & \operatorname{tr}\left(\boldsymbol{N}^{-1} \boldsymbol{N}_{1} \boldsymbol{N}^{-1} \boldsymbol{N}_{n}\right) \\ \vdots & \ddots & \vdots \\ \operatorname{tr}\left(\boldsymbol{N}^{-1} \boldsymbol{N}_{1} \boldsymbol{N}^{-1} \boldsymbol{N}_{n}\right) & \cdots & a_{n}-2 \operatorname{tr}\left(\boldsymbol{N}^{-1} \boldsymbol{N}_{n}\right)+\operatorname{tr}\left(\boldsymbol{N}^{-1} \boldsymbol{N}_{n}\right)^{2} \end{array}\right] $ | (9) |
式中,ai为各组观测数据li的观测量个数。根据式(7)计算新的权重矩阵为:
| $ \hat{\boldsymbol{P}}_{i}=\frac{c}{\hat{\sigma}_{0 i}^{2} \boldsymbol{P}_{i}^{-1}} $ | (10) |
式中,c为任意常数。将求得的新权阵
| $ \hat{\sigma}_{01}^{2} \approx \hat{\sigma}_{02}^{2} \approx \cdots \approx \hat{\sigma}_{0 n}^{2} $ | (11) |
当满足式(11)时,可输出计算结果。各类观测数据差异较大时,往往会导致式(11)出现负方差的情况,这是因为观测方程系数矩阵秩亏,导致矩阵N病态或完全秩亏,使得N-1→∞,N-1与法矩阵Ni的乘积的迹tr(N-1Ni)→∞,从而导致迭代出现负方差。基于此,采用RBFNN算法对负方差的点进行计算。
RBFNN具有自主学习、自主组合和自主适应等特点,可对差异较大的数据进行训练,从而达到数据融合的目的,不仅解决了计算效率的问题,还可完整地表达各组数据在融合中的贡献[14]。RBFNN由3层前向网络构成,第1层为输入层,第2层为隐含层,第3层为输出层,其数学模型表示为:
| $ y_{j}=\sum\limits_{i=1}^{n} w_{i j} \varphi\left(\left\|\boldsymbol{X}-\boldsymbol{x}_{i}\right\|^{2}\right), j=1, \cdots, k $ | (12) |
式中,wij为权值;X为训练样本;xi为基函数中心;φ(‖X-xi‖2)为基函数;k为输出单元数。
RBF函数中心确定的方法不同,RBFNN的学习策略也不同。根据各组观测数据的特点,采用随机选取固定中心的学习策略,使基函数中心和标准差恒定不变。当各组数据比较典型、具有代表性时,这种策略的学习效率会大幅提升。传递函数选择高斯分布函数:
| $ \varphi_{i}(r)=\mathrm{e}^{-\frac{r^{2}}{\sigma_{i}^{2}}} $ | (13) |
式中,r为模糊半径;σ为基函数的标准差。为防止RBF函数过尖或过平,对σ进行选取:
| $ \sigma_{i}=\frac{d_{\max }}{\sqrt{2 n}} $ | (14) |
式中,dmax为选取中心之间的距离;n为隐含节点个数。得到基函数为:
| $ \begin{aligned} \varphi\left(\left\|\boldsymbol{X}-\boldsymbol{x}_{i}\right\|\right) &=\exp \left(-\frac{n}{d_{\max }^{2}}\left\|\boldsymbol{X}-\boldsymbol{x}_{i}\right\|^{2}\right), \\ i &=1,2, \cdots, n \end{aligned} $ | (15) |
最后采用伪逆法计算权值:
| $ \omega_{i j}=\varphi\left(\left\|\boldsymbol{X}-\boldsymbol{x}_{i}\right\|^{2}\right) d_{k j} $ | (16) |
式中,dkj为期望输出值。
2 实验分析 2.1 研究区概况及数据介绍金川西二采矿区位于甘肃省金昌市(图 2),地处河西走廊中段、祁连山北麓,平均海拔1 700 ~2 700 m。该区属大陆性温带干旱气候,光照充足,气候干燥,降水少且蒸发强,地下水系不发育,总体生态环境较弱[15]。矿区地下开采范围南北长420 m,东西宽230 m,总面积约43 512 m2。由于长期受地下开采和断层活动影响,矿区地表塌陷明显,安全隐患极大。

|
(a)矿区地理位置;(b)实验SAR 影像覆盖情况;(c)监测点位分布;(d)地面监测桩 图 2 研究区概况 Fig. 2 Overview of the study area |
本研究在地表均匀布设139个监测点,得到2019-04~2020-06期间GNSS三维形变数据。通过欧洲航天局官网下载同期67景C波段升降轨Sentinel-1A斜距单视复数(SLC)影像,卫星重访周期为12 d,分辨率为5 m×20 m,为提高数据处理效率,裁剪影像至合适区域(图 2(b)),实验参数详见表 1。
|
|
表 1 Sentinel-1A实验参数 Tab. 1 The experimental parameters of Sentinel-1A |
根据前文可知,受SAR卫星飞行轨道影响,InSAR在各方向的敏感程度不同。提取表 1中卫星升降轨入射角和方位角,可由式(1)表示为:
| $ \left\{\begin{array}{l} D_{\mathrm{LOS}}^{\text {升 }}=-0.657\ 89 D_{E}- \\ \quad 0.154\ 83 D_{N}+0.737\ 03 D_{U} \\ D_{\mathrm{LOS}}^{\text {降 }}=0.674\ 72 D_{E}-0.159\ 92 D_{N}+ \\ \quad 0.720\ 53 D_{U} \end{array}\right. $ | (17) |
由式(17)可知,InSAR数据对垂直向形变最敏感,东西向次之,南北向不敏感。
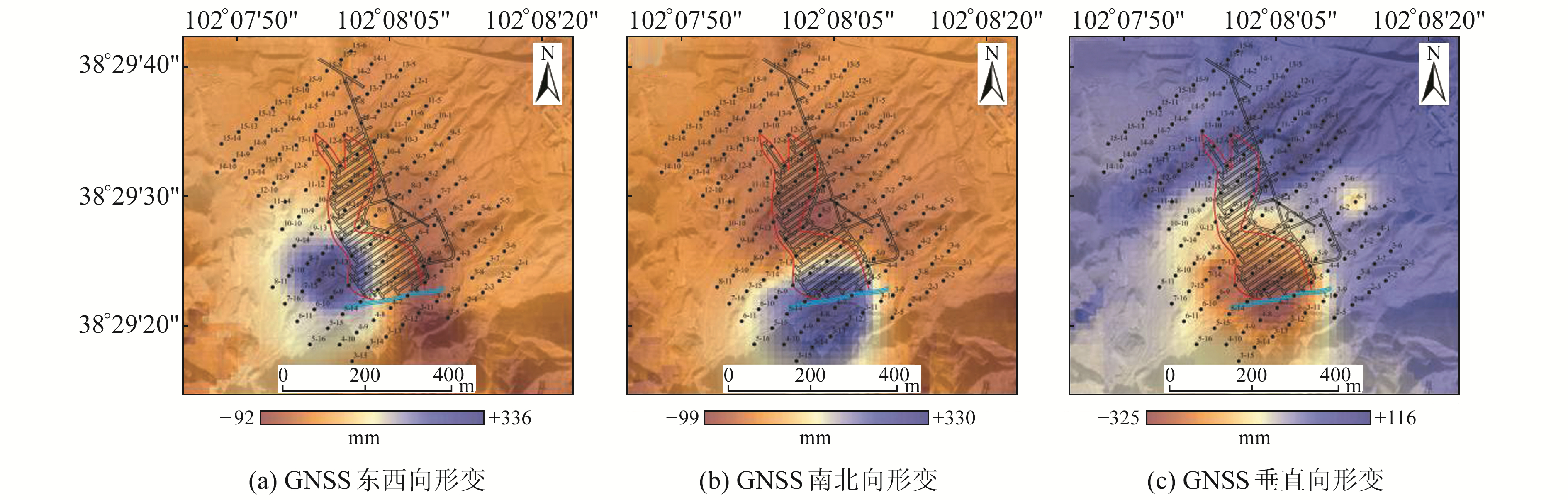
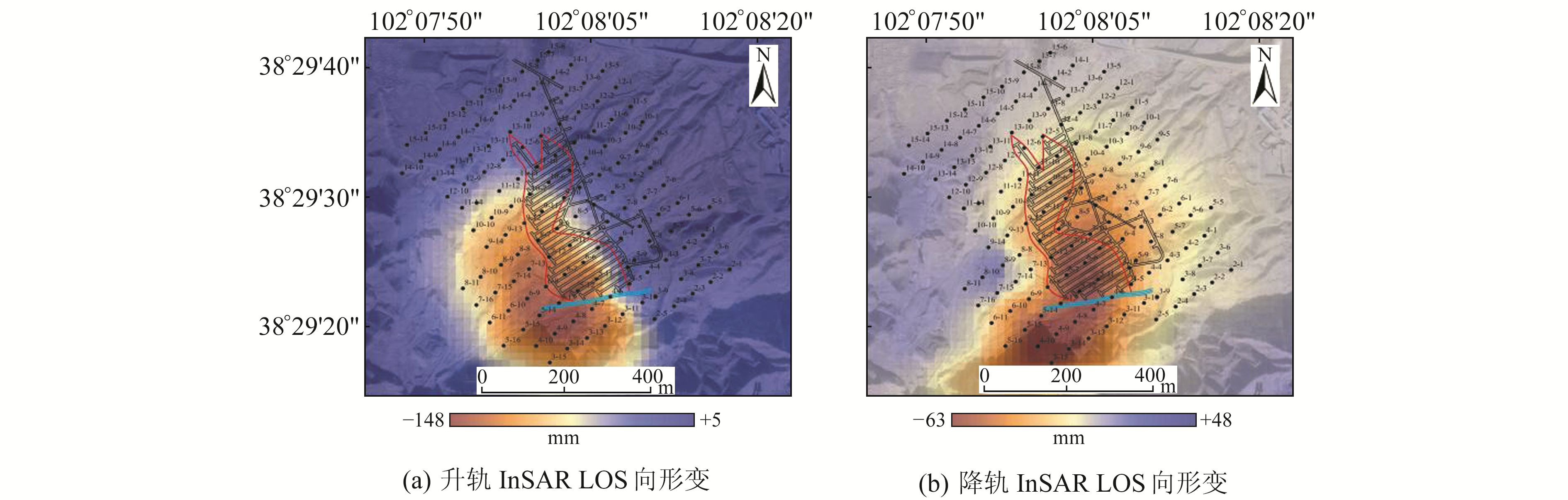
2.2 实验过程与分析针对GNSS监测数据,采用克里金(Kriging)插值法将点数据内插至与InSAR相同像元的面,得到GNSS三维形变场(图 3)。采用短基线集(SBAS)方法处理InSAR数据,并引入AUX_POEORB精密定轨星历和30 m分辨率的SRTM DEM数据去除地形相位,得到升降轨LOS向累积形变场(图 4,其中东、北和上为正方向)。
|
图 3 Kriging插值的GNSS三维形变场 Fig. 3 GNSS 3D deformation fields with Kriging interpolation |
|
图 4 升降轨InSAR LOS向形变场 Fig. 4 InSAR LOS direction deformation fields of ascending and descending |
利用GNSS三维形变与InSAR升降轨LOS向形变结果提取融合后的三维形变场,根据式(2)构建误差方程:
| $ \begin{array}{c} \left[\begin{array}{l} V_{1} \\ V_{2} \\ V_{3} \\ V_{4} \\ V_{5} \end{array}\right]=\left[\begin{array}{cccc} 1 & 0 & 0 & \\ 0 & 1 & 0 & \\ 0 & 0 & 1 & \\ -0.657\ 9 & -0.154\ 8 & 0.737\ 0 \\ \ \ \ 0.674\ 7 & -0.159\ 9 & 0.720\ 5 \end{array}\right] \cdot\\ \left[\begin{array}{c} D_{E} \\ D_{N} \\ D_{U} \end{array}\right]-\left[\begin{array}{c} D_{E}^{\mathrm{GNSS}} \\ D_{N}^{\mathrm{GNSS}} \\ D_{U}^{\mathrm{GNSS}} \\ D_{\mathrm{LOS}}^{\text {升 }} \\ D_{\mathrm{LOS}}^{\text {降 }} \end{array}\right] \end{array} $ | (18) |
根据式(3)~(11)解算融合GNSS与InSAR的三维形变场。解算过程中共有3 080个像素,满足HVCE计算的像素有2 472个。建立RBFNN神经网络,选取满足HVCE的像素作为训练集和验证集进行学习和训练,设置输入层为DEGNSS、DNGNSS、DUGNSS、DLOS升和DLOS降,输出层为DE、DN和DU,对剩余608个像素进行解算,从而获得完整的三维形变场。
为验证HVCE-RBFNN法的有效性,分别用3种方法进行解算:1)结合GNSS南北向形变与InSAR升降轨LOS向形变,解算东西向和垂直向形变场;2)结合GNSS三维形变与InSAR升降轨LOS向形变,采用等权估计法定权,利用最小二乘法解算融合后的东西向、南北向和垂直向形变场;3)采用HVCE-RBFNN法融合解算方法2中的5组形变数据的东西向、南北向和垂直向形变场。由方法1可以解算东西向和垂直向形变场,南北向形变场由GNSS插值代替,方法2和方法3可解算东西向、南北向和垂直向形变场。将139个监测点的观测量作为真值,分析3种方法三维形变的精度,结果如表 2所示。
|
|
表 2 不同方法的三维形变误差 Tab. 2 The 3D deformation errors of different methods |
由表 2可以看出,方法1南北向RMSE为0 mm,但东西向RMSE达到50.22 mm,垂直向RMSE达到75.63 mm,监测精度较低。对比方法1和方法2发现,方法2在综合考虑了GNSS三维形变和InSAR升降轨LOS向形变的情况下,东西向和垂直向的形变精度显著提升,南北向形变精度虽不及方法1,但顾及了InSAR监测在南北向的贡献,精度可达mm级。对比方法2和方法3发现,后者在三维方向的精度略优于前者,尽管二者的精度差别不大,但在一般情况下,方法2利用等权法决定权重难以将各组数据进行合理融合。综上,通过方法3迭代定权解算的三维形变结果精度优于方法1和方法2。
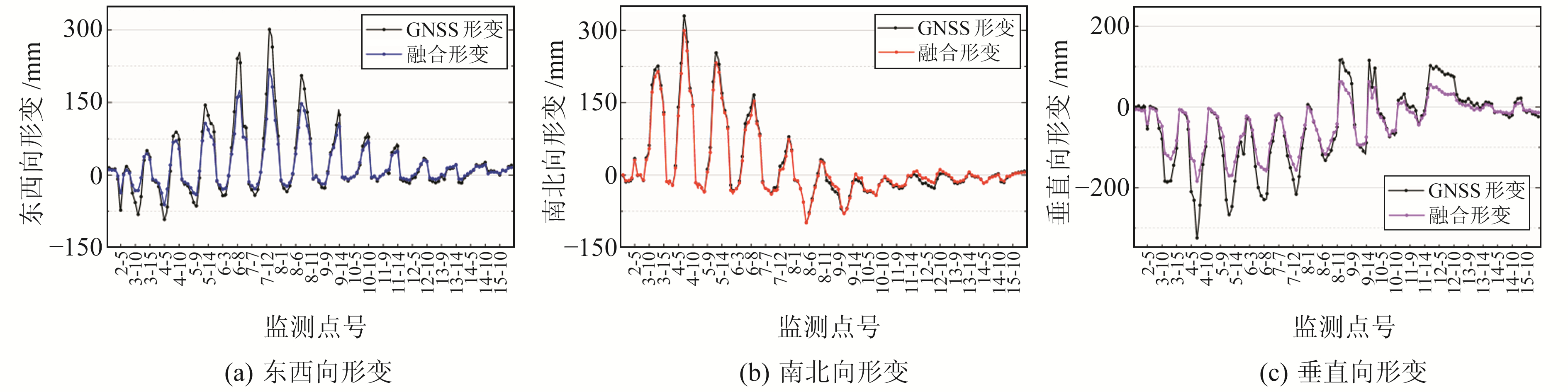
2.3 地表三维形变结果及分析图 5为139个监测点GNSS三维形变结果与方法3得到的结果的对比。不难发现,由于InSAR对垂直向形变最为敏感,对南北向形变最不敏感,因此图 5(c)中融合形变较GNSS形变有一定差异,但曲线走势基本一致;图 5(b)中2种形变曲线高度一致,验证了InSAR对南北向形变贡献小的问题;图 5(a)中曲线走势介于图 5(b)和图 5(c)之间。整体来看,利用HVCE-RBFNN法得到的三维形变结果与GNSS三维形变结果较为一致。
|
图 5 GNSS与HVCE-RBFNN法的三维形变结果对比 Fig. 5 Comparison of 3D deformation results between GNSS and HVCE-RBFNN method |
提取西二采矿区融合后的三维形变场,并与地下采空区位置进行叠加,以分析地下开采对地表的影响。由图 6(a)可知,采空区以西区域向东偏移,最大偏移量为228 mm;采空区以东区域向西偏移,最大偏移量为62 mm。由图 6(b)可知,采空区以南区域向北偏移,最大偏移量为300 mm;采空区以北区域向南偏移,最大偏移量为99 mm。由图 6(c)可知,矿区最大沉降量为193 mm,最大抬升量64 mm,沉降中心与采空区中心重叠,在地表形成沉降盆地。

|
图 6 基于HVCE-RBFNN法的三维形变场 Fig. 6 3D deformation fields based on HVCE-RBFNN method |
采空区地表东西向和南北向的形变量在采空区中心表现平稳,并由中心向两侧先增大后减小,垂直向形变量由采空区中心向四周逐渐减小。整体来看,研究区地表形变受地下开采和断层影响,但其三维形变结果与采空区基本一致,符合开采沉陷规律。
3 结语本文以金昌市金川西二采矿区为研究对象,分别采用GNSS和SBAS-InSAR方法对矿区地表进行监测,得到GNSS在三维方向和升降轨InSAR在LOS向的形变数据;然后根据GNSS和InSAR的优势互补性提出HVCE-RBFNN方法解算矿区地表三维形变,并通过3种不同的融合方法验证其有效性。计算表明,本文方法解算的三维形变结果在东西向、南北向和垂直向的RMSE分别为20.85 mm、7.41 mm和34.47 mm,优于其他2种方法。同时,利用本文方法获取的三维形变场与采空区基本一致,符合开采沉陷的基本规律。由此可知,本文提出的方法可用于矿区地表的三维形变监测。
| [1] |
朱建军, 李志伟, 胡俊. InSAR变形监测方法与研究进展[J]. 测绘学报, 2017, 46(10): 1 717-1 733 (Zhu Jianjun, Li Zhiwei, Hu Jun. Research Progress and Methods of InSAR for Deformation Monitoring[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 717-1 733)
(  0) 0) |
| [2] |
汪云甲. 矿区生态扰动监测研究进展与展望[J]. 测绘学报, 2017, 46(10): 1 705-1 716 (Wang Yunjia. Research Progress and Prospect on Ecological Disturbance Monitoring in Mining Area[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 705-1 716)
(  0) 0) |
| [3] |
Mazzotti S, Dragert H, Hyndman R D, et al. GPS Deformation in a Region of High Crustal Seismicity: N. Cascadia Forearc[J]. Earth and Planetary Science Letters, 2022, 198(1-2): 41-48
(  0) 0) |
| [4] |
刘志敏, 李永生, 张景发, 等. 基于SBAS-InSAR的长治矿区地表形变监测[J]. 国土资源遥感, 2014, 26(3): 37-42 (Liu Zhimin, Li Yongsheng, Zhang Jingfa, et al. An Analysis of Surface Deformation in the Changzhi Mining Area Using Small Baseline InSAR[J]. Remote Sensing for Land and Resources, 2014, 26(3): 37-42)
(  0) 0) |
| [5] |
Zheng M N, Zhang H Z, Deng K Z, et al. Analysis of Pre- and Post-Mine Closure Surface Deformations in Western Xuzhou Coalfield from 2006 to 2018[J]. IEEE Access, 2019, 7: 124
(  0) 0) |
| [6] |
敖萌, 张路, 廖明生, 等. 基于方差分量估计的多源InSAR数据自适应融合形变测量[J]. 地球物理学报, 2020, 63(8): 2 901-2 911 (Ao Meng, Zhang Lu, Liao Mingsheng, et al. Deformation Monitoring with Adaptive Integration of Multi-Source InSAR Data Based on Variance Component Estimation[J]. Chinese Journal of Geophysics, 2020, 63(8): 2 901-2 911)
(  0) 0) |
| [7] |
单新建, 屈春燕, 郭利民, 等. 基于InSAR与GPS观测的汶川同震垂直形变场的获取[J]. 地震地质, 2014, 36(3): 718-730 (Shan Xinjian, Qu Chunyan, Guo Limin, et al. The Vertical Coseismic Deformation Field of the Wenchuan Earthquake Based on the Combination of GPS and InSAR Measurements[J]. Seismology and Geology, 2014, 36(3): 718-730 DOI:10.3969/j.issn.0253-4967.2014.03.014)
(  0) 0) |
| [8] |
Simonetto E, Durand S, Burdack J, et al. Combination of InSAR and GNSS Measurements for Ground Displacement Monitoring[J]. Procedia Technology, 2014, 16: 192-198 DOI:10.1016/j.protcy.2014.10.083
(  0) 0) |
| [9] |
Aghajany S H, Voosoghi B, Yazdian A. Estimation of North Tabriz Fault Parameters Using Neural Networks and 3D Tropospherically Corrected Surface Displacement Field[J]. Geomatics, Natural Hazards and Risk, 2017, 8(2): 918-932 DOI:10.1080/19475705.2017.1289248
(  0) 0) |
| [10] |
王霞迎, 张菊清, 张勤, 等. 升降轨InSAR与GPS数据集成反演西安形变场[J]. 测绘学报, 2016, 45(7): 810-817 (Wang Xiaying, Zhang Juqing, Zhang Qin, et al. Inferring Multi-Dimensional Deformation Filed in Xi'an by Combining InSAR of Ascending and Descending Orbits with GPS Data[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 810-817)
(  0) 0) |
| [11] |
曹海坤. GPS、InSAR数据联合解算地表三维形变场[D]. 西安: 长安大学, 2017 (Cao Haikun. GPS, InSAR Data Combined Methods for Three-Dimensional Surface Deformation Field[D]. Xi'an: Chang'an University, 2017)
(  0) 0) |
| [12] |
周文韬. 融合GNSS与InSAR的矿区地表三维形变监测[D]. 绵阳: 西南科技大学, 2021 (Zhou Wentao. Three-Dimensional Deformation Monitoring of Mining Area with GNSS and InSAR[D]. Mianyang: Southwest University of Science and Technology, 2021)
(  0) 0) |
| [13] |
Hu J, Li Z W, Sun Q, et al. Three-Dimensional Surface Displacements from InSAR and GPS Measurements with Variance Component Estimation[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4): 754-758 DOI:10.1109/LGRS.2011.2181154
(  0) 0) |
| [14] |
曾祥萍. 自适应组合RBF滤波器理论及其应用研究[D]. 成都: 西南交通大学, 2013 (Zeng Xiangping. Theoretical and Practical Research on Adaptive Combination RBF Filter[D]. Chengdu: Southwest Jiaotong University, 2013)
(  0) 0) |
| [15] |
周文韬, 张文君, 杨元继, 等. 矿区地表沉降监测的一种组合模型预测方法[J]. 大地测量与地球动力学, 2021, 41(3): 308-312 (Zhou Wentao, Zhang Wenjun, Yang Yuanji, et al. A Combined Model Prediction Method for Surface Subsidence Monitoring in Mining Areas[J]. Journal of Geodesy and Geodynamics, 2021, 41(3): 308-312)
(  0) 0) |
2. Mianyang Science and Technology City Division, National Remote Sensing Center of China, 59 Mid-Qinglong Road, Mianyang 621010, China;
3. Sichuan Space Remote Sensing and Smart Mapping Technology Co Ltd, 389 Fujin Road, Mianyang 621010, China
 2022, Vol. 42
2022, Vol. 42


