大气可降水量(PWV)是描述大气水汽含量的重要指标,对于GNSS气象学研究、天气预报、灾害预防等具有重要意义。高精度的天顶对流层延迟(ZTD)和大气加权平均温度(Tm)是使用常规GNSS方法得到高精度PWV值的2个重要前提,而模型改正是目前估计ZTD和Tm的主要方法之一。2007年Böehm等[1]提出全球气压与温度模型GPT;2013年Lagler等[2]提出GPT2模型;2015年Böehm等[3]提出GPT2w模型;2018年Landskron等[4]在GPT2w模型的基础上改良离散映射函数系数,提出GPT3模型。在模型精度验证方面,黄良珂等[5]利用IGS站3 a的实测对流层延迟数据分析EGNOS模型估计的ZTD在亚洲地区的精度;施宏凯等[6]利用我国29个探空站的数据,采用箱形图方法检验经GPT2w-1和GPT2w-5模型(GPT2w-1和GPT2w-5分别为分辨率为1°和5°时的GPT2w模型)导出的气压、气温结果在中国区域的精度,得出2个模型精度相当,且在出现异常值时GPT2w-1模型较GPT2w-5模型鲁棒性更好;孟昊霆等[7]研究了GPT2和GPT2w模型估计的ZTD在亚洲区域的精度。基于上述研究,本文使用亚洲地区18个IGS测站和中国区域16个探空站的数据研究GPT3模型反演ZTD和PWV的精度。
1 研究方法与数据来源 1.1 GPT3模型与对流层估计GPT3模型在GPT2w模型的基础上对离散映射函数中的经验系数b、c进行改进,减小了离散映射函数在特定低仰角时存在的误差[4]。GPT3模型仅根据测站的地理位置、时间等信息就可输出测站的大气压强、气温、水汽压等气象参数,其推导公式如下:
| $ \begin{gathered} r(t)=A_{0}+A_{1} \sin \left(\frac{\text { doy }}{365.25} 2 \pi\right)+ \\ B_{1} \cos \left(\frac{\text { doy }}{365.25} 2 \pi\right)+A_{2} \sin \left(\frac{\text { doy }}{365.25} 4 \pi\right)+ \\ B_{2} \cos \left(\frac{\operatorname{doy}}{365.25} 4 \pi\right) \end{gathered} $ | (1) |
式中,r(t)为所求气象参数,A0为最小二乘法估计的平均值,A1、B1和A2、B2分别为年周期和半年周期参数,doy为年积日。采用Saastamoinen模型[8]计算对流层天顶静力学延迟ZHD(zenith hydro-static delay),采用Askne等[9]建立的模型计算对流层天顶湿延迟ZWD(zenith wet delay):
| $ \begin{gathered} \mathrm{ZHD}= \\ \frac{0.0022768 P}{1-0.00266 \cos (2 \varphi)-0.00028 H} \end{gathered} $ | (2) |
| $ \mathrm{ZWD}=10^{-6}\left(k_{2}^{\prime}+k_{3} / T_{m}\right) \frac{R_{d}}{(\lambda+1) g_{m}} e_{s} $ | (3) |
式中,P、φ、H分别为测站处的气压、测站所在纬度以及测站大地高,k′2、k3为大气折射率常数,Rd为干大气普适气体常量,λ为水汽压递减率,Tm为大气加权平均温度,gm为大气质量中心的重力加速度,es为测站处的水汽压。
1.2 PWV反演利用GPT3模型计算得到的ZWD和Tm即可反演求得PWV:
| $ \mathrm{PWV}=\varPi \cdot \mathrm{ZWD} $ | (4) |
| $ \varPi=\frac{10^{6}}{\rho_{\mathrm{w}} R_{v}\left(k_{2}^{\prime}+k_{3} / T_{m}\right)} $ | (5) |
式中,Π为PWV转换系数,Rv为水汽气体常数,ρw为液态水密度,k′2、k3为大气折射率常数。
1.3 研究区域与参考数据选择亚洲区域18个IGS站2016~2018年的数据进行实验,将欧洲定轨中心(Centre for Orbit Determination in Europe,CODE)发布的ZTD产品日均值作为真值对GPT3、GPT2w和GPT2模型计算所得ZTD进行精度评估。选择中国区域16个探空站作为实验站点,以美国怀俄明州立大学官网提供的无线探空资料作为参考值,对探空站基于GPT2w和GPT3模型反演的PWV进行精度验证,选取的IGS站和探空站分布如图 1所示。
|
图 1 IGS站和探空站分布 Fig. 1 Distribution of IGS stations and radiosonde stations |
以亚洲区域18个IGS站的经纬度、高程等信息分别代入GPT2模型、GPT2w模型(1°分辨率和5°分辨率)和GPT3模型(1°分辨率和5°分辨率)的推导公式得到相应的气象参数,再结合式(2)、(3)计算ZTD(GPT2模型的ZHD和ZWD值由Saastamoinen模型计算得到)。以CODE发布的ZTD产品的日均值为参考值,使用bias和RMSE评价各GPT模型反演ZTD的精度,结果如表 1所示。
|
|
表 1 2016~2018年18个IGS站GPT2、GPT2w和GPT3模型反演ZTD的精度 Tab. 1 ZTD accuracy of 18 IGS stations inversed by GPT2, GPT2w and GPT3 models from 2016 to 2018 |
由表 1可见,GPT2w和GPT3模型在相同分辨率下的bias和RMSE非常接近。在模型准确度方面,GPT3-1模型的bias最大值和平均值最小,分别为14.06 mm和1.34 mm,说明GPT3-1模型的偏差最小;在模型精度方面,GPT3-5模型的RMSE最大值最小,为87.71 mm,GPT2w-1和GPT3-1模型的RMSE平均值最小,为43.03 mm。总体来看,GPT3模型的精度高于GPT2模型。
3 PWV精度分析 3.1 GPT3模型反演PWV的总体精度由于相同分辨率的GPT2w和GPT3模型计算得到的PWV结果非常接近,故本节仅分析不同分辨率的GPT3模型反演PWV的精度。因篇幅有限,仅选取中国大陆地区东西南北4个方向各1个测站(45004、50557、51709和58362)进行分析,模型反演的PWV与参考值对比情况如图 2所示。

|
图 2 4个探空站模型反演的PWV与参考值对比 Fig. 2 Comparison of inversed PWV of four radiosonde stations and reference values |
由图 2可见,GPT3模型反演得到的4个测站PWV变化趋势基本与探空参考数据的变化趋势一致,且表现出以年为周期的季节性特征,冬季(12月、1月、2月)的PWV值最低,夏季(6~8月)的PWV值最高。45004站的曲线变化相对于其他测站更加平缓,说明其受时间变化的影响较小,季节性特征相对较弱。4个测站中,只有位于较高海拔的51709站2种不同分辨率的GPT3模型的反演值相差较大,最大差值达到6.81 mm。
3.2 GPT3模型反演PWV精度的时空特征研究表明,GPT系列模型计算的气象数据和ZTD的精度不仅具有很强的季节性特征,还与测站的地理位置有紧密的联系[6-7]。由于PWV精度会受到ZWD和Tm精度的直接影响,所以探索分析PWV精度的时空特征具有重要意义。
3.2.1 GPT3模型反演PWV精度的季节性特征以上述4个站点为例,计算其2017年的PWV月均值(图 3)。由图 3可见,除45004站外,其他测站的PWV月均值的bias和RMSE均表现出较为明显的季节性特征,且bias绝对值在冬季最小、夏季最大。45004站表现出的PWV精度与季节低相关性的原因可能是低纬度地区气压随季节变化较小[7]。但无论是bias值还是RMSE值,GPT3-1模型的精度和稳定性都优于GPT3-5模型,尤其是在51709探空站。
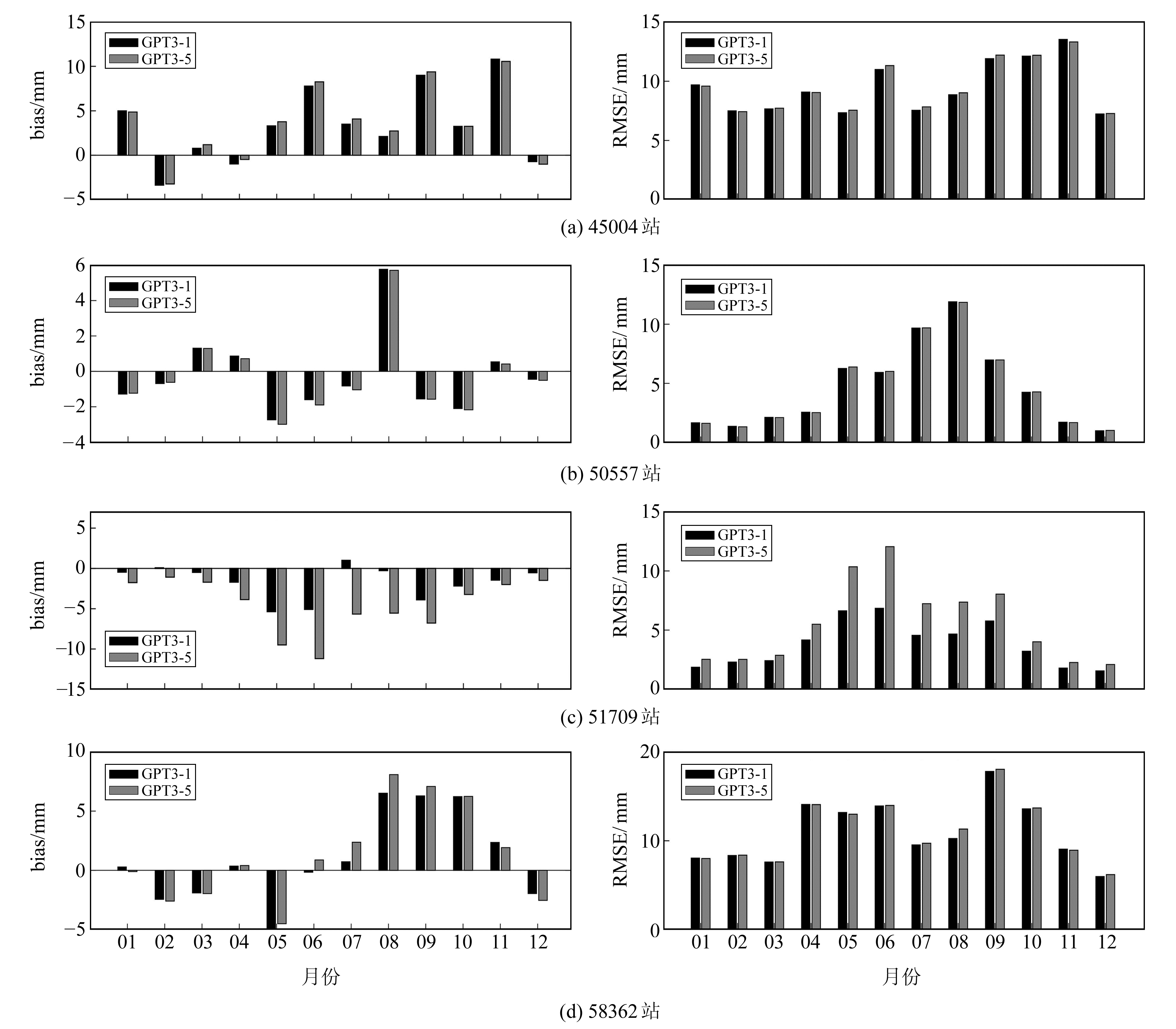
|
图 3 2017年4个探空站PWV的bias和RMSE月均值 Fig. 3 Monthly mean bias and RMSE values of PWV at four radiosonde stations in 2017 |
为分析GPT3模型计算的PWV精度与高程间的相关性,给出GPT3模型PWV的bias和RMSE随高程的变化关系(图 4)。由图可见,当测站高程大于1 500 m时,其PWV的bias绝对值稳定在2 mm以内,RMSE值稳定在6 mm以内。除个别测站外,PWV的bias绝对值大于2 mm或RMSE值大于6 mm的测站几乎都分布在500 m以下。若不考虑纬度对反演结果的影响,则GPT3模型PWV的bias绝对值和RMSE值均随高程的增加而减小,说明高程与PWV精度之间具有较强的相关性。

|
图 4 GPT3模型反演PWV随高程的变化关系 Fig. 4 Relationship between elevation and PWV derived by GPT3 model |
选择测站中高程相当的9个探空测站(纬度从低到高分别为59981、45004、58968、58606、57494、58362、54511、54135、50557)分析GPT3模型反演所得的PWV精度与纬度之间的相关性(图 5)。由图可见,低纬度地区测站PWV的bias和RMSE值无明显的变化规律,但高纬度地区测站PWV的bias绝对值和RMSE值会随着纬度的升高而逐渐减小。综合而言,PWV精度与纬度相关性较弱。除个别测站外,无论是低纬度地区还是高纬度地区,GPT3-1模型反演的PWV的bias绝对值均比GPT3-5模型小,但RMSE值相当。说明同一纬度地区,GPT3-1模型比GPT3-5模型能更有效地改善PWV偏差。
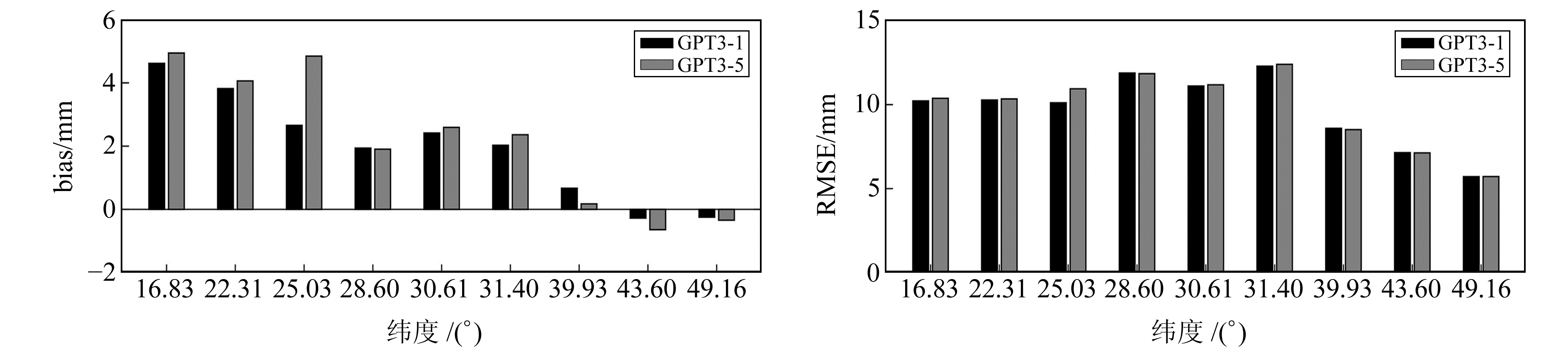
|
图 5 GPT3模型反演PWV随纬度的变化关系 Fig. 5 Relationship between latitude and PWV derived by GPT3 model |
1) 在ZTD精度方面,5个GPT模型中,GPT3-1模型的bias平均值最小,为1.34 mm,说明GPT3-1模型的偏差最小;GPT3-5模型的RMSE最大值最小,为87.71 mm,而GPT2w-1和GPT3-1模型的RMSE平均值最小,为43.03 mm。总体来看,相比于GPT2和GPT2w模型,GPT3模型表现出更高的精确度和稳定性。
2) 在GPT3模型反演PWV方面,测站的PWV曲线与探空站参考值的变化趋势基本一致,且表现出以年为周期的季节性特征,冬季的值最低、夏季的值最高。PWV的精度表现出明显的季节性特征,冬季最高、夏季最低,随着测站高程的升高而增加,与纬度的相关性不高。
| [1] |
Böehm J, Heinkelmann R, Schuh H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679-683 DOI:10.1007/s00190-007-0135-3
(  0) 0) |
| [2] |
Lagler K, Schindelegger M, Böehm J, et al. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1 069-1 073 DOI:10.1002/grl.50288
(  0) 0) |
| [3] |
Böehm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere(GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [4] |
Landskron D, Böehm J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions[J]. Journal of Geodesy, 2018, 92(4): 349-360 DOI:10.1007/s00190-017-1066-2
(  0) 0) |
| [5] |
黄良珂, 刘立龙, 周淼, 等. 亚洲地区EGNOS天顶对流层延迟模型的精度评估[J]. 大地测量与地球动力学, 2013, 33(4): 128-132 (Huang Liangke, Liu Lilong, Zhou Miao, et al. Precision Assessment of Zenith Tropospheric Delay Calculated from EGNOS Model over Asian Area[J]. Journal of Geodesy and Geodynamics, 2013, 33(4): 128-132)
(  0) 0) |
| [6] |
施宏凯, 何秀凤, 王俊杰. 全球气压气温模型在中国地区的精度分析[J]. 大地测量与地球动力学, 2017, 37(8): 841-844 (Shi Hongkai, He Xiufeng, Wang Junjie. Accuracy Analyses of Global Pressure and Temperature Model in China[J]. Journal of Geodesy and Geodynamics, 2017, 37(8): 841-844)
(  0) 0) |
| [7] |
孟昊霆, 张克非, 杨震, 等. GPT2/GPT2w+Saastamoinen模型ZTD估计的亚洲地区精度分析[J]. 测绘科学, 2020, 45(8): 70-76 (Meng Haoting, Zhang Kefei, Yang Zhen, et al. The Determination of GNSS Zenith Tropospheric Delay by GPT2/GPT2w + Saastamoinen Model and Its Performance Analysis in Asia[J]. Science of Surveying and Mapping, 2020, 45(8): 70-76)
(  0) 0) |
| [8] |
李国平. 地基GPS遥感大气可降水量及其在气象中的应用研究[D]. 成都: 西南交通大学, 2007 (Li Guoping. On the Remote Sensing of Precipitable Water Vapor Using Ground-Based GPS Technique and Applications in Meteorology[D]. Chengdu: Southwest Jiaotong University, 2007)
(  0) 0) |
| [9] |
Askne J, Nordius H. Estimation of Tropospheric Delay for Microwaves from Surface Weather Data[J]. Radio Science, 2016, 22(3): 379-386
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

