2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006
大气水汽是对流层的重要组成之一,其变化与降水直接相关。大气可降水量PWV是单位面积空气柱里含有的水汽总数量,通常用来反映对流层中大气水汽的分布和变化。传统的大气水汽探测方法主要包括无线电探空站、微波辐射计、雷达观测和卫星遥感等,但由于费用昂贵,且时空分辨率低,这些方法离监测和预报中小尺度灾害性天气的要求还有很大差距。地基GNSS能较好地弥补传统大气水汽探测在时空分辨率上的不足,并提供精细化气象预报所需要的高精度、近实时的大气水汽资料,已逐渐成为获取大气水汽的主要方法[1-6]。然而,使用地基GNSS反演大气水汽时需要获取地面气压和气温等气象数据,但大部分GNSS观测站未配备气象传感器。因此,本文探讨利用GPT系列模型的最新模型GPT3[7]提供的气象参数来反演PWV,并选用探空站资料验证该模型的有效性。
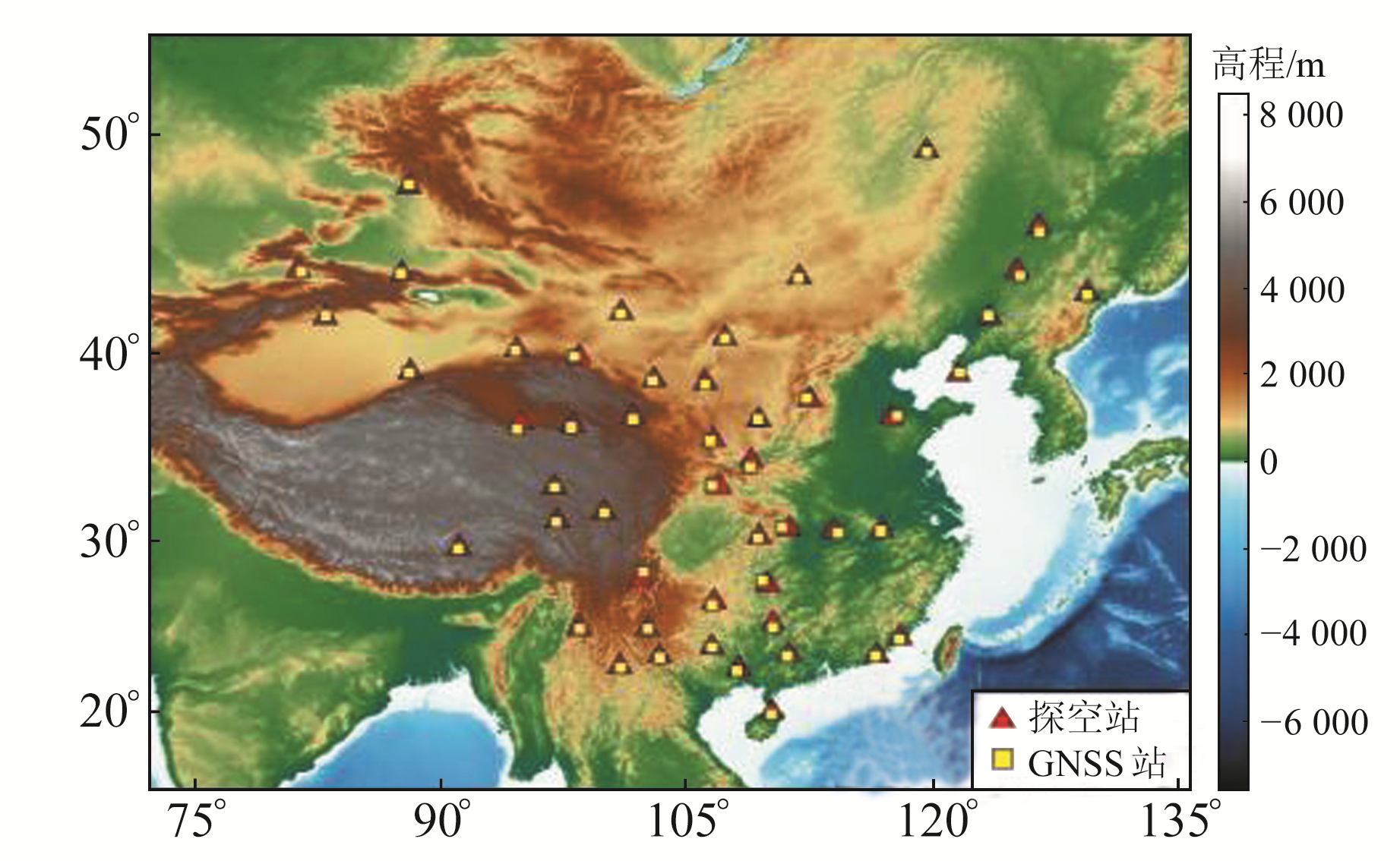
1 数据来源及计算方法 1.1 数据来源探空站资料可提供每天00:00和12:00的实测地表及分层气象数据,数据可从美国怀俄明州立大学网站(http://weather.uwyo.edu/upperair/sounding.html)下载。中国大陆构造环境监测网络(CMONOC)提供的GNSS观测数据可通过中国地震局GNSS数据产品服务平台(http://www.cgps.ac.cn)获取。本文选用2017~2018年49个GNSS站和与其并址的探空站数据进行实验,站点位置见图 1。
|
图 1 GNSS站与探空站分布 Fig. 1 Distribution of GNSS stations and radiosonde stations |
GPT3模型的表达式为:
| $ \begin{gathered} r(t)= \\ A_{0}+A_{1} \cos \left(\frac{\text { doy }}{365.25} 2 \pi\right)+B_{1} \sin \left(\frac{\text { doy }}{365.25} 2 \pi\right)+ \\ A_{2} \cos \left(\frac{\text { doy }}{365.25} 4 \pi\right)+B_{2} \sin \left(\frac{\text { doy }}{365.25} 4 \pi\right) \end{gathered} $ | (1) |
式中,r(t)为模型估计的大地水准面处的气象参数函数;doy为年积日;A0为年平均振幅;A1、B1和A2、B2分别为年周期和半年周期参数。GPT3模型仅需输入测站位置和年积日即可输出气压、气温、Tm等气象参数。本文利用GPT3模型计算出49个探空站和49个GNSS站处的气压、气温和Tm。因探空站采用海拔高,GNSS站采用大地高,故使用EGM2008模型统一高程[8]。
首先利用GNSS观测数据解算对流层天顶总延迟量(ZTD),再根据Saastamoinen模型[9]计算天顶静力延迟量(ZHD),将其从天顶总延迟中减去,从而得到天顶湿延迟(ZWD)。最后利用ZWD与PWV转换系数K计算得到PWV:
| $ \mathrm{PWV}=K \cdot \mathrm{ZWD} $ | (2) |
| $ K=\frac{10^{6}}{\rho_{\mathrm{w}} R_{v}\left[\left(k_{3} / T_{m}+k_{2}^{\prime}\right)\right]} $ | (3) |
式中,ρw=1×103 kg/m3为液态水的密度;Rv=461.495 J/(kg ·K)为水汽气体常数;k′2、k3为大气物理参数,经验值通常为22.13±2.20 K/hPa、(3.739±0.012)×105 K/hPa。采用Bevis经验公式Tm=70.2+0.72Ts计算Tm,其中,Ts为地表温度。
2 精度评估采用偏差(bias)与均方根误差(RMSE)为评估指标,以12 h时间分辨率的探空站资料中的气压、气温和Tm数据为参考值,评估GPT3模型的气压、气温和Tm的精度:
| $ \operatorname{bias}=\frac{1}{N} \sum\limits_{i=1}^{N}\left(X_{m}^{M_{i}}-X_{m}^{R_{i}}\right) $ | (4) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left(X_{m}^{M_{i}}-X_{m}^{R_{i}}\right)^{2}} $ | (5) |
式中,XmMi为模型计算值,XmRi为参考值,N为样本数。
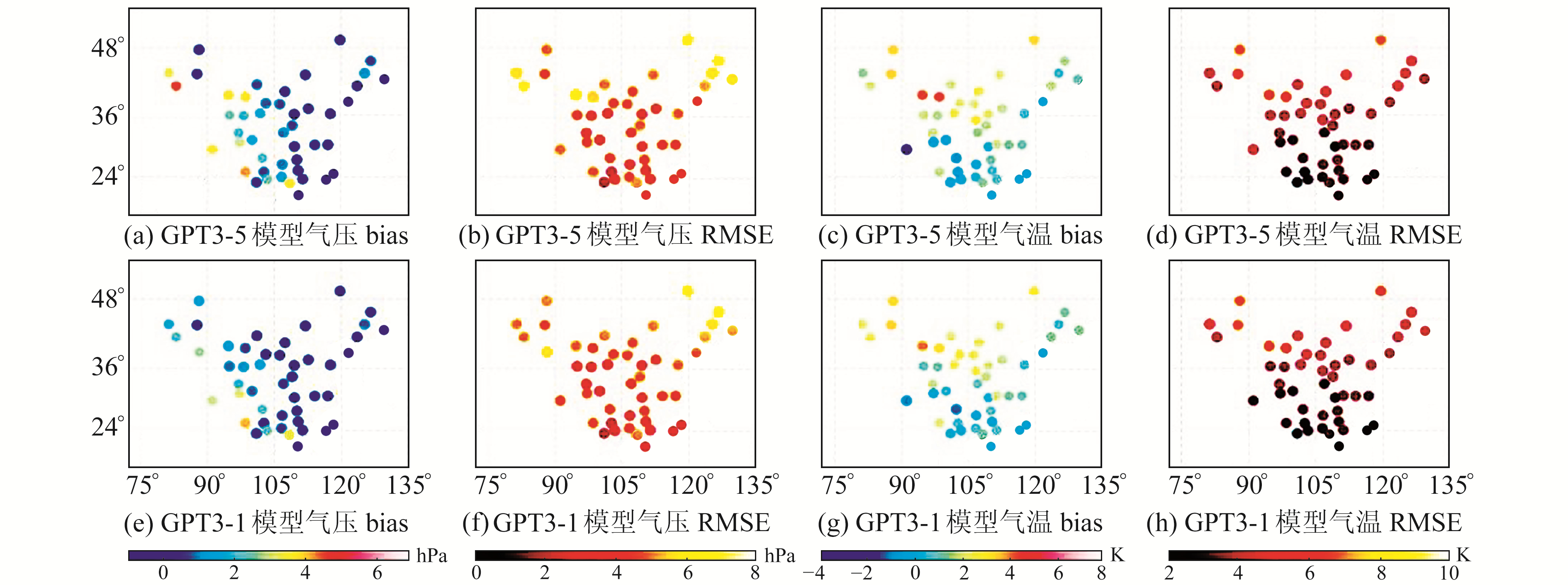
2.1 GPT3模型计算气温、气压的精度评估用GPT3-1和GPT3-5分别表示1°和5°分辨率的GPT3模型,每个站上气压和气温的bias和RMSE见图 2,bias和RMSE统计结果见表 1、2。
|
图 2 利用探空站检验GPT3模型气压和气温的bias和RMSE分布 Fig. 2 Distribution of bias and RMSE values of air pressure and temperature obtained from GPT3 tested by radiosonde stations |
|
|
表 1 气压精度统计 Tab. 1 Accuracy statistics of air pressure |
|
|
表 2 气温精度统计 Tab. 2 Accuracy statistics of temperature |
由图 2可知,GPT3-1和GPT3-5模型气压在中国西部出现较大bias的情况比其他地区多,并且在中国东北地区和西北地区均表现出较大的年均RMSE;GPT3-1和GPT3-5模型气温在中国西部地区不仅表现出较大bias,而且也表现出较大的年均RMSE,其原因可能是西部地区地形起伏较大。
由表 1可知,GPT3-1模型的气压bias均值为0.73 hPa,最大值与最小值之差为4.72 hPa,气压RMSE均值为4.21 hPa,最大值与最小值之差为4.1 hPa;而GPT3-5模型的气压bias和RMSE均值比GPT3-1模型分别高0.35 hPa和0.14 hPa,说明GPT3-1模型的气压精度比GPT3-5模型更优。
由表 2可知,GPT3-1模型的气温bias均值为1.34 K,最大值与最小值之差为5.32 K,气温RMSE均值为3.75 K,最大值与最小值之差为4.41 K;GPT3-5模型的气温bias和RMSE均值与GPT3-1模型接近。
表 1、2说明,GPT3-1模型的气温和气压精度优于GPT3-5模型。
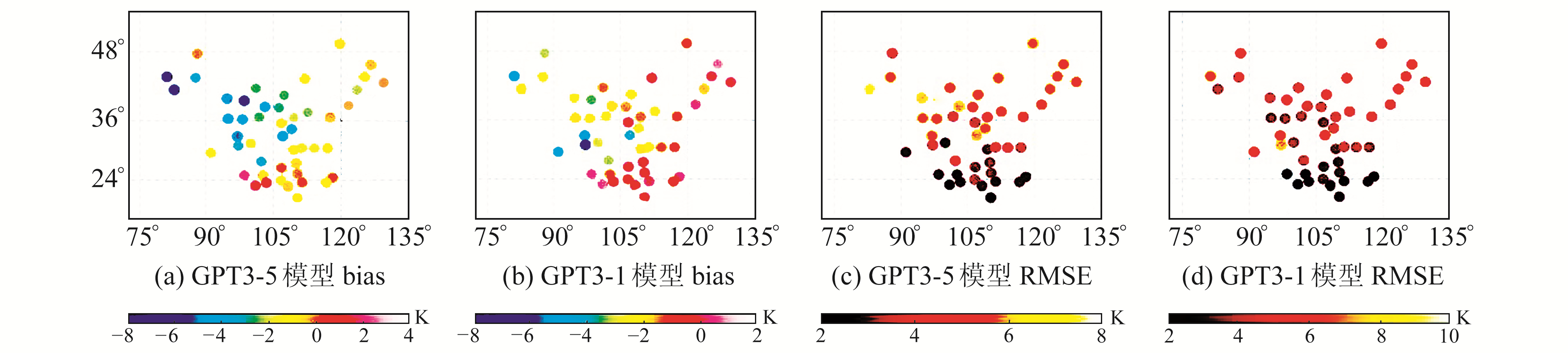
2.2 GPT3模型计算Tm的精度评估同样采用中国地区2017~2018年49个与GNSS站并址的探空站提供的Tm作为参考值来评价GPT3模型Tm的精度,并统计GPT3模型Tm的bias和RMSE,结果见图 3和表 3。
|
图 3 利用探空站检验GPT3模型Tm的bias和RMSE分布 Fig. 3 Distribution of bias and RMSE values of Tm obtained from GPT3 model tested by radiosonde stations |
|
|
表 3 Tm精度统计 Tab. 3 Accuracy statistics of Tm |
由图 3可以看出,GPT3-1和GPT3-5模型高bias主要出现在中国西部地区,其他地区bias较小。2种模型在中国北部及西南地区的RMSE高于南部低纬度地区,其主要原因是西部地区地形起伏大、北部地区存在显著的Tm日均周期,而在南部低纬度地区和东南部地区,Tm的变化振幅低于中纬度地区,有利于对Tm进行精确模型化[10-11]。
由图 3和表 3可知,GPT3模型在中国区域表现出显著的负偏差,且主要集中于西部地区。说明GPT3模型估算的Tm值在多数西部地区测站上要低于探空站计算的Tm值。这是由于GPT3模型在计算Tm时没有考虑高程改正[3],导致在地形起伏相对较大的西部地区产生显著的负偏差。GPT3-5和GPT3-1模型的bias均值分别为-1.91 K和-1.67 K,最大值分别为1.99 K和0.70 K,说明GPT3-1模型比GPT3-5模型更稳定;GPT3-5和GPT3-1模型的RMSE均值分别为4.39 K和4.15 K,也表明GPT3-1模型的性能要优于GPT3-5模型。
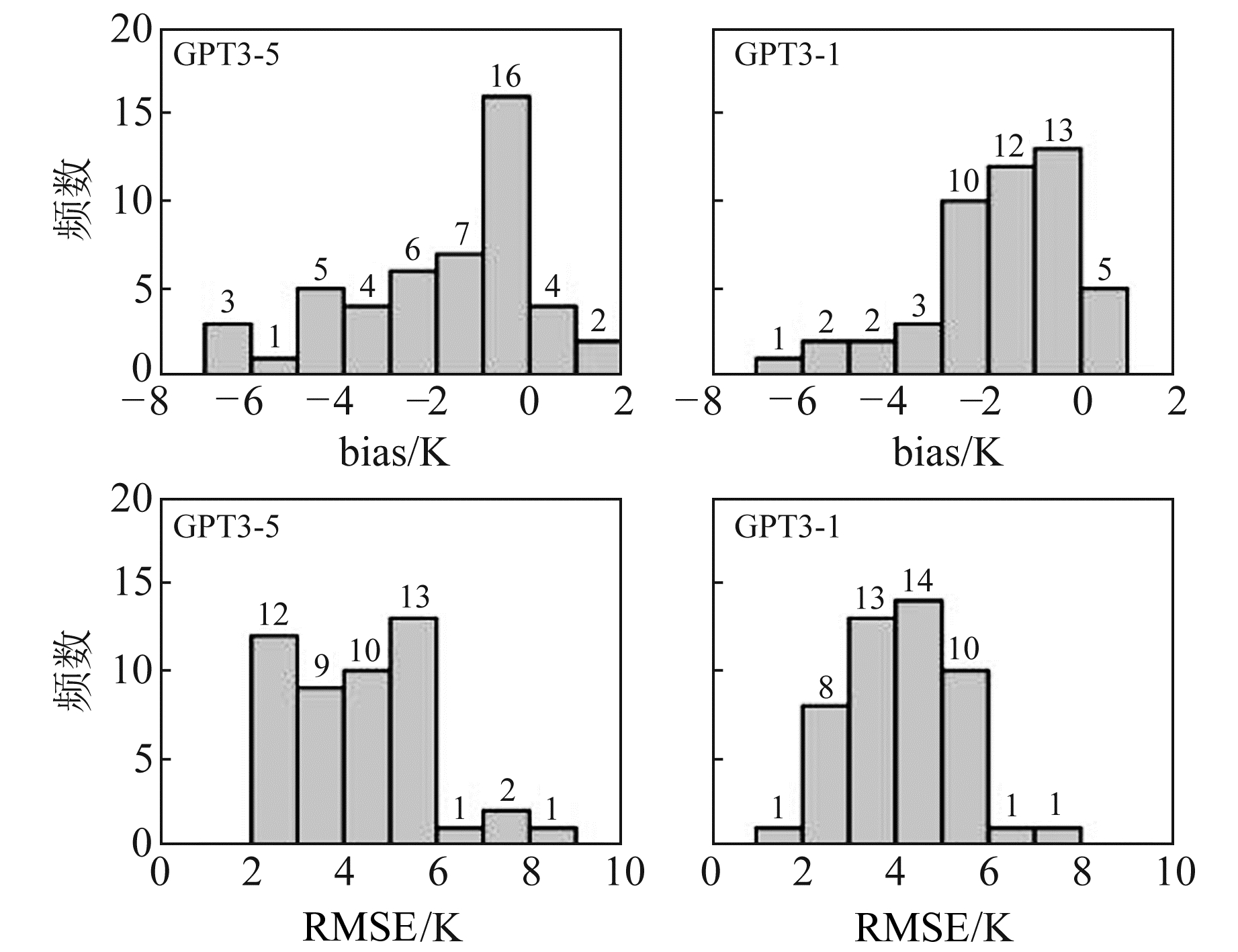
为了进一步分析2种模型Tm的精度,对49个站的bias和RMSE进行统计,结果见图 4。
|
图 4 Tm的bias和RMSE分布直方图 Fig. 4 Histogram of bias and RMSE of Tm |
由图 4可知,GPT3模型的2种分辨率均呈现出明显的负bias,其中GPT3-5模型的bias变化更为显著,说明GPT3-1模型比GPT3-5模型更稳定。同时,GPT3-1模型的RMSE分布要比GPT3-5模型集中,表明GPT3-1模型的性能要比GPT3-5模型好。
2.3 基于GPT3模型的GNSS反演PWV的精度分析由上述分析可知,GPT3-1模型的精度和性能优于GPT3-5模型,因此下文选用GPT3-1模型来反演PWV并进行精度分析。
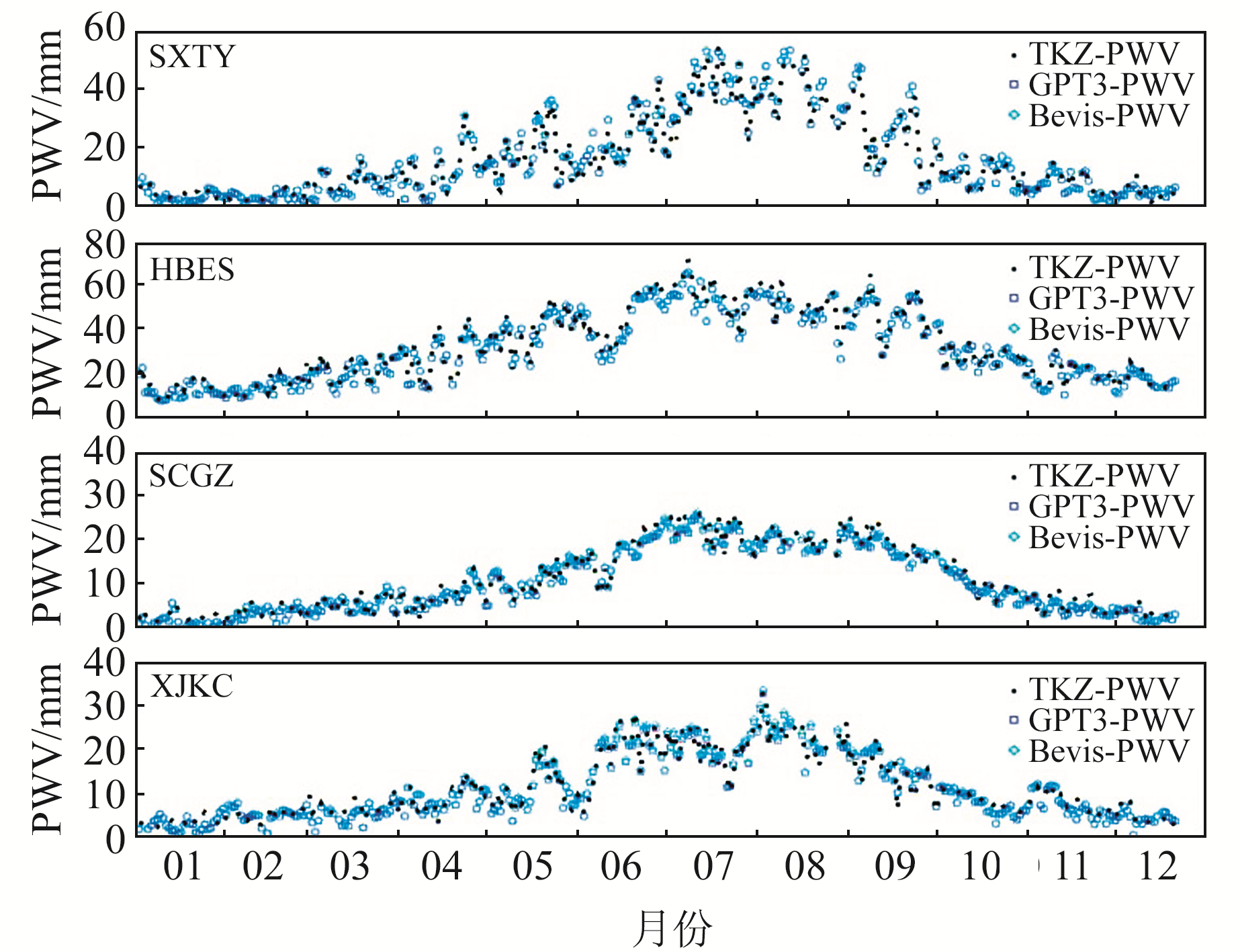
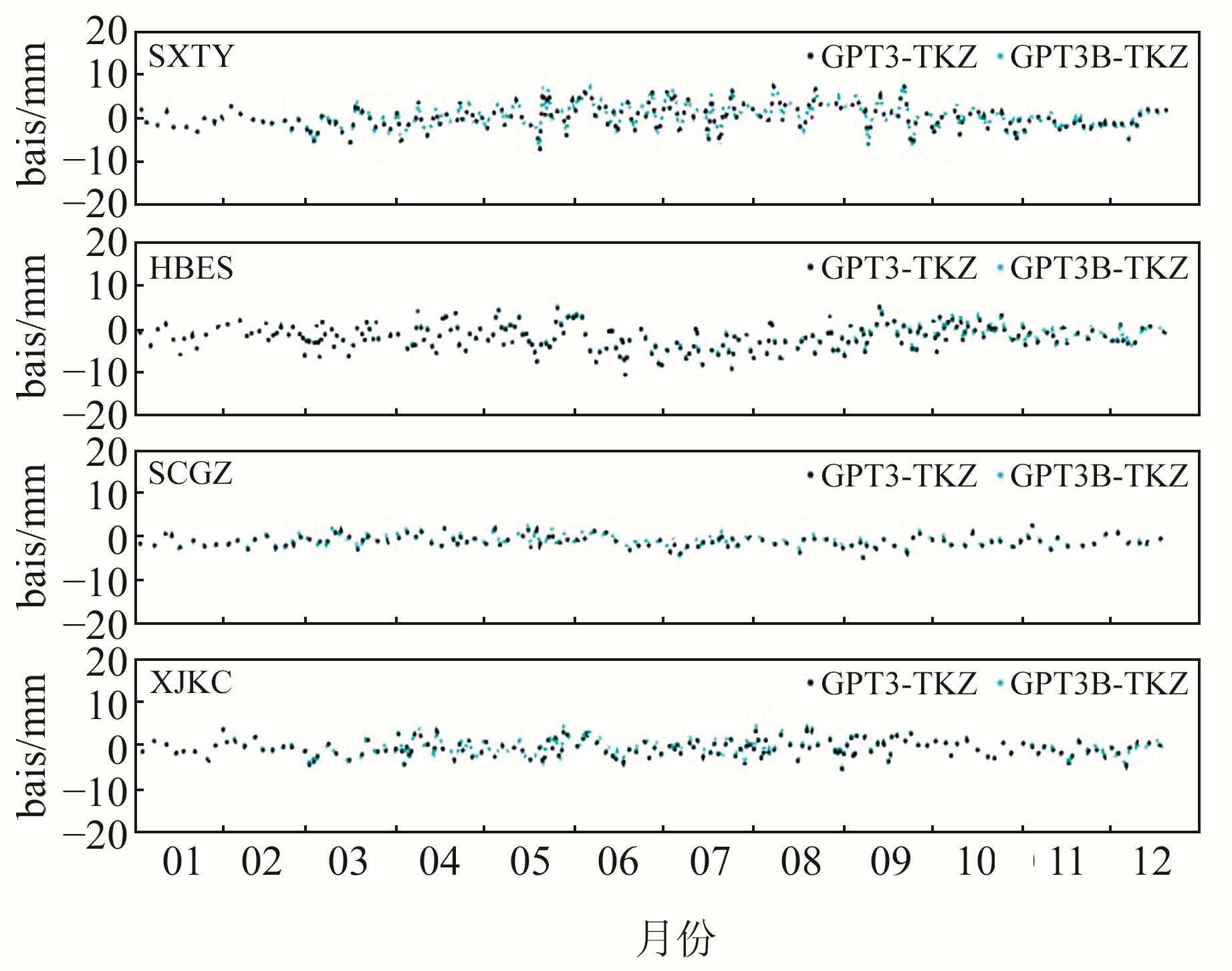
为分析不同区域基于GPT3-1模型2种方案(GPT3-1模型提供的气温结合Bevis经验公式计算得到Tm(Bevis-PWV)和GPT3-1模型提供的Tm(GPT3-PWV))反演的PWV与探空站利用实测地表温度反演的PWV(TKZ-PWV)的偏差,选取SXTY、HBES、SCGZ、XJKC等4个GNSS站(分别代表北方、南方、青藏、西北地区)2018年数据进行分析,结果见图 5。图 6为GPT3-1模型2种方案反演的PWV与探空站反演的PWV的差值时间序列(GPT3-TKZ表示利用GPT3模型Tm反演的PWV与探空站反演的PWV差值,GPT3B-TKZ表示采用GPT3模型提供的气温结合Bevis经验公式得到的Tm反演的PWV与探空站反演的PWV差值)。
|
图 5 SXTY、HBES、SCGZ和XJKC站PWV时间序列 Fig. 5 PWV time series at SXTY, HBES, SCGZ and XJKC stations |
|
图 6 SXTY、HBES、SCGZ和XJKC站GPT3模型反演的PWV与探空站反演的PWV的偏差 Fig. 6 Bias of PWV derived from radiosondes with respect to GPT3 model-derived PWV at SXTY, HBES, SCGZ and XJKC stations |
由图 5可知,Bevis-PWV、GPT3-PWV与TKZ-PWV的整体变化趋势基本吻合,具有很好的一致性,利用GPT3模型2种方法反演的PWV精度相当。由于我国夏季气候温暖湿润,PWV表现出明显的季节性变化,其峰值一般出现在6~9月。其中,HBES站位于我国南方,水汽含量大,因而其PWV明显高于其他3个站。由图 6可知,除HBES站外,2种方法反演的PWV与探空站反演的PWV之间的差值主要集中在5 mm以内。同时,这些差值的时间序列也表现出与PWV相似的季节性变化,其峰值出现在6~9月,表明该时期水汽变化剧烈。另外,由于GNSS站和探空站的位置存在距离,差值之间会出现一些异常值。
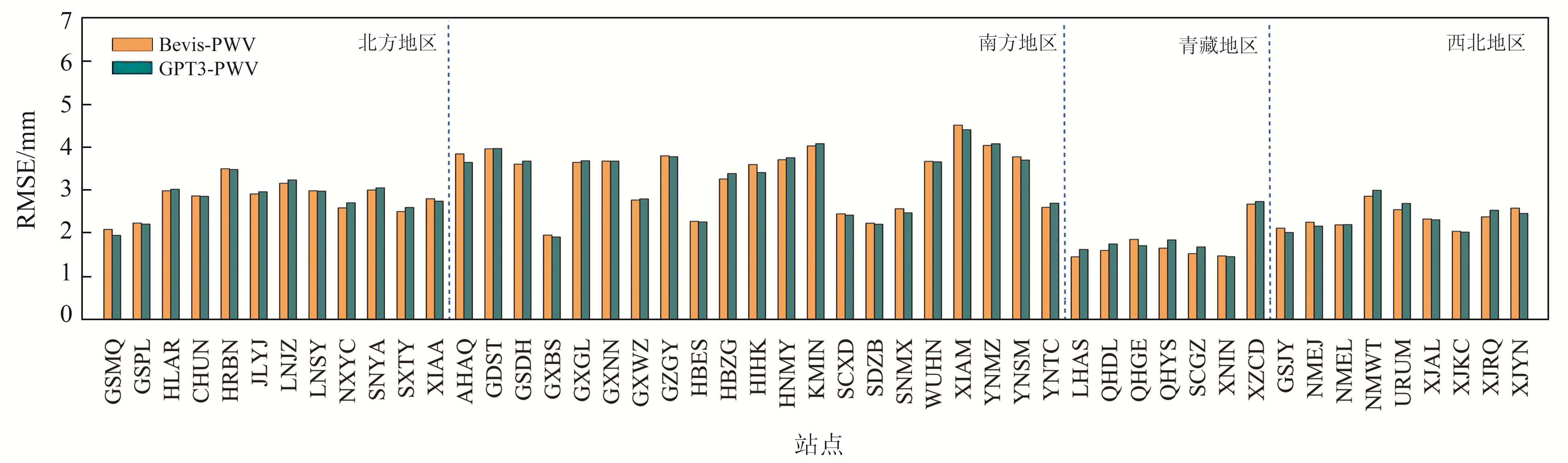
图 7为2018年与探空站并址的49个GNSS站利用2种方法反演出的PWV与探空站推导的PWV之间的RMSE。为便于比较,将中国区域分为4大地区(北方、南方、青藏、西北),同一地区测站放在一起。由图 7可知,在大多数站点,GPT3-PWV、Bevis-PWV与TKZ-PWV之间的RMSE接近且部分几乎相等,说明2种方法反演的PWV的精度相当。由于中国南方地区气候温暖湿润,位于南方地区的多数站点的RMSE大于3 mm;少数位于北方地区的测站存在RMSE大于3 mm的情况,主要是由于这些站靠近海边,水汽含量和变化较大。相比之下,青藏地区和西北地区由于海拔高、气候干燥,其RMSE低于3 mm。由表 4可知,基于GPT3模型反演的PWV精度在青藏和西北地区优于南方和北方地区,但北方和南方地区多数站点也能满足气象学应用要求[12]。
|
图 7 基于GPT3模型反演出的PWV与探空站推导的PWV之间的RMSE Fig. 7 RMSE of GPT3 model-derived PWV with respect to radiosonde station-derived PWV |
|
|
表 4 中国不同地区PWV的RMSE统计 Tab. 4 RMSE statistics of PWV in different areas in China |
本文利用中国地区2017~2018年49个与GNSS站并址的探空站数据对GPT3模型的气压、气温和Tm进行精度分析,并将GPT3模型提供的气象参数应用于GNSS水汽反演,结果表明:
1) 与49个探空站实测的气压、气温相比,GPT3-1模型的气压和气温bias均值分别为0.73 hPa和1.34 K,RMSE均值分别为4.21 hPa和3.75 K;GPT3-5模型的气压和气温bias均值分别为1.08 hPa和1.31 K,RMSE均值分别为4.35 hPa和3.81 K。总体而言,GPT3-1和GPT3-5模型气温和气压在南方地区的精度优于北方地区和西部地区,并且GPT3-1模型优于GPT3-5模型。
2) GPT3-1模型Tm的精度和稳定性优于GPT3-5模型。相对于南方地区,GPT3模型估算的Tm在北方地区和西部地区表现出较大的误差,可能是受地形起伏大和显著的Tm日周期变化影响。
3) 利用GPT3-1模型提供的气温结合Bevis经验公式得到的Tm反演的PWV和GPT3-1模型提供的Tm反演的PWV与探空站推导的PWV呈现出较好的一致性,且2种方法反演精度相当。总体而言,南方和北方地区站点反演的PWV的RMSE要大于青藏和西北地区,因而GPT3模型在青藏和西北地区反演大气水汽的精度更高,但北方和南方地区多数站点精度也能满足气象学应用要求。
| [1] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15 787-15 801 DOI:10.1029/92JD01517
(  0) 0) |
| [2] |
Rocken C, Hove T, Ware R. Near Real-Time GPS Sensing of Atmospheric Water Vapor[J]. Geophysical Research Letters, 1997, 24(24): 3 221-3 224 DOI:10.1029/97GL03312
(  0) 0) |
| [3] |
Huang L K, Jiang W P, Liu L L, et al. A New Global Grid Model for the Determination of Atmospheric Weighted Mean Temperature in GPS Precipitable Water Vapor[J]. Journal of Geodesy, 2019, 93(2): 159-176 DOI:10.1007/s00190-018-1148-9
(  0) 0) |
| [4] |
Huang L K, Mo Z X, Liu L L, et al. Evaluation of Hourly PWV Products Derived from ERA5 and MERRA-2 over the Tibetan Plateau Using Ground-Based GNSS Observations by Two Enhanced Models[J]. Earth and Space Science, 2021, 8(5)
(  0) 0) |
| [5] |
Zhang Y L, Cai C S, Chen B Y, et al. Consistency Evaluation of Precipitable Water Vapor Derived from ERA5, ERA-Interim, GNSS, and Radiosondes over China[J]. Radio Science, 2019, 54(7): 561-571
(  0) 0) |
| [6] |
黄良珂, 彭华, 刘立龙, 等. 顾及垂直递减率函数的中国区域大气加权平均温度模型[J]. 测绘学报, 2020, 49(4): 432-442 (Huang Liangke, Peng Hua, Liu Lilong, et al. An Empirical Atmospheric Weighted Mean Temperature Model Considering the Lapse Rate Function for China[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(4): 432-442)
(  0) 0) |
| [7] |
Landskron D, Böhm J. VMF3/GPT3:Refined Discrete and Empirical Troposphere Mapping Functions[J]. Journal of Geodesy, 2018, 92(4): 349-360 DOI:10.1007/s00190-017-1066-2
(  0) 0) |
| [8] |
章传银, 郭春喜, 陈俊勇, 等. EGM 2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 283-289 (Zhang Chuanyin, Guo Chunxi, Chen Junyong, et al. EGM 2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283-289 DOI:10.3321/j.issn:1001-1595.2009.04.001)
(  0) 0) |
| [9] |
Saastamoinen J. Contributions to the Theory of Atmospheric Refraction[J]. Bulletin Geéodeésique, 1972, 105: 279-298
(  0) 0) |
| [10] |
高壮, 何秀凤, 常亮. GPT3模型在中国地区的精度分析[J]. 武汉大学学报: 信息科学版, 2021, 46(4): 538-545 (Gao Zhuang, He Xiufeng, Chang Liang. Accuracy Analysis of GPT3 Model in China[J]. Geomatics and Information Science of Wuhan University, 2021, 46(4): 538-545)
(  0) 0) |
| [11] |
黄良珂, 李琛, 王浩宇, 等. 基于GPT2w模型计算中国地区对流层加权平均温度的精度分析[J]. 大地测量与地球动力学, 2019, 39(5): 496-501 (Huang Liangke, Li Chen, Wang Haoyu, et al. Precision Analysis of the Tropospheric Weighted Mean Temperature Derived from GPT2w Model over China[J]. Journal of Geodesy and Geodynamics, 2019, 39(5): 496-501)
(  0) 0) |
| [12] |
Wang H, Wei M, Li G P, et al. Analysis of Precipitable Water Vapor from GPS Measurements in Chengdu Region: Distribution and Evolution Characteristics in Autumn[J]. Advances in Space Research, 2013, 52(4): 656-667 DOI:10.1016/j.asr.2013.04.005
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China
 2022, Vol. 42
2022, Vol. 42


