2. 海军工程大学导航工程系,武汉市解放大道717号,430032;
3. 国家卫星海洋应用中心,北京市大慧寺路8号,100081
HY-2B卫星是我国第2颗极轨海洋动力环境卫星,其将与后续发射的HY-2C和HY-2D卫星组成全球大中尺度海洋动力环境卫星监测体系[1]。高精度的轨道是HY-2B卫星海洋测高和重力场模型反演的基础[2],因此有必要对HY-2B卫星的定轨方法和策略进行研究。
低轨卫星精密定轨方法主要可以分为3类:运动学定轨、动力学定轨和简化动力学定轨[3-4]。利用星载GPS数据进行定轨具有精度高、全天时、连续性的特点,目前已被广泛应用[5]。卫星天线相位中心偏差(PCO)和相位中心变化(PCV)是影响定轨精度的重要误差源。在卫星发射前可以得到先验PCO、PCV值,但因卫星发射过程中受力复杂、燃料消耗等因素的影响,实际值与先验值之间会发生较大的变化,因此在轨估计PCO、PCV模型对于定轨结果有较大的影响。数据质量是影响定轨结果的重要因素之一,也是高精度卫星定轨的可靠保障。卫星可见性、周跳比、多路径效应、观测数据的完整性是衡量数据质量的重要标准。
本文利用Anubis软件对HY-2B卫星数据进行质量分析及简化动力学定轨,通过分析不同时间间隔和先验值组合下的SLR结果,寻找出最优伪随机脉冲先验值,并通过载波相位残差、重叠轨道比较、SLR检核3种方法检验其定轨精度;再使用直接法估计出不同分辨率的PCV改正模型,并加入到定轨过程中,分析其对定轨结果的影响,得到高精度的卫星定轨结果。
1 数据处理策略利用2020-12-15~21(doy350~356)的HY-2B星载GPS数据和CODE提供的精密星历EPH、极移ERP、钟差CLK等参数,定轨弧段为24 h,采用简化动力学定轨方法[5]解算HY-2B卫星的精密轨道,寻找HY-2B卫星的最佳伪随机脉冲值,分析不同分辨率PCV对于定轨精度的影响。
基于Bernese5.2软件对HY-2B卫星进行简化动力学精密定轨研究[6],并利用表 1中的力学模型消除HY-2B卫星运行时受到的保守力和非保守力的影响。
|
|
表 1 HY-2B卫星简化动力学定轨策略[7] Tab. 1 Reduced-dynamic orbit determination strategy for HY-2B satellite |
以HY-2B卫星2020年doy350的星载GPS数据为例研究不同的随机脉冲时间间隔和先验标准差对定轨结果的影响。时间间隔分别设置为6 min、9 min、12 min、24 min、60 min,先验标准差分别取1×10-3 m/s、1×10-4 m/s、1×10-5 m/s、1×10-6 m/s、1×10-7 m/s、1×10-8 m/s、1×10-9 m/s、1×10-10 m/s,使用不同的时间间隔和先验标准差组合计算HY-2B卫星轨道,并用SLR检查定轨精度。
星载GPS数据是GPS卫星天线瞬时相位中心到低轨卫星信号接收时刻瞬时天线相位中心的距离。精密轨道的参考点是卫星质心,由于卫星发射及运动中某些因素的影响会导致相位中心发生改变。本研究重新校准了不同分辨率的PCV,并与不添加PCV的定轨结果进行比较。使用PCV直接法对7 d星载GPS数据进行PCV在轨估计,该方法在定轨过程中把未知参数PCV代入观测方程,同时估计轨道参数和PCV,根据最小二乘原理,求得多天PCV并取平均作为最终改正值,受接收机钟差等因素影响较小。
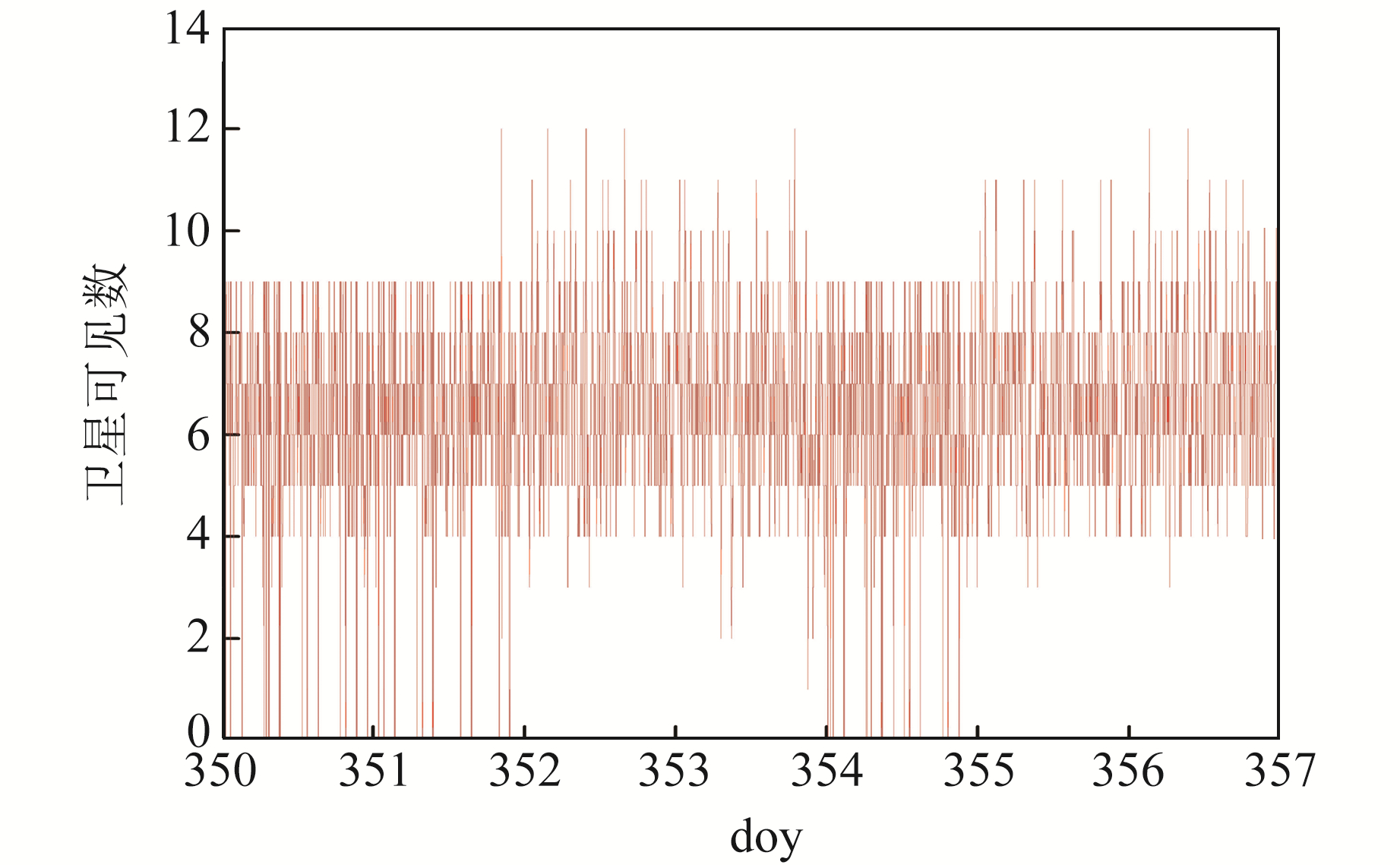
2 数据质量分析 2.1 卫星可见性图 1(采样间隔30 s)为HY-2B卫星在2020年doy350~356的卫星可见数。统计可得,观测到3颗及以下卫星的历元占总历元的0.67%,观测到4颗及以上卫星的历元占总历元的99.33%,观测到5颗及以上卫星的历元占总历元的94.54%,观测到6颗及以上卫星的历元占总历元的78.11%。大部分时间HY-2B卫星能够观测到6颗及以上的卫星,接收机性能良好且稳定。
|
图 1 HY-2B卫星卫星可见数 Fig. 1 Visible satellite numbers of HY-2B satellite |
周跳比(o/slps)表示在一定时间内实际观测到的历元数与发生周跳的历元数之比。数据完整率是GPS接收机在一定时间内获取的实际历元数与理论历元数之比。数据利用率是同时观测到含有4颗以上双频观测值的卫星历元数和预期历元数之比[8]。数据完整率和利用率可以反映接收机获取数据的能力和外部环境的优劣。
表 2为HY-2B卫星GPS数据质量评估结果。可以看出,MP1的RMS值均大于MP2,L1多路径误差RMS均值为15.7 cm,L2多路径误差RMS均值为9.5 cm,周跳比均值为30,数据完整率均值为99.65%,数据利用率均值为98.66%。
|
|
表 2 HY-2B卫星数据质量评估 Tab. 2 Data quality assessment of HY-2B satellite |
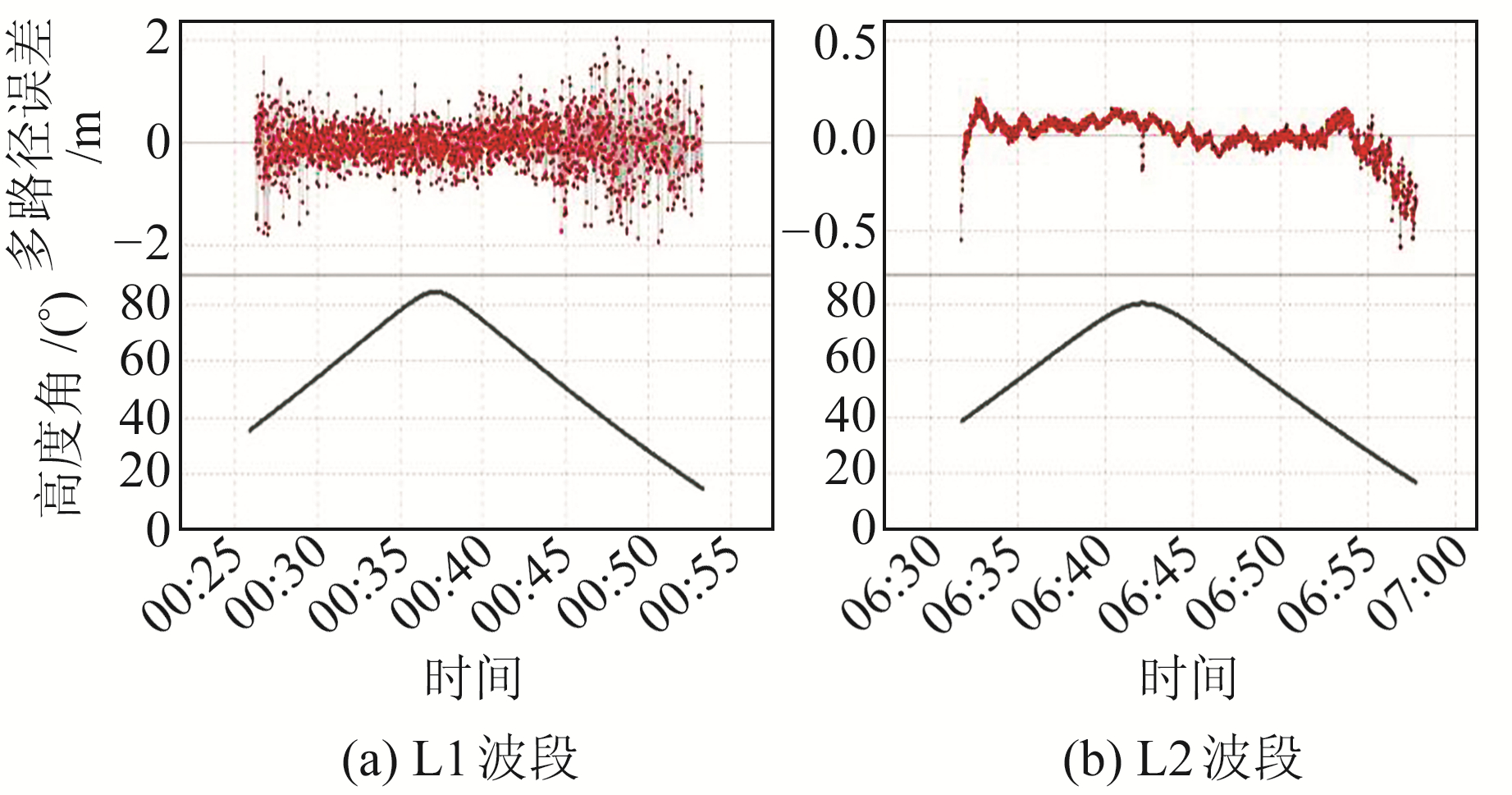
图 2反映了2020年doy350 G03卫星L1、L2波段的多路径误差和高度角的关系。可以看出,随着高度角的降低,多路径误差不断增加。高度角小于40°时,多路径误差显著提升;高度角较大时,多路径误差明显减小,且MP1大于MP2。
|
图 2 G03卫星多路径误差和高度角的变化 Fig. 2 Multipath errors and elevation angle changes of G03 satellite |
当2个频率的载波数据传播路径相同时,电离层延迟可表示为:
| $ \left\{\begin{array}{c} \Delta_{\mathrm{ion}, 1}=\frac{f_{2}^{2}}{f_{1}^{2}-f_{2}^{2}}\left(\lambda_{1} N_{1}-\lambda_{2} N_{2}+\right. \\ \left.M_{1}-M_{2}\right)=\frac{f_{2}^{2}}{f_{1}^{2}-f_{2}^{2}}\left(L_{1}-L_{2}\right) \\ \Delta_{\mathrm{ion}, 2}=\frac{f_{1}^{2}}{f_{1}^{2}-f_{2}^{2}}\left(\lambda_{1} N_{1}-\lambda_{2} N_{2}+\right. \\ \left.M_{1}-M_{2}\right)=\frac{f_{1}^{2}}{f_{1}^{2}-f_{2}^{2}}\left(L_{1}-L_{2}\right) \end{array}\right. $ | (1) |
式中,f1、f2为载波的频率,λ1、λ2为载波的波长,N1、N2为整周模糊度,M1、M2为载波的多路径效应,L1、L2为载波相位观测值。
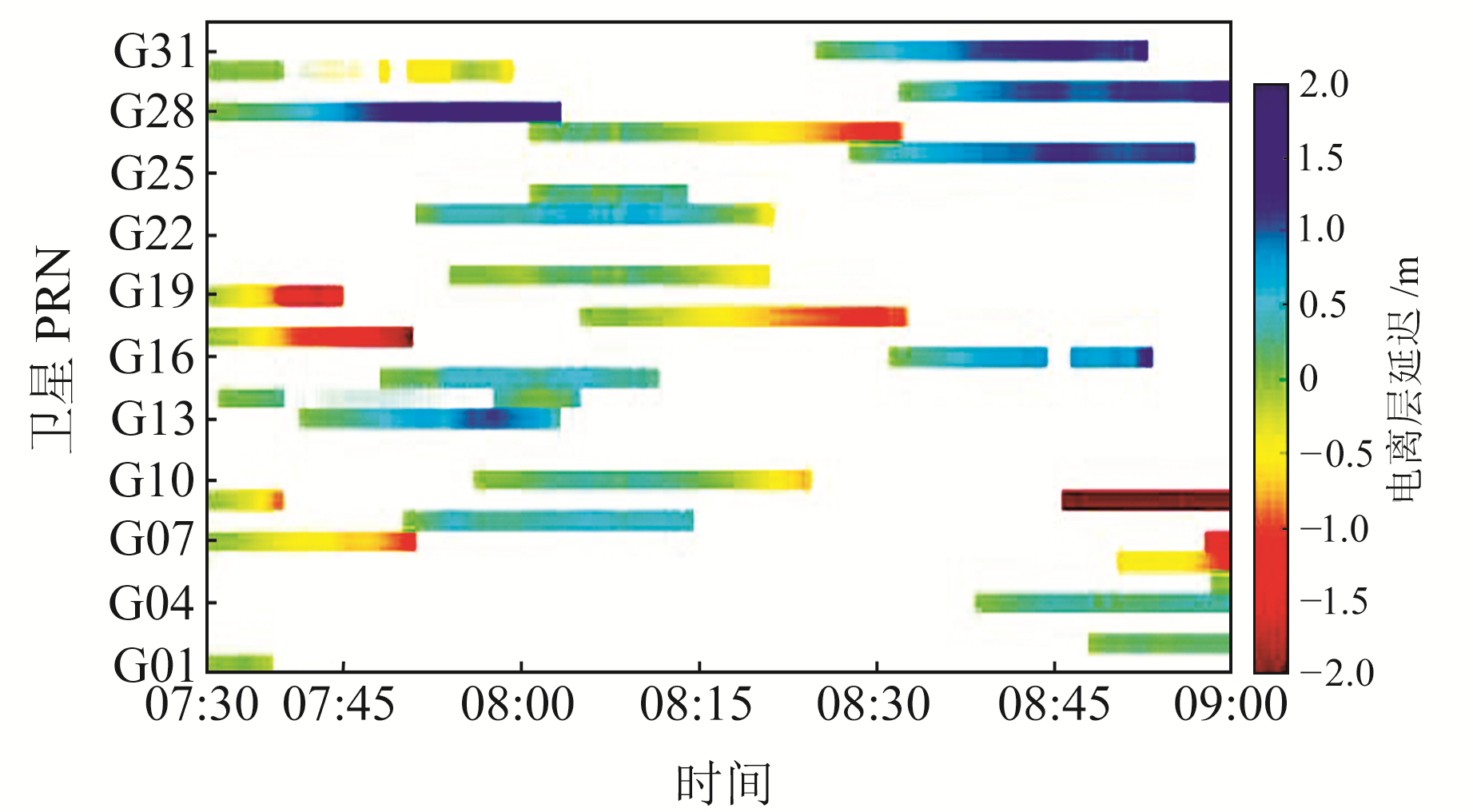
利用相邻历元的电离层延迟可得到电离层延迟变化率(IOD),当IOD>4 m/min时,认为电离层发生跳变。图 3、4分别为doy356 07:30~9:00的电离层延迟以及电离层延迟变化率,载波相位观测数据的中断导致周跳发生频率较大,因此在观测时段末尾会出现一个突变(图 4中棕色到蓝色)。可以看出,G01、G08、G18、G24、G29的GPS观测数据中,周跳的发生频率较大。
|
图 3 电离层延迟 Fig. 3 Ionospheric delay |

|
图 4 电离层延迟变化率 Fig. 4 Ionospheric delay rate |
采用载波相位残差和重叠轨道检验对HY-2B卫星定轨结果进行内符合精度评估,采用SLR检核方法进行外符合精度评估。
3.1 随机脉冲对简化动力定轨的影响分析在不同的伪随机脉冲时间间隔和先验值情况下进行定轨,并使用SLR进行检核得到RMS值,定轨精度如表 3(单位mm)所示。在低轨卫星精密定轨的过程中,随着卫星高度的不同所采用的时间间隔一般设置为6~60 min。这是因为当时间间隔大于60 min时,整体定轨精度较差,无参考意义;当时间间隔小于6 min时,定轨精度不再提高且所用时间会大幅增加[9]。
|
|
表 3 不同伪随机脉冲时间间隔和先验值组合下HY-2B卫星定轨SLR检核RMS值 Tab. 3 RMS values of HY-2B satellite orbit determination SLR check under different combinations of pseudo-random pulse time intervals and prior values |
表 3表明:1)在所有时间间隔下,当先验标准差为1×10-8 m/s2时,定轨精度都是最高的。2)在相同时间间隔下,先验标准差在1×10-3~1×10-6 m/s2变化时,定轨精度变化较小;当先验标准差为1×10-7 m/s2时,定轨精度明显提升;当先验标准差为1×10-8 m/s2时,定轨精度最高,之后开始下降;当先验标准差从1×10-9变为1×10-10 m/s2时,定轨精度大幅降低。综合以上结论,本次HY-2B简化动力学精密实验采用脉冲时间间隔为6 min,先验标准差为1×10-8 m/s2。
3.2 载波相位残差分析用消电离层组合(LC)对HY-2B星载GPS数据进行处理,统计2020年doy350~356的简化动力学定轨相位残差值,结果如表 4(单位mm)所示。
|
|
表 4 载波相位残差统计 Tab. 4 Carrier phase residual statistics |
从表 4可以看出,HY-2B卫星7 d的载波相位残差在7.4~7.9 mm之间,波动很小。说明本次实验采用的计算模型符合实际情况,HY-2B卫星搭载的GPS接收机能够获取稳定的数据,获得可靠的定轨结果。
3.3 重叠轨道检验使用2020年doy350~356的星载GPS数据进行简化动力学重叠轨道的对比,把每天的数据分为2个弧段分别进行定轨,第1段为00:00~18:00,第2段为12:00~24:00,选取13:00~17:00共4 h的重叠弧段进行比较,结果如表 5(单位mm)所示。可以看出,径向(R)RMS均值为7.6 mm,切向(T)RMS均值为12.4 mm,法向(N)RMS均值为9.8 mm,3D RMS均值为17.5 mm,证明了HY-2B星载GPS数据具有较高的精度和稳定性,定轨精度能够达到cm级。
|
|
表 5 重叠轨道RMS值对比 Tab. 5 RMS values comparison of overlap orbits |
在Bernese软件中,天线相位中心变化可以表示为:
| $ \Delta \varphi(\alpha, z)=\Delta \varphi^{\prime}(\alpha, z)+\Delta \boldsymbol{r e} $ | (2) |
式中,Δφ(α, z) 是卫星和接收机之间几何距离的总相位中心校正,α、z是卫星星固坐标系下的卫星方位角和高度角,Δr是平均天线相位中心和天线参考点之间的位置改正,e是接收机天线到卫星方向上的单位矢量。
图 5是在轨估计出的10°× 10°和5°× 5°的PCV格网模型。假设每个格网点都是未知的,直接计算出每一个格网的值,则得到的模型更为精细化,模型图以斑点状显示。可以看出,当高度角较低时,PCV绝对值较小;当高度角为80°~90°时,因只有很少的观测数据,导致计算的PCV值出现“空洞”。

|
图 5 PCV模型 Fig. 5 PCV model |
SLR检核是目前验证定轨结果的最精确手段[10]。大多数低轨卫星都搭载了SLR反射棱镜,测距精度优于1 cm[11]。
利用国际激光测距服务组织(ILRS)提供的HY-2B卫星SLR数据验证定轨精度。在doy350~356期间,共有16个测站对HY-2B卫星进行观测,得到935个标准点(normal point, NP)数据,删除数据很少且质量较差的1873和7403测站,对剩下的NP数据进行计算。从表 6(单位mm)可以看出,加上PCV模型后,每天SLR检核精度均有提升,且对于越差的结果改善效果越好;不加PCV模型7 d RMS均值为27.8 mm,加上10°× 10°和5°× 5° PCV模型后,7 d RMS均值分别为26.9 mm和26.6 mm,精度分别提高0.9 mm和1.2 mm。证明估计出的PCV模型对于定轨精度的提升具有重要意义,简化动力学定轨结果符合精度要求。
|
|
表 6 加PCV模型后HY-2B卫星轨道SLR检核结果 Tab. 6 SLR check results of HY-2B satellite orbit after adding PCV models |
通过以上分析可以证明,HY-2B卫星的星载GPS接收机性能较强、数据稳定、观测质量较高。
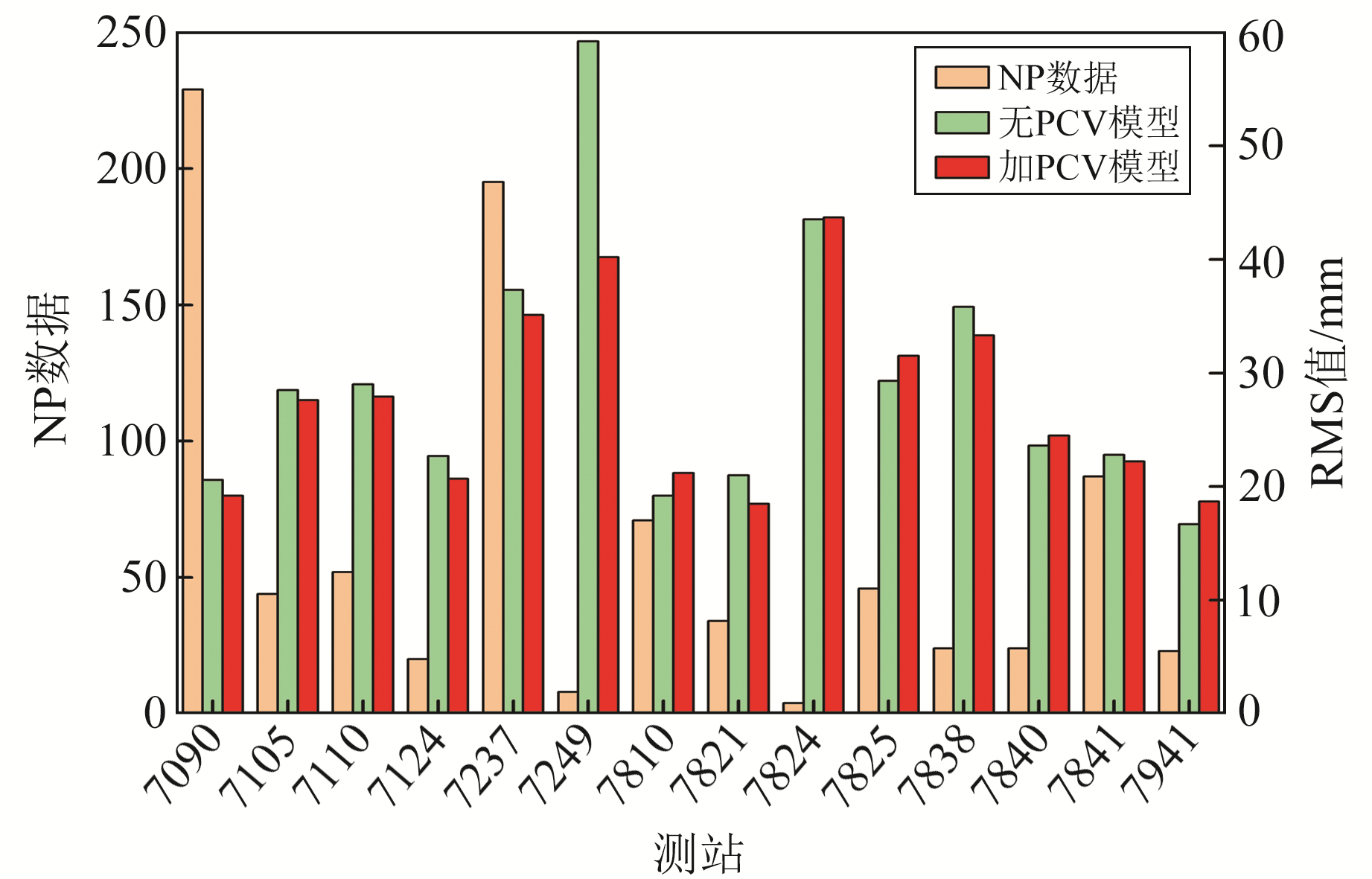
计算剩余14个测站7 d的SLR检核结果,和测站的NP数据一并列出(图 6,图中所加PCV模型为5°×5°)。由图 6可见,7090测站NP数据最多,达到229个,占总数据量的25.5%,不加PCV模型时RMS为20.6 mm,加上5°× 5° PCV模型后RMS降低为19.2 mm。7824和7249测站精度较差,两者共有NP数据12个,占总数据量的1.3%,不加PCV模型时RMS分别为59.2 mm和43.5 mm,加上PCV模型后精度提高到40.2 mm和42.4 mm。精度最高的测站是7941,共有23个NP数据,加入PCV模型后RMS为18.7 mm。大部分测站的RMS低于40 mm,符合预期要求。
|
图 6 NP数据与SLR检核各测站RMS值 Fig. 6 NP data and RMS values with SLR check of each station |
1) HY-2B卫星7 d卫星可见数均值为6.68颗,L1多路径误差RMS均值为15.7 cm,L2多路径误差RMS均值为9.5 cm,数据完整率为99.65%,数据利用率为98.66%,o/slps为30。证明HY2接收机性能良好,获取的数据稳定。
2) 通过分析不同时间间隔和不同先验值的伪随机脉冲参数下的定轨结果,最终选取脉冲时间间隔6 min、先验标准差1×10-8 m/s2作为实验的脉冲先验值进行后续定轨任务。
3) HY-2B卫星2020-12-15~21的7 d载波相位残差在7.4~7.9 mm波动,变化幅度较小。证明卫星观测数据的拟合性较好,采取的力学模型符合实际情况,在解算的过程中能有效地消除保守力和非保守力的影响,得到稳定的定轨结果。重叠轨道实验结果表明,R方向RMS为7.6 mm,T方向RMS为12.4 mm,N方向RMS为9.8 mm,3D RMS为17.5 mm,内符合精度达到cm级。
4) 利用SLR观测数据进行外符合精度检核,无PCV模型改正时,简化动力学定轨精度达到27.8 mm;加入估计得到的5°× 5° PCV模型后,整体检核精度提高1.2 mm。证明估计的PCV模型对提高定轨精度具有重要意义。本次实验的外符合精度也达到cm级,符合预期要求。
致谢: 感谢国家卫星海洋应用中心提供数据支持。
| [1] |
郭倩. "长征"四号B火箭成功发射"海洋"二号B星[J]. 中国航天, 2018, 4(10): 40 (Guo Qian. ALM-4B Successfully Sends HY-2B into Orbit[J]. Aerospace China, 2018, 4(10): 40)
(  0) 0) |
| [2] |
Jäggi A, Dahle C, Arnold D, et al. Swarm Kinematic Orbits and Gravity Fields from 18 Months of GPS Data[J]. Advances in Space Research, 2016, 57(1): 218-233 DOI:10.1016/j.asr.2015.10.035
(  0) 0) |
| [3] |
Prange L, Orliac E, Dach R, et al. CODE's Five-System Orbit and Clock Solution——The Challenges of Multi-GNSS Data Analysis[J]. Journal of Geodesy, 2017, 91(4): 345-360 DOI:10.1007/s00190-016-0968-8
(  0) 0) |
| [4] |
Hackel S, Montenbruck O, Steigenberger P, et al. Model Improvements and Validation of TerraSAR-X Precise Orbit Determination[J]. Journal of Geodesy, 2017, 91(5): 547-562 DOI:10.1007/s00190-016-0982-x
(  0) 0) |
| [5] |
杨洲铭, 郭金运, 夏要伟, 等. GRACE-FO卫星简化动力学精密定轨研究[J]. 地球物理学进展, 2020, 35(5): 1 710-1 716 (Yang Zhouming, Guo Jinyun, Xia Yaowei, et al. Reduced-Dynamic Precise Orbit Determination Research for GRACE-FO Satellites[J]. Progress in Geophysics, 2020, 35(5): 1 710-1 716)
(  0) 0) |
| [6] |
Dach R, Andritsch F, Arnold D, et al. Bernese GNSS Software Version5.2 User Manual[Z]. Astronomical Institute, University of Bern, 2015
(  0) 0) |
| [7] |
Mao X Y, Arnold D, Girardin V, et al. Dynamic GPS-Based LEO Orbit Determination with 1 cm Precision Using the Bernese GNSS Software[J]. Advances in Space Research, 2021, 67(2): 788-805 DOI:10.1016/j.asr.2020.10.012
(  0) 0) |
| [8] |
吴琼宝, 赵春梅. 星载GPS/BDS数据质量评估与分析[J]. 导航定位学报, 2018, 6(1): 81-84 (Wu Qiongbao, Zhao Chunmei. Quality Evaluation and Analysis on Spaceborne GPS/BDS Data[J]. Journal of Navigation and Positioning, 2018, 6(1): 81-84)
(  0) 0) |
| [9] |
张兵兵, 王正涛, 冯建迪, 等. 伪随机脉冲先验值对低轨卫星简化动力学定轨精度的影响[J]. 武汉大学学报: 信息科学版, 2018, 43(8): 1 222-1 227 (Zhang Bingbing, Wang Zhengtao, Feng Jiandi, et al. Inversion of Sound Velocity Profile in Multibeam Survey Based on Simulated Annealing Algorithm[J]. Geomatics and Information Science of Wuhan University, 2018, 43(8): 1 222-1 227)
(  0) 0) |
| [10] |
王友存, 郭金运, 周茂盛, 等. 基于多颗低轨卫星的SLR台站坐标几何解算方法[J]. 地球物理学报, 2020, 63(12): 4 333-4 344 (Wang Youcun, Guo Jinyun, Zhou Maosheng, et al. Geometric Solution Method of SLR Station Coordinate Based on Multi-LEO Satellites[J]. Chinese Journal of Geophysics, 2020, 63(12): 4 333-4 344)
(  0) 0) |
| [11] |
Guo J Y, Wang Y C, Shen Y, et al. Estimation of SLR Station Coordinates by Means of SLR Measurements to Kinematic Orbit of LEO Satellites[J]. Earth, Planets and Space, 2018, 70(1): 1-11
(  0) 0) |
2. Department of Navigation Engineering, Naval University of Engineering, 717 Jiefang Road, Wuhan 430032, China;
3. National Satellite Ocean Application Service, 8 Dahuisi Road, Beijing 100081, China
 2022, Vol. 42
2022, Vol. 42


