精确的位置和速度信息是内河船舶安全航行的重要保障。目前,船舶位速信息主要依赖船载船舶自动识别系统,可获得m级定位精度和dm/s级测速精度[1],但无法满足无人船艇自主导航、航道测量、水下地形测量等特殊场景的精度需求[2-3]。随着BDS-3的建成,GNSS精密定位和测速技术不断完善,使船舶高精度位速测量成为可能[4],但这方面的研究还较少。因此,本文基于长江航段的船载实测数据,重点评估不同水域环境下BDS-2、BDS-3、GPS及多系统组合PPP的定位和测速性能,为BDS以及单站GNSS在内河水域环境下定位和测速提供技术参考。
1 定位测速数据处理方法本文采用BDS、GPS、GLONASS和Galileo双频观测数据进行实时PPP处理。利用双频无电离层组合消除电离层延迟一阶项误差的影响;采用德国地学中心(GFZ)提供的精密轨道和钟差产品进行卫星轨道和钟差改正;对流层延迟中,干分量通过Saastamoinen模型改正,湿分量利用随机游走模型估计,过程噪声设为5.0×10-4m/
采用相位历元间差分法(time-differenced carrier phase,TDCP)计算船舶速度,误差模型与PPP一致,对流层误差仅改正干分量延迟,具体数据处理方法参见文献[6]。最后采用最小二乘准则估计接收机坐标变化量和钟差变化量,进而依据数据采样间隔解算出相邻历元间的平均速度。
2 数据采集数据采集时间为2020-12-09~11,航线从重庆朝天门码头到宜昌秭归港(图 1),全长约650 km。其中,重庆至忠县石宝镇为普通航段(约250 km),江面开阔,卫星遮蔽少,观测条件良好;忠县到宜昌秭归港为库区航段(约400 km),水道相对狭窄,多高山峡谷,卫星信号遮挡较严重。实验采用Trimble接收机和Novatel天线,二者固定在船顶护栏上,数据采样率设为1 Hz,可同时接收4大卫星定位系统的观测数据。

|
图 1 船舶航程轨迹 Fig. 1 Ship trajectory |
千寻位置解算服务利用网络RTK技术可提供cm级定位精度。本文采用该公司解算的船舶位置以及位置差分计算的速度作为参考值,将PPP解算的位置和TDCP解算的速度与其求差,统计差值的均方根(RMS)作为精度评定指标。
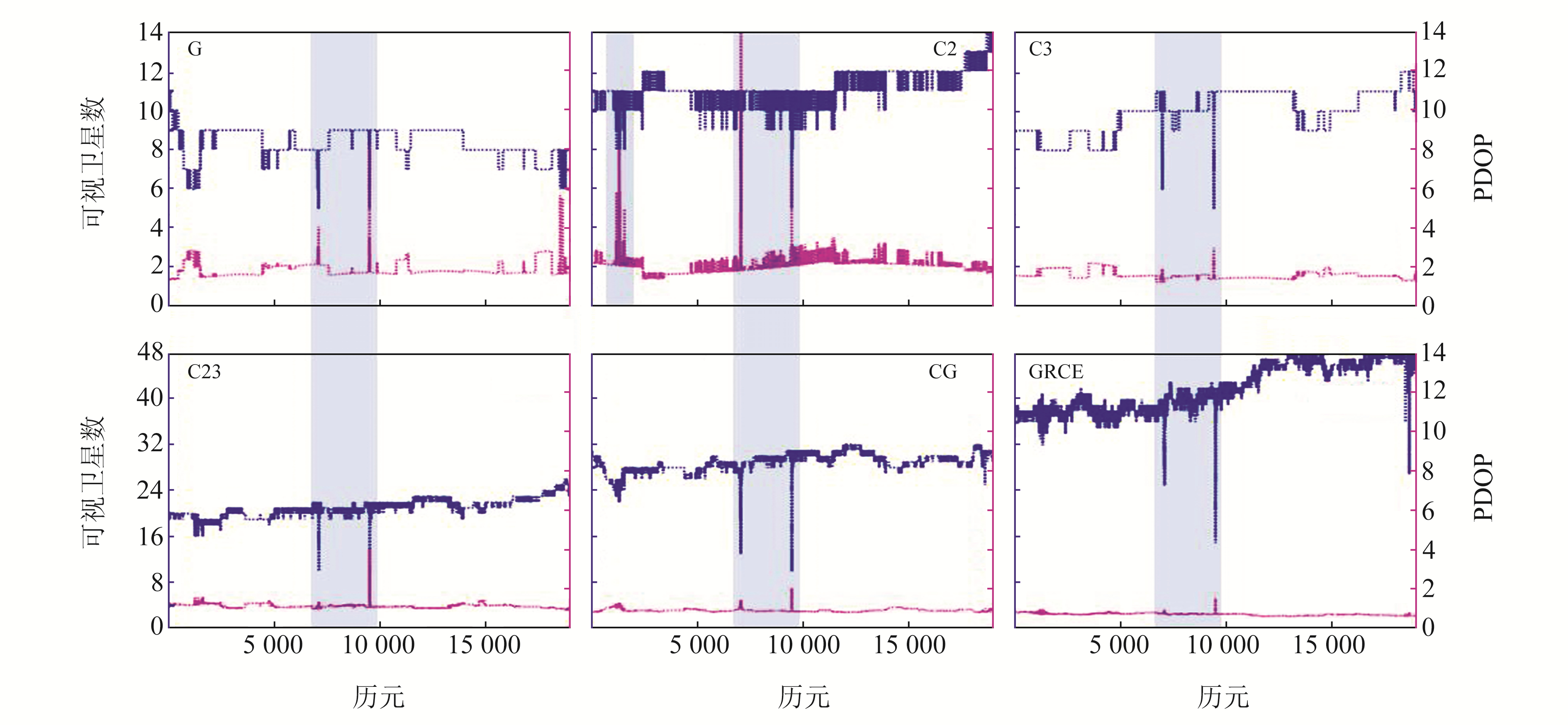
3.1 普通航段定位与测速性能分析 3.1.1 卫星数与位置精度衰减因子统计分析图 2统计了丰都县至忠县石宝镇普通航段GPS(G)、BDS-2(C2)、BDS-3(C3)、BDS(C23)、BDS/GPS(CG)、GPS/GLONASS/BDS/Galileo(GRCE)每个历元观测卫星数与位置精度衰减因子(position dilution of precision,PDOP)值。由图可见,BDS-2可视卫星数大于GPS,基本在10~14颗之间,但其空间几何结构较差,主要原因是68%的BDS-2卫星分布在南半天空,且东西向卫星数较少;BDS全系统在整个观测时段卫星数大于18,PDOP值小于GPS,稳定在1附近,说明川江航道上空BDS卫星空间几何结构优于GPS;CG和GRCE组合可视卫星数达到24颗以上,PDOP值小于单系统,且较为平稳,说明组合系统的卫星空间几何结构优于单系统。阴影表示船舶过桥时段,在此时段内各系统均有2处可视卫星数迅速减少,主要原因是船舶穿越忠州和忠县2座跨江大桥时卫星信号被遮挡。此外,船舶航经丰都时距江岸较近,卫星信号还受到岸边建筑物遮挡,导致BDS-2可视卫星数共有3处迅速减少。对比过桥时段PDOP值变化可见,BDS-3卫星空间几何结构的稳定性优于GPS与BDS-2;多系统组合的卫星几何结构抗干扰性明显优于单系统。
|
图 2 普通航段各系统可视卫星数与PDOP值 Fig. 2 Numbers of visible satellites and PDOP values of each system in normal waterway |
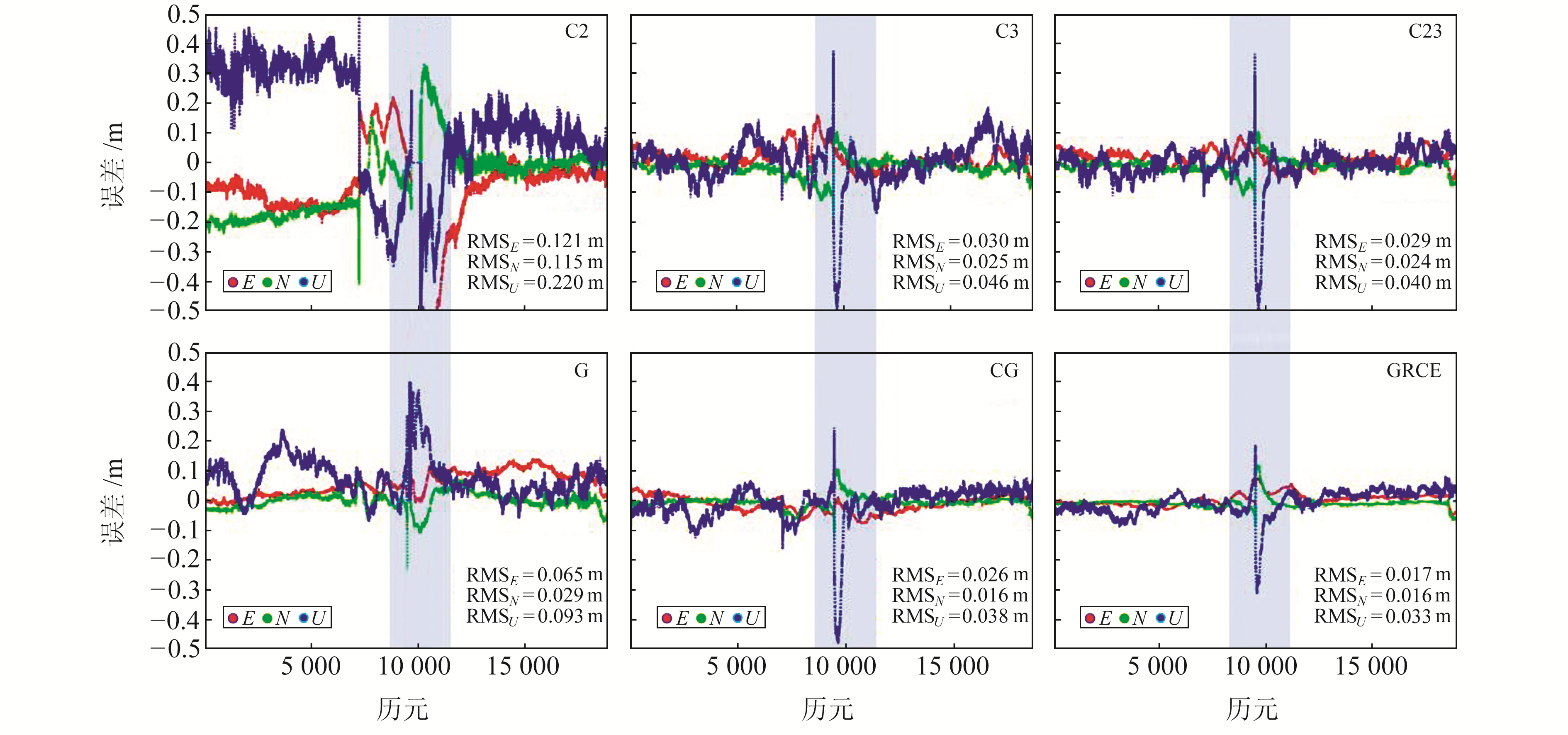
图 3给出了各系统PPP固定解误差时间序列,并统计了整个航段的定位精度。可以看出,无遮挡情况下,BDS-2的U方向定位误差在前半段明显较大,主要是其未能收敛所致,同时其整个航段上水平方向最大定位误差大于0.2 m,垂直方向大于0.4 m,远大于其他系统,且3个方向RMS值均大于0.1 m。这是因为BDS-2卫星空间几何结构较弱,且其观测值质量相对较差[7]。BDS全系统定位精度略大于BDS-3,整体上高于GPS,主要由于其可视卫星数多于GPS,卫星空间几何结构较好。相较于单系统,CG以及GRCE组合观测值冗余多,卫星空间几何结构强度高,定位精度得到进一步提高。阴影表示船舶过桥时段(与图 2一致),在此时段内各系统定位误差迅速增大。这是因为卫星信号被遮挡导致位置解的强度减弱,同时由于信号失锁使得大部分卫星模糊度重新初始化。
|
图 3 普通航段各系统定位误差时间序列 Fig. 3 Time series of positioning errors of each system in normal waterway |
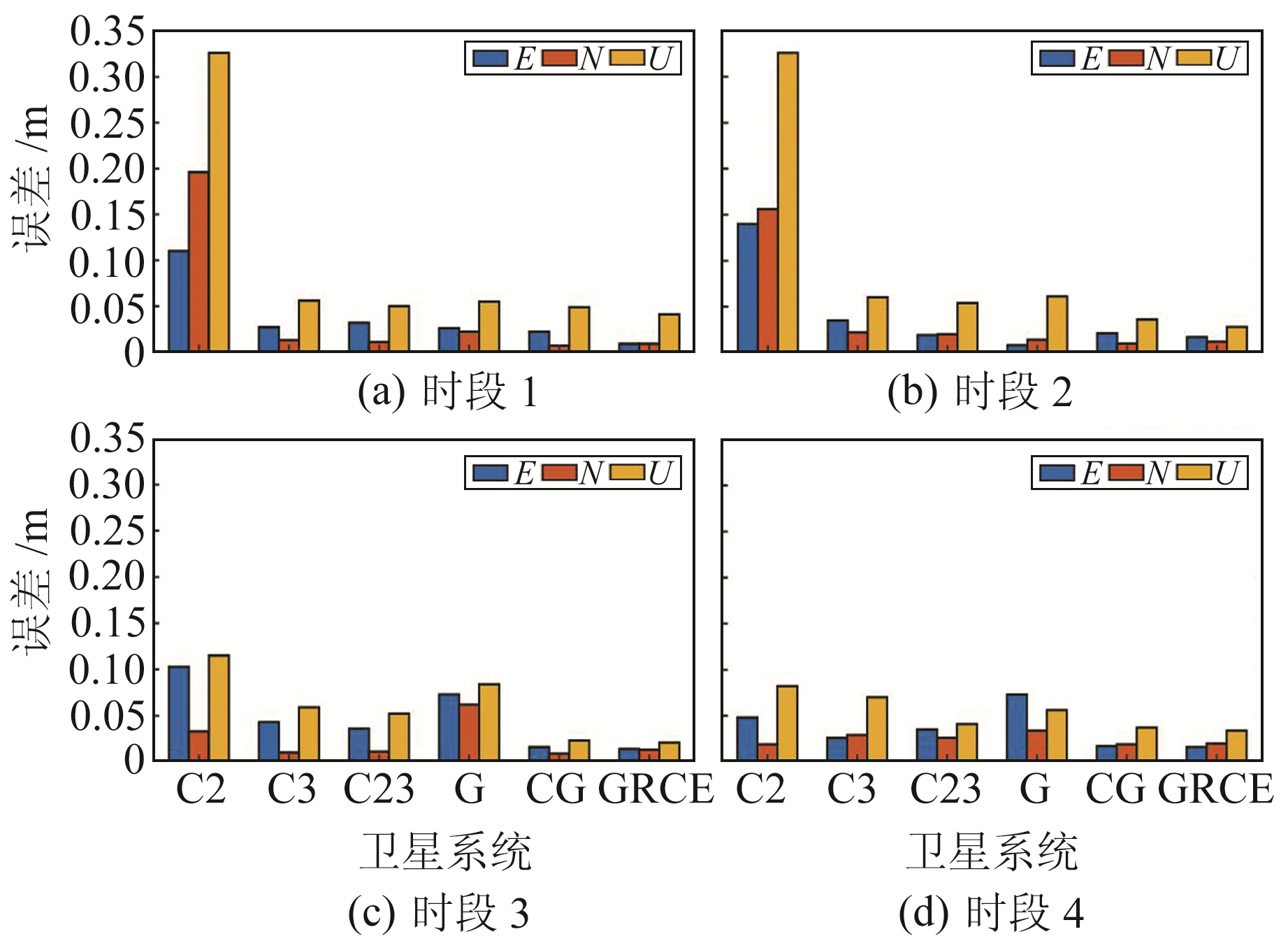
本文以丰都县至忠县石宝镇航段为例,将观测时间2020-12-10 05:40~11:48平均划分成4个时段,统计4个时段内各系统定位误差在3个方向上的RMS值(图 4)。可以看出,BDS-2在时段1、2水平方向定位精度约为0.15 m,垂直方向定位精度约为0.3 m;在时段3水平和垂直方向定位精度略大于0.1 m;在时段4水平方向定位精度优于0.05 m,垂直方向定位精度优于0.1 m。BDS-3与BDS全系统在4个时段内定位精度相当,水平方向均优于0.05 m,垂直方向在0.05~0.07 m。GPS在4个时段中水平方向定位精度在0.02~0.07 m,且在时段2最高、时段3最差,垂直方向定位精度在0.05~0.09 m,说明BDS定位稳定性优于GPS。CG和GRCE组合4个时段3个方向定位精度均优于0.05 m,高于单系统。综上,BDS-2前3个时段定位精度在dm级,第4时段才达到cm级,而其他系统在4个观测时段内均能满足船舶内河航行的定位需求。
|
图 4 普通航段内各系统PPP精度 Fig. 4 PPP accuracy of each system in normal waterway |
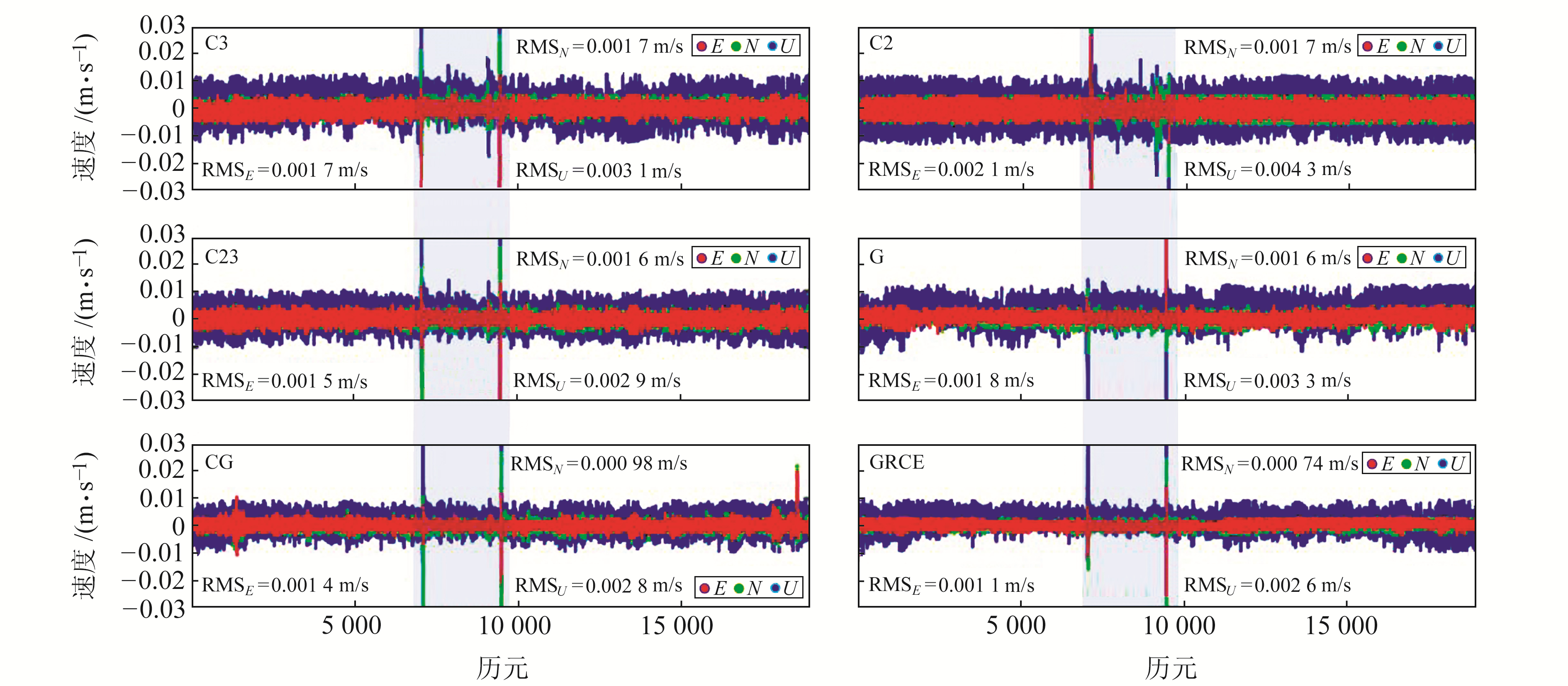
图 5为TDCP解算的船舶速度与参考值之差的时间序列。由图可见,各系统测速精度均在mm/s级,相比于E、N方向,U方向上的误差序列波动更大。BDS-2各方向上误差波动略大于其他系统,E、N、U方向的测速精度分别为2.1 mm/s、1.7 mm/s、4.3 mm/s。BDS-3、BDS全系统和GPS测速精度大致相当,水平方向在1.5~1.8 mm/s,垂直方向在2.9~3.3 mm/s。多系统组合可以显著增加卫星数,降低PDOP值,所以测速精度高于单系统。在2个阴影区观测时段,各系统水平和垂直方向测速误差均超过20 mm/s,主要是因为船舶过桥、卫星信号被遮挡,使得TDCP的测速误差增大。
|
图 5 各系统普通航段测速误差序列 Fig. 5 Velocity error sequence of each system in normal waterway |
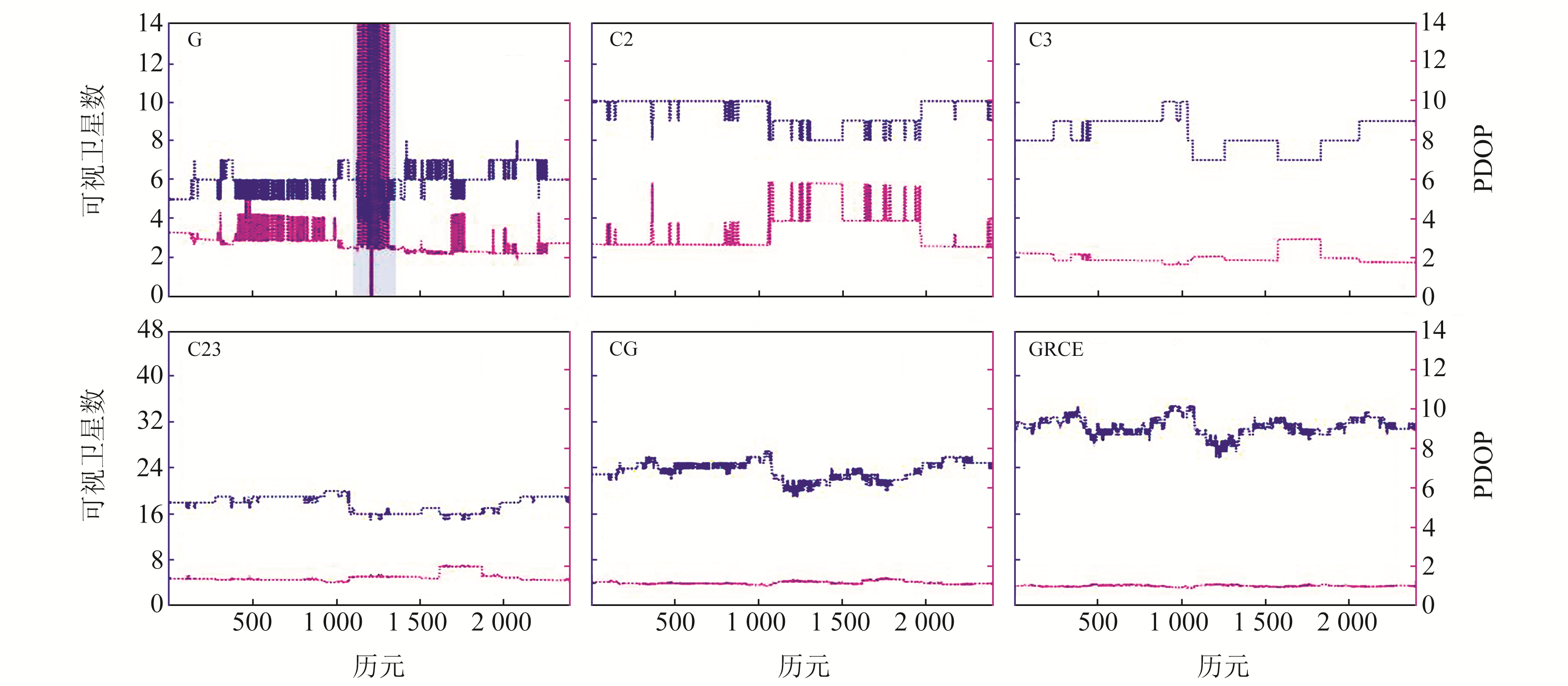
巫峡(库区)航段各系统每个历元的可视卫星数及PDOP值如图 6所示。其中,BDS-2的可视卫星数在8~12颗之间,略高于BDS-3,但BDS-3的PDOP值小于BDS-2,主要是因为BDS-3卫星分布比较均匀,而大部分BDS-2卫星偏南侧分布,东西侧极少。GPS的可视卫星数在4~7颗,阴影区观测时段下降至4颗,同时PDOP值急速增大,主要是由于大部分卫星信号被两侧山体遮挡所致。BDS全系统卫星数在15颗以上,PDOP值略大于1,且比较稳定。CG与GRCE组合可视卫星数达到20颗以上,PDOP值稳定在1左右,其中,GRCE组合可视卫星数高达28颗以上,PDOP值最平稳。
|
图 6 库区航段各系统可视卫星数与PDOP值 Fig. 6 Numbers of visible satellites and PDOP values of each system in reservoir waterway |
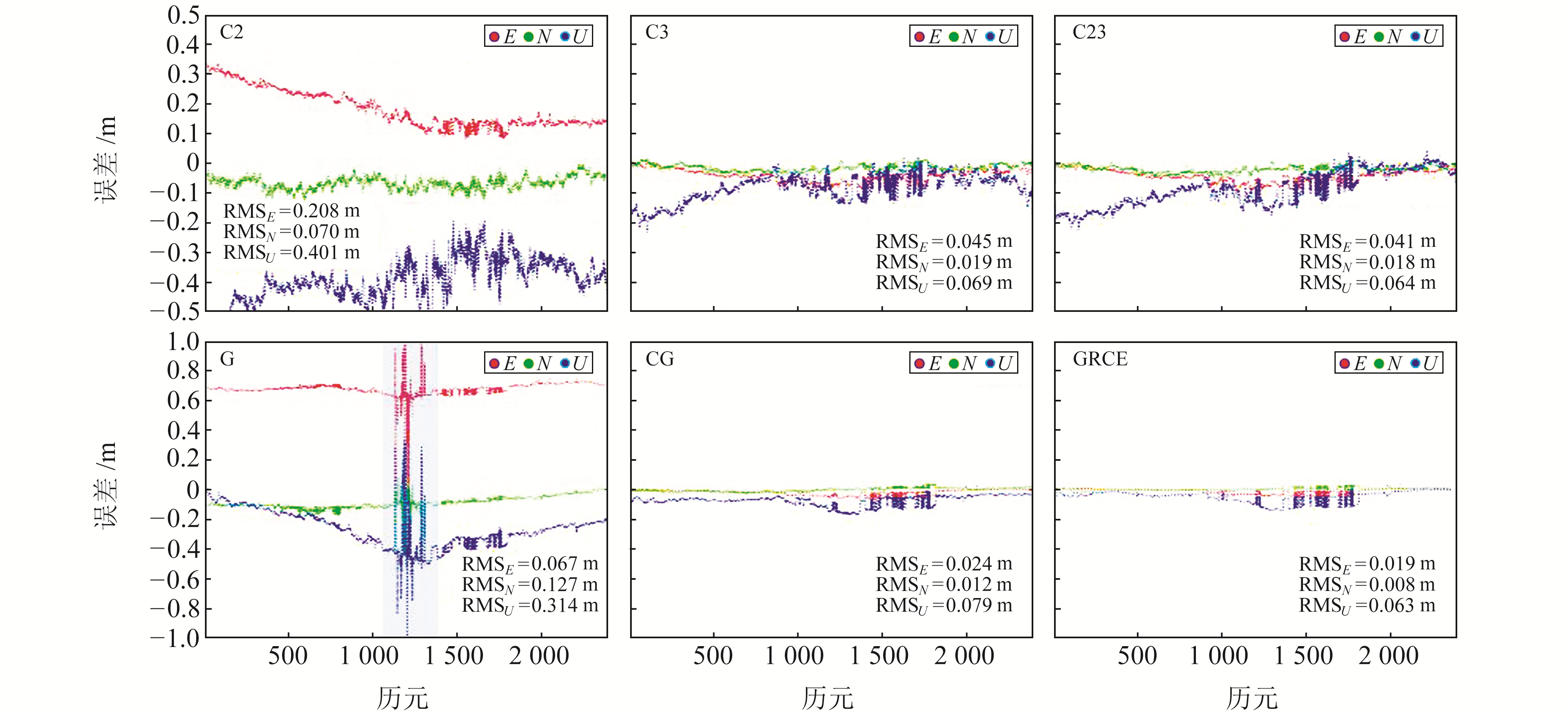
图 7统计了巫峡航段内各系统PPP固定解误差序列及其RMS值。由图可见,BDS-2水平方向误差最大超过0.3 m,垂直方向超过0.4 m。BDS-2与GPS PPP的收敛时间持续整个巫峡航段,这是因为二者PDOP值较大。GPS在E方向上定位误差大于0.6 m,且高于N、U方向,其原因是船舶过巫峡之前由于卫星信号被两岸地物遮挡,导致信号失锁,PPP重收敛;而阴影区观测时段内GPS定位误差突然增大则是由于巫峡两侧山体遮挡所致。BDS-3与BDS全系统虽然也存在PPP重收敛过程,但由于其卫星空间几何结构较好,船驶入巫峡水域后很快收敛;BDS全系统的定位精度略高于BDS-3。CG与GRCE组合拥有更多的观测值冗余和更优的卫星空间几何结构,可以加速收敛,定位精度明显优于单系统。
|
图 7 库区航段各系统定位误差时间序列 Fig. 7 Time series of positioning errors of each system in reservoir waterway |
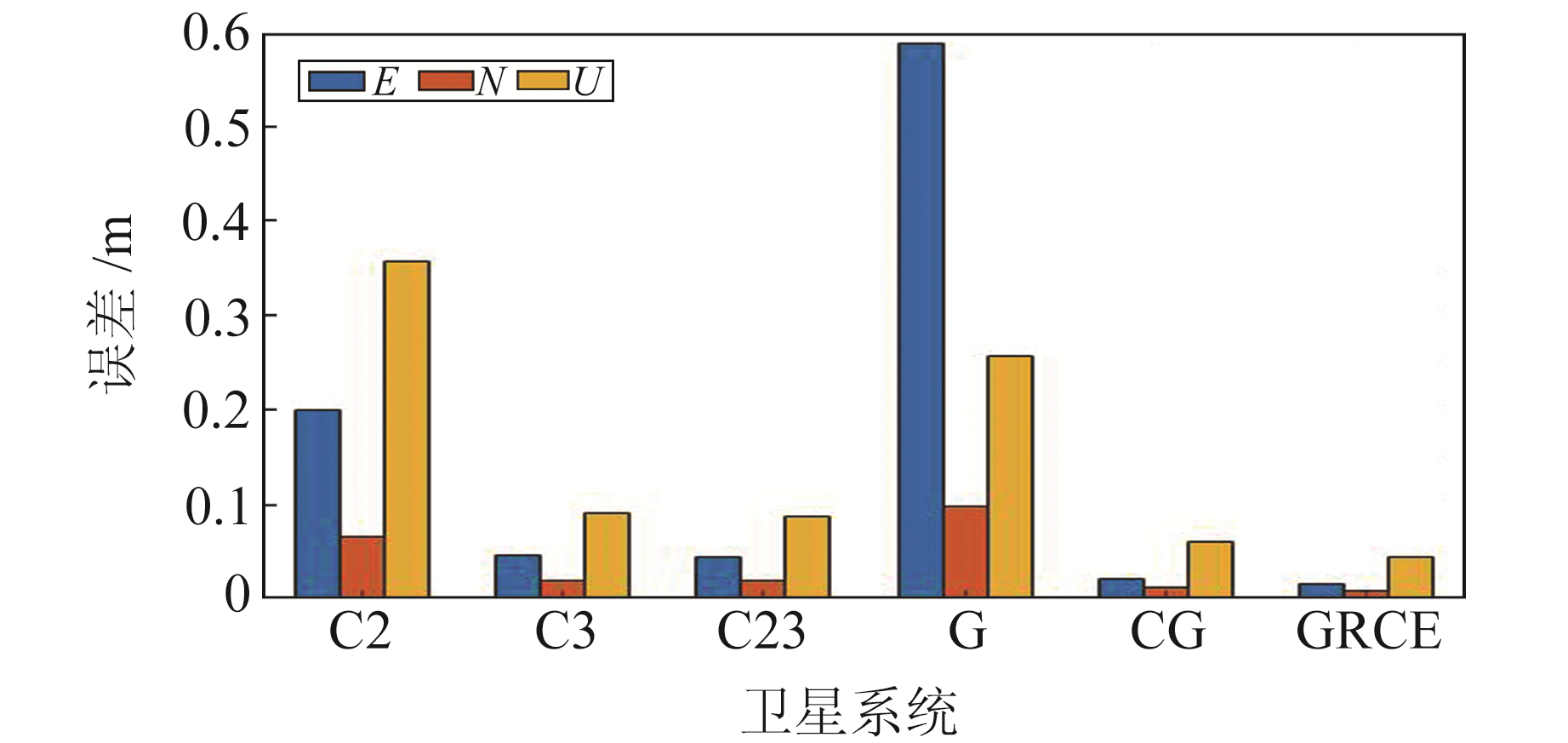
以2020-12-11 00:30~01:00瞿塘峡航段以及09:00~09:30巫峡航段的观测数据来分析不同系统的定位性能。图 8统计了该航段各系统定位误差RMS值。其中,BDS-2定位精度较差,E方向上RMS值达到0.2 m,U方向上接近0.35 m。BDS-3与BDS全系统定位精度相当,水平方向在0.05~0.06 m,垂直方向优于0.1 m。GPS定位精度较差,水平方向约为0.6 m,垂直方向约为0.3 m。多系统组合可提高定位精度与可靠性,其中CG组合水平方向定位精度优于0.05 m,垂直方向定位精度约0.06 m;GRCE组合水平和垂直方向定位精度均优于0.05 m。综上,BDS-2与GPS库区航段dm级的定位精度基本满足内河船舶正常航行需求,BDS-3、BDS全系统、CG以及GRCE组合则能够为内河船舶提供更高的定位精度。
|
图 8 库区航段各系统PPP精度 Fig. 8 PPP accuracy of each system in reservoir waterway |
图 9给出了库区航段内TDCP解算的船舶速度与参考值之差的时间序列。可以看出,库区航段内各系统测速精度依然在mm/s级,测速误差在0 mm/s上下波动,U方向误差波动大于E、N方向。除BDS-2外,各单系统测速精度大体相当,水平方向在1.1~1.8 mm/s,垂直方向在3.3~4.1 mm/s。相对于单系统,CG与GRCE组合的卫星空间几何结构更佳,测速精度得到进一步提高,水平方向优于1.3 mm/s,垂直方向优于3.2 mm/s。此外,由于TDCP测速使用逐历元最小二乘算法,同时采用抗差数据处理策略,数据预处理过程中删除了部分粗差观测值,导致必要观测数不足,无法解算这些历元的速度,而本文中仅对比有信息输出的观测历元,因此在图 9中无法看到测速误差增大的时段。

|
图 9 库区航段各系统速度误差序列 Fig. 9 Velocity error sequence of each system in reservoir waterway |
本文利用川江航道约650 km的GNSS实测数据,以千寻位置解算的结果作为参考,分析了普通航段和库区航段BDS-2、BDS-3、BDS全系统、GPS、CG以及GRCE组合PPP定位性能以及TDCP测速性能。结果显示,普通航段BDS-3、BDS全系统和GPS定位精度均在cm级,且测速精度大致相当,水平方向在1.5~1.8 mm/s,垂直方向在2.9~3.3 mm/s。库区航段受两侧山体遮挡,GPS定位精度水平方向达到了0.6 m,出现较大的波动性;BDS-3与BDS全系统测速精度与普通航段相当,定位精度略有下降,水平方向在0.05~0.06 m,垂直方向优于0.1 m,但定位和测速总体上呈现良好的稳定性。GC和GRCE组合定位和测速精度相较于单系统平均提高30%,且库区航段与普通航段大致相当,表明多系统融合可提高定位和测速精度及可靠性。
| [1] |
段兵兵, 王解先, 王成. 融合速度和方向信息的船舶位置高精度预报[J]. 武汉大学学报: 信息科学版, 2015, 40(3): 422-426 (Duan Bingbing, Wang Jiexian, Wang Cheng. High-Precision Prediction of Ships Including Speed and Orientation[J]. Geomatics and Information Science of Wuhan University, 2015, 40(3): 422-426)
(  0) 0) |
| [2] |
沈海青, 郭晨, 李铁山, 等. 考虑航行经验规则的无人船舶智能避碰导航方法[J]. 哈尔滨工程大学学报, 2018, 39(6): 998-1 005 (Shen Haiqing, Guo Chen, Li Tieshan, et al. An Intelligent Collision Avoidance and Navigation Approach of Unmanned Surface Vessel Considering Navigation Experience and Rules[J]. Journal of Harbin Engineering University, 2018, 39(6): 998-1 005)
(  0) 0) |
| [3] |
赵建虎, 欧阳永忠, 王爱学. 海底地形测量技术现状及发展趋势[J]. 测绘学报, 2017, 46(10): 1 786-1 794 (Zhao Jianhu, Ouyang Yongzhong, Wang Aixue. Status and Development Tendency for Seafloor Terrain Measurement Technology[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 786-1 794)
(  0) 0) |
| [4] |
Prochniewicz D, Szpunar R, Kozuchowska J, et al. Performance of Network-Based GNSS Positioning Services in Poland: A Case Study[J]. Journal of Surveying Engineering, 2020, 146(3)
(  0) 0) |
| [5] |
Wu J T, Wu S C, Hajj G A, et al. Effects of Antenna Orientation on GPS Carrier Phase[J]. Manu-Scripta Geodaetica, 1992, 18(2): 9 198
(  0) 0) |
| [6] |
Freda P, Angrisano A, Gaglione S, et al. Time-Differenced Carrier Phases Technique for Precise GNSS Velocity Estimation[J]. GPS Solutions, 2015, 19(2): 335-341 DOI:10.1007/s10291-014-0425-1
(  0) 0) |
| [7] |
魏二虎, 刘学习, 王凌轩, 等. BDS/GPS组合精密单点定位精度分析与评价[J]. 武汉大学学报: 信息科学版, 2018, 43(11): 1 654-1 660 (Wei Erhu, Liu Xuexi, Wang Lingxuan, et al. Analysis and Assessment of BDS/GPS Combined Precise Point Positioning Accuracy[J]. Geomatics and Information Science of Wuhan University, 2018, 43(11): 1 654-1 660)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


