受观测过程中断和数据处理方法等因素的影响,GNSS坐标时间序列不可避免地存在数据缺失的情况,给数据的使用带来诸多负面影响。因此,有必要对含缺失数据的GNSS坐标时间序列进行插值。
基于单站的插值方法,如拉格朗日插值、三次样条插值、线性插值等适用于缺失比例小或连续缺失数据少的情况。但当数据缺失量较大,特别是连续缺失数据较多时,上述方法插值效果较差[1-2]。基于多站的插值方法利用周围站点数据对含长空缺的目标序列进行插值,可以顾及站点间的相关性[3-5]。但其将目标区域内所有站点数据作为整体进行解算,可能会受到局部信号的污染,影响插值精度[6]。
基于以上问题,本文在数据插值经验正交函数(DINEOF)算法的基础上,考虑站点间的相关性,提出一种相关数据插值经验正交函数(CDINEOF)算法,并与DINEOF算法和多项式插值法的插值效果进行对比分析,验证其有效性。
1 CDINEOF算法原理 1.1 DINEOF算法基本原理DINEOF算法的基本流程如下[7]:假设原始数据可以表示为一个二维观测矩阵X(m, n),其中,m和n分别为历元个数和测站个数;从整个观测矩阵中减去平均值,并将缺失数据设置为0以获得初始数据X0;执行奇异值分解,将X0分解为一组经验正交函数,如式(1)所示:
| $ \boldsymbol{X}_{0}(m, n)=\boldsymbol{U} \boldsymbol{D} \boldsymbol{V}^{\mathrm{T}}=\sum\limits_{p=1}^{q} \boldsymbol{u}_{p} \boldsymbol{\lambda}_{p} \boldsymbol{v}_{p}^{\mathrm{T}} $ | (1) |
式中,U(m×q)和V(q×n)分别为时间和空间EOF模态,up和vp分别为对应的第p列特征向量,对应奇异值为λp。使用第1个模态的空间和时间特征模态对数据进行重构,替换缺失位置数据;使用该重构结果迭代计算第1个模态,替换缺失数据,直至收敛。最后用前k(1, 2, …, q)个保留模态重复该过程,使用交叉验证法计算最优保留模态数。
1.2 CDINEOF算法基本原理为改善DINEOF算法可能会受到局部信号污染的问题,本文加入站点筛选原则,提出CDINEOF算法,算法流程如图 1,具体步骤为:
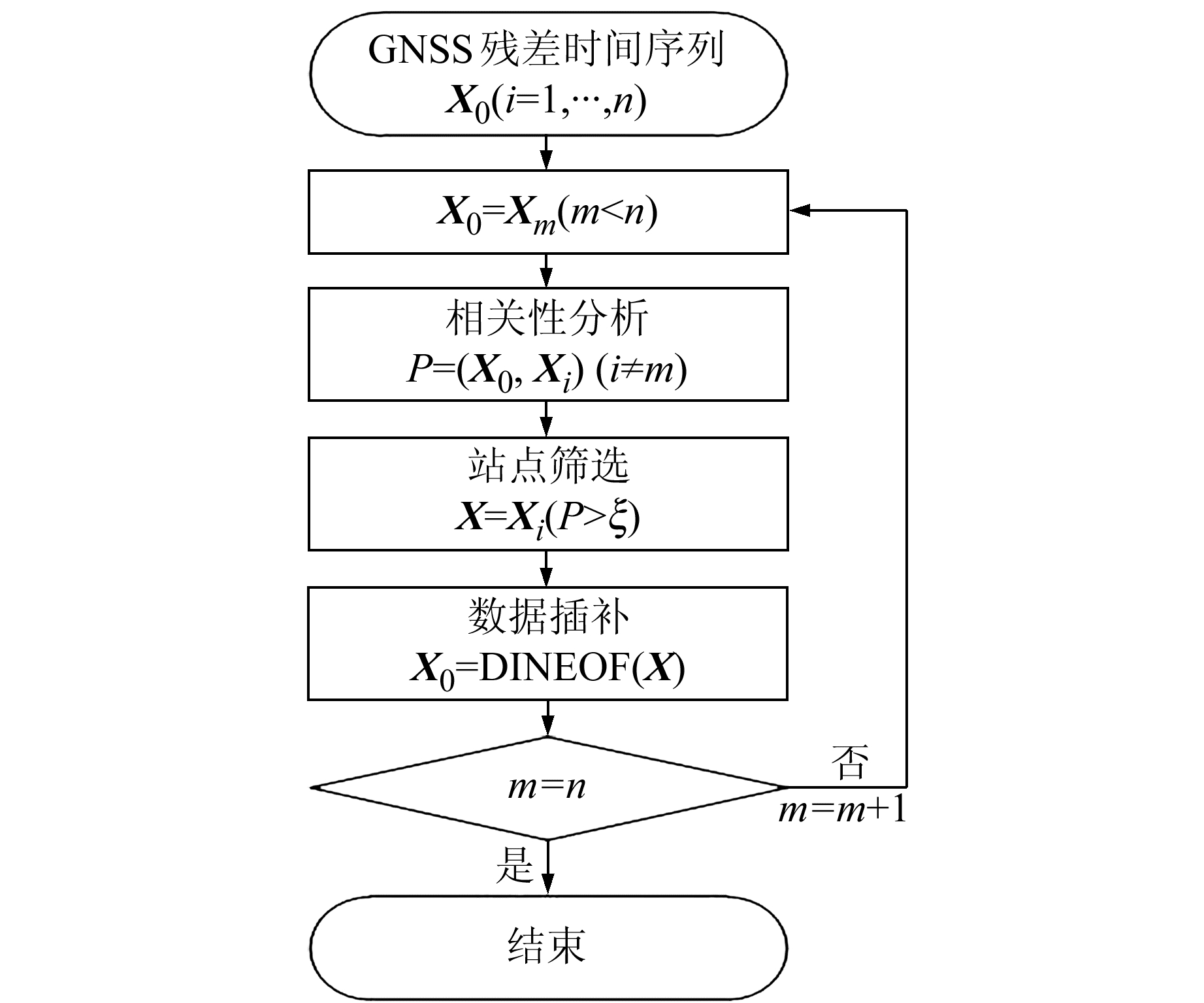
|
图 1 算法流程 Fig. 1 Algorithm flow |
1) 利用公共历元对目标站点与周围站点进行相关性分析,根据分析结果将相关系数最大值设为初始阈值;
2) 将相关性大于阈值的站点坐标时间序列组成观测矩阵X,利用DINEOF算法对含缺失值的观测矩阵X进行迭代插值,得到目标站点插值后数据,然后通过减小阈值获取不同插值结果,采用交叉验证法选取最佳插值结果;
3) 依次对剩余站点进行上述计算,得到各站点完整的坐标时间序列。
2 插值效果评价指标 2.1 模拟数据评价指标采用GNSS坐标时间序列真实值与插补值之间的平均绝对误差MAE、Pearson相关系数R和均方根误差RMSE[4]对CDINEOF算法的插值效果进行评估。其中,MAE和RMSE的值越小、R的绝对值越大,表示插补值和真实值越接近,即插值效果越好。
2.2 实测数据评价指标由于没有真实值作为参考,采用插值后的坐标时间序列投影到各主方向后的方差大小来评价实测数据插值效果,插值后的时间序列应尽可能保持原有方差的最大化方向[5]。计算公式为:
| $ v_{j}=\boldsymbol{w}_{j}^{\mathrm{T}} \boldsymbol{S} \boldsymbol{w}_{j} $ | (2) |
式中,wj为第j个主方向,S为插值后的协方差矩阵。
3 实验分析 3.1 模拟插值实验为避免粗差、阶跃等因素的影响,采用澳大利亚区域内14个经过处理的IGS站坐标残差时间序列进行模拟实验,其中HOB2站在2011年doy048~2016年doy095观测时间段内坐标时间序列完整。为验证CDINEOF算法在不同连续缺失情况下的插值性能,以HOB2站坐标时序为基础,以5个观测历元为步长,移除数据后构成80组实验数据,分别使用DINEOF算法、CDINEOF算法以及二阶多项式插值法对模拟实验数据进行插值。此处给出连续移除400个数据后的插值结果。图 2为插值前HOB2站N、E、U方向上的残差时间序列,其中,空心圆点为后续插值保留的数据,实心圆点为模拟数据缺失而移除的数据。由图可见,N、U方向存在较明显的周期性变化,E方向上以线性趋势为主,变化较为平缓。
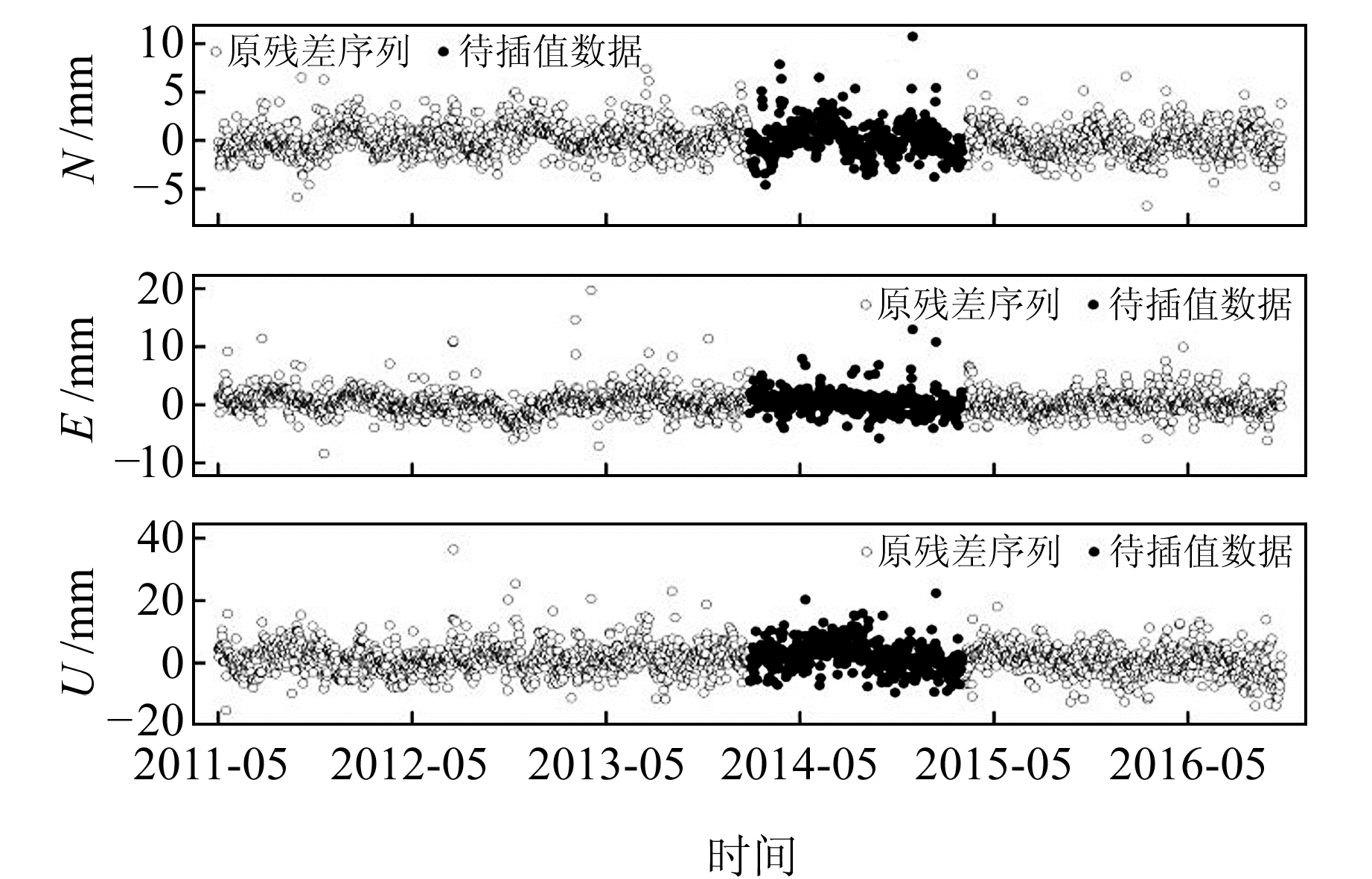
|
图 2 HOB2站坐标残差时间序列 Fig. 2 Coordinate residual time series at HOB2 station |
图 3为利用公共历元计算出的HOB2站与周围站点之间的相关性。由图可见,站点间相关性随距离增加有减弱的趋势,一些站点在U方向上达到负相关,若在插值过程中将这些站点纳入计算过程,可能会对插值结果产生不利的影响。另外,个别站点相关性与上述趋势有所偏离,这可能与站点本身的数据质量有关。根据§1.2中的阈值选取原则,该站点在N、E、U方向的相关性阈值分别为0.3、0.2和0.1。
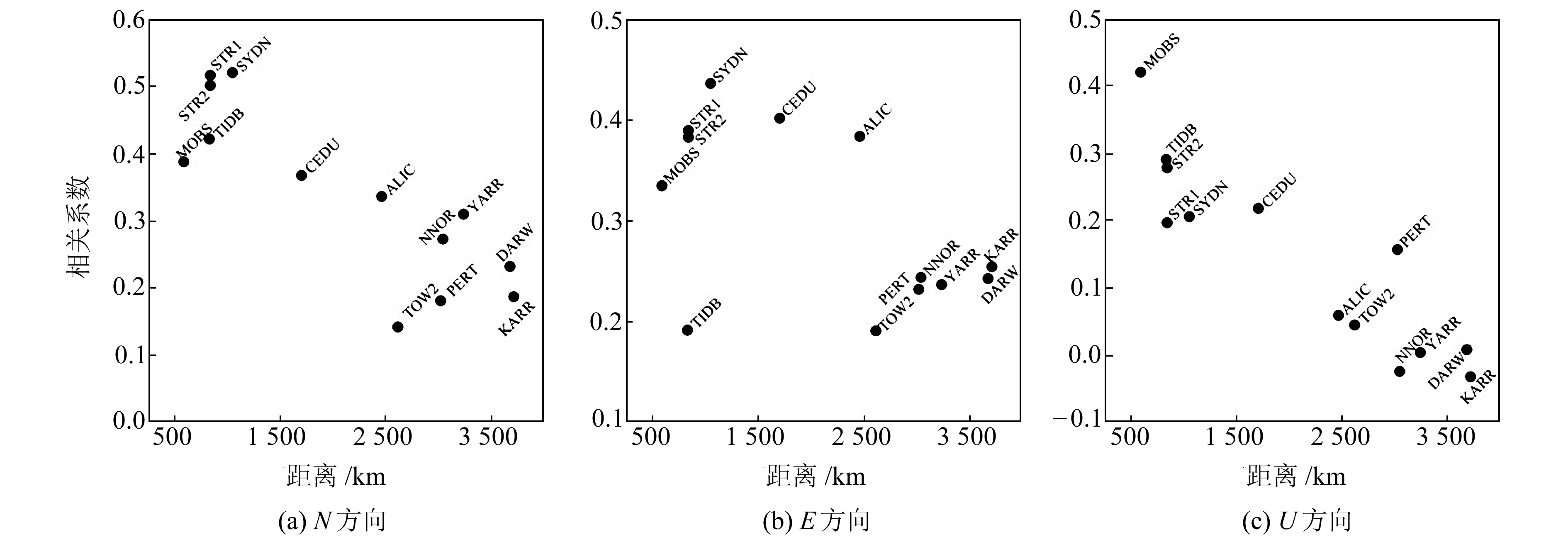
|
图 3 HOB2站与周围站点相关系数 Fig. 3 The correlation coefficient between HOB2 and other stations |
当连续缺失400历元时,3种插值方法在各方向上的MAE、RMSE和R值如表 1所示。可以看出,由CDINEOF算法插值结果计算出的评价指标值在N和U方向上均优于DINEOF算法和多项式插值法。其中,CDINEOF算法的MAE最多减少了33.2%,RMSE最多减少了27.3%,R最多提高了10%。在E方向上,各指标反映出CDINEOF算法插值性能略优于DINEOF算法而略差于多项式插值法。为探究其原因,本文给出插值结果与原残差序列在3个方向上的对比,如图 4所示。
|
|
表 1 不同插值方法性能对比 Tab. 1 Performance comparison of different methods |
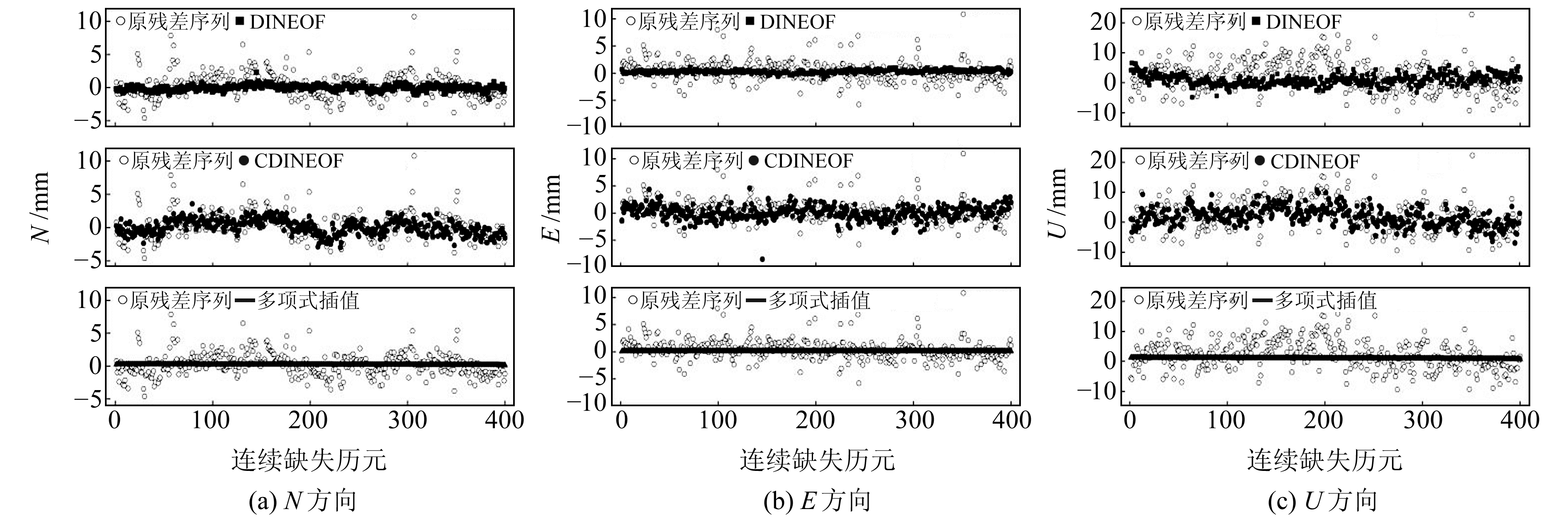
|
图 4 不同方法的插值结果与原残差序列 Fig. 4 Interpolation results of different methods and original residual series |
由图 4可见,在N和U方向上,多项式插值法结果与原残差序列相比呈现出明显的线性变化,虽然保证了数据的连续,但曲线过于光滑,与原残差序列差异较大;相比于多项式插值法,DINEOF算法插值结果保留了一部分原残差序列的高频信息,尤其在U方向上其插值结果表现出明显的波动性,但是整体趋势和原残差序列吻合度不够,周期性变化不明显;CDINEOF算法的插值结果与原残差序列有较高的吻合度,能够在顾及原残差序列周期性变化的同时还原其变化趋势。在E方向上,DINEOF算法和多项式插值法的结果呈现明显的线性变化,与原残差序列较为相符,插值效果较好,CDINEOF算法结果与二者接近。分别计算各插值方法的MAE、RMSE和R值,如图 5所示。

|
图 5 不同方法的插值性能 Fig. 5 Interpolation performance of different methods |
由图 5可见,在周期性明显的N、U方向上,当连续缺失历元在80以内时,3种方法的插值效果相当,无明显差异;当连续缺失历元大于80时,CDINEOF算法的插值性能逐渐优于DINEOF算法和多项式插值法,并且性能优势随着连续缺失历元的增加愈发明显;当连续缺失历元达到400时,CDINEOF算法插值结果与原残差序列的相关系数仍保持在0.92以上,表现出强相关性。而在线性明显的E方向上,不同插值方法之间的插值性能较为接近,这也与前面插值结果相对应。
3.2 实测数据实验选取澳大利亚地区14个IGS站2005~2018年doy069的残差时间序列进行实测数据实验。由于观测中断、孤立值剔除等因素的影响,各站点本身已经存在一定程度的数据缺失,其中最大缺失比例约为19.9%。利用DINEOF算法、CDINEOF算法和多项式插值法对14个站的残差时间序列进行插值,计算插值后坐标时间序列的方差,并统计各插值方法前3个主成分所占总方差的百分比,结果如表 2所示。
|
|
表 2 不同插值方法前3个主成分方差占比 Tab. 2 Variance ratio of the first three principal components of different methods |
由表 2可知,在各方向上CDINEOF算法插值后的坐标时间序列前3个主成分之和占总方差之比均最大。其中,CDINEOF算法所保留的最大方差在DINEOF算法的基础上提升了11.8%,在多项式插值法的基础上提升了6.7%。
4 结语1) 本文提出的CDINEOF算法可以有效避免利用多站点数据进行长时间连续空缺插值时低相关度站点对插值效果产生的不利影响,只使用相关度较高的站点数据进行插值,可以更加准确地还原数据的变化趋势。
2) 多项式插值法会使插值后的序列呈线性变化,因此对于线性趋势明显的坐标时间序列效果较好;CDINEOF算法对数据变化明显的坐标时间序列数据比较敏感,插值效果较好。
3) CDINEOF算法可以很好地保留原有序列方差最大化方向,相比于DINEOF算法和多项式插值法,其插值后坐标时间序列前3个成分之和占总方差之比最大。但其计算效率与基于单站的插值方法相比存在一定劣势。因此,在实际应用中,要根据需求选择合适的插值方法。
| [1] |
武艳强, 黄立人. 时间序列处理的新插值方法[J]. 大地测量与地球动力学, 2004, 24(4): 43-47 (Wu Yanqiang, Huang Liren. A New Interpolation Method in Time Series Analyzing[J]. Journal of Geodesy and Geodynamics, 2004, 24(4): 43-47)
(  0) 0) |
| [2] |
杨登科. 不同插值方法对GPS时间序列的影响分析[J]. 全球定位系统, 2019, 44(5): 66-69 (Yang Dengke. Influences of Different Interpolation Methods on GPS Time Series[J]. GNSS World of China, 2019, 44(5): 66-69)
(  0) 0) |
| [3] |
谢春桥, 匡翠林. 顾及空间相关性的GNSS坐标序列插值比较[J]. 导航定位学报, 2020, 8(4): 85-92 (Xie Chunqiao, Kuang Cuilin. Comparison of Interpolation Methods for GNSS Coordinate Time Series Considering Spatial Correlation[J]. Journal of Navigation and Positioning, 2020, 8(4): 85-92)
(  0) 0) |
| [4] |
明锋. GPS坐标时间序列分析研究[D]. 郑州: 信息工程大学, 2018 (Ming Feng. Research on the GPS Coordinate Time Series Analysis[D]. Zhengzhou: Information Engineering University, 2018)
(  0) 0) |
| [5] |
王方超, 吕志平, 吕浩, 等. 基于RegEM算法的GPS坐标时间序列插值应用分析[J]. 大地测量与地球动力学, 2020, 40(1): 45-50 (Wang Fangchao, Lü Zhiping, Lü Hao, et al. Application Analysis of GPS Coordinate Time Series Interpolation Based on RegEM Algorithm[J]. Journal of Geodesy and Geodynamics, 2020, 40(1): 45-50)
(  0) 0) |
| [6] |
苏利娜, 甘卫军, 苏小宁, 等. 基于模型和空间相关性的GPS时间序列插值方法[J]. 大地测量与地球动力学, 2019, 39(6): 620-624 (Su Lina, Gan Weijun, Su Xiaoning, et al. A New Method of Interpolation of GPS Coordinate Time Series Based on Model and Noise Spatial Correlation[J]. Journal of Geodesy and Geodynamics, 2019, 39(6): 620-624)
(  0) 0) |
| [7] |
Beckers J M, Rixen M. EOF Calculations and Data Filling from Incomplete Oceanographic Datasets[J]. Journal of Atmospheric and Oceanic Technology, 2003, 20(12): 1 839-1 856
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

