微机电系统(micro-electro-mechanical system, MEMS)陀螺仪与其他类型的陀螺仪相比具有体积小、成本低、可靠性高等特点[1]。但受自身元器件和外部环境的影响,MEMS陀螺仪输出的数据误差较大,测量精度相对较低。影响MEMS陀螺仪精度的主要误差源为随机漂移[2]。通过积分解算陀螺仪数据可消除稳态误差,但随机噪声依然存在。
经验模态分解(empirical mode decomposition, EMD)方法[3]不需要信号的先验信息,可自适应地将陀螺仪原始信号分解为一系列高频到低频的本征模态函数(intrinsic mode function, IMF)和1个残差余量,是数据去噪的有效方法[4],但EMD分解时存在模态混叠问题。Torres等[5]提出在EMD分解的每个阶段添加自适应白噪声的完备集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN)方法,可解决EMD分解的模态混叠问题,并精确重构信号。张宁等[6]在CEEMDAN的基础上采用改进的小波阈值对MEMS信号进行去噪,取得了较好的效果。EMD和CEEMDAN方法均将原始信号分解为一系列IMF分量,通过筛选机制确定噪声模态分量,剔除噪声分量后对剩余分量进行重构来消除信号噪声。不同的IMF筛选方法对重构效果具有较大影响。目前常见的IMF筛选方法包括排列熵、相关系数法等[7]。但排列熵方法计算量较大;相关系数法对于非线性、非平稳信号的降噪效果较差[8]。
本文在CEEMDAN分解的基础上,将Hurst指数作为模态筛选机制,把IMF分量划分为噪声模态分量、混合模态分量和信息模态分量,并对混合模态分量进行滤波后重构信号,得到最终结果。
1 去噪模型CEEMDAN算法具体步骤参考文献[9],本文不再赘述。
1.1 Hurst指数本文使用Hurst指数筛选机制对经CEEMDAN处理后得到的IMF分量进行筛选。Hurst指数即有偏的随机游走,最早被用来分析水库与河流的进出水流量,后被应用于股市等行业的分形分析[10]。Hurst指数有3种形式:0 < H < 0.5、H=0.5、0.5 < H < 1。其中,0 < H < 0.5表示该阶模态分量时间序列具有反持续性,即负相关;H=0.5表示该阶模态分量时间序列不相关,即随机序列;0.5 < H < 1表示该阶模态分量时间序列有长期相关特征,具有持续性。
使用R/S分析法计算Hurst指数[11-12]。取一个时间序列IMF1(t)(t=1, 2, …),对于任意正整数τ≥1(τ=1, 2, …, n),该时间序列的平均可表示为:
| $ \mathrm{IMF}_{1 \tau}=\frac{1}{\tau} \sum\limits_{t=1}^{\tau} \operatorname{IMF}_{1}(t) $ | (1) |
累积差X(t)可表示为:
| $ X(t, \tau)=\sum\limits_{u=1}^{t}\left(\mathrm{IMF}_{1}(u)-\mathrm{IMF}_{1 \tau}\right) $ | (2) |
将同一个τ值对应的X(t)的最大值与最小值之差称为极差,记为:
| $ R(\tau)=\max X(t, \tau)-\min X(t, \tau) $ | (3) |
Hurst标准偏差可表示为:
| $ S(\tau)=\left[\frac{1}{\tau} \sum\limits_{t=1}^{\tau}\left(\operatorname{IMF}_{1}(t)-\operatorname{IMF}_{1 \tau}\right)^{2}\right]^{1 / 2} $ | (4) |
在Hurst指数的基础上,可得到更广泛的指数律:
| $ R / S=(\tau / 2)^{H} $ | (5) |
式中,H为Hurst系数。
1.2 AKF混合模态中有用信息与噪声信息共存,因此需对其进行滤波处理。本文采用加入遗忘因子的AKF对信号进行滤波处理。
将卡尔曼状态方程和量测方程设为:
| $ \left\{\begin{array}{l} \boldsymbol{X}(k)=\boldsymbol{F} \boldsymbol{X}(k-1)+\boldsymbol{W}(k) \\ \boldsymbol{Z}(k)=\boldsymbol{H} \boldsymbol{X}(k)+\boldsymbol{V}(k) \end{array}\right. $ | (6) |
式中,X(k)为k时刻的状态向量,取陀螺仪的输出时间序列;F为状态转移矩阵;Z(k)为k时刻对应的量测向量;H为观测矩阵;W(k)、V(k)分别为k时刻系统噪声和量测噪声,且为不相关的零均值白噪声。卡尔曼滤波算法流程如下:
| $ \left\{\begin{array}{l} \hat{\boldsymbol{X}}_{k / k-1}=\boldsymbol{F}_{k / k-1} \hat{\boldsymbol{X}}_{k-1} \\ \boldsymbol{P}_{k / k-1}=\boldsymbol{F}_{k / k-1} \boldsymbol{P}_{k-1} \boldsymbol{F}_{k / k-1}^{\mathrm{T}}+\boldsymbol{W} \\ \hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}_{k / k-1}+\boldsymbol{K}_{k}\left(\boldsymbol{Z}_{k}+\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1}\right) \\ \boldsymbol{K}_{k}=\boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1}+\boldsymbol{V}\right)^{-1} \\ \boldsymbol{P}_{k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1} \end{array}\right. $ | (7) |
式中,Pk/k-1为当前时刻状态预测协方差矩阵。在卡尔曼滤波时间更新中求取Pk/k-1时乘以相应的遗忘因子[13],以抑制历史状态信息产生的影响:
| $ \boldsymbol{P}_{k / k-1}=\lambda_{k+1} \boldsymbol{F}_{k / k-1} \boldsymbol{P}_{k-1} \boldsymbol{F}_{k / k-1}^{\mathrm{T}}+\boldsymbol{W}_{k-1} $ | (8) |
遗忘因子求取方式为[14]:
| $ \lambda_{k}=\max \left\{1, \operatorname{tr}\left(\boldsymbol{N}_{k}\right) / \operatorname{tr}\left(\boldsymbol{M}_{k}\right)\right\} $ | (9) |
其中,
| $ \boldsymbol{M}_{k} =\boldsymbol{H}_{k} \boldsymbol{F}_{k / k-1} \boldsymbol{P}_{k-1} \boldsymbol{F}_{k / k-1}^{\mathrm{T}} \boldsymbol{H}_{k}^{\mathrm{T}} $ | (10) |
| $ \boldsymbol{N}_{k} =\boldsymbol{C}_{k}-\boldsymbol{H}_{k} \boldsymbol{W}_{k-1} \boldsymbol{H}_{k}^{\mathrm{T}}-\boldsymbol{V}_{k} $ | (11) |
式中,残差协方差Ck=HkPk/k-1HkT+Vk。
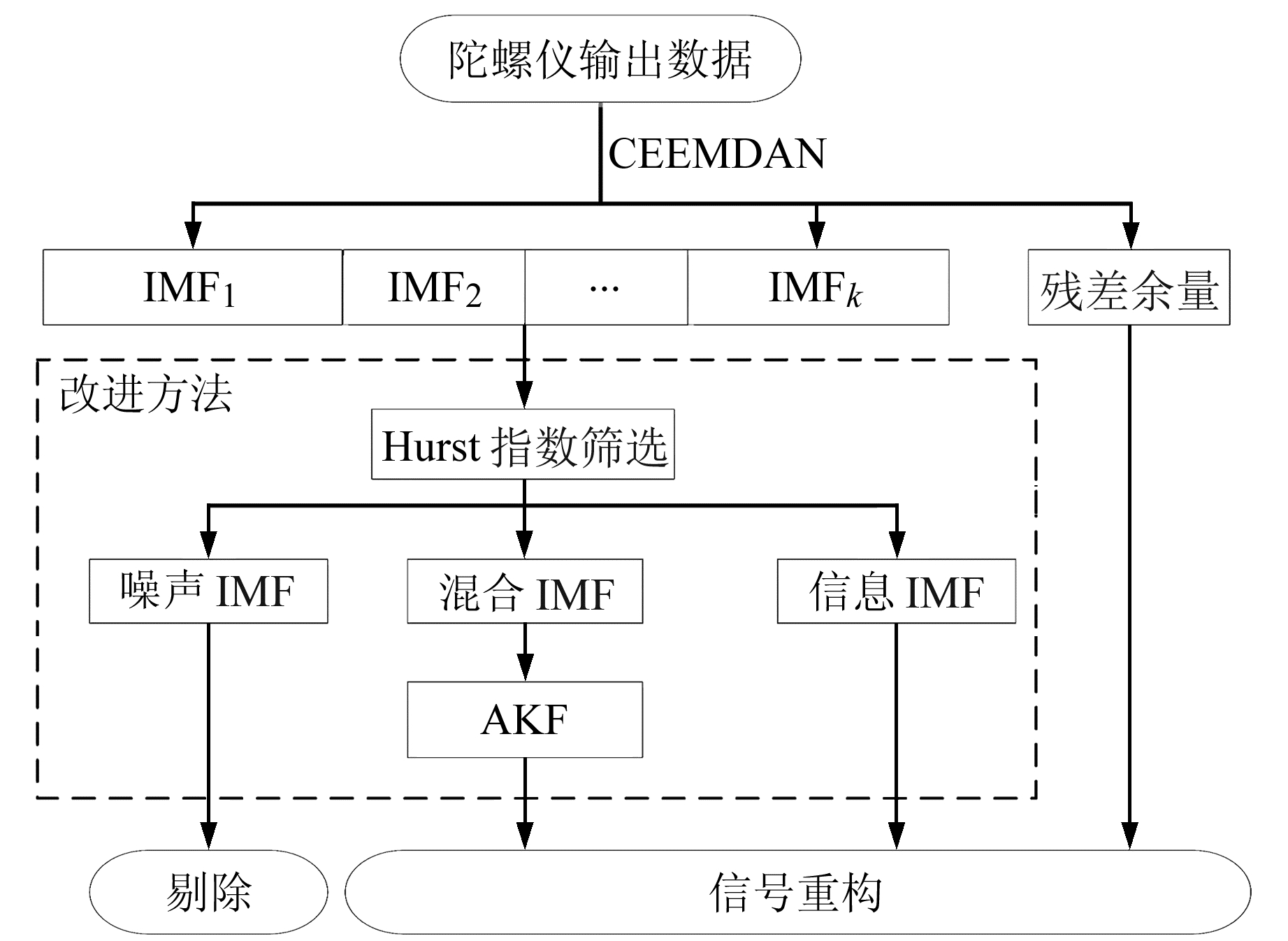
1.3 引入Hurst指数的去噪模型原始信号经CEEMDAN处理后,采用Hurst指数作为模态筛选机制,选择Hurst指数的最低点为噪声模态分量与混合模态分量的分界点M1;将Hurst指数值超过0.5的临界点作为混合模态分量与信息模态分量的分界点M2。本文将本征模态函数划分为噪声IMF、混合IMF和信息IMF。剔除噪声IMF,保留信息IMF,采用AKF处理混合IMF,将滤波后的混合IMF、信息IMF和残差余量进行重构,得到去噪后的信号,具体流程见图 1。
|
图 1 去噪方法流程 Fig. 1 Flow chart of denoising method |
去噪方法大致步骤如下:
1) 对原始陀螺信号s(t)进行CEEMDAN处理,得到n阶IMF和1个残差余量;
2) 计算各IMF分量的Hurst值,确定不同模态分量边界;
3) 采用AKF对混合模态进行滤波处理;
4) 将滤波后的IMF分量及保留的信息模态进行重构,得到去噪后的信号:
| $ s^{\prime}(t)=\sum\limits_{k=M_{1}}^{M_{2}} \operatorname{IMF}_{k}(t)+\sum\limits_{k=M_{2}}^{n} \operatorname{IMF}_{k}(t)+r(t) $ | (12) |
5) 用信噪比(SNR)和均方根误差(RMSE)评价降噪效果。
2 实验分析 2.1 信号分解实验所用陀螺仪为STIM300惯性测量单元,采样时间为3 h,采样频率为100 Hz,陀螺仪参数见表 1。
|
|
表 1 陀螺仪参数 Tab. 1 Gyroscope parameters |
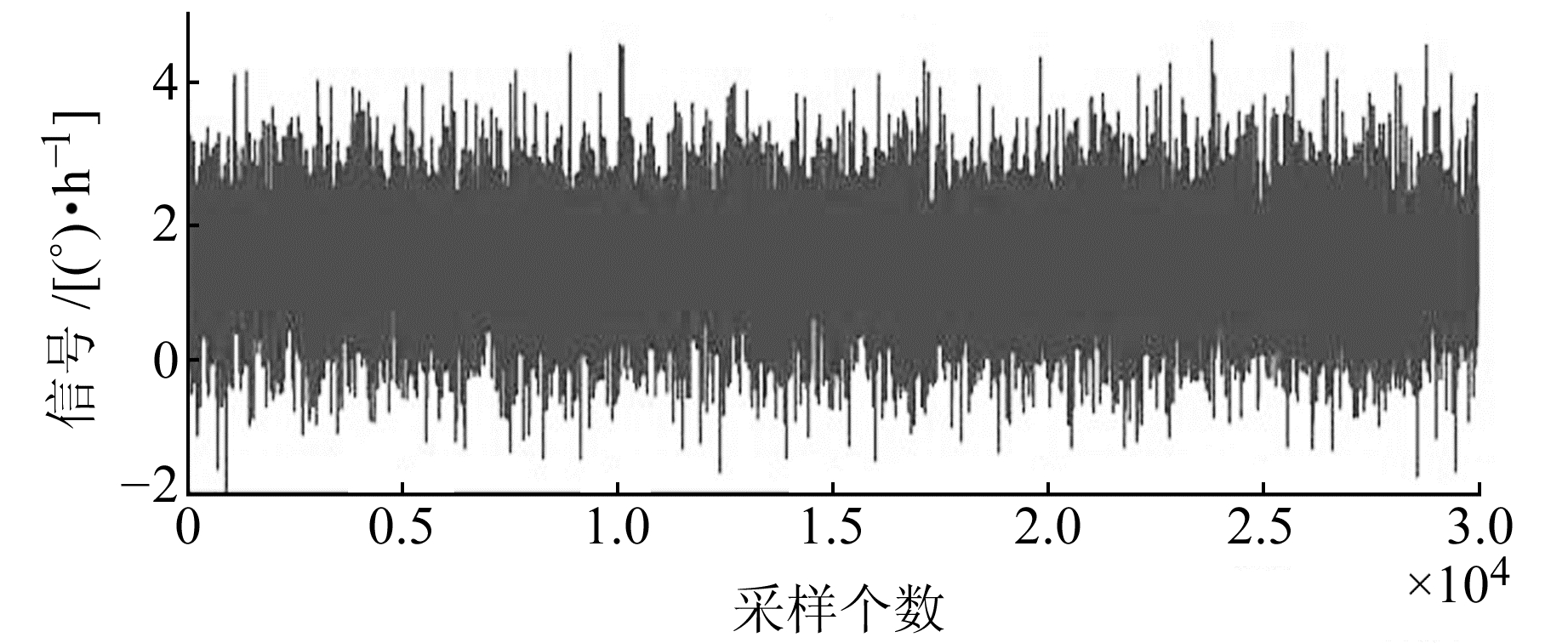
选择3 h静止数据中的5 min进行实验分析,原始信号见图 2。
|
图 2 陀螺仪原始信号 Fig. 2 Gyroscope original signals |
对原始信号分别进行EMD、EEMD和CEEMDAN处理,并将分解后的模态分量直接重构,3种方法误差对比见表 2。
|
|
表 2 不同分解方法误差对比 Tab. 2 Error comparison of different decomposition methods |
从表 2可以看出,EMD和CEEMDAN误差量级太小可忽略不计,EEMD重构误差较大。
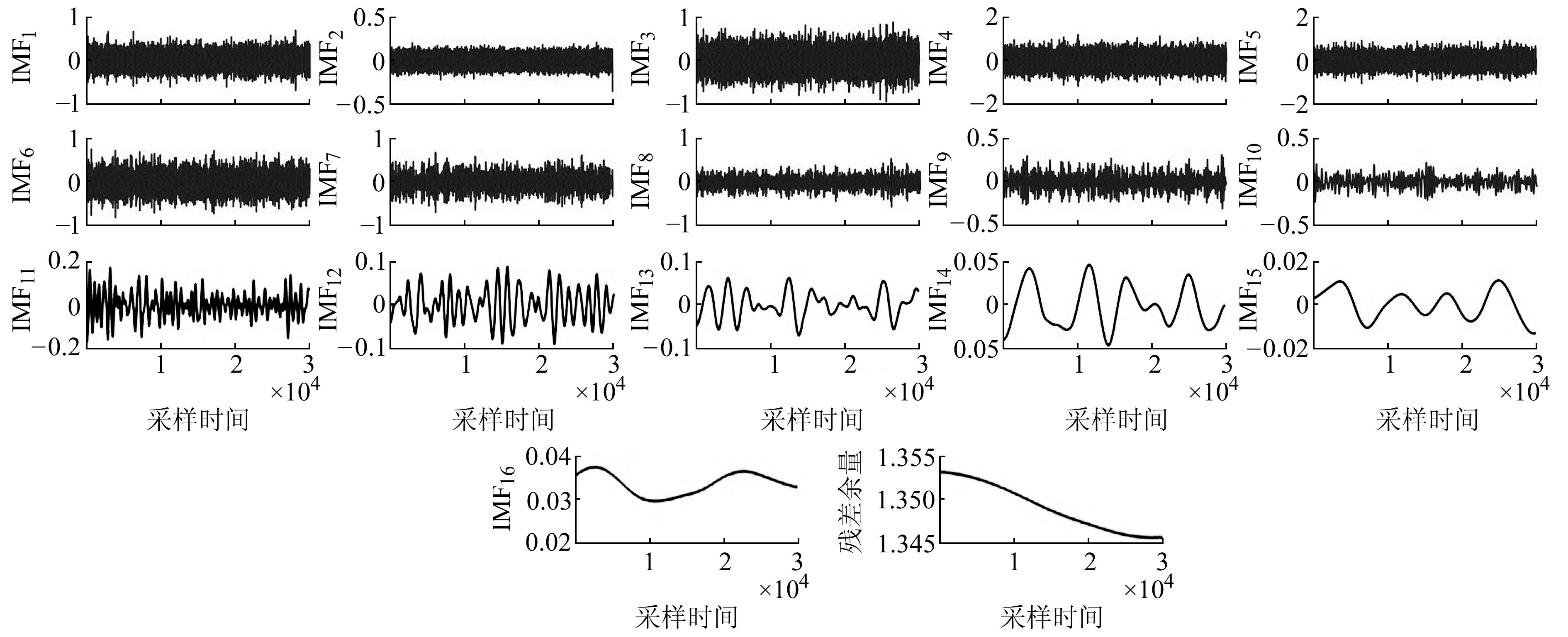
使用CEEMDAN方法将原始信号分解为16阶IMF分量和1个残差余量,结果见图 3。
|
图 3 IMF分量 Fig. 3 IMF components |
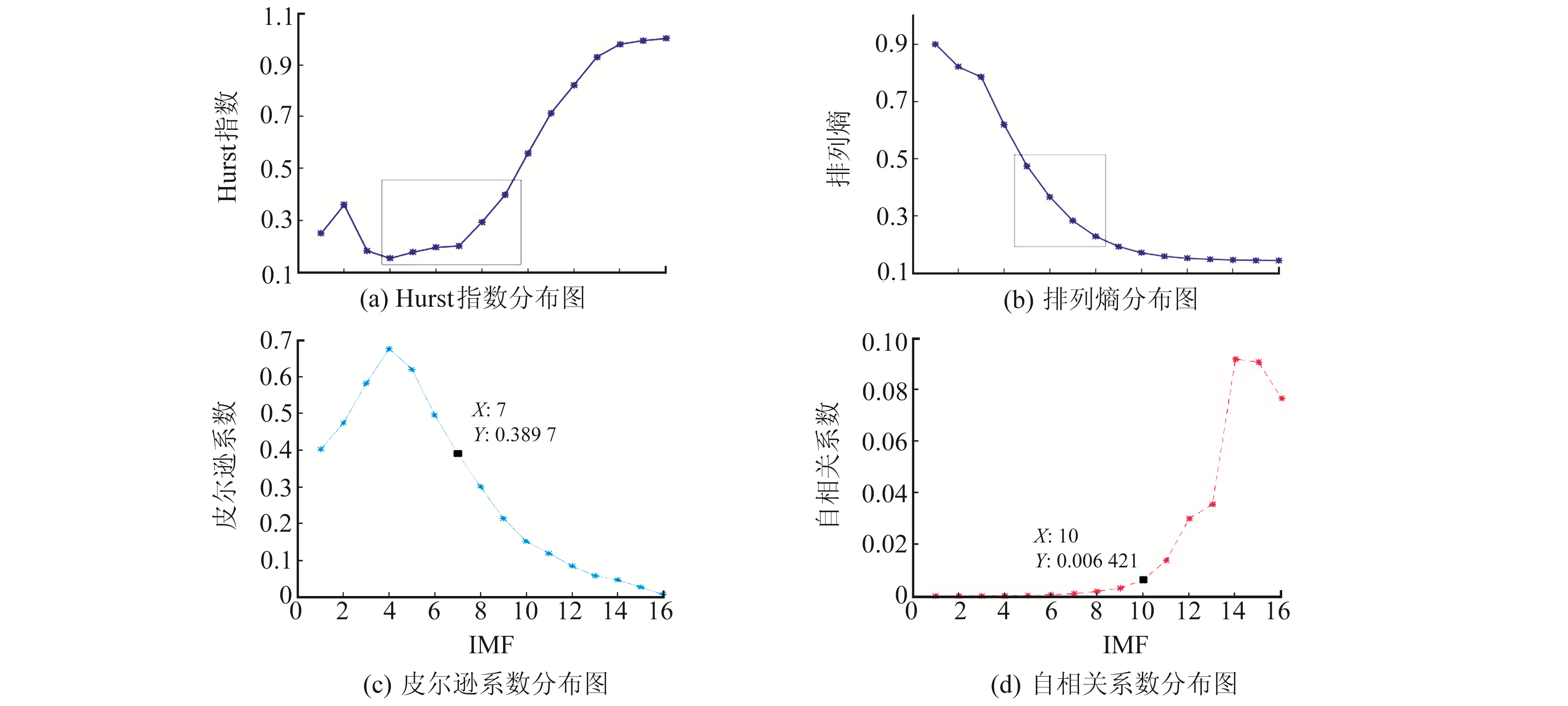
用Hurst指数筛选机制、排列熵和相关系数法分别筛选CEEMDAD处理后的模态分量,其中相关系数法分别采用皮尔逊系数和自相关系数确定上下界,结果见图 4。
|
图 4 相关性分布 Fig. 4 Correlation distribution |
从图 4(a)可以看出,Hurst值呈现先降低后上升的趋势,在模态阶数较小时,IMF分量中噪声信号占比较大,Hurst指数呈负相关,且相关性逐渐增大;随着阶数升高,IMF中噪声成分逐渐减少,噪声对信号的影响随之减小,在IMF5之后Hurst值持续上升,由强负相关逐渐转为正相关。因此,将Hurst指数最低点确定为噪声模态与混合模态的分界点M1,将H=0.5作为混合模态与信息模态的分界线,从而确定M2。从图 4(a)还可以看出,IMF4的Hurst指数最低,为0.154 5;IMF10的Hurst指数超过0.5,为0.559 6。因此,M1=4为噪声模态分量与混合模态分量的分界点,M2=9为混合模态分量与信息模态分量的分界点。
比较3种方法的分界点和运行时间,结果见表 3。可以看出,不同筛选机制确定的分界点不同,但均在一个区间内;排列熵法的运行时间最长,Hurst指数法所需时间最少。
|
|
表 3 筛选结果对比 Tab. 3 Comparison of screening results |
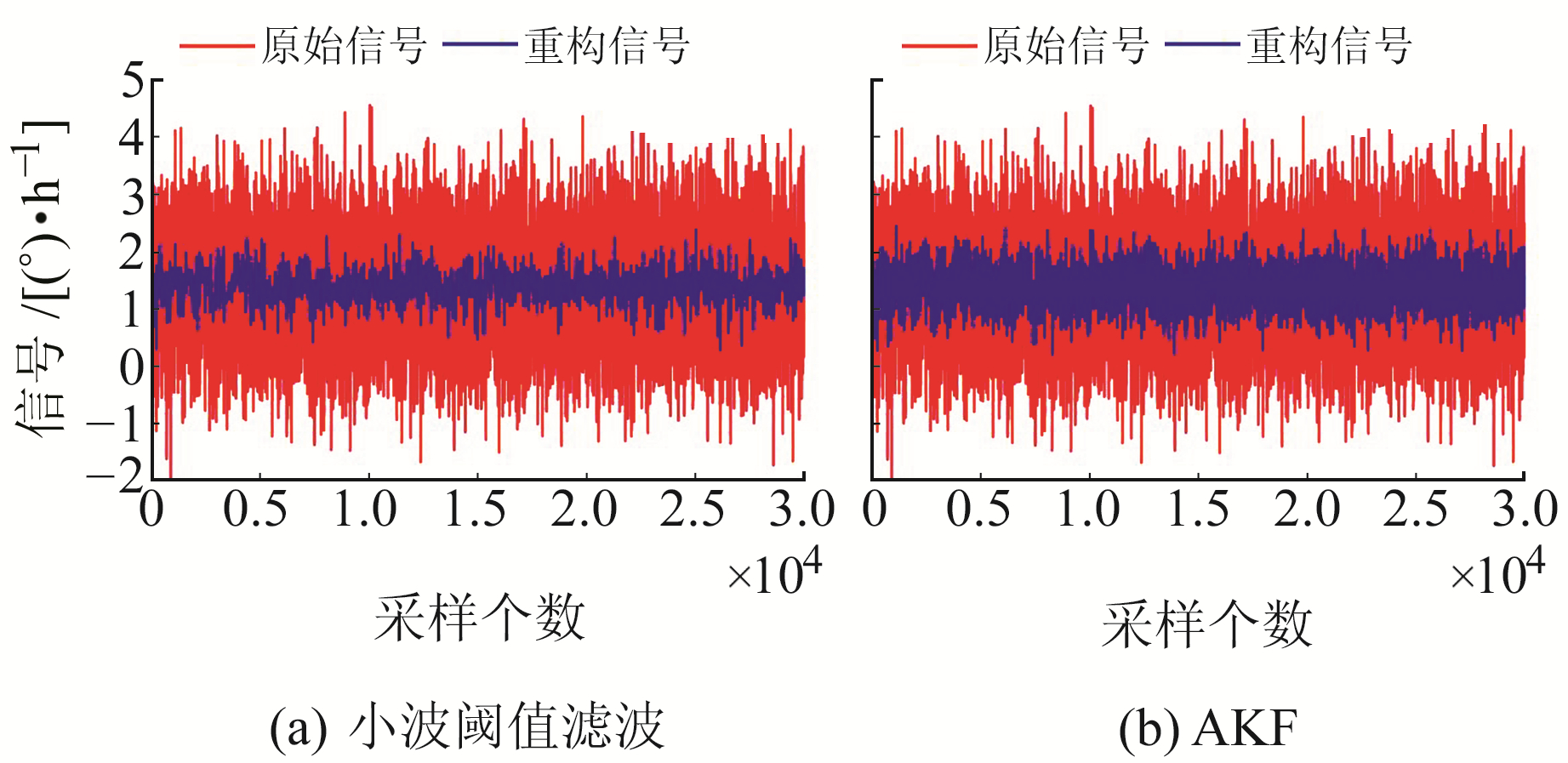
滤波后对混合模态分量进行重构能够有效提升信号的信噪比,本文采用AKF处理混合模态分量,并与小波阈值滤波结果进行对比,结果见图 5。可以看出,2种方法均能去除原始信号中的噪声。进一步分析表明,AKF既能滤除混合模态分量信号中的噪声,还可以有效保留混合模态中的有效信息;小波阈值滤波重构效果直观上优于AKF,但其可能会滤除掉信号中的有用信息。
|
图 5 不同滤波器重构效果 Fig. 5 Reconstruction effect of different filters |
将上节中3种筛选机制得到的混合模态分别进行处理并重构信号,计算其SNR及RMSE,结果见表 4。
|
|
表 4 去噪模型评价 Tab. 4 Denoising model evaluation |
由表 4可以看出,使用同样的滤波方法或筛选方法,本文提出的模型均具有较好的处理效果。使用AKF处理混合模态,Hurst指数筛选机制方法处理得到的信号SNR较排列熵法提高约12%,较相关系数法提高约36%;RMSE较排列熵法降低约10%,较相关系数法降低约23%。采用Hurst指数筛选机制,AKF处理混合模态后重构信号的SNR较小波阈值滤波法提高约36%,RMSE较小波阈值滤波法降低约23%。
3 结语本文采用CEEMDAN方法将陀螺仪原始信号分解为一系列频率由高到低的IMF分量和1个残差余量,通过Hurst筛选机制将IMF分量划分为噪声模态分量、混合模态分量和信息模态分量,并使用AKF处理混合模态分量后重构信号。实验分析表明,本文提出的模型较其他传统方法具有更高的重构精度和计算效率。
| [1] |
马群, 王庆, 阳媛, 等. 基于Allan方差的MEMS陀螺仪随机误差辨识与抑制[J]. 传感器与微系统, 2019, 38(6): 62-65 (Ma Qun, Wang Qing, Yang Yuan, et al. Random Error Identification and Suppression of MEMS Gyroscope Based on Allan Variance[J]. Transducer and Microsystem Technologies, 2019, 38(6): 62-65)
(  0) 0) |
| [2] |
李文华, 汪立新, 沈强, 等. 基于EMD的MEMS陀螺仪随机漂移分析方法[J]. 北京航空航天大学学报, 2021, 47(9): 1 927-1 932 (Li Wenhua, Wang Lixin, Shen Qiang, et al. Random Drift Analysis Method of MEMS Gyroscope Based on EMD[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(9): 1 927-1 932)
(  0) 0) |
| [3] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1 971): 903-995
(  0) 0) |
| [4] |
陈光武, 李文元, 于月. 基于模糊间隔阈值EMD的微机械陀螺消噪[J]. 光学精密工程, 2019, 27(4): 922-931 (Chen Guangwu, Li Wenyuan, Yu Yue. MEMS Gyro Denoising Based on Fuzzy Interval Threshold EMD[J]. Optics and Precision Engineering, 2019, 27(4): 922-931)
(  0) 0) |
| [5] |
Torres M E, Colominas M A, Schlotthauer G, et al. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise[C]. IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP), Prague, 2011
(  0) 0) |
| [6] |
张宁, 刘友文. 基于CEEMDAN改进阈值滤波的微机电陀螺信号去噪模型[J]. 中国惯性技术学报, 2018, 26(5): 665-669 (Zhang Ning, Liu Youwen. Signal De-Noising Model for MEMS Gyro Based on CEEMDAN Improved Threshold Filtering[J]. Journal of Chinese Inertial Technology, 2018, 26(5): 665-669)
(  0) 0) |
| [7] |
戴邵武, 陈强强, 刘志豪, 等. 基于MEEMD与FLP的光纤陀螺去噪[J]. 光电工程, 2020, 47(6): 3-11 (Dai Shaowu, Chen Qiangqiang, Liu Zhihao, et al. De-Noising Algorithm for FOG Based on MEEMD and FLP Algorithm[J]. Opto-Electronic Engineering, 2020, 47(6): 3-11)
(  0) 0) |
| [8] |
徐朗, 蔡德所. 基于最小二乘平滑滤波与CEEMDAN的光纤陀螺信号处理研究[J]. 振动与冲击, 2020, 39(10): 269-278 (Xu Lang, Cai Desuo. Research on Signal Processing of Fiber Optic Gyroscope Based on Least Square Smooth Filtering and CEEMDAN[J]. Journal of Vibration and Shock, 2020, 39(10): 269-278)
(  0) 0) |
| [9] |
徐朗, 蔡德所. CEEMDAN与小波变换混合去噪方法在光纤陀螺监测系统信号去噪中的应用[J]. 水利水电技术, 2018, 49(9): 87-95 (Xu Lang, Cai Desuo. Application of De-Noising Method Mixed with CEEMDAN and Wavelet Transform to Signal De-Noising for Fiber Optic Gyro Monitoring System[J]. Water Resources and Hydropower Engineering, 2018, 49(9): 87-95)
(  0) 0) |
| [10] |
耿庆庆, 李瑞琦, 杨茉. Hurst指数在判别火灾轰燃中的应用[J]. 化工学报, 2019, 70(增2): 369-375 (Geng Qingqing, Li Ruiqi, Yang Mo. Application of Hurst Index in Judging Fire Flashover[J]. CIESC Journal, 2019, 70(S2): 369-375)
(  0) 0) |
| [11] |
潘雅婧, 王仰麟, 彭建, 等. 基于小波与R/S方法的汉江中下游流域降水量时间序列分析[J]. 地理研究, 2012, 31(5): 811-820 (Pan Yajing, Wang Yanglin, Peng Jian, et al. Precipitation Change in Middle and Lower Reaches of Hanjiang River: Based on Wavelet Analysis and R/S Analysis[J]. Geographical Research, 2012, 31(5): 811-820)
(  0) 0) |
| [12] |
王孝礼, 胡宝清, 夏军. 水文时序趋势与变异点的R/S分析法[J]. 武汉大学学报: 工学版, 2002, 35(2): 10-12 (Wang Xiaoli, Hu Baoqing, Xia Jun. R/S Analysis Method of Trend and Aberrance Point on Hydrological Time Series[J]. Engineering Journal of Wuhan University, 2002, 35(2): 10-12)
(  0) 0) |
| [13] |
Gao B B, Gao S S, Zhong Y M, et al. Interacting Multiple Model Estimation-Based Adaptive Robust Unscented Kalman Filter[J]. International Journal of Control, Automation and Systems, 2017, 15(5): 2 013-2 025 DOI:10.1007/s12555-016-0589-2
(  0) 0) |
| [14] |
黄剑雄, 刘小雄, 章卫国, 等. 基于视觉/惯导的无人机组合导航算法研究[J]. 计算机测量与控制, 2021, 29(2): 137-143 (Huang Jianxiong, Liu Xiaoxiong, Zhang Weiguo, et al. Research on Vision/Inertial Based Integrated Navigation Technology of UAVs[J]. Computer Measurement and Control, 2021, 29(2): 137-143)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


