2. 南昌市城市规划设计研究总院,南昌市春晖路599号,330038
如何有效削弱原始时序信号中的各种噪声影响一直是GNSS时序分析的研究热点之一。钱文龙等[1]将改进的经验模态分解(empirical mode decomposition, EMD)算法应用于GPS信号降噪,效果良好,但会出现一定的端点效应及模态混叠现象;张恒璟等[2]改进了基于连续均方误差准则的EEMD噪声识别方法,可以正确识别信号与噪声的分界点,但不具备较高的自适应性;Tao等[3]应用经验小波变换(empirical wavelet transform, EWT)进行GNSS数据降噪,可以较好地反映原始信号的细节特征,降噪效果明显,且不会发生模态混叠及端点现象,但无法自适应选择阈值去除高频噪声。针对以上问题,本文设计一种引入样本熵(sample entropy, SE)优化的EWT-NLM算法应用于GNSS坐标时间序列降噪中,并通过模拟数据和实测数据验证其有效性。
1 原理与方法首先对原始信号进行EWT分解,获取一系列经验小波分量和经验尺度分量,以SE为有效信息分量与混合噪声分量的分界标准,分别提取低频信息分量与中高频混合噪声分量,再对混合噪声分量进行NLM滤波,最后重构有效信息分量和滤波分量得到最终降噪信号。
1.1 EWTEWT算法的核心思想是将原始信号进行傅里叶变换,分割所获取的傅里叶频谱,对不同的分界频率构建经验小波,确定经验尺度函数和经验小波函数后,再进行反傅里叶变换,最后获取具有紧支撑傅里叶频谱的调幅-调频(AM-FM)成分,具体原理见文献[4-5]。其简要过程如下:1)对原始时序信号进行傅里叶变换,求得在支撑区间(0,π)的傅里叶频谱F(ω);2)对傅里叶频谱F(ω)作自适应分割,分解为N个频带与N-1个分界频率;3)根据各分界频率构建经验小波φ(ω),确定经验尺度函数和经验小波函数,再对F(ω)φ(ω)进行反傅里叶变换,获取各模态分量。
原始GNSS坐标信号x(t)进行EWT分解后,分解为1+N个经验模态分量,其中包含1个代表信号整体趋势变化的经验尺度分量和N个代表不同信号频域特征的经验小波分量:
| $ x(t)=f_{0}+\sum\limits_{k=1}^{N} f_{k} $ | (1) |
EWT算法不能准确确定以噪声为主导的经验小波分量界限,而SE可以反映非平稳信号的复杂程度,熵值大表示原始信号中的噪声信号占比高,即噪声信号特征明显;熵值小表示原始信号的趋势性、周期性规律较好,即噪声信号特征不明显。故引入SE来自适应划分信息分量的阈值,将其作为判别所有分量中信息分量与混合分量、噪声分量的标准,可以有效识别GNSS高程时间序列信号分量的界限。具体计算过程如下[6]:
1) 将时间跨度为L的原始时间序列信号x(i)构建为m维向量X(i):
| $ \begin{gathered} \boldsymbol{X}(i)=[x(i) x(i+1) \cdots x(i+m-1)], \\ i=1,2, \cdots, N-m-1 \end{gathered} $ | (2) |
2) 计算向量X(i)与X(j)的距离Dij:
| $ \begin{gathered} D_{i}^{j}=\max |\boldsymbol{X}(i+k)-\boldsymbol{X}(j+k)|, \\ 0<k<m-1 \end{gathered} $ | (3) |
3) 设定相似容限r,假设Ci为Dji小于r的数量,计算Ci与总时间跨度N-m-1的比值Cim(r)及其均值:
| $ C_{i}^{m}(r)=C_{i} /(N-m-1), i=1,2, \cdots, N-m $ | (4) |
| $ C^{m}(r)=\sum\limits_{i=1}^{N-m} C_{i}^{m} /(N-m) $ | (5) |
4) 令m=m+1, 重复上述步骤得Cm+1(r)。
5) 因时间跨度L为有限数,SE值可表示为:
| $ \mathrm{SE}(m, r, L)=\lim \limits_{L \rightarrow m}\left[-\ln \frac{C^{m+1}(r)}{C^{m}(r)}\right] $ | (6) |
可以看出,参数m和r的设定会直接影响熵值。据已有研究,一般m取2, r取原始信号标准差的0.1~0.25倍,考虑到实测GNSS信号的复杂性,本文取r=0.25σ(X)[6]。
1.3 NLM滤波从原始信号中提取出信息分量后,有部分真实信息湮没在混合经验小波分量及噪声小波分量之中,利用NLM算法可以有效地对剩余信号进行降噪,从而获取残余真实信息。NLM算法利用原始信号的自相似特性进行滤波,其设置一个检索跨度窗口,在此跨度内尽可能多地搜寻相似值,然后运用加权平均值获取实际GNSS残差噪声中的真实值,即可以反映原始信号的细节变化,达到降噪的目的[7]。假设噪声信号为x(i),降噪后信号为x(i),则有:
| $ \bar{x}(i)=\sum\limits_{j \in l_{i}} x(i) \omega(i, j) / \sum\limits_{j \in l_{i}} \omega(i, j) $ | (7) |
式中,ω表示两点之间的相似度,即权重,其由两点之间的距离决定,且满足0 < ω < 1,∑ω=1:
| $ \omega(i, j)=\exp \left\{-\frac{\sum\limits_{\delta \in B}[v(i+\delta)-v(j+\delta)]}{2 S \lambda^{2}}\right\} $ | (8) |
式中,B是以i点为中心的相似区域,S为区域B中点的个数,λ为滤波器参数,v为时序值。
1.4 优化的EWT-NLM算法优化的EWT-NLM算法的具体步骤如下:1)对原始信号x(i)进行EWT分解,获取1+N个模态分量。2)计算各分量的SE值,其中,重构维数m=2,阈值r=0.25σ(x),σ为标准差。通过经验阈值判定,将经验尺度、小波分量划分为有效信息分量和混合噪声分量。3)对非信息分量(混合分量、噪声分量)进行NLM滤波。经过多次滤波实验,得到合适的滤波经验参数为:搜索窗口t=50,邻域窗口f=20,滤波参数h=250。4)将NLM滤波后的有效信号主导分量与信息分量重构为最终的降噪信号。
选取信噪比(Rsn)与均方根误差(RMSE)为降噪评价指标,计算公式为:
| $ R_{\mathrm{sn}}=10 \lg \left[\sum\limits_{i=0}^{L-1} x_{i}^{2} / \sum\limits_{i=0}^{L-1}\left(x_{i}-\bar{x}_{i}\right)^{2}\right] $ | (9) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{L} \sum\limits_{i=1}^{L}\left(x_{i}-\bar{x}_{i}\right)^{2}} $ | (10) |
式中,xi为原始时间序列信号,xi为降噪后信号,L为信号长度。
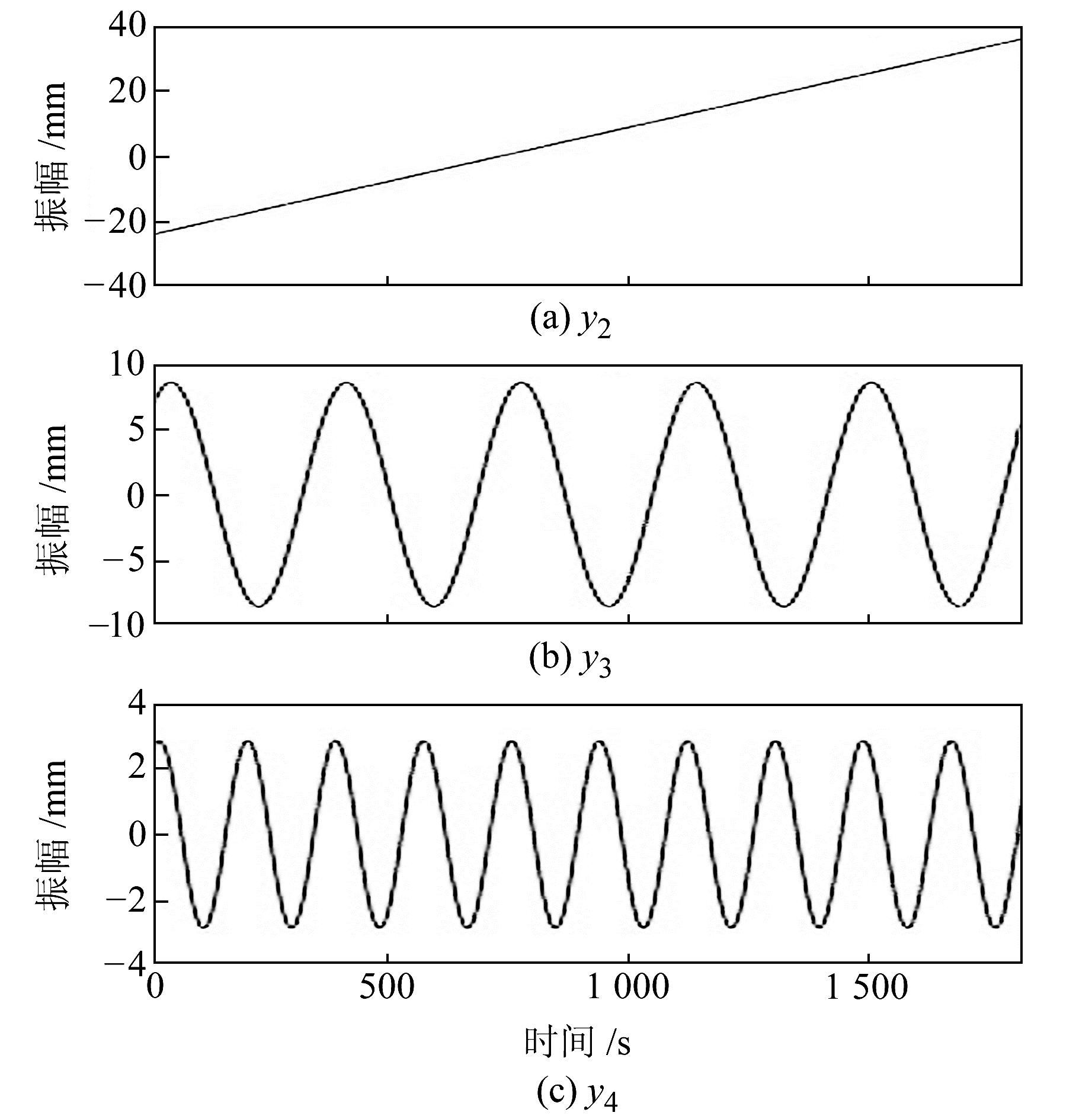
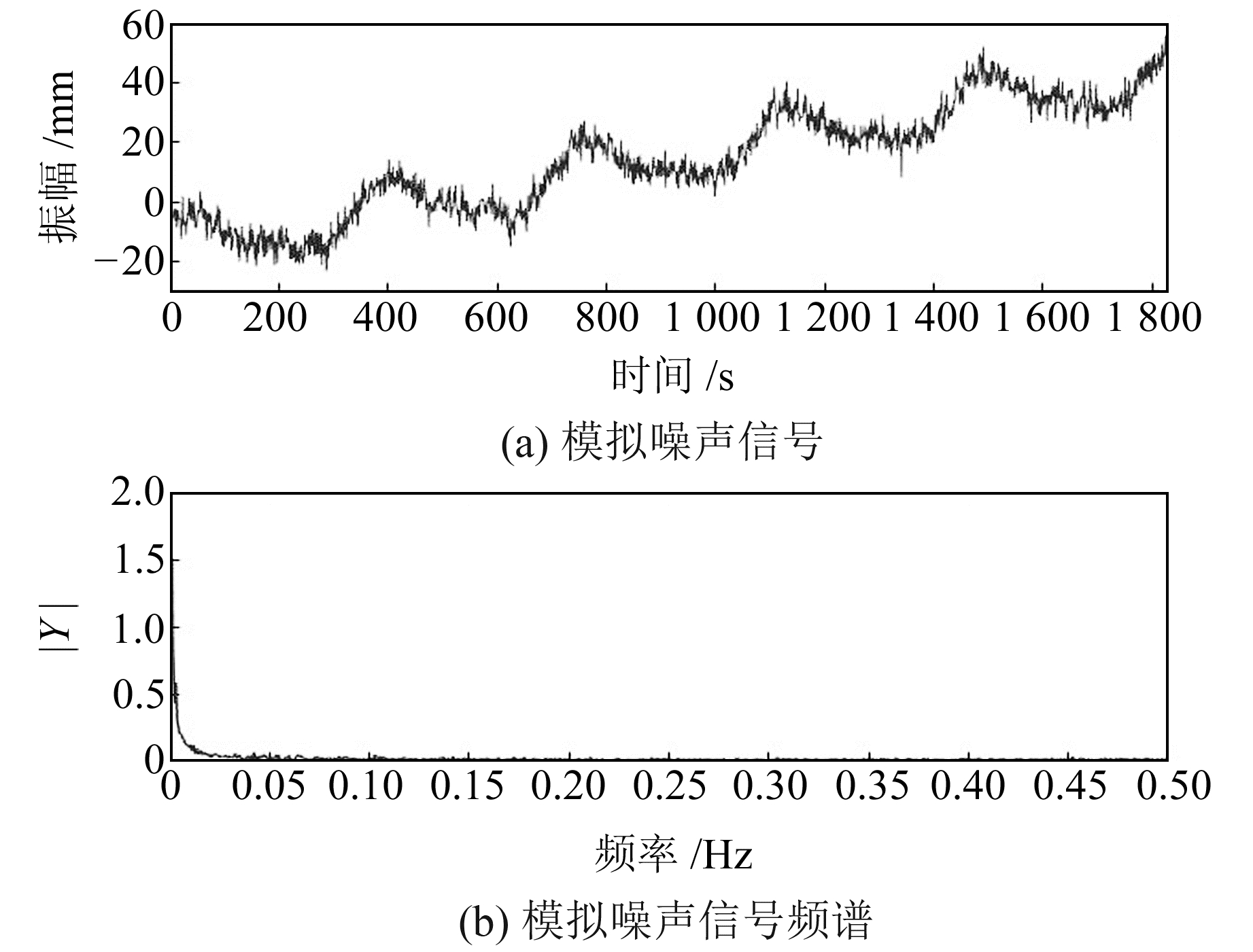
2 实验分析 2.1 模拟数据降噪分析模拟信号采样频率为1 Hz,采样点1 287个。不含噪声的模拟数据见式(11),各分量波形图见图 1。采用白噪声与有色噪声组合模型,见式(12)。包含噪声的模拟数据见式(13),模拟噪声信号及频谱图见图 2。
|
图 1 模拟信号各分量波形 Fig. 1 Waveform of each component of simulated signal |
|
图 2 模拟噪声信号及其频谱 Fig. 2 Simulated noise signal and its spectrum |
| $ \begin{gathered} y_{1}=8, y_{2}=12 t_{i}, \\ y_{3}=6 \sin \left(\frac{2}{5} {\rm{ \mathsf{ π} }} t_{i}\right)+6 \cos \left(\frac{2}{5} {\rm{ \mathsf{ π} }} t_{i}\right), \end{gathered} $ | (11) |
| $ \begin{gathered} y_{4}=2 \sin \left(\frac{2}{5} {\rm{ \mathsf{ π} }} t_{i}\right)+2 \cos \left(\frac{2}{5} {\rm{ \mathsf{ π} }} t_{i}\right) \\ \left\{\begin{array}{l} \boldsymbol{r}\left(t_{i}\right)=\boldsymbol{w}\left(t_{i}\right), i \leqslant 2 \\ \boldsymbol{r}\left(t_{i}\right)=f_{1} \boldsymbol{r}\left(t_{i-1}\right)+f_{2} \cdot \\ \ \ \ \boldsymbol{r}\left(t_{i-2}\right)+\boldsymbol{w}\left(t_{i}\right), i \geqslant 3 \end{array}\right. \end{gathered} $ | (12) |
式中,ti为坐标历元时刻,w(ti)为均值为0、信噪比为4的白噪声,f1和f2均为0.4。则:
| $ x=y_{1}+y_{2}+y_{3}+y_{4}+r_{t} $ | (13) |
式中,rt为组合噪声。
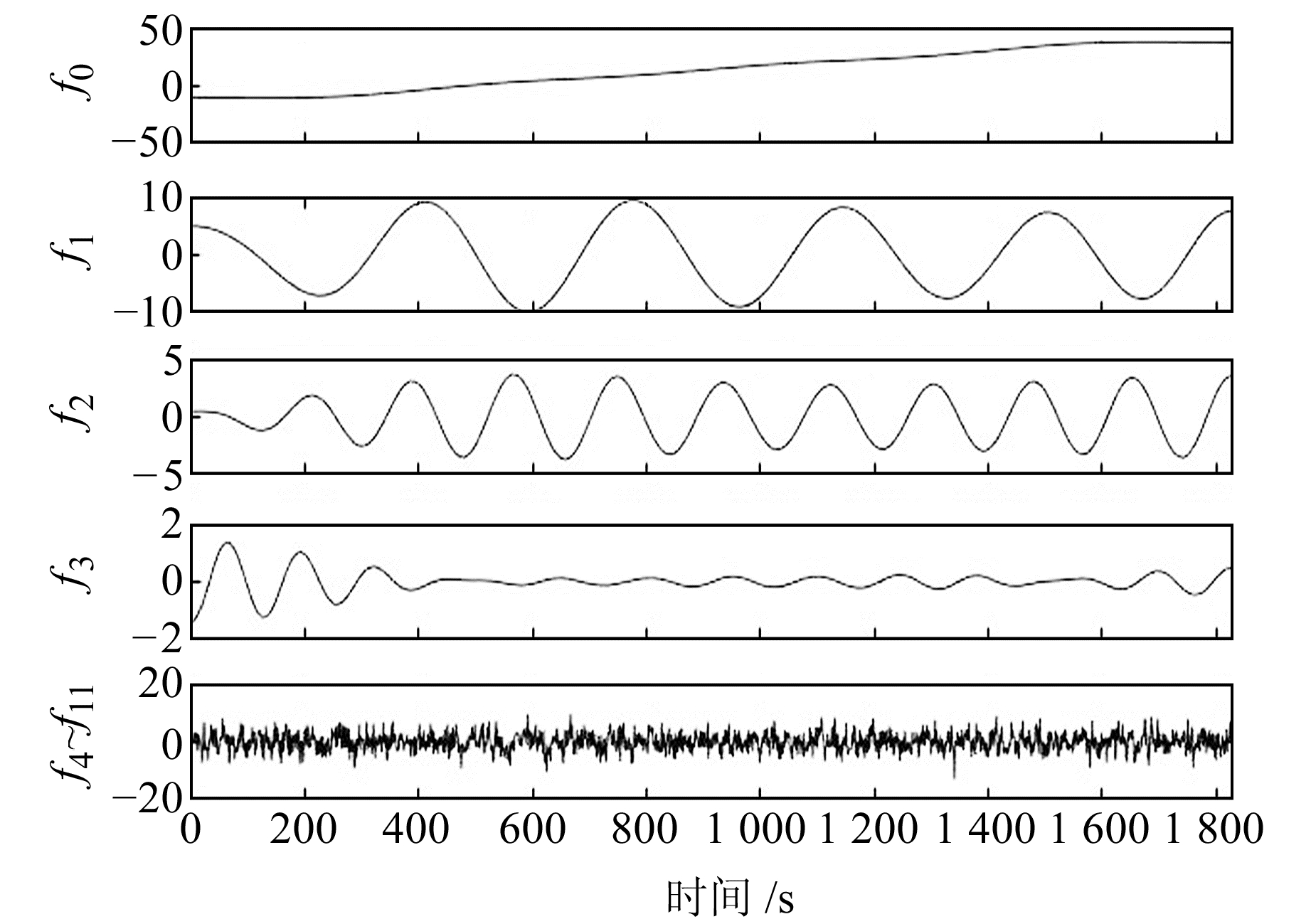
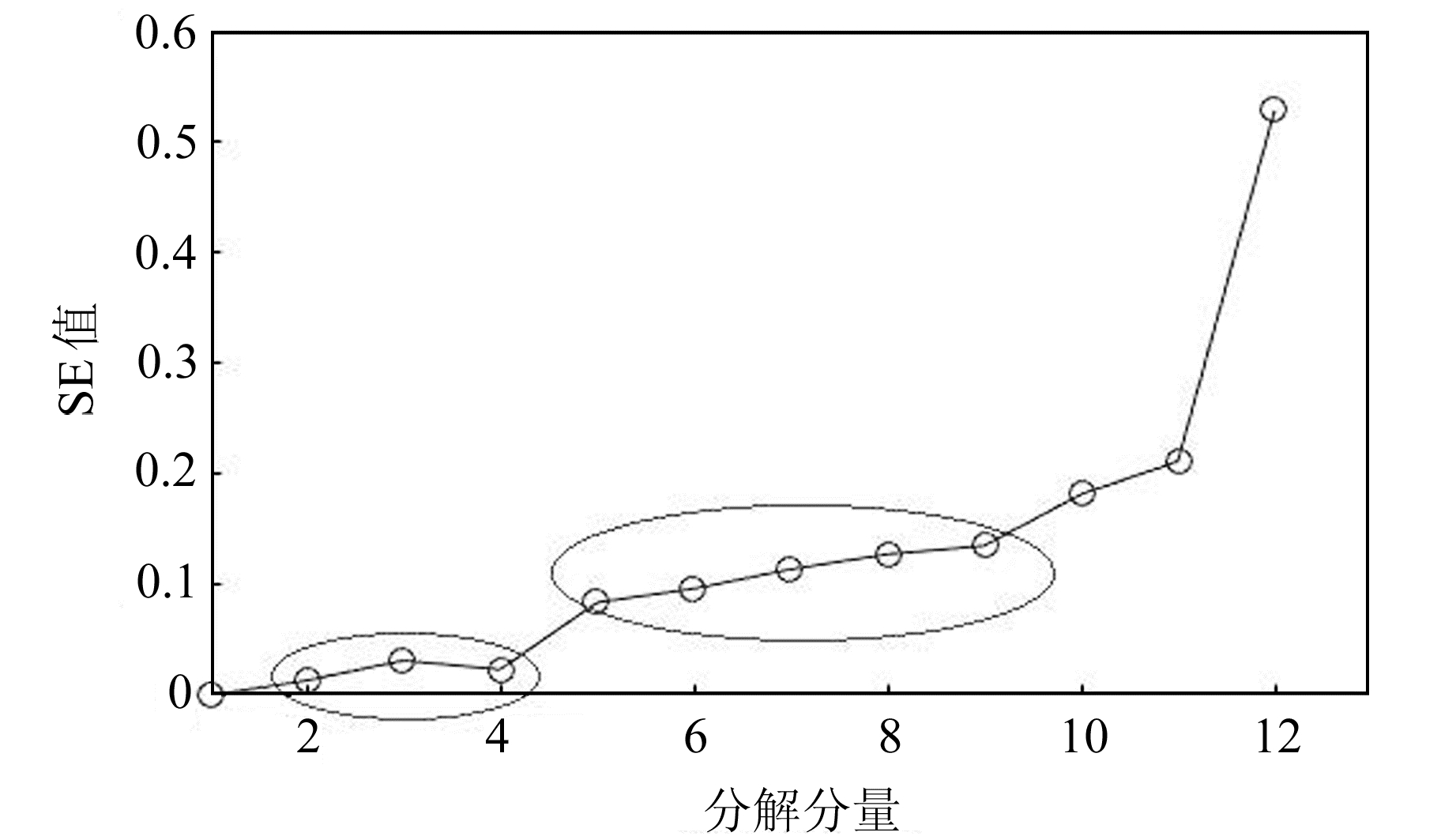
将模拟噪声信号进行EWT分解(图 3)。可以看出,原始信号被分解成1个经验尺度分量和11个经验小波分量(将f4~f11分量合并)。计算各分量SE值,结果见图 4。由图 3和4可见,分解所得的分量频率逐步增大,各分量SE值也依次增大,表明分量的不规则度逐渐增大。选取经验阈值0.05为有效信号界限[7]。可以发现,前4个分量的SE值小于0.05,表明前4个分量为信号主导的模态分量,第5~10个分量为混合信号分量,第11~12个分量大于0.2,为噪声主导的信号分量。
|
图 3 EWT分解模拟噪声信号 Fig. 3 Simulated noise signal decomposed by EWT |
|
图 4 各分量的SE值 Fig. 4 SE values of each component |
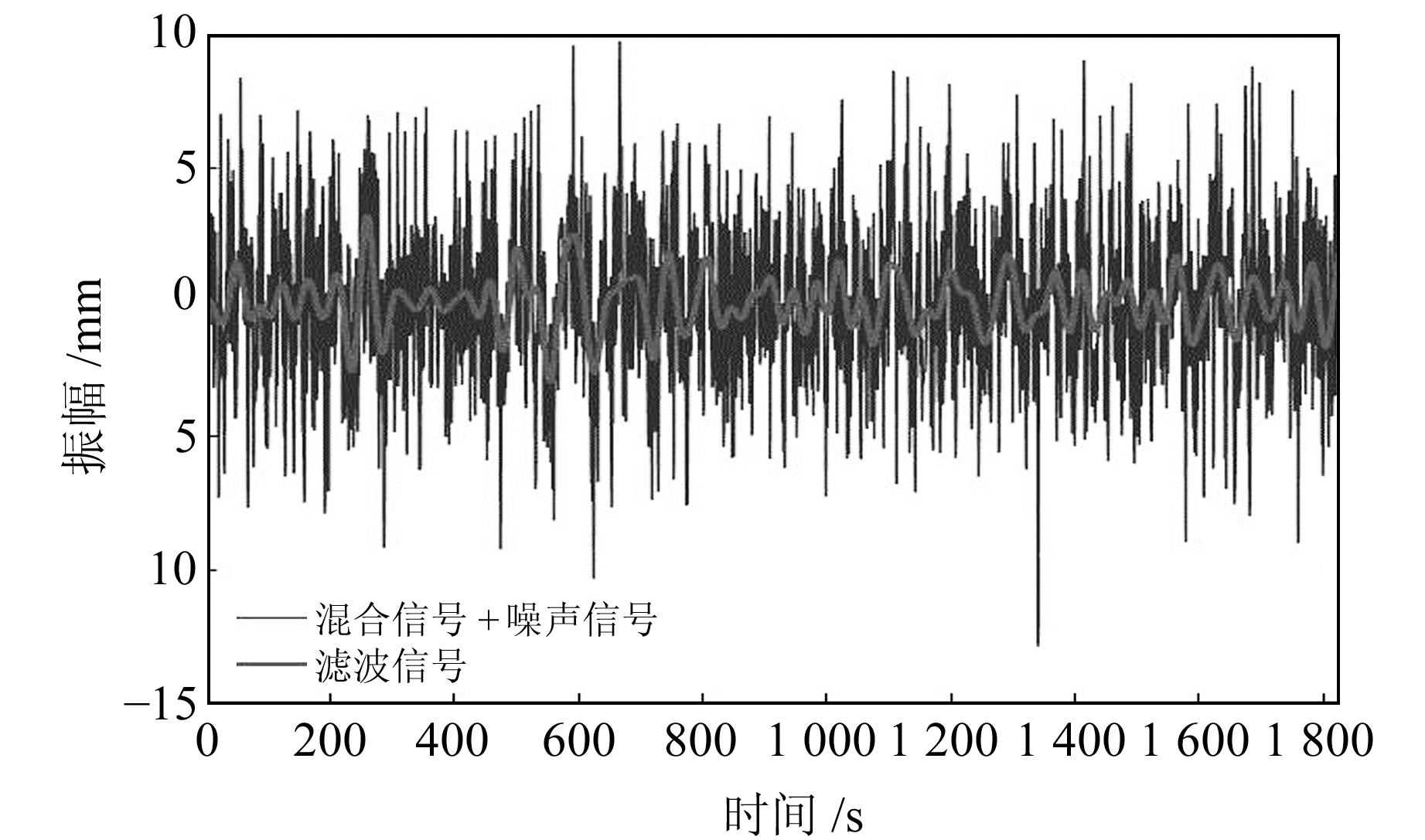
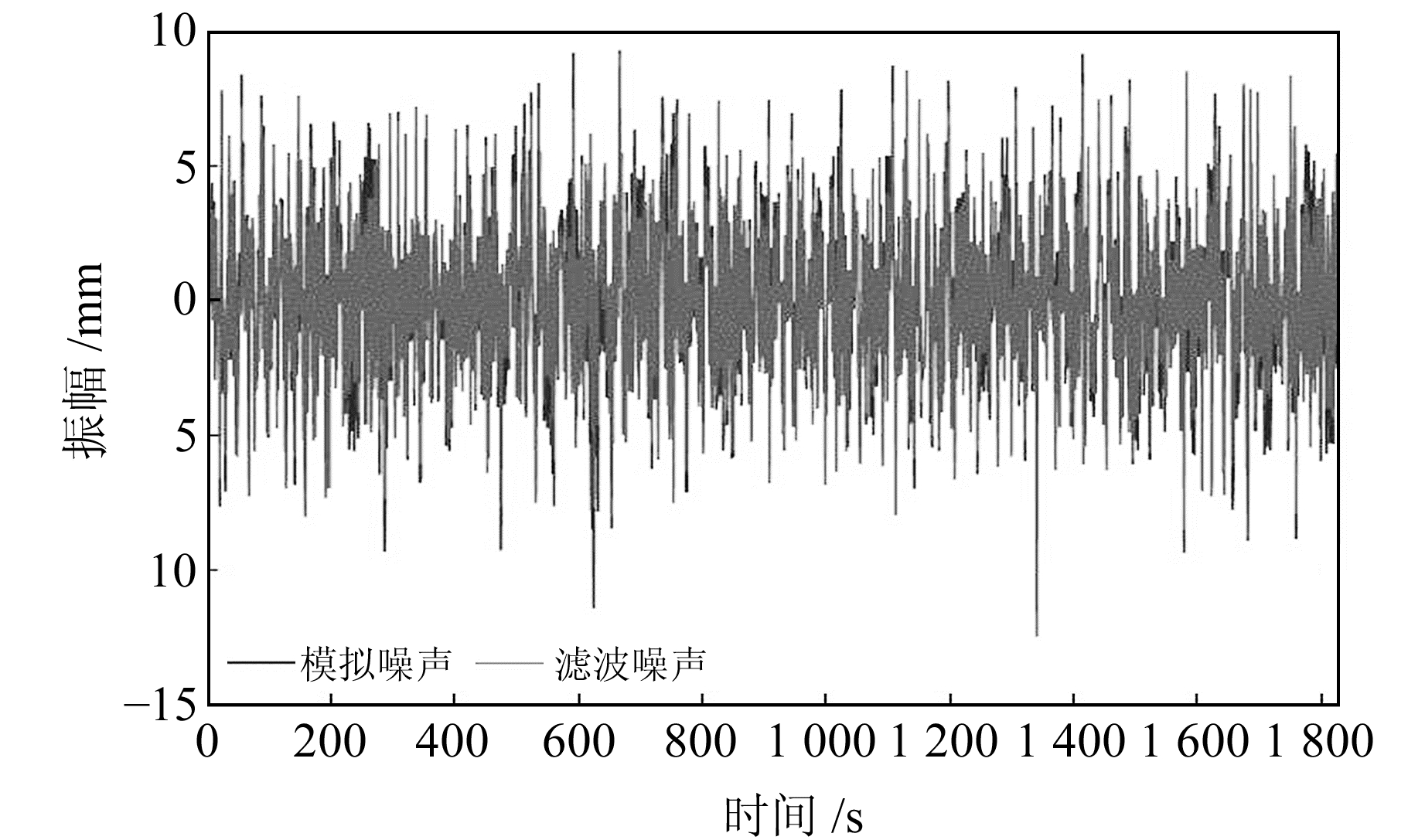
将混合分量和噪声分量重构后进行NLM滤波,结果见图 5。可以看出,NLM能有效滤除较大噪声,提取出混合噪声分量中能量占比较小的真实信号,较好地展示原始信号中的振荡周期变化。图 6为NLM滤波噪声与模拟噪声的对比。可以发现,模拟噪声和滤波噪声基本吻合。
|
图 5 NLM滤波结果 Fig. 5 NLM filtering results |
|
图 6 NLM滤波噪声与模拟噪声对比 Fig. 6 Comparison of NLM filtering noise and simulated noise |
采用自相关系数阈值法结合EMD、EWT和本文方法分别对模拟信号进行降噪,结果见表 1、图 7。
|
|
表 1 不同降噪方法评价参数统计 Tab. 1 Statistics of evaluation parameters for different noise reduction methods |
|
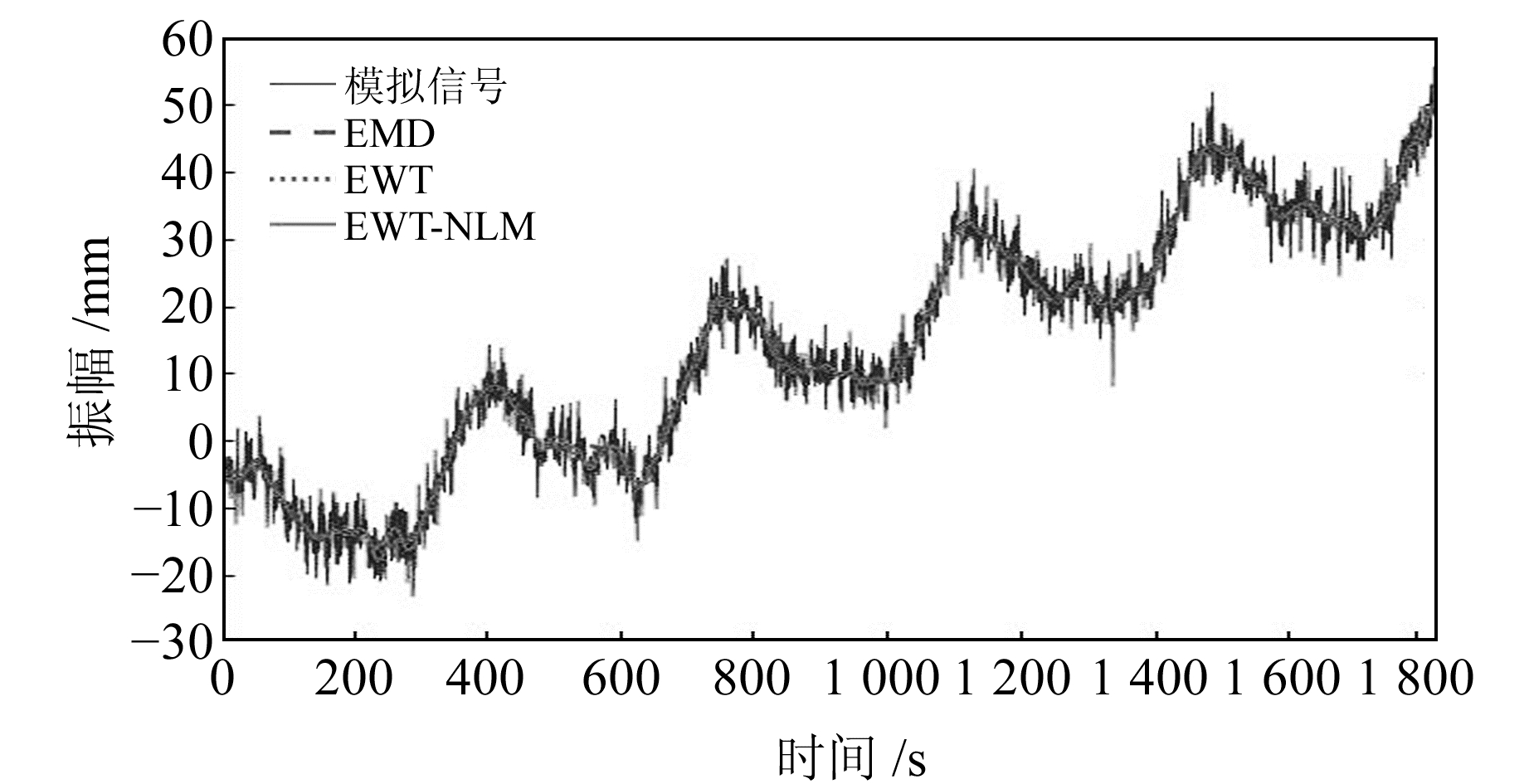
图 7 不同降噪方法对比 Fig. 7 Comparison of different noise reduction methods |
从表 1和图 7可知,使用EMD方法降噪后的信号存在一定的端点效应,从而影响降噪效果;EWT-NLM法可以有效提取出原始信号中的细节趋势变化,更贴合原始信号,降噪的信号也更加平滑。从模拟实验结果的评价指标看,EWT-NLM法整体优于EMD和EWT法,其模拟降噪结果的RMSE为2.876 4 mm、Rsn为17.67,相较于另外2种方法,RMSE分别降低10.63%和5.78%,Rsn分别提升22.54%和7.42%,从而验证了本文方法的有效性。
2.2 GNSS实测高程时间序列降噪分析使用EWT进行实测GNSS坐标时间序列分解时,若分解层数过小会导致不能最大限度地分解信号的不同特征信息,若分解层数过大可能会造成信号之间的差异性被掩盖。同时,EWT分解产生的所有分量中必包含有效信号和混合噪声模态分量,且主要的有效信号大多集中于低频信号中,那么分解的所有经验小波分量可以由低频有效信号分量、中频混合信号分量和高频噪声信号分量3个部分来概括,故分解层数与SE值选择不当会直接影响降噪效果。
选取我国12个陆态网基准站原始高程坐标时间序列进行降噪研究,数据来自中国地震局GNSS数据产品服务平台,时间跨度为2010~2018年,采样间隔为1/365.25 a,采样频率为365.25 Hz。为研究本文方法的自适应性及抗差性,仅对原始高程坐标时间序列进行粗差剔除和阶跃修正,将剔除粗差和修正阶跃后的坐标时间序列作为原始坐标序列。限于篇幅,主要阐述BJFS站的降噪过程,其余站点结果以图表形式展示。
首先对BJFS站高程坐标时间序列进行EWT分解,经多次实验,确定分解层数为14,分解信号见图 8。可以看出,趋势项f1较好地符合原始时间序列信号的趋势变化,f3分量为年周期信号,f5分量呈现0.5 a周期变化。再对各分量进行SE解算,熵重构维数m取2,阈值r取0.25σ(X)(σ为计算序列标准差),各分量SE值见表 2和图 9。因GNSS高程坐标时间序列具有丰富的组合噪声特性,无法确定信号分量与噪声分量的界限,故将所有分量划分为低频有效信号分量和中高频混合噪声分量,再对混合噪声分量进行NLM滤波,最后重构低频有效信号分量与滤波信号为降噪信号,以达到最优的降噪效果。

|
图 8 BJFS站分解信号结果 Fig. 8 The results of decomposing the signal at BJFS station |
|
|
表 2 BJFS站各分量SE值统计 Tab. 2 Statistics of SE values of each component at BJFS station |
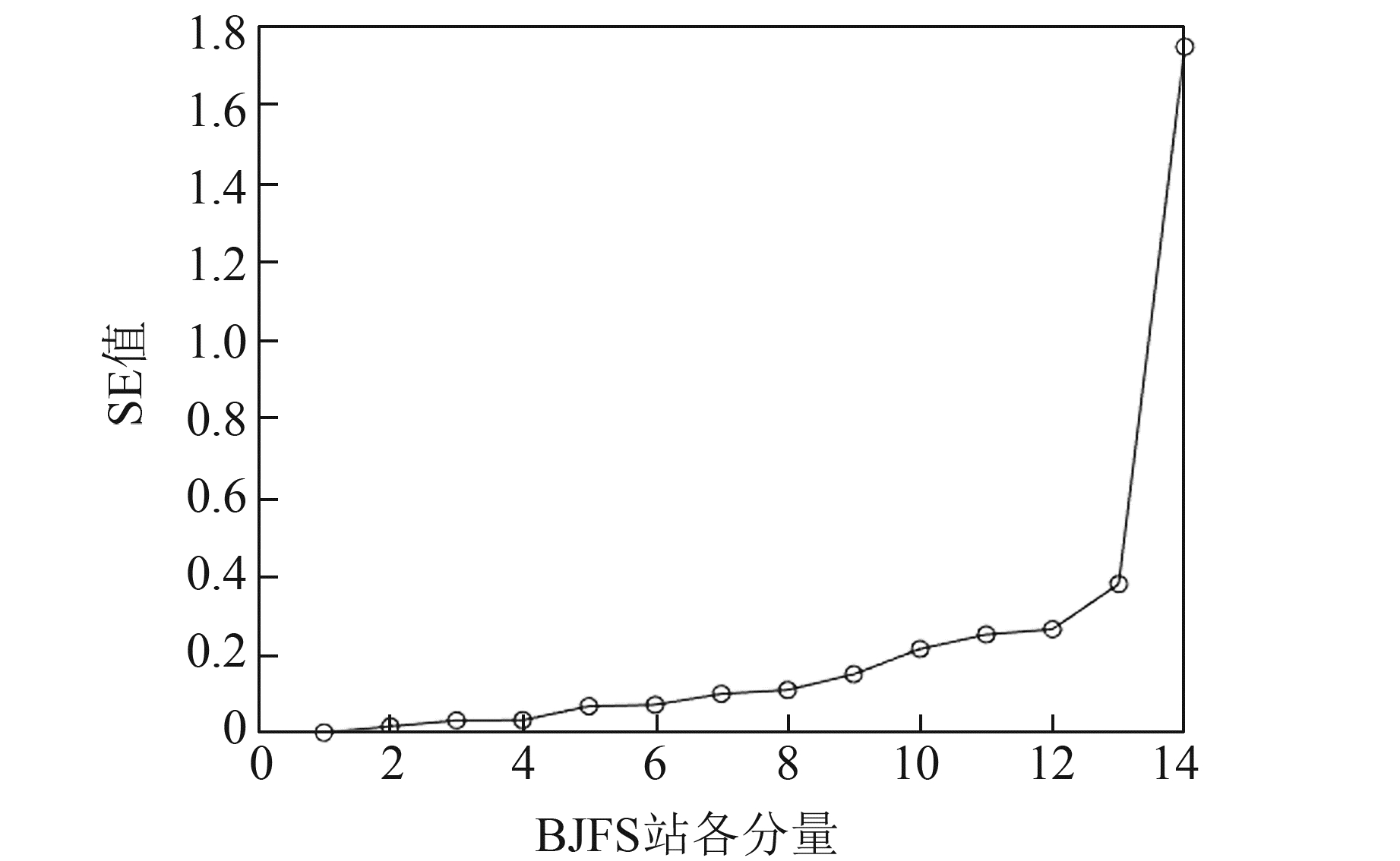
|
图 9 BJFS站各分量SE值 Fig. 9 SE values of each component at BJFS station |
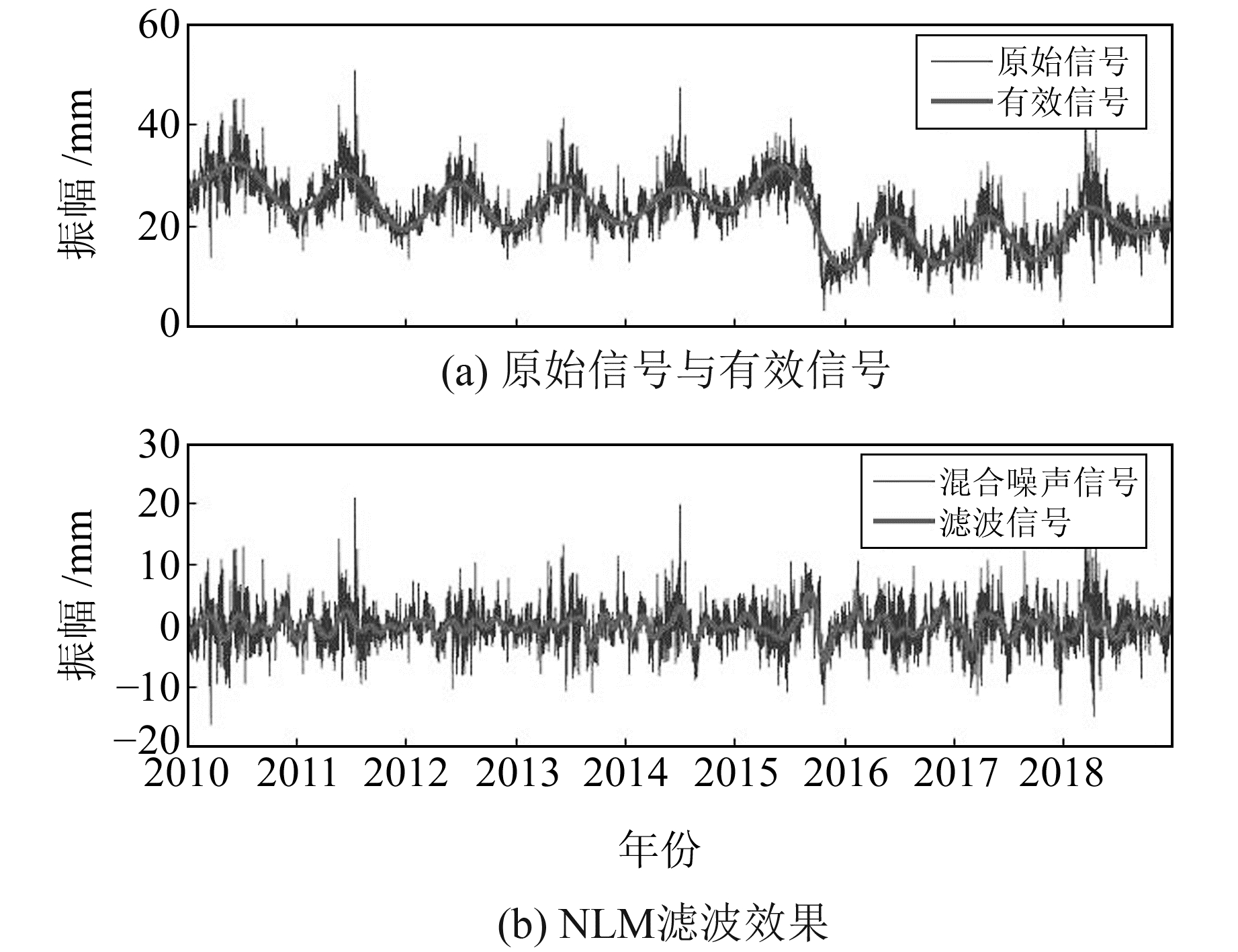
由表 2可见,只有前4个分量的SE值小于0.05,故提取重构前4个分量为有效信号分量,将其余分量重构为混合噪声分量,再对其进行NLM滤波,滤波效果见图 10。可以看出,分解出的有效信号整体较好地贴合原始时序,但不能呈现原始时序中较小的振荡周期变化,在局部甚至出现较大的偏离。NLM有较好的滤波效果,可以有效剔除混合噪声中频率较大的噪声,提取出混合噪声信号中的微小振荡变化。最后叠加滤波信号和有效信号为最终降噪信号。
|
图 10 有效信号分量与滤波效果 Fig. 10 Effective signal components and filtering effect |
使用EMD、EWT和EWT-NLM方法进行对比,各方法降噪效果见图 11,评价参数统计见表 3。

|
图 11 不同降噪方法效果对比 Fig. 11 Comparison of different noise reduction methods |
|
|
表 3 不同降噪方法评价参数统计 Tab. 3 Statistics of evaluation parameters for different noise reduction methods |
由图 11可见,本文方法和EWT方法相比于EMD方法可以较好地避免端点效应造成的影响,在原始信号的首尾两端有较好的降噪效果;经过本文方法降噪的信号更贴合原始信号,可以有效反映局部趋势运动变化及微小的周期振荡。从表 3可以看出,本文方法降噪效果最优,相较于其他2种方法,其RMSE分别降低13.41%、7.13%,Rsn分别提升22.03%、9.72%。
3 结语本文提出一种引入SE优化的EWT结合NLM滤波的组合自适应降噪方法。相较于EMD方法,该方法可以有效削弱端点效应的影响,从而提升降噪效果;相较于EMD与EWT方法,该方法可呈现出原始信号中的局部运动趋势变化及较小振幅的周期振荡变化。在模拟数据和实测数据实验中,该方法降噪效果均最优。
| [1] |
钱文龙, 鲁铁定, 贺小星, 等. GPS高程时间序列降噪分析的改进EMD方法[J]. 大地测量与地球动力学, 2020, 40(3): 242-246 (Qian Wenlong, Lu Tieding, He Xiaoxing, et al. A New Method for Noise Reduction Analysis of GPS Elevation Time Series Based on EMD[J]. Journal of Geodesy and Geodynamics, 2020, 40(3): 242-246)
(  0) 0) |
| [2] |
张恒璟, 程鹏飞. 基于EEMD的GPS高程时间序列噪声识别与提取[J]. 大地测量与地球动力学, 2014, 34(2): 79-83 (Zhang Hengjing, Cheng Pengfei. Noise Recognition and Extraction of GPS Height Time Series Based on EEMD[J]. Journal of Geodesy and Geodynamics, 2014, 34(2): 79-83)
(  0) 0) |
| [3] |
Tao Y, Liu C, Liu C Y, et al. Empirical Wavelet Transform Method for GNSS Coordinate Series Denoising[J]. Journal of Geovisualization and Spatial Analysis, 2021, 5(1): 1-7 DOI:10.1007/s41651-020-00071-6
(  0) 0) |
| [4] |
Tao R, Lu T D, Cheng Y M, et al. An Improved GNSS Vertical Time Series Prediction Model Using EWT[C]. China Satellite Navigation Conference, Nanchang, 2021
(  0) 0) |
| [5] |
Gilles J. Empirical Wavelet Transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3 999-4 010 DOI:10.1109/TSP.2013.2265222
(  0) 0) |
| [6] |
鲁铁定, 谢建雄. 变分模态分解结合样本熵的变形监测数据降噪[J]. 大地测量与地球动力学, 2021, 41(1): 1-6 (Lu Tieding, Xie Jianxiong. Deformation Monitoring Data De-Noising Method Based on Variational Mode Decomposition Combined with Sample Entropy[J]. Journal of Geodesy and Geodynamics, 2021, 41(1): 1-6)
(  0) 0) |
| [7] |
Qian C Q, Su H H, Yu H L. Local Means Denoising of ECG Signal[J]. Biomedical Signal Processing and Control, 2019, 53
(  0) 0) |
2. Nanchang Urban Planning and Design Institute, 599 Chunhui Road, Nanchang 330038, China
 2022, Vol. 42
2022, Vol. 42


