2. 武汉大学测绘学院,武汉市珞喻路129号,430079
陆地水作为全球水循环的重要部分,对经济发展、全球气候、生态环境都有重要影响,因此监测全球范围内水储量变化具有现实意义。大气压力、海底压力、陆地水储量变化等会引起地球重力场变化[1],GRACE重力卫星可捕捉该地球物理信号的波动,为反演陆地质量迁移提供新途径。
目前,采用时变重力场反演地球质量变化主要有球谐系数法[2-3]、Mascon法[4]以及点质量模型法[5]。球谐系数法相比Mascon法和点质量模型法算法简单、易编程实现、应用广泛,但球谐系数法的反演结果存在信号泄露等缺陷。此外,如要达到较好的去条带噪声效果,滤波方法也需要进行详细探究[6-8]。Mascon法可采用GRACE星间距离变率数据反演地表质量迁移,反演结果能以更高的时空分辨率揭示地球物理变化[9],但计算过程复杂。为进一步提高时变重力场模型反演结果的时空分辨率,且减少计算复杂程度,国内外学者提出了各种点质量模型法[2, 10-13]。采用点质量模型法求解地面点质量变化时,法方程会呈现病态,无法获得稳定解。该问题常用的解决方法是进行正则化,构建正则化矩阵的方法主要包括不考虑地表物理信息的纯数学的正则化约束、基于时空相关性进行约束、基于先验信息进行约束等[14-16]。正则化约束是大地测量不适定问题中使用最为广泛的一种方法,点质量模型法中常采用零阶Tikhonov正则化进行约束,该方法的原理是在法方程系数矩阵对角线增加纯数学的正则化参数,以抑制法方程病态,获得稳定解。基于时空相关性进行约束是基于地理相邻点之间的时间、空间相关性,通过权值定义其关系,从而构建约束矩阵。先验信息约束是通过已有的参考模型或先验误差信息构建约束矩阵。这3类方法都涉及正则化参数,而该参数的选取通常会影响反演结果,过大会造成过度平滑,丢失真实地面物理信号,过小则会保留较多噪声,无法获得准确结果。正则化参数的选取一般可使用广义交叉验证法、L曲线法。
本文基于附有空间约束的三维加速度点质量模型法[15],采用水文模型构建地面点之间的空间相关性矩阵,进而抑制法方程病态,并将该方法应用于2009年秋至2010年春云南、贵州、四川地区特大干旱监测,在剔除季节性信号后,采用主成分分析法对2003年至2012年西南地区水储量进行分析。
1 方法与数据处理 1.1 附有空间约束的三维加速度点质量模型法基本原理由于文献[15]已对附有空间约束的三维加速度点质量模型法的基本原理进行详细介绍,本文在此直接给出相关矩阵的构成方法。在构建相关矩阵时,将空间相关性进行量化,采用水文模型提取各点之间的相关系数,从而计算相关矩阵。当质量点之间的球面距离不大于相关距离时(dij≤D),由式(1)构成相关矩阵:
| $ C_{i j}=\left|R_{i j}\right| /|R|_{\text {sum }} $ | (1) |
式中,|Rij|为点i和点j相关系数的绝对值,|R|sum为在相关距离内,各质量点和点i相关系数的绝对值之和。当质量点之间的球面距离大于相关距离D时(dij≥D),Cij=0。由此,可以生成约束矩阵。
1.2 主成分分析法主成分分析法(principal component analysis, PCA)可对数据进行压缩提取,在地学领域通常采用该方法获得空间模态及时间序列。在对利用GRACE重力卫星反演的水储量数据进行主成分分析时,所计算的特征向量可称为空间特征或空间模态,而提取的主成分则认为是时间序列,因此主成分分析也称为时空分析或正交经验分解。主成分分析法计算过程参见文献[17]。
1.3 数据处理及检验方法本文采用CSR发布的60阶Level-2 RL06时变重力模型数据,时间范围为2003~2012年。由于GRACE重力卫星对球谐系数C20不敏感,在计算中采用SLR数据替换C20项[18]。为对比反演结果,分别采用300 km高斯滤波的球谐系数法、零阶Tikhonov正则化约束的三维加速度点质量模型法反演研究区质量变化。在构建水文模型约束矩阵时,为减小各种水文模型的不确定性,采用GLDAS(global land data assimilation system)中2种水文模式和CPC(climate prediction center)水文模型的均值作为最终估值,并采用球谐分析与球谐综合转化为1°×1°格网值。本文利用GLDAS中VIC、NOAH模式,提取0~2 m深度的土壤湿度变化。CPC水文模型数据时间分辨率为1个月,空间分辨率为0.5°,包含0~1.6 m深度的土壤湿度信息。
为检验引入水文模型后的附有空间约束的三维加速度点质量模型法的反演结果,本文采用信噪比(SNR)参数进行评估,具体公式为[15]:
| $ \mathrm{SNR}=\log _{10}\left(\left|\frac{\Delta m_{M}}{\Delta m_{M}-\Delta m_{R}}\right|\right) $ | (2) |
式中,ΔmM为各种方法反演的地面质量变化,ΔmR为参考模型的地面质量变化,当SNR>0时,表明信号大于噪声。
选用CSR发布的RL06 Mascon模型作为参考模型,同样进行格网一致化处理。
2 结果与分析 2.1 空间约束半径选取及各类方法效果对比构建约束矩阵时,以研究点为圆心,约束半径内的点被认为与研究点具有地理相关性,因此约束半径的选择至关重要。在反演东亚地区质量变化时,考虑到在反演质量变化时地理格网间隔为1°,本文设置间隔为100 km,约束半径为200 ~1 100 km,采用SNR进行结果评估。由于广义交叉函数变化平缓,确定最小值存在一定困难,会影响最优正则化参数的确定,因此本文采用L曲线法选取最优正则化参数。
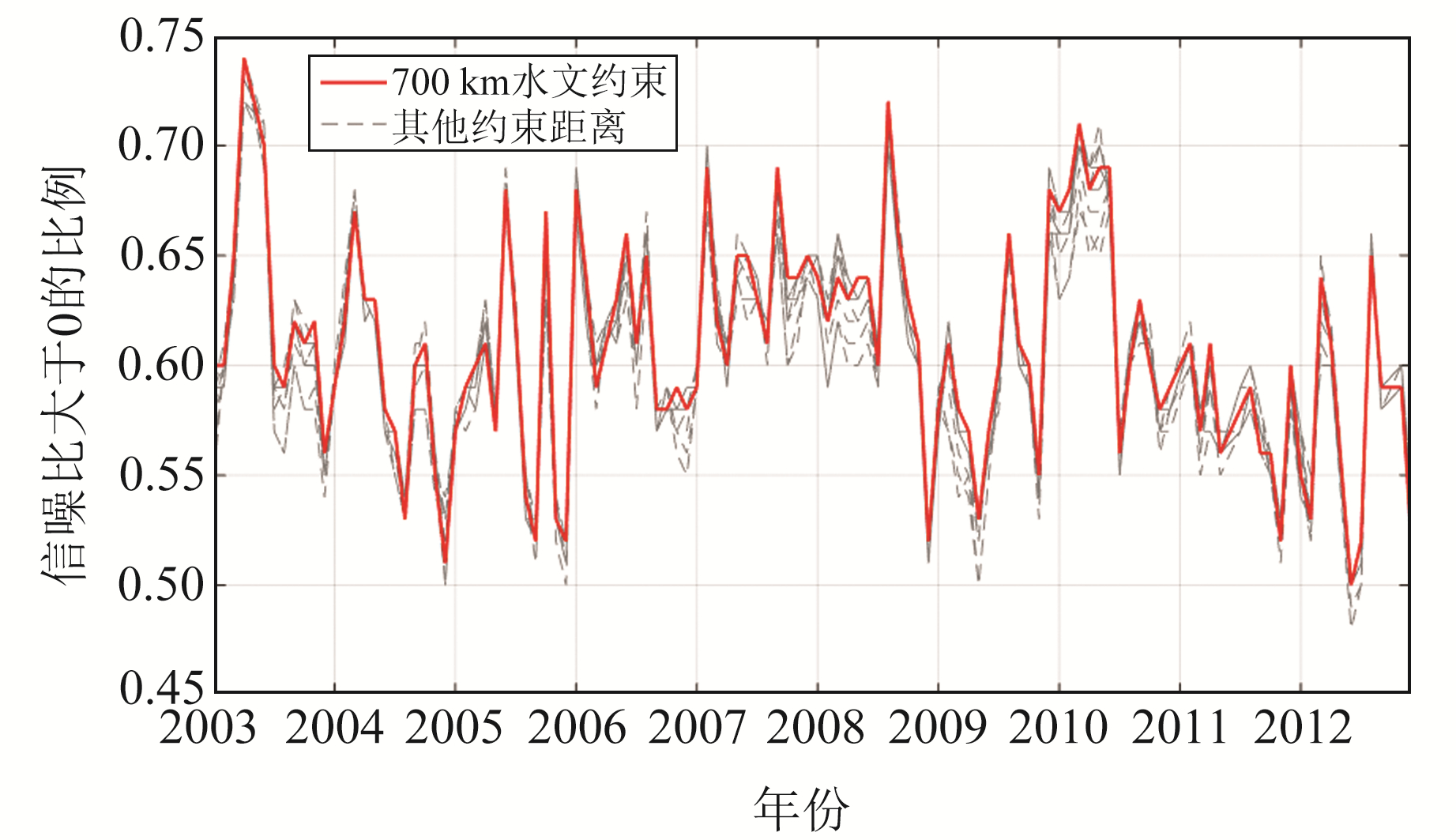
图 1为不同约束半径下2003~2012年东亚区域信噪比比例折线图,即信噪比大于0的点位所占比例。采用统计方法,选择该时间段内峰值最为频繁的700 km约束半径作为最优约束距离。需要注意的是,本文采用信噪比比例作为约束半径的选取准则,而不同空间尺度的研究区所计算的信噪比比例会存在差异,进而会影响最优约束半径的选择,因此本文在计算西南地区水储量变化时,约束半径也进行重新选取。
|
图 1 不同约束半径信噪比比例 Fig. 1 SNR ratio of various spatial constraint distances |
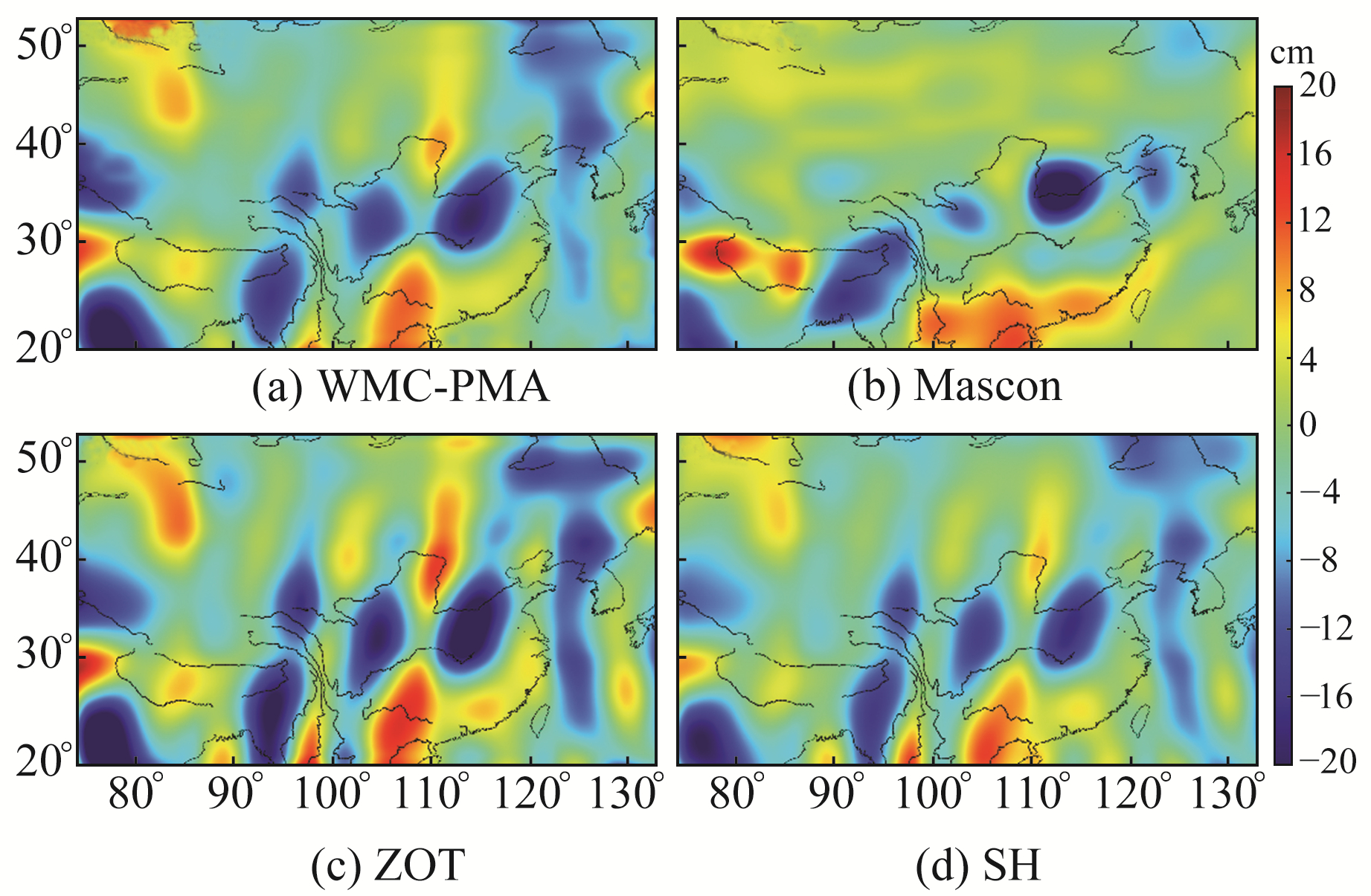
图 2为各种方法反演的2003-01水储量变化空间分布,其中图 2(a)为引入水文模型的附有空间约束的三维加速度点质量模型法的反演结果(WMC-PMA),图 2(b)为CSR Mascon产品结果(Mascon),图 2(c)为采用零阶Tikhonov正则化进行约束的三维加速度点质量模型法的反演结果(ZOT),图 2(d)为球谐系数法的反演结果(SH)。图中(a)、(c)与(d)去条带噪声效果大致相同,但(a)、(c)中地面物理信号更强。(a)、(c)、(d)与(b)相比存在一定区别,但在我国黄河下游区域、印度北部、缅甸、珠穆朗玛峰地区都有明显的质量变化。在信号方面,(b)在保留高空间分辨率情况下,去条带噪声效果更好。(a)与(c)相比在空域上区别较小,为进一步对比2种约束方法的效果,利用信噪比对2种方法进行评估,同时给出球谐系数法的相应结果。
|
图 2 2003-01东亚区域水储量变化 Fig. 2 Terrestrial water storage(TWS) changes in East Asia in January 2003 |
图 3中WMC-PMA方法(约束距离取700 km)相比ZOT方法信噪比大于0的比例更高,其在多数月份均优于ZOT方法。SH方法和WMC-PMA方法信噪比大于0的比例在多数月份相差不大,但由图 2可知,在去条带噪声效果差异较小的情况下,后者在部分地区具有更明显的地面质量变化信号,如我国华北区域。因此,本文方法在保留较好信噪比的情况下,也可保留较强的地面物理信号。

|
图 3 各类方法信噪比比例 Fig. 3 SNR ratio of various methods |
2009年秋至2010年春云南、贵州、四川发生特大干旱。去除季节性信号后,采用本文方法计算2003~2012年中国西南地区水储量变化(在后续计算分析中均采用已去除季节性信号的结果进行分析),水储量变化趋势空间分布如图 4所示,水储量变化时间序列如图 5所示。

|
图 4 2003~2012年西南地区水储量变化趋势 Fig. 4 Trends of TWS in southwest China from 2003 to 2012 |
|
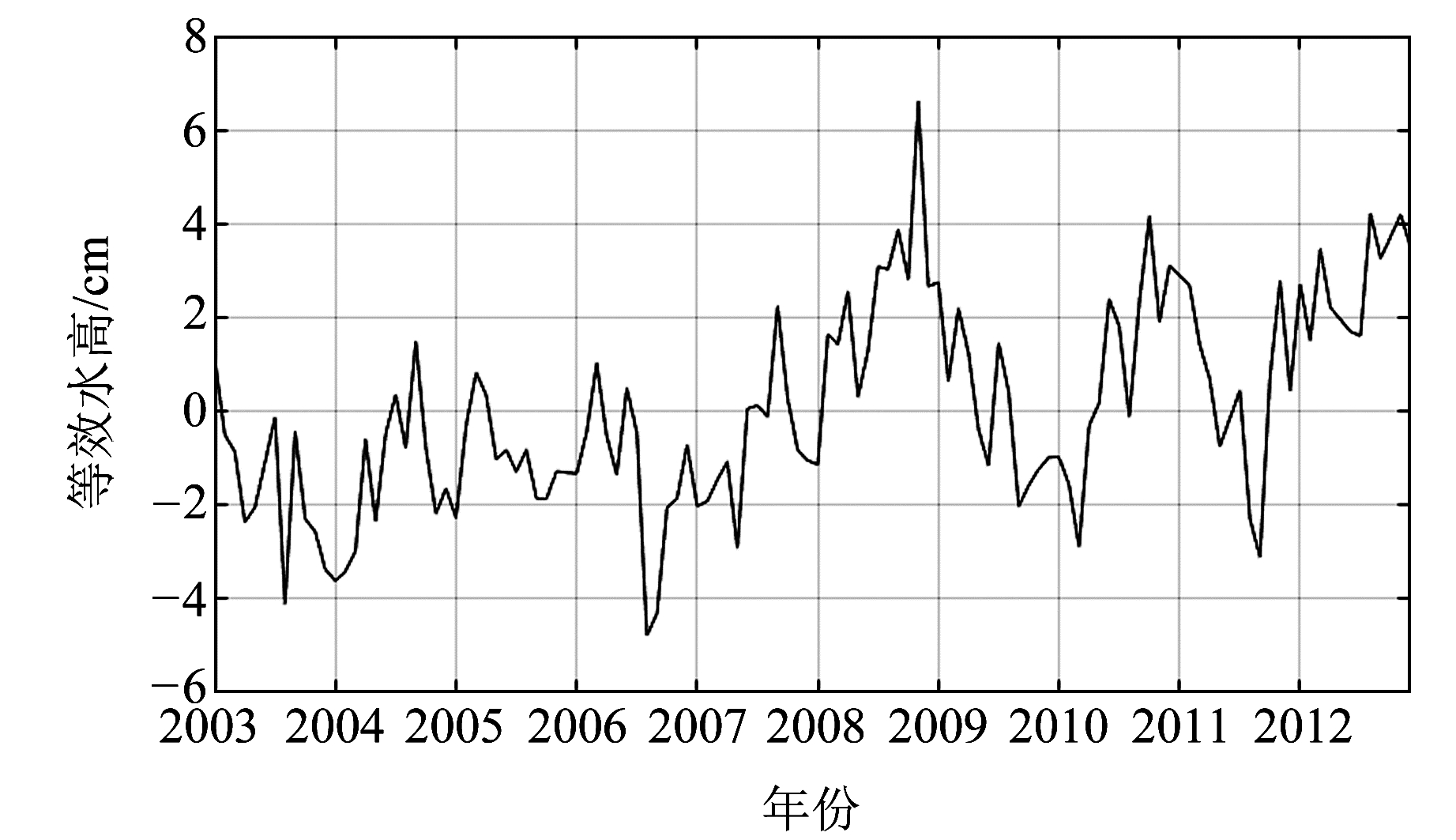
图 5 2003~2012年西南地区水储量变化时间序列 Fig. 5 Time series of TWS changes in southwest China from 2003 to 2012 |
从图 4可以看出,昆明、贵阳、成都具有质量增加趋势,贵阳东北部增加趋势尤为明显,与已有研究结果大致相同[19]。但本文计算结果表明昆明西南方向质量处于增加趋势,文献[19]利用GRACE重力卫星数据反演的结果无该信号特征,而GLDAS反演结果具有质量增加趋势。原因可能为文献[19]采用的时变重力场模型为CSR发布的RL04版本,而不同版本的数据精度和质量均在逐步提高,因此反演结果与本文存在一定区别。
图 5为研究区水储量变化时间序列,从图中可以看出,2006-09存在明显负异常,而2006-07~08云南地区为高温无雨天气,这是导致该异常的主要原因。2007年至2008年末,水储量呈现上升趋势,而2009年水储量变化虽然存在波动,但整体呈现下降趋势。2011年夏季同样存在明显的水储量下降趋势,出现夏季极端干旱事件,该次干旱事件的主要原因为2011年夏季降雨量相比同期明显偏少且干旱区基本与2009年冬至2010年春一致。值得注意的是,在2009年冬,研究区水储量处于上升趋势,本文将在后续对该异常进行分析说明。
为进一步分析西南地区水储量变化,采用主成分分析法(PCA)对反演结果进行处理。经过主成分分析法处理,一般可获取部分贡献率较大的成分,如这几个成分的累积贡献率超过阈值,则认为可以反映当前信息量。
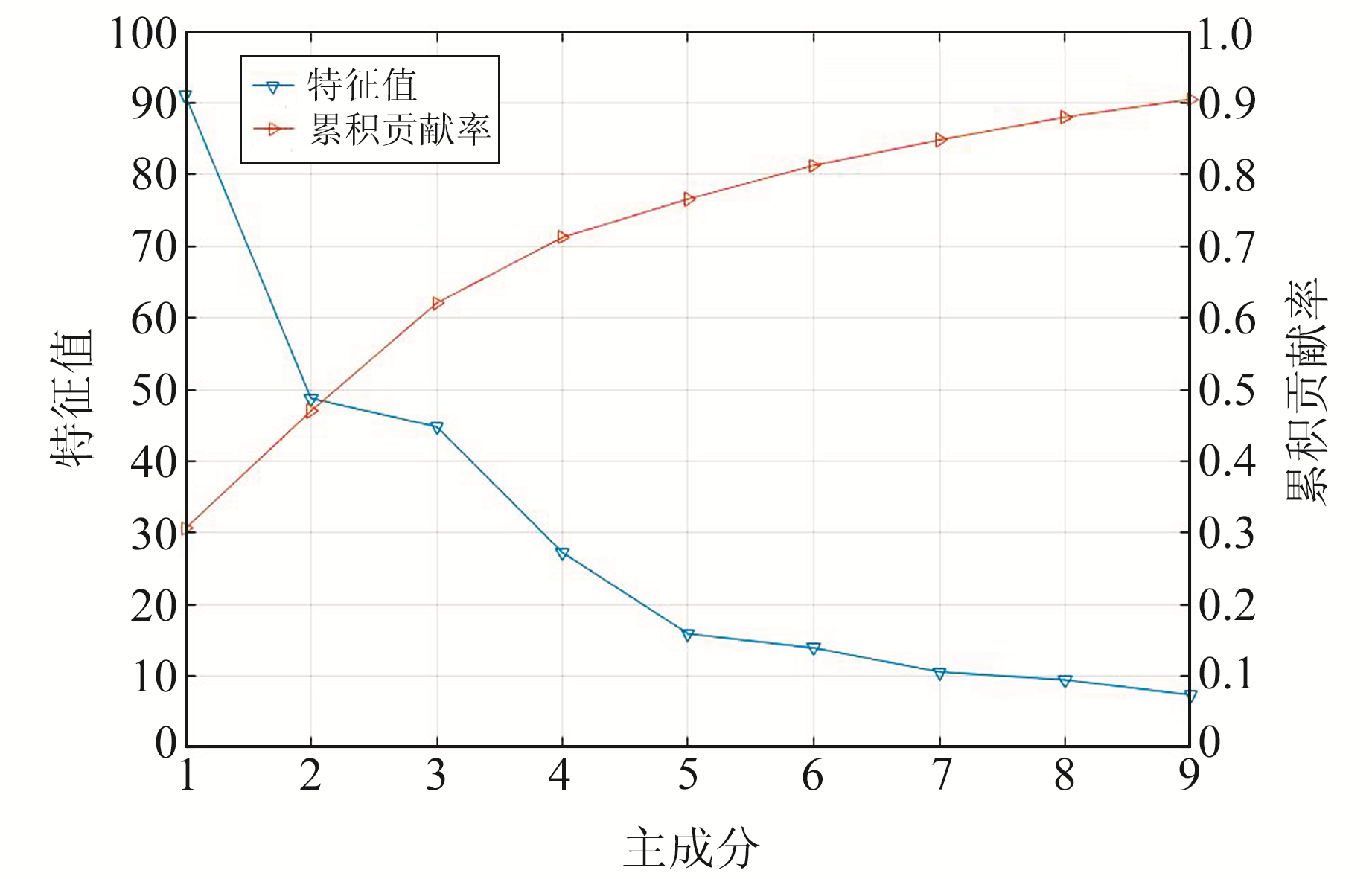
从图 6可以看出,主成分分析法在累积贡献率达到90.48%的情况下,共提取9个成分,其中前6个成分的累积贡献率达到81.25%,可以解释研究区水储量变化。第1个成分的贡献率为30.6%,远大于其他成分的贡献率。西南地区水储量主成分分析结果如图 7、8所示。图 8中所有主成分对应的时间序列均已剔除季节性信号,因此不存在周期性特征。
|
图 6 PCA分解特征值及方差贡献率 Fig. 6 PCA decomposition eigenvalue and variance contribution rate |

|
图 7 西南地区主成分空间模态 Fig. 7 Spatial pattern of principal components in southwest China |
|
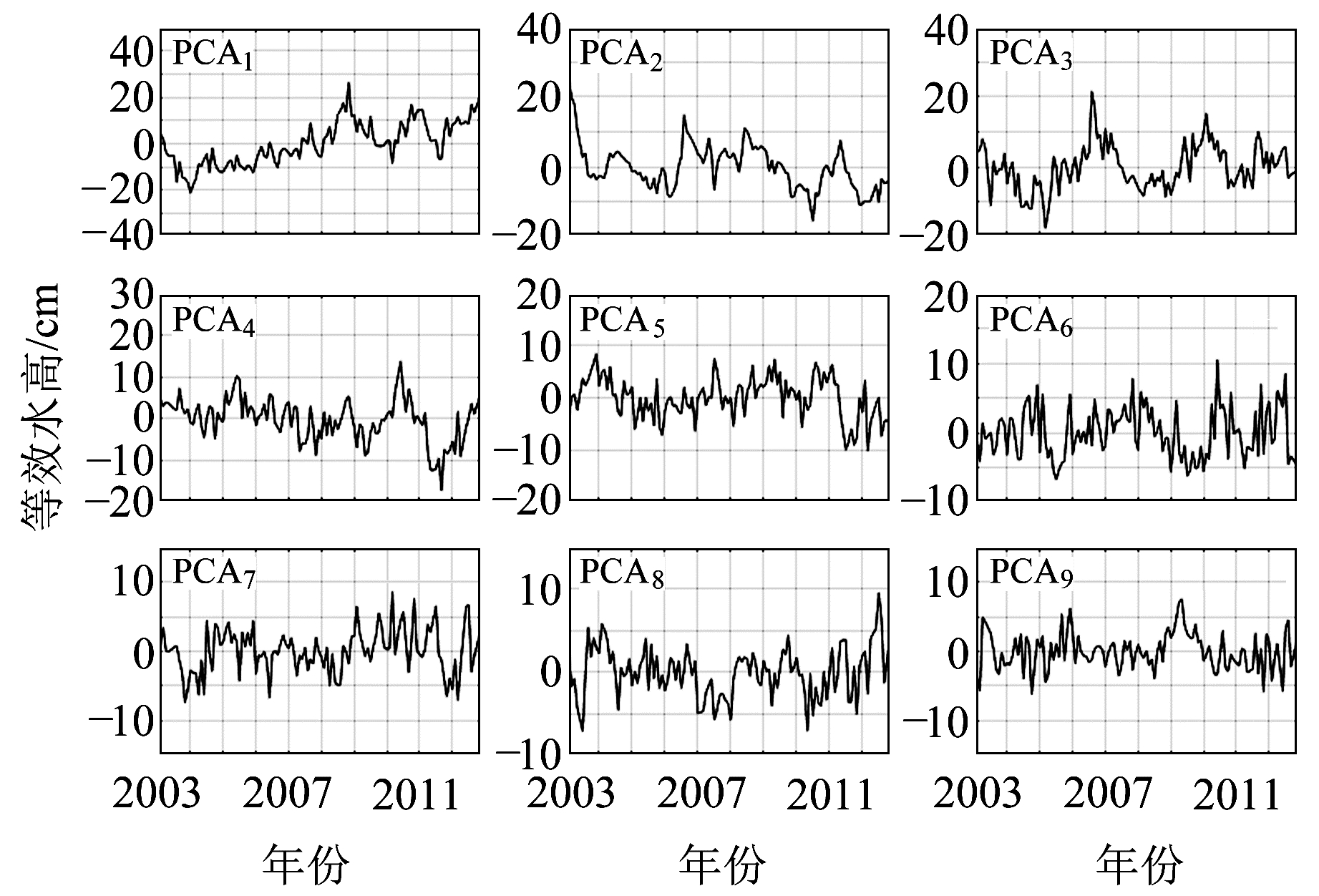
图 8 西南地区主成分时间序列 Fig. 8 Time series of principal components in southwest China |
图 8中PCA1在2009~2010年相比同期具有明显的下降趋势,而对应的空间模态则显示贵阳、昆明具有比其他地区更明显的正变化信号,因此该成分主要代表贵阳、昆明地区水储量变化信号,且贵阳、昆明水储量在该期间也处于下降趋势。在2010年春末,贵阳地区水储量开始恢复,这与图 9中水储量变化的空间分布大致相同;但从图 9可以看出,昆明地区在2010年春末负异常信号增强,与主成分分析结果不一致。该现象可能是由于在计算时间序列主成分时,空间模态在贵阳地区正变化数值较大,与昆明地区信号相互作用导致PCA1时间序列在该时间处于上升趋势。2003~2012年整个研究时间段内PCA1处于增加趋势,因此,在该期间内贵阳、昆明地区水储量处于增加态势,与图 4所反演的水储量变化趋势相同。

|
图 9 西南地区2009-07~2010-06水储量空间分布 Fig. 9 Spatial distribution of TWS in southwest China from July 2009 to June 2010 |
PCA2空间模态在成都、长江中游地区为负变化信号,在我国沿海地区及昆明南部具有较弱的正变化信号,因此PCA2主要表示成都及长江中游地区特征。PCA2时间序列在2009年秋至2010年春处于下降趋势,结合空间模态的正负变化信号可知,成都地区水储量变化呈现增加趋势,与PCA2时间序列的下降趋势相反;昆明南部水储量变化呈现减少趋势,与PCA2时间序列趋势相同。由图 9可知,在去除季节性特征后,成都地区在2009年秋至2010年受干旱影响较小,且多数月份表现为水储量正异常特征,昆明南部则在干旱期内表现为负异常。从研究时间段的整体趋势来看,PCA2时间序列呈现减小趋势,这表明2003~2012年成都及长江中游地区水储量为增加趋势,昆明南部水储量具有减小趋势,与图 4反演的变化趋势相印证。值得注意的是,PCA2时间序列在2006年具有明显的起伏特征,在迅速上升后快速下降,这与云南夏季高温无雨具有一定关系。
由图 7可知,PCA3主要表示青藏高原及云南部分地区,且由该地区负变化信号可知,其与图 8中PCA3时间序列变化趋势相反。2009年PCA3时间序列相比同期具有明显的上升趋势,因此青藏高原及云南部分地区在该时期表现为水储量快速下降趋势。PCA3时间序列在整个时间段内呈现上升趋势,表明青藏高原及云南部分地区在该时间段内水储量处于下降趋势,与图 4中趋势一致。
PCA4、PCA5、PCA6空间模态较为复杂,原始数据在空间模态上进行投影后,无法结合空间模态与时间序列对水储量信号变化进行定量分析,但PCA1、PCA2、PCA3时间序列及空间模态已经可以得出西南地区水储量变化趋势,且主成分分析法也可成功提取出2009年秋至2010年春西南地区水储量亏损信号。
为更好地描述西南地区干旱情况,图 9为西南地区2009年秋至2010年春水储量空间分布。从图中可以看出,青藏高原在2009-07~2010-04水储量一直处于负异常,在2010-02信号达到最大值,随后减弱,并在2010-05恢复为正值。昆明地区则在秋季前期呈现水储量正异常,在2009-09开始表现为负异常,且数值不断增大,并在2009-11开始分别与青藏高原负异常、贵阳地区负异常融合;2010-03西南地区大部分区域呈现水储量负异常,干旱情况加剧,与文献[19]反演结果一致;此后,昆明地区水储量负异常范围开始缩小,但数值不断增大,主要原因还是缺乏有效降雨。贵阳地区相比昆明地区受干旱影响较小,同样在2010-03达到负异常最大值,此后负异常值逐渐减小,在2010-06水储量迅速恢复。成都地区在此次干旱中受影响最小,多数月份表现为正异常。从图 5可以看出,2009年冬季研究区水储量处于上升趋势,结合图 9(d)~(f)可知,在该段时间内青藏高原负异常信号有所减弱,且长江中游、秦岭、成都西北部正异常信号增加,从而导致该时间段内水储量时间序列处于上升趋势,但云南大部分区域为水储量负异常。
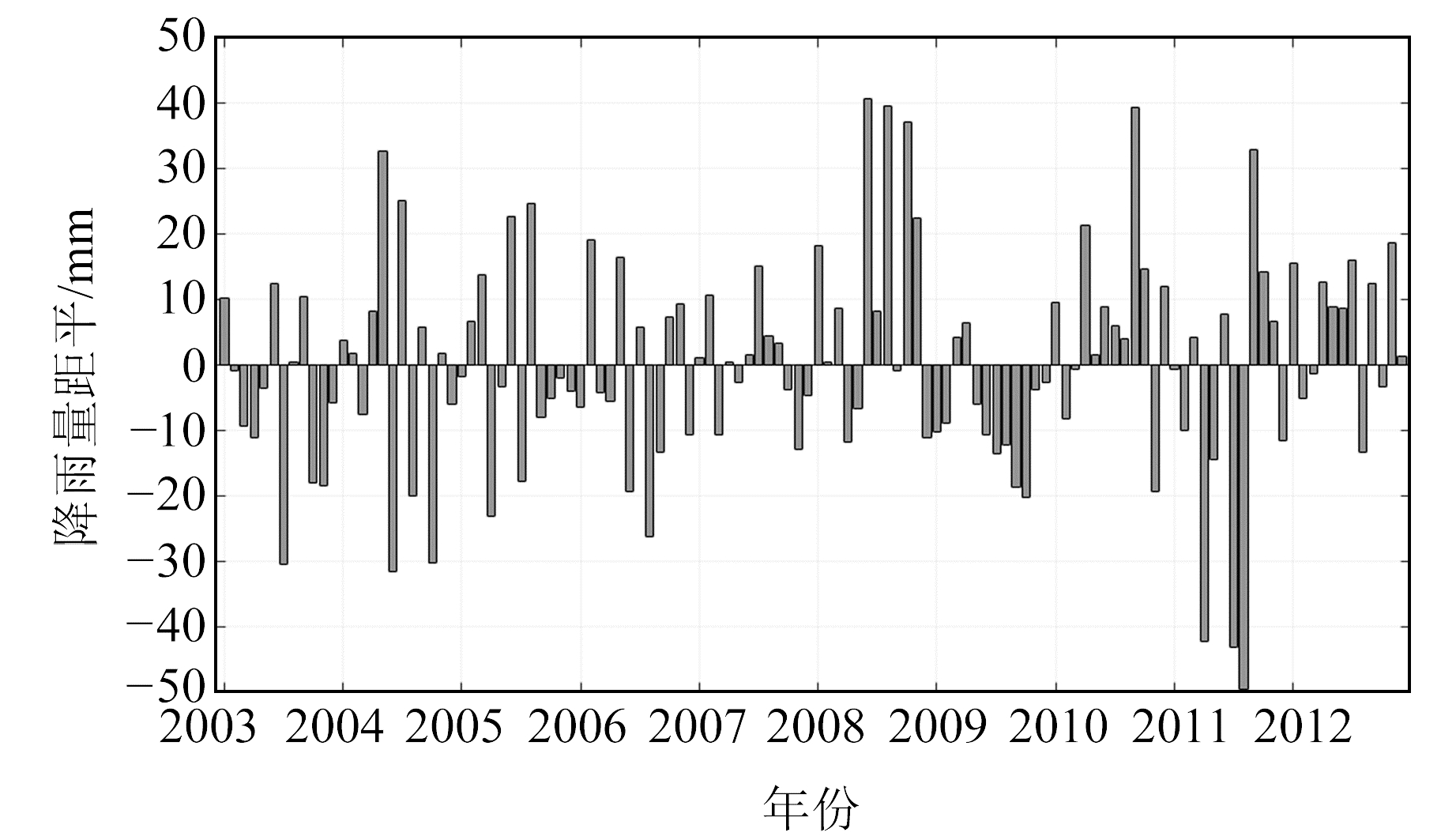
降雨量作为陆地水储量的主要补给来源,可对干旱洪涝事件进行辅助分析。图 10为已去除季节变化的西南地区2003~2012年热带降水测量计划(tropical rainfall measuring missionn, TRMM)的降雨量距平时间序列。
|
图 10 西南地区降雨量距平时间序列 Fig. 10 Time series of rainfall anomaly in southwest China |
由图 10可知,大多年份的降雨量距平处于波动状态,但可以明显看出2009年降雨异常,该年降雨量距平负异常的月份集中,且数值较大,说明2009年降雨量相比同期明显偏少,而雨水减少会削弱对陆地水储量的补给,从而引发干旱,这与GRACE捕捉到的干旱事件相吻合。此外,图 10中2011年出现降雨量距平极端负异常的情况,说明西南地区在2011年也出现一定程度的旱情。
3 结语本文采用空间约束方法处理反演过程中的病态问题,引入水文模型将地理点之间的相关性进行量化,并与球谐系数法、零阶Tikhonov约束的三维加速度点质量模型法进行比较。此外,采用该方法反演2003~2012年我国西南地区水储量变化,去除季节性变化特征后,利用主成分分析法对水储量进行分析。研究结果表明:
1) 2种约束形式的三维加速度点质量模型法均可处理病态问题,且在空间信号特征上差别较小,但本文方法在信噪比方面优于零阶Tikhonov约束的三维加速度点质量模型法。
2) 采用主成分分析法处理2003~2012年我国西南地区去除季节性信号后的水储量变化数据,在累积方差贡献率达到90.48%的情况下,可提取出9个主成分。结果表明,PCA1贡献率最大,该成分主要代表西南地区大部分区域,其所对应的时间序列显示2009年秋至2010年春存在明显的水储量下降趋势。
3) 2009年秋至2010年春,云南地区水储量负异常信号特征最明显、范围最广、持续时间最长。贵阳地区水储量信号在前期呈现正值,后期逐步呈现负异常,贵阳东部尤为明显,但在2010-06,贵阳东部水储量信号迅速恢复为正异常。成都地区在此次干旱中受影响较小。
| [1] |
瞿伟, 安东东, 薛康, 等. GRACE卫星观测到的尼泊尔8.1级地震前后的重力变化[J]. 大地测量与地球动力学, 2017, 37(12): 1 214-1 218 (Qu Wei, An Dongdong, Xue Kang, et al. Gravity Variations before and after the M8.1 Nepal Earthquake Observed by the GRACE[J]. Journal of Geodesy and Geodynamics, 2017, 37(12): 1 214-1 218)
(  0) 0) |
| [2] |
邹芳, 金双根. GRACE估计南极冰川质量变化的泄露影响及其改正[J]. 大地测量与地球动力学, 2016, 36(7): 639-644 (Zou Fang, Jin Shuanggen. Effect and Correction of Leakage Errors in Antarctic Glacier Mass Change from GRACE[J]. Journal of Geodesy and Geodynamics, 2016, 36(7): 639-644)
(  0) 0) |
| [3] |
李圳, 章传银, 柯宝贵, 等. 利用GRACE数据反演东海沉积物变化[J]. 地球物理学报, 2019, 62(7): 2 429-2 440 (Li Zhen, Zhang Chuanyin, Ke Baogui, et al. Inversion for Sediment Variation in the East China Sea Using GRACE Data[J]. Chinese Journal of Geophysics, 2019, 62(7): 2 429-2 440)
(  0) 0) |
| [4] |
Muller P M, Sjogren W L. Mascons: Lunar Mass Concentrations[J]. Science, 1968, 161(3 842): 680-684
(  0) 0) |
| [5] |
苏勇, 于冰, 游为, 等. 基于重力卫星数据监测地表质量变化的三维点质量模型法[J]. 地球物理学报, 2017, 60(1): 50-60 (Su Yong, Yu Bing, You Wei, et al. Surface Mass Distribution from Gravity Satellite Observations by Using Three-Dimensional Point-Mass Modeling Approach[J]. Chinese Journal of Geophysics, 2017, 60(1): 50-60 DOI:10.3969/j.issn.1672-7940.2017.01.009)
(  0) 0) |
| [6] |
Swenson S, Wahr J. Methods for Inferring Regional Surface-Mass Anomalies from Gravity Recovery and Climate Experiment(GRACE)Measurements of Time-Variable Gravity[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B9)
(  0) 0) |
| [7] |
Swenson S, Wahr J. Post-Processing Removal of Correlated Errors in GRACE Data[J]. Geophysical Research Letters, 2006, 33(8)
(  0) 0) |
| [8] |
Han S C, Shum C K, Jekeli C, et al. Non-Isotropic Filtering of GRACE Temporal Gravity for Geophysical Signal Enhancement[J]. Geophysical Journal International, 2005, 163(1): 18-25 DOI:10.1111/j.1365-246X.2005.02756.x
(  0) 0) |
| [9] |
李琼. 地表物质迁移的时变重力场反演方法及其应用研究[D]. 武汉: 武汉大学, 2014 (Li Qiong. Earth's Surface Mass Transport Recovered from Temporal Gravity Field and Its Applications[D]. Wuhan: Wuhan University, 2014)
(  0) 0) |
| [10] |
Han S C, Shum C K, Jekeli C, et al. Improved Estimation of Terrestrial Water Storage Changes from GRACE[J]. Geophysical Research Letters, 2005, 32(7)
(  0) 0) |
| [11] |
Baur O, Sneeuw N. Assessing Greenland Ice Mass Loss by Means of Point-Mass Modeling: A Viable Methodology[J]. Journal of Geodesy, 2011, 85(9): 607-615 DOI:10.1007/s00190-011-0463-1
(  0) 0) |
| [12] |
Baur O. Greenland Mass Variation from Time-Variable Gravity in the Absence of GRACE[J]. Geophysical Research Letters, 2013, 40(16): 4 289-4 293 DOI:10.1002/grl.50881
(  0) 0) |
| [13] |
郭飞霄, 苗岳旺, 肖云, 等. 采用点质量模型方法反演中国大陆及周边地区陆地水储量变化[J]. 武汉大学学报: 信息科学版, 2017, 42(7): 1 002-1 007 (Guo Feixiao, Miao Yuewang, Xiao Yun, et al. Recovery Water Storage Variation in China and Its Adjacent Area by Method of Point-Mass Model[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 1 002-1 007)
(  0) 0) |
| [14] |
Zhong B, Li Q, Chen J L, et al. Improved Estimation of Regional Surface Mass Variations from GRACE Intersatellite Geopotential Differences Using a Priori Constraints[J]. Remote Sensing, 2020, 12(16)
(  0) 0) |
| [15] |
苏勇, 郑文磊, 余彪, 等. 反演地表质量变化的附有空间约束的三维加速度点质量模型法[J]. 地球物理学报, 2019, 62(2): 508-519 (Su Yong, Zheng Wenlei, Yu Biao, et al. Surface Mass Distribution Derived from Three-Dimensional Acceleration Point-Mass Modeling Approach with Spatial Constraint Methods[J]. Chinese Journal of Geophysics, 2019, 62(2): 508-519)
(  0) 0) |
| [16] |
Ran J, Ditmar P, Klees R, et al. Statistically Optimal Estimation of Greenland Ice Sheet Mass Variations from GRACE Monthly Solutions Using an Improved Mascon Approach[J]. Journal of Geodesy, 2018, 92(3): 299-319 DOI:10.1007/s00190-017-1063-5
(  0) 0) |
| [17] |
王陈燕, 游为, 范东明. 利用独立成分分析检测2004年和2012年印度洋地震的重力变化[J]. 地球物理学报, 2019, 62(11): 4 142-4 155 (Wang Chenyan, You Wei, Fan Dongming. Using Independent Component Analysis to Detect the Gravity Changes in the Indian Ocean Earthquakes of 2004 and 2012[J]. Chinese Journal of Geophysics, 2019, 62(11): 4 142-4 155)
(  0) 0) |
| [18] |
Loomis B D, Rachlin K E, Luthcke S B. Improved Earth Oblateness Rate Reveals Increased Ice Sheet Losses and Mass-Driven Sea Level Rise[J]. Geophysical Research Letters, 2019, 46(12): 6 910-6 917 DOI:10.1029/2019GL082929
(  0) 0) |
| [19] |
李琼, 罗志才, 钟波, 等. 利用GRACE时变重力场探测2010年中国西南干旱陆地水储量变化[J]. 地球物理学报, 2013, 56(6): 1 843-1 849 (Li Qiong, Luo Zhicai, Zhong Bo, et al. Terrestrial Water Storage Changes of the 2010 Southwest China Drought Detected by GRACE Temporal Gravity Field[J]. Chinese Journal of Geophysics, 2013, 56(6): 1 843-1 849)
(  0) 0) |
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2022, Vol. 42
2022, Vol. 42

