2. 苏州科技大学北斗导航与环境感知研究中心,苏州市学府路99号,215009
大气可降水量(precipitable water vapor, PWV)作为反映水汽含量的重要指标,与实际降水之间具有较高的相关性,在描述水汽含量、监测和预报天气变化等方面具有重要意义。Bevis等[1]提出利用GPS技术获取高时空分辨率的GPS-PWV;石小龙等[2]研究发现GPS-PWV能够较好地反映水汽含量的时空分布变化;向玉春等[3]研究发现,与探空法相比,地面气象资料推算的PWV偏差较小,而GPS-PWV偏差较大;卢士庆等[4]将部分求解PWV的方法进行比较发现,GPS-PWV精度较高且不受天气状况影响,具有广阔的应用前景,而基于地面露点资料计算PWV方法简便且可以得到实时结果;翟树峰等[5]提出一种基于GPT2w获取Tm,进而利用地基GPS反演PWV的方法,该方法获取的PWV精度与基于Bevis-Tm反演的PWV精度相当。本文利用探空资料、地面露点资料、GNSS数据以及GPT3模型[6]计算长三角地区PWV,并以探空法计算得到的PWV为参考评估其他方法,从精度、可靠性和时效性等方面比较分析以上各方法。
1 数据来源及处理方法 1.1 数据来源实验数据主要来自2017年长三角地区7个探空站和2个GNSS基准站,位置信息如表 1所示。由表 1可知,射阳GNSS站与探空站经纬度完全一致,安庆GNSS站与探空站位置非常接近,因此GNSS站与探空站之间的差异主要为高程差,安庆和射阳两站高程差分别为51.6 m和28.3 m。为确保GNSS-PWV与探空PWV精度对比的可靠性和准确性,进一步利用静力平衡方程分析GNSS站与探空站高程差对PWV的影响。结果表明,安庆和射阳GNSS站与探空站之间高程差对PWV的误差影响分别为1.3 mm和0.7 mm,影响程度较小,因此可以直接利用探空站PWV评估GNSS-PWV和其他方法得到的PWV精度。
|
|
表 1 长三角地区7个探空站及2个GNSS站位置信息 Tab. 1 Information of 7 radiosonde stations and 2 GNSS stations in Yangtze river delta |
采用探空数据和数值积分法获取的Tm精度较高,可作为参考值对其他方法获取的Tm进行评估,其计算公式为:
| $ T_{m}=\frac{\int(e / T) \mathrm{d} z}{\int\left(e / T^{2}\right) \mathrm{d} z} $ | (1) |
式中,z为分层高度,e为地面水汽压,可通过2008年世界气象组织提出的饱和水汽压公式计算得到。
1.3 PWV计算方法 1.3.1 基于探空资料PWV是指单位面积空气柱内所含的水汽总量,计算公式为:
| $ \mathrm{PWV}=\frac{1}{g_{m}} \int_{0}^{P_{0}} q \mathrm{~d} p $ | (2) |
式中,q为各气压层空气比湿,p为对流层上界气压,P0为地面气压。
1.3.2 基于地面气象资料建立PWV与地面露点资料之间的关系可为缺乏探空数据的地区获取PWV提供新途径,本文分别采用杨景梅等[7]和张学文[8]建立的经验关系式反演PWV。
文献[7]基于地面露点温度、高程和纬度建立的PWV经验关系式为:
| $ \mathrm{PWV}=\exp \left(b_{0}^{\prime}+b_{1}^{\prime} t_{d}\right) $ | (3) |
式中,PWV为整层大气可降水量,b′0、b′1为经验系数,td为地面露点温度。
文献[8]建立的PWV与水汽压(根据露点温度计算)的关系式为:
| $ {\rm{PWV}}=1.74e $ | (4) |
利用精密单点定位技术可解算GNSS站观测数据,从而获取高精度的GNSS-ZTD。其中ZHD可根据Saastamonien模型[9]获取:
| $ \left\{\begin{array}{l} \mathrm{ZHD}=0.0022768 \times \frac{P_{c}}{f\left(\varphi_{c}, H_{c}\right)} \\ f\left(\varphi_{c}, H_{c}\right)=1-0.00266 \cos 2 \varphi_{c}-0.00028 H_{c} \end{array}\right. $ | (5) |
式中,Pc、φc和Hc分别为测站气压、纬度和海拔。
GNSS-PWV与ZWD(ZWD=ZTD-ZHD)的关系式为:
| $ \left\{\begin{array}{l} \mathrm{PWV}=K \times \mathrm{ZWD} \\ K=\frac{10^{5}}{R_{v}\left(k_{3} / T_{m}+k_{2}^{\prime}\right)} \end{array}\right. $ | (6) |
式中,K为大气水汽转换系数,Rv为水汽的比气体常数,k′2、k3为大气折射率常数,具体数值参见文献[9]。
1.3.4 基于GPT3模型基于欧洲中期天气预报中心(ECMWF)数据建立的对流层延迟模型GPT3是获取PWV所需气象参数的有效方法之一,其计算公式为:
| $ \begin{array}{c} r(t)=\alpha_{0}+\alpha_{1} \cos \left(2 {\mathtt{π}} \frac{\text { doy }}{365.25}\right)+\\ \beta_{1} \sin \left(2 \pi \frac{\text { doy }}{365.25}\right)+\alpha_{2} \cos \left(4 {\mathtt{π}} \frac{\text { doy }}{365.25}\right)+ \\ \beta_{2} \sin \left(4 {\mathtt{π}} \frac{\operatorname{doy}}{365.25}\right) \end{array} $ | (7) |
式中,r(t)为格网点处气象参数值,α0为平均值,α1、β1为年周期振幅,α2、β2为半年周期振幅。利用式(7)可得到基于GPT3模型的各类气象参数,GPT3-PWV与GNSS-PWV计算原理相同,均可利用式(6)计算得到。
1.4 精度统计方法采用偏差bias和均方根误差RMSE作为精度评定标准:
| $ \text { bias }=\frac{\sum\limits_{i=1}^{n}\left(X_{\text {model }, i}-X_{\text {real }, i}\right)}{n} $ | (8) |
| $ \mathrm{RMSE}=\sqrt{\frac{\sum\limits_{i=1}^{n}\left(X_{\text {model }, i}-X_{\text {real }, i}\right)^{2}}{n}} $ | (9) |
式中,Xmodel, i、Xreal, i分别为PWV的模型值和参考值,n为样本数。
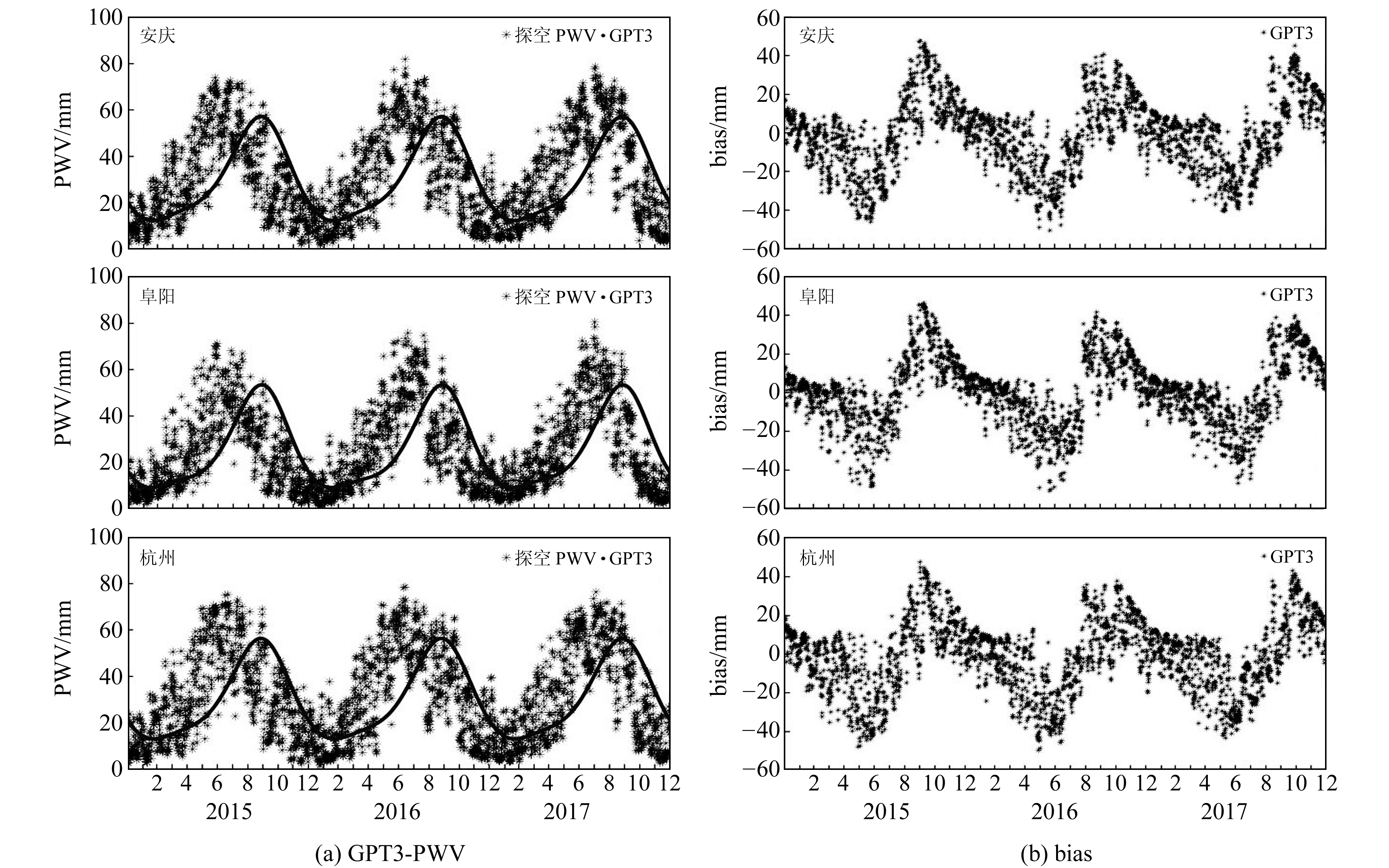
2 PWV精度分析 2.1 GPT3-PWV根据GNSS-PWV计算原理和GPT3模型提供的气象参数,可在无气象参数情况下获取PWV。由于篇幅所限,本文只列举安庆、阜阳及杭州站GPT3-PWV及其bias(图 1)。由图可知,GPT3-PWV与探空PWV变化趋势基本一致,呈周期性变化,春冬季精度优于夏季精度。这是由于长三角地区主要为亚热带季风气候,雨热同期,春冬季空气中的水汽含量远低于夏季。
|
图 1 2015~2017年安庆、阜阳、杭州站GPT3-PWV及其bias Fig. 1 GPT3-PWV and their biases at Anqing, Fuyang and Hangzhou stations from 2015 to 2017 |
表 2为2015~2017年7个探空站获取的GPT3-PWV精度统计(单位mm)。由表可知,平均bias和RMSE分别为0.57 mm和9.15 mm,未达到理想精度。这是由于GPT3模型获取的平滑气象参数会丢失实时气象参数的细节信息,缺乏时效性,且与实测数据存在较大差异。而采用Askne-Nordius模型计算的GPT3-ZWD涉及到e、Tm等参数,与P、T和高程均有很强的相关性,多种气象误差累积和交叉影响,造成ZWD精度下降,从而导致由GPT3模型反演的PWV精度较低,仅可作为无实测气象参数时的参考。
|
|
表 2 2015~2017年7个探空站GPT3-PWV精度统计 Tab. 2 GPT3-PWV accuracy statistics of 7 radiosonde stations from 2015 to 2017 |
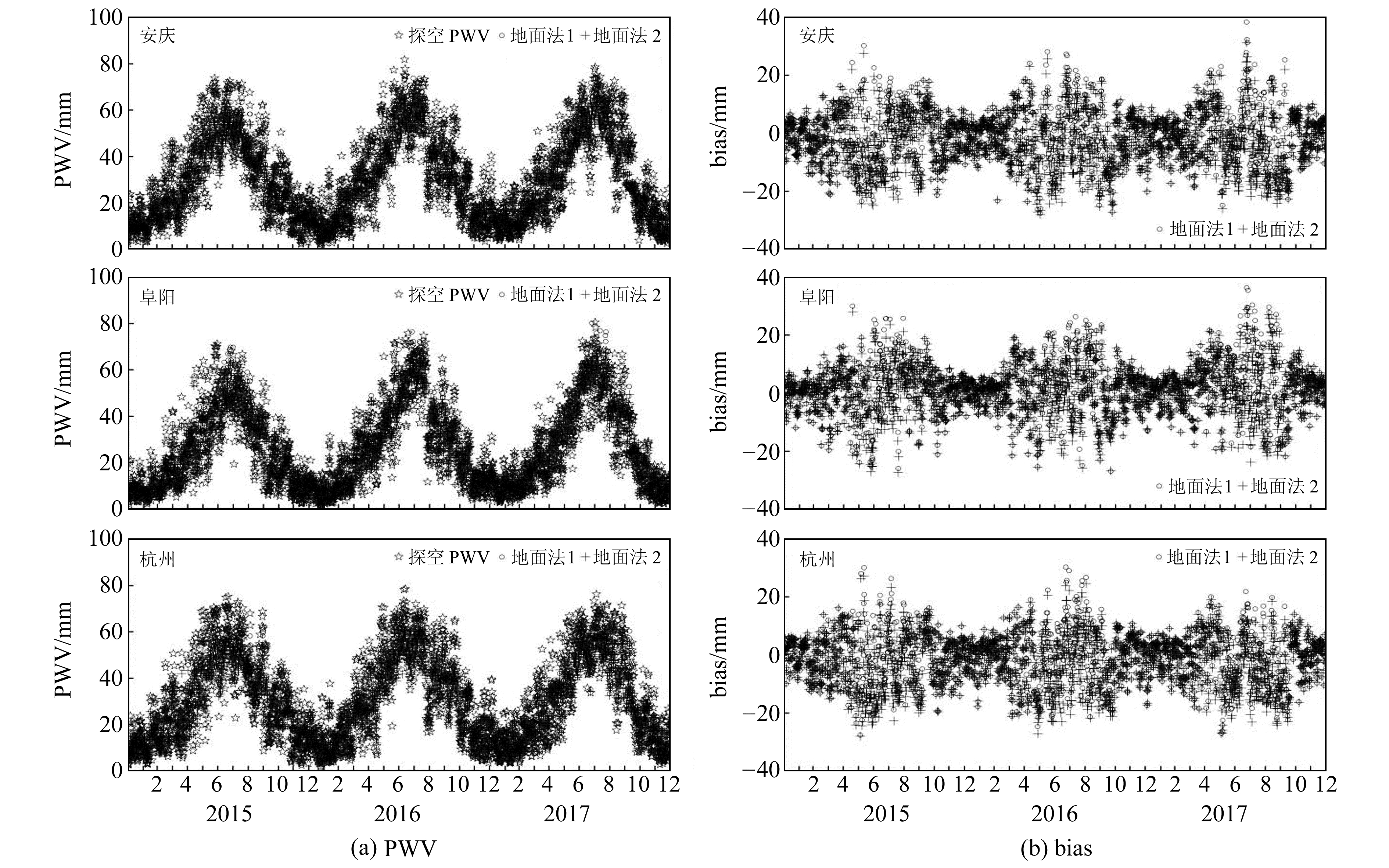
图 2为基于地面气象资料法计算的2015~2017年部分探空站的PWV及其偏差。由于篇幅所限,本文仅列出安庆、阜阳和杭州站。由图可知,地面测得的露点资料能很好地反映空气中的水汽状况。此外,地面法获取的PWV呈季节性变化,冬季精度明显优于夏季精度,且基于地面法1推算的PWV值比地面法2推算的PWV值大,更接近于真实值,尤其是在夏季。
|
图 2 2015~2017年地面法PWV及其bias Fig. 2 PWV and their biases of surface methods from 2015 to 2017 |
表 3为基于两种地面法获取的PWV精度统计(单位mm)。基于地面法1获取的PWV平均bias和RMSE分别为0.22 mm和8.00 mm,基于地面法2获取的PWV平均bias和RMSE分别为-0.51 mm和8.34 mm。总体而言,地面法1的精度稍优于地面法2,虽然地面法1与地面法2均是利用气象资料建立的经验公式,但地面法1考虑了露点温度、纬度和高程,而地面法2仅考虑了地面水汽压。由于地面露点资料仅能反映地面附近的湿度状况,由此得到的经验关系式仍存在20%的误差[7]。与GPT3-PWV相比,两种地面法计算的PWV精度略有提升,但仍未达到理想水平。
|
|
表 3 2015~2017年基于地面法的PWV精度统计 Tab. 3 PWV accuracy statistics based on surface methods from 2015 to 2017 |
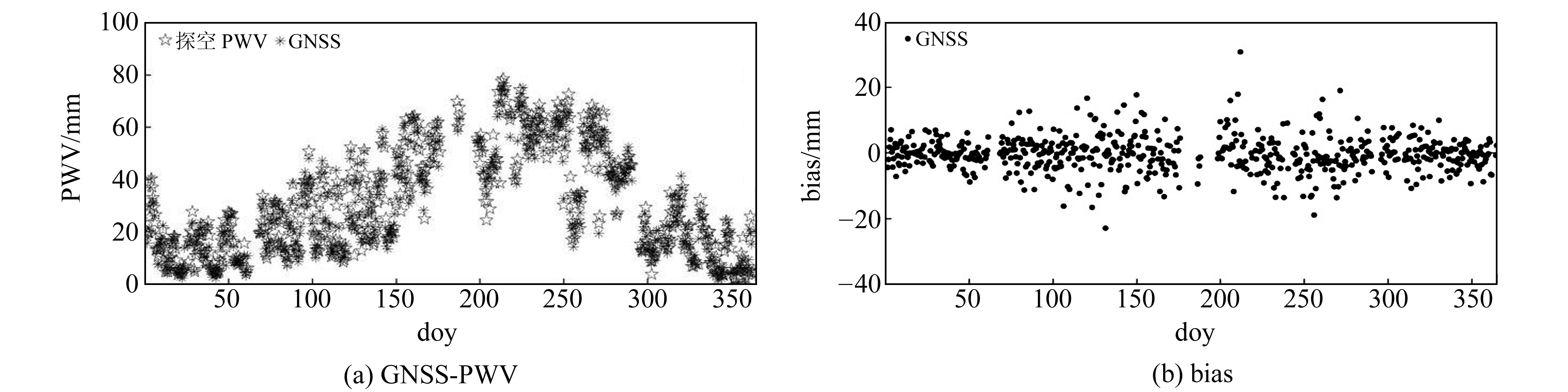
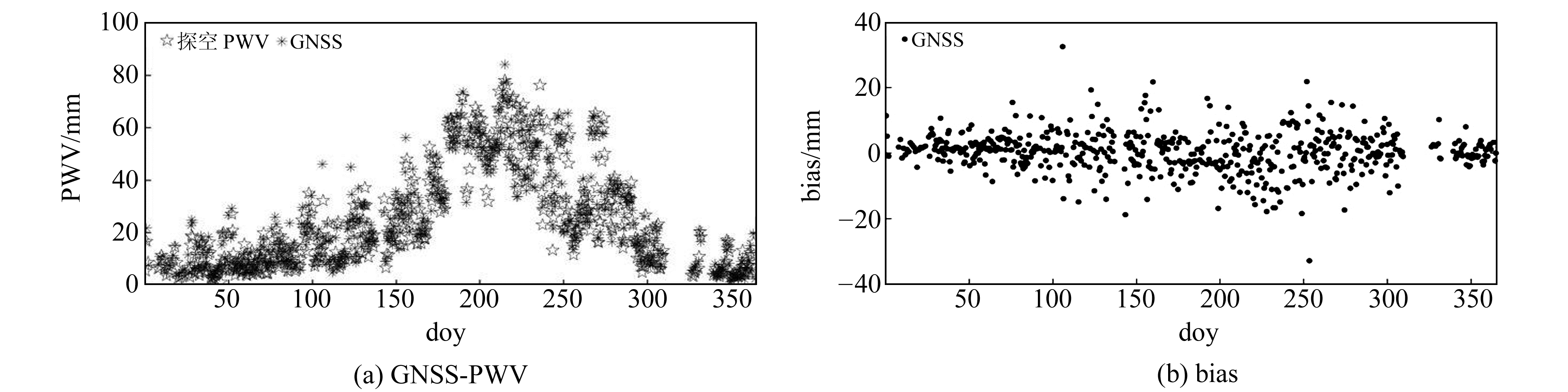
图 3、图 4分别为安庆站和射阳站2017年GNSS-PWV及其bias,表 4为两站2017年GNSS-PWV的精度统计(单位mm)。由图可知,GNSS-PWV与探空PWV在2017年的差值基本保持在10 mm以内,且冬季偏差小于夏季偏差。由表 4可知,GNSS-PWV的平均bias和RMSE分别为0.05 mm和3.50 mm,与探空PWV具有较好的一致性。
|
图 3 2017年安庆站GNSS-PWV及其bias Fig. 3 GNSS-PWV and their biases at Anqing station in 2017 |
|
图 4 2017年射阳站GNSS-PWV及其bias Fig. 4 GNSS-PWV and their biases at Sheyang station in 2017 |
|
|
表 4 2017年安庆站和射阳站GNSS-PWV精度统计 Tab. 4 Accuracy statistics of GNSS-PWV at Anqing and Sheyang stations in 2017 |
总体而言,GNSS-PWV精度最高,不受天气状况影响且仪器长期稳定无需标定,具有广阔的应用前景;地面法PWV精度较低,但计算简单、可实时获取结果,在无法实时处理GNSS数据以及缺乏GNSS站的情况下具有很强的实用价值。但上述两种方法均需要探空站或GNSS站的观测数据,在很多无法获取气象参数的地区具有较大的局限性,因此可利用GPT3模型在精度要求较低的地区获取实时PWV。
3 结语1) 从精度上看,GNSS-PWV精度最高,地面气象资料法次之,GPT3-PWV精度最低。其中,地面气象资料法1的精度优于地面气象资料法2,4种方法获取的PWV均呈现出季节特性,冬季精度优于夏季精度。
2) 从时效性和数据依赖程度上看,GPT3模型无需任何气象参数,可实时获取PWV;地面法需要露点温度、纬度和高程等参数;GNSS-PWV同时需要GNSS数据和实测气象数据。
3) 在同时拥有气象资料和GNSS数据的情况下,可基于GNSS获得精度最高的GNSS-PWV;在仅有地面气象资料而缺乏GNSS数据时,可利用地面露点资料得到实时PWV;若GNSS数据和气象数据均缺失,则可利用GPT3模型计算PWV。
| [1] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15 787-15 801 DOI:10.1029/92JD01517
(  0) 0) |
| [2] |
石小龙, 尚伦宇, 尹远渊, 等. 大连地区GPS反演大气可降水量的变化特征[J]. 高原气象, 2014, 33(6): 1 648-1 653 (Shi Xiaolong, Shang Lunyu, Yin Yuanyuan, et al. Variation Characteristics of Precipitable Water Vapor Inversed by GPS in Dalian[J]. Plateau Meteorology, 2014, 33(6): 1 648-1 653)
(  0) 0) |
| [3] |
向玉春, 陈正洪, 徐桂荣, 等. 三种大气可降水量推算方法结果的比较分析[J]. 气象, 2009, 35(11): 48-54 (Xiang Yuchun, Chen Zhenghong, Xu Guirong, et al. A Comparison and Analysis of the Results of Three Methods for the Calculation of Water Vapor Resources[J]. Meteorological Monthly, 2009, 35(11): 48-54 DOI:10.7519/j.issn.1000-0526.2009.11.006)
(  0) 0) |
| [4] |
卢士庆, 闫宾, 刘晓东. 几种求算大气可降水量方法比较[J]. 内蒙古气象, 2009(1): 15-18 (Lu Shiqing, Yan Bin, Liu Xiaodong. Comparison among Some Calculation Methods on Atmosphere Precipitation[J]. Inner Mongolia Meteorological, 2009(1): 15-18 DOI:10.3969/j.issn.1005-8656.2009.01.004)
(  0) 0) |
| [5] |
翟树峰, 吕志平, 李林阳, 等. 基于GPT2w模型化加权平均温度反演可降水量[J]. 大地测量与地球动力学, 2019, 39(7): 733-737 (Zhai Shufeng, Lü Zhiping, Li Linyang, et al. Precipitable Water Vapor Retrieval Based on Weighted Mean Temperature from GPT2w[J]. Journal of Geodesy and Geodynamics, 2019, 39(7): 733-737)
(  0) 0) |
| [6] |
Landskron D, Böhm J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions[J]. Journal of Geodesy, 2018, 92(4): 349-360 DOI:10.1007/s00190-017-1066-2
(  0) 0) |
| [7] |
杨景梅, 邱金桓. 用地面湿度参量计算我国整层大气可降水量及有效水汽含量方法的研究[J]. 大气科学, 2002, 26(1): 9-22 (Yang Jingmei, Qiu Jinhuan. A Method for Estimating Precipitable Water and Effective Water Vapor Content from Ground Humidity Parameters[J]. Chinese Journal of Atmospheric Sciences, 2002, 26(1): 9-22 DOI:10.3878/j.issn.1006-9895.2002.01.02)
(  0) 0) |
| [8] |
张学文. 可降水量与地面水汽压力的关系[J]. 气象, 2004, 30(2): 9-11 (Zhang Xuewen. A Relationship between Precipitable Water and Surface Vapor Pressure[J]. Meteorological Monthly, 2004, 30(2): 9-11)
(  0) 0) |
| [9] |
Saastamoinen J. Introduction to Practical Computation of Astronomical Refraction[J]. Bulletin Géodésique, 1972, 106(1): 383-397
(  0) 0) |
2. Research Center of Beidou Navigation and Environmental Remote Sensing, Suzhou University of Science and Technology, 99 Xuefu Road, Suzhou 215009, China
 2022, Vol. 42
2022, Vol. 42

