电离层作为近地空间环境的重要组成部分,其发生的任何细微变化都有可能对导航定位系统、无线电传播与通讯、测量及人类空间活动产生重大影响[1]。卫星信号的传播误差与电离层总电子含量直接相关,提高电离层TEC短期预报精度可以有效提高导航定位精度。目前电离层TEC短期预报主要有数理统计和人工智能两种方法。由于TEC具有随时间发生周期性变化的特点,国内有关TEC预报的研究多以数学统计法中的时间序列分析为主[1-4]。
人工智能法则以神经网络模型为代表,相较于时间序列分析方法,神经网络模型具有更高的预报精度及计算速度[5-7]。电离层在时空上的随机性和不平衡性使TEC具有非线性和不平稳的特点[8],由于神经网络能够以任意精度逼近任意N维到M维映射,从而达到预报效果,其作为一种典型的非线性预报模型可有效预报电离层TEC。许多学者采用神经网络模型对TEC进行有效预报,然而神经网络在参数选择及网络优化等方面较为复杂,且存在过度拟合导致精度下降的情况,群优化算法可有效改善该缺陷。因此,本文提出一种群优化算法改进Elman神经网络的电离层TEC短期预报模型。
1 模型算法原理 1.1 BP神经网络和Elman神经网络BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络[9]。相比于BP神经网络的3层结构,Elman神经网络在隐含层上增加一个承接层,可以记忆隐含层前一时刻的输出,使系统具有适应时变特性的能力。
1.2 SSA-Elman组合模型目前,国内外已有很多有关群优化算法的研究,许多学者提出一些性能优异的群优化算法,其中粒子群算法(particle swarm optimization, PSO)和蚁群算法(ant colony optimization, ACO)最具代表性。与粒子群算法和蚁群算法相比,麻雀搜索算法(SSA)[10]具有良好的稳定性和收敛速度,并具有探索未知区域和避免陷入局部最优的能力。
SSA-Elman组合模型将SSA寻优获得的最优初始权值和阈值赋值给Elman神经网络,在Elman神经网络迭代过程中通过计算网络误差,进一步更新Elman神经网络的权值和阈值,当满足精度要求后则可以进行电离层TEC预报。
1.3 模型参数及处理电离层TEC受地磁活动、太阳活动及引力波等因素影响,随昼夜、季节变化而发生周期性变化。本文在建立电离层TEC预报模型时,选取地磁活动指数Dst及TEC作为输入参数,其中地磁活动指数是描述一个时段内地磁扰动强度的分级指标[9]。
在使用BP神经网络进行TEC预报时,选取1个输入层、1个隐含层和1个输出层的3层网络结构,将最大学习次数设置为5 000,学习速率设置为0.01,期望误差设置为0.000 1。Elman神经网络和SSA-Elman组合神经网络参数设置与BP神经网络保持一致,通过调整参数,将SSA种群数量设置为20,最大迭代次数为30,发现者占种群总数20%,安全系数设置为0.8,进行预警行为的个体数量为3。采用15 d预报5 d的方法对电离层TEC进行预报,其中网络训练样本选取前15 d的TEC及Dst作为网络的输入层,后5 d的TEC及Dst作为网络的输出层进行网络训练,并分别对TEC及Dst进行归一化处理,将数值控制在[-1, 1]范围内以便于网络训练。
2 实验与分析本文所用数据来源于CODE中心,时间分辨率为1 h,选取2018年全年低中纬度地区(5°N, 120°E)和(40°N, 120°E)的TEC数据进行实验分析。图 1(a)和1(b)分别为(5°N, 120°E)和(40°N, 120°E)处全年的电离层TEC变化趋势,图 1(c)为2018年全年的地磁活动指数。通过对比可以发现,当地磁活动指数发生扰动时,对应TEC也会发生明显变化,TEC与地磁活动指数具有较强的相关性。选取均方根误差(RMSE)、残差(Δ)及相关系数(ρ)用于分析比较,计算公式参见文献[8]。

|
图 1 2018年电离层TEC及地磁活动指数 Fig. 1 Ionospheric TEC and Dst index in 2018 |
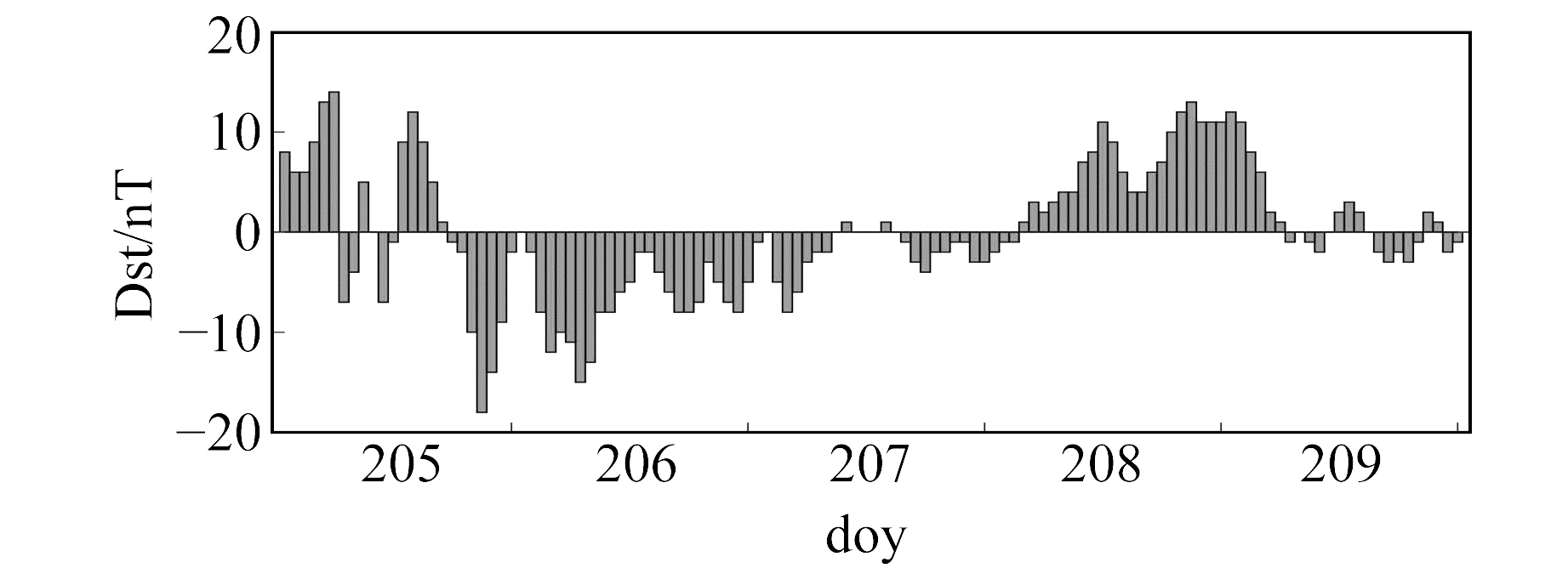
选取平静期对应时段,图 2为doy205~209对应的地磁活动指数,从图中可以看出,该时间段Dst指数都维持在-20~20 nT范围内,均大于-30 nT。
|
图 2 平静期地磁活动指数 Fig. 2 The Dst index in quiet period |
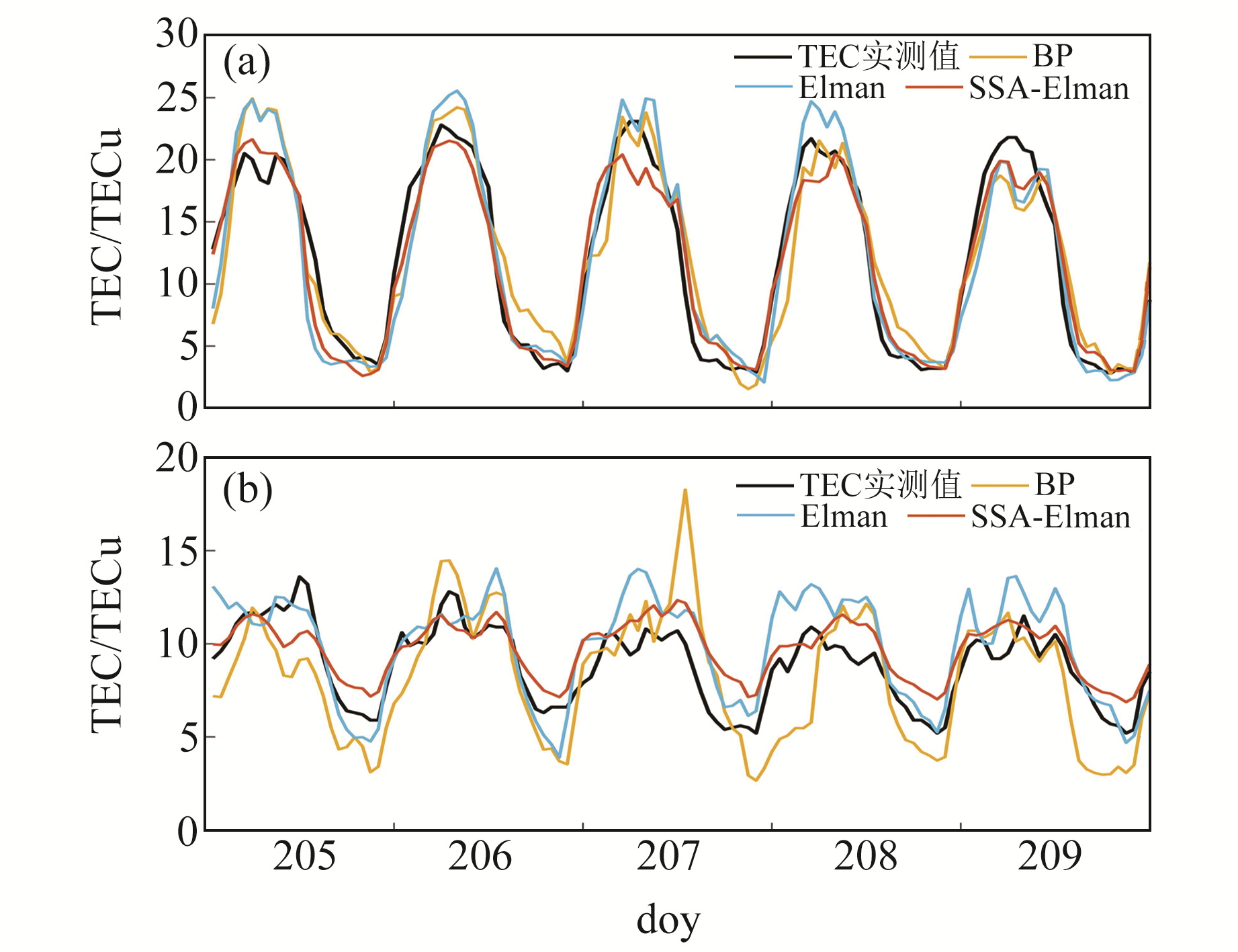
图 3为利用3种模型预报不同纬度的TEC,其中图 3(a)和3(b)分别对应低纬度和中纬度。从图 3(a)可以看出,低纬度的TEC变化较为平缓,3种模型预报值的变化趋势相近,但SSA-Elman组合模型的预报值相比BP模型和Elman模型更加接近实测值,SSA-Elman组合模型在峰值处和谷值处的预报效果优于另外2种模型。从图 3(b)来看,不同于低纬度TEC平缓的变化趋势,中纬度TEC在峰值处出现突变,因此突变处的拟合程度可作为模型精度的评价指标之一。BP模型的预报值明显偏离TEC实测值,在doy207出现极端峰值,Elman模型和SSA-Elman组合模型对峰值处的预报效果优于BP模型,但从图中可以明显看出,Elman模型的残差大于SSA-Elman组合模型。综上所述,SSA-Elman组合模型和Elman模型的预报效果明显优于BP模型,SSA-Elman组合模型的预报精度相较Elman模型具有一定程度的提高。
|
图 3 平静期3种模型TEC预报值与实测值对比 Fig. 3 Comparison between predicted and measured TEC values of three models in quiet period |
评价模型精度的另一项指标为残差(Δ),图 4为平静期3种模型TEC预报残差值对比情况,其中图 4(a)和4(b)分别对应低纬度和中纬度。从图 4(a)可以看出,SSA-Elman组合模型的预报残差值基本在4 TECu以内,最大残差接近6 TECu,Elman模型的预报残差值多数集中在4~6 TECu之间,BP模型的部分预报残差值高达8 TECu,预报误差最大。同时,BP模型和Elman模型的残差值分布相较SSA-Elman组合模型更为离散,BP模型的残差值分布在3种模型中最为离散,该现象在中纬度情况下更加明显。使用SSA-Elman组合模型预报得到的残差值绝对值基本在3 TECu以内,Elman模型在4 TECu以内,而BP模型最大残差值可达9 TECu,其残差值在doy207、208、209比其他2个模型多出将近4 TECu,离散程度大于Elman模型和SSA-Elman组合模型。因此,BP模型预报精度最差,总体误差大于其他2个模型,SSA-Elman组合模型相比Elman模型精度更优。

|
图 4 平静期3种模型TEC预报残差值对比 Fig. 4 Comparison between residual errors of predicted TEC values of three models in quiet period |
表 1为中低纬度地区doy205~209期间3个模型预报结果的均方根误差(RMSE)、残差(Δ)及相关系数(ρ)对比结果。由表可知,对平静期进行5 d的低纬度TEC预报时,BP模型5 d的RMSE平均值为2.763 TECu,残差平均值为2.218 TECu,相关系数为0.929;Elman模型5 d的RMSE平均值为2.402 TECu,平均残差为1.876 TECu,相关系数为0.946;SSA-Elman组合模型5 d的RMSE平均值为1.776 TECu,平均残差为1.382 TECu,相关系数为0.972。对中纬度地区TEC进行预报时,BP模型5 d的RMSE平均值为2.360 TECu,平均残差为1.974 TECu,相关系数为0.837;Elman模型5 d的RMSE平均值为1.785 TECu,平均残差为1.468 TECu,相关系数为0.887;SSA-Elman组合模型5 d的RMSE平均值为1.358 TECu,平均残差为1.168 TECu,相关系数为0.904。从上述分析可知,SSA-Elman组合模型的3个评价指标均优于其他2个模型,预报精度最优。
|
|
表 1 平静期不同纬度下3个模型预报指标对比 Tab. 1 Comparison of prediction indexes of three models at different latitudes in quiet period |
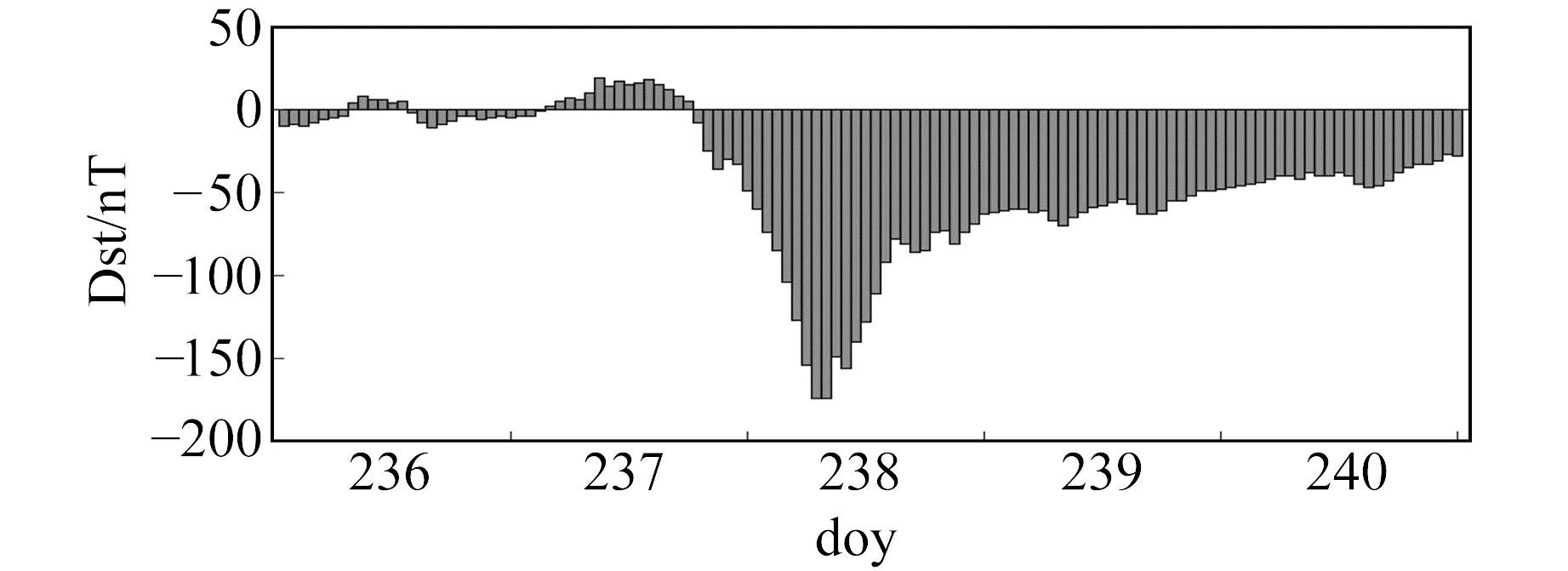
图 5为doy236~240对应的地磁活动指数,从图中可以看出,该时间段Dst指数在-180~20 nT范围内变化,根据国际磁暴划分标准,这5 d发生较大磁暴,与平静期Dst指数相比,扰动期Dst指数跨度极大,正负峰值相差近200 nT。
|
图 5 扰动期地磁活动指数 Fig. 5 The Dst index in disturbance period |
图 6为扰动期中低纬度TEC实测值与3种模型TEC预报值对比结果,其中图 6(a)和6(b)分别为低纬度和中纬度处TEC变化趋势。由图 6(a)可知,BP模型相比其他2种模型在doy237出现极端值。由于受磁暴影响,doy238中低纬度TEC实测值远大于其他4 d,3种模型在该天的预报残差均较大。BP模型和Elman模型的预报值在doy236谷值处出现突变,与之相比,SSA-Elman组合模型的预报值变化更平缓,且预报值更加接近实测值,预报效果相比其他2种模型更好。从图 6(b)来看,与低纬度TEC相比,中纬度TEC在峰值处存在突变,BP模型在谷值处的预报结果呈现出与实测值相反的变化趋势。此外,Elman模型与SSA-Elman组合模型在峰值处的拟合度优于BP模型,且SSA-Elman组合模型比Elman模型的预报残差值更小。由此可知,SSA-Elman模型在中纬度和低纬度地区均具有更高的预报精度。

|
图 6 扰动期3种模型TEC预报值与实测值对比 Fig. 6 Comparison between predicted and measured TEC values of three models in disturbance period |
图 7为扰动期3种模型TEC预报残差值对比,其中图 7(a)和7(b)分别对应低纬度和中纬度。从图中可以看出,低纬度的预报残差值为中纬度的2倍,中低纬度在doy238的TEC预报残差值均发生较大波动。由于当日受磁暴影响,Dst指数低至-174 nT,导致3种模型的预报残差值均较大。利用BP模型预报其余4 d低纬度TEC时,最大残差接近12 TECu,而利用Elman模型与SSA-Elman组合模型预报时,残差值均小于8 TECu,因此BP模型在低纬度的预报效果在3种模型中最差。在中纬度地区,BP模型预报其余4 d的残差值在0.5~7 TECu范围内波动,Elman模型的预报残差值在2~4.5 TECu范围内波动,SSA-Elman组合模型的预报残差值在2~4 TECu范围内波动,由此可见,BP模型在中纬度的预报效果不如其他2种模型。

|
图 7 扰动期3种模型TEC预报残差值对比 Fig. 7 Comparison between residual errors of predicted TEC values of three models in disturbance period |
由于图 7中Elman模型和SSA-Elman组合模型预报残差值的变化趋势相似,残差值大小相近,为分析2种模型的预报精度,表 2为中低纬度地区doy236~240期间3个模型预报结果的均方根误差(RMSE)、残差(Δ)及相关系数(ρ)对比结果。由表可知,对扰动期进行5 d的低纬度TEC预报时,BP模型5 d的RMSE平均值为4.775 TECu,平均残差为3.803 TECu,相关系数为0.883;Elman模型5 d的RMSE平均值为3.945 TECu,平均残差为3.237 TECu,相关系数为0.924;SSA-Elman组合模型5 d的RMSE平均值为2.955 TECu,平均残差为2.372 TECu,相关系数为0.952。对扰动期进行5 d的中纬度TEC预报时,BP模型5 d的RMSE平均值为2.846 TECu,平均残差为2.446 TECu,相关系数为0.749;Elman模型5 d的RMSE平均值为2.255 TECu,平均残差为1.988 TECu,相关系数为0.803;SSA-Elman组合模型5 d的RMSE平均值为1.896 TECu,平均残差为1.586 TECu,相关系数为0.826。3种模型扰动期TEC预报精度均低于平静期,BP模型的相关系数低于0.8,预报效果最差,SSA-Elman组合模型的预报效果优于Elman模型,其对电离层扰动期TEC的预报效果相较Elman模型具有一定程度的提高。
|
|
表 2 扰动期不同纬度下3个模型预报指标对比 Tab. 2 Comparison of prediction indexes of three models at different latitudes in disturbance period |
为进一步验证模型在不同经度地区预测值的可靠性,利用CODE中心提供的2018年(5°N, 120°W)和(40°N, 120°W)处TEC值,使用3种预报模型进行建模,并利用中科院提供的同位置、同时段TEC作为实测值进行精度验证。表 3为3种模型在平静期(doy205~209)和扰动期(doy236~240)均方根误差(RMSE)、残差(Δ)和相关系数(ρ)的均值。从表中可以看出,使用SSA-Elman组合模型对平静期和扰动期进行低纬度TEC预报时,预报精度均优于BP模型和Elman模型,其中平静期的RMSE为1.970 TECu,残差为1.499 TECu,相关系数为0.984;扰动期的RMSE为3.818 TECu,残差为2.702 TECu,相关系数为0.934。对中纬度TEC进行预报时,平静期SSA-Elman组合模型的RMSE为1.640 TECu,残差为1.402 TECu,相关系数为0.900,优于BP模型和Elman模型;扰动期SSA-Elman组合模型的RMSE为2.347 TECu,残差为1.928 TECu,相关系数为0.916,优于BP模型和Elman模型。经过对比分析可知,SSA-Elman组合模型可对中低纬度不同经度地区的TEC进行有效预报,且预报效果优于BP模型和Elman模型。
|
|
表 3 120°W处不同纬度地区3个模型预报指标对比 Tab. 3 Comparison of prediction indexes of three models at different latitudes at 120°W |
根据电离层TEC序列非线性和不平稳的特点,针对传统BP神经网络模型在对TEC进行预报时易陷入局部最优的缺陷,本文选取网络全局稳定性更强并具有适应时变特性能力的Elman神经网络模型,利用麻雀算法对Elman模型进行优化,构建SSA-Elman组合模型。采用地磁活动指数Dst及TEC作为输入,分别对中低纬度平静期和扰动期电离层TEC进行5 d的短期预报,并将其与BP神经网络模型及Elman神经网络模型的预报效果进行对比分析。结果表明,SSA-Elman组合模型具有更好的预报效果。由于TEC不仅受地磁活动影响,还会受到诸如太阳风、引力波等因素影响,并且在不同时间、空间条件下进行预报存在不稳定性,随着预报时长的增加,个别时段还存在预报精度下降的问题,可尝试使用更多的数据进行训练以提高网络的泛用性,或将太阳风、引力波等参数加入到模型训练中以提高预报的准确度。
| [1] |
陈鹏, 姚宜斌, 吴寒. 利用时间序列分析预报电离层TEC[J]. 武汉大学学报: 信息科学版, 2011, 36(3): 267-270 (Chen Peng, Yao Yibin, Wu Han. TEC Prediction of Ionosphere Based on Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 267-270)
(  0) 0) |
| [2] |
汤俊, 姚宜斌, 陈鹏, 等. 利用EMD方法改进电离层TEC预报模型[J]. 武汉大学学报: 信息科学版, 2013, 38(4): 408-411 (Tang Jun, Yao Yibin, Chen Peng, et al. Prediction Models of Ionospheric TEC Improved by EMD Method[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 408-411)
(  0) 0) |
| [3] |
张小红, 任晓东, 吴风波, 等. 自回归移动平均模型的电离层总电子含量短期预报[J]. 测绘学报, 2014, 43(2): 118-124 (Zhang Xiaohong, Ren Xiaodong, Wu Fengbo, et al. Short-Term TEC Prediction of Ionosphere Based on ARIMA Model[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 118-124)
(  0) 0) |
| [4] |
鲁铁定, 黄佳伟, 鲁春阳, 等. 基于EWT- ARMA的短期电离层TEC预测模型[J]. 大地测量与地球动力学, 2021, 41(4): 331-335 (Lu Tieding, Huang Jiawei, Lu Chunyang, et al. Short-Term Ionospheric TEC Prediction Model Based on EWT-ARMA[J]. Journal of Geodesy and Geodynamics, 2021, 41(4): 331-335)
(  0) 0) |
| [5] |
陆建华, 王斌, 胡伍生. 利用BP神经网络改进电离层短期预报模型[J]. 测绘科学技术学报, 2017, 34(1): 1-4 (Lu Jianhua, Wang Bin, Hu Wusheng. Improved Prediction Model of Ionospheric TEC by BP Neural Network[J]. Journal of Geomatics Science and Technology, 2017, 34(1): 1-4)
(  0) 0) |
| [6] |
汤俊, 高鑫. 贝叶斯正则化的Elman神经网络电离层TEC预报模型[J]. 大地测量与地球动力学, 2020, 40(8): 799-805 (Tang Jun, Gao Xin. Prediction Models of Ionospheric TEC by Elman Neural Network with Bayesian Regularization[J]. Journal of Geodesy and Geodynamics, 2020, 40(8): 799-805)
(  0) 0) |
| [7] |
黄文喜, 祝芙英, 翟笃林, 等. BP神经网络和ARMA模型在中纬度TEC短期预测中的对比分析[J]. 大地测量与地球动力学, 2021, 41(3): 262-267 (Huang Wenxi, Zhu Fuying, Zhai Dulin, et al. Comparative Analysis of BP Neural Network and ARMA Model in Short-Term Prediction of Mid-Latitude TEC[J]. Journal of Geodesy and Geodynamics, 2021, 41(3): 262-267)
(  0) 0) |
| [8] |
刘淑琼, 高鑫, 李长春. EEMD-RBF神经网络的电离层TEC预报模型[J]. 测绘工程, 2020, 29(3): 15-19 (Liu Shuqiong, Gao Xin, Li Changchun. Prediction Models of Ionospheric TEC by EEMD and Radial Basis Function Neural Network[J]. Engineering of Surveying and Mapping, 2020, 29(3): 15-19)
(  0) 0) |
| [9] |
Gonzalez W D, Joselyn J A, Kamide Y, et al. What is a Geomagnetic Storm?[J]. Journal of Geophysical Research: Space Physics, 1994, 99(A4): 5 771-5 792 DOI:10.1029/93JA02867
(  0) 0) |
| [10] |
Xue J K, Shen B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm[J]. Systems Science and Control Engineering, 2020, 8(1): 22-34 DOI:10.1080/21642583.2019.1708830
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

