2. 中国科学院大学,北京市玉泉路19号甲,100049;
3. 中国科学院时间频率基准重点实验室,西安市书院东路3号,710600
远程高精度时间频率传递技术主要有卫星双向时间频率传递(TWSTFT)、基于全球导航卫星系统(GNSS)的时间频率传递、光纤时间频率传递和激光时间传递等[1-4],其中GNSS载波相位时间传递(CPTT)作为一种远程时间传递手段,具有设备简单、成本低、测量精度高、全球可覆盖等特点,多年来一直是国内外时间频率传递领域的研究热点,其实现方式主要有非差精密单点定位(PPP)、站间单差Phase-CV和网解法[5-7]。相比于TWSTFT和其他GNSS时间传递技术,GNSS CPTT具有良好的短期频率稳定度和更高的分辨率,其典型代表GPS PPP自2009年开始被国际权度局(BIPM)用于TAI计算,时间传递精度可达亚ns级。PPP以双频无电离层码伪距和载波相位组合作为观测量,采用IGS/MGEX提供的卫星精密轨道、钟差、差分码偏差(DCB)及地球自转参数等,消除卫星钟、轨道和地球自转等误差的影响,可获得静态cm级定位精度和ps量级定时精度,多年来一直是高精度定位和时间传递领域的研究热点[8-9]。目前,全球参与TAI计算的84个守时实验室中有50个实验室已建立GPS PPP链路[10]。而随着欧盟Galileo和中国北斗卫星导航系统(BDS)的逐步完善及GNSS多系统实验专项(MGEX)精密轨道和钟差产品的出现,采用融合GNSS多系统来提高PPP时间传递的准确度和链路的稳健性已成为当前及今后的发展趋势[11-13]。
传统PPP通常以1 d为1个批单元进行测站钟差估计,测站钟差序列在天与天边界历元出现跳变,从而产生日界不连续现象。对大多数测站而言,钟差估计结果的日界不连续误差量值一般为几十ps至1 ns,但部分测站的日界不连续误差量值会大于1 ns。日界不连续误差的出现成为实现连续GNSS载波相位时间传递的最大障碍,无法准确反映实时连续运行的两地时钟性能,严重影响两地时钟比对长期频率稳定度的提升。研究表明,日界不连续误差主要由码噪声(包括接收机硬件时延、多径误差等)和卫星精密产品不连续性所引起,相位模糊度与测站钟差估计结果不连续的本质具有一致性[14-17]。
为分析日界不连续误差对GNSS载波相位频率传递的影响,本文基于MGEX/BIPM并址站GPS/BDS观测数据及欧洲定轨中心(CODE)提供的精密轨道和钟差产品,首先分析日界不连续误差的统计特性,然后从理论方面分析日界不连续误差对两地时钟相对频率偏差估计的影响,最后通过实验来验证日界不连续误差对两地时钟频率比对的影响。
1 GNSS载波相位时间传递 1.1 GNSS CP时间传递数学模型基于码伪距和载波相位测量的GNSS基本观测模型可参见文献[17]。双频组合消除电离层一阶延迟误差的无电离层码伪距和载波相位组合观测模型,即传统PPP模型,可表示为:
| $ \begin{array}{c} P_{\mathrm{IF}}=\frac{f_{1}^{2} P_{1}-f_{2}^{2} P_{2}}{f_{1}^{2}-f_{2}^{2}}=\rho+c\left(\mathrm{~d} t_{r}-\mathrm{d} T^{s}\right)+ \\ d_{\text {trop }}+D_{P_{\mathrm{IF}}}+d_{P_{\mathrm{IF}}}+d_{\mathrm{mul} / P_{\mathrm{IF}}}+\varepsilon_{P_{\mathrm{IF}}} \end{array} $ | (1) |
| $ \begin{array}{c} L_{\mathrm{IF}}=\frac{f_{1}^{2} L_{1}-f_{2}^{2} L_{2}}{f_{1}^{2}-f_{2}^{2}}=\rho+c\left(\mathrm{~d} t_{r}-\mathrm{d} T^{s}\right)+d_{\text {trop }}+ \\ D_{L_{\mathrm{IF}}}+d_{L_{\mathrm{IF}}}+\lambda_{\mathrm{IF}} N_{\mathrm{IF}}+d_{\mathrm{mul} / L_{\mathrm{IF}}}+\varepsilon_{L_{\mathrm{IF}}} \end{array} $ | (2) |
式中,PIF和LIF分别为无电离层码伪距和载波相位组合观测值,单位m;dPIF、DPIF、dLIF和DLIF分别为码伪距和载波相位接收机与卫星硬件时延,单位s;NIF为组合模糊度,单位周。
对式(1)和式(2)进行线性化后,采用序贯最小二乘平差对未知参数进行估计,包括测站位置、接收机钟差、天顶对流层延迟和组合模糊度。在解算出两测站钟差后,通过逐历元作差可获得两地时钟比对结果:
| $ \begin{array}{c} \Delta T_{A B}=\mathrm{d} t_{r, A}-\mathrm{d} t_{r, B}= \\ \left(T_{r, A}-\operatorname{IGST}\right)-\left(T_{r, B}-\operatorname{IGST}\right) \end{array} $ | (3) |
测站钟差参数的准确估计是实现两地时间传递的基础,估计结果的连续性对两测站间连续时间传递至关重要。在GNSS观测模型中,测站钟差平均值主要由码伪距观测值决定,而钟差的变化量则取决于载波相位。传统PPP通常以1 d为1个批单元,起始历元处测站钟差的无偏估计是基于码伪距观测值,由于多径及硬件时延等码噪声影响,相位模糊度不再是无偏估计,每日相位模糊度相对真值均存在不确定度,从而使相邻两天的相位模糊度出现不连续现象。而测站钟差与模糊度线性相关,因此测站钟差序列在天与天边界历元处出现时间跳变,即日界不连续误差,如图 1中红圈所示。

|
图 1 PPP测站钟差估计结果中日界不连续现象 Fig. 1 Day-boundary discontinuities in GPS PPP clock offset estimation |
除周跳、卫星信号被遮挡或接收机失锁等非正常观测外,如图 1中绿框所示,测站外接参考时钟正常工作时钟差序列应具有连续性,然而PPP测站钟差估计结果却在相邻两天边界处出现不连续现象。这种不连续误差主要在PPP数据处理时产生,与测站外接参考时钟无关,其量值甚至大于1 ns,而PPP测站钟差解算的精度通常为几百ps,因此日界不连续误差是限制PPP测站钟差估计结果频率稳定度提升的主要因素。
假设PPP测站钟差估计结果dtr可表示为X+Δ,其中X表示钟差真值,Δ表示由于码噪声引起的钟差偏移,日界不连续误差DBD可表示为:
| $ \mathrm{DBD}_{M, M+1}^{1}=\Delta_{M+1, M+1}^{1}-\Delta_{M, M}^{1} $ | (4) |
式中,DBD表示日界不连续误差,上标1表示批单元长度为1 d,下标M、M+1表示第M天与第M+1天。由于Δ取决于整个批单元码噪声的平均值和第1个历元的相位噪声,因此日界不连续误差与码噪声、载波相位噪声等引起的误差均有关。而相位噪声远小于码噪声,因此Δ主要取决于整个批单元所有历元码噪声的平均值。
1.2.2 统计分布为分析测站钟差估计结果的日界不连续误差,首先需将其提取出来。日界不连续误差可采用2种方法进行提取:1)将当前批单元(1 d)的前5 min测站钟差序列减去前1个批单元的最后5 min结果,称为原始法(图 2);2)对相邻2个批单元(2 d)的观测数据进行单独PPP解算,测站钟差分别为X1和X2,然后对这相邻2个批单元进行连续PPP测站钟差解算,测站钟差为X1→2,将X1与X1→2作差得到Δ1-X,X1→2与X2作差得到ΔX-2,最后可得相邻批单元间测站钟差的日界不连续误差为Δ1-2=ΔX-2-Δ1-X。

|
图 2 日界不连续误差提取方法 Fig. 2 Extraction method of the day-boundary discontinuities |
上述2种方法提取的日界不连续误差的均值基本相同,虽然重叠法(第2种方法)提取的不连续误差STD偏小,但重叠过程会消除短期噪声,无法真实反映码噪声的影响,因此,本文采用原始法(第1种方法)提取PPP测站钟差估计结果的日界不连续误差。
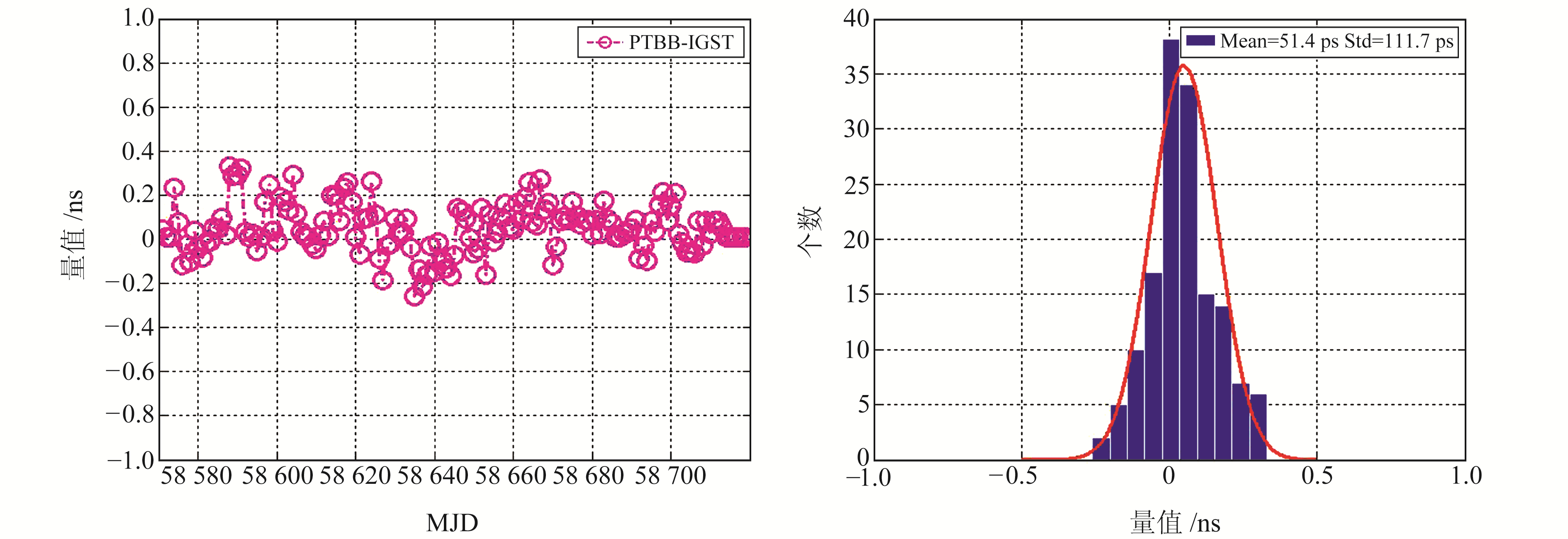
采用传统PPP模型对欧洲3个MGEX测站GPS/BDS观测数据进行解算,分别统计各测站钟差的日界不连续误差。所选测站不仅是MGEX测站,还是BIPM测站,测站外接参考时间分别为UTC(PTB)、UTC(ORB)和UTC(OP)。采用CODE提供的MGEX产品将参考时间统一对齐到IGST后,对2019-03-28~08-24共150 d的GPS/BDS观测数据进行PPP测站钟差解算,即约化儒略日(MJD)为58 570~58 719时段,然后提取测站钟差估计结果的日界不连续误差,结果见图 3~5。
|
图 3 PTBB测站钟差的日界不连续误差统计结果 Fig. 3 Statistical results of day-boundary discontinuities of clock offset estimation at PTBB station |
|
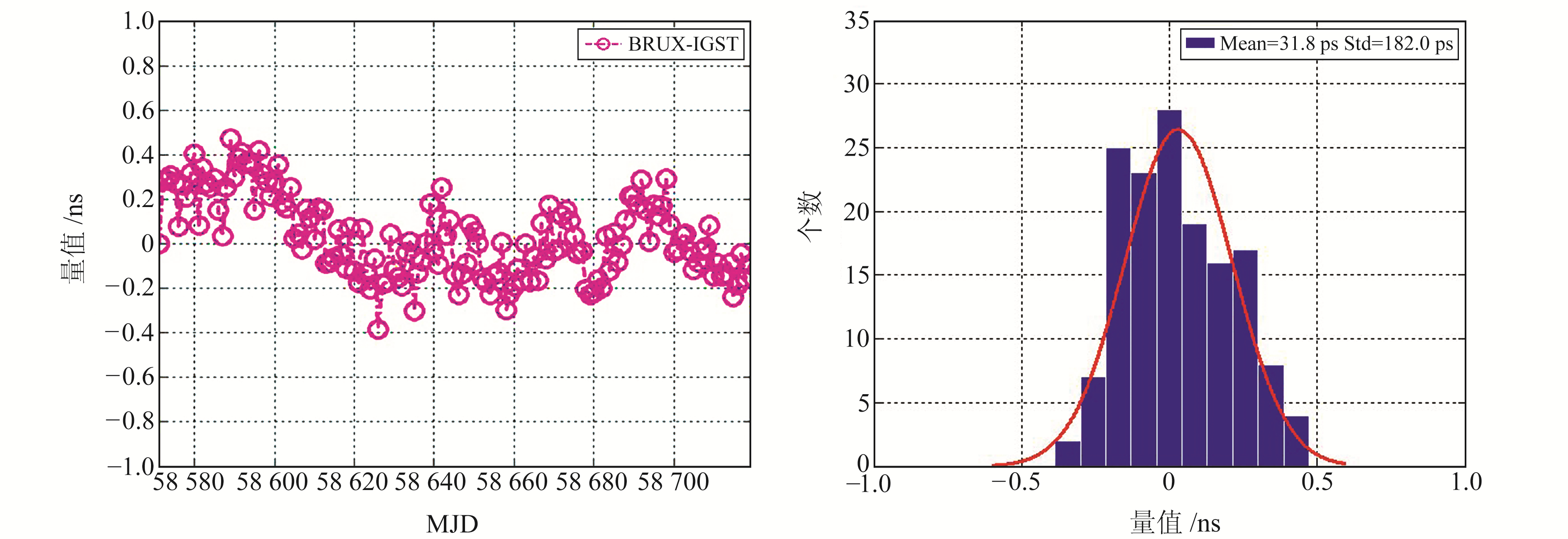
图 4 BRUX测站钟差的日界不连续误差统计结果 Fig. 4 Statistical results of day-boundary discontinuities of clock offset estimation at BRUX station |
|
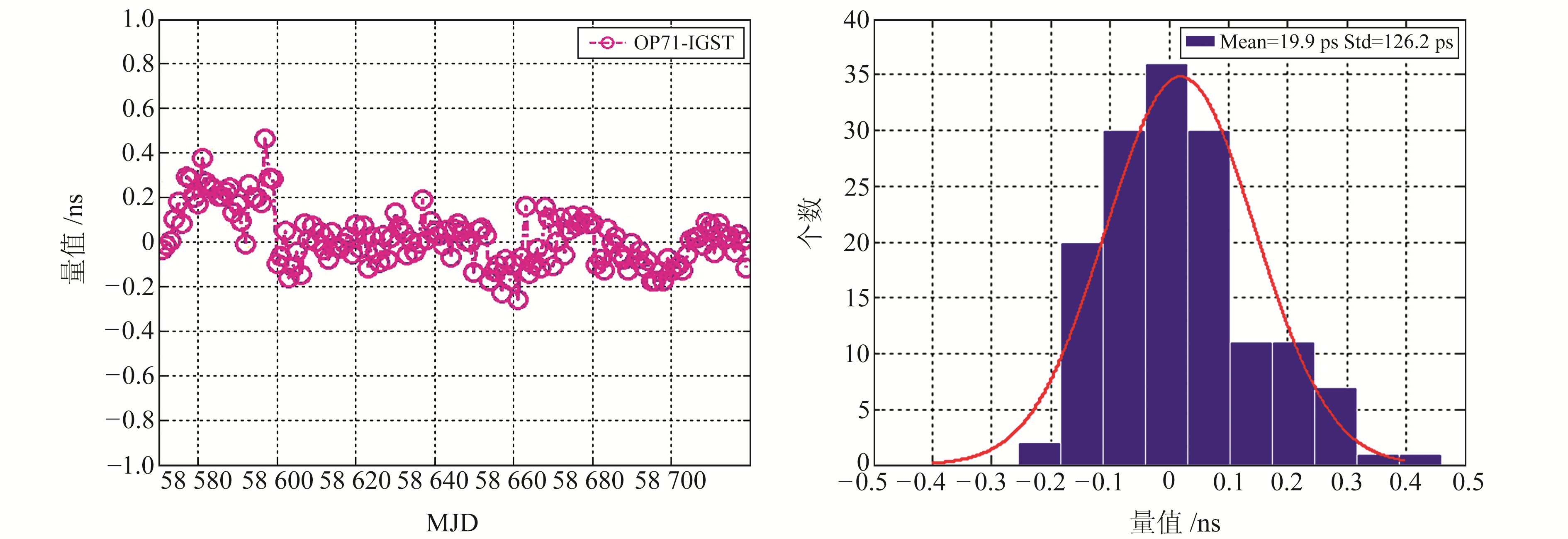
图 5 OP71测站钟差的日界不连续误差统计结果 Fig. 5 Statistical results of day-boundary discontinuities of clock offset estimation at OP71 station |
从图 3~5可以看出,PTBB、BRUX和OP71测站钟差估计结果的日界不连续误差基本在0.4 ns内波动,均值小于100 ps,Std小于200 ps,基本服从高斯分布。各测站钟差估计结果在相同边界历元处的日界不连续误差水平均不相同,由此可知,PPP测站钟差估计结果的日界不连续误差与测站有关。产生日界不连续误差的原因主要为码噪声和卫星精密产品的不连续性[15, 17],日界不连续误差更符合随机游走噪声特性。
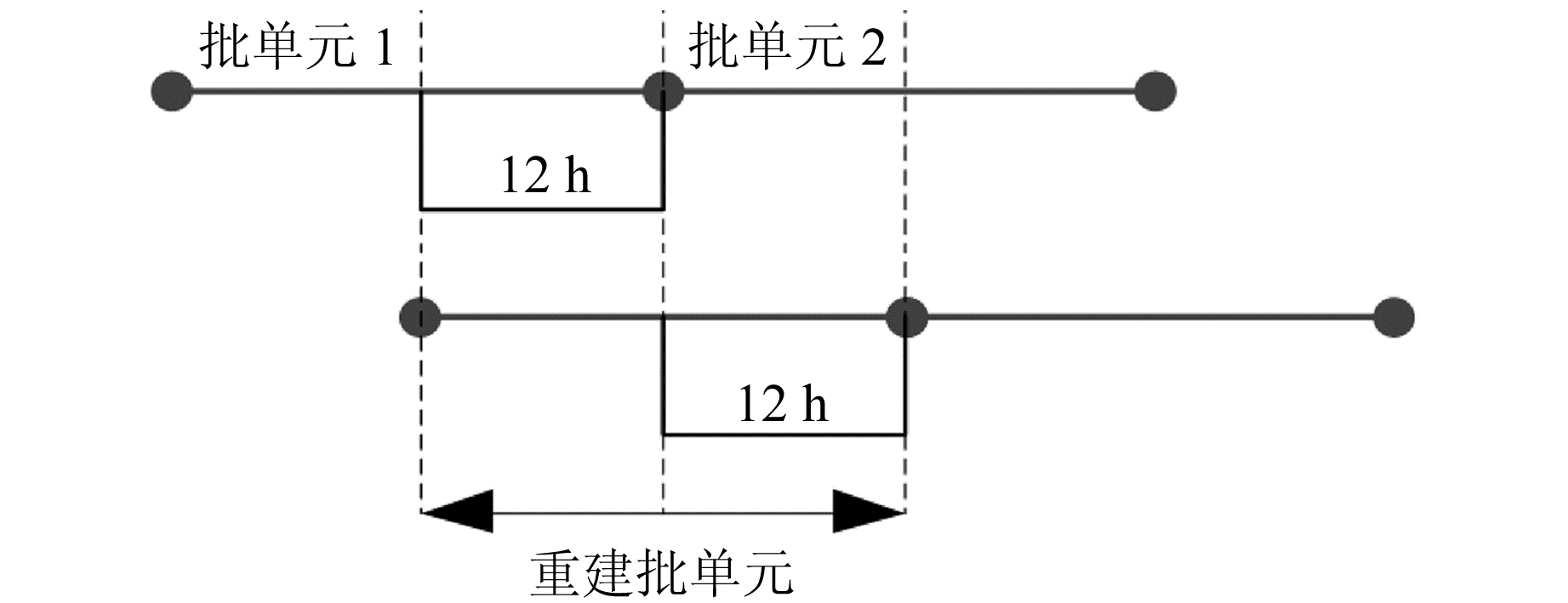
1.2.3 改正方法码噪声是引起PPP测站钟差估计和时间传递中日界不连续误差的主要原因,尽管无法彻底去除码噪声引起的误差,但可以采取多种方法尽量减弱其影响,从而减小相邻批单元间的不连续误差。为消除日界不连续误差,国内外学者相继提出多种方法[18-23],其中移位重叠法简单实用且计算量较小。对于更长批单元PPP,采用移位重叠可显著减小日界不连续误差,提升PPP时间传递的频率稳定度。移位重叠法的原理是在进行第1个批单元(24 h)PPP解算后,从4 h、8 h和12 h历元处重新开始1个新批单元PPP解算,新批单元与先前批单元重叠20 h、16 h或12 h,新批单元会跨越原来2个相邻批单元边界历元,可规避原相邻边界历元处的时间跳变;然后采用重叠段差值来估算不连续误差改正量,采用加权平均来平滑短期噪声;最后重构所需时段的测站钟差。如果重叠时长为12 h,则可以选用相邻2 d中间时段数据作为最终结果,从而减小残余的系统误差,最后逐次遍历所有时段。按此操作原理,可在PPP数据处理时将批单元长度为1 d推广为多天,从而最大程度地减小日界不连续误差,实现连续PPP时间传递(图 6)。
|
图 6 移位重叠法原理 Fig. 6 Principle of shift and overlapping method |
日界不连续误差使得通过PPP时间传递无法准确反映两地氢原子钟本身的性能。为规避日界不连续误差的影响,首先要消除日界不连续误差,获得连续的时间传递结果,再计算两地时钟的相对频率偏差。
假设PPP解算中第j个批单元包含Nes个时差估计值xj, 1, xj, 2, …, xj, i, xj, Nes,采样间隔为Δt,则相对频率偏差yi可表示为:
| $ y_{j}=\frac{1}{N_{e s}-1} \sum\limits_{i=1}^{N_{e s}-1} y_{j, i}=\frac{1}{N_{e s}-1} \sum\limits_{i=1}^{N_{e s}-1} \frac{x_{j, i+1}-x_{j, i}}{\Delta t} $ | (5) |
式中,xj, i和xj, i+1表示第j个批单元中相邻2个历元钟差估计。在获得第j个批单元的相对频率偏差后,可将每个批单元中获得的相对频率偏差进行组合,即可获得任意时段的相对频率偏差,取平均值则为最优频率估计。
在日界不连续误差存在的情况下,要计算相对频率偏差,首先可采用移位重叠法消除PPP时间传递中日界不连续误差而获得连续序列,该过程可表示为:
| $ x_{r+n, k}^{\prime}-x_{r, l}^{\prime}=x_{r+n, k}-x_{r, l}-\sum\limits_{j=r}^{r+n-1} m_{j} $ | (6) |
式中,mj为第j个和j+1个批单元间的不连续误差。需要强调的是,如果n=0,则xr+n, k-xr, l在同一批批单元中,此时无不连续误差项。由式(6)可以得到:
| $ x_{N, N_{e s}}^{\prime}-x_{1, 1}^{\prime}=x_{N, N_{e s}}-x_{1, 1}-\sum\limits_{j=1}^{N-1} m_{j} $ | (7) |
因此,包含日界不连续误差项的时间传递钟差序列的相对频率可表示为:
| $ y_{\text {merge }}=\frac{x_{N, N_{e s}}-x_{1, 1}-\sum\limits_{j=1}^{N-1} m_{j}}{N \tau_{0}} $ | (8) |
假设批单元中日界不连续误差估计值的不确定度为um,ux代表 1个批单元内相邻钟差估计值的噪声,则根据误差随机模型由式(8)可得含有不连续误差的钟差序列的相对频率不确定度为:
| $ \begin{array}{c} u_{y_{\text {merge }}^{2}}=\frac{u_{x_{N, N_{es}}}^{2}+u_{x_{1, 1}}^{2}+(N-1) u_{m}^{2}}{\left(N \tau_{0}\right)^{2}}= \\ \frac{2 u_{x}^{2}+(N-1) u_{m}^{2}}{\left(N \tau_{0}\right)^{2}} \end{array} $ | (9) |
式(9)需基于以下假设:1)xN, N与x1, 1之间互不相关,这在批单元长度N≠1时完全成立;2)第j个批单元与第k个批单元的不连续误差互不相关(如果第j个和第k个批单元为相邻批单元,该项假设将不成立)。从式(9)可以看出,相对频率偏差因为日界不连续误差的存在而出现偏移项,可能导致相对频率偏差估计值在两相邻批单元边界历元处出现跳变,从而难以准确估计总时段中相对频率偏差。
2 实验设计及数据预处理为验证以上理论分析的正确性,对MGEX/BIPM并址站PTBB、SPT0和USN8在2019-05-21~30(MJD 58 624~58 633)共10 d的GPS/BDS观测数据进行PPP测站钟差估计,采用移位重叠法对PPP时间传递中日界不连续误差进行改正,对比日界不连续误差改正前后UTC(SP)-UTC(PTB)、UTC(USNO)-UTC(PTB)的相对频率偏差。其中,GNSSsave表示日界不连续误差改正后的相对频率偏差估计结果,GNSSmerge表示日界不连续误差改正前的相对频率偏差估计结果,同时以BIPM公布的TAIPPP结果的相对频率偏差作为参考,实验所选测站信息见表 1。
|
|
表 1 实验所选MGEX测站信息 Tab. 1 Information of the selected MGEX stations |
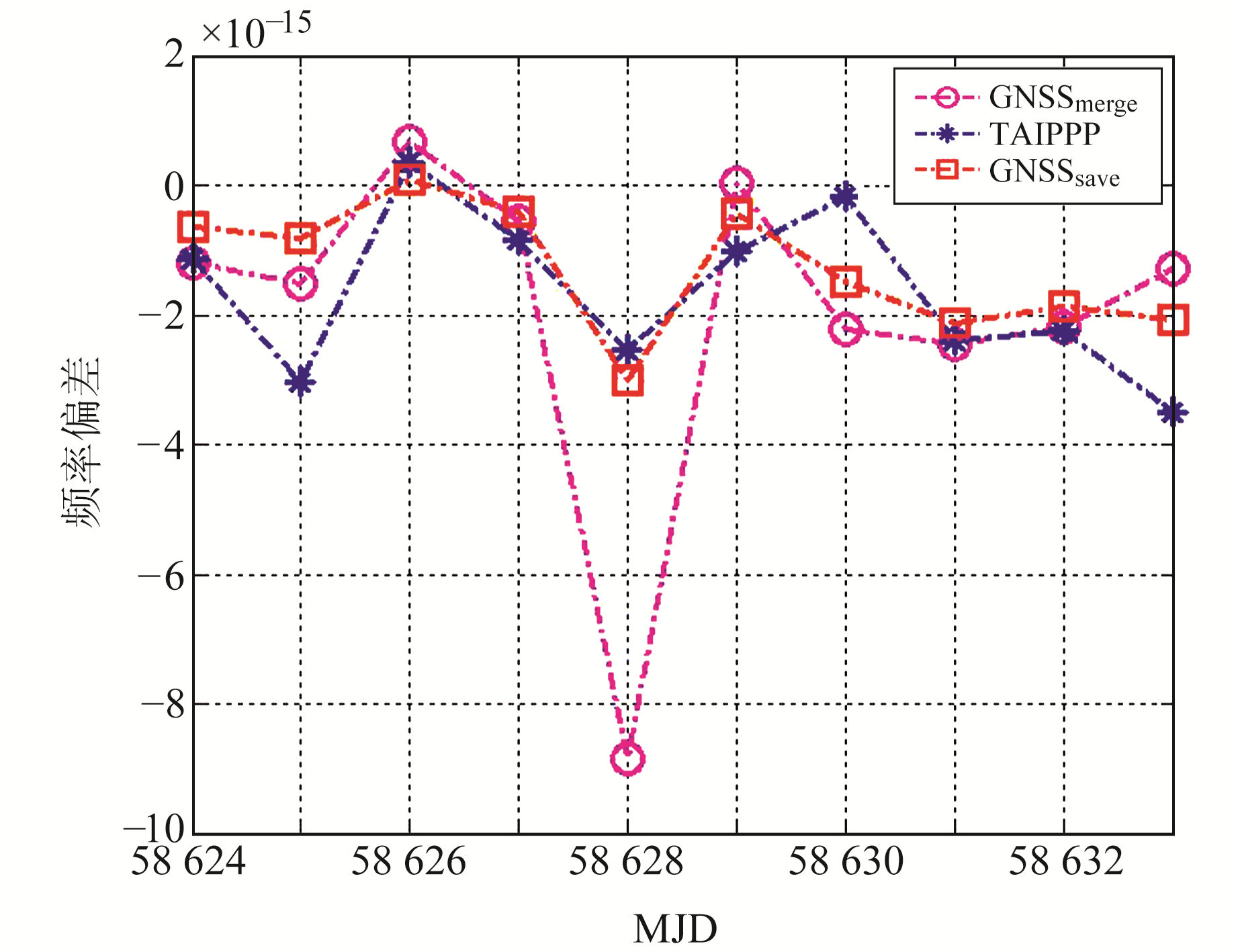
日界不连续误差改正前后UTC(SP)相对UTC(PTB)的频率偏差及TAIPPP结果如图 7所示,10 d平均相对频率偏差见表 2。从图中可以看出,未对UTC(SP)-UTC(PTB)中日界不连续误差进行改正时,相对频率偏差估计结果在批单元边界历元处出现很大量值的跳变,导致相对频率偏差出现偏移;对日界不连续误差进行改正后,UTC(SP)与UTC(PTB)相对频率偏差在相应批单元边界处的偏移基本得到消除,相对频率偏差估计结果的变化趋势与TAIPPP基本一致。日界不连续误差改正后,UTC(SP)与UTC(PTB)的10 d平均相对频率偏差GNSSsave为-1.275 2×10-15,TAIPPP平均相对频率偏差为-1.455 1×10-15,日界不连续误差未改正时UTC(SP)与UTC(PTB)平均相对频率偏差GNSSmerge为-1.956 8×10-15。由此可知,未进行日界不连续误差改正时,相对频率偏差在批单元边界处存在很大跳变,导致频率偏差出现偏移;而对日界不连续误差进行改正后,相对频率偏差在相应批单元边界处的偏移基本得到抑制,且变化趋势与TAIPPP基本一致。
|
图 7 UTC(SP)与UTC(PTB)相对频率偏差 Fig. 7 Relative frequency deviation between UTC(SP) and UTC(PTB) |
|
|
表 2 UTC(SP)与UTC(PTB)的10 d平均相对频率偏差 Tab. 2 Average relative frequency deviation between UTC(SP) and UTC(PTB) for 10 days |
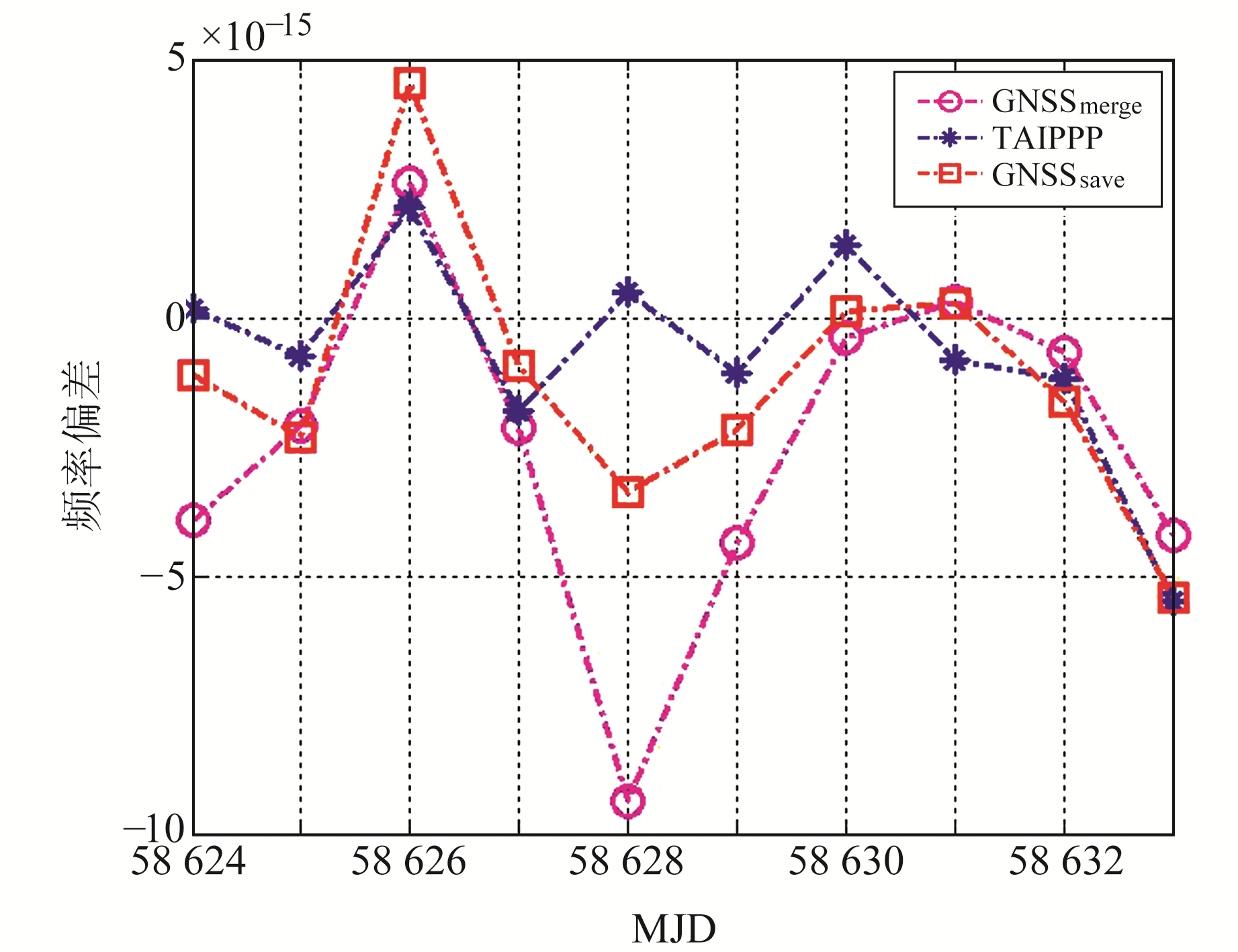
日界不连续误差改正前后UTC(USNO)-UTC(PTB)的相对频率偏差如图 8所示,10 d平均相对频率偏差见表 3。从图中可以看出,日界不连续误差改正前UTC(USNO)与UTC(PTB)相对频率偏差在批单元边界处存在很大跳变,而日界不连续误差改正后相对频率偏差跳变减小,变化趋势与TAIPPP基本一致。日界不连续误差改正后,UTC(USNO)与UTC(PTB)的10 d平均相对频率偏差GNSSsave为-8.220 7×10-16,TAIPPP平均相对频率偏差为-6.968 6×10-16,而日界不连续误差未改正时平均相对频率偏差GNSSmerge为-3.426 7×10-15。
|
图 8 UTC(USNO)与UTC(PTB)相对频率偏差 Fig. 8 Relative frequency deviation between UTC(USNO) and UTC(PTB) |
|
|
表 3 UTC(USNO)与UTC(PTB)的10 d平均相对频率偏差 Tab. 3 Average relative frequency deviation between UTC(SP) and UTC(PTB) for 10 days |
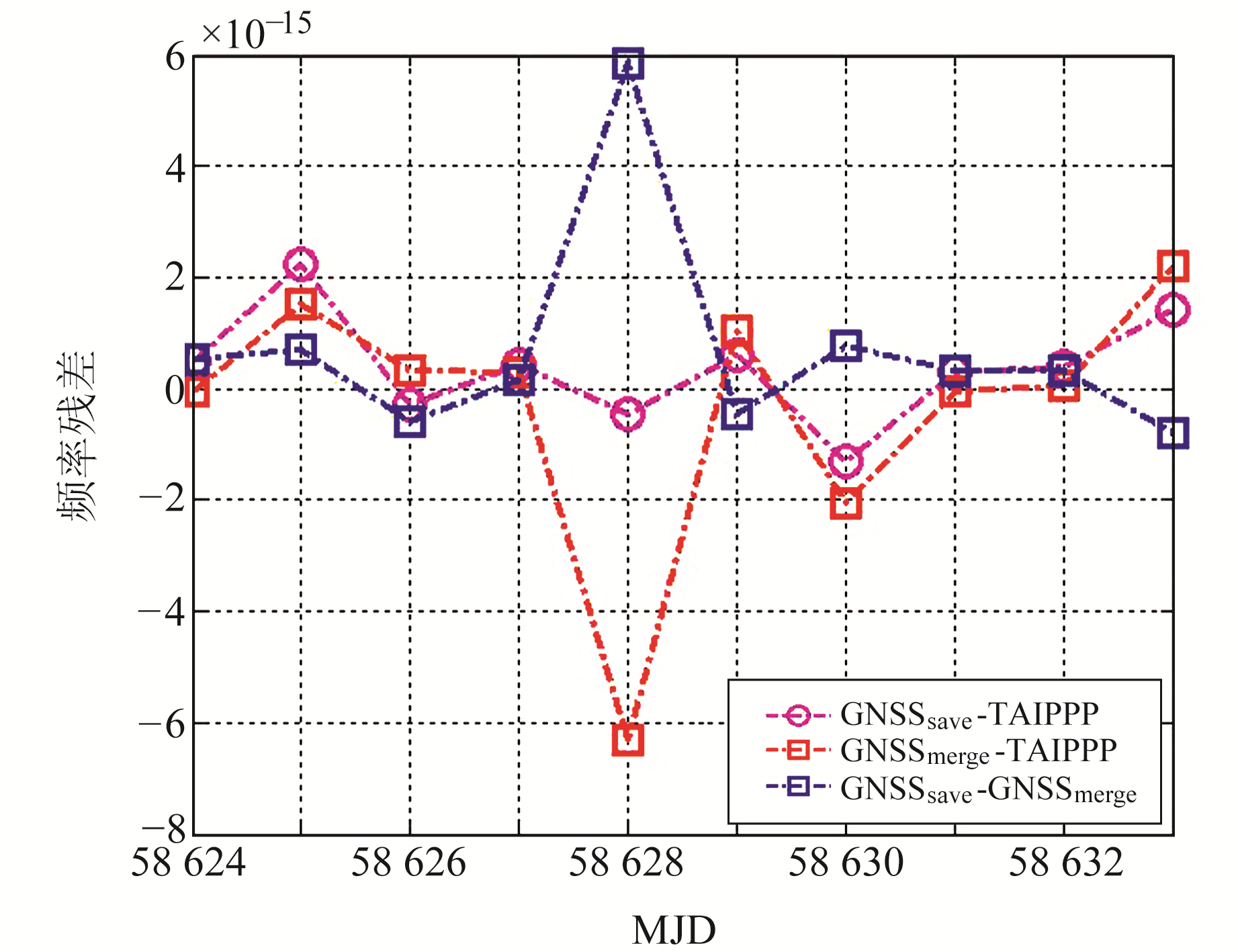
为进一步分析日界不连续误差对相对频率偏差的影响,以TAIPPP结果的相对频率偏差为参考,分别计算UTC(SP)-UTC(PTB)、UTC(USNO)-UTC(PTB)日界不连续误差改正前后相对频率偏差与TAIPPP结果相对频率偏差的残差,结果如图 9和10所示。从图中可以看出,日界不连续误差改正后,UTC(SP)-UTC(PTB)、UTC(USNO)-UTC(PTB)相对频率偏差的变化趋势更接近TAIPPP,而日界不连续误差改正前UTC(SP)-UTC(PTB)、UTC(USNO)-UTC(PTB)的相对频率偏差与TAIPPP结果相比存在明显跳变。另外,UTC(SP)-UTC(PTB)、UTC(USNO)-UTC(PTB)在日界不连续误差改正后GNSSsave变化趋势更接近TAIPPP,而日界不连续误差改正前GNSSmerge与TAIPPP结果相比存在明显跳变。
|
图 9 UTC(SP)-UTC(PTB)相对频率偏差与TAIPPP的残差 Fig. 9 Residuals of relative frequency deviation between UTC(SP)-UTC(PTB) and TAIPPP |

|
图 10 UTC(USNO)-UTC(PTB)相对频率偏差与TAIPPP的残差 Fig. 10 Residuals of relative frequency deviation between UTC(USNO)-UTC(PTB) and TAIPPP |
综上所述,当测站接收机外接氢钟等高稳时钟时,PPP时间传递中日界不连续误差将引起两地参考频标的相对频率偏差在批单元边界处出现偏移,导致相对频率偏差估计准确度降低。
4 结语本文首先介绍GNSS载波相位时间传递中日界不连续误差的统计特性和改正方法,然后从理论上分析日界不连续误差对相对频率偏差估计的影响,最后采用实际数据进行实验验证。结果表明,PPP测站钟差估计结果中日界不连续误差与测站紧密相关,其概率密度基本服从高斯分布;日界不连续误差是限制PPP时间传递准确度和链路稳健性提升的主要障碍;采用PPP估计两测站时钟的相对频率偏差时,日界不连续误差会使相对频率偏差估计结果在相邻批单元边界处出现偏移,使得总时段中相对频率偏差估计结果的准确度降低,严重影响两地时钟频率比对结果。
| [1] |
Kirchner D. Two-Way Time Transfer via Communication Satellites[J]. Proceedings of the IEEE, 1991, 79(7): 983-990 DOI:10.1109/5.84975
(  0) 0) |
| [2] |
Baeriswyl P, Schildknecht T, Springer T, et al. Time Transfer with Geodetic GPS Receivers Using Code and Phase Observations[C]. 10th International Conference on European Frequency and Time, Brighton, 1996
(  0) 0) |
| [3] |
Śliwczyński Ƚ, Krehlik P, Czubla A, et al. Dissemination of Time and RF Frequency via a Stabilized Fibre Optic Link over a Distance of 420 km[J]. Metrologia, 2013, 50(2): 133-145 DOI:10.1088/0026-1394/50/2/133
(  0) 0) |
| [4] |
Samain E, Fridelance P. Time Transfer by Laser Link(T2L2) Experiment on Mir[J]. Metrologia, 1998, 35(3): 151-159 DOI:10.1088/0026-1394/35/3/3
(  0) 0) |
| [5] |
Ray J, Senior K. IGS/BIPM Pilot Project: GPS Carrier Phase for Time/Frequency Transfer and Timescale Formation[J]. Metrologia, 2003, 40(3): S270-S288 DOI:10.1088/0026-1394/40/3/307
(  0) 0) |
| [6] |
Píriz R, Cerretto G, Perucca A, et al. Evaluation of the Time and Frequency Transfer Capabilities of a Network of GNSS Receivers Located in Timing Laboratories[C]. Proceedings of the 41st Annual Precise Time and Time Interval Systems and Applications Meeting, Santa Ana Pueblo, 2009
(  0) 0) |
| [7] |
Skakun I, Mitrikas V. GNSS Carrier-Phase Network Time and Frequency Transfer Technique[C]. Proceedings of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation, Tampa, 2015
(  0) 0) |
| [8] |
Kouba J, Héroux P. Precise Point Positioning Using IGS Orbit and Clock Products[J]. GPS Solutions, 2001, 5(2): 12-28 DOI:10.1007/PL00012883
(  0) 0) |
| [9] |
Kouba J. A Guide to Using International GNSS Service(IGS) Products[EB/OL]. http://acc.igs.org/UsingIGSProductsVer21.pdf, 2009
(  0) 0) |
| [10] |
Petit G, Jiang Z H. Precise Point Positioning for TAI Computation[C]. Proceedings of the IEEE International Frequency Control Symposium and Exposition, Geneva, 2007
(  0) 0) |
| [11] |
Defraigne P, Baire Q. Combining GPS and GLONASS for Time and Frequency Transfer[J]. Advances in Space Research, 2011, 47(2): 265-275 DOI:10.1016/j.asr.2010.07.003
(  0) 0) |
| [12] |
Zhang P F, Tu R, Zhang R, et al. Combining GPS, Beidou, and Galileo Satellite Systems for Time and Frequency Transfer Based on Carrier Phase Observations[J]. Remote Sensing, 2018, 10(2)
(  0) 0) |
| [13] |
Ge Y L, Zhou F, Dai P P, et al. Precise Point Positioning Time Transfer with Multi-GNSS Single-Frequency Observations[J]. Measurement, 2019, 146: 628-642 DOI:10.1016/j.measurement.2019.07.009
(  0) 0) |
| [14] |
Dach R, Beutler G, Hugentobler U, et al. Time Transfer Using GPS Carrier Phase: Error Propagation and Results[J]. Journal of Geodesy, 2003, 77(1-2): 1-14 DOI:10.1007/s00190-002-0296-z
(  0) 0) |
| [15] |
Defraigne P, Bruyninx C. On the Link between GPS Pseudorange Noise and Day-Boundary Discontinuities in Geodetic Time Transfer Solutions[J]. GPS Solutions, 2007, 11(4): 239-249 DOI:10.1007/s10291-007-0054-z
(  0) 0) |
| [16] |
Yao J, Levine J. GPS Carrier-Phase Time Transfer Boundary Discontinuity Investigation[C]. Proceedings of the 44th Annual Precise Time and Time Interval Systems and Applications Meeting, Reston, 2012
(  0) 0) |
| [17] |
Zhang X B, Guo J, Hu Y H, et al. Influence of Precise Products on the Day-Boundary Discontinuities in GNSS Carrier Phase Time Transfer[J]. Sensors, 2021, 21(4)
(  0) 0) |
| [18] |
Dach R, Schildknecht T, Hugentobler U, et al. Continuous Geodetic Time-Transfer Analysis Methods[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2006, 53(7): 1 250-1 259 DOI:10.1109/TUFFC.2006.1665073
(  0) 0) |
| [19] |
Defraigne P, Guyennon N, Bruyninx C. GPS Time and Frequency Transfer: PPP and Phase-Only Analysis[J]. International Journal of Navigation and Observation, 2008, 2008
(  0) 0) |
| [20] |
Delporte J, Mercier F, Laurichesse D, et al. GPS Carrier-Phase Time Transfer Using Single-Difference Integer Ambiguity Resolution[J]. International Journal of Navigation and Observation, 2008, 2008
(  0) 0) |
| [21] |
Yao J, Levine J. A New Algorithm to Eliminate GPS Carrier-Phase Time Transfer Boundary Discontinuity[C]. Proceedings of the 45th Annual Precise Time and Time Interval Systems and Applications Meeting, Bellevue, 2013
(  0) 0) |
| [22] |
Petit G, Kanj A, Loyer S, et al. 1×10-16 Frequency Transfer by GPS PPP with Integer Ambiguity Resolution[J]. Metrologia, 2015, 52(2)
(  0) 0) |
| [23] |
Zhang X B, Guo J, Hu Y H, et al. Research of Eliminating the Day-Boundary Discontinuities in GNSS Carrier Phase Time Transfer through Network Processing[J]. Sensors, 2020, 20(9)
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China;
3. Key Laboratory of Time and Frequency Primary Standards, CAS, 3 East-Shuyuan Road, Xi'an 710600, China
 2022, Vol. 42
2022, Vol. 42


