全球气候变暖导致海平面不断升高,这不仅会影响气候变化,也对人类生命安全造成严重威胁。因此,监测海平面高度变化意义重大[1]。近年来,GNSS多路径反射测量(GNSS multipath reflectometry, GNSS-MR)被用于海面高度探测,目前利用GNSS-MR技术进行潮位监测在国内外已有一定的研究基础。Larson等[2]利用大地测量型接收机获取的GPS实测数据对潮位进行反演,实验表明GPS-MR反演结果与验潮站实测数据具有较好的一致性。Lfgren等[3]分别使用GPS和GLONASS系统L1和L2频段信号进行潮位反演,证实GLONASS系统也可用于潮位反演。Roussel等[4]基于最小二乘方法,对GPS和GLONASS系统反演的潮位值进行融合。张双成等[5]利用不同时间段的GPS信噪比数据进行海面高度反演,研究表明GPS-MR反演结果与实测潮位较差约为10 cm。Jin等[6]首次使用Beidou系统SNR(signal-to-noise ratio)和相位组合方法估计海面变化。Wang等[7]利用基于稳健估计的数据融合方法进行4个系统(GPS、GLONASS、Galileo和Beidou)联合潮位反演,结果表明多模多频GNSS-MR可以有效提高潮位反演精度和时间分辨率。从国内外研究来看,GNSS-MR技术可以用于监测潮位变化。
目前GNSS-MR潮位反演的原理和方法已经相对成熟,即利用LSP[8]方法提取SNR中频率信息,再将该信息转换为垂直反射高度RH值,最后统一到潮位基准上[9]。但是,基于LSP的潮位反演方法在一段SNR序列中通常只能得到一个时刻的潮位值,这样可能会出现反演点缺失且难以刻画潮位起伏变化的情况。虽然多模多频观测可以提供更多有效卫星弧段的SNR数据,但存在个别信号质量较差,从而影响潮位反演结果的精度。针对GNSS-MR技术反演时间分辨率不足的问题,Wang等[10]提出利用小波分析方法提取SNR序列瞬时频率,进而得到潮位值,可大幅提高反演点的时间分辨率。但是小波分析方法过于依赖SNR数据质量,使得该方法反演潮位的精度有时比LSP方法低。
本文针对小波分析精度偏低的问题,利用多模多频GNSS数据,分析各个频段SNR数据质量,选取质量更好的SNR数据进行小波分析潮位反演,分别以法国BRST站和香港HKQT站15 d的数据进行实验,并与LSP反演结果进行分析比较。
1 方法与原理 1.1 GNSS-MR反演潮位原理当GNSS测站位于海边时,卫星直射信号与海水表面反射信号相干的合成SNR可表示为[11]:
| ${\rm{SN}}{{\rm{R}}^2} = A_d^2 + A_m^2 + 2{A_d}{A_m}\cos \psi $ | (1) |
式中,Am和Ad分别为直射信号和反射信号振幅,ψ为直射信号与反射信号之间的相位偏差。
直射信号与反射信号相位差为:
| $\psi = \frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }D = \frac{{4{\rm{ \mathsf{ π} }}h}}{\lambda }{\rm{sine}}$ | (2) |
式中,D为反射信号与直射信号的路径差,λ为信号波长,e为卫星高度角,h为垂直反射距离。
假设反射面静止,根据式(2)可知:
| $2{\rm{ \mathsf{ π} }}f = \frac{{{\rm{d}}\psi }}{{{\rm{dsine}}}} = 4{\rm{ \mathsf{ π} }}\frac{{\bar h}}{\lambda }$ | (3) |
式中,f为SNR中受干涉影响部分的信号频率,为静态假设下得到的反射高度。对于频率f,经典方法是先用低阶多项式去除SNR序列中直射信号,得到反射信号的残差序列δSNR,再用LSP分析方法从δSNR中求解f,从而确定反射高度h。
顾及到海面动态变化,反射高度h求解时会存在误差。Larson等[12]首次提出对海面动态变化引起的高度误差进行改正。设
| $\bar h = \frac{{\tan e}}{{\dot e}}\dot h + h$ | (4) |
为求解动态变化的高度h,首先需要得到时间序列h,再用潮汐调和分析函数求解
小波分析是一种多分辨率时频分析方法,通过伸缩和平移形成一系列灵活窗口对信号进行多尺度细化分析[14]。在小波分析中,分析函数为一个小波ψ,小波通常被定义为[15]:
| ${\psi _{m, n}}\left( t \right) = {2^{\frac{m}{2}}}\psi ({2^m}t - n)$ | (5) |
式中,m、n分别为缩放因子和平移因子,二者属于整数集合Z={0, ±1, ±2, …},t为时间。对于去除趋势项后的SNR序列在尺度a(>0)和位置b的小波变换可表示为[10]:
| $\begin{array}{c} W\left( {a, b;\delta S\left( {\sin e} \right), \psi \left( {\sin e} \right)} \right) = \\ \int_{ - \infty }^\infty {S(\sin e)\frac{1}{{\sqrt a }}{\psi ^*}\left( {\frac{{\sin e - b}}{a}} \right){\rm{d}}\sin e} \end{array}$ | (6) |
式中,δS(sine)为去除趋势项后的SNR序列,*表示复共轭,W(a, b)为小波变换系数。MATLAB中‘centfrq’和‘scal2frq’两个函数可以在给定小波尺度情况下计算尺度与采样频率之间的关系。
为进一步说明小波分析反演潮位过程,以美国PBAY站(59.6°N, 151.3°W)为例,选取2020年年积日106的GPS观测数据进行分析。图 1(a)为当日PRN14卫星的SNR残差序列,小波分析频谱如图 1(b)所示,图中纵坐标频率已由
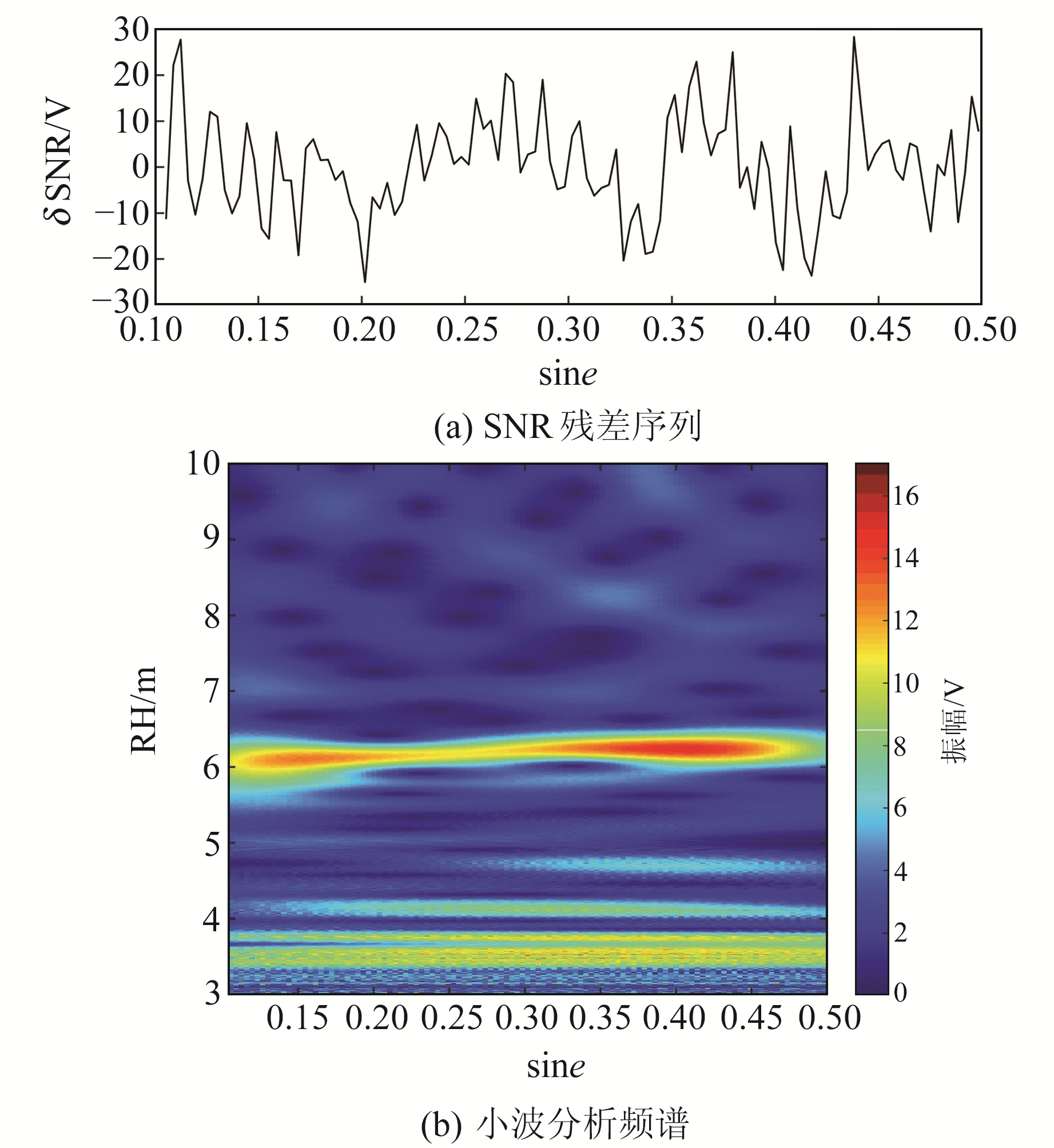
|
图 1 小波分析频谱 Fig. 1 The wavelet analysis spectrum |
对于PBAY站,3~11 m是能够反映潮位变化的有效高度区间[12],区间以外的能量聚集部分则认为是噪声。在3~11 m范围内,有两个明显的能量聚集区,分别位于横轴sine=0.15、纵轴6.1 m和横轴sine=0.41、纵轴6.3 m处。找出每个sine对应的最大振幅值(图 2(a)),再确定其对应的有效高度,即可将sine、振幅值、有效高度的三维图转变成sine和垂直反射距离的二维图(图 2(b))。
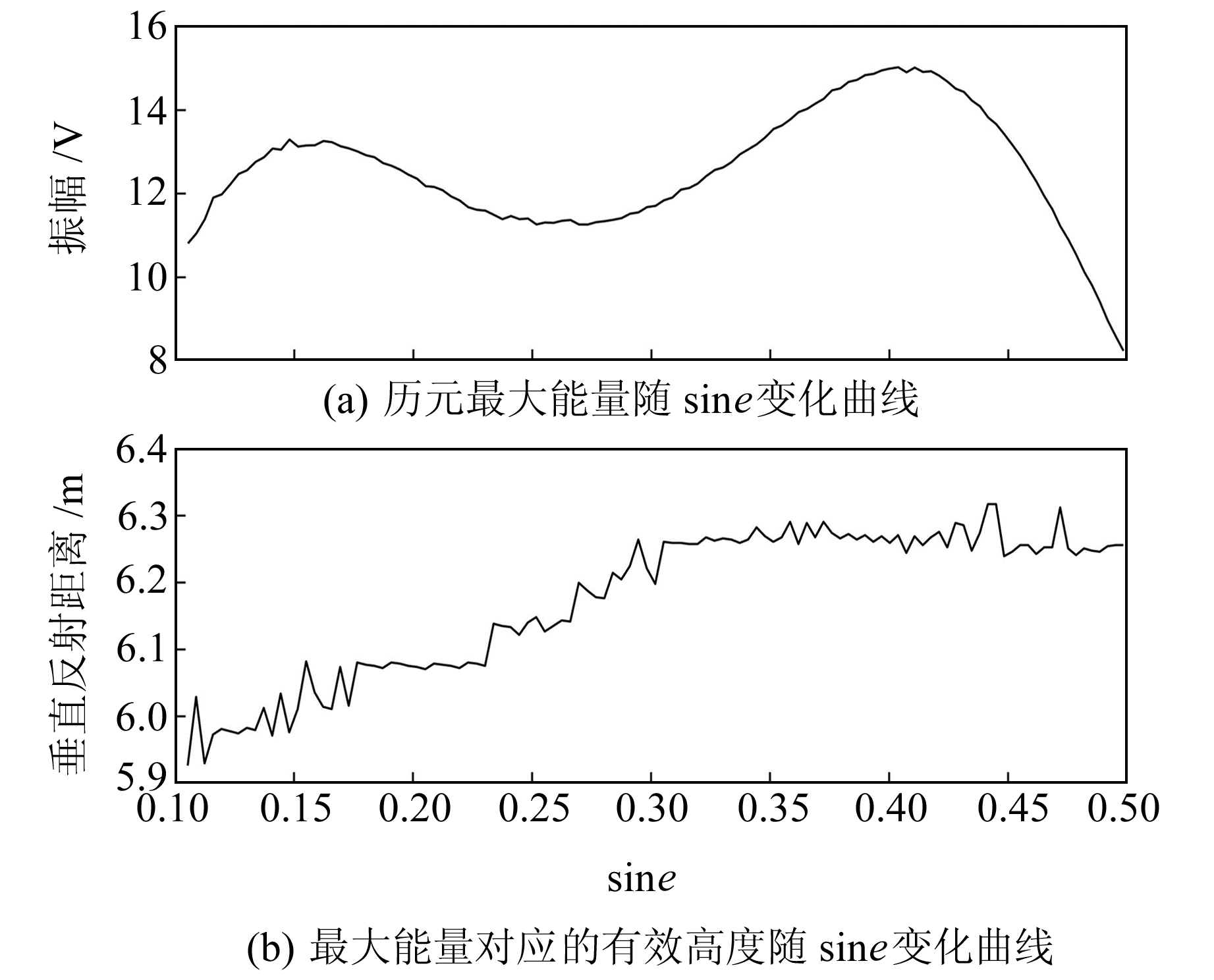
|
图 2 小波分析频谱二维表示 Fig. 2 Two dimensional representation of wavelet analysis spectrum |
根据以上步骤即可提取SNR序列瞬时频率,进而得到瞬时潮位反演值,但由于SNR数据质量原因,即便选取每个历元能量最大值对应的有效高度,依然会存在反演值出现跳变的情况。为剔除这种粗差,本文根据LSP方法获取的RH值计算标准偏差σ和均值μ,剔除在[μ-3σ, μ+3σ]区间外的瞬时垂直反射距离,同时利用小波分析得到的瞬时潮位反演值也需要采用潮汐调和函数进行海面动态改正[10],技术流程如图 3所示。
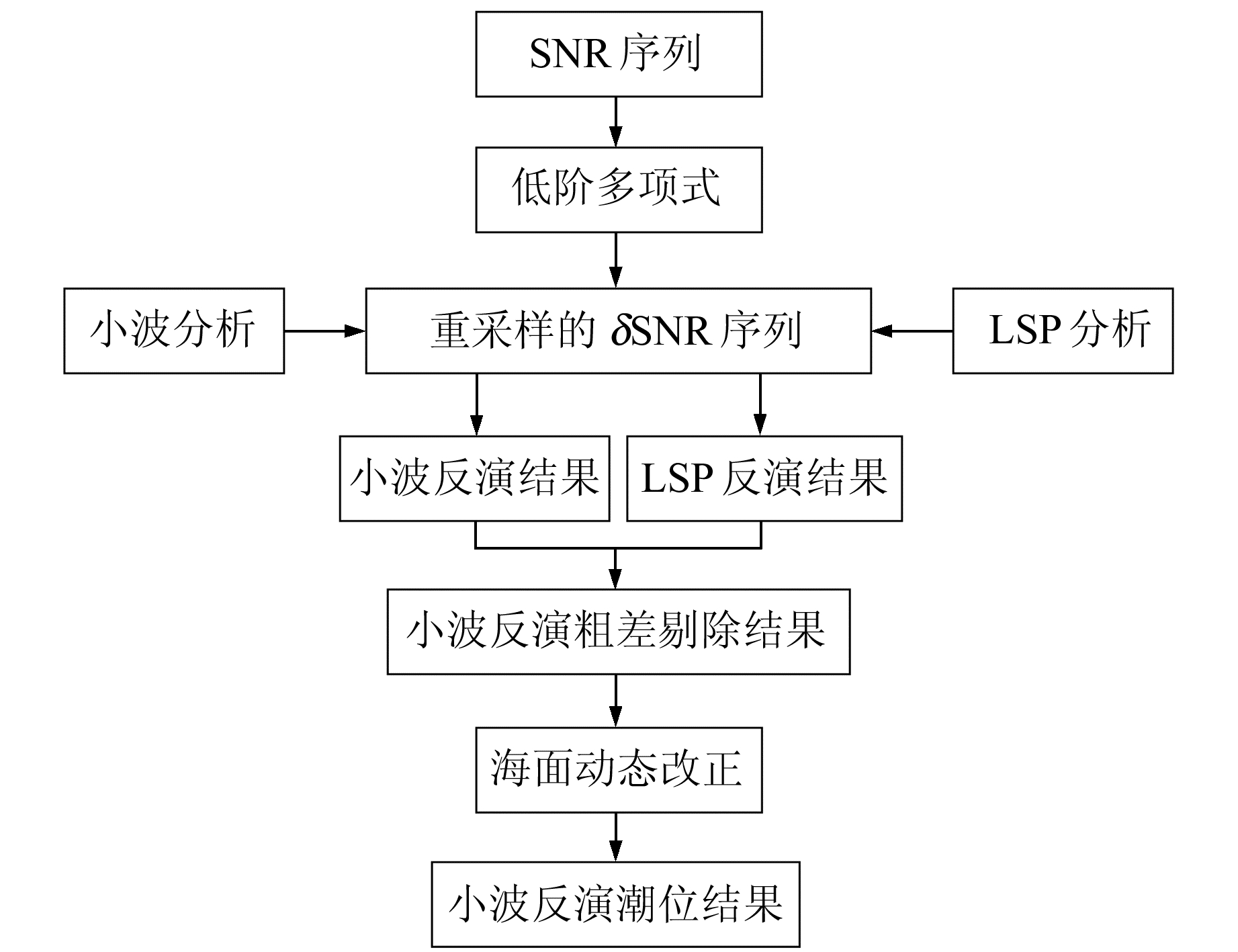
|
图 3 基于小波分析反演潮位流程图 Fig. 3 Flow chart of sea level inversion using wavelet analysis |
BRST站(48.4°N,4.5°W)位于法国西海岸Brest海港岸边,距离BRST站292 m的Brest验潮站可提供实测数据[16]。BRST站配备有Trimble NetR9大地测量型接收机,可提供GPS、GLONASS、Galileo、Beidou和SBAS卫星观测数据,采样间隔为30 s。为获取来自海面的反射信号,方位角区间设置为130°~270°,有效高度角区间为5°~30°。
HKQT站(22.3°N,114.1°E)位于香港北边海岸,安装有Trimble NetR5大地测量型接收机,可提供GPS、GLONASS、Galileo、Beidou、QZSS和SBAS卫星观测数据,采样间隔为1 s、5 s和30 s[17]。该站点海面反射信号所对应区域的方位角为-60°~105°,有效高度角为4°~9°。距离HKQT站2 m的Quarry Bay实测潮位数据可用于对比分析。
2.2 数据分析以BRST站为例,本文选取BRST站2020年年积日197~211的SNR数据进行实验,其中信噪比数据GPS有4种(S1C、S2W、S2X、S5X),GLONASS有4种(S1C、S1P、S2C、S2P),Galileo有5种(S1X、S5X、S7X、S8X、S6X),Beidou有5种(S1X、S5X、S2I、S7I、S6I)。其中,Galileo中S6X和Beidou中S7I数据记录有缺失,因此在后续实验中未采用这两种信号。为获取质量更高的SNR数据,本文分别从GNSS不同SNR类型数据LSP反演结果的精度及其小波谱表现来评定SNR数据的质量等级。
表 1为BRST站4个卫星系统每种SNR类型数据LSP反演结果的日均反演点数量、均方根误差(RMSE)和相关系数(CORR)统计结果,以评估采样率及反演精度。BRST站GPS、GLONASS、Galileo和Beidou系统中反演精度最高的SNR类型依次为S5X、S2P、S7X和S6I。不同SNR类型数据质量等级为:对于GPS,S5X>S2X>S2W>S1C;对于GLONASS,S2P>S2C>S1P>S1C;对于Galileo,S7X>S1X>S5X>S8X;对于Beidou,S6I>S5X>S2I>S1X。
|
|
表 1 BRST站每种SNR类型的日均反演点数量、RMSE和CORR Tab. 1 The number of daily average inversion points, RMSE and CORR of each SNR type at BRST station |
图 4为BRST站2020年年积日201的GPS PRN27、GLONASS PRN16、Galileo PRN33和Beidou PRN21卫星不同类型SNR序列小波谱图。从图中可以看出,小波谱图不仅可以确定每一时刻不同垂直反射距离RH的功率,而且还可以反映SNR序列的质量。质量较好的SNR序列具有明显的功率集中区且由噪声引起的散乱区较少,而质量较差的SNR序列功率分布较离散且噪声多[9]。从小波谱图可以看出,每种SNR类型数据质量等级为:对于GPS,S5X>S2X>S2W>S1C;对于GLONASS,S2P>S2C>S1C>S1P;对于Galileo,S7X>S5X>S1X>S8X;对于Beidou,S6I>S2I>S5X>S1X。
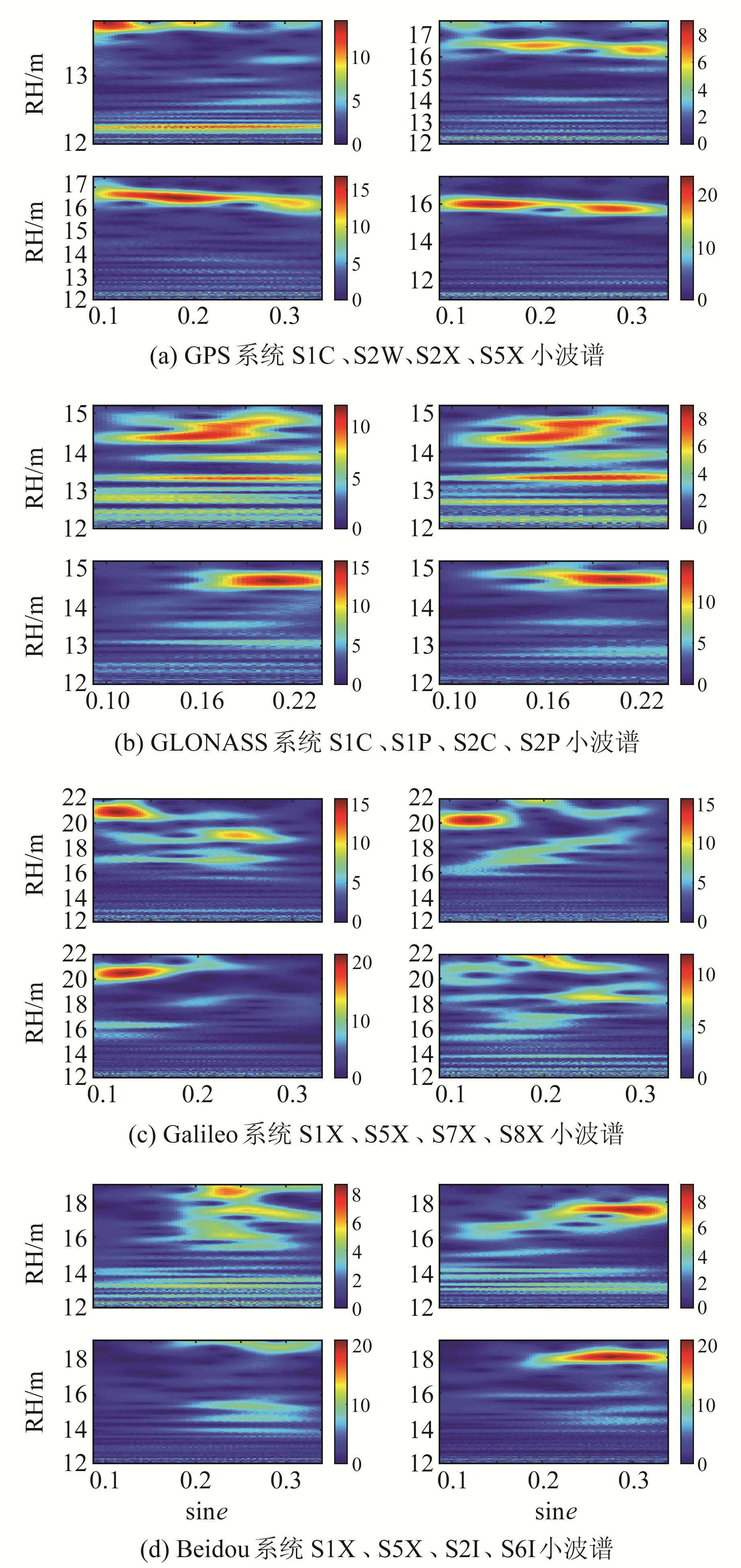
|
图 4 BRST站GNSS不同类型SNR序列小波谱 Fig. 4 Wavelet spectrum of different types of GNSS SNR series at BRST station |
比较根据LSP反演结果对SNR数据质量进行评定可以发现,质量最好的SNR类型两种方法评定结果一致,其他类型存在个别差异。小波谱的表现可直接决定瞬时反演结果的准确性,因此需要筛选质量较好的SNR类型进行反演以保证精度。
3 实验与结果 3.1 BRST站GNSS-MR瞬时潮位结果根据上节分析,本文最终选择GPS系统S5X、S2X,GLONASS系统S2P,Galileo系统S7X,Beidou系统S6I数据进行GNSS-MR瞬时潮位反演,同时与LSP方法得到的潮位反演结果进行对比。BRST站LSP和小波分析反演结果如图 5所示。

|
图 5 BRST站LSP和小波分析方法潮位反演值 Fig. 5 Sea level estimated by LSP and wavelet analysis at BRST station |
由图 5可知,BRST站利用LSP方法和小波分析方法获得的潮位结果均与实际潮位对应良好。其中,LSP方法得到的结果较少,而小波分析得到的瞬时反演结果基本能描绘潮位的变化趋势,满足潮位监测需求。为对两种方法进行评定并验证小波分析方法获取潮位的精度是否可靠,本文将小波分析结果以及LSP结果与验潮站实测数据进行比较,表 2为RMSE值、相关系数值、日均反演点数量和时间间隔统计。
|
|
表 2 BRST站小波分析和LSP方法反演结果统计 Tab. 2 Statistics of inversion results of LSP and wavelet analysis methods at BRST station |
从表 2可以看出,小波分析方法和LSP方法相关系数均优于98%,小波分析方法的反演精度比LSP方法低3%~10%,但日均反演点数量却比LSP方法提高约12倍,且平均时间间隔约为0.2 h,表明小波分析方法可大大提高反演结果的时间分辨率。
3.2 HKQT站GNSS-MR瞬时潮位结果为进一步验证基于小波分析的多模多频瞬时潮位反演的有效性,本文又选取HKQT站2020年年积日211~225的SNR数据进行实验。其中信噪比数据GPS有S1C、S2W、S2X、S5X,GLONASS有S1C、S1P、S2C、S2P,Galileo有S1X、S5X、S7X、S8X,Beidou有S2I、S7I。同样进行LSP反演结果精度分析和小波谱图质量分析,最终选择GPS系统S5X,GLONASS系统S2P,Galileo系统S5X,Beidou系统S7I数据。LSP和小波分析反演结果如图 6所示。
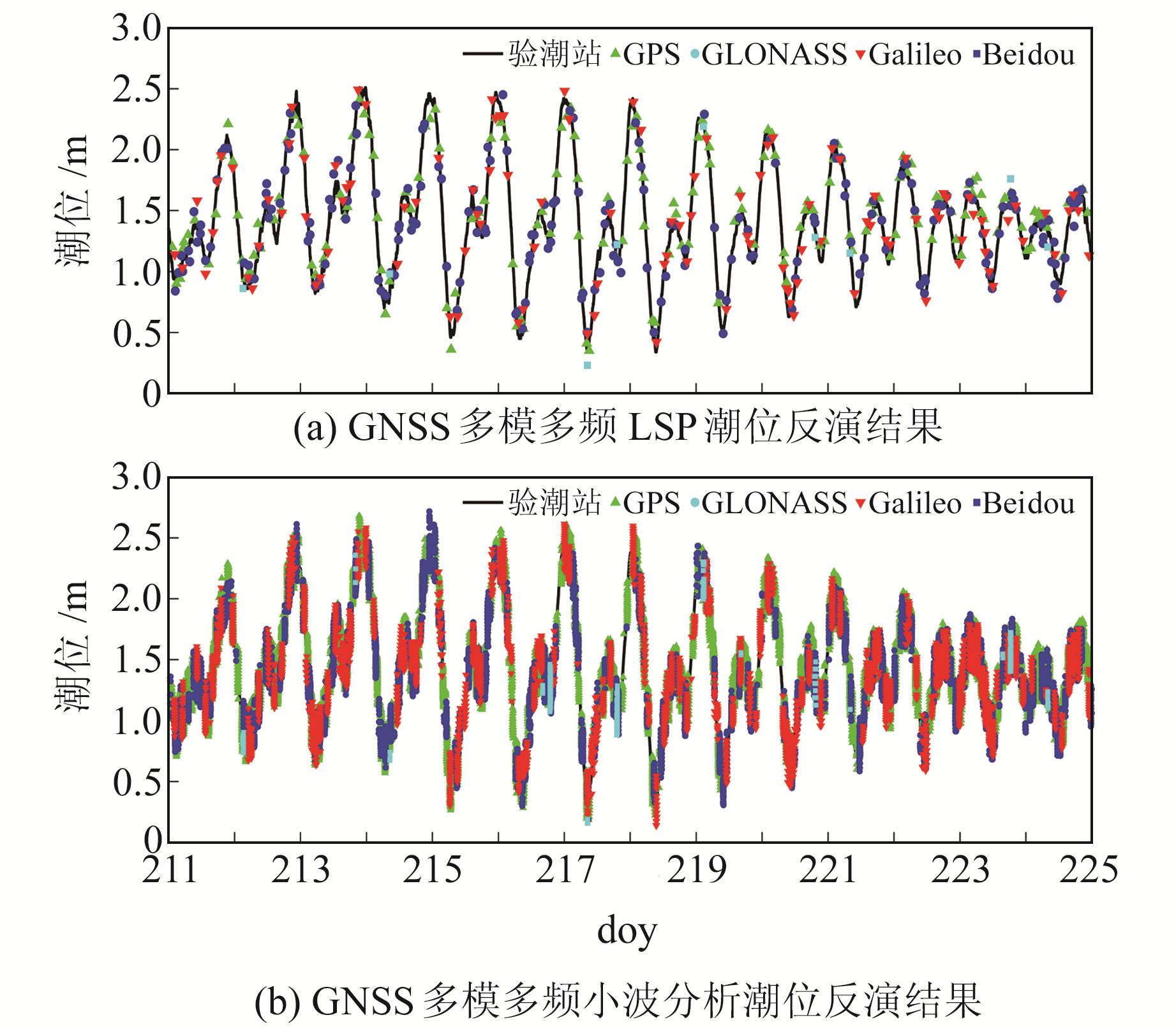
|
图 6 HKQT站LSP和小波分析方法潮位反演值 Fig. 6 Sea level estimated by LSP and wavelet analysis at HKQT station |
由图 6可知,HKQT站利用LSP方法和小波分析方法获得的潮位结果均与实测数据具有良好的对应关系。但LSP方法得到的结果较少,而小波分析的反演结果可以清晰反映潮位起伏变化。表 3为小波分析结果和LSP结果RMSE值、相关系数值、日均反演点数量和时间间隔统计。
|
|
表 3 HKQT站小波分析和LSP方法反演结果统计 Tab. 3 Statistics of inversion results of LSP and wavelet analysis methods at HKQT station |
从表 3可以看出,HKQT站LSP方法反演结果的相关性优于小波分析方法,小波分析方法的反演精度比LSP方法低8%~17%,但日均反演点数量却比LSP方法提高约13倍,除Beidou外小波分析方法的平均时间间隔也为0.2 h左右。
4 结语利用小波分析方法从SNR序列中获取潮位值可以大大提高GNSS-MR技术反演潮位的时间分辨率,但小波分析方法的反演精度易受SNR数据质量的影响。本文针对该问题,利用多模多频数据从LSP反演精度和小波谱图质量两个方面分析评定4种系统不同SNR类型数据的质量,进而选择最优的SNR数据类型进行瞬时频率潮位反演。从BRST站和HKQT站的反演结果来看,基于小波分析的多模多频GNSS-MR潮位反演方法能够在精度损失较小的情况下大幅提高反演点数量和数据采样率。这种基于多模多频SNR数据的小波分析方法,可充分利用海面多路径反射信号,实现对SNR数据的最大利用。
但是小波分析方法无法脱离LSP方法单独使用,目前其粗差还需要根据LSP反演结果的标准偏差σ和均值μ计算的淘汰区间进行剔除。同时利用小波分析得到的瞬时潮位反演值也需要采用LSP反演的时间序列进行潮波函数拟合来确定海面动态变化情况。未来需要更加合理的粗差剔除方法,从小波谱图的表现来对粗差进行探测和去除,进一步提高小波分析方法用于潮位反演的精度。
| [1] |
王瑞芳. 利用EMD进行GNSS-MR潮位监测研究[J]. 测绘通报, 2020(10): 114-117 (Wang Ruifang. Research on GNSS-MR Tide Level Monitoring Based on EMD[J]. Bulletin of Surveying and Mapping, 2020(10): 114-117)
(  0) 0) |
| [2] |
Larson K M, Löfgren J S, Haas R. Coastal Sea Level Measurements Using a Single Geodetic GPS Receiver[J]. Advances in Space Research, 2013, 51(8): 1 301-1 310 DOI:10.1016/j.asr.2012.04.017
(  0) 0) |
| [3] |
Löfgren J S, Haas R. Sea Level Measurements Using Multi-Frequency GPS and GLONASS Observations[J]. EURASIP Journal on Advances in Signal Processing, 2014, 2014(1)
(  0) 0) |
| [4] |
Roussel N, Ramillien G, Frappart F, et al. Sea Level Monitoring and Sea State Estimate Using a Single Geodetic Receiver[J]. Remote Sensing of Environment, 2015, 171(2): 261-277
(  0) 0) |
| [5] |
张双成, 南阳, 李振宇, 等. GNSS-MR技术用于潮位变化监测分析[J]. 测绘学报, 2016, 45(9): 1 042-1 049 (Zhang Shuangcheng, Nan Yang, Li Zhenyu, et al. Analysis of Tide Variation Monitored by GNSS-MR[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1 042-1 049)
(  0) 0) |
| [6] |
Jin S G, Qian X D, Wu X R. Sea Level Change from Beidou Navigation Satellite System-Reflectometry(BDS-R): First Results and Evaluation[J]. Global and Planetary Change, 2017, 149: 20-25 DOI:10.1016/j.gloplacha.2016.12.010
(  0) 0) |
| [7] |
Wang X L, He X F, Zhang Q. Evaluation and Combination of Quad-Constellation Multi-GNSS Multipath Reflectometry Applied to Sea Level Retrieval[J]. Remote Sensing of Environment, 2019, 231(2)
(  0) 0) |
| [8] |
Lomb N R. Least-Squares Frequency Analysis of Unequally Spaced Data[J]. Astrophysics and Space Science, 1976, 39(2): 447-462 DOI:10.1007/BF00648343
(  0) 0) |
| [9] |
王笑蕾. 地基GNSS近地空间水环境遥感监测研究[D]. 西安: 长安大学, 2018 (Wang Xiaolei. Ground GNSS Remote Sensing for Near-Surface Water Environmental Parameters[D]. Xi'an: Chang'an University, 2018)
(  0) 0) |
| [10] |
Wang X L, Zhang Q, Zhang S C. Sea Level Estimation from SNR Data of Geodetic Receivers Using Wavelet Analysis[J]. GPS Solutions, 2019, 23(1)
(  0) 0) |
| [11] |
Larson K M, Small E E, Gutmann E, et al. Using GPS Multipath to Measure Soil Moisture Fluctuations: Initial Results[J]. GPS Solutions, 2008, 12(3): 173-177 DOI:10.1007/s10291-007-0076-6
(  0) 0) |
| [12] |
Larson K M, Ray R D, Nievinski F G, et al. The Accidental Tide Gauge: A GPS Reflection Case Study from Kachemak Bay, Alaska[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(5): 1 200-1 204 DOI:10.1109/LGRS.2012.2236075
(  0) 0) |
| [13] |
Larson K M, Ray R D, Williams S D P. A 10-Year Comparison of Water Levels Measured with a Geodetic GPS Receiver versus a Conventional Tide Gauge[J]. Journal of Atmospheric and Oceanic Technology, 2017, 34(2): 295-307 DOI:10.1175/JTECH-D-16-0101.1
(  0) 0) |
| [14] |
孙云莲, 刘敦敏. 时频分析与小波变换及其应用[J]. 武汉大学学报: 工学版, 2003, 36(2): 103-106 (Sun Yunlian, Liu Dunmin. Time-Frequency Analysis and Wavelet Transform and Their Applications[J]. Engineering Journal of Wuhan University, 2003, 36(2): 103-106)
(  0) 0) |
| [15] |
Torrence C, Compo G P. A Practical Guide to Wavelet Analysis[J]. Bulletin of the American Meteorological Society, 1998, 79(1): 61-78 DOI:10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2
(  0) 0) |
| [16] |
Santamaría-Gómez A, Watson C, Gravelle M, et al. Levelling Co-Located GNSS and Tide Gauge Stations Using GNSS Reflectometry[J]. Journal of Geodesy, 2015, 89(3): 241-258 DOI:10.1007/s00190-014-0784-y
(  0) 0) |
| [17] |
何秀凤, 王杰, 王笑蕾, 等. 利用多模多频GNSS-IR信号反演沿海台风风暴潮[J]. 测绘学报, 2020, 49(9): 1 168-1 178 (He Xiufeng, Wang Jie, Wang Xiaolei, et al. Retrieval of Coastal Typhoon Storm Surge Using Multi-GNSS-IR[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(9): 1 168-1 178)
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42

