精密单点定位(PPP)技术[1]仅采用单台接收机即可获得高精度位置参数,具有精度高、不受地理位置限制等特点,还可以提供额外参数用于物理、气象等其他方面研究[2]。目前全球卫星系统主要有GPS、GLONASS、Galileo和BDS,由于测站分布和卫星星座几何分布存在差异,各卫星系统在定位精度和收敛时间方面表现各不相同,为得到稳定精确的坐标,融合多系统的PPP应运而生。多数研究选择忽略伪距IFB误差或按照频率号的一次线性函数估计载波IFB[3-6]。Zhou等[7]总结各卫星系统的最优伪距IFB模型,但仅对GLONASS单系统和GPS/GLONASS组合系统进行分析。同时大多数研究采用的组合观测值会放大噪声误差,也无法对其他参数进行估计。
因此,本文提出多系统非差非组合PPP函数模型,对两种IFB模型在不同卫星组合模式下的定位精度和收敛速度进行统计分析。
1 多系统融合PPP的函数模型线性化后不同卫星系统的伪距和载波观测方程可表示为:
| $ \begin{gathered} p_{r, i}^{s, T}=\boldsymbol{u}_{r}^{s, T} \cdot \boldsymbol{x}+c\left(\mathrm{~d} t_{r}-\mathrm{d} t^{s, T}\right)+ \\ \boldsymbol{\gamma}_{i}^{T} \cdot I_{r, 1}^{s, T}+m \cdot \mathrm{zwd}_{r}+d_{r, i}^{s, T}-d_{i}^{s, T}+e_{r, i}^{s, T} \end{gathered} $ | (1) |
| $ \begin{gathered} l_{r, i}^{s, T}=\boldsymbol{u}_{r}^{s, T} \cdot \boldsymbol{x}+c\left(\mathrm{~d} t_{r}-\mathrm{d} t^{s, T}\right)-\boldsymbol{\gamma}_{i}^{T} \cdot I_{r, 1}^{s, T}+ \\ m \cdot \mathrm{zwd}_{r}+\lambda_{i}^{s, T} \cdot\left(N_{r, i}^{s, T}+D_{r, i}^{s, T}-D_{i}^{s, T}\right)+\xi_{r, i}^{s, T} \end{gathered} $ | (2) |
式中,s、T、r、i分别为卫星PRN号码、卫星系统(GPS、BDS、GLONASS、Galileo)、接收机以及载波频段,pr, is, T、lr, is, T分别为伪距和载波的观测值与相应计算值的差值,urs, T为接收机到卫星的单位矢向量,x为接收机坐标的增向量,c为光速,dtr为接收机钟差,dts, T为卫星钟差,γiT=(f1s, T)2/(fis, T)2为不同频率的电离层参数比率因子,fs, T为信号频率(i=1, 2),Ir, 1s, T为第一频率上的电离层参数,m为对流层湿延迟的映射函数,zwdr为对流层天顶湿延迟,λis, T为载波长度,Nr, is, T为整周模糊度,dr, is, T和dis, T分别为接收机和卫星的非校正码延迟(UCDs),Dr, is, T和Dis, T分别为接收机和卫星的非校正载波延迟(UPDs),er, is, T为伪距观测值的噪声总和,ξr, is, T为载波观测值的噪声总和。其他误差如相对论效应、对流层干延迟等已通过模型进行改正。
为方便理解,通常对符号进行如下定义:
| $ \left\{\begin{array}{l} \alpha_{m, n}^{T}=\frac{\left(f_{m}^{s, T}\right)^{2}}{\left(f_{m}^{s, T}\right)^{2}-\left(f_{n}^{s, T}\right)^{2}} \\ \beta_{m, n}^{T}=\frac{-\left(f_{n}^{s, T}\right)^{2}}{\left(f_{m}^{s, T}\right)^{2}-\left(f_{n}^{s, T}\right)^{2}} \\ \mathrm{DCB}_{P_{m} P_{n}}^{s, T}=d_{m}^{s, T}-d_{n}^{s, T} \\ \mathrm{DCB}_{r, P_{m} P_{n}}^{s, T}=d_{r, m}^{s, T}-d_{r, n}^{s, T} \\ d_{\mathrm{IF}_{m, n}^{s, T}}=\alpha_{m, n}^{T} \cdot d_{m}^{s, T}+\beta_{m, n}^{T} \cdot d_{n}^{s, T} \\ d_{r, \mathrm{IF}_{m, n}}^{s, T}=\alpha_{m, n}^{T} \cdot d_{r, m}^{s, T}+\beta_{m, n}^{T} \cdot d_{r, n}^{s, T} \end{array}\right. $ | (3) |
式中,m、n=1、2(m≠n),αm, nT、βm, nT均为与频率相关的放大因子,DCBPmPns, T、DCBr, PmPns, T分别为卫星端和接收机端差分码偏差,dIFm, ns, T、dr, IFm, ns, T分别为在m、n频段上卫星端和接收机端UCDs的线性组合。
由于在PPP中已使用基于无电离层模型计算的精密卫星钟差产品,因此其提供的卫星钟差产品包含卫星端UCDs的线性组合[8]。将式(3)代入式(1)和式(2)可得:
| $ \left\{\begin{array}{l} p_{r, 1}^{s, T}=\boldsymbol{u}_{r}^{s, T} \cdot \boldsymbol{x}+c \cdot \mathrm{d} t_{r}+d_{r, 1}^{s, T}+m \cdot \mathrm{zwd}_{r}+ \\ \ \ \ \ I_{r, 1}^{s, T}-\beta_{12}^{T} \cdot \mathrm{DCB}_{P_{1} P_{2}}^{s, T}+e_{r, 1}^{s, T} \\ l_{r, 1}^{s, T}=\boldsymbol{u}_{r}^{s, T} \cdot \boldsymbol{x}+c \cdot \mathrm{d} t_{r}+m \cdot \mathrm{zwd}_{r}-I_{r, 1}^{s, T}+ \\ \ \ \ \ d_{\mathrm{IF}_{12}}^{s, T}+\lambda_{1}^{s, T} \cdot\left(N_{r, 1}^{s, T}+D_{r, 1}^{s, T}-D_{1}^{s, T}\right)+\xi_{r, 1}^{s, T} \end{array}\right. $ | (4) |
| $ \left\{\begin{array}{l} p_{r, 2}^{s, T}=\boldsymbol{u}_{r}^{s, T} \cdot \boldsymbol{x}+c \cdot \mathrm{d} t_{r}+d_{r, 2}^{s, T}+m \cdot \mathrm{zwd}_{r}+ \\ \ \ \ \ \gamma_{2}^{T} \cdot I_{r, 1}^{s, T}+\alpha_{12}^{T} \cdot \mathrm{DCB}_{P_{1} P_{2}}^{s, T}+e_{r, 2}^{s, T} \\ l_{r, 2}^{s, T}=\boldsymbol{u}_{r}^{s, T} \cdot \boldsymbol{x}+c \cdot \mathrm{d} t_{r}+m \cdot \mathrm{zwd}_{r}-\gamma_{2}^{T} \cdot I_{r, 1}^{s, T}+ \\ \ \ \ \ d_{\mathrm{IF}_{12}^{s}, T}+\lambda_{2}^{s, T} \cdot\left(N_{r, 2}^{s, T}+D_{r, 2}^{s, T}-D_{2}^{s, T}\right)+\xi_{r, 2}^{s, T} \end{array}\right. $ | (5) |
在进行多系统融合PPP时,需要考虑不同卫星系统间的系统偏差ISB,ISB可看作为不同卫星系统接收机钟差的差异[6],需要选择一个卫星系统作为基准。例如以GPS为基准,则GLONASS卫星的ISB参数为:
| $ \mathrm{ISB}_{r}^{\mathrm{R}}=c \cdot\left(T^{\mathrm{R}}-T^{\mathrm{G}}\right)+\left(d_{r, \mathrm{IF}}^{\mathrm{R}}-d_{r, \mathrm{IF}}^{\mathrm{G}}\right) $ | (6) |
式中,ISBrR为GLONASS使用GPS接收机钟差而引入的ISB参数,TR、TG分别为GLONASS和GPS系统的时间基准,dr, IFR、dr, IFG分别为GLONASS和GPS系统在接收机端UCDs的无电离层组合。为增强模型强度,本文只设定一个ISB参数,即如果选定一个卫星系统作为基准,则ISB为其他所有卫星系统在使用该基准系统接收机钟差时引入的系统偏差参数[8]。
3 两种伪距IFB模型 3.1 第一种伪距IFB模型第一种模型是对每个GLONASS卫星估计一个IFB参数:
| $ d_{r, i}^{s, \mathrm{R}}=d_{r, i}^{\mathrm{R}}+\varphi_{r, i}^{s, \mathrm{R}} $ | (7) |
式中,dr, iR表示频率号(取值范围为-7~6)为0的卫星伪距IFB,φr, is, R为IFB的一部分,与卫星PRN号码和频率有关。由于该伪距IFB模型的ISB与IFB参数强相关[7],故将ISB与IFB合并为参数ISFB进行估计。将式(7)代入式(4)和式(5)并重新进行参数化可得[9]:
| $ \left\{\begin{aligned} &c \cdot \mathrm{d} \bar{t}_{r}^{T}=c \cdot \mathrm{d} t_{r}+d_{r, \mathrm{IF}_{12}}^{T} \\ &\mathrm{ISFB}_{r, 12}^{s, \mathrm{R}}=\varphi_{r, 2}^{s, \mathrm{R}}-\gamma_{2}^{\mathrm{R}} \cdot \varphi_{r, 1}^{s, \mathrm{R}}+\mathrm{ISB}_{r}^{M}\\ &\bar{I}_{r, 1}^{s, \mathrm{C}}=I_{r, 1}^{s, \mathrm{C}}+\beta_{12}^{\mathrm{C}} \cdot \mathrm{DCB}_{r, P_{1} P_{2}}^{\mathrm{C}}\\ &\bar{I}_{r, 1}^{s, \mathrm{R}}=I_{r, 1}^{s, \mathrm{R}}+\beta_{12}^{\mathrm{R}} \cdot \mathrm{DCB}_{r, P_{1} P_{2}}^{\mathrm{R}}+\varphi_{r, 1}^{s, \mathrm{R}}\\ &\bar{N}_{r, 1}^{s, \mathrm{C}}=\lambda_{1}^{\mathrm{C}} \cdot\left(N_{r, 1}^{s, \mathrm{C}}+D_{r, 1}^{\mathrm{C}}-D_{1}^{s, \mathrm{C}}\right)+d_{\mathrm{IF}_{12}}^{s, \mathrm{C}}-d_{r, \mathrm{IF}_{12}}^{\mathrm{C}}+\beta_{12}^{\mathrm{C}} \cdot \mathrm{DCB}_{r, P_{1} P_{2}}^{\mathrm{C}}\\ &\bar{N}_{r, 2}^{s, \mathrm{C}}=\lambda_{2}^{\mathrm{C}} \cdot\left(N_{r, 2}^{s, \mathrm{C}}+D_{r, 2}^{\mathrm{C}}-D_{2}^{s, \mathrm{C}}\right)+d_{\mathrm{IF}_{12}}^{s, \mathrm{C}}-d_{r, \mathrm{~F}_{12}}^{\mathrm{C}}+\gamma_{2}^{\mathrm{C}} \cdot \beta_{12}^{\mathrm{C}} \cdot \mathrm{DCB}_{r, P_{1} P_{2}}^{\mathrm{C}}\\ &\bar{N}_{r, 1}^{s, \mathrm{R}}=\lambda_{1}^{s, \mathrm{R}} \cdot\left(N_{r, 1}^{s, \mathrm{R}}+D_{r, 1}^{s, \mathrm{R}}-D_{1}^{s, \mathrm{R}}\right)+d_{\mathrm{I} \mathrm{F}_{12}}^{s, \mathrm{R}}-d_{r, \mathrm{IF}_{12}}^{\mathrm{R}}+\varphi_{r, 1}^{s, \mathrm{R}}+\beta_{12}^{\mathrm{R}} \cdot \mathrm{DCB}_{r, P_{1} P_{2}}^{\mathrm{R}}\\ &\bar{N}_{r, 2}^{s, \mathrm{R}}=\lambda_{2}^{s, \mathrm{R}} \cdot\left(N_{r, 2}^{s, \mathrm{R}}+D_{r, 2}^{s, \mathrm{R}}-D_{2}^{s, \mathrm{R}}\right)+d_{\mathrm{IF}_{12}}^{s, \mathrm{R}}-d_{r, \mathrm{IF}_{12}}^{\mathrm{R}}+\gamma_{2}^{\mathrm{R}} \cdot \varphi_{r, 1}^{s, \mathrm{R}}+\gamma_{2}^{\mathrm{R}} \cdot \beta_{12}^{\mathrm{R}} \cdot \mathrm{DCB}_{r, P_{1} P_{2}}^{\mathrm{R}} \end{aligned}\right. $ | (8) |
式中,M为选取某种卫星信号的接收机钟差作为参考后其他的卫星信号,ISBrM为选定某种卫星系统作为基准后其他所有参与PPP解算的卫星系统在使用基准卫星系统接收机钟差时引入的ISB参数,C为采用CDMA技术的卫星系统。该模型需要估计的参数包括坐标增量x、接收机钟差dtrT、参数ISFBr, 12s, R、对流层延迟ZTDr、电离层延迟Ir, 1s, C、Ir, 1s, R以及浮点模糊度Nr, 1s, C、Nr, 2s, C、Nr, 1s, R、Nr, 2s, R。
3.2 第二种伪距IFB模型第二种模型是用频率号的一次线性函数来估计伪距IFB参数:
| $ d_{r, i}^{s, \mathrm{R}}=d_{r, i}^{\mathrm{R}}+K^{s, \mathrm{R}} \cdot \Delta_{r, i}^{\mathrm{R}} $ | (9) |
式中,Ks, R为卫星s的频率号,Δr, iR为IFB的一部分,与卫星频率号有关[7]。该模型将1 d内的ISB参数作为常数进行估计[8]。将式(9)代入式(4)和式(5)并重新进行参数化可得:
| $ \left\{\begin{array}{l} c \cdot \mathrm{d} \bar{t}_{r}^{T}=c \cdot \mathrm{d} t_{r}+d_{r, \mathrm{IF}_{12}}^{\mathrm{T}} \\ \Delta_{r, 12}^{\mathrm{R}}=\Delta_{r, 2}^{\mathrm{R}}-\gamma_{2}^{\mathrm{R}} \cdot \Delta_{r, 1}^{\mathrm{R}} \\ \bar{I}_{r, 1}^{s, \mathrm{C}}=I_{r, 1}^{s, \mathrm{C}}+\beta_{12}^{\mathrm{C}} \cdot \mathrm{DCB}_{r, P_{1} P_{2}}^{\mathrm{C}} \\ \bar{I}_{r, 1}^{s, \mathrm{R}}=I_{r, 1}^{s, \mathrm{R}}+\beta_{12}^{\mathrm{R}} \cdot \mathrm{DCB}_{r, P_{1} P_{2}}^{\mathrm{R}}+K^{s, \mathrm{R}} \cdot \Delta_{r, 1}^{\mathrm{R}}\\ \bar{N}_{r, 1}^{s, \mathrm{C}}=\lambda_{1}^{\mathrm{C}} \cdot\left(N_{r, 1}^{s, \mathrm{C}}+D_{r, 1}^{\mathrm{C}}-D_{1}^{s, \mathrm{C}}\right)+d_{\mathrm{IF}_{12}}^{s, \mathrm{C}}-d_{r, \mathrm{IF}_{12}}^{\mathrm{C}}+\beta_{12}^{\mathrm{C}} \cdot \mathrm{DCB}_{r, P_{1} P_{2}}^{\mathrm{C}}\\ \bar{N}_{r, 2}^{s, \mathrm{C}}=\lambda_{2}^{\mathrm{C}} \cdot\left(N_{r, 2}^{s, \mathrm{C}}+D_{r, 2}^{\mathrm{C}}-D_{2}^{s, \mathrm{C}}\right)+d_{\mathrm{IF}_{12}}^{s, \mathrm{C}}-d_{r, \mathrm{IF}_{12}}^{\mathrm{C}}+\gamma_{2}^{\mathrm{C}} \cdot \beta_{12}^{\mathrm{C}} \cdot \mathrm{DCB}_{r, P_{1} P_{2}}^{\mathrm{C}}\\ \bar{N}_{r, 1}^{s, \mathrm{R}}=\lambda_{1}^{s, \mathrm{R}} \cdot\left(N_{r, 1}^{s, \mathrm{R}}+D_{r, 1}^{s, \mathrm{R}}-D_{1}^{s, \mathrm{R}}\right)+d_{\mathrm{IF}_{12}}^{s, \mathrm{R}}-d_{r, \mathrm{IF}_{12}}^{\mathrm{R}}+K^{s, \mathrm{R}} \cdot \Delta_{r, 1}^{\mathrm{R}}+\beta_{12}^{\mathrm{R}} \cdot \mathrm{DCB}_{r, P_{1} P_{2}}^{\mathrm{R}} \\ \bar{N}_{r, 2}^{s, \mathrm{R}}=\lambda_{2}^{s, \mathrm{R}} \cdot\left(N_{r, 2}^{s, \mathrm{R}}+D_{r, 2}^{s, \mathrm{R}}-D_{2}^{s, \mathrm{R}}\right)+d_{\mathrm{IF}_{12}}^{s, \mathrm{R}}-d_{r, \mathrm{IF}_{12}}^{\mathrm{R}}+\gamma_{2}^{\mathrm{R}} \cdot K^{s, \mathrm{R}} \cdot \Delta_{r, 1}^{\mathrm{R}}+\gamma_{2}^{\mathrm{R}} \cdot \beta_{12}^{\mathrm{R}} \cdot \mathrm{DCB}_{r, P_{1} P_{2}}^{\mathrm{R}} \end{array}\right. $ | (10) |
该模型需要估计的参数包括坐标增量x、接收机钟差dtrT、系统偏差ISBrM、对流层延迟ZTDr、电离层延迟Ir, 1s, C、Ir, 1s, R,浮点模糊度Nr, 1s, C、Nr, 2s, C、Nr, 1s, R、Nr, 2s, R以及IFB参数Δr, 12R。
4 两种伪距IFB模型性能分析为研究两种伪距IFB模型在多系统融合PPP中的性能,随机选取52个MGEX测站在2020-04-09~15期间的数据(采样间隔为30 s)进行分析。在进行数据解算时发现有些测站大部分历元搜索到的GLONASS卫星个数小于4,在数理统计上无意义,因此仅对G/R、R/B、R/E、G/R/B、G/R/E、R/B/E和G/R/B/E等卫星组合模式进行性能评定。将不同组合估计的坐标与IGS周解坐标[10]进行对比,获得E、N、U三个方向上的坐标残差,并分析不同组合模式在静态和动态条件下采用不同伪距IFB模型对定位精度和收敛时间的影响。
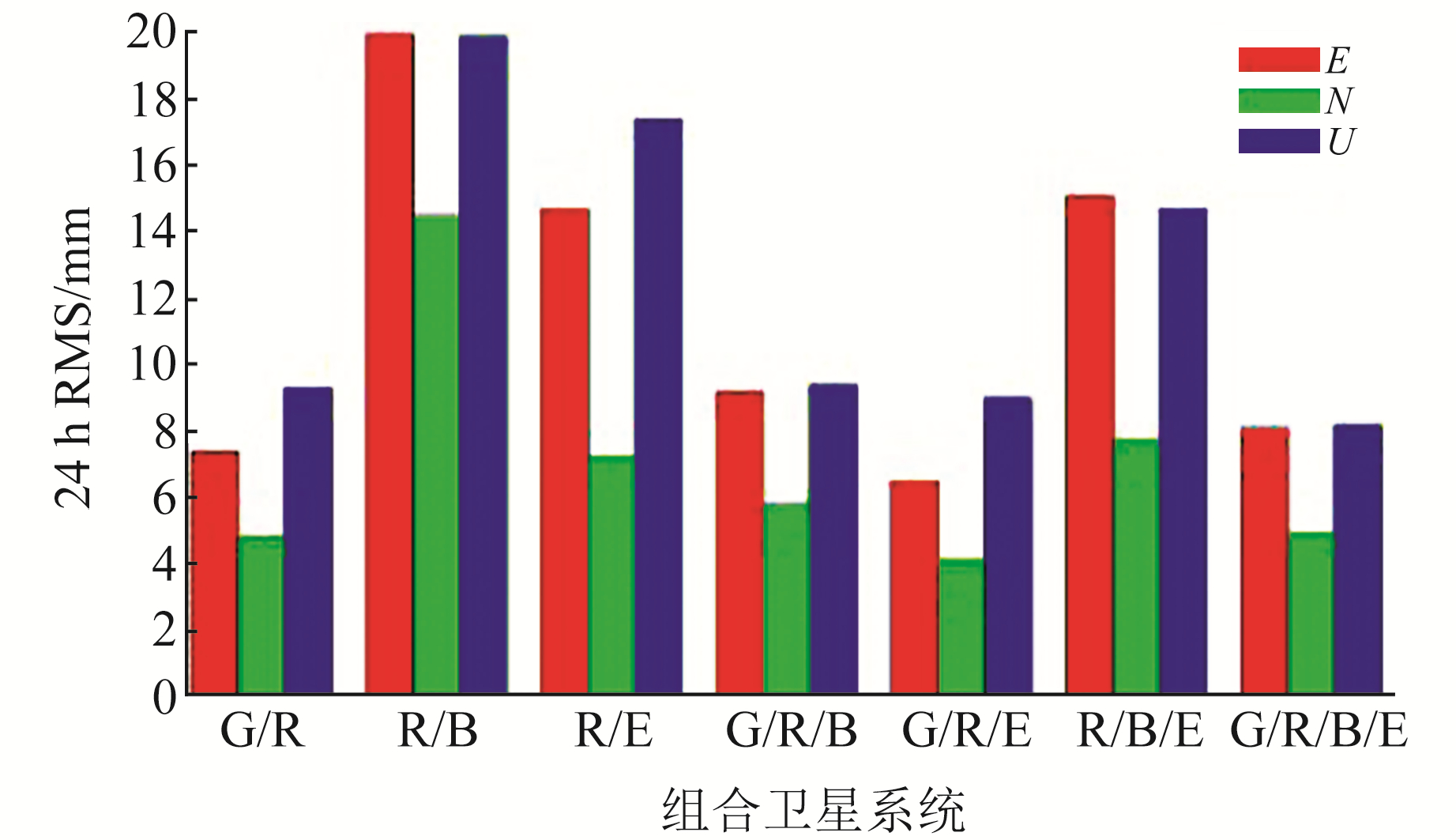
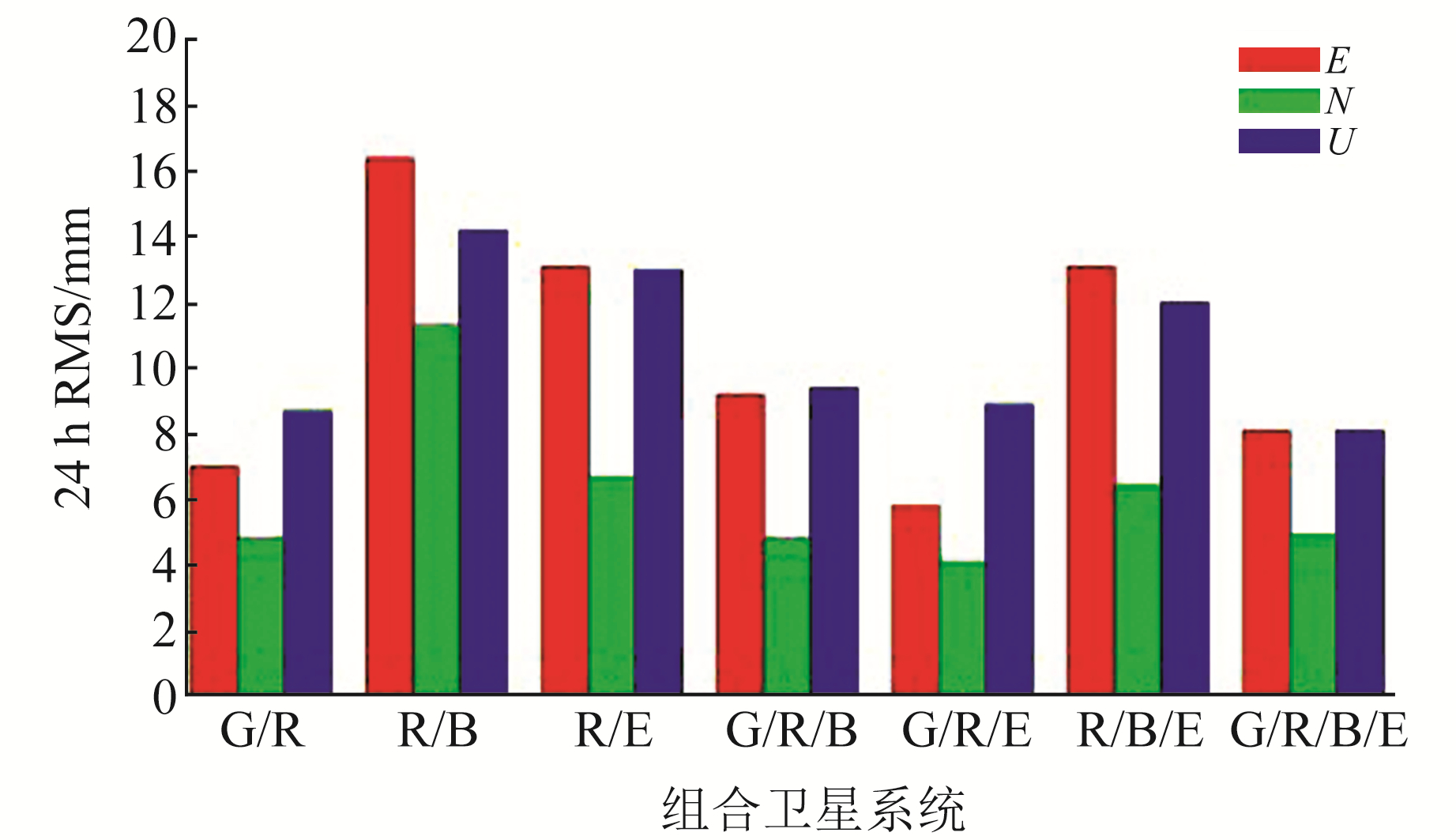
4.1 静态定位精度分析图 1和图 2为不同组合模式下两种伪距IFB模型在静态条件下的定位精度。从图中可以看出,两种伪距IFB模型的定位精度在3个方向上大致相当。在E方向上,R/B、R/B/E组合第二种模型的精度略优于第一种模型,其他组合精度相当;在N方向上,R/B组合第二种模型的精度略优于第一种模型,其他组合精度相当;在U方向上,R/B、R/E、R/B/E第二种模型的精度略优于第一种模型,其他组合精度相当。综上所知,在卫星数量较少的情况下,第一种伪距IFB模型的参数个数多于第二种模型,从而使定位精度降低。
|
图 1 第一种IFB模型静态定位结果 Fig. 1 Static positioning results of the first IFB model |
|
图 2 第二种IFB模型静态定位结果 Fig. 2 Static positioning results of the second IFB model |
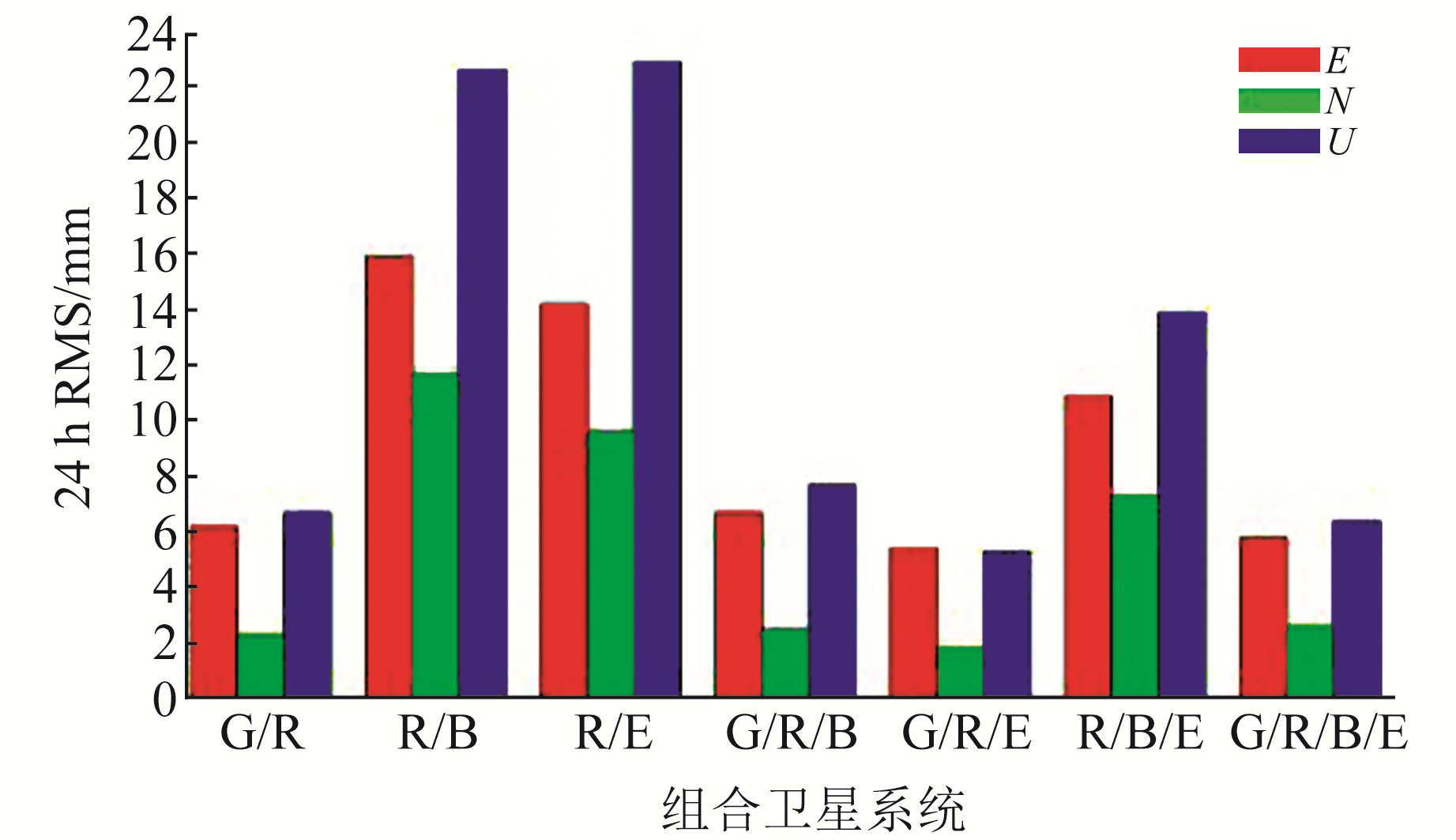
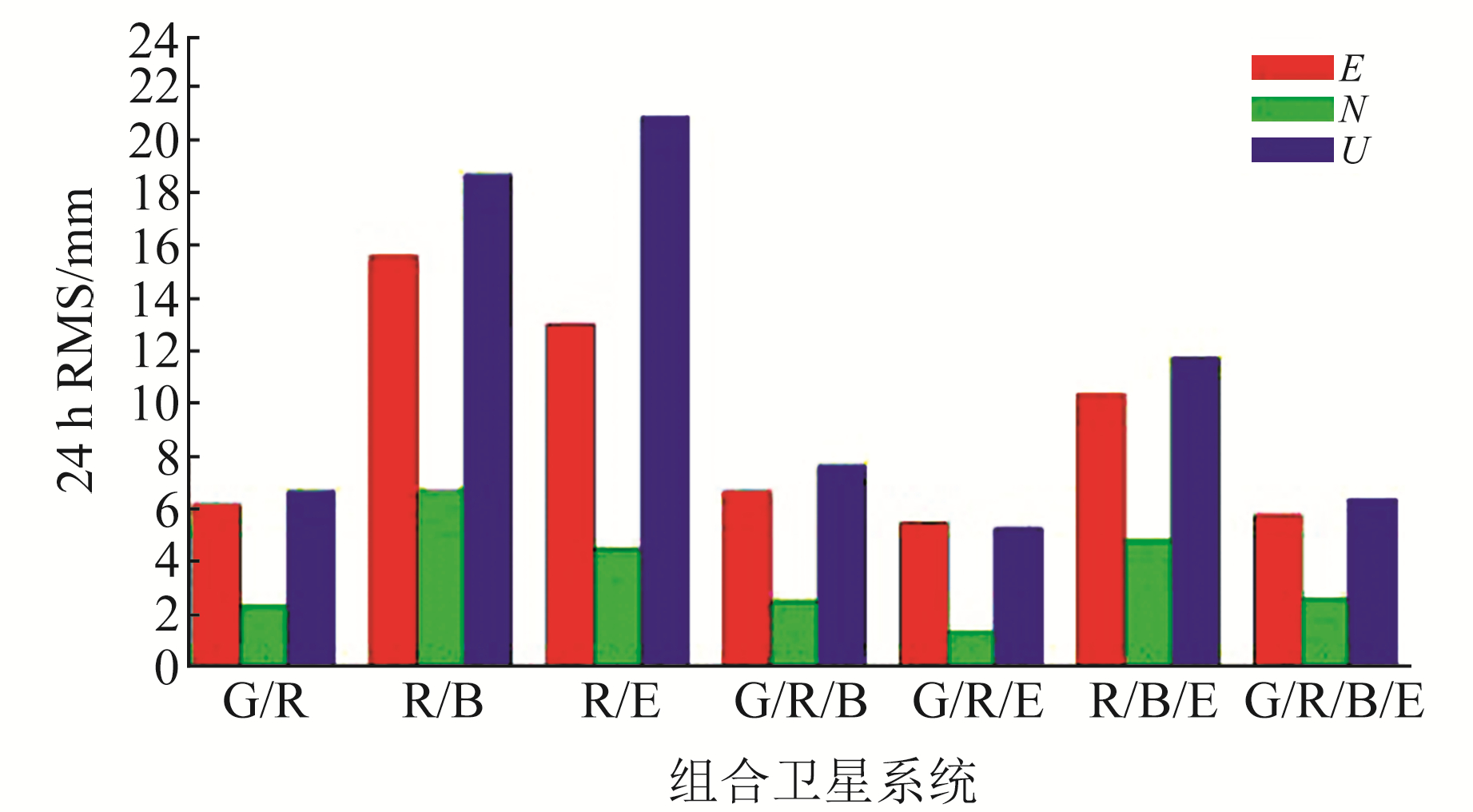
图 3和图 4为不同组合模式下两种伪距IFB模型在动态条件下的定位精度。通过对比可知,在N方向上,第二种IFB模型的定位精度比第一种模型提升约21%;在E方向上,R/E组合第二种模型的定位精度优于第一种模型;在U方向上,R/E、R/B、R/B/E组合第二种模型的定位精度优于第一种模型。其他组合在E、U方向上定位精度大致相当。
|
图 3 第一种IFB模型动态定位结果 Fig. 3 Dynamic positioning results of the first IFB model |
|
图 4 第二种IFB模型动态定位结果 Fig. 4 Dynamic positioning results of the second IFB model |
为评估两种伪距IFB模型在多系统融合PPP中的收敛速度,将收敛时间定义为:68%和95%的总测站在3个方向上均达到一定精度并在随后的一段时间内保持稳定所需的时间。静态条件下3个方向上精度达到0.03 m并在随后至少20个历元内保持稳定的历元时间为收敛时间,动态条件下3个方向上精度达到0.1 m并在随后至少20个历元内保持稳定的历元时间为收敛时间。表 1~7(单位min)分别为G/R、R/B、R/E、G/R/B、G/R/E、R/B/E和G/R/B/E在静态和动态条件下3个方向上的收敛时间。
|
|
表 1 G/R收敛时间 Tab. 1 The convergence time of G/R |
|
|
表 2 R/B收敛时间 Tab. 2 The convergence time of R/B |
|
|
表 3 R/E收敛时间 Tab. 3 The convergence time of R/E |
|
|
表 4 G/R/B收敛时间 Tab. 4 The convergence time of G/R/B |
|
|
表 5 G/R/E收敛时间 Tab. 5 The convergence time of G/R/E |
|
|
表 6 R/B/E收敛时间 Tab. 6 The convergence time of R/B/E |
|
|
表 7 G/R/B/E收敛时间 Tab. 7 The convergence time of G/R/B/E |
由表 1~7可知,在包含GPS星座的组合中,第一种模型在部分方向的收敛速度略快于第二种模型,但提升幅度有限。原因可能为GPS卫星在全球分布较广,每个历元能观测到的GPS卫星数目较多且随时间变化较小。但其他不包含GPS卫星的组合在动态条件下第一种模型的收敛速度普遍比第二种模型慢,且部分方向的收敛速度相差巨大。原因主要为第一种伪距IFB模型包含大量被估参数,并且该组合的卫星会受到地域、时间等因素影响,每个历元观测到的可用卫星数量变化很大,数值解不稳定。
5 结语1) 静态条件下,两种伪距IFB模型在3个方向上定位精度相当;动态条件下,两种伪距IFB模型在E、U方向上精度相当,第二种IFB模型能够提高N方向上定位精度,提升幅度约为21%。
2) 两种模型在不同卫星组合模式下的收敛速度略有不同。包含GPS星座的组合在静态和动态条件下第一种模型的收敛速度在部分方向上略快于第二种模型,但提升效果有限;不包含GPS星座的组合第一种模型的收敛速度在3个方向上普遍比第二种模型慢,且部分方向的收敛速度相差巨大。
3) 两种伪距IFB模型在3个方向上均可达到设定精度,但第一种模型会增加被估参数的个数,这在数值运算中会影响解算精度,特别是在观测方程较少的情况下。因此从模型简易程度、定位精度和收敛时间等方面考虑,第二种伪距IFB模型要优于第一种伪距IFB模型。
| [1] |
Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5 005-5 017 DOI:10.1029/96JB03860
(  0) 0) |
| [2] |
王利, 张勤, 涂锐, 等. 基于原始观测值的单频精密单点定位算法[J]. 测绘学报, 2015, 44(1): 19-25 (Wang Li, Zhang Qin, Tu Rui, et al. A Kind of Single-Frequency Precise Point Positioning Algorithm Based on the Raw Observations[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1): 19-25)
(  0) 0) |
| [3] |
Wanninger L. Carrier-Phase Inter-Frequency Biases of GLONASS Receivers[J]. Journal of Geodesy, 2012, 86(2): 139-148 DOI:10.1007/s00190-011-0502-y
(  0) 0) |
| [4] |
Al-Shaery A, Zhang S, Rizos C. An Enhanced Calibration Method of GLONASS Inter-Channel Bias for GNSS RTK[J]. GPS Solutions, 2013, 17(2): 165-173 DOI:10.1007/s10291-012-0269-5
(  0) 0) |
| [5] |
Xia F Y, Ye S R, Xia P F, et al. Assessing the Latest Performance of Galileo-Only PPP and the Contribution of Galileo to Multi-GNSS PPP[J]. Advances in Space Research, 2019, 63(9): 2 784-2 795 DOI:10.1016/j.asr.2018.06.008
(  0) 0) |
| [6] |
Lou Y D, Zheng F, Gu S F, et al. Multi-GNSS Precise Point Positioning with Raw Single-Frequency and Dual-Frequency Measurement Models[J]. GPS Solutions, 2016, 20(4): 849-862 DOI:10.1007/s10291-015-0495-8
(  0) 0) |
| [7] |
Zhou F, Dong D N, Ge M R, et al. Simultaneous Estimation of GLONASS Pseudorange Inter-Frequency Biases in Precise Point Positioning Using Undifferenced and Uncombined Observations[J]. GPS Solutions, 2018, 22(1)
(  0) 0) |
| [8] |
Liu T, Yuan Y B, Zhang B C, et al. Multi-GNSS Precise Point Positioning(MGPPP) Using Raw Observations[J]. Journal of Geodesy, 2017, 91(3): 253-268
(  0) 0) |
| [9] |
Teunissen P J G. Zero Order Design: Generalized Inverses, Adjustment, the Datum Problem and S-Transformations[M]//Grafarend E W, Sansò F. Optimization and Design of Geodetic Networks. Heidelberg: Springer, 1985
(  0) 0) |
| [10] |
Kouba J. A Guide to Using International GNSS Service (IGS) Products[Z]. 2015
(  0) 0) |
 2022, Vol. 42
2022, Vol. 42


