2. 中铁第一勘察设计院集团有限公司,西安市西影路2号,710043
近年来随着GPS和GLONASS现代化的逐步推进以及Galileo和BDS的逐步完善,提供高精度、高可靠性的实时位置服务已成为全球导航卫星系统(GNSS) 精密定位的发展趋势和研究热点[1]。精密单点定位(PPP) 作为一种高精度的绝对定位手段已在多个领域得到广泛应用,收敛后可在全球任意范围内提供静态cm级、动态dm级的定位精度[2]。然而,由于卫星几何构型变化缓慢以及受实际复杂环境引起的噪声影响,PPP通常需要20~30 min才能收敛到cm量级[3]。
PPP模糊度的正确固定能够显著缩短PPP收敛时间。按照PPP窄巷模糊度的恢复方式可将PPP模糊度固定方法分为两类,一类为估计窄巷硬件延迟小数部分(fractional cycle bias, FCB) 方法,如Ge等[4]提出将相位未校准硬件延迟偏差(UPD) 与实数模糊度进行分离,服务端通过星间单差方式消除接收机端UPD并发送给用户端,恢复模糊度的整周特性;Li等[5]提出以某一卫星或地面某一测站UPD作为基准,用户端采用非差法整网平差,同时解算出卫星端和接收机端UPD。另一类称为整数恢复钟差(integer-recovery clock, IRC) 方法,如Laurichesse等[6]直接将卫星钟差与窄巷硬件延迟进行合并解算,服务端将解算的整数相位钟产品进行播发,用户端无需进行窄项UPD改正即可固定模糊度;Geng等[7]已证明FCB方法与IRC方法在数学上具有等价性,FCB方法在服务端估计时较为方便,IRC方法在用户端固定时较为便捷;Li等[2]针对部分情况下固定模糊度全集较为困难,提出部分模糊度固定策略,根据一定的准则挑选部分模糊度进行固定;Wang等[8]为解决服务端与用户端产品不统一的问题,证明3种FCB产品具有等价性,并进行实验验证;Hu等[9]对服务端多系统FCB产品质量进行分析,并在用户端采用星间单差方式进行PPP模糊度固定。
然而,目前研究主要是针对服务端FCB产品的解算及质量评估,对于用户端PPP模糊度固定的研究较少。当前用户端采用星间单差方式消除接收机端UPD的影响,基准星选取不当会对模糊度固定造成极大影响,从而使PPP模糊度无法固定。因此,本文提出一种顾及接收机UPD的PPP分步模糊度固定方法,用户端基于非差法和服务端FCB产品估计接收机端UPD,并依据PPP窄巷模糊度协方差大小进行分步模糊度固定。
1 数学模型 1.1 传统星间单差方法对伪距和载波观测量消电离层组合,消除电离层延迟一阶项影响:
| $\left\{ {\begin{array}{*{20}{l}} {P_{{\rm{IF}}, k}^i = {\mathit{\boldsymbol{\mu }}}_k^i{\mathit{\boldsymbol{r}}} + c\left( {\delta {{\hat t}_k} + {d_{{\rm{IF}}, k}}} \right) - }\\ {\quad c\left( {\delta {t^i} + d_{{\rm{IF}}}^i} \right) + M_k^i \cdot {d_{{\rm{trop}}, k}}}\\ {L_{{\rm{IF}}, k}^i = {\mathit{\boldsymbol{\mu }}}_k^i{\mathit{\boldsymbol{r}}} + c\left( {\delta {{\hat t}_k} + {d_{{\rm{IF}}, k}}} \right) - }\\ {\quad c\left( {\delta {t^i} + d_{{\rm{IF}}}^i} \right) + M_k^i \cdot {d_{{\rm{trop }}, k}} + {\lambda _{{\rm{IF}}}}B_{{\rm{IF}}, k}^i} \end{array}} \right.$ | (1) |
式中,P和L分别表示GNSS伪距和载波观测量,上标i、下标k分别表示卫星编号和测站编号,下标IF表示消电离层组合。μki=(αi, βi, γi)表示站星间方向向量,r表示坐标改正数,c表示光速。
由于NIF, ki不具备整数特性,将其分为宽巷NWL, ki和窄巷NNL, ki分别进行固定。为消除接收机端UPD的影响,通常选取高度角最高的卫星作为基准星,进行星间单差,因此固定的模糊度为星间单差的宽巷模糊度和窄巷模糊度。设基准站为i,则星间单差的消电离层模糊度可表示为:
| $B_{{\rm{IF}}, k}^{i, j} = \frac{{{f_1}}}{{{f_1} + {f_2}}}B_{{\rm{NL}}, k}^{i, j} + \frac{{{\rm{ }}{f_1}{f_2}}}{{f_1^2 - f_2^2}}B_{{\rm{WL}}, k}^{i, j}$ | (2) |
式中,BWL, ki, j和BNL, ki, j分别表示包含硬件延迟的宽巷和窄巷模糊度,宽巷模糊度可按照MW组合历元间平滑获得:
| $\begin{array}{c} B_{{\rm{WL}}, k}^i = \left[ {{\rm{ }}\left( {\frac{{{f_1}}}{{{f_1} - {f_2}}}L_{1, k}^i - {\rm{ }}\frac{{{f_2}}}{{{f_1} - {f_2}}}L_{1, k}^i} \right) - } \right.\\ \left. {\left( {\frac{{{f_1}}}{{{f_1} + {f_2}}}P_{1, k}^i + \frac{{{f_2}}}{{{f_1} + {f_2}}}P_{2, k}^i} \right)} \right]/{\lambda _{\rm{W}}} = \\ N_{{\rm{WL}}, k}^i + {f_{{\rm{WL}}, k}} - f_{{\rm{WL}}}^i \end{array}$ | (3) |
式中,[*]表示历元间平滑,fWL, k和fWLi分别表示接收机端和卫星端硬件延迟,将得到的宽巷模糊度进行星间单差即可消除接收机端硬件延迟,即BWL, ki, j=NWL, ki, j-fWLi, j。由于宽巷模糊度波长λW为0.86 m,经星间单差FCB改正后可直接取整固定[10]。将固定后的星间单差宽巷模糊度代入消电离层模糊度中,即可得到星间单差窄巷模糊度:
| $B_{{\rm{NL}}, k}^{i, j} = \frac{{{\rm{ }}{f_1} + {f_2}}}{{{f_1}}}B_{{\rm{IF}}, k}^{i, j} - \frac{{{f_1}}}{{{f_1} - {f_2}}}N_{{\rm{WL}}, k}^{i, j}$ | (4) |
由于窄巷模糊度波长之间存在相关性且其波长较短,通常采用LAMBDA[11]算法进行模糊度搜索固定。固定后的单差模糊度作为约束条件代入滤波器,可得到PPP固定解。
1.2 顾及接收机UPD的分步模糊度固定方法考虑到接收机端UPD,将UPD表示成虚拟观测方程:
| $l_{i, r}^j = B_{i, r}^j - N_{i, r}^j = {f_{i, r}} - f_i^j$ | (5) |
式中,li, rj为虚拟观测量,fi, r和fij分别为接收机端和卫星端UPD。可以看出,PPP模糊度固定的关键在于UPD与整周模糊度的准确分离。当已知卫星端UPD,可对实数模糊度Bi, rj进行改正,并将其就近取整,以其相差的小数部分构造虚拟观测量。
对于用户端,利用各卫星端UPD对观测卫星的模糊度进行改正,理论上改正后的模糊度仅剩接收机端UPD,具有相近的小数部分。需要注意的是,服务端UPD产品为星间单差UPD,因此改正后的模糊度除接收机端UPD外还包括参考星UPD。将这些接收机端UPD的近似值采用与整数无关的三角函数进行计算,得到接收机端UPD的估计值:
| ${f_{i, r}} = \frac{{{\rm{arc}}\left( {\frac{{\sum\limits_{{\rm{ }}j}^m {\sin \left( {2{\rm{ \mathsf{ π} }}\left( {B_{i, r}^j - f_i^j} \right)} \right)} }}{{\sum\limits_{{\rm{ }}i}^m {\cos \left( {2{\rm{ \mathsf{ π} }}\left( {B_{i, r}^j - f_i^j} \right)} \right)} }}} \right)}}{{2{\rm{ \mathsf{ π} }}}}$ | (6) |
将得到的接收机端UPD代入PPP模糊度浮点解中,扣除卫星端UPD即可得到整周模糊度估计值。由于估计的接收机端UPD包括参考星UPD,同时服务端UPD为星间单差UPD,因此PPP模糊度浮点解经卫星端UPD产品和所估计的接收机端UPD改正后,可得到整周模糊度估计值。
同理,由于消电离层模糊度不具备整数特性,将其分为宽巷、窄巷分别进行固定。非差宽巷模糊度波长较长,可直接取整固定。
| $\begin{array}{c} {P_0} = 1 - \sum\limits_{i = 1}^\infty {\left[ {{\rm{erfc}}\left( {\frac{{i - \left| {B - N} \right|}}{{\sqrt 2 \sigma }}} \right)} \right. - } \\ {\rm{}}\left. {{\rm{erfc}}\left( {\frac{{i - \left| {B - N} \right|}}{{\sqrt 2 \sigma }}} \right)} \right], {\rm{erf}}c\left( x \right) = \frac{2}{{\sqrt {\rm{ \mathsf{ π} }} }}\int_x^\infty {{{\rm{e}}^{ - {t^2}}}{\rm{d}}t} \end{array}$ | (7) |
式中,B为宽巷模糊度浮点解,N为其取整结果,σ为宽巷模糊度中误差。当取整成功率大于0.999时,认为其正确固定。由固定的宽巷模糊度和消电离层模糊度可得到窄巷模糊度浮点解:
| $B_{{\rm{NL}}, k}^i = \frac{{{f_1} + {f_2}}}{c}L_{{\rm{IF}}, k}^i - \frac{{{f_2}}}{{{f_1} - {f_2}}}N_{{\rm{WL}}, k}^i$ | (8) |
同理,窄巷模糊度浮点解经卫星端和接收机端UPD改正后,由于其波长较短且模糊度之间具有相关性,可采用分步模糊度固定方法:
1) 对非差窄巷模糊度依据其协方差大小σN12≤σN22≤…≤σNi2≤…≤σNm2进行排序。
2) 采用LAMBDA[11]算法对非差窄巷模糊度进行降相关并搜索,若通过Ratio值检验则认为PPP模糊度固定成功,否则进入步骤3)。
3) 对非差窄巷模糊度进行降维处理,即删去协方差最大的模糊度,对剩余模糊度子集进行固定,若通过Ratio值检验则输出PPP固定解。否则重复步骤2)、3),直至PPP模糊度成功固定,或者窄巷模糊度维数小于4按照PPP浮点解输出。
2 实验与分析选取全球225个MGEX(multi-GNSS experiment) 测站作为服务端进行UPD产品的生成与发布,观测日期为2019年年积日81。另选取未参与服务端解算的14个MGEX测站作为用户端,以验证方法的有效性。测站真值坐标选取SINEX(solution independent exchange format)周解。表 1为服务端UPD解算策略,采用消电离层组合消去电离层延迟一阶项影响,数据采样率为30 s,卫星截止高度角设为10°。卫星轨道和钟差均采用德国地学研究中心(German research centre for geosciences, GFZ) 发布的精密产品进行改正,对流层湿延迟采用随机游走模型进行估计,接收机钟差当作白噪声进行估计。
|
|
表 1 服务端UPD解算策略 Tab. 1 UPD solution strategy at server station |
服务端采用非差法进行UPD估计,由于卫星宽巷UPD较为稳定,一天估计一组,而卫星窄巷UPD波动较大,通常15 min估计一组。将生成的UPD产品播发给225个MGEX测站以检验UPD产品的精度。经UPD改正后的PPP宽巷和窄巷模糊度残差分布如图 1所示,从图中可以看出,97.4%的宽巷残差和93.6%的窄巷残差分布在±0.25周之内,表明服务端生成的UPD产品具有较好的精度,可以播发给用户端使用。
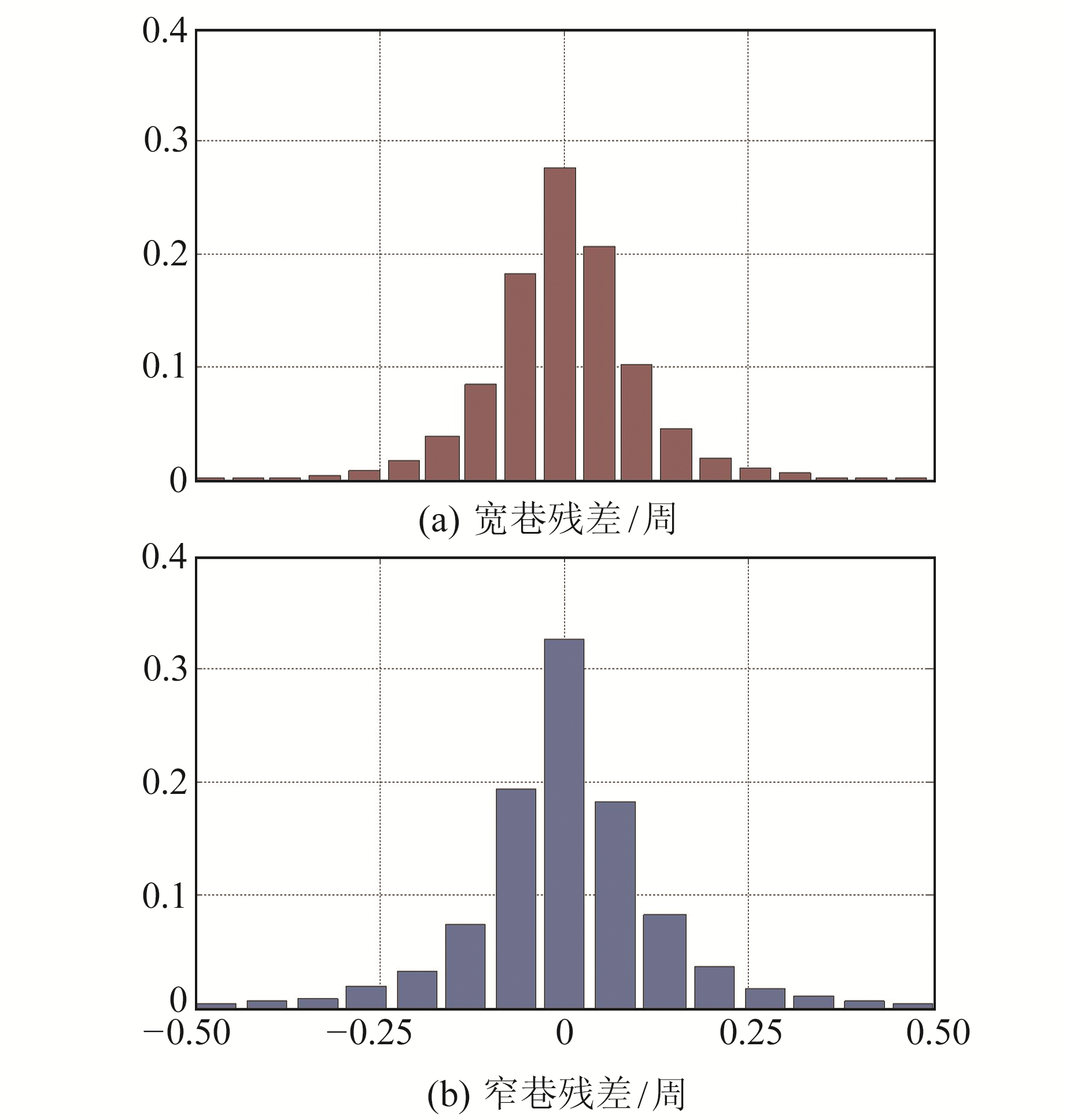
|
图 1 经UPD产品改正后的宽巷残差和窄巷残差分布 Fig. 1 Residual distribution of wide-lane and narrow-lane corrected by UPD products |
对于全球用户端14个MGEX测站,分别采用PPP浮点解(PPP-Float)、常规PPP星间单差法固定模糊度(PPPAR-SD)和顾及接收机UPD的分步模糊度固定方法(PPPAR-UD)进行求解。图 2为静态和仿动态条件下CEDU测站3种方法的解算结果,从图中可以看出,PPP模糊度的正确固定能够显著缩短PPP初始化时间,较之传统方法,新方法效果更加显著。
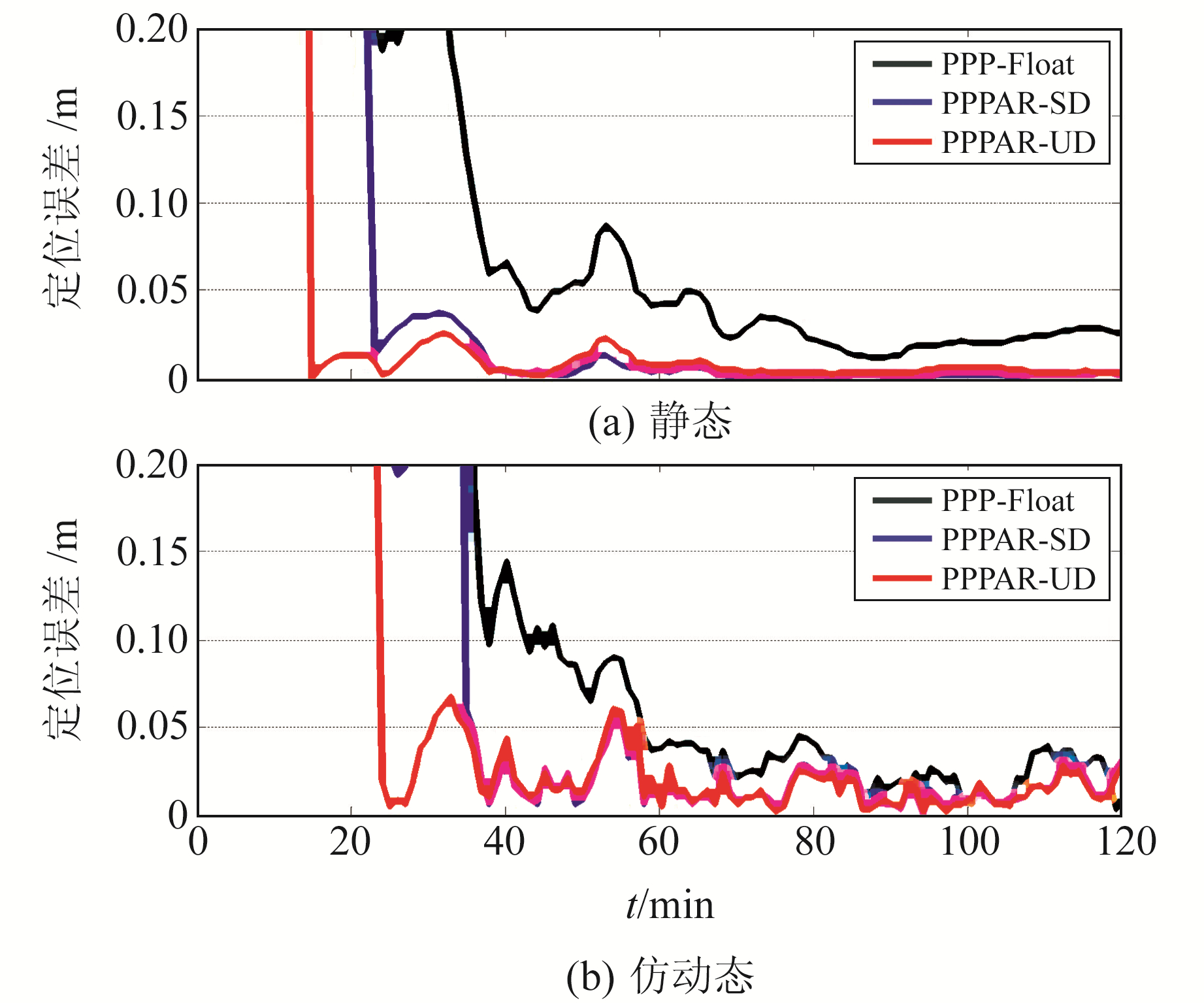
|
图 2 静态和仿动态情况下3种方法的定位结果 Fig. 2 Positioning results of three methods under static and dynamic conditions |
图 3为静态和仿动态条件下用户端14个MGEX测站采用3种方法在30 min的定位精度,从图中可以看出,静态情况下,PPP浮点解平均精度为7.8 cm,传统星间单差方法为2.5 cm,本文所提方法为1.8 cm。与PPP浮点解相比,静态情况下传统方法和新方法定位精度分别提升68.3%和76.4%。仿动态情况下,PPP浮点解平均精度为14.4 cm,传统星间单差方法为4.9 cm,本文所提方法为2.2 cm。与PPP浮点解相比,仿动态情况下传统方法和新方法定位精度分别提升65.7%和84.7%。从上述分析可以看出,与传统方法相比,无论静态还是仿动态情况下,本文方法都能够显著提高PPP短时间内的定位精度。
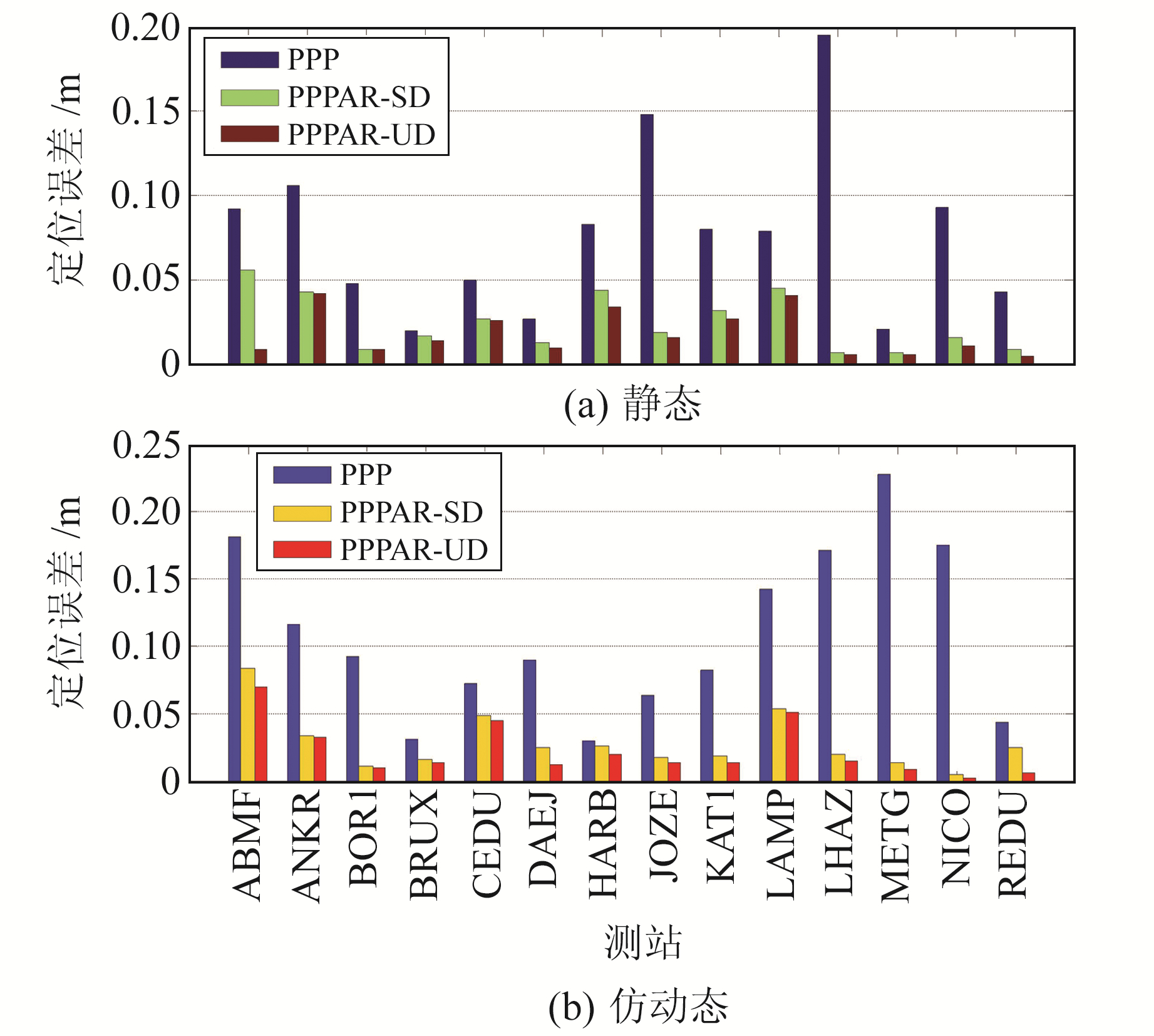
|
图 3 静态和仿动态情况下用户端14个MGEX测站的定位精度 Fig. 3 Positioning accuracy of 14 MGEX stations under static and dynamic conditions |
为分析用户端14个MGEX测站的收敛时间,收敛条件为N、E、U方向的定位偏差均小于10 cm且其后5 min均满足该条件[12]。图 4为静态和仿动态情况下用户端14个MGEX测站采用3种方法的收敛时间,从图中可以看出,静态情况下,PPP浮点解平均精度为22.3 min,传统星间单差方法为9.8 min,本文所提方法为6.7 min。与PPP浮点解相比,静态情况下传统方法和新方法收敛时间分别缩短56.3%和69.9%。仿动态情况下,PPP浮点解平均精度为41.0 min,传统星间单差方法为15.7 min,本文所提方法为11.9 min。与PPP浮点解相比,仿动态情况下传统方法和新方法收敛时间分别缩短61.8%和71.1%。表 2为用户端14个MGEX测站的定位精度及收敛时间,从表中可以看出,与传统方法相比,本文所提方法无论在静态还是仿动态情况下均能显著提高PPP短时间内的定位精度和缩短PPP收敛时间。
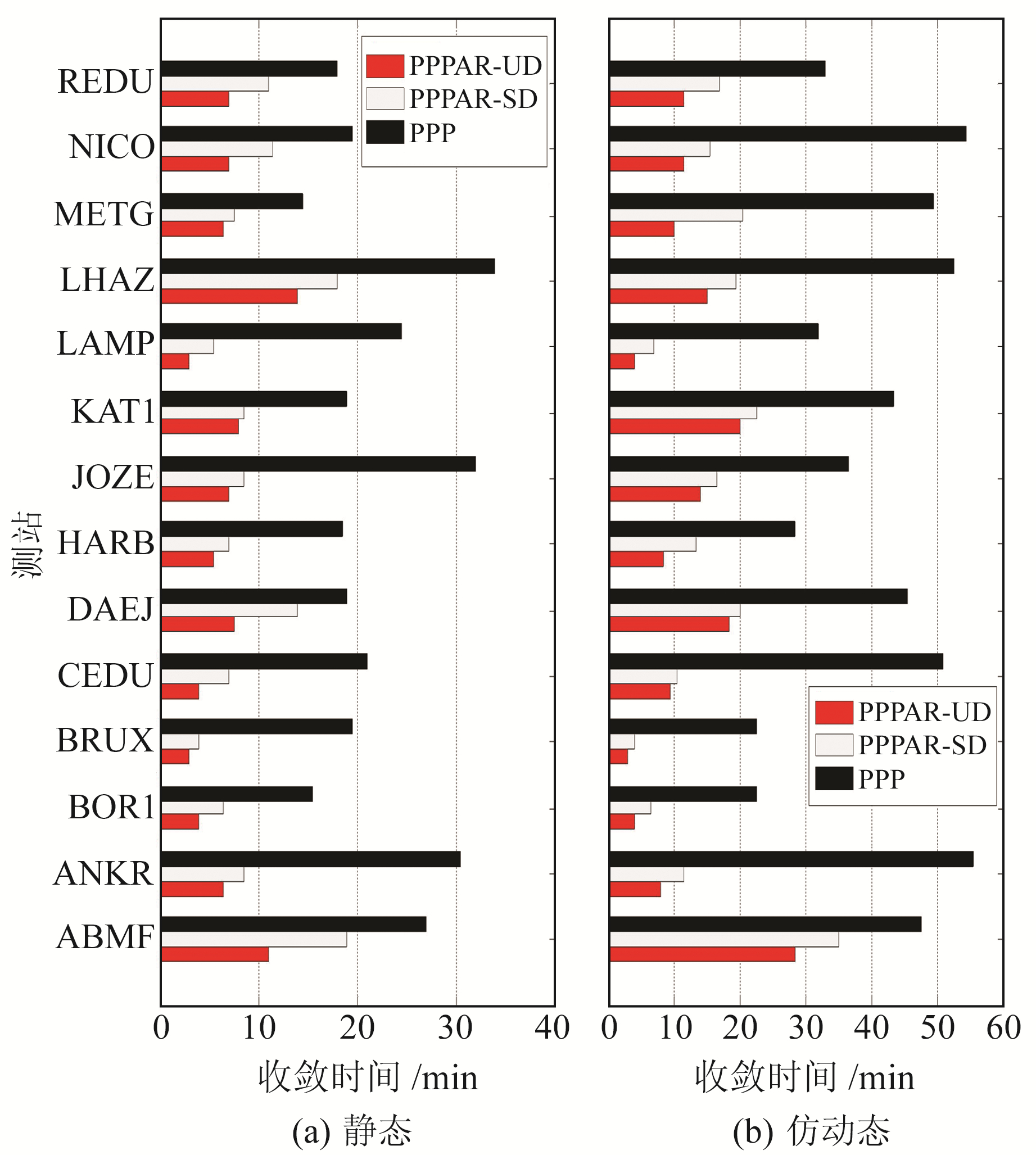
|
图 4 静态和仿动态情况下用户端14个MGEX测站的收敛时间 Fig. 4 Convergence time of 14 MGEX stations under static and dynamic conditions |
|
|
表 2 用户端14个MGEX测站的定位精度及收敛时间统计 Tab. 2 Statistical results of positioning accuracy and convergence time of 14 MGEX stations |
针对用户端基准星选取不当对PPP模糊度固定造成干扰,使模糊度固定错误或无法固定的问题,本文提出顾及接收机UPD的PPP分步模糊度固定方法。基于非差法和服务端FCB产品,采用与整数无关的三角函数得到接收机端UPD估计值,依据非差窄巷模糊度协方差大小进行分步模糊度固定。选取全球225个MGEX测站作为服务端进行UPD产品的生成与发布,未参与服务端解算的14个MGEX测站作为用户端进行方法验证。实验结果表明,与PPP浮点解相比,静态情况下传统方法和新方法定位精度分别提升68.3%和76.4%;收敛时间分别缩短56.3%和69.9%。仿动态情况下传统方法和新方法定位精度分别提升65.7%和84.7%;收敛时间分别缩短61.8%和71.1%。与传统方法相比,本文所提方法无论在静态还是仿动态情况下均能显著提升PPP定位精度和缩短收敛时间。
| [1] |
Li X X, Ge M R, Dai X L, et al. Accuracy and Reliability of Multi-GNSS Real-Time Precise Positioning: GPS, GLONASS, Beidou, and Galileo[J]. Journal of Geodesy, 2015, 89(6): 607-635 DOI:10.1007/s00190-015-0802-8
(  0) 0) |
| [2] |
Li P, Zhang X H, Ge M R, et al. Three-Frequency BDS Precise Point Positioning Ambiguity Resolution Based on Raw Observables[J]. Journal of Geodesy, 2018, 92(12): 1 357-1 369 DOI:10.1007/s00190-018-1125-3
(  0) 0) |
| [3] |
胡豪杰, 赵兴旺, 刘超, 等. 一种适用于PPP动力学模型异常的自适应Kalman滤波[J]. 大地测量与地球动力学, 2020, 40(8): 822-826 (Hu Haojie, Zhao Xingwang, Liu Chao, et al. An Adaptive Kalman Filter for Dynamics Model Abnormity of PPP[J]. Journal of Geodesy and Geodynamics, 2020, 40(8): 822-826)
(  0) 0) |
| [4] |
Ge M R, Gendt G, Rothacher M, et al. Resolution of GPS Carrier-Phase Ambiguities in Precise Point Positioning(PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389-399 DOI:10.1007/s00190-007-0187-4
(  0) 0) |
| [5] |
Li X X, Zhang X H. Improving the Estimation of Uncalibrated Fractional Phase Offsets for PPP Ambiguity Resolution[J]. Journal of Navigation, 2012, 65(3): 513-529 DOI:10.1017/S0373463312000112
(  0) 0) |
| [6] |
Laurichesse D, Mercier F, Berthias J P, et al. Real Time Zero-Difference Ambiguities Fixing and Absolute RTK[C]. Proceedings of the Institute of Navigation, National Technical Meeting, San Diego, 2008
(  0) 0) |
| [7] |
Geng J H, Meng X L, Dodson A H, et al. Integer Ambiguity Resolution in Precise Point Positioning: Method Comparison[J]. Journal of Geodesy, 2010, 84(9): 569-581 DOI:10.1007/s00190-010-0399-x
(  0) 0) |
| [8] |
Wang J, Huang G W, Yang Y X, et al. FCB Estimation with Three Different PPP Models: Equivalence Analysis and Experiment Tests[J]. GPS Solutions, 2019, 23(4)
(  0) 0) |
| [9] |
Hu J H, Zhang X H, Li P, et al. Multi-GNSS Fractional Cycle Bias Products Generation for GNSS Ambiguity-Fixed PPP at Wuhan University[J]. GPS Solutions, 2019, 24(1)
(  0) 0) |
| [10] |
Bock H, Dach R, Yoon Y, et al. GPS Clock Correction Estimation for near Real-Time Orbit Determination Applications[J]. Aerospace Science and Technology, 2009, 13(7): 415-422 DOI:10.1016/j.ast.2009.08.003
(  0) 0) |
| [11] |
Teunissen P J G. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82 DOI:10.1007/BF00863419
(  0) 0) |
| [12] |
王正军. GPS/GLONASS组合精密单点定位性能分析[J]. 大地测量与地球动力学, 2012, 32(2): 105-109 (Wang Zhengjun. Performance Assessment of GPS/GLONASS Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2012, 32(2): 105-109)
(  0) 0) |
2. China Railway First Survey and Design Institute Group Co Ltd, 2 Xiying Road, Xi'an 710043, China
 2022, Vol. 42
2022, Vol. 42

