2. 江西理工大学土木与测绘工程学院,江西省赣州市红旗大道86号,341000
受多路径效应、地质构造活动、测站相关误差以及外界环境影响,GNSS坐标时间序列中不可避免地存在粗差[1-3],从而对建模精度和结果的可靠性产生重大影响。因此,探测并剔除GNSS坐标时间序列中的粗差就显得尤为重要。
经典的统计量粗差探测方法有3σ准则、四分位距法(inter-quartile range,IQR)以及中位数绝对偏差法(median absolute deviation,MAD)。其中,3σ法是利用最小二乘法求得观测序列的残差,然后对残差进行粗差探测。但最小二乘本身难以抵抗粗差,使得3σ法对残差的中误差估计有偏,从而影响粗差探测的可靠性[2]。IQR法相比3σ准则受粗差影响较小,具有更好的稳健性[4];但对于离散度较大的数据会使估计值偏大,从而影响粗差探测的效果[5]。MAD法具有抗差性强、对粗差敏感的优点,相比3σ准则和IQR法具有更好的稳健性[6-7],已广泛应用于粗差探测领域[7-9]。
在GNSS坐标时间序列粗差探测中,首先需构建合适的时间序列模型,获取残差序列[2]。近年来,国内部分学者利用小波分析[10](wavelet analysis,WA)、奇异谱分析[1, 5](singular spectrum analysis, SSA)、L1范数[3](L1-norm) 获取GNSS坐标时间序列的残差向量,并构造粗差判别统计量进行粗差探测。这些方法的关键在于如何准确地提取原始序列的趋势项和周期项,以分离出含粗差的残差项。其中,奇异谱分析在选取滞后窗口时具有一定主观性,不同的滞后窗口对信号的提取影响较大[11];而文献[3]中L1范数与IQR组合算法可能会对粗差产生“误判”或“漏判”。小波分析具有局部化时频分析能力和多分辨率分析特性,能准确提取时间序列的趋势项和周期项,进而反映出时间序列的内在特征[12-13]。
因此,本文在MAD法基础上结合小波分析,建立一种WT-MAD粗差探测方法,以提高传统MAD法对GNSS高程时间序列中偏离度较小的粗差的探测能力。
1 原理及方法 1.1 MAD粗差探测方法黄博华等[7]在传统MAD方法基础上对其数学表达式进行改进,得到式(1)形式的表达式。对于服从正态分布的观测序列Xn={x1, x2, …, xi, …xn},将观测数据xi与其中位数K及中位数绝对偏差(MAD)数倍之和进行比较,若xi满足
| $|{x_i} - K| > n\cdot{\rm{MAD}}$ | (1) |
则认为xi为粗差点。式中,K=Med{xi},MAD=Med{|xi-K|/0.674 5}(Med表示求中位数),常数n取值按实际需求确定,n值较大不易剔除偏离度较小的粗差,而n值较小可能产生误判,一般取3~5[7, 9]。在探测出粗差后,将粗差值设为0或其他值予以剔除。
1.2 WT-MAD粗差探测方法GNSS高程时间序列可看作由不同频率部分组成的信号,趋势项、周期项主要集中在低频信号中,噪声和粗差干扰项主要集中在高频信号中[14]。本文在传统MAD方法基础上,利用小波分析对其进行改进,主要思路如下:利用小波多尺度分解提取原始时间序列的低频系数,将其重构为趋势项和周期项;原始时间序列减去重构序列得到残差序列,再利用MAD法对残差序列进行粗差探测,进而确定粗差位置。具体步骤如下:
1) 利用3σ准则剔除原始时间序列X(t)中偏离度较大的粗差,以避免小波分解和重构受到影响。对于剔除粗差后的缺失值,采用线性插值法插补得到X′(t)。
2) 利用小波分解提取X′(t)的低频系数,并重构得到
| ${r_{j + 1}} = \frac{{{\rm{RMS}}{{\rm{E}}_{j + 1}}}}{{{\rm{RMS}}{{\rm{E}}_j}}}$ | (2) |
式中,RMSEj表示分解层数为j时原始信号与降噪信号间的均方根误差,可由式(3)求得;r为相邻层数均方根误差之比,当r接近于1时,则取最佳层数为j或j+1。
| ${\rm{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{[\hat y{_i} - {y_i}]}^2}} } $ | (3) |
式中,N为信号长度,
3) 利用步骤2)中低频系数重构数据
| $\mathit{\boldsymbol{R}}\left( t \right) = \mathit{\boldsymbol{X}}\prime \left( t \right) - \mathit{\boldsymbol{\tilde X}}' \left( t \right)$ | (4) |
4) 利用MAD估计值探测残差序列中的粗差,当残差ri满足
| $|{r_i} - K| > n\cdot{\rm{MAD}}$ | (5) |
时,则认为ri为粗差点,即原始数据中xi为粗差点。式中,K为残差序列的中位数。步骤1)和4)中探测的粗差即为WT-MAD法探测出的所有粗差。
2 实验与分析 2.1 模拟数据为验证WT-MAD方法的有效性,采用由趋势项、周期项和噪声项所组成的函数模型[15]对GNSS坐标时间序列进行建模,构造模拟时间序列,函数表达式如下:
| $\begin{array}{*{20}{c}} {y\left( t \right) = b + {v_0}{t_i} + }\\ {\sum\limits_{m = 1}^{{m_0}} {[{a_m}\sin (2{\rm{ \mathsf{ π} }}{f_m}{t_i}) + {b_m}cos(2{\rm{ \mathsf{ π} }}{f_m}{t_i})] + {r_{{t_i}}}} } \end{array}$ | (6) |
式中,i为坐标历元时刻标识,y(ti)为GNSS测站某一分量ti时刻的坐标,b为横轴截距,v0为线性速度,m0为周期性信号个数,fm为周期项频率,am和bm表示频率为fm的周期项对应的振幅,rti为随机噪声。
将利用式(6)模拟的高程方向坐标时间序列作为原始数据,各参数设置为:b=5.0,v0=2,m0=2,a1=b1=5,a2=b2=3,σwn=4。
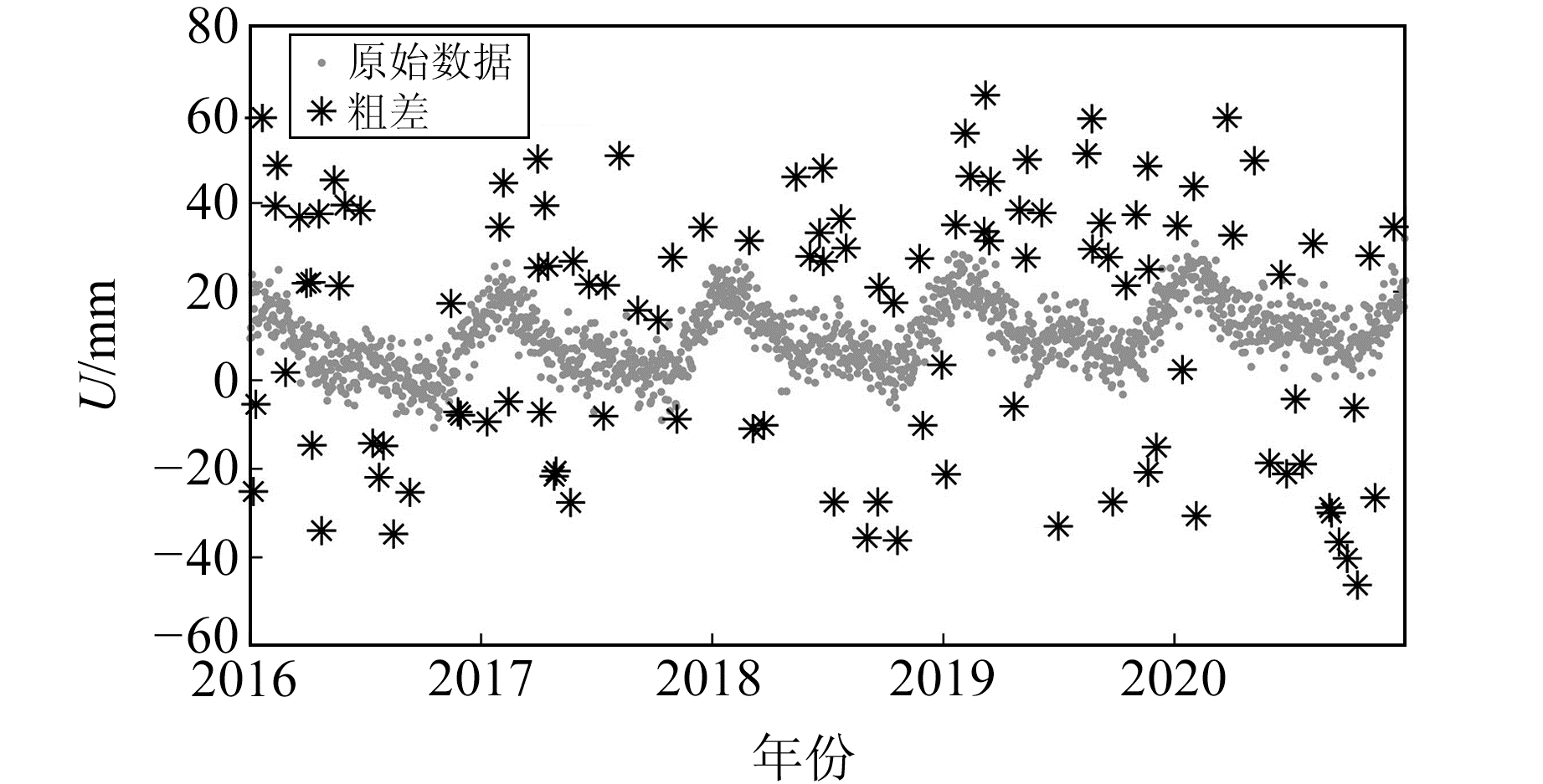
向原始数据中加入粗差:首先模拟服从正态分布且标准差为6σwn(σwn为噪声标准差)的随机误差序列;然后提取大于3σwn的数据,并将其随机插入到原始数据中,得到一组被粗差污染的GNSS高程时间序列。模拟时间序列的时间跨度为2016~2020年,历元间隔为1 d,总历元数为1 827,粗差总数为115,粗差占总历元比例为6.29%(图 1)。
|
图 1 模拟的高程时间序列 Fig. 1 The simulated elevation time series |
模拟实验采用4种方法进行对比:LS-3σ法、LS-IQR法、LS-MAD法、WT-MAD法。前3种方法均基于式(6),利用最小二乘法去除趋势项和周期项以获取残差序列,再构造粗差判别式进行粗差探测。在LS-MAD法中,经筛选取n=3;在WT-MAD法中,经筛选取n=3,选用db4小波基函数,并利用式(2)求解最佳小波分解层数,相邻层数均方根误差之比见表 1。由表可知,第4层和第5层间的均方根误差之比最小,因此取小波分解层数为5。粗差探测结果如图 2和表 2所示。
|
|
表 1 相邻分解层数均方根误差之比 Tab. 1 RMSE ratio of adjacent decomposition layers |

|
图 2 LS-3σ法、LS-IQR法、LS-MAD法和WT-MAD法粗差探测结果 Fig. 2 Results of gross error detection by LS-3σ method, LS-IQR method, LS-MAD method and WT-MAD method |
|
|
表 2 各方法粗差探测结果对比 Tab. 2 Comparison of gross error detection results of different methods |
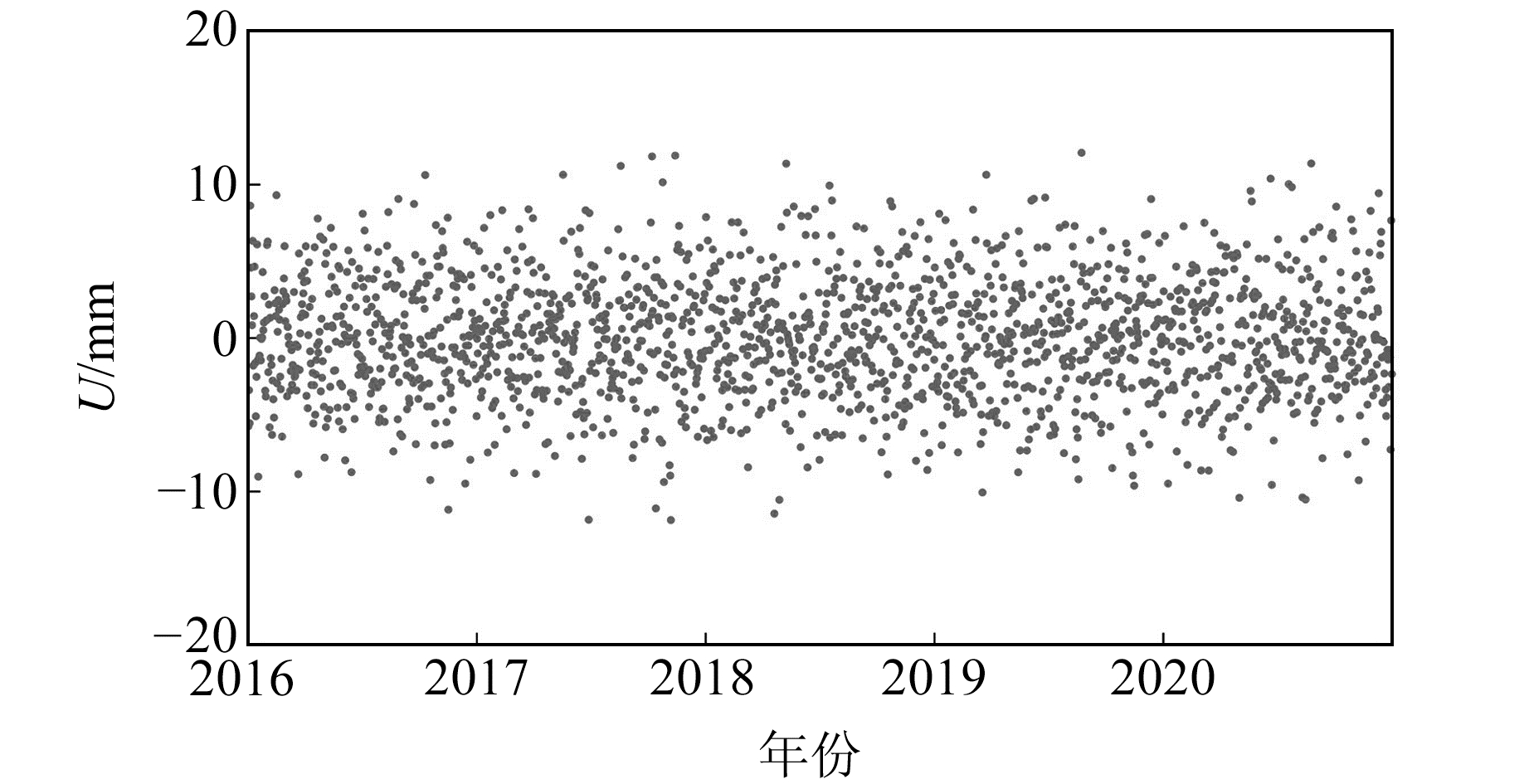
从图 2可以看出,LS-3σ法可探测出大部分粗差,但对偏离度较小的粗差探测效果有限,而LS-IQR法、LS-MAD法和WT-MAD法均可探测出绝大部分粗差。由表 2可知,WT-MAD法粗差剔除率为98.3%,高于其他3种方法;虽然LS-IQR法和LS-MAD法均存在1个误判,但这两种方法的粗差探测率与WT-MAD法相近,这主要是因为模拟时间序列未考虑季节项、阶跃等非线性变化,且加入的噪声仅为白噪声。在先验模型准确的情况下,利用最小二乘法同样能准确获取模拟数据的残差,从而得到较好的粗差探测效果。在利用WT-MAD法剔除粗差后,通过小波分析可得到去除趋势项和周期项后的残差,结果如图 3所示。从图 3可以看出,残差序列为白噪声序列,无明显异常值,表明WT-MAD法可有效探测出模拟时间序列中的粗差。
|
图 3 WT-MAD法剔除粗差后的残差序列 Fig. 3 Residual sequence after eliminating gross errors by WT-MAD method |
本文选用SOPAC(scrips orbit and permanent array center) 提供的“Raw”和“Clean”类型的单天高程(U)时间序列作为实测数据,其中“Raw”为原始时间序列,“Clean”为删除异常值的时间序列。
本次实验选取LHAZ、BJFS、TWTF三个IGS站2006~2020年共15 a的“Raw”数据进行分析。在IGS站中,GNSS坐标时间序列数据缺失的情况较为常见[16],而小波分析要求原始数据均匀采样,因此在粗差探测前先利用线性插值法插补缺失值。得到完整时间序列后,以LHAZ站为例,分别利用小波变换与LS法获取去除趋势项和周期项后的残差序列(图 4)。由图可知,小波变换所得残差趋近为白噪声,而LS法获取的残差序列含有残余的周期性信号,表明LS法难以抵御粗差和有色噪声的影响,而小波变换在无需数据先验信息的情况下,能够更为准确地提取原始数据的趋势项和周期项。

|
图 4 LHAZ站高程方向残差序列 Fig. 4 Residual sequence of LHAZ station in elevation direction |
利用WT-MAD法对各IGS站的时间序列进行粗差探测,与模拟实验相同,采用db4小波基函数,由式(2)求得各站最佳小波分解层数均为5,取n=3,探测结果见表 3。
|
|
表 3 LHAZ、BJFS、TWTF三个IGS站粗差探测结果 Tab. 3 Gross error detection results of LHAZ, BJFS and TWTF stations |
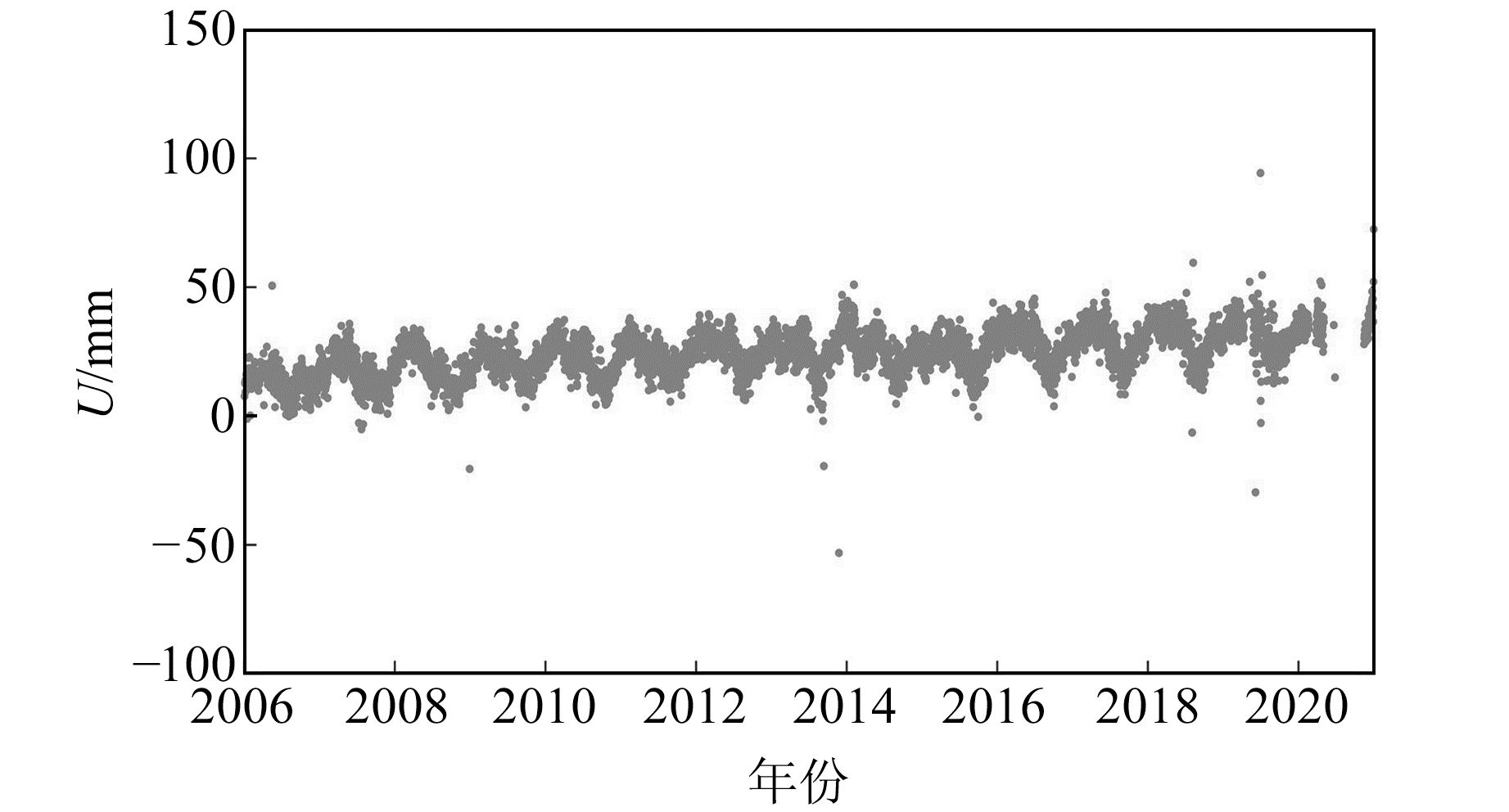
表 3中粗差探测结果表明,3个IGS站均含有粗差,其中LHAZ站探测出的粗差最少,为100个;BJFS站最多,为104个。为验证WT-MAD方法的有效性,以LHAZ站为例,得到该方法剔除粗差后的高程时间序列,并与SOPAC提供的“Raw”数据进行对比,结果如图 5~6所示。
|
图 5 LHAZ站“Raw”高程时间序列 Fig. 5 "Raw" elevation time series of LHAZ station |
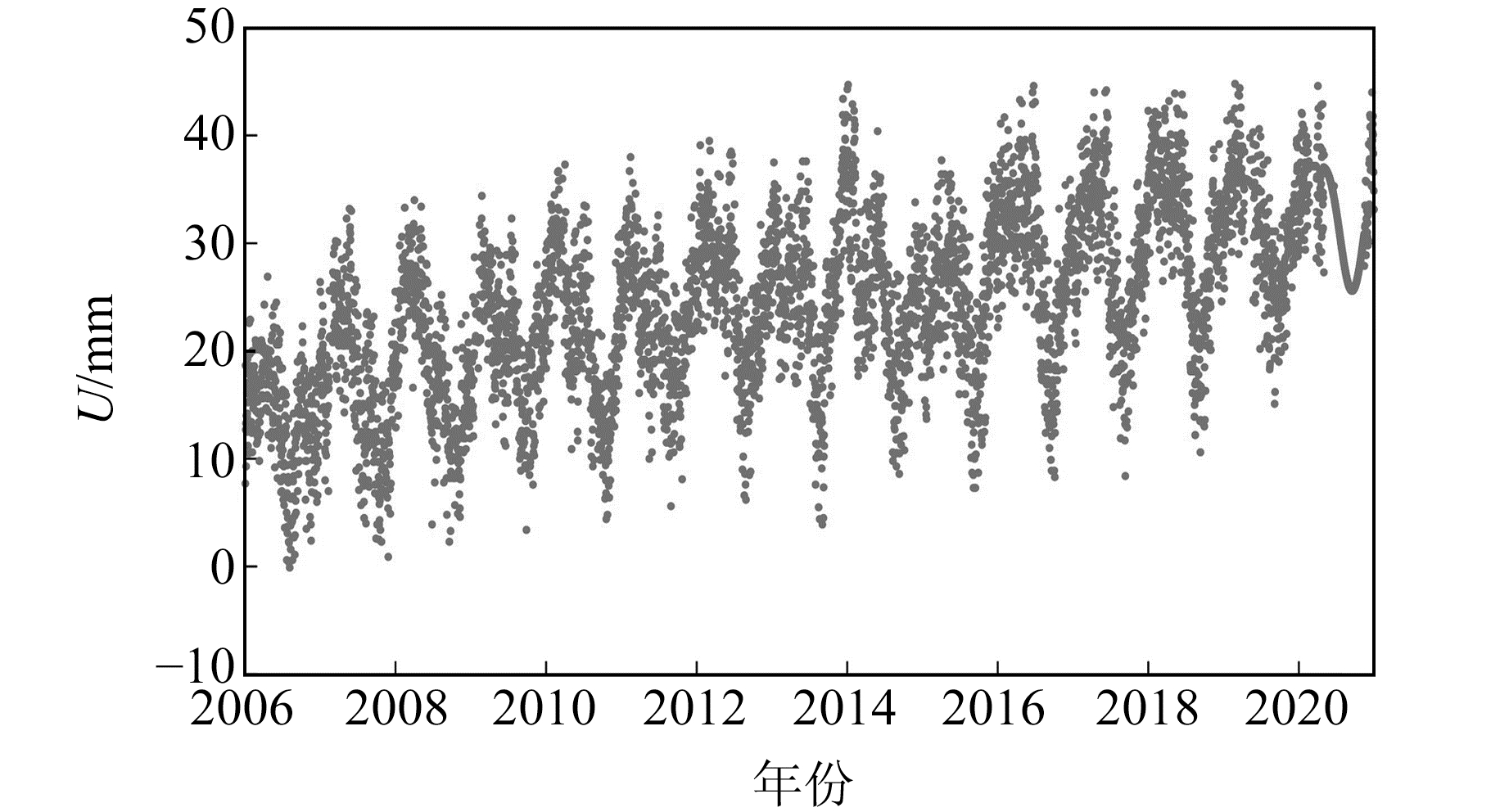
|
图 6 WT-MAD法剔除粗差后的LHAZ站高程时间序列 Fig. 6 Elevation time series of LHZA station after eliminating gross errors by WT-MAD method |
从图 5~6可以看出,原始时间序列在历元2006.5 a、历元2009.0 a、历元2014.0 a、历元2016.0 a以及历元2019.0 a附近均含有偏离度较大的粗差,而WT-MAD法可剔除这些粗差。
在利用WT-MAD法剔除LHAZ站原始高程时间序列的粗差后,通过小波变换可得到去除趋势项和周期项后的残差,结果如图 7(a)所示。图 7(b)为SOPAC提供的LHAZ站去除粗差、趋势项和周期项后的残差。对比图 7(a)和图 7(b)可知,图 7(b)中历元2014.0 a和历元2021.0 a附近仍含有粗差,而图 7(a)中这两个历元附近均无异常值,且残差序列近似为白噪声序列,表明WT-MAD法可更有效地剔除原始时间序列中的粗差。

|
图 7 LHAZ站残差序列 Fig. 7 Residual sequence of LHAZ station |
为进一步验证WT-MAD方法的有效性,分别利用LS-3σ法、LS-IQR法、LS-MAD法和WT-MAD法对表 3中3个IGS站的数据进行粗差探测,并将利用小波分析提取的趋势项和周期项作为参照,计算原始时间序列剔除粗差前后的RMSE,以此作为评判标准,结果如表 4所示。从表 4可以看出,3个测站中WT-MAD法探测出的粗差数量均多于LS-3σ法、LS-IQR法和LS-MAD法,且RMSE均小于其他3种方法,表明WT-MAD法可得到较好的探测效果。
|
|
表 4 4种方法粗差探测结果及精度统计 Tab. 4 Gross error detection results and accuracy statistics of four methods |
本文针对GNSS高程时间序列非线性、不平稳性导致粗差探测困难的问题,构建一种基于MAD改进的WT-MAD粗差探测方法。该方法在进行粗差探测时不易受趋势项和周期项等影响,同时可降低数据非对称分布对MAD法的影响,从而可有效探测粗差。模拟实验和实测结果均表明,相比LS-3σ法、LS-IQR法和LS-MAD法,WT-MAD法可得到较好的探测效果,说明本文方法具有适用性和有效性。
在进行小波分析时,小波基函数及分解层数根据经验来选取,且需要进行重复实验确定,这会影响粗差探测效率,且在一定程度上具有主观性;若分解层数过大可能会造成粗差误判,过小则可能造成漏判。因此,如何快速、准确地选取小波基函数及分解层数还需进一步研究。
| [1] |
蔡晓军, 杨建华. 基于多通道奇异谱的GNSS坐标序列粗差探测与数据插值[J]. 测绘工程, 2019, 28(5): 20-28 (Cai Xiaojun, Yang Jianhua. Gross Error Detection and Data Interpolation for GNSS Coordinates Time Series Based on Multichannel Singular Spectrum[J]. Engineering of Surveying and Mapping, 2019, 28(5): 20-28)
(  0) 0) |
| [2] |
张恒璟, 程鹏飞. 基于GPS高程时间序列粗差的抗差探测与插补研究[J]. 大地测量与地球动力学, 2011, 31(4): 71-75 (Zhang Hengjing, Cheng Pengfei. Study on Robust Detection and Interpolation from Gross Errors of GPS Height Time Series[J]. Journal of Geodesy and Geodynamics, 2011, 31(4): 71-75)
(  0) 0) |
| [3] |
明锋, 曾安敏, 景一帆. L1范数与IQR统计量组合的GNSS坐标序列粗差探测算法[J]. 测绘科学技术学报, 2016, 33(2): 127-132 (Ming Feng, Zeng Anmin, Jing Yifan. A New Method of Outlier Detection for GNSS Position Time Series Based on the Combination of L1-Norm and IQR Statistic[J]. Journal of Geomatics Science and Technology, 2016, 33(2): 127-132)
(  0) 0) |
| [4] |
Nikolaidis R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D]. San Diego: University of California, 2002
(  0) 0) |
| [5] |
Wang X, Cheng Y, Wu S, et al. An Effective Toolkit for the Interpolation and Gross Error Detection of GPS Time Series[J]. Survey Review, 2016, 48(348): 202-211 DOI:10.1179/1752270615Y.0000000023
(  0) 0) |
| [6] |
Huber P J. Robust Statistics[M]. New York: Wiley, 2009
(  0) 0) |
| [7] |
黄博华, 杨勃航, 李明贵, 等. 一种改进的MAD钟差粗差探测方法[EB/OL]. https://doi.org/10.13203/j.whugis20190430, 2020-12-05 (Huang Bohua, Yang Bohang, Li Minggui, et al. An Improved Method for MAD Gross Error Detection of Clock Error[J]. https://doi.org/10.13203/j.whugis20190430, 2020-12-05)
(  0) 0) |
| [8] |
郭建锋. 尺度因子的MAD估计及其在测量平差中的应用[J]. 武汉大学学报: 信息科学版, 2021, 46(11): 1 636-1 640 (Guo Jianfeng. MAD Estimate of Scale Factor and Its Applications in Measurement Adjustment[J]. Geomatics and Information Science of Wuhan University, 2021, 46(11): 1 636-1 640)
(  0) 0) |
| [9] |
王宇谱. GNSS星载原子钟性能分析与卫星钟差建模预报研究[D]. 郑州: 信息工程大学, 2017 (Wang Yupu. Research on Modeling and Prediction of the Satellite Clock Bias and Performan Evaluation of GNSS Satellite Clocks[D]. Zhengzhou: Information Engineering University, 2017)
(  0) 0) |
| [10] |
吴浩, 卢楠, 邹进贵, 等. GNSS变形监测时间序列的改进型3σ粗差探测方法[J]. 武汉大学学报: 信息科学版, 2019, 44(9): 1 282-1 288 (Wu Hao, Lu Nan, Zou Jingui, et al. An Improved 3σ Gross Error Detection Method for GNSS Deformation Monitoring Time Series[J]. Geomatics and Information Science of Wuhan University, 2019, 44(9): 1 282-1 288)
(  0) 0) |
| [11] |
嵇昆浦, 沈云中. 含缺值GNSS基准站坐标序列的非插值小波分析与信号提取[J]. 测绘学报, 2020, 49(5): 537-546 (Ji Kunpu, Shen Yunzhong. Dyadic Wavelet Transform and Signal Extraction of GNSS Coordinate Time Series with Missing Data[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(5): 537-546)
(  0) 0) |
| [12] |
徐洪钟, 吴中如, 李雪红, 等. 基于小波分析的大坝变形观测数据的趋势分量提取[J]. 武汉大学学报: 工学版, 2003, 36(6): 5-8 (Xu Hongzhong, Wu Zhongru, Li Xuehong, et al. Abstracting Trend Component of Dam Observation Data Based on Wavelet Analysis[J]. Engineering Journal of Wuhan University, 2003, 36(6): 5-8)
(  0) 0) |
| [13] |
文鸿雁. 基于小波理论的变形分析模型研究[D]. 武汉: 武汉大学, 2004 (Wen Hongyan. Research on Deformation Analysis Model Based on Wavelet Transform Theory[D]. Wuhan: Wuhan University, 2004)
(  0) 0) |
| [14] |
宋唐龙, 肖付民, 邓凯亮, 等. 基于小波变换的潮位粗差探测定位方法研究[J]. 海洋测绘, 2019, 39(4): 27-30 (Song Tanglong, Xiao Fumin, Deng Kailiang, et al. Detection and Location of Tidal Level's Gross Error Based on Wavelet Transform[J]. Hydrographic Surveying and Charting, 2019, 39(4): 27-30 DOI:10.3969/j.issn.1671-3044.2019.04.007)
(  0) 0) |
| [15] |
李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496-503 (Li Zhao, Jiang Weiping, Liu Hongfei, et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series inside China[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 496-503)
(  0) 0) |
| [16] |
李威, 鲁铁定, 贺小星, 等. Prophet模型在GNSS坐标时间序列中的插值分析[J]. 大地测量与地球动力学, 2021, 41(4): 362-367 (Li Wei, Lu Tieding, He Xiaoxing, et al. Interpolation Analysis of Prophet Model in GNSS Coordinate Time Series[J]. Journal of Geodesy and Geodynamics, 2021, 41(4): 362-367)
(  0) 0) |
2. School of Civil and Surveying and Mapping Engineering, Jiangxi University of Science and Technology, 86 Hongqi Road, Ganzhou 341000, China
 2022, Vol. 42
2022, Vol. 42


