2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054;
3. 中国科学院国家授时中心,西安市书院东路3号,710600
地球自转参数(ERP)可为地球动力学特性研究提供重要的基础信息,可表征地球自转运动的整体变化,是地球各圈层、海洋和大气等综合作用的直接反映。ERP包含极移运动、世界时变化(UT1-UTC)和日长变化(LOD),对卫星精密定轨、深空探测、天文自主导航等具有重要意义,同时也是地球参考框架和天球参考框架相互转换[1]的必要参数。
ERP测定是利用空间大地测量技术对天体或天体卫星进行观测并获取测站及观测源位置矢量来实现。目前卫星激光测距(SLR)、激光测月(LLR)、全球卫星导航系统(GNSS)、甚长基线干涉测量(VLBI)、星基多普勒定轨和无线电组合系统(DORIS)等已成为地球自转参数测定的重要技术手段[2],其中,VLBI技术可同时测定地球定向参数(EOP)所有分量,精度高且稳定性强[2];GNSS技术可提供高分辨率全天候监测数据,其极移解算精度在现有技术中最高。
由于现代大地测量手段数据处理的复杂性和各种观测技术之间时空基准的不一致性,高精度ERP数据的获取往往存在滞后现象,目前ERP产品主要由国际地球自转服务(IERS)定期推出,并免费为地球自转研究提供基础数据[3]。但这些提供基础资料的数据中心均不在我国境内,多种地球物理观测数据在获取时存在一定程度的阻碍。考虑到ERP观测结果的重要性及数据来源的不稳定性等因素,建立我国独立技术状态的ERP观测和预报机制,实现高精度ERP观测和预报产品的自主供给具有重要的科学价值和现实意义。
数字天顶摄影定位系统虽然仍为一种光学测量技术,但考虑到其具有观测自动化、测量时间短、测量精度高、无人仪差等优势[4-9],相比于传统天文大地测量技术,仍不失为地球自转参数测定的一种有效技术手段。德国、瑞士等欧洲国家率先开展新型光学天文定位设备的研制工作,其中具有代表性的天顶仪工程样机有德国汉诺威大学研制的TZK2-D[5]和瑞士苏黎世联邦理工学院GGL(geodesy and geodynamics laboratory)研制的DIADEM[6],奥地利维也纳技术大学基于小型CCD相机研制出ZC-G1[7],中国科学院国家天文台与山东科技大学于2011年成功研制出DZT-1[8],中国人民解放军第一○○一工厂先后研制出TDY、TDY2、CTDY、STDY数字天顶摄影定位系统[9],四种型号分别顾及轻便、快速、高精度等不同应用需求。数字天顶摄影定位系统可作为我国地球自转参数自主测定的备用技术手段,是对国际高精度ERP常规测定手段的有效补充。
1 理论分析 1.1 数字天顶摄影定位原理数字天顶摄影定位是实现测站精密天文定位的一种天文大地测量技术[9],其基本原理是通过数字天顶摄影仪(简称天顶仪)在对称位置上对测站天顶恒星进行数字图像拍摄,根据天顶摄影测量原理构造相关数据拟合及时空基准转换模型,实现天顶仪旋转轴方向天文经纬度的精确测定[9-12],并利用倾角敏感器的倾斜测量数据完成天顶仪旋转轴方向天文经纬度至测站铅垂线方向的精密归算[11-12]。
数字天顶摄影定位的数学模型可表示为:
| $ \left\{\begin{array}{l} \varphi=\varphi_{x}+\Delta \varphi_{n} \\ \lambda=\lambda_{x}+\Delta \lambda_{n} \end{array}\right. $ | (1) |
式中,λ、φ为测站点的天文经纬度;λx、φx为天顶仪旋转轴方向的天文经纬度;Δλn、Δφn为倾角敏感器测定的倾斜量改正。
顾及倾角传感器双敏感轴读数的线性漂移[11]及各种误差的综合影响,同时考虑到倾角敏感器状态参数的测定需求,数字天顶摄影定位一般按照循环观测方法进行,每个循环观测需拍摄16幅星图,并将对称位置取中数得到最终的测站天文经纬度。图 1为天顶仪循环观测位置示意图。
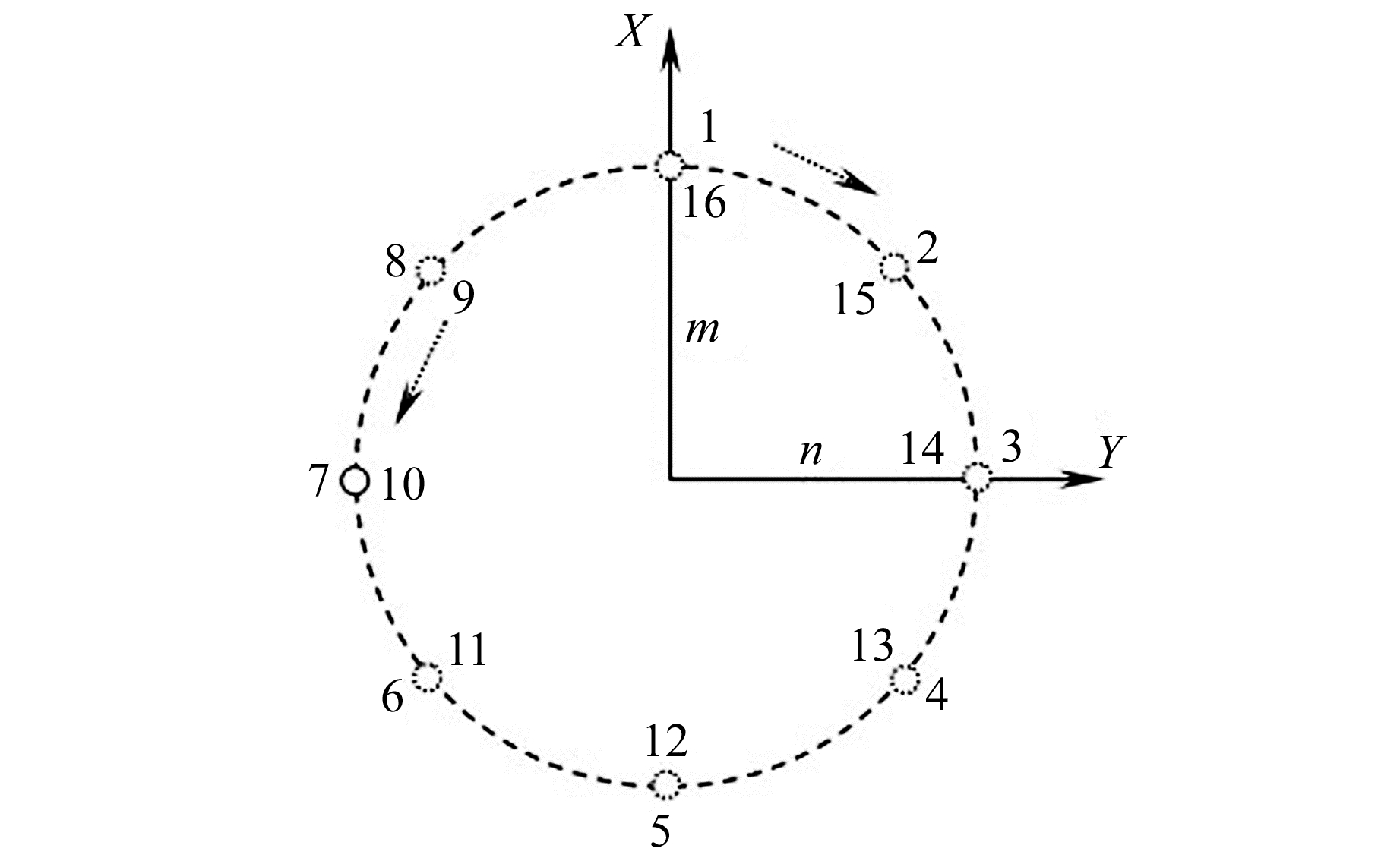
|
图 1 天顶仪每个循环观测位置 Fig. 1 Observation location of zenith camera of each cycle |
数字天顶摄影仪旋转轴方向位置解算是根据天体方向较差原理,按照对称位置拍摄的作业流程,将天顶仪旋转中心依靠数据拟合方法内插至测站天顶星场,并多次迭代后得到其天文坐标[12]。具体技术流程如下:
1) 视位置计算。根据天顶仪转台对称旋转前、后恒星图像的拍摄时刻及测站的概略坐标计算两对称位置上各恒星的第二赤道坐标(赤经α、赤纬δ)。
2) 恒星时角计算。根据测站概略天文经度λ和转台对称旋转前、后恒星图像的拍摄时刻T(经世界时变化改正后的UT1),按下式计算各恒星的时角t:
| $ t=\mathrm{GAST}+1.002\ 737\ 891 * T+\lambda-\alpha $ | (2) |
式中,GAST为世界时(UT1)0 h的真恒星时。
3) 切平面坐标计算。根据对称位置各恒星的第一赤道坐标(δ,t),按下式计算各恒星以天顶仪旋转轴方向为基准的切平面[13]坐标(ξ,η):
| $ \left\{\begin{array}{l} \xi=\frac{\cos \varphi \tan \delta-\sin \varphi \cos t}{\sin \varphi \tan \delta+\cos \varphi \cos t} \\ \eta=\frac{-\sin t}{\sin \varphi \tan \delta+\cos \varphi \cos t} \end{array}\right. $ | (3) |
4) 投影变换。根据各恒星的切平面坐标(ξ,η)及对应星像点的像平面坐标(x,y),按下式进行数据拟合计算,建立星像点像平面坐标与恒星切平面坐标之间的投影变换模型:
| $ \left\{\begin{array}{l} \xi=\frac{a_{1}+b_{1} x+c_{1} y}{1+d x+e y} \\ \eta=\frac{a_{2}+b_{2} x+c_{2} y}{1+d x+e y} \end{array}\right. $ | (4) |
式中,a1、a2为平移参数,b1、c1、b2、c2为尺度变换、旋转变换参数,d、e为投影变换顾及两平面倾斜的系统分项。
5) 旋转中心内插。根据建立的投影变换模型,按迭代趋近解方法计算天顶仪旋转中心的图像坐标(x0,y0),其中旋转中心像平面坐标初始值采用CCD靶面中心坐标参与计算,并根据式(4)数值拟合模型计算天顶仪旋转轴方向与切平面交点的切平面坐标(ξ0,η0)。
6) 旋转轴天文经纬度计算。根据计算的切平面坐标(ξ0,η0),按下式计算天顶仪旋转轴方向天文经纬度(φ,λ):
| $ \left\{\begin{array}{l} \Delta t=\arctan \left[-\eta_{0} /\left(\cos \varphi_{0}-\xi_{0} \sin \varphi_{0}\right)\right] \\ \varphi=\arctan \left[\left(\xi_{0} \cos \varphi_{0}+\sin \varphi_{0}\right) \cos \Delta t\right. \\ \ \ \ \ \left./\left(\cos \varphi_{0}-\xi_{0} \sin \varphi_{0}\right)\right] \\ \lambda=\lambda_{0}-\Delta t \end{array}\right. $ | (5) |
在首次趋近计算中按上述流程求得旋转轴方向天文经纬度后,再以此经纬度为基准计算两对称位置各恒星的第一赤道坐标及切平面坐标,并按照上述要求重新迭代计算。一般情况下,3~5次迭代计算即可满足定位精度要求。
1.2 误差来源及影响分析根据数字天顶摄影定位原理及应用实例,可将其误差来源归纳为3部分:硬件综合误差、CCD成像误差、星表及算法鲁棒性误差。本文通过构建误差模型对不同误差源展开系统性分析,并对削弱不同误差源提出相关改进方法。
针对硬件综合误差应在设备研制生产及安装过程中严格控制其机加、工艺及电控水平,并通过对称位置测量、安装双倾角敏感器等方法进行削弱。
影响数字天顶摄影定位精度的CCD成像误差主要是由星点坐标量算误差引起。本文采用顾及各向异性的高斯曲面拟合方法[13]进行星点坐标量算,星图匹配过程中采用基于亮星辅助的坐标差匹配方法[14],可有效提高星点坐标量算精度及星图匹配效率。
目前用于数字天顶摄影定位测量的起算星表主要包含Hipparcos星表、Tycho-2星表和GAIA DR2星表。其中,Hipparcos星表与Tycho-2星表各天体测量特征及精度基本一致,GAIA DR2星表目前已成为国际天球参考框架精度最高的光学实现方法。任磊等[10]对Hipparcos星表和GAIA DR2星表的天体测量参数进行对比,并通过实例验证GAIA DR2星表可有效提高天文定位测量精度,具有一定参考意义。
时延误差属于硬件综合误差,其直接关系到测站天文经度的精确测定,数字天顶摄影定位系统通过GNSS授时模式以秒脉冲信号触发相机拍照并获取UTC整秒时间信息。因此,相机曝光时延是影响测量过程中时间对准的主要误差源。针对相机曝光时延,可通过基于平行光原理的曝光时延标定设备精确测定,另外,将相机机械快门更换为电子快门也可大幅降低硬件时延对天文经度测量的影响。
1.3 地球自转参数测定原理基于数字天顶摄影定位的地球自转参数测定,是通过对以世界协调时(UTC)为基准的平极天文经纬度测定值和以世界时(UT1)为基准的已知值进行差分处理来实现。设以世界协调时UTC为基准的测站平极天文定位结果为(λ,φ),测站点的精确天文经纬度(即以世界时UT1为基准,且归算至IERS参考极的已知值)为(λ0,φ0)。根据时间参考基准转换与极移参数对天文定位的影响,可得到测站天顶摄影定位的关系式为:
| $ \left\{\begin{array}{l} \varphi_{0}=\varphi-\left(x_{p} \cos \lambda-y_{p} \sin \lambda\right) \\ \lambda_{0}=\lambda-\Delta t-\left(x_{p} \sin \lambda+y_{p} \cos \lambda\right) \tan \varphi \end{array}\right. $ | (6) |
式中,xp、yp为地球瞬时极相对IERS参考极(IRP)的极坐标;Δt=1.002 737 891×(UT1-UTC),为世界时变化对测站点天文经度测定结果的影响值。
令式(6)中Δt的近似值为Δt0,误差值为δt,即Δt=Δt0+δt,则式(7)可表示为:
| $ \left\{\begin{array}{l} \varphi_{0}=\varphi-\left(x_{p} \cos \lambda-y_{p} \sin \lambda\right) \\ \lambda_{0}=\lambda-\left(\Delta t_{0}+\delta t\right)-\left(x_{p} \sin \lambda+y_{p} \cos \lambda\right) \tan \varphi \end{array}\right. $ | (7) |
令该式中
| $ \left\{\begin{array}{l} \Delta \varphi=\varphi-\varphi_{0} \\ \Delta \lambda=\lambda-\Delta t_{0}-\lambda_{0} \end{array}\right. $ | (8) |
则式(7)又可表示为:
| $ \left\{\begin{array}{l} \Delta \varphi=x_{p} \cos \lambda-y_{p} \sin \lambda \\ \Delta \lambda=\delta t+\left(x_{p} \sin \lambda+y_{p} \cos \lambda\right) \tan \varphi \end{array}\right. $ | (9) |
基于数字天顶摄影定位的地球自转参数测定正是根据式(9)参与解算。根据测量平差原理,至少需要2个测站的观测值才可联立求解上述3个未知数,为提高所求参数的测量精度,应顾及冗余观测,因此一般考虑布设多个测站。
设各测站点(i=1, 2, …, n)以世界协调时UTC为基准的天顶摄影定位结果为(λi, φi),测站点天文经纬度已知值为(λ0, φ0),由式(9)可得各测站点的误差方程式为:
| $ \left\{\begin{array}{l} V_{\varphi i}=x_{p} \cos \lambda_{i}-y_{p} \sin \lambda_{i}-\Delta \varphi_{i} \\ V_{\lambda i}=\delta t+\left(x_{p} \sin \lambda_{i}+y_{p} \cos \lambda_{i}\right) \tan \varphi_{i}-\Delta \lambda_{i} \end{array}\right. $ | (10) |
在实际计算时,Δt的近似值Δt0可取各测站点天文经度观测值(以世界协调时UTC为基准)与已知值之差的平均值,即
| $ \Delta t_{0}=\frac{1}{n} \sum\limits_{i=1}^{n}\left(\lambda-\lambda_{0}\right)_{i} $ | (11) |
式中,n为测站点个数。
由各测站点的天文经纬度,根据式(10)即可得到误差方程组的系数阵为:
| $ \boldsymbol{B}=\left[\begin{array}{ccc} 0 & \cos \lambda_{1} & -\sin \lambda_{1} \\ 1 & \sin \lambda_{1} \tan \varphi_{1} & \cos \lambda_{1} \tan \varphi_{1} \\ \vdots & \vdots & \vdots \\ 0 & \cos \lambda_{n} & -\sin \lambda_{n} \\ 1 & \sin \lambda_{n} \tan \varphi_{n} & \cos \lambda_{n} \tan \varphi_{n} \end{array}\right] $ | (12) |
根据误差理论与测量平差中的间接平差原理,按下式即可求得地球自转参数X的最小二乘解为:
| $ \boldsymbol{X}=\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{l}=\boldsymbol{N}_{B B}^{-1} \boldsymbol{W} $ | (13) |
式中,B为误差方程组的系数阵;P为观测值的权阵;l为误差方程组的自由项,其表达式为:
| $ \boldsymbol{l}=\left[\begin{array}{ccc} \Delta \varphi_{1} & \Delta \lambda_{1} \cdots \Delta \varphi_{n} & \Delta \lambda_{n} \end{array}\right]^{\mathrm{T}} $ | (14) |
在基于数字天顶摄影定位的地球自转参数测定中,各测站采用同类型仪器按照相同的观测循环数测定Δφ、Δλ值时,可视为观测精度相同。设不同测站测得的观测值li(Δφi,Δλi)分别为Ni个循环中同精度观测值的平均值,则各观测值li的权重可定义为:
| $ P_{i}=\frac{N_{i}}{C} $ | (15) |
一般取观测循环数最多的测站经纬度观测值作为单位权观测值,即取C=Nmax。显然,当各测站的观测循环数相同时,各测站的观测值权值均为1。
1.4 单台站UT1-UTC测定原理UT1-UTC是变化最快且无法精确预测的ERP分量。从其各激发源来看,引起UT1-UTC变化的因素可分为地球内部荷载的不规则运动及地球外部受日月引力作用影响的受摄运动[15]。为满足部分特定军事工程实时性、机动性、无外部依托、精度要求较低等需求,考虑到极移参数的数值一般较小,本文提出单台站UT1-UTC测定方法。
由式(6)可知,单台站测定UT1-UTC的数学模型为:
| $ \Delta t=\lambda-\lambda_{0}-\left(x_{p} \sin \lambda+y_{p} \cos \lambda\right) \tan \varphi $ | (16) |
式中,λ为以UTC时间为基准测得的测站天文经度,λ0为以UT1时间为基准的测站天文经度已知值。由此可知,单台站测定UT1-UTC中数据处理的关键是如何处理极移参数的影响。
地球自转轴在本体内运动引起的地极移动称作极移[16]。精密观测表明,地极在地面约24 m×24 m范围内按逆时针方向依循近似圆的螺旋线作周期运动(图 2)。地极绕行一周约432 d,近似于6 a内绕行5周,且极移在不同年份中略有差异。
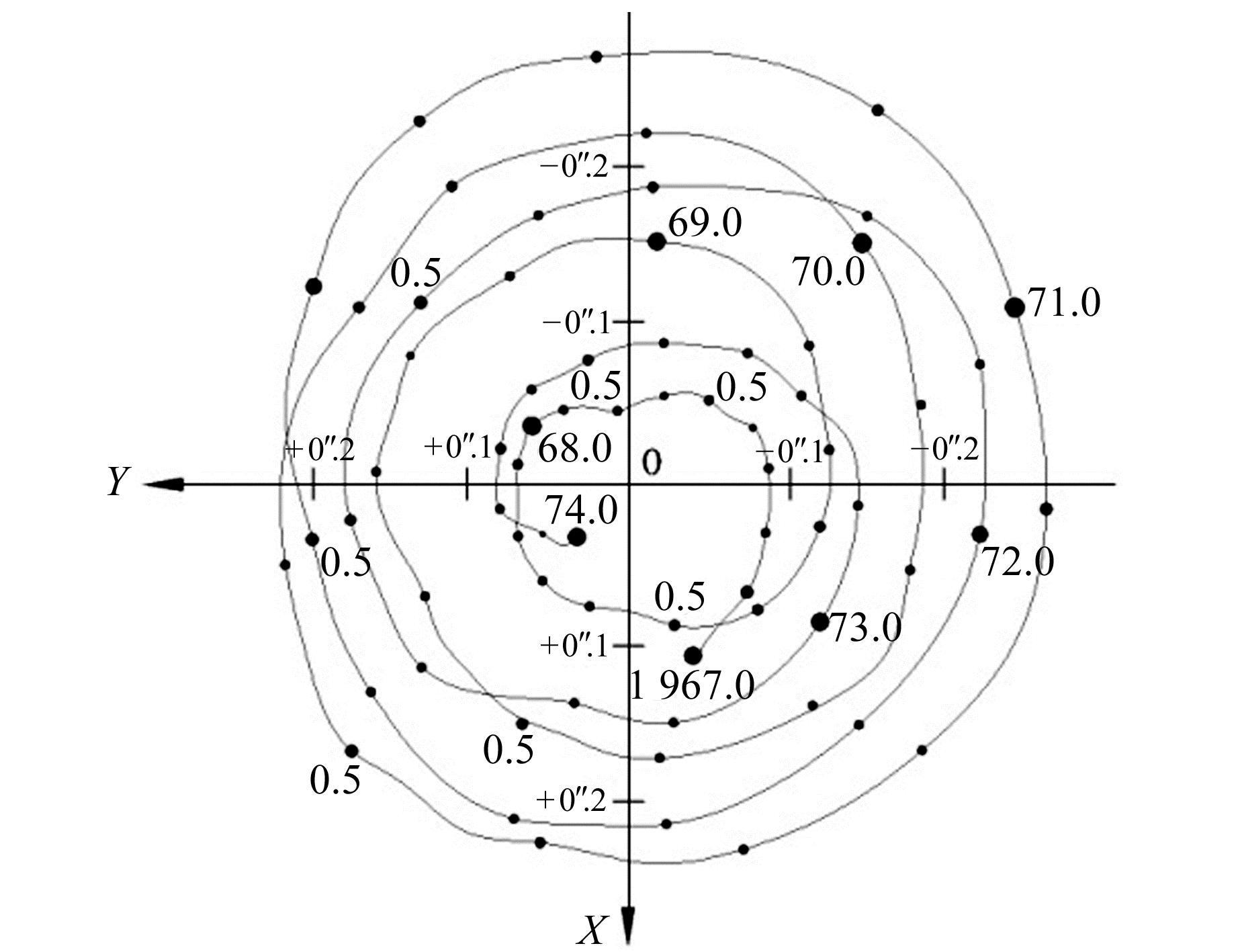
|
图 2 地极移动示意图 Fig. 2 Schematic diagram of polar movement |
考虑到地极运动特点,为最大限度地减弱极移影响,同时顾及极移运动的周期特性,一般取最接近测定日的前6 a极移参数(由IERS公布)的平均值进行极移影响的修正计算,从而可将极移参数对UT1-UTC测定的影响控制在指定精度范围内。
对于单测站UT1-UTC测定,由式(16)可知,设mΔλ为Δλ=λ-λ0的中误差,极移参数xp、yp的中误差分别为mx、my,令ΔUT1=UT1-UTC,忽略ΔUT1在天文经度测定结果中的系数影响,则ΔUT1测定的中误差mΔu为:
| $ m_{\Delta u}^{2}=m_{\Delta x}^{2}+\left(m_{x}^{2} \sin ^{2} \lambda+m_{y}^{2} \cos ^{2} \lambda\right) \tan ^{2} \varphi $ | (17) |
本文研究分析发现,用于参数测定的测站配置在地球自转参数计算中具有至关重要的作用。在相同测量模式下,不同的测站数量及测站空间几何分布对地球自转参数测定精度影响较大。综合考虑观测环境、运行维护、建设成本等因素,本文在模拟分析时仅考虑在我国境内合理布站,并对不同数量及不同空间网形分布的模拟测站进行大量的数据验证。限于篇幅,文中仅对5个分布较优的模拟测站进行数据分析。
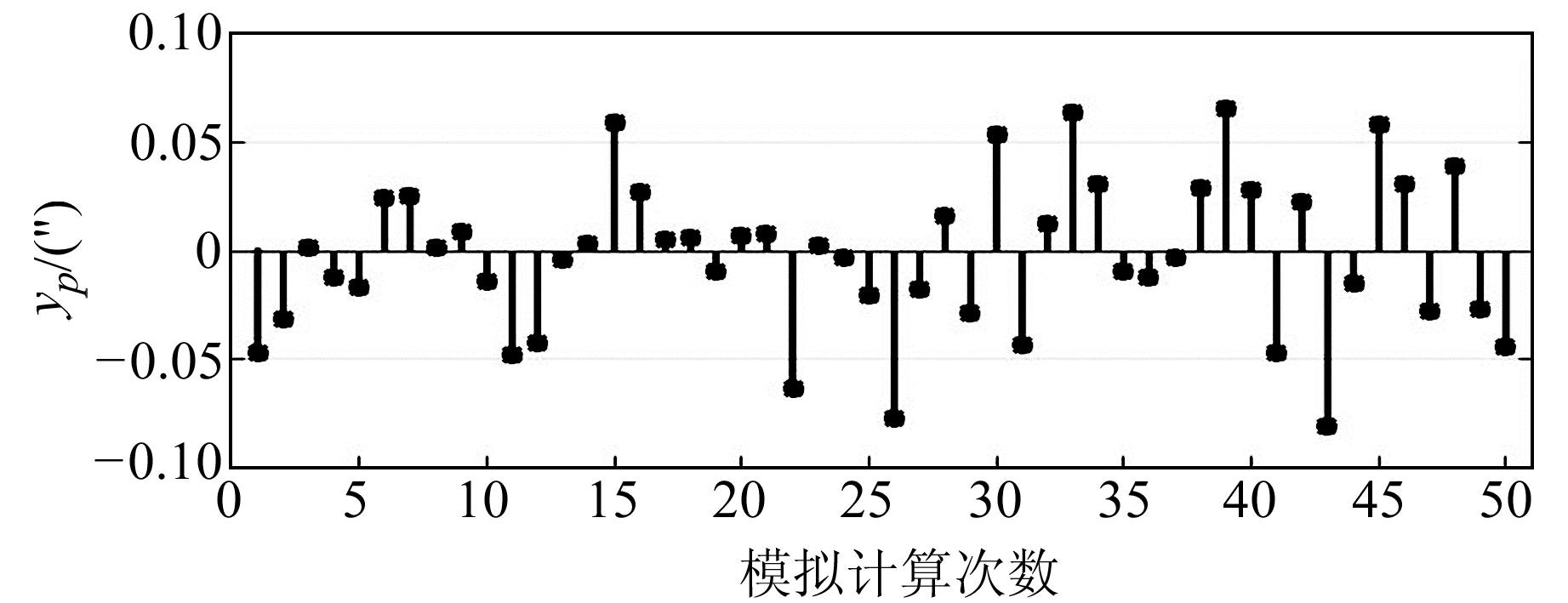
在地球自转参数模拟计算时,以通化、黄山、西安、库尔勒、昆明5个模拟测站构成的观测网进行计算,并使所有测站的观测系统和观测方法保持一致,且在单日观测中采用同步观测时段解。计算中取数字天顶摄影定位精度σ0=0.05″。图 3~5分别为UT1-UTC、极移xp、极移yp参数50次模拟计算的平差结果。
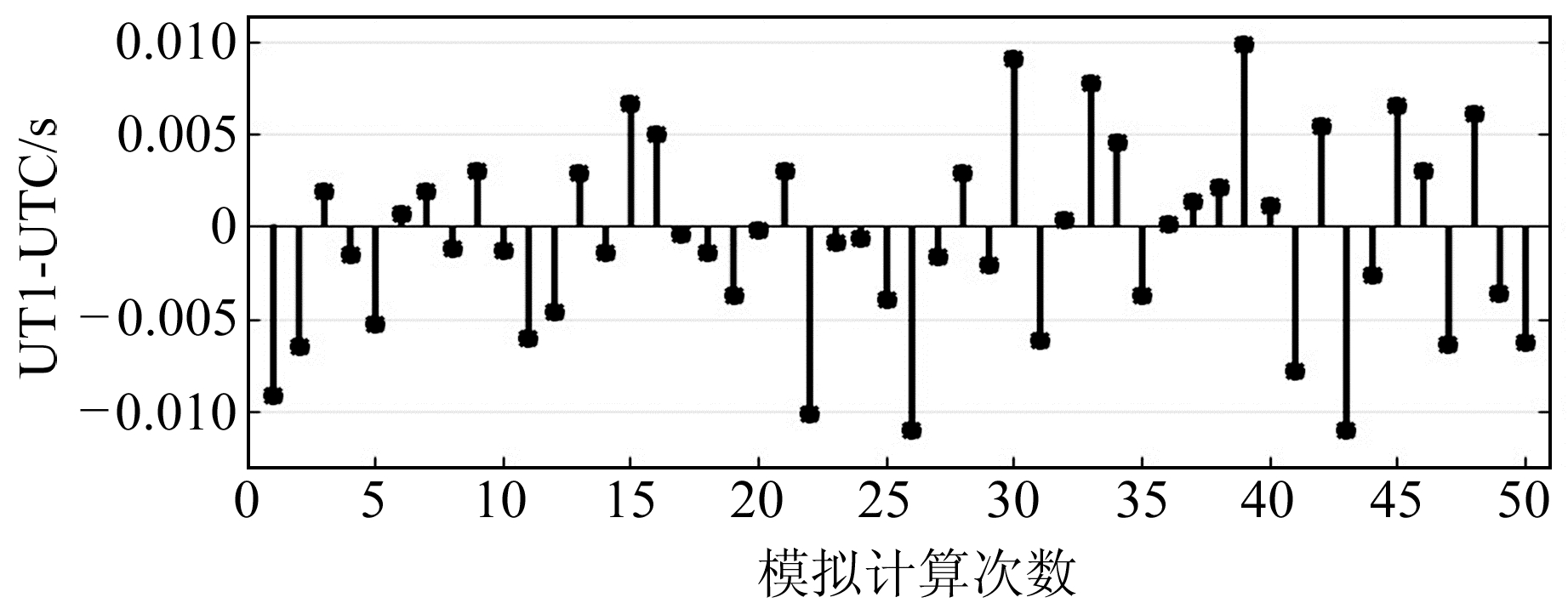
|
图 3 UT1-UTC平差计算结果针状图 Fig. 3 Needle chart of UT1-UTC adjustment calculation results |
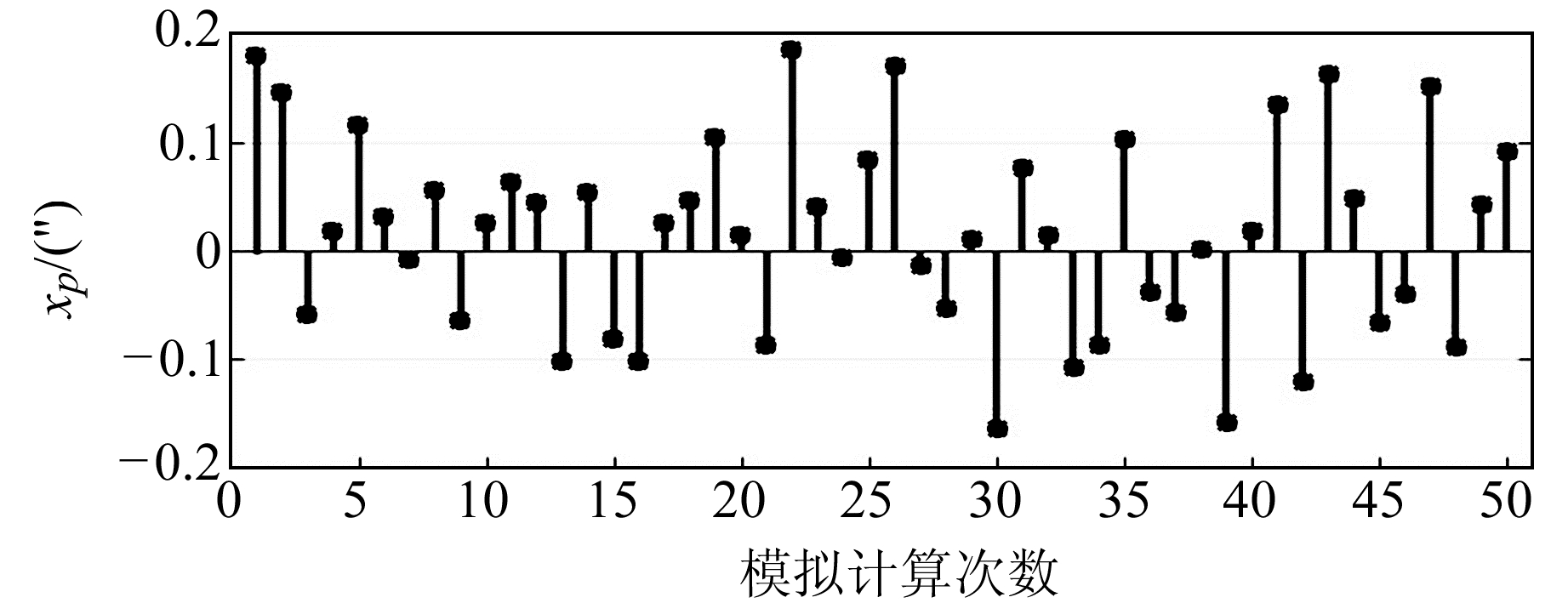
|
图 4 极移xp平差计算结果针状图 Fig. 4 Needle chart of xp adjustment calculation results |
|
图 5 极移yp平差计算结果针状图 Fig. 5 Needle chart of yp adjustment calculation results |
以上50次模拟计算的结果统计详见表 1,从表中可以看出,采用高精度天顶摄影定位系统,通过在全国范围内合理布站可实现地球自转参数的精确测定,能满足UT1-UTC参数±5 ms、极移参数±0.06″的测量精度。同时可以发现,仅在我国境内设置测站时,尽管已经顾及到测站数量和网形分布,但仍然受到地域引起的经纬差限制,导致极移两参数测定精度存在较大差异。
|
|
表 1 参数平差计算结果统计 Tab. 1 Statistical results of parameter adjustment calculation |
表 2为各平差参数精度估计结果统计,对比表 1和表 2可知,相应数据在量级上基本一致。同时,精度估计中单位权中误差的平均值为0.047 5″,与数字天顶摄影定位精度σ0=0.05″也保持一致,充分验证了多台站测定地球自转参数的合理性。此外,如何规避在我国境内建站时经纬差受限引起的各参数测定精度不一致的问题,以及如何进一步提高地球自转参数测定的精度,还有待更深入研究。
|
|
表 2 精度估计结果统计 Tab. 2 Statistical results of precision estimation |
为进一步验证利用数字天顶摄影定位方法测定地球自转参数的可行性与准确性,本文对西安某天文基准点(简称西安站)和国家授时中心骊山天文基准点(简称骊山站)进行单台站UT1-UTC实测,将IERS公布值作为真值,统计最终测算结果并分析各测站UT1-UTC实测精度。
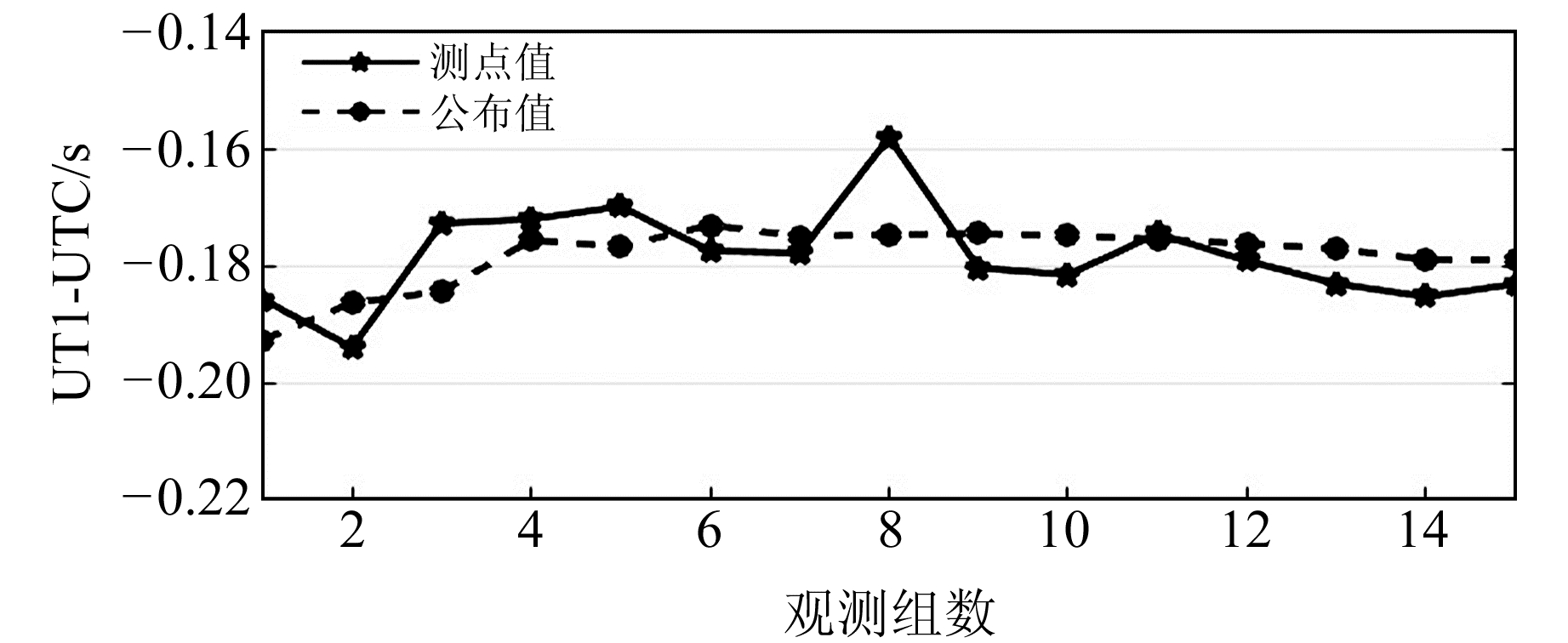
需要说明的是,西安站并非固定天文台站,在西安站进行数字天顶摄影定位测量时,按照1+5(1个参数校正循环和5个实测工作循环)测量模式实施作业。非固定台站多天观测时需重复架设仪器,这会不可避免地影响倾角传感器的状态参数,引入对点误差等,从而影响天文定位精度。现取西安站2020-08~11期间15组有效数据参与UT1-UTC数据解算,图 6为该站UT1-UTC实测序列。
|
图 6 西安站UT1-UTC实测序列 Fig. 6 UT1-UTC measured sequence of Xi'an station |
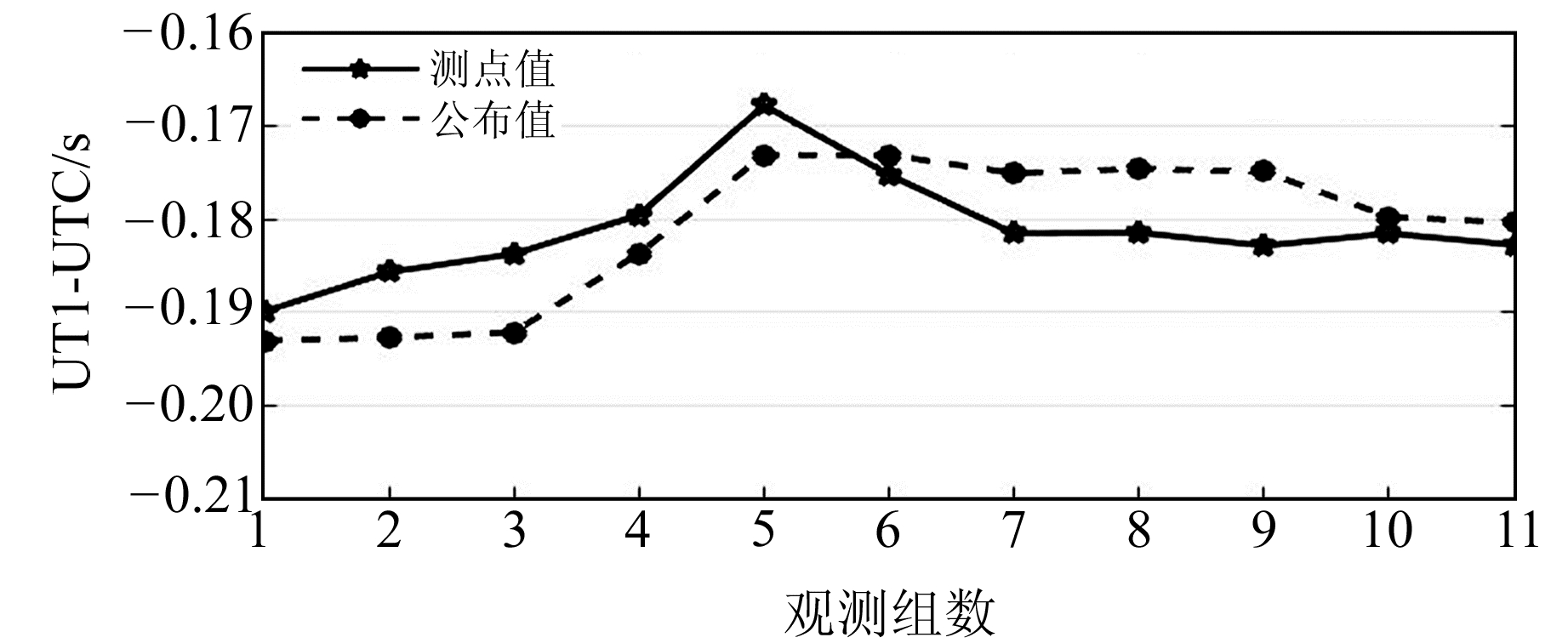
骊山站为无人值守固定天文台站,在该站进行数字天顶摄影定位测量时,按照1+24(注解同上)测量模式实施作业。该站仪器固连于观测墩,多天观测时无需重复架设与对中整平,且观测期间可远程操控。台站地处骊山山顶,受城市光污染影响较小,适合整夜连续性观测。现取骊山站2020-08~12期间11组有效数据参与UT1-UTC数据解算,图 7为其实测序列。
|
图 7 骊山站UT1-UTC实测序列 Fig. 7 UT1-UTC measured sequence of Lishan station |
两测站均采用高精度天顶摄影定位系统(CTDY),在数据解算过程中,由于采用天顶对称观测,其蒙气差影响可忽略不计。两测站在单日观测中采用不同的循环数,且观测条件不同,因此其观测值中误差也有所差异。西安站单日观测值中误差为0.047″,骊山站单日观测值中误差为0.021″。
分析两测站UT1-UTC实测序列可知,单台站UT1-UTC实测序列与IERS公布序列的分布趋势较为一致,尤其是在固定台站实施作业,实测序列趋势项与公布序列基本保持一致。另外,IERS公布的最终ERP产品为经过平滑滤波后的理想数据,在后续单台站UT1-UTC测定工作中,随着历史数据的不断积累,对实测序列进行粗差探测、平滑滤波等相关研究分析,其测量精度将有可能进一步提高。
对西安站和骊山站UT1-UTC测定值与公布值差值的相关结果进行精度计算(表 3),表中最大值、最小值按照残差绝对值参与统计。
|
|
表 3 UT1-UTC实测精度统计 Tab. 3 Statistics of UT1-UTC measurement accuracy |
结合两测站UT1-UTC测定序列与精度统计结果可知,采用高精度数字天顶摄影定位系统进行单台站UT1-UTC测定时,相关参数的实测精度可达到5~8 ms。另外,非固定台站模式下建站灵活,机动作业能力强,其精度相对不高,但仍可满足特定军事工程的相关需求;固定台站模式下可实现无人值守自动观测,可为后续多台站联合解算ERP提供历史数据支撑。
3 结语本文基于数字天顶摄影定位原理及时空基准转换模型,分析地球自转参数对天文大地测量的影响,并对数字天顶摄影定位工程实现过程中存在的误差源及改正方法作出系统阐述,在此基础上推导利用数字天顶摄影定位方法测定地球自转参数的相关数学模型及技术途径。利用仿真实验证实,合理的测站配置可实现高精度ERP参数测定,并进一步根据实测数据验证单台站UT1-UTC测算精度。本文旨在讨论将数字天顶摄影仪应用于地球自转参数测定的可行性,相关研究可为我国综合不同空间大地测量技术建立有关高精度地球自转服务体系提供数据支撑和有益参考。
| [1] |
许才军, 申文斌, 晁定波. 地球物理大地测量学原理与方法[M]. 武汉: 武汉大学出版社, 2006 (Xu Caijun, Shen Wenbin, Chao Dingbo. Geophysical Geodesy Principles and Methods[M]. Wuhan: Wuhan University Press, 2006)
(  0) 0) |
| [2] |
魏二虎, 刘文杰, Wei Jianan, 等. VLBI和GPS观测联合解算地球自转参数和日长变化[J]. 武汉大学学报: 信息科学版, 2016, 41(1): 66-71 (Wei Erhu, Liu Wenjie, Wei Jianan, et al. Estimation of Earth Rotation Parameters and ΔLOD with Combining VLBI and GPS Observations[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 66-71)
(  0) 0) |
| [3] |
金文敬, 唐正宏, 黄乘利, 等. 国际地球自转服务(IERS)评介[J]. 天文学进展, 2003, 21(1): 26-32 (Jin Wenjing, Tang Zhenghong, Huang Chengli, et al. Evaluation of International Earth Rotation Service[J]. Progress in Astronomy, 2003, 21(1): 26-32 DOI:10.3969/j.issn.1000-8349.2003.01.003)
(  0) 0) |
| [4] |
Halicioglu K, Deniz R, Ozener H. Digital Zenith Camera System for Astro-Geodetic Applications in Turkey[J]. Journal of Geodesy and Geoinformation, 2012, 1(2): 115-120 DOI:10.9733/jgg.131212.1
(  0) 0) |
| [5] |
Hirt C, Gruber T, Featherstone W E. Evaluation of the First GOCE Static Gravity Field Models Using Terrestrial Gravity, Vertical Deflections and EGM2008 Quasigeoid Heights[J]. Journal of Geodesy, 2011, 85(10): 723-740 DOI:10.1007/s00190-011-0482-y
(  0) 0) |
| [6] |
Bürki B, Somieski A E, Sorber P, et al. The Digital Astronomical Deflection Measuring System(DIADEM)[C]. XXIV General Assembly of the International Union for Geodesy and Geophysics, Perugia, 2007
(  0) 0) |
| [7] |
Gerstbach G, Pichler H. A Small CCD Zenith Camera (ZC-G1)-Developed for Rapid Geoid Monitoring in Difficult Projects[J]. Publications of the Astronomical Observatory of Belgrade, 2003, 75: 221-228
(  0) 0) |
| [8] |
王博, 田立丽, 王政, 等. 数字化天顶望远镜观测图像及数据处理[J]. 科学通报, 2014, 59(12): 1 100-1 107 (Wang Bo, Tian Lili, Wang Zheng, et al. Image and Data Processing of Digital Zenith Telescope(DZT-1) of China[J]. Chinese Science Bulletin, 2014, 59(12): 1 100-1 107)
(  0) 0) |
| [9] |
艾贵斌, 龚建. 数字天顶摄影定位原理与方法[M]. 北京: 解放军出版社, 2014 (Ai Guibin, Gong Jian. Principle and Method of Digital Zenith Photographing and Positioning[M]. Beijing: PLA Press, 2014)
(  0) 0) |
| [10] |
任磊, 徐天河, 龚建, 等. GAIA DR2星表在数字天顶摄影定位中的应用[J]. 测绘科学技术学报, 2020, 37(3): 226-231 (Ren Lei, Xu Tianhe, Gong Jian, et al. Application of GAIA DR2 Star Catalogue in Digital Zenith Photographing and Positioning[J]. Journal of Geomatics Science and Technology, 2020, 37(3): 226-231)
(  0) 0) |
| [11] |
周召发, 徐志浩, 刘先一, 等. 数字化天顶摄影仪倾角补偿的影响分析[J]. 光子学报, 2019, 48(8) (Zhou Zhaofa, Xu Zhihao, Liu Xianyi, et al. Analysis on the Effect of Tilt Compensation of Digital Zenith Camera[J]. Acta Photonica Sinica, 2019, 48(8))
(  0) 0) |
| [12] |
翟广卿, 艾贵斌. 数字天顶摄影天文定位测量的工程实现[J]. 测绘科学技术学报, 2014, 31(3): 232-235 (Zhai Guangqing, Ai Guibin. Digital Zenith Camera Astronomical Positioning Measurement of Project Implementation[J]. Journal of Geomatics Science and Technology, 2014, 31(3): 232-235 DOI:10.3969/j.issn.1673-6338.2014.03.003)
(  0) 0) |
| [13] |
王敏, 赵金宇, 陈涛. 基于各向异性高斯曲面拟合的星点质心提取算法[J]. 光学学报, 2017, 37(5) (Wang Min, Zhao Jinyu, Chen Tao. Center Extraction Method for Star-Map Targets Based on Anisotropic Gaussian Surface Fitting[J]. Acta Optica Sinica, 2017, 37(5))
(  0) 0) |
| [14] |
刘先一, 周召发, 张志利, 等. 亮星辅助下基于坐标转换的快速星图识别方法[J]. 航空学报, 2020, 41(8) (Liu Xianyi, Zhou Zhaofa, Zhang Zhili, et al. Fast Star Identification Based on Coordinate Transformation Assisted by Bright Stars[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(8))
(  0) 0) |
| [15] |
孙张振. 高精度地球自转参数预报模型与算法研究[D]. 威海: 山东大学, 2020 (Sun Zhangzhen. Research on the Models and Algorithms for High Accuracy Prediction of Earth Rotation Parameters[D]. Weihai: Shandong University, 2020)
(  0) 0) |
| [16] |
宋贯一, 王吉易, 曹志成, 等. 极移的成因及其移动特征[J]. 地球物理学进展, 2006, 21(2): 416-425 (Song Guanyi, Wang Jiyi, Cao Zhicheng, et al. The Cause of Polar Movement and Its Characteristics[J]. Progress in Geophysics, 2006, 21(2): 416-425 DOI:10.3969/j.issn.1004-2903.2006.02.013)
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
3. National Time Service Center, CAS, 3 East-Shuyuan Road, Xi'an 710600, China
 2022, Vol. 42
2022, Vol. 42

